ANOVA III: Varianzanalyse mit Messwiederholung
ANOVA mit Messwiederholung
In den letzten beiden Sitzungen ging es darum Unterschiede zwischen Personen zu untersuchen, indem wir Mittelwertsunterschiede zwischen verschiedenen Gruppen von Personen geprüft haben (in englischsprachiger Literatur wird dies als between subjects ANOVA bezeichnet). In dieser Sitzung soll es darum gehen, Unterschiede innerhalb von Personen (im Englischen within subjects ANOVA) mithilfe der ANOVA mit Messwiederholung zu untersuchen. Diese Unterschiede können dabei z.B. dadurch entstehen, dass wir unterschiedliche Messzeitpunkte untersuchen. Die Messwiederholung muss nicht zwingend durch Zeit zustande kommen - andere Möglichkeiten der Messwiederholung sind z.B. unterschiedliche Tests oder Informationsquellen. Wir könnten z.B. Verhaltensauffälligkeiten von Kindern erheben, indem wir sie durch Psychotherapeutinnen und -therapeuten beobachten lassen und die Eltern sowie die Kita-Erzieher und -Erzieherinnen befragen. Auch so messen wir wiederholt das Gleiche und können untersuchen, inwiefern sich hierbei mittlere Unterschiede zeigen. Diese Analysen von Messwiederholungen lassen sich zudem mit den Zwischen-Subjekt Analysen kombinieren, die wir bereits behandelt haben. Mehr zur ANOVA mit Messwiederholung finden Sie in Eid, Gollwitzer und Schmitt (2017, Kapitel 14 und insb. 14.1 und folgend).
Datensatz laden
Wir laden zunächst die Daten, entweder lokal von Ihrem Rechner:
load("C:/Users/Musterfrau/Desktop/alc.rda")oder wir laden sie direkt über die Website:
load(url("https://pandar.netlify.app/post/alc.rda"))dim(alc)## [1] 82 7head(alc)## id male peer coa alcuse.14 alcuse.15 alcuse.16
## 1 1 0 1.2649111 1 1.732051 2 2.000000
## 4 2 1 0.8944272 1 0.000000 0 1.000000
## 7 3 1 0.8944272 1 1.000000 2 3.316625
## 10 4 1 1.7888544 1 0.000000 2 1.732051
## 13 5 0 0.8944272 1 0.000000 0 0.000000
## 16 6 1 1.5491934 1 3.000000 3 3.162278Der Datensatz stammt aus einer Erhebung von Curran, Stice und Chassin (1997) in der der Alkoholkonsum von Jugendlichen längsschnittlich untersucht wurde. Die enthaltenen Variablen sind der Personen-Identifikator (id), das dichotom kodierte Geschlecht (male, mit 0 = weiblich), das berichtete Ausmaß, in dem Peers Alkohol konsumieren (peer, ein Durchschnittswert über mehrere Items mit 0 = keine und 5 = alle) und ob derjenige/diejenige Kind eines/einer Alkoholikers/Alkoholikerin ist (coa, “child of alcoholic”, mit 0 = nein). Darüber hinaus gibt es zu drei verschiedenen Zeitpunkten (jeweils im Alter von 14, 15 und 16) die selbstberichtete Häufigkeit, mit der Alkohol konsumiert wird (alcuse, ein Durchschnittswert über mehrere Items mit 0 = nie und 7 = täglich).
Datenformat und reshape
Bei der Formatierung von sozialwissenschaftlichen Datensätzen können zwei generelle Typen unterschieden werden: das Long-Format und das Wide-Format (bzw. lang und breit). Die Bezeichnung bezieht sich dabei (meistens) auf die Anordnung von Messwiederholungen der gleichen Personen. Manche Analyseverfahren benötigen Datensätze im langen Format (wie z.B. die Messwiederholte ANOVA mit ez), andere benötigen Datensätze im breiten Format (wie z.B. multivariate Regression). Im breiten Format ist wird jedem Objekt bzw. jeder Versuchsperson eine Zeile zugeordnet. Verschiedene Messzeitpunkte derselben Variable werden also in verschiedenen Spalten abgebildet. Beispielsweise könnte das so aussehen:
| ID | alc14 | alc15 | alc16 | male |
|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 1 |
| 2 | 1 | 1 | 1 | 1 |
| 3 | 1 | 2 | 3 | 0 |
Im langen Format hingegen bekommt jede Versuchsperson für jeden Messzeitpunkt eine Spalte. Variablen, die häufiger gemessen wurden, ändern sich dann je nach Zeile für eine Person, während einmal gemessene Variablen gleich bleiben. Als Indikator für den Messzeitpunkt wird eine neue Spalte eingeführt. Die gerade aufgeführte Tabelle würde dann so aussehen:
| ID | age | alc | male |
|---|---|---|---|
| 1 | 14 | 0 | 1 |
| 1 | 15 | 1 | 1 |
| 1 | 16 | 1 | 1 |
| 2 | 14 | 1 | 1 |
| 2 | 15 | 1 | 1 |
| 2 | 16 | 1 | 1 |
| 3 | 14 | 1 | 0 |
| 3 | 15 | 2 | 0 |
| 3 | 16 | 3 | 0 |
Wenn wir uns den Datensatz alc anschauen sehen wir, dass er erstmal im breiten Format vorliegt. Eine weitere Bestätigung dafür ist, dass jede ID auch nur einmal vorkommt.
table(alc$id)##
## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
## 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
## 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78
## 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## 79 80 81 82
## 1 1 1 1Wie bereits geschildert benötigt das ez-Paket für die ANOVA mit Messwiederholung allerdings einen Datensatz im langen Format. Für die Transformation der Daten aus einem in das andere Format gibt es die reshape-Funktion, welche unterschiedliche Argumente benötigt, je nachdem, in welche Richtung die Daten transformiert werden sollen. Hier wollen wir aus dem breiten Format ins lange Format transformieren, um die Daten hinterher für die Varianzanalyse mit Messwiederholung nutzen zu können.
Weil die Benennung und Handhabung von Argumenten in reshape mitunter etwas unübersichtlich ist, empfiehlt es sich mit ?reshape (in einem neuen R-Fenster) die Hilfe aufzurufen. Für die Umwandlung von breit nach lang sind drei Argumente zwingend erforderlich:
data: der Datensatzvarying: eine Liste der Variablen, die wiederholt gemessen wurdendirection: die Richtung, in die der Datensatz transformiert werden soll (hier'long')
Den umgewndelten Datensatz wollen wir direkt ablegen. Allerdings wollen wir den Datensatz im breiten Format nicht überschreiben, weshalb wir den Namen alc_long verwenden. Im Minimalfall sieht die Umwandlung also so aus:
alc_long <- reshape(data = alc,
varying = list(c('alcuse.14', 'alcuse.15', 'alcuse.16')),
direction = 'long')
head(alc_long)## id male peer coa time alcuse.14
## 1.1 1 0 1.2649111 1 1 1.732051
## 2.1 2 1 0.8944272 1 1 0.000000
## 3.1 3 1 0.8944272 1 1 1.000000
## 4.1 4 1 1.7888544 1 1 0.000000
## 5.1 5 0 0.8944272 1 1 0.000000
## 6.1 6 1 1.5491934 1 1 3.000000Das Argument varying bedarf einer zweiten Betrachtung: hier wird eine Liste von Vektoren erstellt. Die Vektoren enthalten jeweils die Namen der Variablen, die zusammen Messwiederholungen der gleichen Variable sind. Wenn wir z.B. einen weiteren Satz aus drei Variablen hätten, die weeduse hieße, würde diese Liste so aussehen:
varying = list(c('alcuse.14', 'alcuse.15', 'alcuse.16'),
c('weeduse.14', 'weeduse.15', 'weeduse.16'))Per Voreinstellung werden alle Variablen übernommen, die nicht explizit als varying angegeben werden. Diese Variablen haben dann für jede Zeile, die die gleiche Person betrifft, auch den gleichen Wert. Wenn wir die Werte für die erste Person betrachten:
alc_long[alc_long$id == 1, ]## id male peer coa time alcuse.14
## 1.1 1 0 1.264911 1 1 1.732051
## 1.2 1 0 1.264911 1 2 2.000000
## 1.3 1 0 1.264911 1 3 2.000000sehen wir diese Variablen in den ersten vier Spalten wieder (id, male, peer, coa). Die nächste Variable ist die Zeitvariable, die von R automatisch als time benannt wird. Wenn wir etwas anderes nutzen möchten, können wir mit timevar explizit einen Namen vergeben (weil die Wiederholungen das Alter der Jugendlichen sind, bietet sich age an):
alc_long <- reshape(data = alc,
varying = list(c('alcuse.14', 'alcuse.15', 'alcuse.16')),
direction = 'long',
timevar = 'age')
head(alc_long)## id male peer coa age alcuse.14
## 1.1 1 0 1.2649111 1 1 1.732051
## 2.1 2 1 0.8944272 1 1 0.000000
## 3.1 3 1 0.8944272 1 1 1.000000
## 4.1 4 1 1.7888544 1 1 0.000000
## 5.1 5 0 0.8944272 1 1 0.000000
## 6.1 6 1 1.5491934 1 1 3.000000Das Problem mit dieser neuen Variable ist jetzt noch, dass sie nicht das korrekte Alter der Jugendlichen kodiert, sondern stattdessen einfach bei 1 anfängt und hoch zählt. Auch das können wir per Argument ändern:
alc_long <- reshape(data = alc,
varying = list(c('alcuse.14', 'alcuse.15', 'alcuse.16')),
direction = 'long',
timevar = 'age',
times = c(14, 15, 16))
head(alc_long)## id male peer coa age alcuse.14
## 1.14 1 0 1.2649111 1 14 1.732051
## 2.14 2 1 0.8944272 1 14 0.000000
## 3.14 3 1 0.8944272 1 14 1.000000
## 4.14 4 1 1.7888544 1 14 0.000000
## 5.14 5 0 0.8944272 1 14 0.000000
## 6.14 6 1 1.5491934 1 14 3.000000Zu guter Letzt wird für die neuen Variablen automatisch der erste Name wiederverwendet. Hier ist der Name der neuen, messwiederholten Variable also alcuse.14. Weil in der Variable aber jetzt nicht mehr nur der Alkoholkonsum im 14. Lebensjahr enthalten ist, sondern für alle Jahre von 14 bis 16, bietet es sich an, hier auch einen allgemeineren Namen zu verwenden:
alc_long <- reshape(data = alc,
varying = list(c('alcuse.14', 'alcuse.15', 'alcuse.16')),
direction = 'long',
timevar = 'age',
times = c(14, 15, 16),
v.names = 'alcuse')
head(alc_long)## id male peer coa age alcuse
## 1.14 1 0 1.2649111 1 14 1.732051
## 2.14 2 1 0.8944272 1 14 0.000000
## 3.14 3 1 0.8944272 1 14 1.000000
## 4.14 4 1 1.7888544 1 14 0.000000
## 5.14 5 0 0.8944272 1 14 0.000000
## 6.14 6 1 1.5491934 1 14 3.000000Rückübertragung in breites Format
Der Vollständigkeit halber können wir auch noch überlegen, wie man diesen Datensatz dann wieder in das breite Format zurück übertragen kann. Dafür benötigt man fünf Argumente:
data: der Datensatzv.names: Variablen die wiederholt gemessen wurden (und sich über die Messungen unterscheiden können)timevar: die Variable, die Wiederholungen kennzeichnetidvar: der Personen-Identifikatordirection: das Zielformat des neuen Datensatzes
alc_wide <- reshape(alc_long,
v.names = 'alcuse',
timevar = 'age',
idvar = 'id',
direction = 'wide')
head(alc_wide)## id male peer coa alcuse.14 alcuse.15 alcuse.16
## 1.14 1 0 1.2649111 1 1.732051 2 2.000000
## 2.14 2 1 0.8944272 1 0.000000 0 1.000000
## 3.14 3 1 0.8944272 1 1.000000 2 3.316625
## 4.14 4 1 1.7888544 1 0.000000 2 1.732051
## 5.14 5 0 0.8944272 1 0.000000 0 0.000000
## 6.14 6 1 1.5491934 1 3.000000 3 3.162278Für Variablen, die nicht explizit aufgeführt werden, wird von reshape wieder angenommen, dass es nicht wiederholt gemessene “feste” Variablen sind. Im vorliegenden Fall sind Geschlecht (male) und die Menge alkoholkonsumierender Peers (peer) nur ein Mal gemessen worden und können daher nicht über Messzeitpunkte variieren. Um Variablen bei der Transformation aus dem Datensatz zu entfernen, kann das drop Argument genutzt werden.
Wenn ein Datensatz durch reshape umgewandelt wurde - z.B. dann, wenn man einen Datensatz mit unterschiedlichen Auswertungsansätzen untersucht und zwischen den Formaten wechseln muss - kann er mit reshape(data) direkt in seine Ursprungsform zurückgewandelt werden.
Einfaktorielle ANOVA (mit Messwiederholung)
Nun haben wir den Datensatz umgebaut und unsere Analyse soll sich logischerweise auch auf die 3 Messungen von Alkohol fokussieren. Doch warum brauchen wir jetzt überhaupt ein anderes Verfahren als die einfaktorielle Varianzanalyse? Können wir nicht jede Altersgruppe als eigene Gruppe betrachten und dann unser schon gelerntes Vorgehen anwenden? Die Begründung, warum das nicht so einfach möglich ist, ähnelt natürlich der Unterscheidung zwischen unabhängigem und abhängigem t-Test. Wenn wir den Messwert einer Person in verschiedene Einflüsse zerlegen, gibt es neben dem Effekt des Messzeitpunktes also auch einen Effekt der Person. Daher müssen wir eine andere mathematische Formulierung nutzen.
Die Umsetzung in R funktioniert aber ähnlich mit den in den letzten Sitzungen behandelten Funktionen aus dem ez-Paket. Im Folgenden betrachten wir zunächst die Deskriptivstatistik und führen dann die ANOVA durch.
Deskriptivstatistik
In diesem Fall ist von Interesse, wie sich der Alkoholkonsum von Jugendlichen zwischen 14 und 16 verändert. Dafür können wir zunächst deskriptiv betrachten, wie die Mittelwerte sich über die Zeit verändern:
library(ez)## Warning: Paket 'ez' wurde unter R Version 4.2.3 erstelltezStats(alc_long, alcuse, id, within = age)## Warning: "age" will be treated as numeric.## Warning: There is at least one numeric within variable, therefore aov() will be
## used for computation and no assumption checks will be obtained.## age N Mean SD FLSD
## 1 14 82 0.6304662 0.938912 0.2500601
## 2 15 82 0.9636295 1.047373 0.2500601
## 3 16 82 1.1717690 1.135350 0.2500601ezStats wartet hier direkt mit einer Warnung auf, die darauf hinweist, dass age als numerische Variable vorliegt. Weil in der Varianzanalyse davon ausgegangen wird, dass die unabhängigen Variablen nominalskaliert sind, möchte das ez-Paket sie auch im dazugehörigen Format. Deswegen wandeln wir die Altersvariable schnell in einen factor um:
alc_long$age <- as.factor(alc_long$age)Jetzt sollte der ezStats-Befehl ohne die Warnung funktionieren:
ezStats(alc_long, alcuse, id, within = age)## age N Mean SD FLSD
## 1 14 82 0.6304662 0.938912 0.2165844
## 2 15 82 0.9636295 1.047373 0.2165844
## 3 16 82 1.1717690 1.135350 0.2165844Statt das Argument between wie in den letzten Sitzungen zu nutzen, wird mithilfe des within Arguments die Variable benannt, die zwischen Messungen innerhalb der gleichen Personen unterscheidet. In diesem Fall unterscheiden sich die Messungen der gleichen Personen bezogen auf das Alter, zu dem Sie befragt wurden. Deskriptiv zeigt sich (vielleicht nicht allzu überraschend) ein Anstieg des Alkoholkonsums über die Jahre. Grafisch dargestellt:
ezPlot(alc_long, alcuse, id, within = age,
x = age)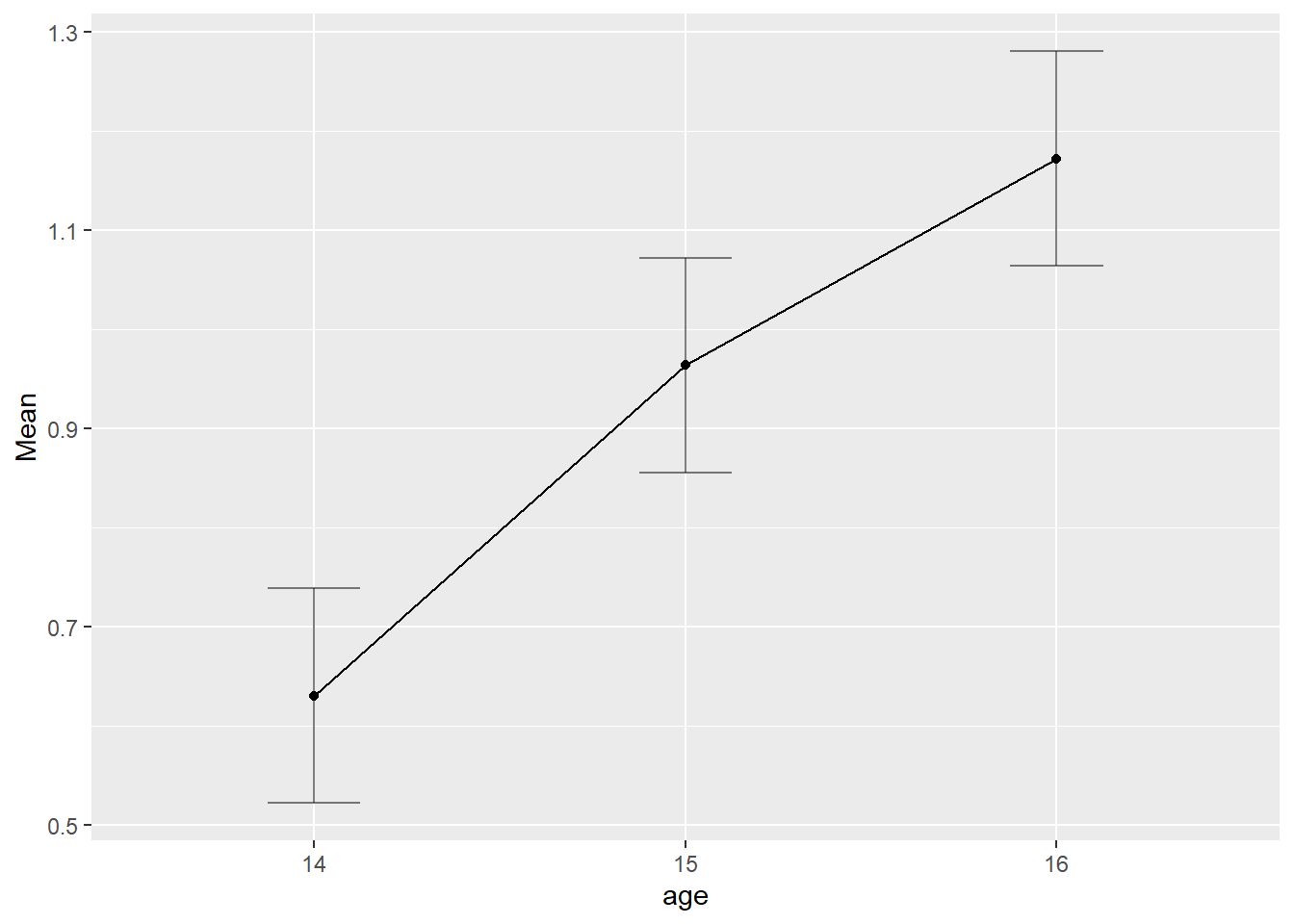
Wie schon in der letzten Sitzung erklärt, sind die Intervalle um die Mittelwerte herum die Fisher’s Least Significant Difference (FLSD) - wenn sich zwei Mittelwerte um diesen Betrag unterscheiden, sollten sie auch statistisch bedeutsam sein.
ezANOVA für Messwiederholungen
Als Äquivalent zur Homoskedastizitätsannahme in der ANOVA ohne Messwiederholung, wird in der ANOVA mit Messwiederholung die Sphärizitätsannahme getroffen. Unter dieser Annahme sollten die Varianzen der Differenzen zwischen allen Zeitpunkten identisch sein (vgl. Eid et al., 2017, S. 474 f.). Im breiten Datenformat sind diese Differenzen einfach zu erstellen:
alc$diff_1415 <- alc$alcuse.15 - alc$alcuse.14
alc$diff_1416 <- alc$alcuse.16 - alc$alcuse.14
alc$diff_1516 <- alc$alcuse.16 - alc$alcuse.15
var(alc[, c('diff_1415', 'diff_1416', 'diff_1516')])## diff_1415 diff_1416 diff_1516
## diff_1415 0.7235404 0.5391093 -0.1844311
## diff_1416 0.5391093 1.2951897 0.7560804
## diff_1516 -0.1844311 0.7560804 0.9405115Wir konzentrieren uns auf die Diagonale. Rein deskriptiv lässt sich erkennen, dass die Varianz der Differenz zwischen 14 und 16 Jahren beinahe doppelt so groß ist, wie die zwischen 14 und 15 Jahren. Wie schon bei der Homoskedastizitätsannahme, wird auch die Sphärizität von ezANOVA mitgetestet:
ezANOVA(data = alc_long, dv = alcuse, wid = id, within = age)## $ANOVA
## Effect DFn DFd F p p<.05 ges
## 2 age 2 162 12.39539 9.793248e-06 * 0.0441567
##
## $`Mauchly's Test for Sphericity`
## Effect W p p<.05
## 2 age 0.8858857 0.007854286 *
##
## $`Sphericity Corrections`
## Effect GGe p[GG] p[GG]<.05 HFe p[HF] p[HF]<.05
## 2 age 0.8975739 2.342158e-05 * 0.9166239 1.991144e-05 *Der sogenannte Mauchly Test (Mauchly's Test for Sphericity) zeigt hier an, dass es bedeutsame Abweichungen von der Annahme der Sphärizität gibt (\(p\) < .05), die Annahme also nicht als gegeben betrachtet werden kann. Weil diese Situation sehr häufig vorkommt, gibt es eine Reihe verbreiteter Korrekturen, von denen ezANOVA die Greenhouse-Geisser (GGe) und die Huynh-Feldt Korrekturen (HFe) anbietet. Es hat sich gezeigt, dass die Greenhouse-Geisser Korrektur mitunter zu strikt ist (also zu selten bedeutsame Ergebnisse gefunden werden), weswegen beide Varianten ausgegeben werden. Beide Korrekturen führen zu kleineren Freiheitsgraden (durch Multiplikation mit dem Faktor \(\epsilon\) in Bestimmung des kritischen F-Wertes. Im Output der Funktion sehen wir die Korrektur durch einen darauf angepassten p-Wert - die korrigierten Freiheitsgrade werden nicht aufgeführt (aber \(\epsilon\), wenn man diese selbst ausrechnen will). Eine Empfehlung für eine der beiden Korrekturen zu geben ist schwer, da sie sich häufig nur leicht unterscheiden. Verschiedene Daumenregeln existieren, doch sollte im besten Fall die Power im Versuchsplan so gestaltet werden, dass der kleine Unterschied in keinen unterschiedlichen Signifikanzentscheidungen resultiert.
In unserem Beispiel können also der ersten Tabelle der empirische \(F\)-Wert und das generalisierte \(\eta^2\) entnommen werden, der korrekte \(p\)-Wert bezüglich der Hypothesenprüfung sollte allerdings der dritten, korrigierten Tabelle entnommen werden, weil der Mauchly Test gezeigt hat, dass die Sphärizitätsannahme nicht hält. In unserem Fall (egal, ob wir Greenhouse-Geisser oder Huynh-Feldt nutzen) zeigt sich ein bedeutsamer Unterschied im Alkoholkonsum zwischen dem 14, 15 und 16. Lebensjahr (\(p\) < .05).
Ob es sich hier um einen konstanten Anstieg handelt, der Alkoholkonsum stetig abnimmt, oder aber im Alter von 15 Jahren den Höhepunkt erreicht wird, können wir aus diesen Ergebnissen allein nicht unterscheiden. Wie bereits aus den letzten beiden Sitzungen bekannt ist, bietet die ANOVA uns einen Omnibustest dafür, ob es Unterschiede gibt. Um genauer zu verstehen, welche Unterschiede es gibt, können wir Kontraste nutzen.
Effektgröße und Intraklassenkorrelation
Die Intraklassenkorrelation (ICC) bezeichnet generell das Ausmaß, in dem die Varianz von Beobachtungen von der “Klasse” abhängen, aus dem diese Beobachtungen kommen. Im Fall von Längsschnittanalysen bedeutet das, dass die ICC das Ausmaß von intraindividueller Stabilität anzeigt. Effektgrößen sollten unter Berücksichtigung dieser Stabilität interpretiert werden. Eine generelle Richtlinie für die ICC-bedingte Interpretation von \(\eta^2\) liefert Cohen (1988), hier dargestellt nach Eid et al. (2017, S. 478):
| ICC | klein | mittel | groß |
|---|---|---|---|
| .20 | .012 | .074 | .169 |
| .40 | .016 | .096 | .213 |
| .60 | .024 | .138 | .289 |
| .80 | .048 | .242 | .449 |
Die ICC kann generell als \(\frac{\sigma^2_{\pi}}{\sigma^2_{\pi} + \sigma^2_{\epsilon}}\) berechnet werden. Dabei ist \(\sigma^2_{\pi}\) die Personenvarianz und \(\sigma^2_{\epsilon}\) die Residualvarianz. Beide können direkt aus den mittleren Quadratsummen berechnet werden. Alternativ kann die ICC-Funktion aus dem psych-Paket genutzt werden:
psych::ICC(alc[, c('alcuse.14', 'alcuse.15', 'alcuse.16')])## Call: psych::ICC(x = alc[, c("alcuse.14", "alcuse.15", "alcuse.16")])
##
## Intraclass correlation coefficients
## type ICC F df1 df2 p lower bound upper bound
## Single_raters_absolute ICC1 0.51 4.1 81 164 1.4e-14 0.38 0.63
## Single_random_raters ICC2 0.51 4.6 81 162 6.3e-17 0.37 0.64
## Single_fixed_raters ICC3 0.55 4.6 81 162 6.3e-17 0.42 0.66
## Average_raters_absolute ICC1k 0.75 4.1 81 164 1.4e-14 0.64 0.83
## Average_random_raters ICC2k 0.76 4.6 81 162 6.3e-17 0.64 0.84
## Average_fixed_raters ICC3k 0.78 4.6 81 162 6.3e-17 0.69 0.85
##
## Number of subjects = 82 Number of Judges = 3
## See the help file for a discussion of the other 4 McGraw and Wong estimates,Der in diesem Fall relevante ICC-Typ (type) ist als ICC1 gelistet. In diesem Fall (ICC = .51) bedeutet es also, dass ca. 50% der Unterschiede zwischen Messungen auf stabile Personeneigenschaften zurückgehen. In Anbetracht dieser ICC, hat das Alter mit einem \(\eta^2\) von .016 < \(\eta^2\) = .0442 < .096 also einen kleinen Effekt auf das Ausmaß an Alkoholkonsum bei Jugendlichen.
Kontraste
Wie für eine ANOVA ohne Messwiederholung, kann auch in diesem Fall mit dem emmeans-Paket die Kontrastanalyse durchgeführt werden.
#### Kontraste ----
library(emmeans)Kontraste sind hier hilfreich, da spezifischere Hypothesen getesten werden können, während unsere bisherige Analyse nur einen globalen Effekt feststellen konnte. Die contrast-Funktion des Pakets benötigt als Input ein aov-Objekt. Wir haben bereits gelernt, dass solch ein Objekt mit der Funktion aov erstellt werden kann (aov(alcuse ~ age, data = alc_long; links steht die abhängige Variable Nutzung von Alkohol getrennt von der ~ stehen dann die Gruppenvariablen hier die Zeit). Wenn wir diesen Code jetzt so übernehmen würden, würden aber die Abhängigkeiten in unserem Datensatz durch die Messwiederholung nicht berücksichtigt. Genauer gesagt muss die Abhängigkeit in den Fehlern modelliert werden, die duch die Messwiederholung entsteht. In aov wird dies durch die Hinzunahme von Error() erreicht. Die Fehler sind abhängig von der Personen ID zu den verschiedenen Messungen. In Error müssen beide Informationen getrennt durch einen Backslash \ aufgegührt werden. Wir schreiben also zunächst id, da alle gleichen Ausprägungen zur gleichen Person gehören. Nach dem Backslash schreiben wir age, da es sich hierbei um eine Innersubjektvariable (eine Within-Variable). Diese Schreibweise sagt quasi, dass wir die Messzeitpunkte innerhalb einer Person als Gruppe betrachten.
# aov-Objekt erzeugen
wdh_aov <- aov(alcuse ~ age + Error(id/age),
data = alc_long)
wdh_aov##
## Call:
## aov(formula = alcuse ~ age + Error(id/age), data = alc_long)
##
## Grand Mean: 0.9219549
##
## Stratum 1: id
##
## Terms:
## Residuals
## Sum of Squares 184.7733
## Deg. of Freedom 81
##
## Residual standard error: 1.510348
##
## Stratum 2: id:age
##
## Terms:
## age Residuals
## Sum of Squares 12.22698 79.89952
## Deg. of Freedom 2 162
##
## Residual standard error: 0.7022869
## Estimated effects may be unbalancedIn den aov-Objekten werden uns ein paar zusätzliche Infos mit ausgegen, nämlich die Quadratsummenzerlegung in Effekt, Person und Fehler. Die Variation, die auf die Personen zurückzuführen ist, steht unter Stratum 1: id, während die Effekte der Zeit unter Stratum 2: id:age zu finden sind. Genauso kann uns natürlich auch ezANOVA ein aov-Objekt als Output mitgeben, indem wir das nötige Argument spezifizieren, allerdings scheint es hier zurzeit Probleme mit dem Paket zu geben, weswegen wir hier nun auf aov ausweichen müssen. Nachdem wir nun ein Objekt erstellt haben, müssen wir die Funktion emmeans auf dieses anwenden und damit ein Objekt vorbereiten, das bei den Kontrasten verwendet werden kann.
# Kontraste vorbereiten
em <- emmeans(wdh_aov, ~ age)## Note: re-fitting model with sum-to-zero contrastsem## age emmean SE df lower.CL upper.CL
## 14 0.630 0.115 152 0.403 0.858
## 15 0.964 0.115 152 0.736 1.191
## 16 1.172 0.115 152 0.944 1.399
##
## Warning: EMMs are biased unless design is perfectly balanced
## Confidence level used: 0.95Polynomiale Kontraste und Trendanalysen
In der letzten Sitzung hatten wir den contrast-Befehl genutzt, um beliebige Kontraste zu definieren. Bei messwiederholten Designs mit dem Ziel, Veränderung über die Zeit zu untersuchen, ist es meist sinnvoll zu prüfen, ob die Veränderung über die Zeit durch eine einfache Funktion der Zeit beschrieben werden kann. Für den Zeitverlauf werden häufig Polynome genutzt, wie Sie sie in der 4. Regressionssitzung gesehen haben. Hierbei ist zu beachten, dass herkömmliche Kontraste immer so aufgestellt werden, dass das Verwerfen der Null-Hypothese gegen den Kontrast spricht. Bspw. wenn wir annehmen, dass zwei bestimmte Mittelwerte gleich sind, dann verwerfen wir diese Hypothese bei einem signifikanten Hypothesentest und einer entsprechend großen Teststatistik.
Bei sogenannten Trendanalysen, bei denen wir Veränderungen über bspw. die Zeit bei Messwiederholungsdesigns untersuchen, ist dies anders. Hier wird in der Regel eine ganze Batterie an orthogonalen Kontrasten verwendet, die sukzessive verschiedene Verläufe testet, wobei hier die Null-Hypothese besagt, dass der jeweilige Verlauf nicht gilt. Dies bedeutet im Umkehrschluss, dass bei Trendanalysen die Signifikanz einer Hypothese besagt, dass mindestens dieser Verlauf gilt (auf das “mindestens” gehen wir noch näher ein).
In unserem Beispiel haben wir 3 Messzeitpunkte, also 3 Mittelwerte, die wir auf Trends testen können. Bei 3 Mittelwerten können wir maximal einen quadratischen Verlauf testen und es können maximal zwei orthogonale Kontraste aufgestellt werden (immer K - 1 viele, wobei K die Anzahl an Gruppen ist; hier Gruppen = Messzeitpunkte). Welche Verläufe sind nun möglich? Die Null-Hypothese einer normalen ANOVA besagt, dass alle Mittelwerte gleich sind. Übersetzt in das Messwiederholungsdesign bedeutet dies, dass sich die Mittelwerte nicht über die Zeit verändern: die Mittelwerte folgen einer horizontalen Linie (im Regressionssetting bedeutet dies, dass es keine Beziehung mit der Zeit/der Wiederholungsmessung gibt; die Steigung ist Null). Folgen die Mittelwerte keiner horziontalen Linie, sondern verändern sich gleichmäßig über die Zeit, so steigen sie linear an oder fallen linear ab. Zeigen die Mittelwerte hingegen ein beschleunigtes Wachstum oder einen beschleunigten Abfall oder steigen sie erst an und fallen dann ab oder fallen erst ab und steigen dann an, so folgen sie vermutlich keinem linearen Trend mehr. Hier wäre der quadratische Trend geeigneter, um dieses Verhalten zu erklären.
Folglich haben wir drei Trends, die wir untersuchen können: horizontal, linear und quadratisch. Entsprechend werden auch die Hypothesen aufgestellt. Die erste Nullyhpothese des Kontrasts in diesem Beispiel ist, dass ein horizontaler Verlauf gilt. Ist dieser Kontrast signifikant, so wird sie verworfen und es gilt kein horizontaler Verlauf. Aus diesem Grund wird diese Hypothesenstellung auch häufig die Hypothese auf linearen Trend genannt (was zur Verwirrung führen kann, weil der lineare Trend in der H1 steckt); ist die Testung signifikant, so gilt mindestens ein linearer Trend in den Daten (mit einer Irrtumswahrscheinlichkeit von \(5\%\) - bzw. einem gewählten \(\alpha\)). Das mindestens steht hier, weil auch ein quadratischer Trend dem horizontalen Verlauf widerspricht. Wir brauchen also noch einen weiteren Hypothesentest, der den linearen gegen den quadratischen Verlauf testet. Sie denken es sich vielleicht schon, die nächste Null-Hypothese repräsentiert einen linearen Trend. Wird diese verworfen, so gilt kein linearer Verlauf sondern ein quadratischer. Der quadratische Trend beschreibt die Daten signifikant besser als der lineare. Aus diesem Grund wird dieser Kontrast auch häufig der Kontrast auf quadratischen Trend genannt. Ist er signifikant, so können wir für die Daten einen quadratischen Trend annehmen. Diese Informationen sind in folgender Tabelle nochmals zusammengefasst:
| Kontrastnahme | \(H_0\) | \(H_1\) |
|---|---|---|
| linear | horizontal: \(y = c\) | linear: \(y = bx + c\) |
| quadratisch | linear: \(y = bx + c\) | quadratisch: \(y = ax^2 +bx + c\) |
Der Tabelle entnehmen wir, dass quasi immer ein Term hinzukommt (von “\(c\)” zu “\(bx + c\)” zu “\(ax^2 + bx + c\)”). Die Signifikanzentscheidung entspricht also dem inkrementellen Vorgehen, welches wir bereits aus der Regressionsanalyse kennen! Das bedeutet also, falls der lineare Trend signifikant ist, dann verbessert er gegenüber der H0 vom horizontalen Verlauf die Vorhersage der Entwicklung der Mittelwerte. Genauso spricht ein signifikanter quadratischer Trend für eine Verbesserung der Vorhersage gegenüber des linearen Trends!
Die erste Funktion, die üblicherweise getestet wird, ist der lineare Verlauf. Dabei wird unterstellt, dass die Mittelwerte auf einer geraden Linie liegen, die eine uns vorerst unbekannte Steigung hat. Wie bei Eid et al. (2017, S. 481) dargestellt, ergibt sich daraus die Linearkombination
\[\Lambda = K_1 \cdot \mu_1 + K_2 \cdot \mu_2 + \ldots + K_J \cdot \mu_J\]
wobei \(K_j\) die jeweiligen Kontrastkoeffizienten sind. Wie in der letzten Sitzung behandelt, wird für Kontrastkoeffizienten die Restriktion aufgestellt, dass \(\sum_{j=1}^{J} K_j = 0\) (die Summe aller Kontrastkoeffizienten muss 0 sein). Im Kontext von Messwiederholungen müssen die \(K_j\) jetzt so gewählt werden, dass sie mit den Zeitabständen zwischen den Wiederholungen korrespondieren. In unserem Fall geht es um 3 aufeinanderfolgende Jahre - die Abstände zwischen den Wiederholungen sind also gleich (jeweils 1 Jahr) praktischerweise gleich. Wie beschrieben wird für die Überprüfung auf linearen Trend in der H0 ein horizontaler Trend aufgeführt und für diesen die Kontrastkoeffizienten bestimmt.
Horizontaler Trend würde bedeuten, dass unsere Messwerte eine horizontale Linie bilden. Für die Bestimmung der Koeffizienten müssen wir zunächst einige mathematische (theoretische) Überlegungen anstellen. Eine horizontale Linie entsteht, wenn sich die Mittelwerte über die Zeit nicht verändern, also der Abstand vom Mittelpunkt in beide Richtungen gleich groß ist und sich das Vorzeichen nicht verändert: \(\mu_2 - \mu_1 = \mu_2 - \mu_3\). Hier ist es extrem wichtig, dass wir das gleiche \(\mu\) (hier \(\mu_2\)) zuerst nennen, da wir sonst fälschlicherweise andere Effekte testen würden. Wenn wir diese kleine Gleichung nun umformen und auf beiden Seiten \(\mu_2\) abziehen und anschließend beide Seiten mit \(\mu_3\) addieren, dann erhalten wir: \(-\mu_1 + \mu_3 = 0\) also die Kontrastkoeffizienten (-1, 0, 1), wie wir sie oben schon aufgeschrieben hatten. Wie schon für die Kontraste in der letzten Sitzung wird hierbei die Nullhypothese getestet, dass \(H_0 : -1 \cdot \mu_1 + 0 \cdot \mu_2 + 1 \cdot \mu_3 = 0\). Diese Koeffizienten müssen wir in einem eigenen Objekt ablegen.
lin_cont <- c(-1, 0, 1)Wir können uns erstmal rein deskriptiv anschauen, inwiefern der lineare Verlauf eine realistische Behauptung über den Mittelwertsverlauf ist. Wie in der letzten Sitzung behandelt, erstellen wir mit ezPlot automatisch einen ggplot mit der gleichen Snytax wie bei ezANOVA. Der Grund, aus dem ggplot2 als Paket so beliebt ist, ist, dass es modular funktioniert und wir unsere Abbildungen schichten können (wie in der 2. Sitzung behandelt). Wenn Pakete also ggplot2-Abbildungen erstellen, können wir diese einfach durch andere ggplot2-Komponenten ergänzen (wenn wir vorher ggplot2 geladen haben):
library(ggplot2)Zur Erinnerungen können Sie die Abbildung nach Ihren Wünschen umgestalten, wie in der 2. Sitzung besprochen:
# ezPlot siehe oben
ezPlot(alc_long, alcuse, id, within = age,
x = age) +
# beliebige ggplot Erweiterungen anfügen
theme_minimal() +
xlab('Alter')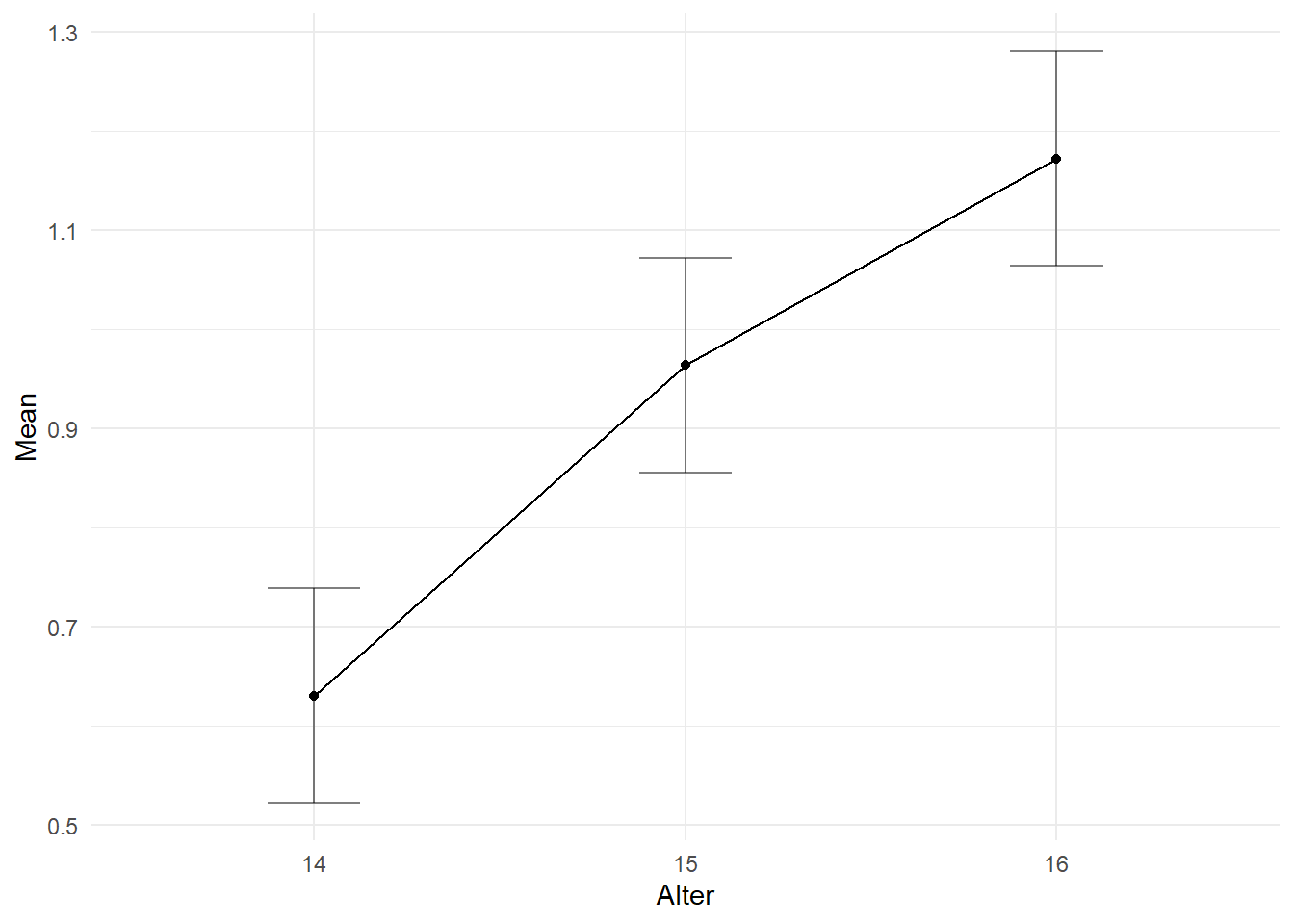
Um Verläufe darzustellen, hatten wir in der 2. Sitzung und der 8. Sitzung geom_smooth() kennen gelernt. Weil diese Geometrie als Schicht auf den ursprünglichen Plot gelegt werden kann, können wir den linearen Verlauf veranschaulichen:
ezPlot(alc_long, alcuse, id, within = age,
x = age) +
geom_smooth(aes(x = as.numeric(age)), method = 'lm', se = FALSE)## `geom_smooth()` using formula = 'y ~ x'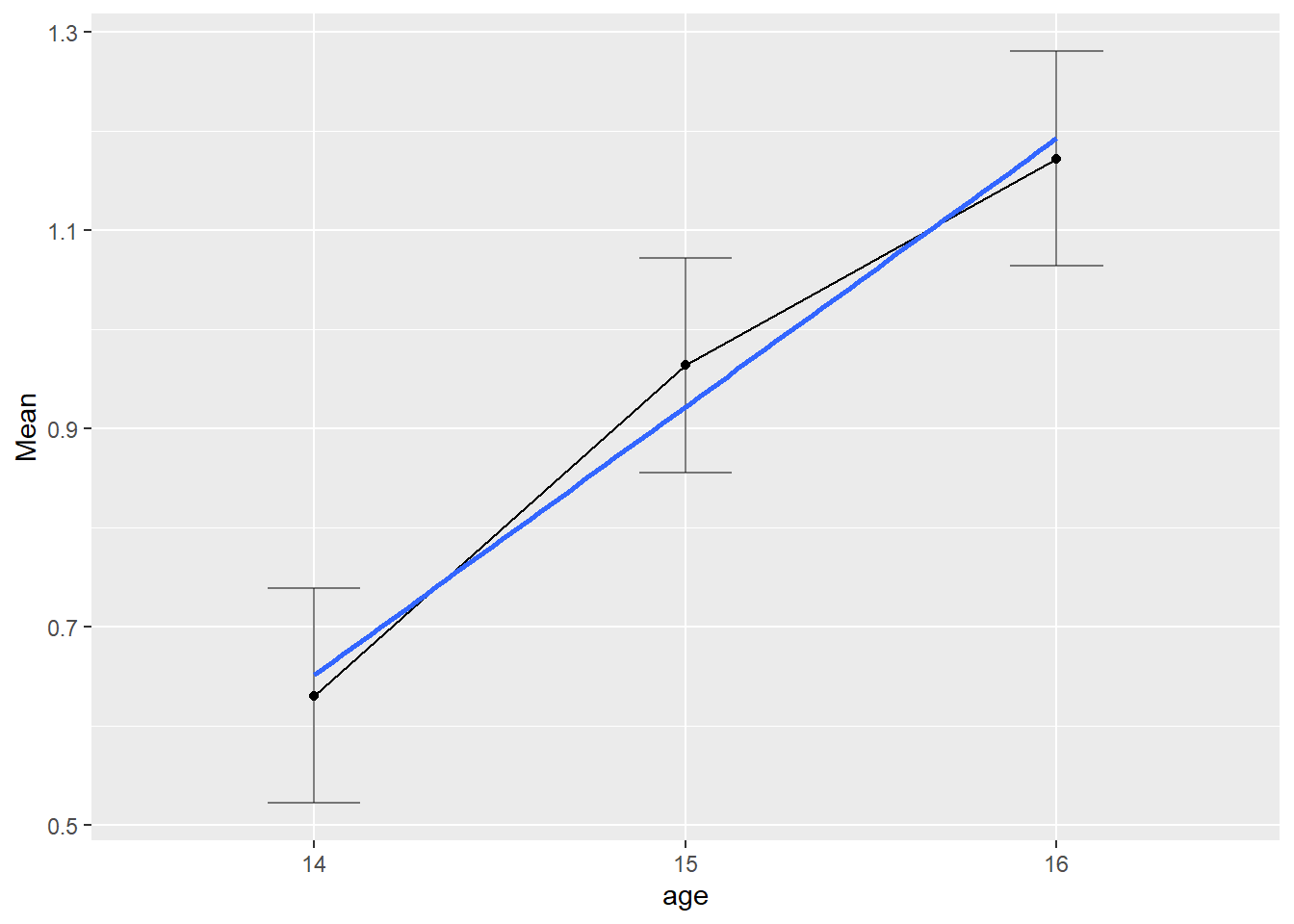
Weil wir für ezANOVA das Alter in einen Faktor umgewandelt hatten, müssen wir es für geom_smooth erst noch in eine numerische Variable zurücküberführen (as.numeric). Dann wählen wir mit method = 'lm' das lineare Modell und unterdrücken mit se = FALSE das Konfidenzintervall um die Regressionsgerade. In unserem Kontrast für den linearen Effekt prüfen wir den Anstieg dieser Geraden (oben als \(\Lambda\) notiert):
contrast(em, list(lin_cont))## contrast estimate SE df t.ratio p.value
## c(-1, 0, 1) 0.541 0.11 162 4.935 <.0001Wie wir an dem p.value erkennen können, ist der Kontrast signifikant, es liegt also mindestens ein linearer Trend vor. Im nächsten Schritt können wir prüfen, ob ein quadratischer Effekt vorliegt. Für diesen Effekt ist es eventuell nicht so direkt einleuchtend, wie der Kontrastvektor auszusehen hat. Auch hier gilt, dass \(\sum_{j=1}^{J} K_j = 0\) sein muss. Wir wissen, dass der Test auf den quadratischen Trend dem des linearen Trends widersprechen soll. Dies erreichen wir, indem wir tatsächlich in der H0 einen linearen Verlauf aufstellen. Das erscheint jetzt etwas paradox, da wir uns ja im zuvorigen Test bereits dafür entschlossen hatten, dass in den Daten mindestens ein linearer Trend verborgen ist. Wir wollen allerdings einen Kontrast erstellen, der, falls er signifikant ist, gegen einen linearen und für einen quadratischen Verlauf spricht. Folglich müssen wir Linearität annehmen, indem wir uns vorstellen, dass die Veränderung von \(\mu_1\) zu \(\mu_2\) genauso groß ist, wie von \(\mu_2\) zu \(\mu_3\). Hier ist nun die Richtung (und damit das Vorzeichen) entscheidend, denn in Worten gesprochen klingt das zunächst sehr ähnlich zu dem, was wir oben getestet haben. Wenn wir allerdings die Richtung berücksichtigen, so erhalten wir bspw: \(\mu_2 - \mu_1 = \mu_3 - \mu_2\), was sich umformen lässt zu \(\mu_1 - 2\mu_2 + \mu_3 = 0\). Für eine gleichzeitige Testung der beiden bisher aufgestellten Kontraste müssen diese orthogonal sein (siehe Eid et al., 2017, S. 426).
Dies kann man leicht prüfen: \(-1*1 + 0*-2 + 1*1 = 0\) (hier ist die erste Zahl pro Summand jeweils der Koeffizient des ersten Kontrasts und die zweite jeweils die vom zweiten: (-1, 0, 1) und (1, -2, 1)).
Um Ihnen das Leben ein wenig zu erleichtern, können Sie folgende Tabelle konsultieren, wenn Sie gleichabständige Messungen vorliegen haben und polynomiale Kontraste definieren wollen:
| Zeitpunkte | Polynom | Vektor |
|---|---|---|
| 2 | 1 (linear) | \([-1, 1]\) |
| 3 | 1 (linear) | \([-1, 0, 1]\) |
| 2 (quadratisch) | \([1, -2, 1]\) | |
| 4 | 1 (linear) | \([-3, -1, 1, 3]\) |
| 2 (quadratisch) | \([1, -1, -1, 1]\) | |
| 3 (kubisch) | \([-1, 3, -3, 1]\) |
Diese Tabelle ist natürlich ziemlich lang erweiterbar. Wie Sie sehen, können Polynome immer für \(t-1\) Grade bestimmt werden - für drei Messzeitpunkte, kann also bis zum quadratischen Trend geprüft werden. Abgebildet sieht der quadratische Verlauf der Mittelwerte (rote Linie) so aus:
ezPlot(alc_long, alcuse, id, within = age,
x = age) +
geom_smooth(aes(x = as.numeric(age)), method = 'lm', se = FALSE) +
geom_smooth(aes(x = as.numeric(age)), method = 'lm', se = FALSE,
formula = y ~ x + I(x^2), color = 'red')## `geom_smooth()` using formula = 'y ~ x'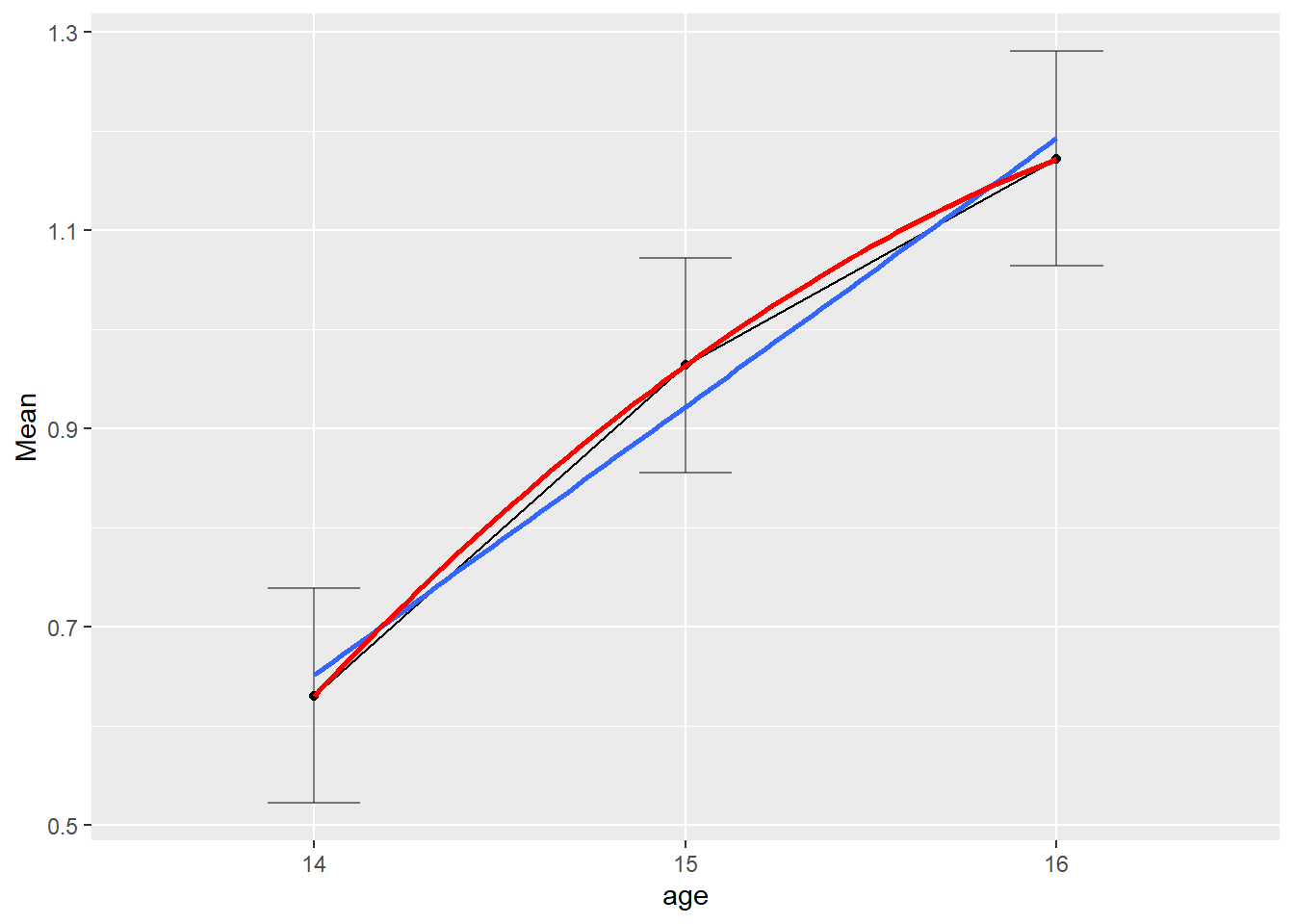
Wir erkennen deutlich, dass alle Mittelwerte auf dem quadratischen Trend liegen. Das ist allerdings auch einleuchtend, da es immer so ist, dass für \(t\) Zeitpunkte ein Polynom bis zum Grad \(t-1\) (also: \(a_0 + a_1X + a_2X^2 + \dots + a_{t-1}X^{t-1}\)) gefunden werden kann, dass alle Punkte trifft, solang nicht mehrere Punkte den gleichen \(x\)-Wert haben. Die Frage ist nun, ob der quadratische Trend eine signifikante Verbesserung gegenüber dem linearen Trend ist!
Wir wollen nun also untersuchen, ob es in den Daten einen quadratischen Trend gibt, indem wir dafür den entsprechenden Kontrast definieren und die Kontrastprüfung gleichzeitig für den linearen und quadratischen Effekt durchführen! Wir sollten dabei nicht vergessen, die \(p\)-Werte einer Bonferroni-Korrektur zu unterziehen!
lin_cont <- c(-1, 0, 1)
qua_cont <- c(1, -2, 1)
contrast(em, list(lin_cont, qua_cont),
adjust = 'bonferroni')## contrast estimate SE df t.ratio p.value
## c(-1, 0, 1) 0.541 0.11 162 4.935 <.0001
## c(1, -2, 1) -0.125 0.19 162 -0.658 1.0000
##
## P value adjustment: bonferroni method for 2 testsWie Sie erkennen können, ist nur der lineare Trend-Kontrast signifikant! Wir gehen also nur von einem linearen und nicht von einem quadratischen Trend aus, denn der Test auf “Modellverbesserung” durch das Hinzufügen des quadratischen Trends brachte keine signifikante Verbesserung. Genauso kann man dies so interpretieren, dass die Datenlage zwar einem horizontalen (Gleichheit aller Mittelwerte) Verlauf widerspricht, nicht aber einem linearen Verlauf!
Hier muss allerdings aufgepasst werden. Diese Kontraste, die aus sogenannten orthognalen Polynomen entstehen, sollten immer gemeinsam getestet werden. Wenn beispielsweise der quadratische Verlauf der richtige wäre, er aber perfekt U-förmig verläuft, so könnte es passieren, dass der lineare Trend nicht signifikant wird, wir aber im quadratischen erkennen, dass tatsächlich die Daten einem quadratischen Trend folgen. Hier ist das beste Vorgehen immer alle möglichen Trends gleichzeitig zu prüfen. Es wird dann immer der höchste signifikante Trend angenommen. Falls z.B. der lineare und der quadratische signifikant sind, so entscheiden wir uns für den quadratischen. Falls Sie mehr dazu wissen wollen, schauen Sie doch in Appendix A vorbei.
Abkürzungen für typische Kontraste
Damit wir nicht für jede Datenkonstellation riesige Tabellen von orthogonalen Kontrasten parat haben müssen, können wir in der contrast-Funktion einige typische Kontraste in abgekürzter Fassung anfordern. Für polynomiale Kontraste, z.B.
contrast(em, interaction = 'poly')## age_poly estimate SE df t.ratio p.value
## linear 0.541 0.11 162 4.935 <.0001
## quadratic -0.125 0.19 162 -0.658 0.5114Es zeigt sich in diesem Fall also ein bedeutsamer linearer, aber kein bedeutsamer quadratischer Trend. Die Interpretation ist identisch zu oben — es ist ja auch die gleiche Analyse (alle Koeffizienten sind identisch zu oben)! Wie schon zuvor, können wir hier mit adjust eine Bonferroni-Korrektur vornehmen:
contrast(em, interaction = 'poly',
adjust = 'bonferroni')## age_poly estimate SE df t.ratio p.value
## linear 0.541 0.11 162 4.935 <.0001
## quadratic -0.125 0.19 162 -0.658 1.0000
##
## P value adjustment: bonferroni method for 2 testsEs ergibt sich die gleiche Tabelle wie zuvor.
Wollen wir einen herkömmlichen Kontrast prüfen (also keinen Trend), so müssen wir in unserer Interpretation wieder umschwenken! Der direkte Vergleich aller Zeitpunkte kann via method = 'pairwise' erreicht werden. Außerdem resultieren die Voreinstellungen in einem Vergleich aller Zeitpunkte mit dem globalen Mittel:
# Alle paarweisen Vergleiche
contrast(em, method = 'pairwise',
adjust = 'bonferroni')## contrast estimate SE df t.ratio p.value
## age14 - age15 -0.333 0.11 162 -3.038 0.0083
## age14 - age16 -0.541 0.11 162 -4.935 <.0001
## age15 - age16 -0.208 0.11 162 -1.898 0.1785
##
## P value adjustment: bonferroni method for 3 testsHier erkennt man, dass sich vor allem Unterschiede zwischen 14 und 15 Jahren (\(p = 0.0083\)) sowie zwischen 14 und 16 Jahren (\(p < .001\)) ergeben, da hier die Mittelwertsvergleiche signifikant sind. Genauso könnten wir auch den jeweiligen Gruppenmittelwert gegen den globalen Mittelwert testen.
# Vergleiche mit dem Mittel
contrast(em,
adjust = 'bonferroni')## contrast estimate SE df t.ratio p.value
## age14 effect -0.2915 0.0633 162 -4.603 <.0001
## age15 effect 0.0417 0.0633 162 0.658 1.0000
## age16 effect 0.2498 0.0633 162 3.945 0.0004
##
## P value adjustment: bonferroni method for 3 testsDer Vergleich mit dem Mittel ist dann nützlich, wenn man sehr viele Zeitpunkte (oder Gruppen) hat. Dann bietet es sich an zu prüfen, ob es spezifische Instanzen gibt, die “auffällig” vom Durchschnittswert abweichen, statt sehr viele Einzelvergleiche zu definieren. Dies gilt besonders dann, wenn man keine natürliche Referenzkategorie hat - wie z.B. einen Prätest oder eine Kontrollgruppe. In unserem Fall weichen das Alter 14 (\(p < .001\)) und 16 (\(p = .0004\)) von Mittel ab.
Würden wir beispielsweise bei p Gruppen paarweise Vergleiche durchführen, so bräuchten wir insgesamt \(\frac{p(p-1)}{2}\) Vergleiche, während wir beim Test gegen das globale Mittel nur \(p\) Tests brauchen:
| Anzahl Gruppen: \(p\) | Anzahl paarweise Vergleiche: \(\frac{p(p-1)}{2}\) | Anzahl Vergleiche zum Mittel: \(p\) |
|---|---|---|
| 2 | 1 | 2 |
| 3 | 3 | 3 |
| 4 | 6 | 4 |
| 5 | 10 | 5 |
Wir sehen also, dass die paarweisen Vergleiche extrem schnell anwachsen, was natürlich verherende Folgen im Hinblick auf die Irrtumswahrscheinlichkeit hat!
Split-Plot ANOVA
Untersuchungen, in denen mehrere Gruppen und mehrere Messungen gleichzeitig betrachtet werden, werden häufig Split-Plot Designs genannt. Im aktuellen Datensatz können Jugendliche danach in Gruppen eingeteilt werden, ob ihre Eltern Alkoholiker sind (coa). Die entsprechende Syntax für das ez-Paket ist eine einfache Kombination aus der Syntax für die beiden Typen der ANOVA, die wir bereits behandelt haben:
# Deskriptive Statistiken
ezStats(alc_long,
dv = alcuse,
wid = id,
within = age, #zwischen den jährlichen Messungen
between = coa) #zwischen den Jugendlichen Gruppen## Warning: Data is unbalanced (unequal N per group). Make sure you specified a
## well-considered value for the type argument to ezANOVA().## Warning in ezStats(alc_long, dv = alcuse, wid = id, within = age, between =
## coa): Unbalanced groups. Mean N will be used in computation of FLSD## coa age N Mean SD FLSD
## 1 0 14 45 0.2903221 0.6253560 0.3080161
## 2 0 15 45 0.6601661 0.8840523 0.3080161
## 3 0 16 45 0.8762325 1.1225959 0.3080161
## 4 1 14 37 1.0441549 1.0885821 0.3080161
## 5 1 15 37 1.3327066 1.1215570 0.3080161
## 6 1 16 37 1.5312054 1.0573837 0.3080161# Grafische Darstellung
ezPlot(alc_long,
dv = alcuse,
wid = id,
within = age,
between = coa,
x = age, split = coa)## Warning: Data is unbalanced (unequal N per group). Make sure you specified a
## well-considered value for the type argument to ezANOVA().## Warning in ezStats(data = data, dv = dv, wid = wid, within = within, within_full
## = within_full, : Unbalanced groups. Mean N will be used in computation of FLSD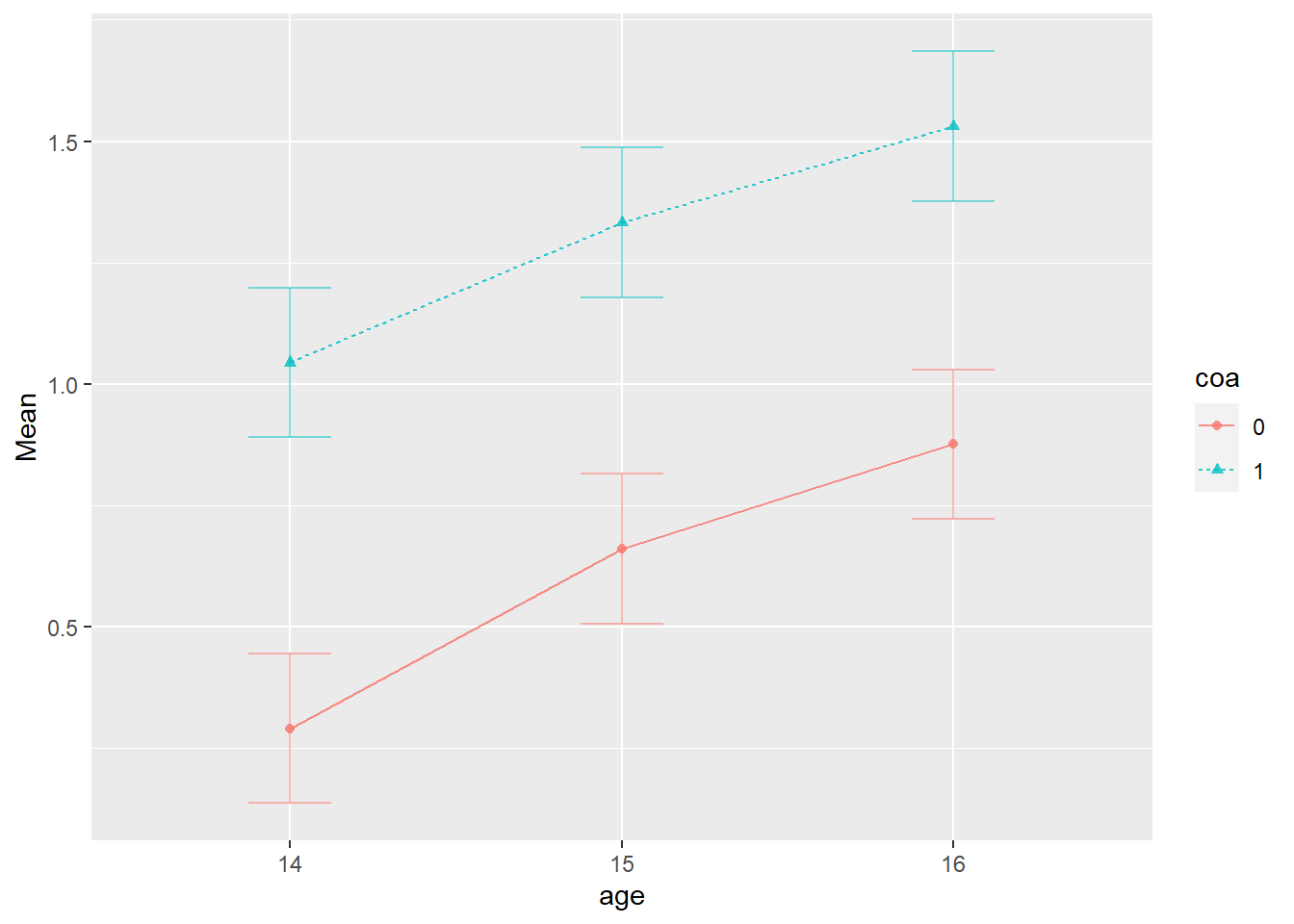
Der Plot verdeutlicht bereits, was in dieser Situation die drei zentralen Fragestellungen sind:
- Verändert sich der Alkoholkonsum über die Zeit? (Haupteffekt A)
- Unterscheiden sich Jugendliche von Alkoholikern von Jugendlichen nicht alkoholabhängiger Eltern in ihrem mittleren Alkoholkonsum? (Haupteffekt B)
- Unterscheidet sich die Veränderung mit der Zeit im Alkoholkonsum zwischen den beiden Gruppen von Jugendlichen? (Interaktionseffekt)
Wir erkennen leicht, dass die ANOVA mit Messwiederholung mit einem between Faktor sehr viel mit der zweifaktoriellen ANOVA gemein hat! Allerdings müssen wir unbedingt die Ähnlichkeit der Messungen, die durch die wiederholten Messungen entsteht, berücksichtigen, was wir ja über das “Within”-Design getan haben!
In sehr vielen psychologischen Studien ist der Interaktionseffekt der relevante Effekt. Insbesondere wenn experimentelle Studien durchgeführt werden, ist die Annahme, dass die Gruppen sich zu Beginn nicht unterscheiden (randomisierte Gruppenzuweisung), dann aber durch eine Intervention eine Veränderung eintritt und diese in der Experimentalgruppe anders ist, als die Veränderung in der Kontrollgruppe.
Um diese Effekte zu untersuchen, können wir wieder die ezANOVA nutzen:
ezANOVA(alc_long,
dv = alcuse,
wid = id,
within = age,
between = coa)## Warning: Data is unbalanced (unequal N per group). Make sure you specified a
## well-considered value for the type argument to ezANOVA().## $ANOVA
## Effect DFn DFd F p p<.05 ges
## 2 coa 1 80 15.0889366 2.101590e-04 * 0.1108265719
## 3 age 2 160 12.2596915 1.112344e-05 * 0.0494086230
## 4 coa:age 2 160 0.1132673 8.929835e-01 0.0004799824
##
## $`Mauchly's Test for Sphericity`
## Effect W p p<.05
## 3 age 0.8859965 0.008386194 *
## 4 coa:age 0.8859965 0.008386194 *
##
## $`Sphericity Corrections`
## Effect GGe p[GG] p[GG]<.05 HFe p[HF] p[HF]<.05
## 3 age 0.8976633 2.626605e-05 * 0.9169621 2.233274e-05 *
## 4 coa:age 0.8976633 8.726825e-01 0.9169621 8.768214e-01Obwohl ez den Mauchly Test für Sphärizität mitliefert, ist im Fall des Split-Plot Designs die eigentliche Annahme die Gleichheit der Varianz-Kovarianz-Matrizen der messwiederholten Variablen über alle Gruppen hinweg. Diese Annahme kann mithilfe des Box-M-Tests geprüft werden, welcher allerdings in nur wenigen Paketen implementiert ist, weil er in der Mehrheit aller empirischen Anwendungen statistisch bedeutsam ist. Wer ihn dennoch durchführen möchte, findet ihn z.B. im heplots Paket:
heplots::boxM(alc[, c('alcuse.14', 'alcuse.15', 'alcuse.16')], group = alc$coa)##
## Box's M-test for Homogeneity of Covariance Matrices
##
## data: alc[, c("alcuse.14", "alcuse.15", "alcuse.16")]
## Chi-Sq (approx.) = 21.486, df = 6, p-value = 0.0015Auch in unserem Fall wird eine signifikante Verletzung der Annahme angezeigt. Nach Eid et al. (2017, S. 494) ist die ANOVA gegenüber der Verletzung der Homgenitätsannahme bezüglich der Kovarianzmatrizen dann robust, wenn die Sphärizitätsannahme nicht verworfen werden muss. In dem Output von der ANOVA haben wir aber gesehen, dass auch hier eine signifikante Verletzung vorliegt. Für die Interpretaion können nun die zuvor dargestellten Korrekturen oder eine “echte” robuste Variante (z.B. im WRS2-Paket) genutzt werden. Betrachten wir nun nochmal genauer den oben schon gezeigten Output.
## $ANOVA
## Effect DFn DFd F p p<.05 ges
## 2 coa 1 80 15.0889366 2.101590e-04 * 0.1108265719
## 3 age 2 160 12.2596915 1.112344e-05 * 0.0494086230
## 4 coa:age 2 160 0.1132673 8.929835e-01 0.0004799824
##
## $`Mauchly's Test for Sphericity`
## Effect W p p<.05
## 3 age 0.8859965 0.008386194 *
## 4 coa:age 0.8859965 0.008386194 *
##
## $`Sphericity Corrections`
## Effect GGe p[GG] p[GG]<.05 HFe p[HF] p[HF]<.05
## 3 age 0.8976633 2.626605e-05 * 0.9169621 2.233274e-05 *
## 4 coa:age 0.8976633 8.726825e-01 0.9169621 8.768214e-01Bezüglich der Ergebnisse der ANOVA zeigt sich, dass das Alter (korrigierte Effekte nach HF) und ob ein Elternteil Alkoholiker (coa) ist einen bedeutsamen Einfluss auf das Trinkverhalten von Jugendlichen haben. Da coa nur einmal gemessen wurde, wird für den Effekt keine Korrektur verwendet. Dass die Interaktion nicht statistisch bedeutsam ist, deutet darauf hin, dass die Entwicklung über die Zeit zwischen beiden Gruppen von Jugendlichen parallel verläuft.
Appendix A
Trendanalysen
Wir schauen uns im Folgenden simulierte Daten an und betrachten nochmals die 3 Trends (horizontal, linear, quadratisch). Wir beginnen mit einem horiziontalen Trend in den Daten an. Die wahren Mittelwerte werden als (0, 0, 0) gewählt:
set.seed(123) # für Vergleichbarkeit
Means <- c(0, 0, 0) # wahren Mittelwerte pro Zeitpunkt
Y <- Means[1] + rnorm(30)
Y <- c(Y, Means[2] + rnorm(30))
Y <- c(Y, Means[3] + rnorm(30))
times <- c(rep("1", 30), rep("2", 30), rep("3", 30))
id <- c(1:30, 1:30, 1:30)
df <- data.frame(Y, times, id)
df$times <- as.factor(times)
df$id <- as.factor(df$id)
head(df)## Y times id
## 1 -0.56047565 1 1
## 2 -0.23017749 1 2
## 3 1.55870831 1 3
## 4 0.07050839 1 4
## 5 0.12928774 1 5
## 6 1.71506499 1 6ezPlot(df, Y, id, within = times,
x = times) +
geom_smooth(aes(x = as.numeric(times)), method = 'lm', se = FALSE,
formula = y ~ x) +
geom_smooth(aes(x = as.numeric(times)), method = 'lm', se = FALSE,
formula = y ~ x + I(x^2), color = 'red')+
geom_smooth(aes(x = as.numeric(times)), method = 'lm', se = FALSE,
formula = y ~ 1, color = 'gold3')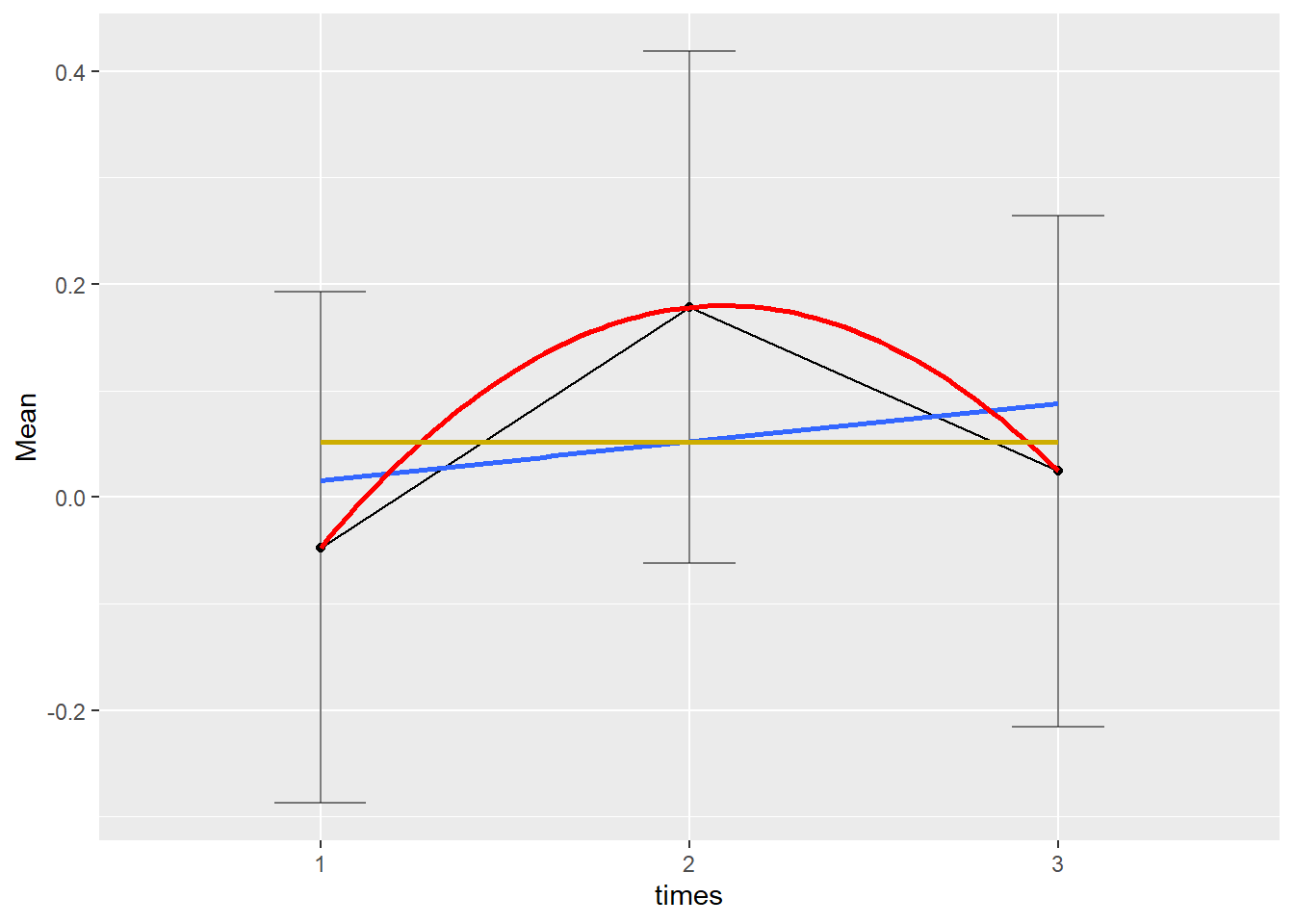
whd_aov <- aov(Y ~ times + Error(id/times), data = data.frame(df))
em <- emmeans(whd_aov, ~ times)
contrast(em, interaction = 'poly')## times_poly estimate SE df t.ratio p.value
## linear -0.635 0.475 84 -1.337 0.1848
## quadratic -0.531 0.823 84 -0.645 0.5205Sowohl der lineare als auch der quadratische Trend sind nicht signifikant! Die gelbe Linie stellt einen horizontalen Verlauf dar, die blaue einen linearen Verlauf und die rote einen quadratischen.
Nun schauen wir uns einen linearen Trend mit Mittelwerten (0, 1, 2) an:
set.seed(123) # für Vergleichbarkeit
Means <- c(0, 1, 2) # wahren Mittelwerte pro Zeitpunkt
Y <- Means[1] + rnorm(30)
Y <- c(Y, Means[2] + rnorm(30))
Y <- c(Y, Means[3] + rnorm(30))
times <- c(rep("1", 30), rep("2", 30), rep("3", 30))
id <- c(1:30, 1:30, 1:30)
df <- data.frame(Y, times, id)
df$times <- as.factor(times)
df$id <- as.factor(df$id)
head(df)## Y times id
## 1 -0.56047565 1 1
## 2 -0.23017749 1 2
## 3 1.55870831 1 3
## 4 0.07050839 1 4
## 5 0.12928774 1 5
## 6 1.71506499 1 6ezPlot(df, Y, id, within = times,
x = times) +
geom_smooth(aes(x = as.numeric(times)), method = 'lm', se = FALSE,
formula = y ~ x) +
geom_smooth(aes(x = as.numeric(times)), method = 'lm', se = FALSE,
formula = y ~ x + I(x^2), color = 'red')+
geom_smooth(aes(x = as.numeric(times)), method = 'lm', se = FALSE,
formula = y ~ 1, color = 'gold3')
whd_aov <- aov(Y ~ times + Error(id/times), data = data.frame(df))
em <- emmeans(whd_aov, ~ times)
contrast(em, interaction = 'poly')## times_poly estimate SE df t.ratio p.value
## linear 1.365 0.475 84 2.872 0.0052
## quadratic -0.531 0.823 84 -0.645 0.5205Diesmal ist nur der lineare Trend signifikant. Die Mittelwerte steigen mit jedem Zeitpunkt um 1 Einheit!
Nun schauen wir uns einen (umgekehrt) U-förmigen Verlauf an mit Mittelwerten: (0, 1, 0):
set.seed(123) # für Vergleichbarkeit
Means <- c(0, 1, 0) # wahren Mittelwerte pro Zeitpunkt
Y <- Means[1] + rnorm(30)
Y <- c(Y, Means[2] + rnorm(30))
Y <- c(Y, Means[3] + rnorm(30))
times <- c(rep("1", 30), rep("2", 30), rep("3", 30))
id <- c(1:30, 1:30, 1:30)
df <- data.frame(Y, times, id)
df$times <- as.factor(times)
df$id <- as.factor(df$id)
head(df)## Y times id
## 1 -0.56047565 1 1
## 2 -0.23017749 1 2
## 3 1.55870831 1 3
## 4 0.07050839 1 4
## 5 0.12928774 1 5
## 6 1.71506499 1 6ezPlot(df, Y, id, within = times,
x = times) +
geom_smooth(aes(x = as.numeric(times)), method = 'lm', se = FALSE,
formula = y ~ x) +
geom_smooth(aes(x = as.numeric(times)), method = 'lm', se = FALSE,
formula = y ~ x + I(x^2), color = 'red')+
geom_smooth(aes(x = as.numeric(times)), method = 'lm', se = FALSE,
formula = y ~ 1, color = 'gold3')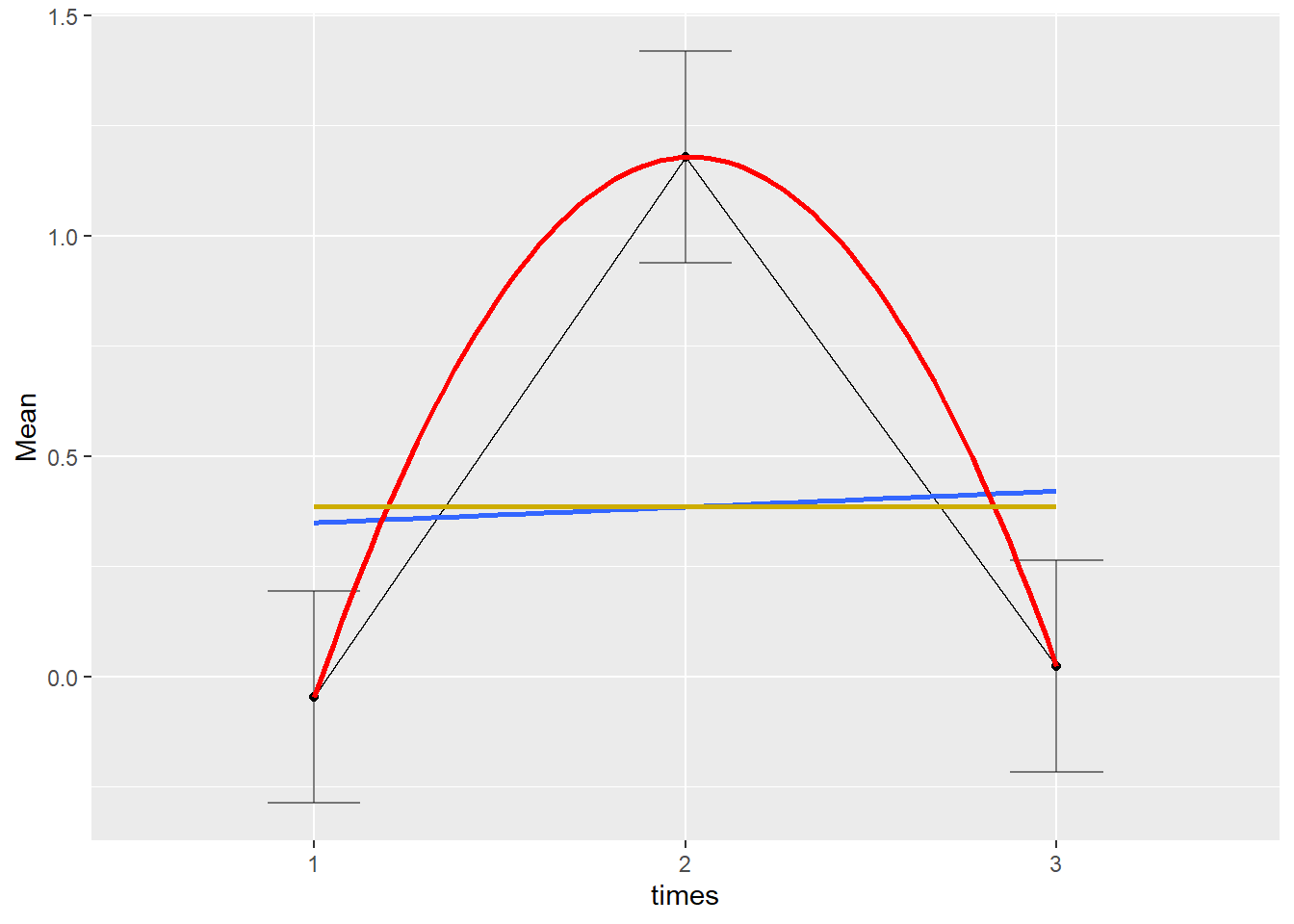
whd_aov <- aov(Y ~ times + Error(id/times), data = data.frame(df))
em <- emmeans(whd_aov, ~ times)
contrast(em, interaction = 'poly')## times_poly estimate SE df t.ratio p.value
## linear -0.635 0.475 84 -1.337 0.1848
## quadratic -2.531 0.823 84 -3.075 0.0028Es ist nur der quadratische Trend signifikant, da wir ja gesehen hatten, dass der Kontrast für den linearen Trend nur die beiden äußeren Mittelwerte gegeneinander testet (\(\mu_1\) vs \(\mu_3\)), welche sich aber nicht unterscheiden und somit auch die blau Gerade horizontal erscheint (sie ist nicht/kaum von der gelben zu unterscheiden)! Schauen wir uns doch einmal einen Verlauf an, in welchem sowohl der lineare als auch de quadratische Trend signifikant ist. Das ist der Fall, wenn die Mittelwerte bspw. “beschleunigt” steigen mit den Zeitpunkten. wir wählen die Mittelwerte als (1, 4, 9), also \(t^2\).
set.seed(1234) # für Vergleichbarkeit
Means <- c(1^2, 2^2, 3^2) # wahren Mittelwerte pro Zeitpunkt
Y <- Means[1] + rnorm(30)
Y <- c(Y, Means[2] + rnorm(30))
Y <- c(Y, Means[3] + rnorm(30))
times <- c(rep("1", 30), rep("2", 30), rep("3", 30))
id <- c(1:30, 1:30, 1:30)
df <- data.frame(Y, times, id)
df$times <- as.factor(times)
df$id <- as.factor(df$id)
head(df)## Y times id
## 1 -0.2070657 1 1
## 2 1.2774292 1 2
## 3 2.0844412 1 3
## 4 -1.3456977 1 4
## 5 1.4291247 1 5
## 6 1.5060559 1 6ezPlot(df, Y, id, within = times,
x = times) +
geom_smooth(aes(x = as.numeric(times)), method = 'lm', se = FALSE,
formula = y ~ x) +
geom_smooth(aes(x = as.numeric(times)), method = 'lm', se = FALSE,
formula = y ~ x + I(x^2), color = 'red')+
geom_smooth(aes(x = as.numeric(times)), method = 'lm', se = FALSE,
formula = y ~ 1, color = 'gold3')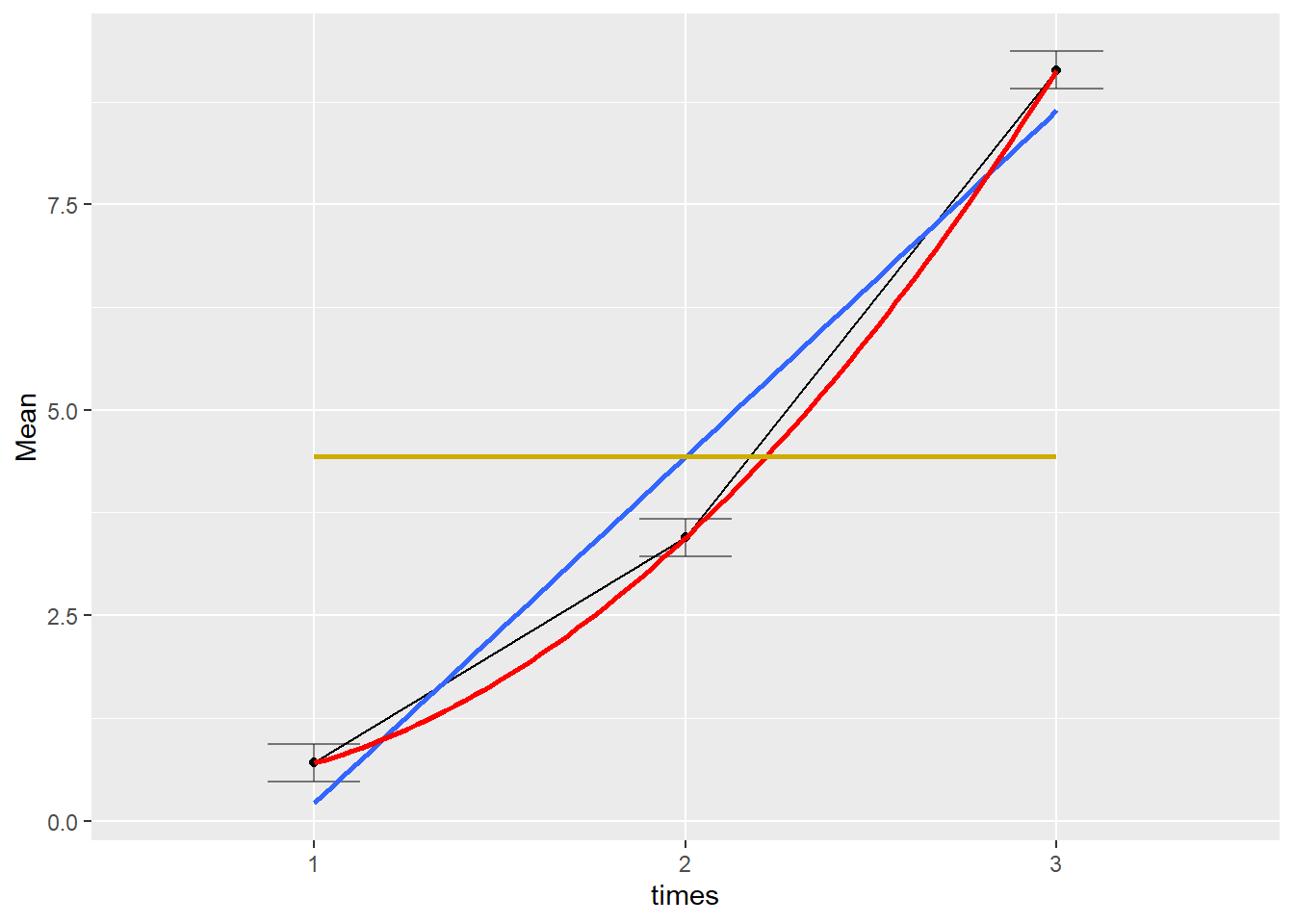
whd_aov <- aov(Y ~ times + Error(id/times), data = data.frame(df))
em <- emmeans(whd_aov, ~ times)
contrast(em, interaction = 'poly')## times_poly estimate SE df t.ratio p.value
## linear 9.04 0.497 84 18.194 <.0001
## quadratic 4.13 0.861 84 4.793 <.0001Wir erkennen, dass sowohl der lineare als auch der quadratische Trend signifikant ist. Die blau Linie passt besser als einen horiziontale und die rote passt besser als die blau Linie! Hier entscheiden wir uns final für den quadratischen Trend!
Literatur
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden (5. korrigierte Auflage, 1. Auflage: 2010). Weinheim: Beltz.
- Blau hinterlegte Autor:innenangaben führen Sie direkt zur universitätsinternen Ressource.
