Konjugierte Prior
Wie man Bayes betreibt, wenn man wirklich Ahnung hat
Im ersten Beitrag hatten wir uns mal angeguckt, wie Bayes im Allgemeinen funktioniert. Auch, wenn das Ganze an einem Beispiel orientiert war, war das ganze Vorgehen dabei eher hands-off. Das ändern wir jetzt: in diesem Beitrag gucken wir uns an, wie man Bayesianische Analysen betreiben kann, wenn man sich ein bisschen mit Verteilungen auskennt. Keine Sorge, über die grundlegenden Konzepte von Verteilungen hinaus, setzt dieser Beitrag nichts voraus - er soll eher dazu dienen, ein bisschen besser zu verstehen, wie, warum und wozu man Bayesianische Schätzung so einsetzt. Wer die Grundkonzepte von Verteilungen nochmal auffrischen möchten, kann z.B. diesen Beitrag mal querlesen (oder auch ganz).
Datenbeispiel
Wir knüpfen wieder beim gleichen Beispiel an, wie im letzten Beitrag. Es geht darum, dass Sie ein neues Ausgangskonzept für Ihre Patient:innen in einer Suchtklinik entwickelt haben. Dieses Konzept haben Sie nun ein paar Wochen getestet und dabei eine erstaunliche Erfolgsquote von 70% verbuchen können. Leider haben Sie das Ganze aber bisher nur mit \(n = 10\) Personen ausprobieren können. Die Daten dazu:
# Beobachtungen
obs <- c(0, 1, 1, 0, 1, 1, 1, 0, 1, 1)
# N
length(obs)## [1] 10# Erfolgsquote
mean(obs)## [1] 0.7Wie wir schon gesehen haben, brachten uns die klassischen Analyseanstäze hier keine statistisch bedeutsamen Ergebnisse und demzufolge auch nur wenig Erkenntnisgewinn.
Die Binomialverteilung
Wenn wir in der Psychologie mit Variablen arbeiten, die nur eine von zwei Ausprägungen annehmen kann, notieren wir sie idealerweise als Dummy-Variable. Für diese Variablen nutzen wir die 0, um die Zugehörigkeit zu einer Gruppe zu notieren (z.B. Personen, bei denen keine depressive Störung vorliegt) und die 1, zum die Zugehörigkeit zur anderen Gruppe festzuhalten (z.B. Personen, die an einer Depression leiden). Dabei gehen wir davon aus, dass eine Person einer und nur einer der beiden Gruppen angehört. In unserem Fall sind die beiden Gruppen Patient:innen die im Ausgang rückfällig geworden sind (obs = 0) und Patient:innen, die nicht rückfällig geworden sind (obs = 1).
Bei jeder Untersuchung versuchen wir dann möglichst voneinander unabhängige Beobachtungen als Stichprobe zu gewinnen. Bei vielen klassischen Tests ist die Unabhängigkeit der Beobachtungen eine Voraussetzung, um adäquate Inferenzstatistik betreiben zu können. Wenn wir eine Dummy-Variable mehrfach in unabhängigen Beobachtungen festhalten, folgt die Anzahl der Beobachtungen der Kategorie 1 der Binomialverteilung. In unserem Fall lässt sich die Verteilung der Anzahl der “Erfolge” (Personen, die im Ausgang nicht rückfällig werden) in einer Stichprobe so beschreiben:
\[ P(X = x | n, \pi) = {n \choose x} \cdot \pi^x \cdot (1 - \pi)^{n-x} \] Dabei ist \(x\) die Anzahl der von uns beobachteten Erfolge, \(n\) die Anzahl der Beobachtungen, die wir insgesamt durchgeführt haben und \(\pi\) die Grundrate in der Population. Eine super detaillierte Darstellung der Binomialverteilung haben wir z.B. in diesem Beitrag aufgeschrieben. Wie wir schon im letzten Bayes-Beitrag besprochen haben, können wir diese Formel einfach nutzen, um die Likelihood zu bestimmen:
\[ L(P = \pi | N = n, X = x) = {n \choose x} \cdot \pi^x \cdot (1 - \pi)^{n-x} \]
In unserem Fall war \(n\) length(obs) also 10. Die Anzahl der Erfolge (einer der vielen Vorteile davon, mit 0 und 1 zu arbeiten und nicht z.B. mit 1 und 2, wenn man zwei Gruppen kodiert) lässt sich einfach über
sum(obs)## [1] 7ermitteln. Welches \(\pi\) die höchste Likelihood hat, hatten wir auch bereits ausprobiert. Dazu können wir zum Beispiel einfach alle möglichen Werte für \(\pi\) in die Gleichung einsetzen:
pi <- c(.2, .5, .7, .9)
L <- choose(10, 7) * pi^7 * (1 - pi)^(10 - 7)
d <- data.frame(pi, L)
d## pi L
## 1 0.2 0.000786432
## 2 0.5 0.117187500
## 3 0.7 0.266827932
## 4 0.9 0.057395628Statt immer die ganze Gleichung aufschreiben zu müssen, können wir natürlich auch die in R integrierte Verteilungsfunktionalität nutzen. Dazu gibt es ein allgemeines Muster, nach dem Verteilungsfunktionen aufgebaut sind. Für die Binomialverteilun können wir also dbinom benutzen, um uns die Dichtefunktion ausgeben zu lassen:
dbinom(7, 10, .2)## [1] 0.000786432Um das Ganze in einer hübschen Abbildung darzustellen, statt eine Tabelle für alle Werte aufstellen zu müssen, hatten wir auch schon hiermit gearbeitet:
likeli_plot <- ggplot(d, aes(x = pi, y = L)) +
xlim(0, 1) +
geom_function(fun = dbinom, args = list(x = 7, size = 10)) +
labs(x = expression(pi), y = 'Likelihood')
likeli_plot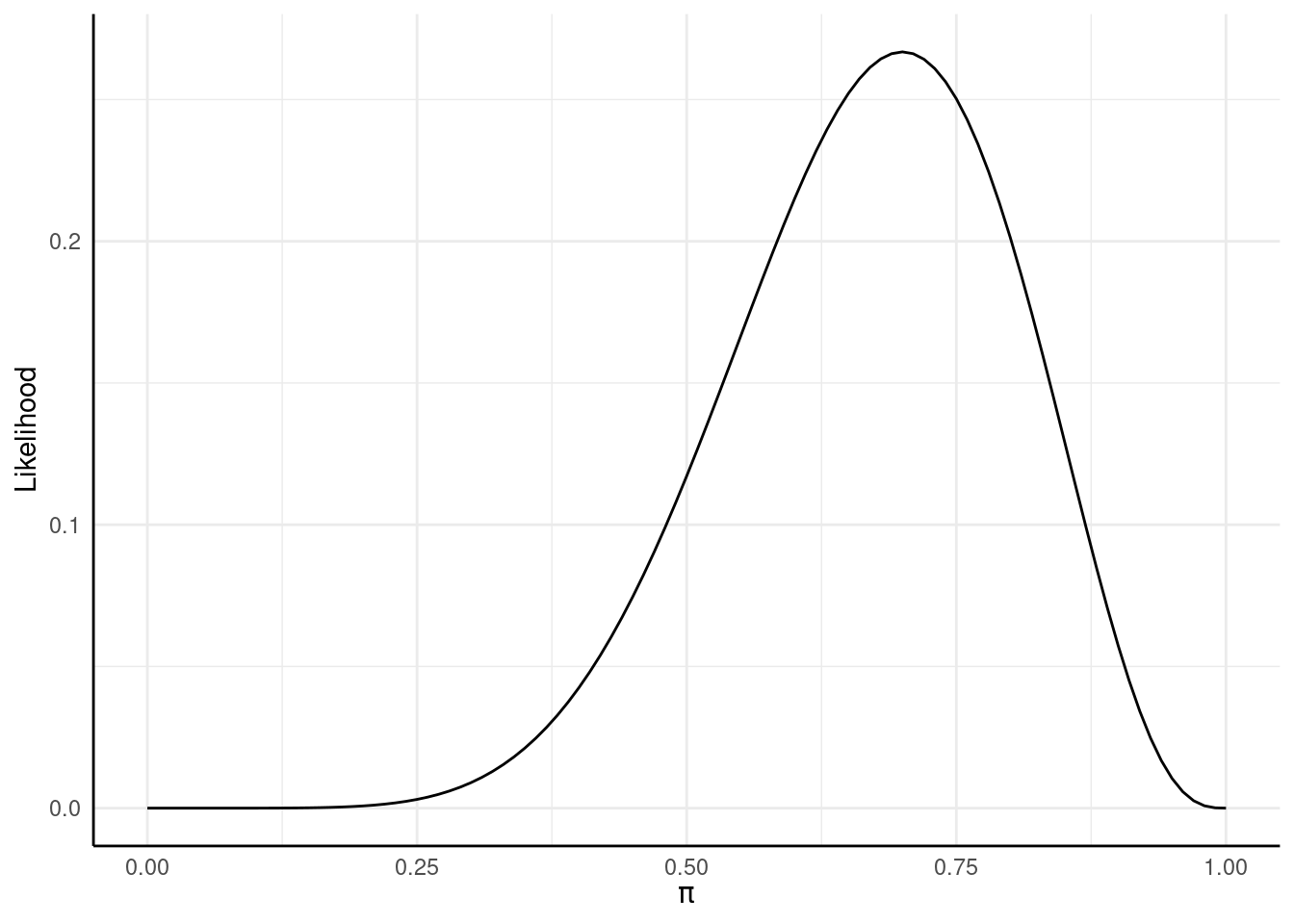
Ein geeigneter Prior für Wahrscheinlichkeiten
Wie wir im Bayes-Intro besprochen haben.
