Grundkonzepte Bayesianischer Analysen
An einem fiktiven klinischen Beispiel mit viel zu kleinem $n$
In vielen Bereichen der Psychologie haben wir ein Problem. Also, eigentlich mehrere, aber eins beschäftigt uns außerordentlich häufig, auch während des Studiums: unsere Studien arbeiten oft mit sehr kleinen Stichproben. Insbesondere in klinischen Untersuchungen liegt das oft einfach daran, dass es sehr aufwendig ist Probanden zu erheben. Wenn wir psychotherapeutische Interventionen untersuchen bedeutet oft jedes einzelne zusätzliche \(n\), dass wir dutzende Stunden Arbeit aufwenden müssen. Auf der anderen Seite steht das Problem, dass wir bei jeder Verringerung des \(n\) unsere Fähigkeit einschränken, aus unserer Stichprobe auch zulässige Rückschlüsse auf die Population ziehen zu können. In diesem Abschnitt wird es - wie der Titel hoffentlich klar gemacht hat - um eine Einführung in Bayes gehen. Wie die beiden Dinge zusammenhängen, sollte idealerweise nach ungefähr der Hälfte dieses Beitrags klar geworden sein. Danach gibt es ein paar technische Spielereien.
Ein einfaches Beispiel
Nehmen wir an, dass Sie in einer Suchtklinik arbeiten - oder vielleicht ein Praktikum machen. Das bisherige System, nach welchem Patient:innen Ausgang außerhalb des Klinikgeländes gewährt wird bezieht sich vor allem auf die Zeit, die die Person schon in der Klinik ist. Als Sie anfangen, finden Sie das System irgendwie suboptimal und Sie denken sich: “Das sollte doch eigentlich vom Therapiefortschritt abhängen…”. Obwohl Sie vielleicht Recht haben, ist auch für die Patient:innen Planbarkeit wichtig: ein Termin beim Bürgeramt, zum Beispiel, muss etliche Wochen vorab vereinbart werden. Also denken Sie sich etwas Neues aus, das alle super glücklich machen sollte. Sie können dieses System aber nicht an 42 Leuten testen (wie Ihre Poweranalyse Ihnen rät), sondern probieren es zunächst mit den zehn Patient:innen, die im Rahmen des Praktikums in Ihre Obhut übergeben wurden.
Ihr neues System führt dazu, dass 7 von 10 Patient:innen aus dem Ausgang zurück kommen ohne Drogen genommen zu haben. Angesichts der Tatsache, dass es bei den Kolleg:innen, die sich an das alte System halten immer knapp die Hälfte ist, verbuchen Sie das als Erfolg. Übertragen wir das Ganze mal in R:
# Beobachtungen
obs <- c(0, 1, 1, 0, 1, 1, 1, 0, 1, 1)
# N
length(obs)## [1] 10# Erfolgsquote
mean(obs)## [1] 0.7Jede 1 stellt eine Person dar, die erfolgreich aus dem Ausgang zurückkam, ohne Drogen genommen zu haben. Jede 0 ein Scheitern, dass Sie an Ihrer Berufswahl zweifeln lässt.
Etwas formaler ausgedrückt: wir wollen jetzt prüfen, ob die Erfolgsquote Ihres Systems sich von der Quote Ihrer Kolleg:innen unterscheidet. Die Nullhypothese ist also, dass wir vermuten, dass auch Ihr System eine Erfolgsquote von 50% produziert: \(H_0: \pi = .5\). \(\pi\) stellt hierbei die Wahrscheinlichkeit des “erfolgreichen” Ausgangs in der Population aller Personen dar, die jemals an diesem System teilnehmen könnten.
Frequentistische Ansätze
Parametrischer Ansatz: \(\chi^2\)-Test
Gucken wir uns zunächst die Möglichkeiten an, zu prüfen, ob Ihr System besser ist als das Ihrer Kolleg:innen. Ein klassischer Ansatz (den Sie hier in Fragestellung C nachlesen können) ist der \(\chi^2\)-Test. In unserem Fall haben wir zwar nicht vier sondern nur zwei Felder, aber das macht das Ganze einfach nur einfacher:
# Häufigkeitstabelle der Erfolge
tab <- table(obs)
# Tabelle in den Chi2-Test
chisq.test(tab)##
## Chi-squared test for given probabilities
##
## data: tab
## X-squared = 1.6, df = 1, p-value = 0.2059Was hier geprüft wird ist die gleichmäßige Besetzung der Zellen. Unter der Nullhypothese \(H_0 : \pi = .5\) müssten wir also fünf Erfolge und fünf Misserfolge beobachten:
chisq.test(tab)$expected## 0 1
## 5 5In diesem Fall erhalten wir ein nicht bedeutsames Ergebnis - wir behalten die Nullhypothese also bei.
Den Aufmerksamen unter Ihnen ist vielleicht aufgefallen, dass der \(\chi^2\)-Test, den wir hier nutzen, mit ein paar Annahmen einhergeht. Das liegt daran, dass wir die Diskrepanz zwischen Erwartung und Beobachtung zu einer Zahl verrechnen und die erzeugte Zahl dann mit einer bekannten Verteilung (der \(\chi^2\)-Verteilung) abgleichen, um festzustellen wie wahrscheinlich unser Ergebnis wäre, wenn die Nullhypothese wahr wäre. Die Übertragung funktioniert nur unter bestimmten Annahmen, vor allem aber funktioniert Sie immer besser, je größer \(n\) ist. Das gilt nicht nur für den \(\chi^2\)-Test, sondern für alle parametrischen Tests - also Tests, die sich darauf verlassen, eine Prüfgröße zu erstellen und diese mit einer bekannten Verteilung abzugleichen.
Diese Tatsache führt dazu, dass insbesondere in klinischen Studien häufig gefordert wird, stattdessen mit Tests zu arbeiten, die sich nicht auf asymptotische Eigenschaften verlassen - sogenannte non-parametrische Tests. Für unser Beispiel gibt es da zum Glück eine recht einfache Möglichkeit!
Wenn Ihre Statistik I Vorlesung noch nicht allzu lange her ist, erinnern Sie sich vielleicht, dass die Anzahl von Erfolgen \(x\) aus \(n\) unabhängigen Versuchen binomialverteilt ist. Das ist, im Gegensatz zu dem was in parametrischen Tests wie z.B. dem \(\chi^2\)-Test vorausgesetzt wird, keine Annahme, sondern einfach eine Realität der Welt in der wir leben. Wir können also mit einer Gleichung direkt bestimmen, wie wahrscheinlich es ist, dass sieben Ihrer zehn Patient:innen aus dem Ausgang zurückkommen ohne rückfällig geworden zu sein, wenn ihr Ausgangsprinzip genauso gut funktioniert, wie das Ihrer Kolleg:innen (\(H_0: \pi = .5\)).
\[ P(X = x | n, \pi) = {n \choose x} \cdot \pi^x \cdot (1 - \pi)^{n-x} \]
Für diesen Fall also:
\[ P(X = 7 | 10, .5) = {10 \choose 7} \cdot .5^7 \cdot (1 - .5)^{10-7} = .117 \]
# Wahrscheinlichkeit händisch bestimmen
choose(10, 7) * .5^7 * (1 - .5)^(10 - 7)## [1] 0.1171875Uns interessiert aber nicht, wie wahrscheinlich es ist, dass Sie genau sieben Erfolge haben. In der Inferenzstatistik interessiert uns typischerweise, wie wahrscheinlich es ist dieses oder ein extremeres (im Fall der ungerichteten Nullhypothese) Ergebnis zu finden. Dafür können wir einfach die Funktion zur Binomialverteilung nutzen:
# Gerichtet
pbinom(6, 10, .5, lower.tail = FALSE)## [1] 0.171875# Ungerichtet
pbinom(6, 10, .5, lower.tail = FALSE) + pbinom(3, 10, .5)## [1] 0.34375Wir setzen hier 6 und nicht 7 in die Funktion ein, weil uns pbinom die Überschreitungswahrscheinlichkeit ausgibt. Wir brauchen also die Wahrscheinlichkeit dafür einen Wert von 6 zu überschreiten (weil wir die 7 ja einschließen wollen). Der Test, den wir gerade durchgeführt haben, nennt man Binomialtest und auch für diesen gibt es eine eigene Funktion in R, die dem gleichen Schema folgt, wie z.B. die t.test-Funktion:
binom.test(7, 10, .5)##
## Exact binomial test
##
## data: 7 and 10
## number of successes = 7, number of trials = 10, p-value = 0.3438
## alternative hypothesis: true probability of success is not equal to 0.5
## 95 percent confidence interval:
## 0.3475471 0.9332605
## sample estimates:
## probability of success
## 0.7Auch hier also keine statistische Bedeutsamkeit.
Power in unseren frequentistischen Möglichkeiten
Wir haben jetzt also zwei Ansätze gesehen die einfache Frage zu prüfen, ob Ihr Ausgangssystem zu anderen Erfolgsquoten führt, als das Ihrer Kolleg:innen. Dabei hatten wir zunächst den klassischen, parametrischen Weg gewählt und einen \(\chi^2\)-Test durchgeführt. Allerdings fällt es uns bei kleinen Stichproben häufig schwer uns auf die asymptotischen Eigenschaften von Tests zu verlassen. Bei anderen parametrischen Tests - wie z.B. \(t\)-Tests oder ANOVAs - kann es bei kleinen Stichproben auch quasi unmöglich werden überhaupt zu prüfen, ob die Annahmen haltbar sind, die diese Verfahren voraussetzen.
Also sind wir auf einen non-parametrischen Test ausgewichen (den Binomialtest). Das Problem dabei ist, dass wir die Power unsere Inferenzstatistik sogar noch verringern. In parametrischen Tests “gewinnen” wir ein wenig Power dadurch, dass wir Annahmen machen. Wenn wir weniger Annahmen machen, brauchen wir mehr Daten, um zur gleichen Sicherheit zu kommen. Mehr zur Poweranalyse in frequentistischen Analysen finden Sie hier.
Neyman-Pearson Nullhypothesentests
In unseren frequentistischen Berechnungen haben wir unsere Analysen stets mit der Betrachtung des \(p\)-Werts abgeschlossen und dabei den einfachen Nullhypothesentest zugrundegelegt. In beiden Fällen ist das Ergebnis (vermutlich wegen geringer Power) nicht statistisch bedeutsam. Die logische Frage, die sich an diesen - deprimierenden - Ausgang unserer Studie anschließt ist: “Was haben wir an Erkenntnis gewonnen?”.
Im klassischen Neyman-Pearson Nullhypothesentest haben wir an dieser Stelle keine belastbare Erkenntnis generiert. Wir behalten unsere Nullhypothese bei, weil wir keinen echten Anlass haben, von dieser Abstand zu nehmen. In der nächsten Untersuchung (die vielleicht die nächste Praktikantin an der gleiche Klinik durchführen wird) werden wir wieder mit der Nullhypothese anfangen, dass Ihr Plan genauso gut ist, wie der Ihrer Kolleg:innen (es wird also wieder \(H_0 : \pi = .5\) getestet werden) und die Ergebnisse der hier untersuchten 10 Patient:innen werden in Vergessenheit geraten.
Um uns noch einmal kurz zu verdeutlichen, warum das ist, gucken wir uns noch einmal an, was ein \(p\)-Wert eigentlich ist. Hervorragende Einleitungen in die Grundidee des klassischen, frequentistischen Testens gibt es viele, sodass wir uns hier nur auf die, für uns in diesem spezifischen Fall relevanten Komponenten beschränken.
Der \(p\)-Wert, den wir erzeugt haben ist die Wahrscheinlichkeit dieses - oder ein extremeres - Ergebnis zu finden, wenn die Nullhypothese wahr wäre. Also, wenn die Grundrate mit der Leute nach Ihrem Schema rückfällig werden, tatsächlich \(\pi = .5\) wäre, könnte es per Zufall passieren, dass sie nur 3 Rückfälle finden, wenn Sie nur 10 Personen untersuchen. Etwas formaler könnte man notieren \(P(X = x|H_0)\): die Wahrscheinlichkeit des empirischen Ergebnisses, gegeben die Nullhypothese. Wenn dieses Ergebnis unwahrscheinlich genug wäre (also \(p < .05\)), hätten wir abgeleitet, dass wir die Nullhypothese verwerfen und uns stattdessen für die Alternativhypothese entscheiden sollten. Das Problem dabei ist, dass wir nichts Neues wissen, wenn \(p > .05\), weil dieses Ergebnis eine Aussage über die Daten, nicht über die Nullyhypothese ist: \(P(X = x|H_0) \neq P(H_0|X = x)\). Darüber hinaus ist \(P(X = x|H_0) \neq 1-P(x|H_1)\) - das Ergebnis ist also auch keine Aussage über die Alternativhypothese.
Ein kurzer Einschub zur klassischen Wissenschaftstheorie
Das klassische Nullhypothesentesten ist konzeptuell sehr nah an Karl Poppers naivem Falsifikationismus. Dieses Konzept haben Sie im Verlauf des Studiums bestimmt schon etliche Male gehört: wir haben eine Theorie, leiten aus dieser eine Hypothese (hier die \(H_0\)) ab und prüfen diese. Wenn wir die Hypothese verwerfen, verwerfen wir die generierende Theorie. Wenn wir die Hypothese nicht verwerfen (korroborieren), behalten wir die Theorie bei, generieren eine neue Hypothese und bleiben in dieser Schleife, bis wir die Theorie irgendwann verwerfen werden. Das Neyman-Pearson Nullhypothesentesten (mit \(H_0\) und \(H_1\)) ist konzeptuell eng mit Poppers raffiniertem Falsifikationismus verwandt, in dem Theorien unter Konkurrenzdruck stehen und wir uns beim Test einer Hypothese dann zwischen Theorien entscheiden können.
In den 60er und 70er Jahren wurde diese Ansicht des wissenschaftlichen Erkenntnisgewinns stark kritisiert. Vor allem Thomas Kuhn und Imre Lakatos (aber auch Popper selbst) integrierten in wissenschaftstheoretische Konzept, dass wissenschaftlicher Fortschritt durch schrittweise Anpassung von Theorien, das einpflegen neuer Erkenntnisse und die subjektiven Ansichten von Forscher:innen hinsichtlich der Nützlichkeit von Theorien geleitet wird. Nur in äußerst seltenen Fällen wird eine Theorie in Gänze über Bord geworfen, wenn eine aus ihr abgeleitete Hypothese falsifiziert wird. Viel häufiger kommt es vor, dass neue (empirische) Erkenntnisse genutzt werden, um unsere Theorien zu verfeinern. Leider wird dieses Vorgehen in unserer Art Hypothesen zu prüfen nicht direkt reflektiert. Stattdessen entscheiden wir bei jeder Studie erneut über die Ablehnung der Nullhypothese und schreiten nur dann mit unserem Wissen voran, wenn dies erfolgreich ist.
Wenn Sie eine etwas detaillierte Betrachtung des Nullhypothesentestens und bayesianischer Alternativen aus wissenschaftstheoretischer Sicht interessiert, ist das Buch von Dienes (2008) sehr empfehlenswert.
Likelihood
Leider bekommen wir von unseren Tests also eine Aussage über Daten, gegeben der Hypothesen und keine Aussagen über unsere Hypothesen. Naiv verstehen wir aber meistens die Daten als “fix” und unsere Hypothesen als das, was mit Unsicherheit behaftet ist. Also interessiert uns eher wie wahrscheinlich unsere Hypothese ist, gegeben der Daten - \(P(H|X = x)\).
Gucken wir uns noch einmal den Binomialtest an, den wir durchgeführt haben, um zu bestimmen wie wahrscheinlich es ist sieben “Erfolge” zu verbuchen, wenn wir zehn Patient:innen in den Ausgang schicken:
\[
P(X = x | n, \pi) = {n \choose x} \cdot \pi^x \cdot (1 - \pi)^{n-x}
\]
In R dann für unseren spezifischen Fall:
choose(10, 7) * .5^7 * (1 - .5)^(10 - 7)## [1] 0.1171875Wenn die Grundrate in der Population also \(\pi = .5\) wäre, bestünde eine Wahrscheinlichkeit von 0.117, dass wir in unserem Fall sieben Erfolge verbuchen. Aber ist dieses \(\pi\) eine gute Erklärung, bzw. eine gute Annahme, gegeben unserer Daten? Dafür könnten wir mit roher Gewalt einfach alle möglichen Werte von \(\pi\) ausprobieren, um zu sehen, unter welcher Grundrate das Ergebnis am wahrscheinlichsten ist:
pi <- c(.5, .6, .7, .8, .9, 1)
L <- choose(10, 7) * pi^7 * (1 - pi)^(10 - 7)
d <- data.frame(pi, L)
d## pi L
## 1 0.5 0.11718750
## 2 0.6 0.21499085
## 3 0.7 0.26682793
## 4 0.8 0.20132659
## 5 0.9 0.05739563
## 6 1.0 0.00000000Wir haben den Prozess also umgedreht: statt \(\pi\) als gegeben anzunehmen, haben wir die Daten (\(n\) und \(x\)) festgesetzt und dann die Annahmen variiert. Ich habe das Ergebnis davon oben schon mit L bezeichnet, weil es statistisch als Likelihood bezeichnet wird:
\[ L(\pi = .5 | n = 10, X = 7) = {10 \choose 7} \cdot .5^7 \cdot (1 - .5)^{10-7} = .117 \] Wenig überraschend ist, dass \(\pi = .7\) in diesem fall die höchste Likelihood erreicht - schließlich ist .7 auch die von uns in diesem Fall beobachtete relative Häufigkeit. Wenn wir zwei Grundraten vergleichen wollen, können wir einfach deren Verhältnis - die sogenannte Likelihood Ratio - bestimmen:
L_H0 <- dbinom(7, 10, .5)
L_H1 <- dbinom(7, 10, .7)
L_H1/L_H0## [1] 2.276932Eine Grundrate von .7 ist - gegeben der von uns beobachteten Daten - also 2.28-mal so likely wie eine Grundrate von .5. Der Begriff Likelihood Ratio ist Ihnen bestimmt schon einmal begegnet: genau das gleiche Prinzip nutzen wir, um verschiedene Modelle z.B. in hierarchischer Regression oder Faktorenanalyse zu vergleichen. In unserem Fall hier sind die “Modelle” nur sehr simpel: in einem ist die Grundrate .5 in dem anderen ist sie .7.
In der R-Syntax benutze ich hier jetzt dbinom statt die komplette Binomialverteilung händisch aufzuschreiben - es passiert aber genaus das Gleiche. Wir können die Dichteverteilung sogar nutzen, um uns anzugucken, wie die Likelihood so über verschiedene Werte von \(\pi\) aussieht:
likeli_plot <- ggplot(d, aes(x = pi, y = L)) +
xlim(0, 1) +
geom_function(fun = dbinom, args = list(x = 7, size = 10)) +
labs(x = expression(pi), y = 'Likelihood')
likeli_plot + geom_vline(xintercept = .5, lty = 2) +
annotate('text', x = .48, y = .02, label = 'H[0]', parse = TRUE) +
geom_vline(xintercept = .7, lty = 2) +
annotate('text', x = .68, y = .02, label = 'H[1]', parse = TRUE)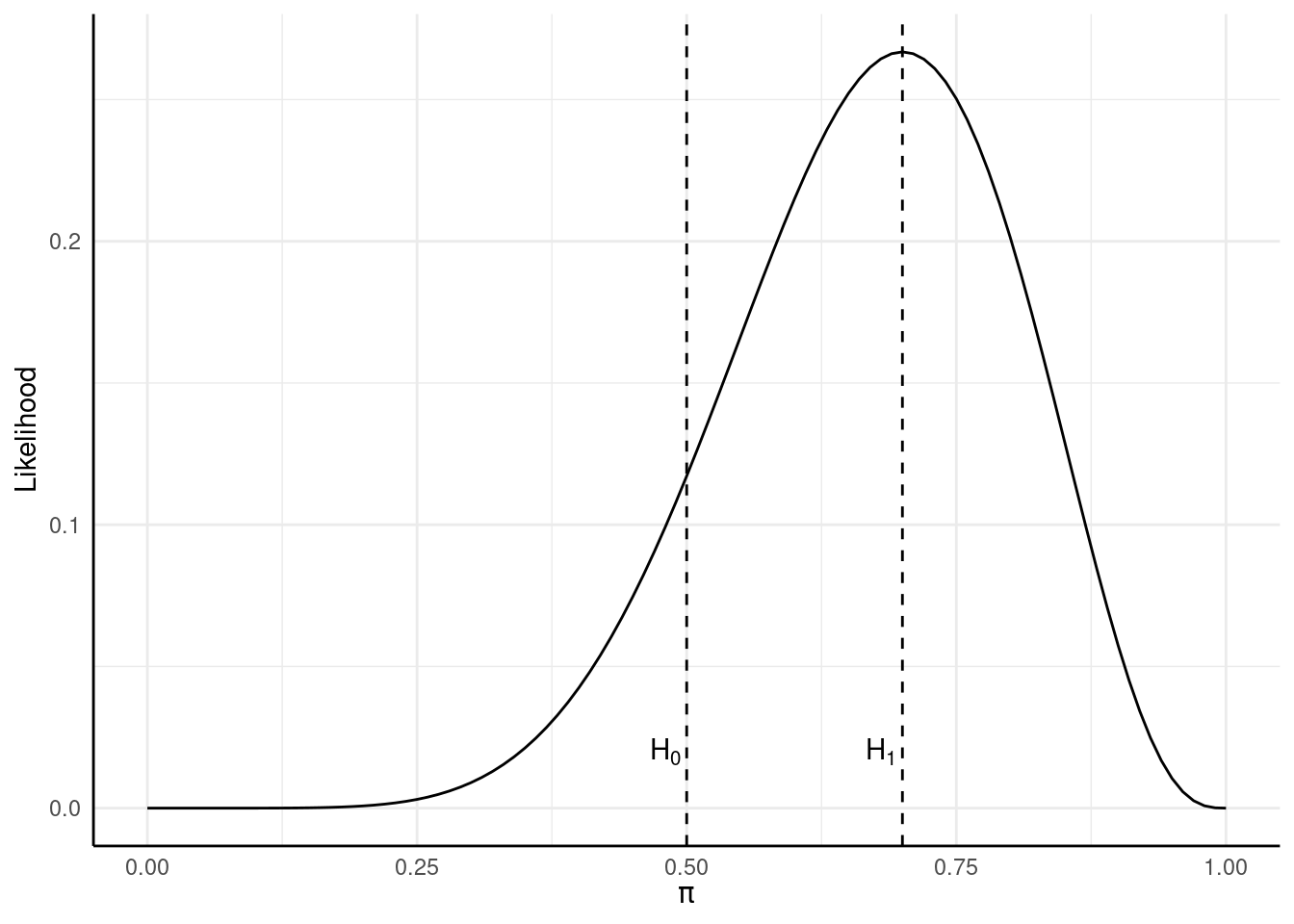
Basic Bayes
Für einen Beitrag, der eigentlich “Grundideen Bayesianischer Analysen” betitelt ist, war das ganz schön viel Vorgeplänkel bis ich jetzt endlich bei Bayes angekommen bin. Aber all das war nötig, um ein Verständnis von dem zu bekommen, was jetzt passiert (vermute ich… mir ging es zumindest so).
Die Grundidee der Bayesianischen Analysen lässt sich eigentlich in folgender Gleichung zusammenfassen:
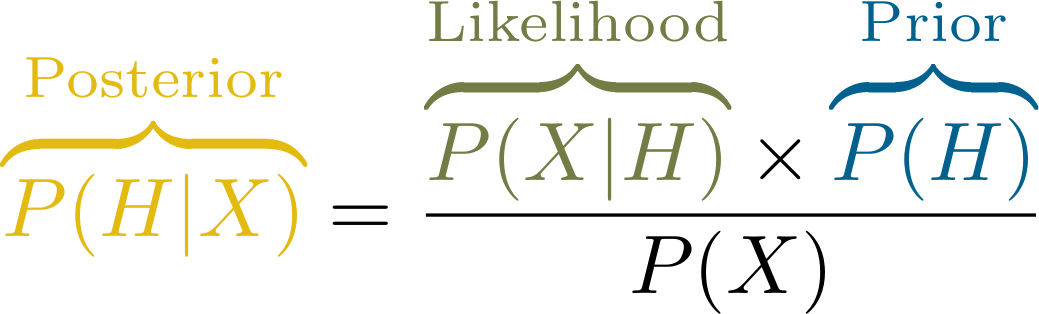 Auf der linken Seite steht also die uns eigentlich interessierende Aussage - wie wahrscheinlich ist unsere Hypothese \(H\), wenn wir unsere Daten \(X\) berücksichtigen? Diese Information wird Posterior genannt - weil es unseren Wissensstand nach der Studie darstellt.
Auf der linken Seite steht also die uns eigentlich interessierende Aussage - wie wahrscheinlich ist unsere Hypothese \(H\), wenn wir unsere Daten \(X\) berücksichtigen? Diese Information wird Posterior genannt - weil es unseren Wissensstand nach der Studie darstellt.
Das Gegenstück ist die Wahrscheinlichkeit, die Daten \(X\) zu beobachten, wenn die Theorie \(H\) wahr wäre. Dies entspricht - wie gerade im Detail gesehen - der Likelihood \(L(H|X)\). Die Inferenzstatistik, die wir in den klassischen Varianten oben betrieben haben, betrachtet ausschließlich die Daten - wir nehmen an, dass wir keinerlei Vorwissen über unsere Hypothesen und deren Beziehung zu den Daten haben. Jedes Mal, wenn wir unseren Arbeitsalltag damit erschweren, dass wir irgendwie wieder zehn Personen erheben, um festzustellen, ob Ihr Ausgangsplan besser ist als die altmodischen Varianten, tun wir so, als ob es das allererste Mal wäre, dass wir auf diese Idee kommen. Und wir tun so, als hätten wir niemals zuvor Ergebnisse zu diesem Thema gesehen. Etwas vereinfacht ausgedrückt, basiert unsere Entscheidung ausschließlich auf der Likelihood bzw. dem \(p\)-Wert, den wir erzeugen können \(P(X | H)\).
Warum dann überhaupt so Forschung betreiben und diese klassischen \(p\)-Werte betrachten? Der immense Vorteil dieses Abschnitts der Gleichung ist, dass er direkt aus den Daten gewonnen werden kann. Er ist also quasi objektiv bestimmbar. Um aber eine bedingte Wahrscheinlich drehen zu können brauchen wir - nach Satz von Bayes - die Grundwahrscheinlichkeit der Hypothesen: Wir brauchen also irgendeine Annahme darüber wie wahrscheinlich unsere Hypothesen wahr sind. Diese Vorannahme wird Prior genannt: die Informationen, die wir vor unserer Erhebung kennen (z.B. als unseren vorherigen, gescheiterten \(n=10\) Studien).
Als letzte Information benötigen wir noch die Wahrscheinlichkeit der Daten, die wir gefunden haben. Diese Wahrscheinlichkeit kann sehr schwierig zu bestimmen sein und hat letztlich nur einen konkreten Zweck: sie relativiert das Produkt aus Likelihood und Prior so, dass wir am Ende auch wirklich eine Wahrscheinlichkeit (also einen Wert zwischen 0 und 1) erhalten. Deswegen wird die Grundformel Bayesianischer Statistik häufig von dieser Komponente befreit und so notiert:
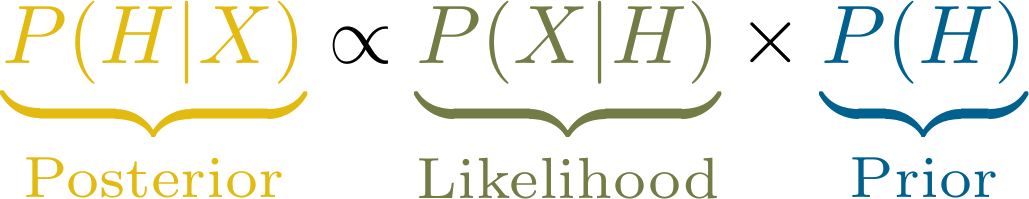
Der Posterior ist also propotional zu der Mischung aus Prior (unseren Vorannahmen) und den, in dieser Studie neu gewonnenen Daten. Wir “updaten” unsere Annahmen bzw. Theorien also anhand der Daten (die wir in Form der Likelihood berücksichtigen).
Uninformative Prior
Wenn das Vorwissen, das wir über den Gegenstand unserer Untersuchung haben quasi Null ist, können wir Prior setzen, die keine Information enthalten. In solchen Fällen sollen alle Möglichkeiten (also in unserem Fall alle Werte der Grundrate \(\pi\)) gleich wahrscheinlich sein - dass immer alle Personen rückfällig werden ist genauso wahrscheinlich, wie der totale Erfolg des Programms und alles dazwischen.
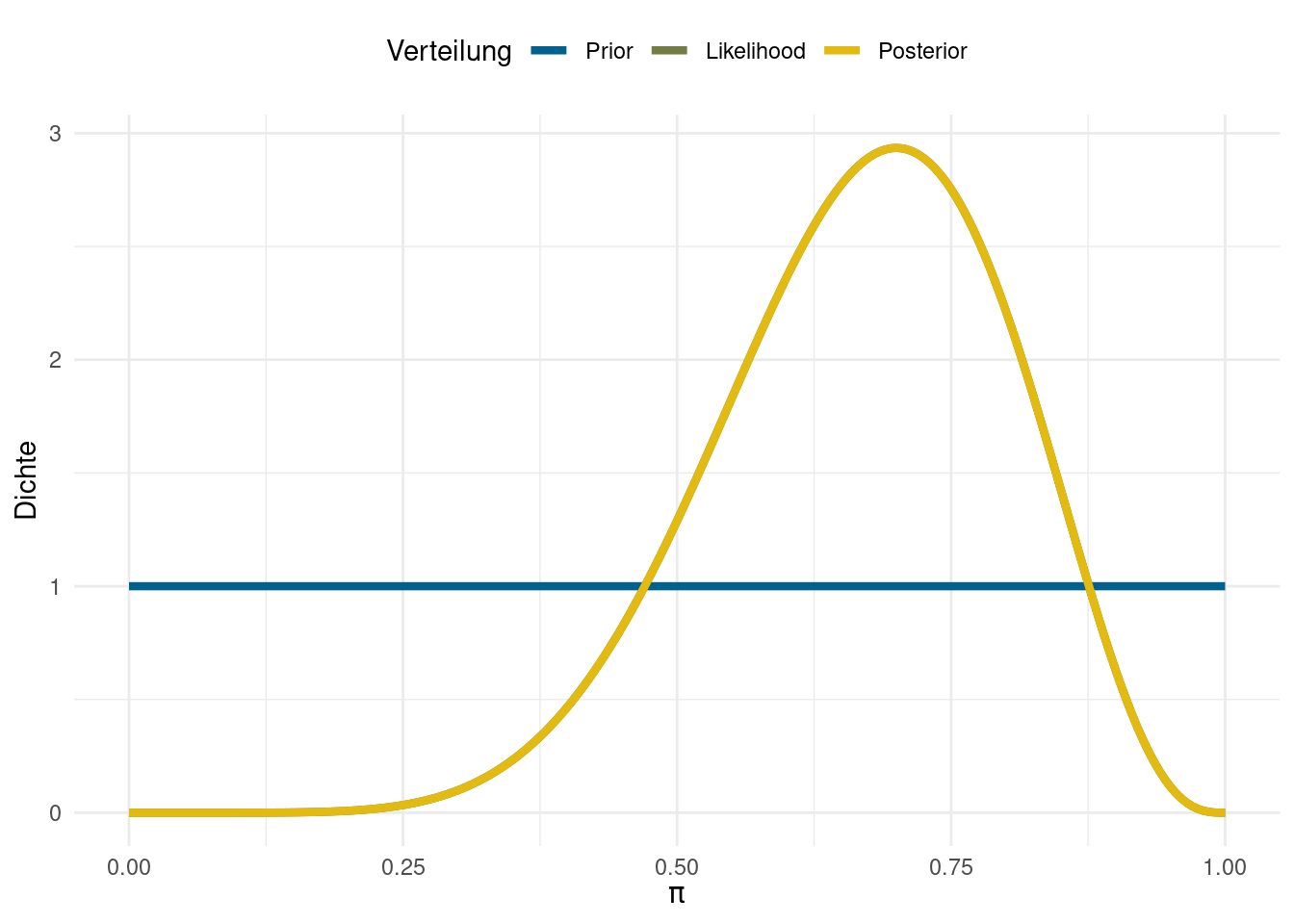
Sie fragen Sich vielleicht, warum Sie nur zwei Linien sehen, wenn wir doch drei Komponenten (Prior, Likelihood und Posterior) haben. Das liegt daran, dass unser Prior keinerlei Information beinhält - jedes \(\pi\) ist gleich wahrscheinlich. Also wird die Likelihood für jeden Ausprägung von \(\pi\) mit dem gleichen Wert multipliziert, sodass dieser Teil in der Gleichung einfach irrelevant wird. So geht unser Posterior also ausschließlich auf unsere Daten zurück und entspricht genau der Likelihood-Verteilung.
Schwache Prior
Jetzt haben wir also einen sehr umständlichen Weg besprochen, exakt das Gleiche zu bekommen, wie vorher auch. Interessant wird das Ganze erst, wenn man über Prior Informationen in das System hineingibt, die Vorinformationen darstellen. Zum Beispiel könnten wir davon ausgehen, dass die Extreme unwahrscheinlicher Sind, als Werte in der Mitte - z.B. weil wir von unseren Kolleg:innen wissen, dass es keine Ausgangskonzepte gibt, die bewirken, dass niemand rückfällig wird oder alle rückfällig werden.
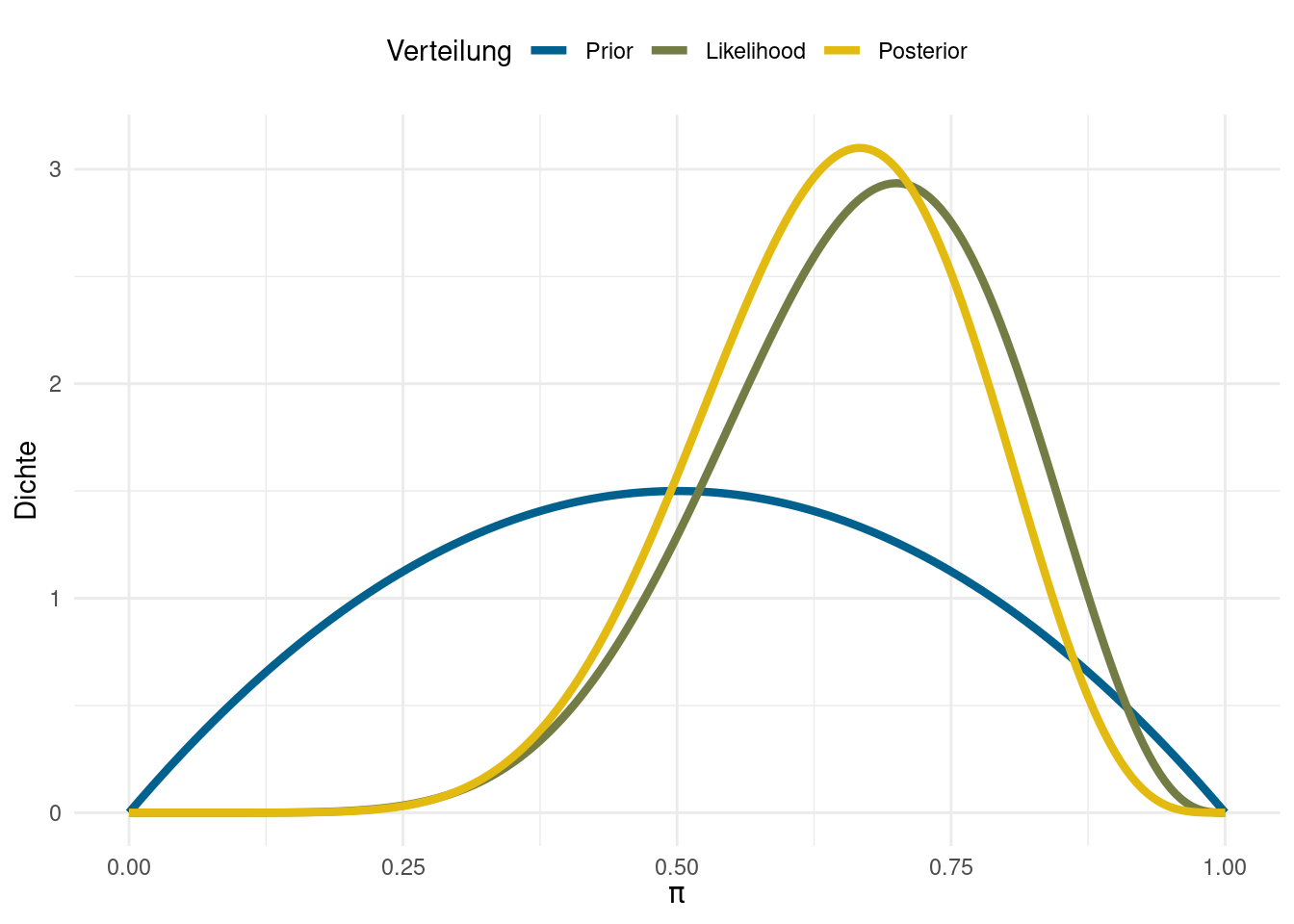
Wenn wir dermaßen schwache Annahmen in unsere Analysen einbauen, weicht die Posterior Verteilung nur leicht von unserer Likelihood Verteilung ab. Weil wir als Vorannahme hatten, dass \(\pi = .5\) der wahrscheinlichste Wert ist, ist die ermittelte Grundrate in der Population auch im Posterior nicht mehr die beobachtete relative Häufigkeit von .7.
Starke Prior
Noch deutlicher wird dieser Effekt, wenn wir z.B. Informationen aus vorherigen Untersuchungen zum gleichen System einspeisen, dass Sie jetzt untersuchen wollen. Vielleicht stehen Sie im Kontakt zu anderen Kliniken, an denen schon mal ähnliche System erprobt wurden - immer wieder mit sehr kleinen Stichproben. All diese Informationen wollen Sie aber berücksichtigen, weil Ihre Studie mit \(n=10\) nicht die einzige Quelle der Weisheit ist. Wenn es stichhaltige Informationen aus anderen Studien gibt, können wir diese als starke Prior einbauen:
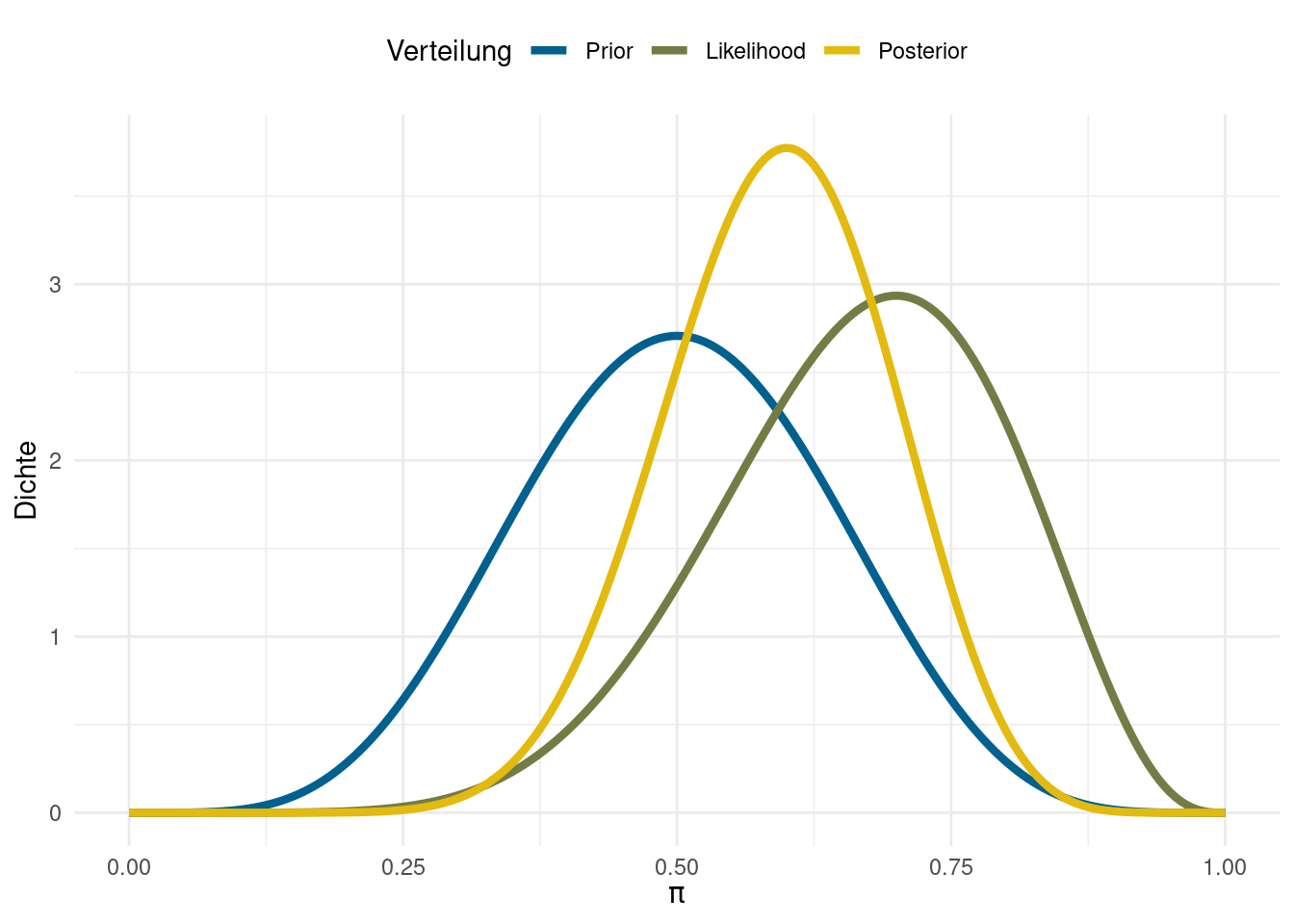 In diesem Fall stellt der Posterior wirklich eine Mischung aus Ihren vorherigen Kenntnissen und den Informationen aus Ihrer eigenen Datenerhebung dar. Aus vorherigen Studien hatten Sie abgeleitet, dass die Erfolgsquote dieses Ausgangssystems (wie bei allen Anderen) bei ungefähr \(\pi = .5\) liegen sollte. Nachdem Sie das Ganze mit zehn Personen ausprobiert haben und dabei festgestellt haben, dass sieben von denen nicht rückfällig geworden sind, erscheint es Ihnen eher naheliegend, dass der “wahre” Effekt vermutlich irgendwo dazwischen liegt.
In diesem Fall stellt der Posterior wirklich eine Mischung aus Ihren vorherigen Kenntnissen und den Informationen aus Ihrer eigenen Datenerhebung dar. Aus vorherigen Studien hatten Sie abgeleitet, dass die Erfolgsquote dieses Ausgangssystems (wie bei allen Anderen) bei ungefähr \(\pi = .5\) liegen sollte. Nachdem Sie das Ganze mit zehn Personen ausprobiert haben und dabei festgestellt haben, dass sieben von denen nicht rückfällig geworden sind, erscheint es Ihnen eher naheliegend, dass der “wahre” Effekt vermutlich irgendwo dazwischen liegt.
In weiteren Studien - z.B. wenn Sie den Standort wechseln oder einer Freundin in einer anderen Klinik empfehlen, das gleiche System mal auszuprobieren - können Sie diesen Posterior wiederum als Prior nutzen. So entsteht auch in der statistischen Auswertung kumulativer Erkenntnisgewinn.
Wie genau diese Posterior-Verteilungen zustandekommen werden wir uns im nächsten Bayes-Beitrag noch genauer angucken. Das wird dann ein Beitrag mit ein paar mehr tatsächlien Umsetzungen in R … versprochen.
Inferenzstatistische Schlüsse mit Bayes
Im letzten Abschnitt hat in allen drei Variante eins gefehlt: eine eindeutige Enstscheidung, ob Ihr Ausgangssystem jetzt besser ist, als das Ihrer Kolleg:innen. Was Ihnen in solchen Analysen eher sehr selten begegnen wird sind \(p\)-Werte. Diese haben die spezifische Bedeutung, die wir oben schon besprochen haben und sind deswegen in Bayesianischer Analyse eher fehl am Platz. Stattdessen wird in diesen Analysen vor allem mit zwei Mitteln gearbeitet: dem Credible Interval und dem Bayes Factor.
Credible Interval
In frequentistischer Statistik können wir Konfidenzintervalle um unsere Punktschätzer generieren, die von Parameter, Standardfehler und der angestrebten Sicherheit abhängen. Z.B. hatten wir oben im Binomialtest von R folgendes Konfidenzintervall ausgegeben bekommen:
binom.test(7, 10, .5)##
## Exact binomial test
##
## data: 7 and 10
## number of successes = 7, number of trials = 10, p-value = 0.3438
## alternative hypothesis: true probability of success is not equal to 0.5
## 95 percent confidence interval:
## 0.3475471 0.9332605
## sample estimates:
## probability of success
## 0.7Wenn wir unsere Studie unendlich häufig unter diesen Bedingungen durchführen würden, würde dieses Intervall in 95% aller Fälle den “wahren Wert” Ihres Ausgangssystems enthalten. Wenn wir uns nochmal die Likelihoodverteilung vor Augen führen, können wir an dieser erkennen, dass wir dabei einfach die extremen 5% der Verteilung abtrennen und die mittleren 95% betrachten:
ki <- binom.test(7, 10, .5)$conf.int
likeli_plot +
geom_vline(xintercept = ki[1], lty = 3) +
geom_vline(xintercept = ki[2], lty = 3)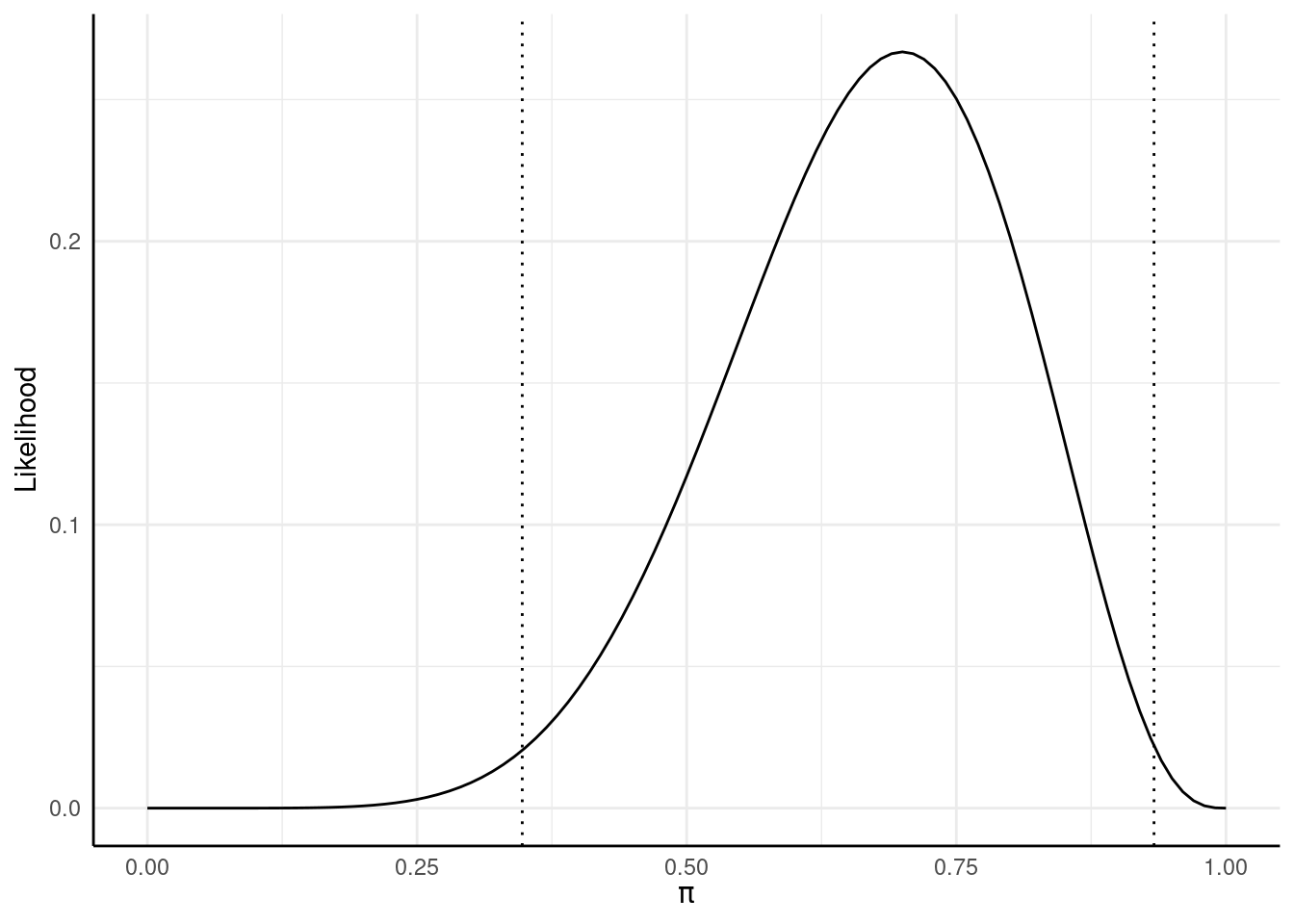
Mit unserer Bayes-Analyse können wir etwas Ahnliches bestimmen, das Credible Interval. Dieses Intervall entspricht dem Intervall in das der unbeobachtete Wert in der Population mit z.B. 95%iger Wahrscheinlichkeit fällt. Dieses Intervall bestimmen wir naheliegenderweise nicht aus der Likelihood-Verteilung, sondern aus unserer Posterior-Verteilung. Für diese interessieren uns dann ebenfalls die mittleren 95%. Für den Fall mit uninformativen Priors, ist das Credible Interval numerisch identisch zum Konfidenzintervall, das wir anhand des Binomial-Tests erzeugt haben. Am Beispiel mit starken Priors sieht das Intervall hingegen so aus:
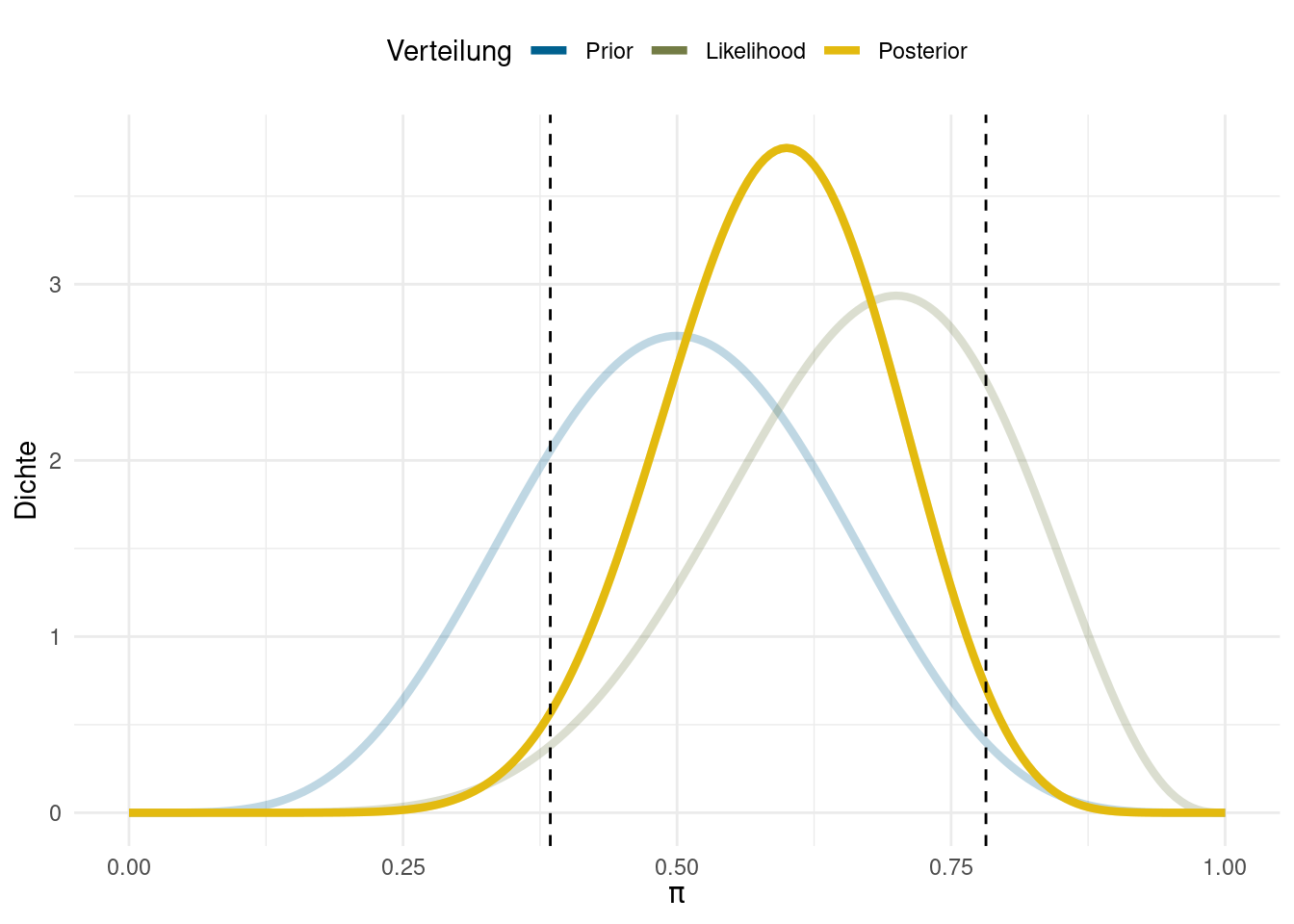
Das 95%-Credible Interval ist in diesem Fall \([0.38; 0.78]\). Wie diese Werte genau entstehen, bzw. wie wir sie mit R ermitteln können besprechen wir im zweiten Bayes-Beitrag, hier geht es erst einmal um das Prinzip: Credible Intervals sind die mittleren z.B. 95% der Posterior Verteilung.
Bayes-Factor
Der Bayes-Factor ist eine Kennzahl, die uns einen etwas direkteren Einblick in das Verhältnis zweier konkurrierender Theorien bzw. Hypothesen gibt. Dabei ist sie - anders als klassische \(p\)-Werte - auch in der Lage, das Ausmaß darzustellen, in dem unsere Daten für die Nullhypothese sprechen. Im Wesentlichen gibt es dabei zwei Wege, auf denen ein Bayes-Factor berechnet werden kann.
Der erste Weg ist es, zu vergleichen wie wahrscheinlich die Daten sind, wenn man zwei unterschiedliche Theorien annimmt. Letztlich nutzen wir also die Likelihood-Ratio: \(\frac{P(D | H_1)}{P(D|H_0)} = \frac{L(H_1|D)}{L(H_0|D)}\), was zeigt wie eng dieses Konzept mit dem Likelihood-Ratio-Test verwandt ist, mit dem wir z.B. in der Faktorenanalyse konkurrierende Modelle vergleichen. Letztlich ist dieses Verhältnis die Aussage darüber, wie viel wahrscheinlicher unserer Daten aufgrund des einen Modells (hier \(H_1\)) als aufgrund eines anderen Modells (hier \(H_0\)) sind.
Der Zweite Weg ist der Vergleich der beiden anderen Terme unserer generellen Gleichung. Dabei können wir die Prior Odds \(\frac{P(H_1)}{P(H_0)}\) bestimmen: das Wahrscheinlichkeitsverhältnis unserer beiden Modelle bevor sie mit Daten konfrontieren. Die andere Komponente \(\frac{P(H_1|D)}{P(H_0|D)}\) wird als Posterior Odds bezeichnet: das Wahrscheinlichkeitsverhältnis unserer beiden Modelle nachdem wir sie mit Daten konfrontiert haben. Das Verhältnis zwischen den beiden \(\frac{\text{Posterior Odds}}{\text{Prior Odds}}\) zeigt dann an, um welchen Faktor unser Modell \(H_1\) im Verhätlnis zum Modell \(H_0\) durch die Daten Wahrscheinlicher geworden ist.
Falls Sie sich wundern: beide Wege sind komplett identisch - der erste Weg bietet sich lediglich als einfachere Konzeptualisierung an, wenn wir ganze Modelle vergleichen, der zweite Weg dann, wenn wir spezifische Punkt- (ungerichtete) oder Flächenhypothesen (gerichtete) vergleichen.
In unserem einfachen Beispiel gab es zunächst nicht direkt zwei “konkurrierende Modelle” - diesen Fall des Bayes-Factors werden wir im Beitrag zur Regression mit Bayes genauer beleuchten. Wir gucken uns hier also erst einmal nur den Vergleich einer Punkt-Hypothese an. Nehmen wir den Fall mit starkem Prior. Dort hatten wir angenommen, dass der Wert von \(\pi = .5\) für neues Ausgangskonzept am wahrscheinlichsten ist: für \(\pi = .5\) ist die Dichte der Prior-Verteilung 2.71. Wenn wir von dieser Punkt-Hypothese ausgehen (dass Ihr neues Ausgangskonzept genauso gut funktioniert, wie das aller Anderen, also \(\pi = .5\)), können wir die Dichte des Wertes in der Prior-Verteilung mit der Dichte des Wertes in der Posterior-Verteilung vergleichen. Dieses Verhältnis wir Savage-Dickey Density Ratio genannt und ist für einzelne Werte in Bayes-Analysen eine relativ simple Approximation des Bayes-Factors. In unserem Bespiel sieht man direkt, dass Posterior und Prior bei \(\pi = .5\) fast die gleiche Dichte haben. Im Posterior ist diese 2.52. Der Bayes-Factor von \(\pi = .5\) ist hier also \(\frac{2.71}{2.52} = 0.93\). Die Annahme, dass die Grundrate Ihres Ausgangskonzepts sich von .5 unterscheidet ist nach der durchgeführten Untersuchung also nur minimal weniger Wahrscheinlich wahr, als sie es vor der Untersuchung war.
Dieser Vergleich lässt sich für jeden beliebigen Wert von \(\pi\) durchführen. Die Annahme, dass Ihr Ausgangskonzept eine Erfolgsquote von .3 hat, ist beispielsweise nach der Untersuchung nur \(\frac{1.13}{0.08} = 0.07\)-mal so wahrscheinlich annehmnbar, wie vor der Untersuchung. Dadurch, dass wir das für jeden einzelnen Wert machen können, können wir es auch für ganze Regionen von Werten machen. Z.B. könnten wir prüfen, wie viel sicherer wir uns nun sein können, dass Ihr Ausgangskonzept eine Erfolgsquote von über \(\pi = .5\) hat. Dafür vergleichen wir die beiden eingfärbten Regionen unseres Priors und unseres Posteriors:
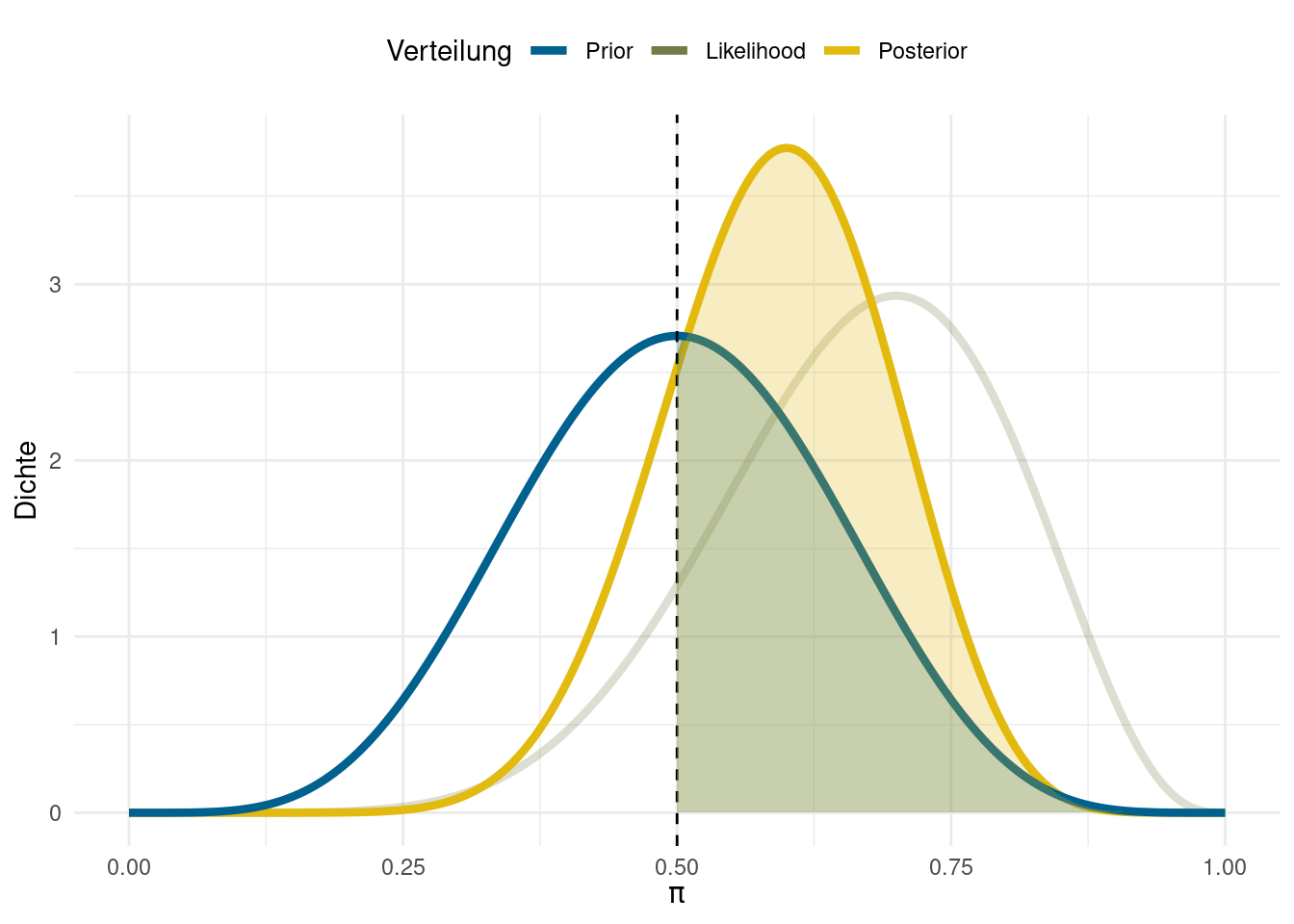 Die Fläche unter den beiden Verteilungen können wir durch Integrale (yay!) bestimmen. In diesem Fall ergibt sich ein Bayes-Factor von \(\frac{0.808}{0.5} = 1.617\). Es ist also 1.617-mal so wahrscheinlich, dass Ihr neues Ausgangsschema eine bessere Erfolgsquote hat, als die Ihrer Kolleg:innen (\(\pi > .5\)) als es ist, dass Ihr Schema genausogut oder schlechter (\(\pi \leq .5\)) ist.
Die Fläche unter den beiden Verteilungen können wir durch Integrale (yay!) bestimmen. In diesem Fall ergibt sich ein Bayes-Factor von \(\frac{0.808}{0.5} = 1.617\). Es ist also 1.617-mal so wahrscheinlich, dass Ihr neues Ausgangsschema eine bessere Erfolgsquote hat, als die Ihrer Kolleg:innen (\(\pi > .5\)) als es ist, dass Ihr Schema genausogut oder schlechter (\(\pi \leq .5\)) ist.
Der Bayes-Factor ist eine Aussage über die relative Evidenz für eine Hypothese gegenüber einer anderen. Weil viele Menschen etwas dagegen haben, Werte auch interpretieren zu müssen, hat sich für den Bayes-Factor die Daumenregel eingebürgert, dass ein Wert \(1/3 < BF < 3\) als schwache oder anekdotische Evidenz gewertet werden sollte. Ein \(BF < 1/3\) stellt hingegen eine Unterstützung der “Nullhypothese” (in unserem Fall, dass Ihr Ausgangsystem schlechter als das Ihrer Kolleg:innen ist) dar. Umgekehrt heißt es, dass ein \(BF > 3\) Unterstützung für “Alternativhypothese” anzeigt (in unserem Fall also, dass Ihr System besser ist, als dass Ihrer Kolleg:innen). Wie Sie sehen, kann ein Bayes-Factor also auch dafür genutzt werden eine Aussage zu treffen, wenn die Nullyhpothese beibehalten wird.
Hier beenden wir erst einmal die generelle Einführung in Bayes. In den kommenden Abschnitten werden wir an diesem gleichen Beispiel noch zeigen, wie man mit R händisch Bayesianische Analysen rechnen kann, wenn man Verteilungen kennt oder sich selbst eine Verteilung sampeln muss, weil man Verteilungen nicht kennt. Für die praktische Umsetzung mit echten Daten, gucken wir uns auch noch an, wie man mit dem R-Paket brms Bayesianisch Regressionen rechnen kann.
Literatur
Dienes, Z. (2008). Understanding psychology as a science: an introduction to scientific and statistical inference. Palgrave Macmillan.
