Netzwerkanalyse im Querschnitt
Einführung
Netzwerkanalyse kommt aus einem eher technischen Feld. Sie wurde dafür genutzt, Systeme darzustellen, bei denen verschiedene Einheiten miteinander verbunden sind. Beispielsweise wurden Computer als Knotenpunkte gesehen und dann über Kanten deren Verbindung (oder eben auch Nicht-Verbindung) dargestellt. Den vermutlich ersten Einzug in die Psychologie hatten Netzwerke in Gruppenanalysen. Dabei sind nun nicht mehr Computer die Knotenpunkte, sondern eben Menschen aus einer spezifischen Gruppe. Bestimmte Arten der Beziehung werden dabei durch eine Verbindung zwischen zwei Personen abgebildet.
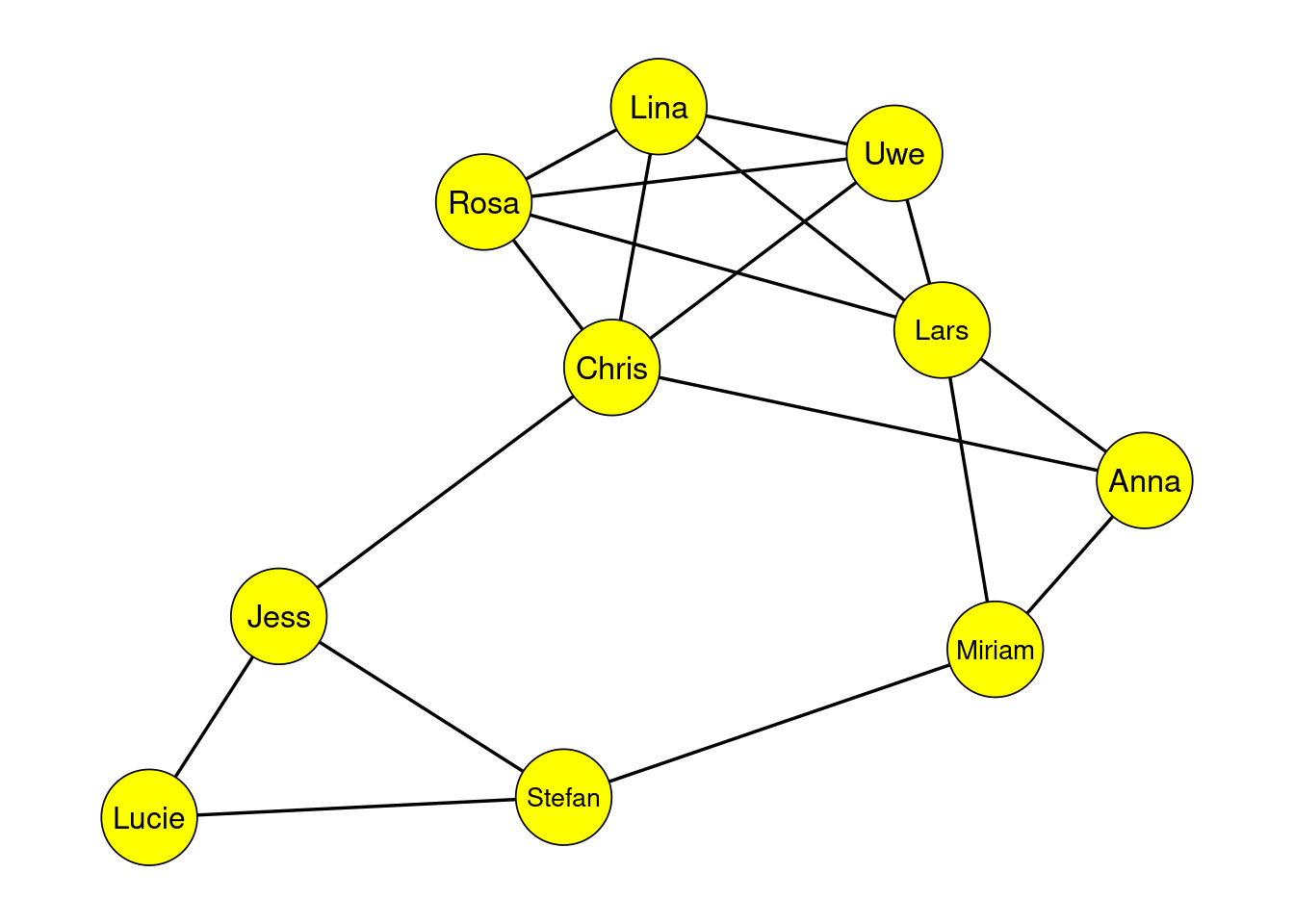
In der neueren Literatur werden Netzwerke aber auch zur Darstellung von Psychologischen Konstrukten genutzt. Beispielsweise können die einzelnen Symptome der Depression (wie in der nächsten Grafik abgebildet) die Knotenpunkte darstellen und die Kanten deren Zusammenhang. Dies hat gegenüber einem globalen Skalenwert, der die Erkankung nur als homogene Masse betrachtet, den Vorteil, dass die Dynamik zwischen verschiedenen Symptomen aufgezeigt werden kann. Vielfalt und Komplexität der psychischen Erkankungen werden deutlich. Die ursprüngliche Idee war, dass so auch zentrale Punkte identifiziert werden können, die bei einer Intervention angesteuert werden sollten. Hierüber gibt es aber aktuell eine Diskussion in der (methodischen) Literatur. Generell lässt sich aber festhalten, dass das Wissen über die Idee der Netzwerkanalyse in der modernen klinischen Forschung ein hilfreiches Tool ist. Zunächst befassen wir uns mit grundlegenden Begriffen und der Berechnung der Netzwerkstruktur.
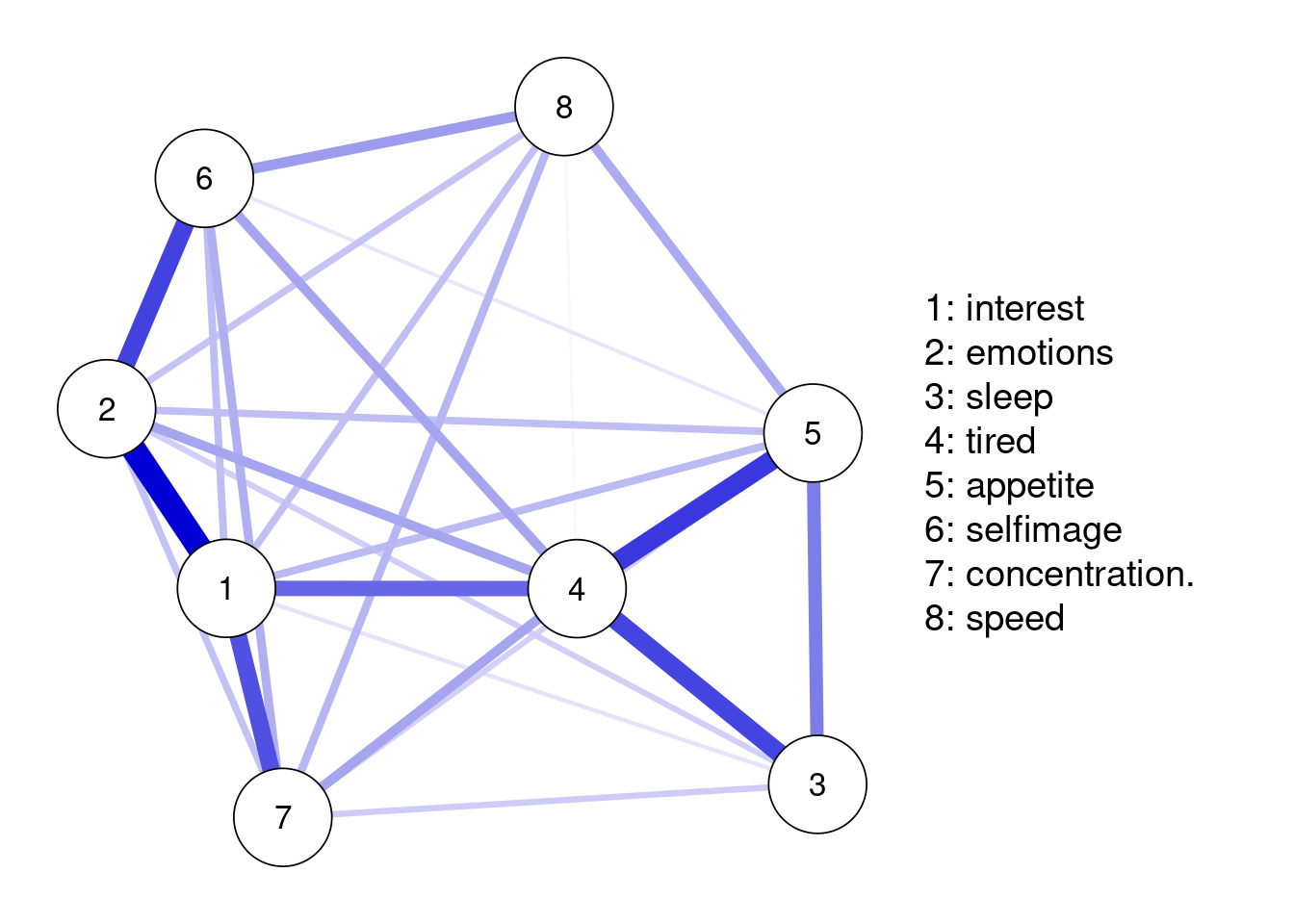
Begriffsklärung und Netzwerktypen
Betrachten wir an dieser Stelle nochmal zwei grundlegende Begriffe der Netzwerkanalyse. Wie bereits angedeutet wurde, bestehen diese aus Knoten und Kanten. Knoten - oder englisch nodes - repräsentieren unterschiedliche psychologische Variablen (z.B. Störungen, Symptome oder Items), die über Messungen aus verschiedenen Skalen oder Subskalen erhoben werden können. Kanten - oder englisch edges - repräsentieren statistische Beziehungen zwischen den Nodes (z.B. Korrelationen), die anhand der Daten geschätzt werden. Während Werte auf den Knoten also gemessen werden, muss deren Beziehung (also die Kanten) geschätzt werden. Dies steht auch im fundamentalen Gegensatz zu der ursprünglichen Anwendung der Netzwerke (bspw. im sozialen Bereich), bei der die Knoten Einheiten sind und deren Verbindung (oder das Fehlen der Verbindung) bekannt ist.
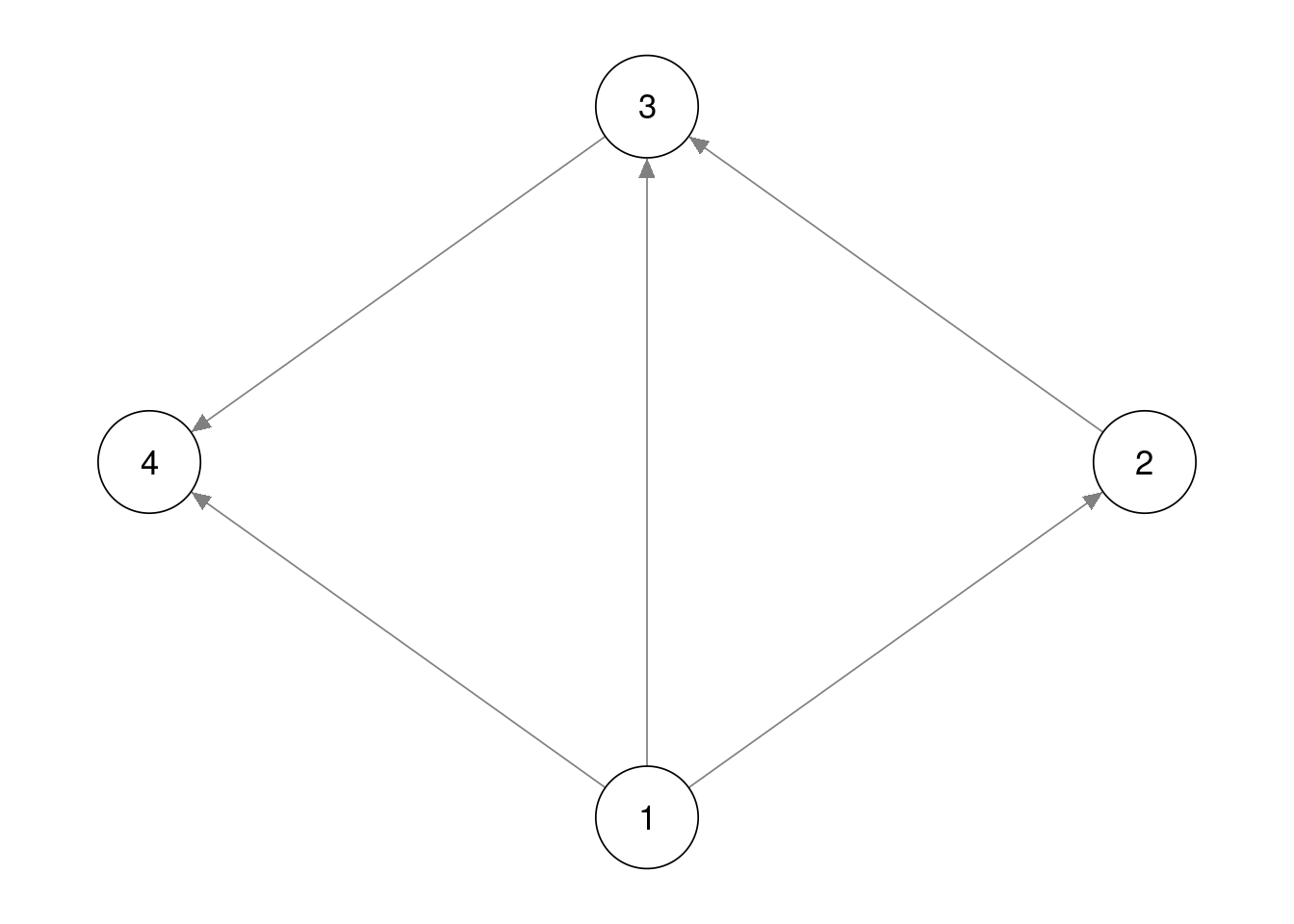
Kanten können sowohl gerichtet als auch ungerichtet sein, wobei gerichtete Kanten durch einen Pfeil gekennzeichnet werden, der einen einseitigen Effekt andeutet (siehe nächste Grafik). Ungerichtete Kanten hingegen haben wir bereits bei dem sozialen und psychologischen Netzwerk gesehen. Sie werden durch eine einfache Linie zwischen zwei Knoten abgebildet. Ein Netzwerk, das nur gerichtete Kanten enthält, bezeichnet man als gerichtetes Netzwerk. Netzwerke aus ungerichteten Kanten nennt man hingegen ungerichtetes Netzwerk. Im Querschnitt sind keine zeitlichen Abfolgen bekannt, weshalb wir heute zunächst nur ungerichtete Netzwerke betrachten werden.
Eine weitere interessante Eigenschaft eines Netzwerkes besteht darin, ob die Kanten ein Gewicht inne haben. Die Unterscheidung besteht dabei zwischen gewichteten und ungewichteten Netzwerken. Für beide Arten haben wir in diesem Tutorial bereits Beispiele gesehen. Das soziale Netzwerk der 10 Personen zeigte nur an, ob zwischen diesen eine Beziehung besteht oder nicht. Der Beziehung wird kein Gewicht zugegeben, weshalb es sich um ein ungewichtetes Netzwerk handelt. Das präsentierte psychologische Netzwerk hingegen hat unterschiedliche Kantenformen. Diese sind unterschiedlich dick, wodurch die unterschiedliche Stärke des Zusammenhangs zwischen den Symptomen demonstriert wird. Dabei wird auch durch die Farbe dargestellt, ob eine positive oder negative Beziehung vorliegt. Ursprünglich wurde dies durch grüne und rote Kanten demonstriert, wobei jetzt eine Wahl von blau für positive Beziehung eine höhere Differenzierbarkeit garantiert. In unserem abgebildeten Beispiel für psychologische Netzwerke existieren keine Kanten mit einem negativen Gewicht. Da es sich insgesamt um ein Konstrukt handelt, ist es aber auch wünschenswert, dass alle Symptome positiv miteinander zusammenhängen.
Nachdem nun die wichtigsten Basics über Netzwerke abgehandelt wurden, können wir uns mit den ersten kleinen Umsetzungen in R beschäftigen. Zunächst brauchen wir aber natürlich einen Datensatz.
Daten
In dieser Sitzung wollen wir einen Datensatz von Rubin (2020). verwenden. Dieser steht auf OSF zum Download zur Verfügung kann aber auch über den folgenden Befehl direkt ins Environment eingeladen werden.
raw_data <- readRDS(url("https://osf.io/awz3d/download"))Mit head können wir uns wie gewohnt die ersten 6 Zeilen des Datensatzes anschauen.
head(raw_data)## FFMQ.obs FFMQ.des FFMQ.aw FFMQ.nj FFMQ.nr PHQ8_1
## 176 0.3067478 1.79571268 -1.7452668 0.4913721 0.83620916 0.9014022
## 177 -0.6750700 -1.68548010 0.2927406 -0.7290201 -0.17361531 1.9346512
## 178 -0.1328100 -0.81038081 -0.5246719 -0.2616628 -0.89540458 1.9346512
## 179 0.2398591 0.08341658 -0.1104417 -0.4186422 -0.08913244 -0.1318469
## 180 0.2398591 0.92071465 0.7069709 0.3343926 0.42022136 -0.1318469
## 181 0.4357006 -0.84818204 0.1020567 -1.1963775 0.20778590 -0.1318469
## PHQ8_2 PHQ8_3 PHQ8_4 PHQ8_5 PHQ8_6 PHQ8_7
## 176 0.91147081 0.3521987 -0.4176933 0.6863475 -0.89672924 0.8543800
## 177 -0.09429008 -0.5805206 1.5147671 -1.1895061 -0.89672924 -1.0586341
## 178 1.91723170 1.2849181 1.5147671 1.6242743 1.05422843 1.8108870
## 179 -0.09429008 -0.5805206 -0.4176933 -0.2515793 -0.89672924 -1.0586341
## 180 -1.10005097 0.3521987 0.5485369 0.6863475 -0.89672924 -0.1021271
## 181 -0.09429008 -1.5132400 0.5485369 1.6242743 0.07874959 -1.0586341
## PHQ8_8
## 176 -0.5906521
## 177 2.1922977
## 178 0.8008228
## 179 -0.5906521
## 180 -0.5906521
## 181 0.8008228Dabei ist auffällig, dass der Datensatz bereits auf rein inhaltliche Items reduziert wurde. Allerdings ist die Benennung durch das Erhebungsinstrument und ein Kürzel bzw. die dazu gehörige Nummer für die Interpretation noch etwas unschön, weshalb wir die Bedeutung im folgenden Code als Spaltenname zuordnen. In Voraussicht auf spätere Zeichnungen kürzen wir manche längeren Namen etwas ab.
names(raw_data) <- c("observe", "describe", "awaren.", "nonjudg.",
"nonreact.", "interest", "emotions", "sleep",
"tired", "appetite", "selfim.",
"concentr.", "speed")Die Variablen observe, describe, awareness, nonjudging und nonreactivity bezeichnen die fünf Facetten der Achtsamkeit von Baer et al. (2006), über die mehr in diesem Paper steht. Die 8 weiteren Variablen beschreiben eine dysfunktionale, meist negative Veränderung in dem bezeichneten Lebensaspekt im Zuge einer Depression; so steht interest beispielsweise für einen Interessensverlust, während selfimage ein negatives Selbstbild abbildet. Die angezeigten Werte weisen auf eine Inervallskalierung der Daten hin. Die weiterführende Berechnung ist auch deshalb ein wenig besonders, da nicht nur ein Konstrukt im Netzwerk enthalten ist, sondern zwei verschiedene interagierende Eigenschaften.
Netzwerkschätzung
Es gibt in R einige Pakete, die sich mit der Netzwerkanalyse auseinandersetzen (bspw. psychonetrics, GGMnonreg oder auch mgm). Ein häufig verwendetes Paket ist bootnet, das einige vorher entwickelte Pakete vereint und daher für verschiedene Fragestellungen einsetzbar ist. Weiterhin werden wir auch in der Auswertung auf Funktionen dieses Pakets zurückgreifen, weshalb wir uns in diesem Tutorial für seine Nutzung entschieden haben. Vor der ersten Verwendung muss das Paket natürlich installiert werden - die vorher entwickelten Pakete werden als Dependencies automatisch mit installiert.
install.packages("bootnet")Anschließend müssen wir das Paket zur Verwendung natürlich noch aktivieren.
library(bootnet)## Loading required package: ggplot2## This is bootnet 1.4.3## For questions and issues, please see github.com/SachaEpskamp/bootnet.Die Schätzung von Netzwerken funktioniert in dem Paket fast ausschließlich durch die Sammelfunktion estimateNetwork. In ihr können durch Argumente verschiedene Netzwerkanalysen durchgeführt werden, wie wir im weiteren Verlauf sehen werden.
Starten wir zunächst mit der einfachsten Berechnung von Zusammenhängen, die wir für intervallskalierte Variablen kennengelernt haben - die Produkt-Moment-Korrelation. Wenn wir eine Netzwerkstruktur erstellen wollen, indem das Gewicht der Kanten der Korrelation zwischen den zugehörigen Knoten entspricht, muss das Argument default mit "cor" gefüllt werden. Weiterhin muss natürlich der Datensatz mit aufgeführt werden, für den die Schätzung durchgeführt werden soll. Wir weisen dieses Netzerk dem Objekt cor_net zu und betrachten die summary.
cor_net <- estimateNetwork(raw_data, default = "cor")## Estimating Network. Using package::function:
## - psych::corr.p for significance thresholdingsummary(cor_net)##
## === Estimated network ===
## Number of nodes: 13
## Number of non-zero edges: 78 / 78
## Mean weight: 0.1274807
## Network stored in object$graph
##
## Default set used: cor
##
## Use plot(object) to plot estimated network
## Use bootnet(object) to bootstrap edge weights and centrality indices
##
## Relevant references:
##
## Epskamp, S., Borsboom, D., & Fried, E. I. (2016). Estimating psychological networks and their accuracy: a tutorial paper. arXiv preprint, arXiv:1604.08462.Bei der Schätzung erhalten wir zunächst eine Warning Message, die wir aber nicht weiter betrachten müssen. In der summary() sind einige Informationen abgetraten. Über das Netzwerk wird dabei ausgesagt, dass es 13 Knoten gibt. Weiterhin wird angezeigt, dass alle Korrelationen (also die Gewichte der Kanten) nicht gleich 0 sind. Auch das durchschnittliche Gewicht der Kanten wird bestimmt. Wir erhalten zusätzliche einige Hinweise zum weiteren Vorgehen und der Zitation. Dabei konzentrieren wir uns jetzt zunächst erst einmal darauf, das Netzwerk zu zeichnen.
plot(cor_net)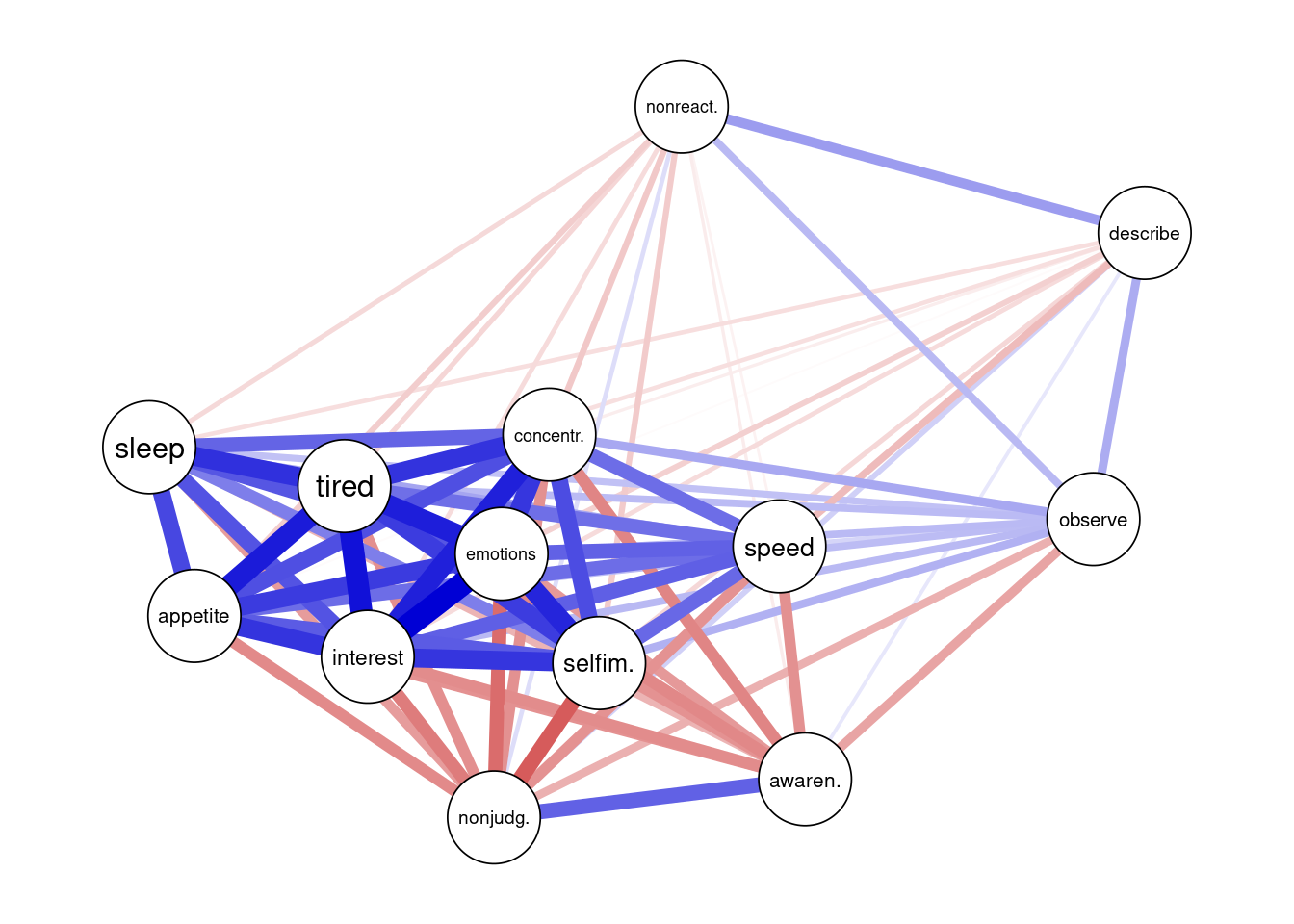
Das Paket zeichnet - wie wir es bereits gesehen haben - positive Beziehungen als blaue Striche. Je stärker das Gewicht einer Kante ist, desto dicker ist die zugehörige Linie . Die Erstellung der Struktur in der Grafik (also an welchem Ort welcher Knoten passiert wird), wird durch einen Algorithmus berechnet. Das Ziel dabei ist es, Knoten mit starken Verbindungen möglichst eng zu platzieren, welche mit schwächeren Verbindungen weiter entfernt. Die dahinter liegende Mathematik werden wir an dieser Stelle nicht besprechen. Neben Plots ist auch eine Darstellung als Matrix mit Zahlen möglich (in diesem Fall also die Korrelationsmatrix). Diese wird im Objekt abgelegt und kann daher sehr simpel ausgegeben werden.
cor_net$graph## obs dsc aw. nnj. nnr. int
## obs 0.0000000 0.23346309 -0.25541487 -0.2222614 0.19805461 0.1969371
## dsc 0.2334631 0.00000000 0.06687903 0.1331660 0.27784544 -0.1011692
## aw. -0.2554149 0.06687903 0.00000000 0.4450588 -0.05401572 -0.3248143
## nnj. -0.2222614 0.13316604 0.44505878 0.0000000 0.09581370 -0.3692725
## nnr. 0.1980546 0.27784544 -0.05401572 0.0958137 0.00000000 -0.1017167
## int 0.1969371 -0.10116925 -0.32481434 -0.3692725 -0.10171673 0.0000000
## emt 0.1934157 -0.13326343 -0.28714643 -0.4129465 -0.15351137 0.7174187
## slp 0.1731551 -0.09329764 -0.21099657 -0.2782807 -0.10744319 0.4843885
## trd 0.1925480 -0.09036251 -0.33511996 -0.3163092 -0.11603613 0.6694402
## app 0.1885348 -0.01217114 -0.30812835 -0.3289537 -0.14141308 0.5714895
## sl. 0.2188235 -0.11260390 -0.30566888 -0.4617085 -0.14576964 0.5683146
## cn. 0.2444282 -0.05065239 -0.34285231 -0.3092825 -0.10888137 0.6264498
## spd 0.1187273 -0.19014945 -0.31011608 -0.3056252 -0.03571703 0.4512196
## emt slp trd app sl. cn.
## obs 0.1934157 0.17315515 0.19254797 0.18853485 0.2188235 0.24442824
## dsc -0.1332634 -0.09329764 -0.09036251 -0.01217114 -0.1126039 -0.05065239
## aw. -0.2871464 -0.21099657 -0.33511996 -0.30812835 -0.3056689 -0.34285231
## nnj. -0.4129465 -0.27828074 -0.31630918 -0.32895373 -0.4617085 -0.30928247
## nnr. -0.1535114 -0.10744319 -0.11603613 -0.14141308 -0.1457696 -0.10888137
## int 0.7174187 0.48438851 0.66944023 0.57148955 0.5683146 0.62644975
## emt 0.0000000 0.47417461 0.63290470 0.55255929 0.6145474 0.56554626
## slp 0.4741746 0.00000000 0.58281105 0.51825404 0.3617876 0.43671632
## trd 0.6329047 0.58281105 0.00000000 0.64236068 0.5473139 0.57256379
## app 0.5525593 0.51825404 0.64236068 0.00000000 0.4617999 0.49424939
## sl. 0.6145474 0.36178756 0.54731393 0.46179987 0.0000000 0.50260557
## cn. 0.5655463 0.43671632 0.57256379 0.49424939 0.5026056 0.00000000
## spd 0.4447632 0.25262260 0.40557975 0.40985862 0.4258437 0.41213178
## spd
## obs 0.11872732
## dsc -0.19014945
## aw. -0.31011608
## nnj. -0.30562521
## nnr. -0.03571703
## int 0.45121961
## emt 0.44476319
## slp 0.25262260
## trd 0.40557975
## app 0.40985862
## sl. 0.42584371
## cn. 0.41213178
## spd 0.00000000Die Koeffizienten liegen wie immer bei der Korrelation zwischen -1 und 1. Wir können uns exemplarisch noch die Beziehung der ersten beiden Variablen in der Matrix und im Plot anschauen. Das Gewicht wird als 0.2334631 ausgegeben. Im Plot findet man beide Items am Rand rechts. Sie sind durch einen dünnen (weil kleinerer Wert), blauen (weil positiver Wert) Strich verbunden.
Aus einiger Arbeit mit Korrelationen in multivariaten Settings wissen wir, dass die Einzigartigkeit einer Beziehung durch einfache Korrelationen nicht abgebildet wird. Obwohl zwei Variablen in unserem Plot also verbunden sind, könnten sie eigentlich keinen eigenen Zusammenhang haben, sondern durch eine Drittvariable gesteuert sein. Deshalb betrachtet man für solche Darstellungen üblicherweise nicht Korrelationen. Stattdessen werden die Partialkorrelationen berechnet. Die Gewichte der Kanten sollen die Beziehungen zwischen den Knoten abbilden, nachdem auf alle anderen Informationen im Datensatz kontrolliert wurde. Im Bachelor haben wir Formeln für das Herauspartialisieren einer Variable aus der Beziehung für die Berechnung der Partialkorrelation kennen gelernt. Dies würde viel rechnerischen Aufwand bedeuten. Zum Glück können Partialkorrelationen auch aus der Inversen der Kovarianzmatrix berechnet werden.
\[ \Theta = \Sigma^{-1} \] \(\Sigma\) bezeichnet die Kovarianzmatrix, während \(\Theta\) die Inverse dieser symbolisiert. Die Berechnung der Partialkorrelation \(\rho\) zweier Variablen \(j\) und \(p\) anhand der Einträge aus \(\Theta\) folgt dann folgender Formel:
\[ \rho(y_py_j) = -\frac{\Theta_{y_py_j}}{\sqrt{\Theta_{y_py_p}}\sqrt{\Theta_{y_jy_j}}}\]
Für das Vorgehen in R hat diese Verwendung eines anderen Maßes erstmal keine großen Konsequenzen. In default muss jetzt "pcor" angegeben werden. Wir nennen das resultierende Objekt pcor_net und lassen uns wieder das summary() ausgeben.
pcor_net <- estimateNetwork(raw_data, default = "pcor")## Estimating Network. Using package::function:
## - qgraph::qgraph(..., graph = 'pcor') for network computation
## - psych::corr.p for significance thresholdingsummary(pcor_net)##
## === Estimated network ===
## Number of nodes: 13
## Number of non-zero edges: 78 / 78
## Mean weight: 0.04296311
## Network stored in object$graph
##
## Default set used: pcor
##
## Use plot(object) to plot estimated network
## Use bootnet(object) to bootstrap edge weights and centrality indices
##
## Relevant references:
##
## Epskamp, S., Borsboom, D., & Fried, E. I. (2016). Estimating psychological networks and their accuracy: a tutorial paper. arXiv preprint, arXiv:1604.08462.Der Output verändert seine Struktur dabei nicht, nur die Werte werden für die neue Berechnung angepasst. Weiterhin sind jedoch keine Gewichte von Kanten 0, wozu wir gleich nochmal kommen werden. Zunächst wollen wir uns aber das Netzwerk nochmal zeichnen lassen.
plot(pcor_net)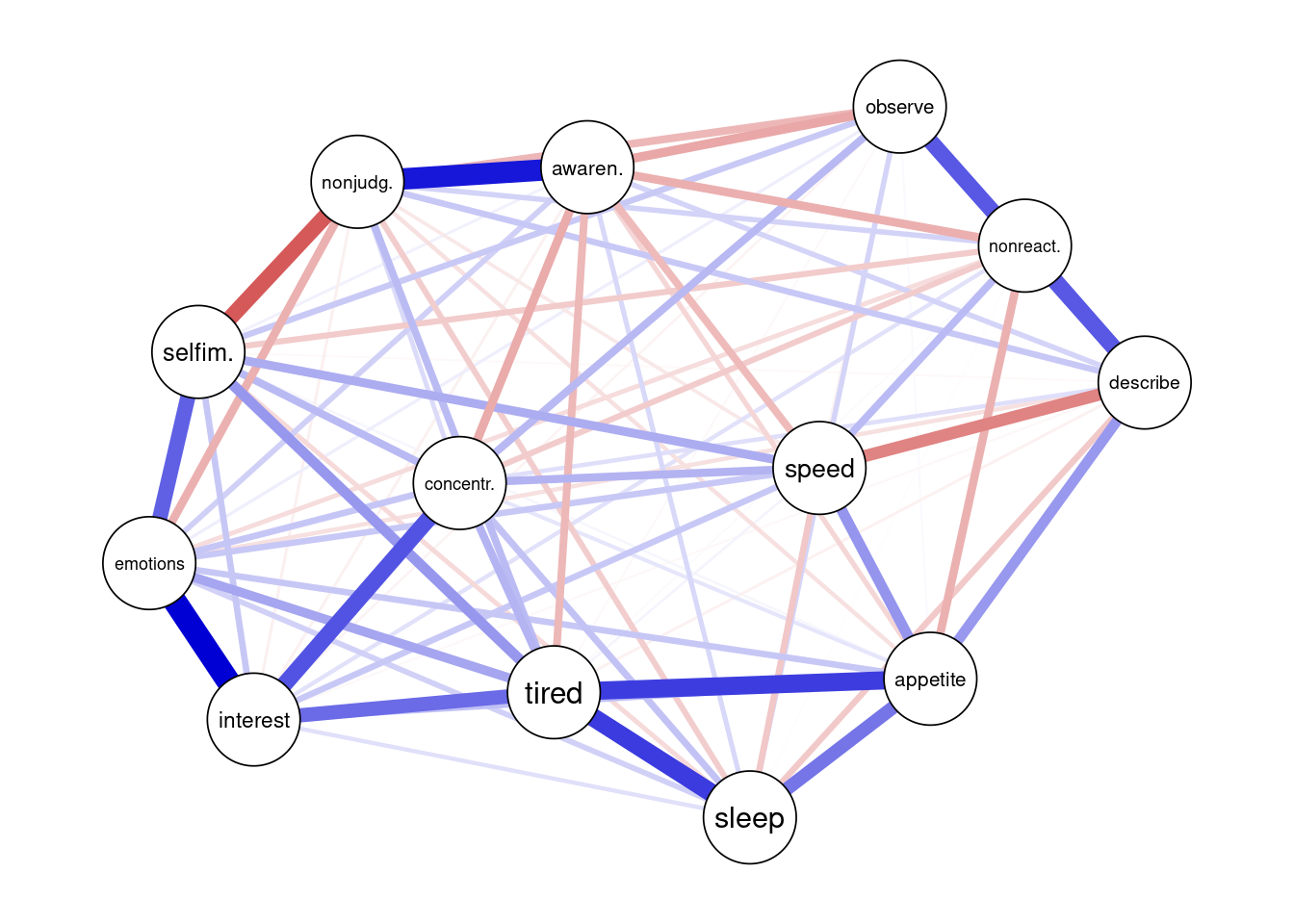
Zunächst sehen wir, dass sich die Struktur geändert hat. Da der Algorithmus nun andere Werte verwendet, platziert er auch die Knoten an anderen Orten. Ein Problem der Analyse von ehobenen Daten ist es, dass durch die Fehlervarianz in den Messung eigentlich immer alle Knoten untereinander verbunden sind. Dies führt vor allem bei komplexen Netzwerken mit vielen Knoten dazu, dass die Visualisierung des Netzwerkes unübersichtlich wird und man sich mit Kanten beschäftigt, die keine relevante Beziehung zwischen zwei Knoten darstellen. Es gibt verschiedene Ansätze, um relevante Beziehungen für die Darstellung auszuwählen (bspw. in der Statistik nach Bayes oder durch extensive Modellsuche). Wir benutzen im weiteren Verlauf allerdings nur den Ansatz der Regularisierung, da wir nicht ausreichend Zeit für alle Möglichkeiten haben und die Regularisierung als noch unbekanntes Prinzip am lehrreichsten sein sollte.
Regularisierung und Netzwerkauswahl
Ein regularisiertes Partialkorrelations-Netzwerk ist eine visualisierte gewichtete Netzwerkstruktur, das durch Regulations-Techniken aus dem Feld des Machine-Learnings geschätzt wird. Daraus resultiert eine sogenannte sparse network structure (also eine spärlich besetzte Netzwerkstruktur). Das bedeutet, dass viele der Parameter auf den Kanten exakt 0 sind. Die theoretische Reichweite der bestraften (siehe nächster Absatz) Partialkorrelationen liegt dabei weiterhin zwischen 0 und 1.
Regularisierte Netzwerke werden durch die Lasso-Regulation geschätzt. Der Mechanismus ist so aufgestellt, dass falsche Kanten nicht auftreten sollen. Falsche Kanten bedeutet, dass diese in der Population nicht existieren, aber in der Stichprobe trotzdem keine Partialkorrelationen von 0 vorliegen würde. Die Lasso-Regularisierung hat gegenüber anderen Regularisierungs-Techniken den Vorteil, dass Werte genau 0 sein können. Man nennt das Vorgehen bei der Regularisierung auch eine Bestrafung des Parameters, da er in seiner Größe und Richtung (oder genau auf 0) reduziert wird.
Lasso kommt ursprünglich aus der multiplen Regression und wurde zur Selektion von Prädiktoren genutzt. Friedman et al. (2008) haben eine Überleitung in die Analyse von Graphen (Netzwerke sind eigentlich auch nur Graphen) gespannt - daher kommt auch die Bezeichnung als graphical lasso (glasso). Obwohl es um Werte von 0 in der Partialkorrelationsmatrix geht, wird mathematisch die Bestrafung und Schätzung in der inversen Kovarianzmatrix \(\Theta\) vorgenommen. Wenn dort ein Eintrag 0 ist, folgt daraus nach der bereits dargestellten Form der Berechnung der Partialkorrelation aber auch, dass diese den Wert 0 annimmt. Dabei werden die einzelnen Einträge in \(\Theta\) bestraft. Für die Schätzung der regularisierten inversen Kovarianzmatrix wird die folgende Gleichung maximiert.
\[\log \det(\Theta) - trace(S\Theta) - \lambda \|\Theta\|_1\]
Dabei steht \(S\) für die empirisch gefundene Kovarianzmatrix. \(\|\Theta\|_1\) bezeichnet die absolute Summe aller Einträge in \(\Theta\). Da der Maximierungsprozess unter anderem duale Räumen verwendet, werden wir uns damit nicht näher befassen. Anhand der Gleichung sehen wir aber, dass hohe Werte in der inversen Matrix einen niedrigeren Gesamtwert ergeben, weshalb diese runter regularisiert werden. Weiterhin sehen wir, dass das Ergebnis der Maximierung abhängig von der Wahl eines \(\lambda\)-Wertes ist, den man auch als Bestrafungsparameter bezeichnet. Für eine gute Auwahl wird die Schätzung standardmäßig mit verschiedenen Bestrafungsparametern durchgeführt. Üblich sind dabei 100 \(\lambda\)-Werte. Als obere Grenze \(\lambda_{max}\) wird der Wert gewählt, der alle Einträge auf 0 regularisieren würde. Bis zu einer gewählten unteren Grenze (meist $_{max} $) werden die andere Werte in einer logarithmischen Verteilung festgelegt.
Nachdem 100 verschiedene inverse Kovarianzmatrizen geschätzt wurden, muss noch eine Auswahl der besten Werte geschehen. Üblicherweise wird dabei die Minimierung des Informationskriteriums EBIC nach Foygel und Drton (2010) genutzt.
\[ EBIC = -2LL + E \cdot \log(n) + 4 \cdot \gamma \cdot E \cdot \log(p) \] In die Berechnung gehen einige Größen ein, wobei wir die meisten auch schon gesehen haben. Ein Loglikelihood-Wert (\(LL\)) wird für das Modell bestimmt, während \(n\) die Größe der Stichprobe ist. \(p\) bezeichnet die Größe des Netzwerkes (Anzahl der Knoten) - also die Zeilen- und auch Spaltenanzahl der Matrix. \(E\) hingegen ist Anzahl der Elemente der Matrix, die nicht Null sind. Nicht direkt aus der bestraften inversen Kovarianzmatrix \(\Theta\) lässt sich \(\gamma\) ablesen. Dies ist ein weiterer freier Parameter (auch Hyperparameter genannt), der gewählt werden muss. Üblicherweise wird hier ein Wert von 0.5 gewählt. Aus der Gleichung lässt sich ablesen, dass ein hoher Wert Netzwerke mit mehr Kanten mehr bestrafen würde, da der letzte Term größer und damit durch die Subtraktion der Gesamtwert kleiner wird. Für einen explorativen Ansatz wird deshalb auch ein \(\gamma\)-Wert von 0 empfohlen.
Nachdem die beiden wichtigen Schritte (Regularisierung und Auswahl) nun theoretisch dargestellt wurden, können wir uns mit der praktischen Umsetzung befassen. bootnet bietet natürlich eine Möglichkeit, beide Schritte auf einmal durchzuführen. Die Kombination der Bestrafung anhand des grafischen Lasso mit der Auswahl des besten Netzwerkes durch EBIC führt zu der Benennung als "EBICglasso in dem Argument default in der bereits bekannten Funktion. Wir legen das Objekt unter reg_net als Netzwerk mit regularisierten Werten ab. Die Anzahl der geschätzten Werte, die anhand ihres EBICs anschließend bewertet werden, kann mit nlambda festgelegt werden. Weiterhin interessant ist das Argument tuning, in dem \(\gamma\) als Hyperparameter zur Bestrafung für Netzwerke mit vielen Edges festgelegt werden kann. Die hier gewählten Werte sind dabei die Standardeinstellungen des Paketes, aber eine Variation ist (wie zum Teil auch beschrieben) durchaus situativ nötig.
reg_net <- estimateNetwork(raw_data, default = "EBICglasso",
nlambda = 100, tuning = 0.5)## Estimating Network. Using package::function:
## - qgraph::EBICglasso for EBIC model selection
## - using glasso::glasso## Warning in EBICglassoCore(S = S, n = n, gamma = gamma, penalize.diagonal =
## penalize.diagonal, : A dense regularized network was selected (lambda < 0.1 *
## lambda.max). Recent work indicates a possible drop in specificity. Interpret the
## presence of the smallest edges with care. Setting threshold = TRUE will enforce
## higher specificity, at the cost of sensitivity.summary(reg_net)##
## === Estimated network ===
## Number of nodes: 13
## Number of non-zero edges: 54 / 78
## Mean weight: 0.03944097
## Network stored in object$graph
##
## Default set used: EBICglasso
##
## Use plot(object) to plot estimated network
## Use bootnet(object) to bootstrap edge weights and centrality indices
##
## Relevant references:
##
## Friedman, J. H., Hastie, T., & Tibshirani, R. (2008). Sparse inverse covariance estimation with the graphical lasso. Biostatistics, 9 (3), 432-441.
## Foygel, R., & Drton, M. (2010). Extended Bayesian information criteria for Gaussian graphical models.
## Friedman, J. H., Hastie, T., & Tibshirani, R. (2014). glasso: Graphical lasso estimation of gaussian graphical models. Retrieved from https://CRAN.R-project.org/package=glasso
## Epskamp, S., Cramer, A., Waldorp, L., Schmittmann, V. D., & Borsboom, D. (2012). qgraph: Network visualizations of relationships in psychometric data. Journal of Statistical Software, 48 (1), 1-18.
## Epskamp, S., Borsboom, D., & Fried, E. I. (2016). Estimating psychological networks and their accuracy: a tutorial paper. arXiv preprint, arXiv:1604.08462.Der Aufbau der summary() verändert sich auch im Fall der Regularisierung nicht. Wir sehen allerdings, dass nun nicht mehr alle Gewichte der Kanten ungleich null sind - nur 54 der ursrünglichen 78 haben noch ein solches. Anscheinend wurde ein Netzwerk ausgewählt, in dem manche Kanten als falsch angesehen werden. Im abgelegten Objekt reg_net kann man sich unter results diese auch noch genauer anschauen. Unter optnet sind die Gewichte der Kanten abgelegt, die später zum Aufzeichnen der Struktur verwendet werden.
reg_net$results$optnet## observe describe awaren. nonjudg. nonreact.
## observe 0.00000000 0.166635996 -0.112455981 -0.064210464 0.120279093
## describe 0.16663600 0.000000000 0.000000000 0.053792547 0.184887657
## awaren. -0.11245598 0.000000000 0.000000000 0.274658761 -0.009476879
## nonjudg. -0.06421046 0.053792547 0.274658761 0.000000000 0.000000000
## nonreact. 0.12027909 0.184887657 -0.009476879 0.000000000 0.000000000
## interest 0.00000000 0.000000000 -0.008306110 -0.007143912 0.000000000
## emotions 0.00000000 -0.009943722 0.000000000 -0.085549714 -0.034081467
## sleep 0.01645887 0.000000000 0.000000000 -0.016629399 0.000000000
## tired 0.00000000 0.000000000 -0.048598933 0.000000000 0.000000000
## appetite 0.01765258 0.000000000 -0.034685093 -0.022566660 -0.034701150
## selfim. 0.04827669 0.000000000 0.000000000 -0.204644007 -0.040229725
## concentr. 0.08130007 0.000000000 -0.080922301 0.000000000 0.000000000
## speed 0.00000000 -0.102393195 -0.095378108 -0.025354316 0.000000000
## interest emotions sleep tired appetite
## observe 0.000000000 0.000000000 0.01645887 0.000000000 0.01765258
## describe 0.000000000 -0.009943722 0.00000000 0.000000000 0.00000000
## awaren. -0.008306110 0.000000000 0.00000000 -0.048598933 -0.03468509
## nonjudg. -0.007143912 -0.085549714 -0.01662940 0.000000000 -0.02256666
## nonreact. 0.000000000 -0.034081467 0.00000000 0.000000000 -0.03470115
## interest 0.000000000 0.328215474 0.04261040 0.201402370 0.09475036
## emotions 0.328215474 0.000000000 0.06213000 0.123247456 0.08407725
## sleep 0.042610403 0.062130003 0.00000000 0.243721052 0.17015695
## tired 0.201402370 0.123247456 0.24372105 0.000000000 0.25782853
## appetite 0.094750361 0.084077251 0.17015695 0.257828532 0.00000000
## selfim. 0.089100199 0.218062872 0.00000000 0.113293692 0.02334907
## concentr. 0.226661590 0.084354353 0.06402587 0.116453004 0.05843849
## speed 0.082618845 0.071390648 0.00000000 0.008733832 0.10041545
## selfim. concentr. speed
## observe 0.04827669 0.08130007 0.000000000
## describe 0.00000000 0.00000000 -0.102393195
## awaren. 0.00000000 -0.08092230 -0.095378108
## nonjudg. -0.20464401 0.00000000 -0.025354316
## nonreact. -0.04022973 0.00000000 0.000000000
## interest 0.08910020 0.22666159 0.082618845
## emotions 0.21806287 0.08435435 0.071390648
## sleep 0.00000000 0.06402587 0.000000000
## tired 0.11329369 0.11645300 0.008733832
## appetite 0.02334907 0.05843849 0.100415453
## selfim. 0.00000000 0.09135646 0.109372709
## concentr. 0.09135646 0.00000000 0.083957947
## speed 0.10937271 0.08395795 0.000000000Im Endeffekte ist das aber die selbe Information, die in reg_net$graph abgelegt wird. results ist als Unterpunkt besonders interessant, wenn man sich den Ablauf der Berechnung nochmal klar machen möchte.
Zunächst hat die Funktion 100 Bestrafungsparameter bestimmt. Diese sind unter lambda abgelegt.
reg_net$results$lambda## [1] 0.007174187 0.007515791 0.007873661 0.008248572 0.008641334 0.009052797
## [7] 0.009483853 0.009935434 0.010408517 0.010904126 0.011423335 0.011967265
## [13] 0.012537096 0.013134059 0.013759447 0.014414613 0.015100976 0.015820020
## [19] 0.016573303 0.017362453 0.018189179 0.019055271 0.019962602 0.020913136
## [25] 0.021908931 0.022952141 0.024045024 0.025189946 0.026389384 0.027645935
## [31] 0.028962317 0.030341379 0.031786107 0.033299626 0.034885213 0.036546299
## [37] 0.038286478 0.040109518 0.042019363 0.044020146 0.046116199 0.048312056
## [43] 0.050612471 0.053022422 0.055547125 0.058192043 0.060962901 0.063865695
## [49] 0.066906708 0.070092522 0.073430030 0.076926456 0.080589367 0.084426691
## [55] 0.088446731 0.092658189 0.097070178 0.101692248 0.106534401 0.111607116
## [61] 0.116921373 0.122488672 0.128321063 0.134431167 0.140832208 0.147538039
## [67] 0.154563174 0.161922816 0.169632893 0.177710091 0.186171891 0.195036605
## [73] 0.204323420 0.214052434 0.224244701 0.234922282 0.246108283 0.257826914
## [79] 0.270103537 0.282964720 0.296438298 0.310553431 0.325340666 0.340832007
## [85] 0.357060979 0.374062707 0.391873984 0.410533359 0.430081214 0.450559855
## [91] 0.472013601 0.494488884 0.518034345 0.542700940 0.568542054 0.595613612
## [97] 0.623974202 0.653685203 0.684810916 0.717418704Der größte Bestrafungsparameter ist der letzte Eintrag in der Matrix. Für diesen sollten alle Gewichte der Kanten auf 0 herunterregularisiert worden sein.
Die Werte aller 100 bestraften inversen Kovarianzmatrizen sind unter reg_net$results$results$wi. Beispielsweise ist das komplett leere Netzwerke (also mit dem größten Bestrafungsparameter \(\lambda\)) als 100. Objekt abgelegt.
reg_net$results$results$wi[,,100]## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13]
## [1,] 1 0 0 0 0 0 0 0 0 0 0 0 0
## [2,] 0 1 0 0 0 0 0 0 0 0 0 0 0
## [3,] 0 0 1 0 0 0 0 0 0 0 0 0 0
## [4,] 0 0 0 1 0 0 0 0 0 0 0 0 0
## [5,] 0 0 0 0 1 0 0 0 0 0 0 0 0
## [6,] 0 0 0 0 0 1 0 0 0 0 0 0 0
## [7,] 0 0 0 0 0 0 1 0 0 0 0 0 0
## [8,] 0 0 0 0 0 0 0 1 0 0 0 0 0
## [9,] 0 0 0 0 0 0 0 0 1 0 0 0 0
## [10,] 0 0 0 0 0 0 0 0 0 1 0 0 0
## [11,] 0 0 0 0 0 0 0 0 0 0 1 0 0
## [12,] 0 0 0 0 0 0 0 0 0 0 0 1 0
## [13,] 0 0 0 0 0 0 0 0 0 0 0 0 1Für jede dieser Strukturen hat die Funktion dann automatisch den EBIC mitbestimmt. Diese sind unter ebic abgelegt.
reg_net$results$ebic## [1] 3848.108 3848.427 3848.777 3849.158 3838.489 3838.935 3839.423 3839.954
## [9] 3840.534 3841.166 3841.855 3842.605 3843.423 3833.215 3823.006 3823.908
## [17] 3813.751 3803.658 3782.561 3783.647 3773.731 3763.672 3764.778 3765.982
## [25] 3756.104 3757.257 3758.513 3759.878 3761.364 3751.870 3753.366 3754.994
## [33] 3756.763 3758.688 3760.778 3763.050 3765.516 3768.195 3737.815 3740.574
## [41] 3743.572 3746.827 3750.361 3731.498 3723.963 3716.634 3709.605 3713.964
## [49] 3718.702 3712.578 3717.820 3723.517 3729.707 3736.431 3743.737 3751.674
## [57] 3749.210 3758.522 3768.637 3779.626 3791.566 3793.409 3796.310 3788.930
## [65] 3804.667 3810.438 3828.706 3836.553 3846.066 3868.504 3893.019 3897.005
## [73] 3912.586 3930.102 3961.161 3983.920 3996.667 4022.143 4049.351 4068.050
## [81] 4100.386 4125.118 4176.429 4209.728 4256.744 4321.919 4384.476 4417.105
## [89] 4488.278 4542.934 4574.671 4642.817 4718.780 4791.972 4839.630 4903.552
## [97] 4964.138 4972.465 4985.504 4992.000Der niedrigste dieser Werte hat für die Funktion den Ausschlag gegeben, welche Matrix als Struktur für das optimale Netzwerk ausgewählt wurde. Das Paket nutzt also genau das Vorgehen, dass zu Beginn dieses Abschnitts theoretisch beschrieben wurde.
Zur Veranschaulichung des Einfluss von \(\gamma\) ziehen wir hier nochmal einen Vergleich mit einem größeren Parameter in tuning von 2.
reg_net2 <- estimateNetwork(raw_data, default = "EBICglasso",
nlambda = 100, tuning = 2)## Estimating Network. Using package::function:
## - qgraph::EBICglasso for EBIC model selection
## - using glasso::glassosummary(reg_net2)##
## === Estimated network ===
## Number of nodes: 13
## Number of non-zero edges: 48 / 78
## Mean weight: 0.03710894
## Network stored in object$graph
##
## Default set used: EBICglasso
##
## Use plot(object) to plot estimated network
## Use bootnet(object) to bootstrap edge weights and centrality indices
##
## Relevant references:
##
## Friedman, J. H., Hastie, T., & Tibshirani, R. (2008). Sparse inverse covariance estimation with the graphical lasso. Biostatistics, 9 (3), 432-441.
## Foygel, R., & Drton, M. (2010). Extended Bayesian information criteria for Gaussian graphical models.
## Friedman, J. H., Hastie, T., & Tibshirani, R. (2014). glasso: Graphical lasso estimation of gaussian graphical models. Retrieved from https://CRAN.R-project.org/package=glasso
## Epskamp, S., Cramer, A., Waldorp, L., Schmittmann, V. D., & Borsboom, D. (2012). qgraph: Network visualizations of relationships in psychometric data. Journal of Statistical Software, 48 (1), 1-18.
## Epskamp, S., Borsboom, D., & Fried, E. I. (2016). Estimating psychological networks and their accuracy: a tutorial paper. arXiv preprint, arXiv:1604.08462.Das gewählte Netzwerk hätte jetzt noch 48 Kanten, die ein Gewicht ungleich 0 aufweisen würden. Natürlich ist tuning = 2 ein unrealistisch hoher Wert, da dieser wie empfohlen stets zwischen 0 und 0.5 liegen sollte. Mathematisch macht dies jedoch keinen Unterschied und das Beispiel demonstriert seinen Zweck sehr gut: Ein größerer Hyperparameter \(\gamma\) führt dazu, dass ein Netzwerk mit weniger Gewichten unterschiedlich von 0 ausgewählt wird. Bei anderen Netzwerkkonstellationen wird dort auch ein Unterschied zwischen der Wahl von 0 oder 0.5 vorliegen.
Zum Abschluss dieses Abschnitts wollen wir natürlich das geschätzte Netzwerk auch nochmal zeichnen
plot(reg_net)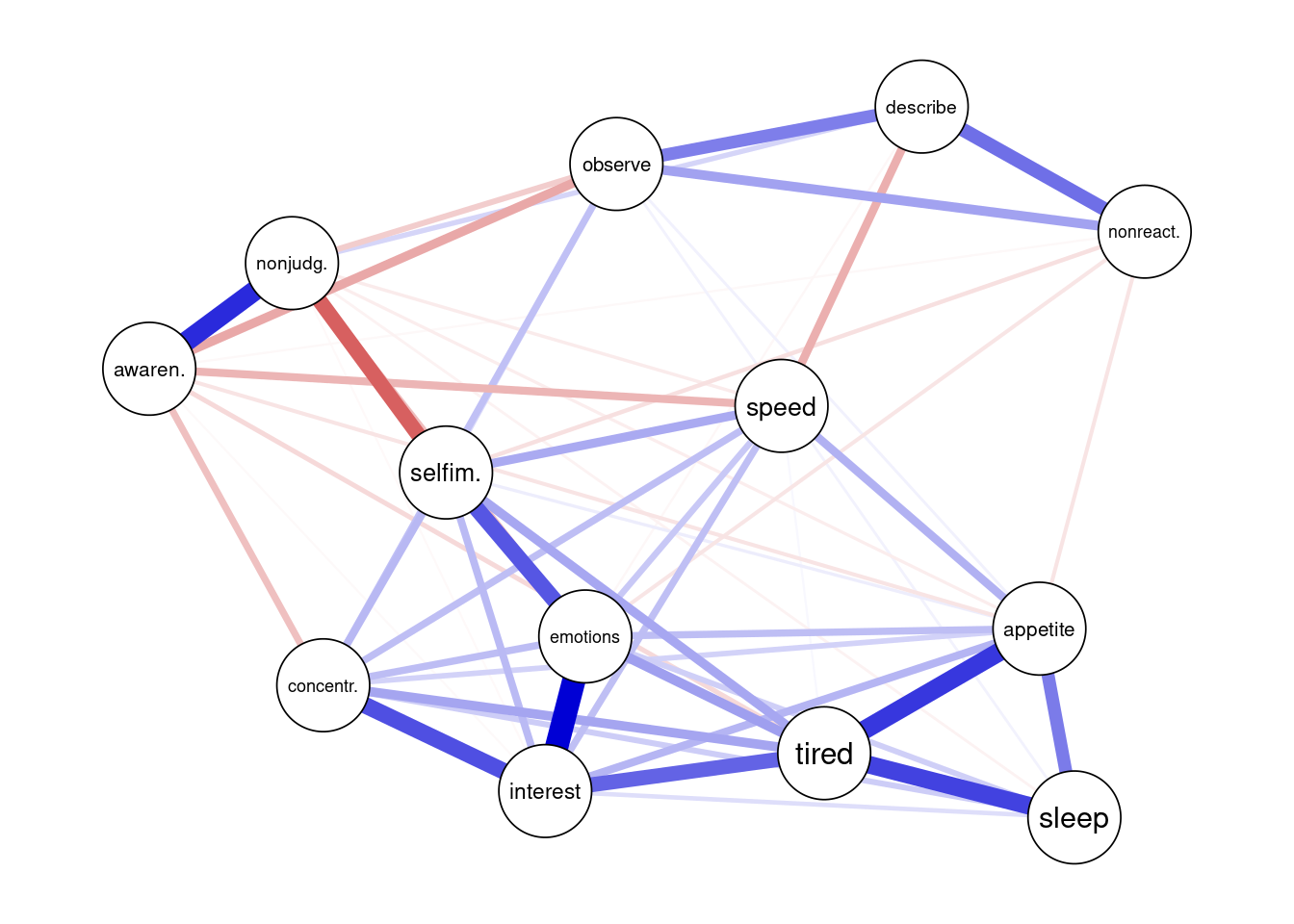
Dabei wird nochmal deutlich, dass einige Kanten nun nicht mehr gezeichnet werden, da sie ein Gewicht von 0 haben. Trotzdem ist die Struktur der beiden Konstrukte noch gut zu erkennen. Die fünf Facetten der Achtsamkeit sind am oberen Rand mit großteils positiven Zusammenhängen, während die depressiven Symptome einen gemeinsamen Kern bilden. Die meisten Verbindungen zwischen den beiden Konstrukten sind dabei auch negativ, was darauf hindeutet, dass Menschen, die eine hohen Achtsamkeit zeigen, auch weniger depressive Symptome zeigen.
Zentralitätsindizes
Nachdem durch die eben durchgeführte Analyse ein Netzwerk für die Präsentation ausgewählt und auch gezeichnet wurde, stellt sich die Frage, welche weiteren Aussagen durch die Netzwerkanalyse durchführbar sind. In den technischen und sozialen Netzwerken wurde dafür die Zentralität der Knoten untersucht. Darin wird durch verschiedene Facetten aufgezeigt, welcher Knoten im Netzwerk am meisten Einfluss hat. Die Aktivierung dieser Knoten sollte zu einer (De-)Aktivierung anderer, verbundener Knoten im Netzwerk führen. Die Herangehensweise wurde mit kleinen Anpassungen für die Psychologischen Netzwerke übernommen. Die Anwendung steht aktuell in der Kritik aufgrund von instabiler Schätzung und der Frage nach inhaltlicher Relevanz. Die methodische Diskussion ist jedoch nicht abgeschlossen. Weiterhin setzt sich ein Maß über die Kritikpunkte (zumindest der Instabilität) hinweg und wird auch zur Beantwortung von Fragestellungen empfohlen, weshalb wir es hier genauer betrachten.
Die Zentralität eines Knoten ist hoch, wenn er starke oder viele Verbindungen hat, alle anderen Knoten schnell erreichbar sind oder viele Verbindungen zwischen anderen Knoten gehen durch diesen Knoten gehen. Im Folgenden werden die Zentralitätsindizes beschrieben und berechnet, die diese Eigenschaften repräsentieren. Während bootnet später wieder zum Einsatz kommt, ist es für die einfache Berechnung der Indizes nicht geeignet, weshalb wir das Paket qgraph aktivieren müssen. Dieses ist bei der Installation von bootnet mitinstalliert worden.
library(qgraph)Einige Zentralitätsindizes werden über die Funktion centrality() gemeinsam berechnet. Als graph Argument braucht man die Struktur des Graphen, die wie besprochen in reg_net$graph vorhanden ist. Wir legen die Resultate erstmal in ein Objekt centrality_indices an und
centrality_indices <- centrality(graph = reg_net$graph)Die Anzahl von Verbindungen eines Knoten zu anderen Knoten im Netzwerk wird üblicherweise als Grad der Zentralität (eng: degree) bezeichnet. Dieser Wert ist besonders in ungewichteten Netzwerken von Interesse. Wenn Gewichte mit im Spiel sind, wird häufig die Stärke des Knoten (eng: strength) betrachtet. Diese wird durch die aufsummierten und gewichteten Werte aller Kanten eines Knoten zu allen anderen im Netzwerk vorhandenen Knoten dargestellt. Um die Stärke eines Knoten zu berechnen, müssen daher nur die Gewichte aller mit ihm verbundenen Kanten aufaddiert werden.
\[s_{i} = \sum^{p}_{j = 1} w_{ij}\]
Die Differenzierung zwischen strength und degree ist leider nicht immer komplett konsistent. Wir werden gleich sehen, dass in R die Ausfabe generell als degree bezeichnet wird, da diese Funktion für ungewichtete als auch gewichtete Netzwerke nutzbar ist. Daher müssen wir uns in dem erstellten Objekt auf den Unterpunkt OutDegree konzentrieren.
centrality_indices$OutDegree## observe describe awaren. nonjudg. nonreact. interest emotions sleep
## 0.6272698 0.5176531 0.6644822 0.7545498 0.4236560 1.0808093 1.1010530 0.6157325
## tired appetite selfim. concentr. speed
## 1.1132789 0.8986216 0.9376854 0.8874701 0.6796151Eine hohe Zahl im Output bedeutet also einen starken direkte Bindung zu anderen Knoten. Den höchsten Wert in unserem Netzwerk hat dabei die Müdigkeit. Noch eine kleine Anmerkung: Die Unterpunkte InDegree und OutDegree im Objekt centrality_indices sind gleich, da es sich um ein ungerichtetes Netzwerk handelt.
Auch eine grafische Übersicht für die Zentralitätsindizes aller Knoten ist im Paket graph integriert. Diese kann mit der Funktion centralityPlot erstellt werden. Im Argument include kann angegeben werden, welche Zentralitätsindizes aufgezeichnet werden sollen. Wir nehmen alle drei besprochenen Werte.
centralityPlot(reg_net, include = c("Strength"))## Note: z-scores are shown on x-axis rather than raw centrality indices.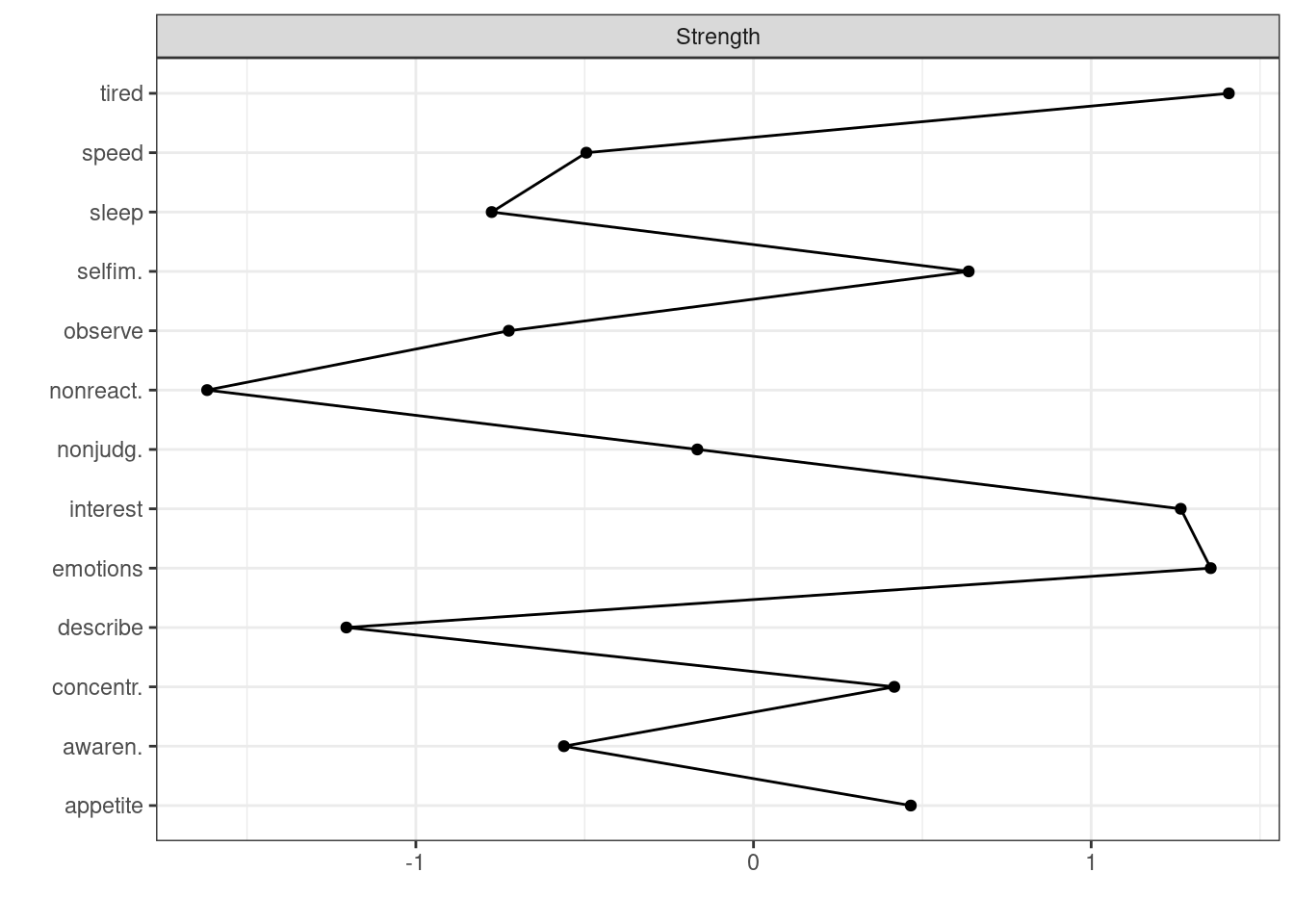
Dabei wird standardmäßig statt der normalen Wert der z-Score ausgegeben. Ein negativer Wert bedeutet hier demnach nicht eine negative Stärke, sondern eine kleinere Stärke im Vergleich zu den anderen Knoten. Wenn man stattdessen die Rohwerte haben möchte, müsste man das Argument scale mit "raw" füllen.
centralityPlot(reg_net, scale = "raw", include = c( "Strength"))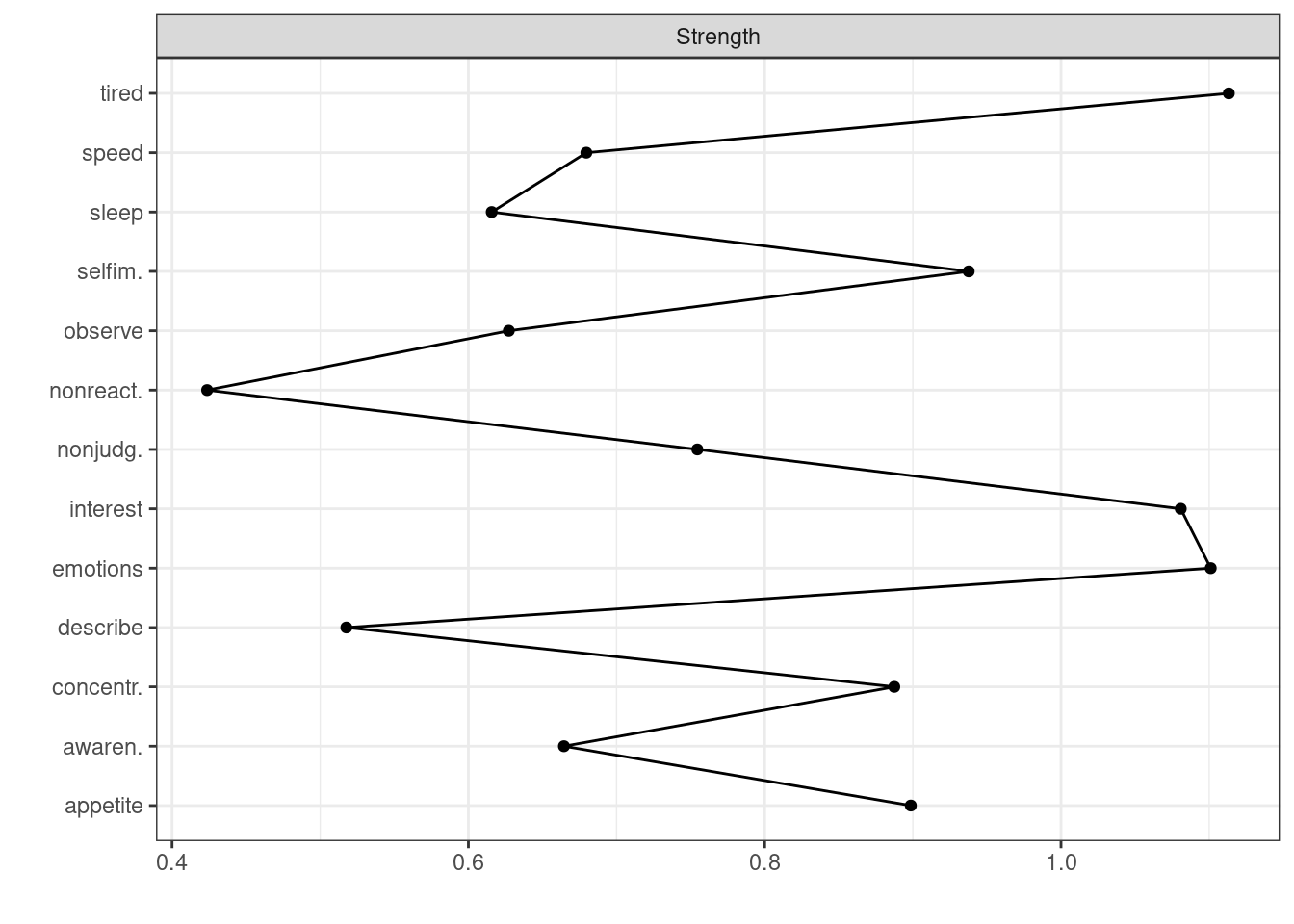
Bootstrap
Ein wichtiges Kriterium für aussagekräftige Parameter einer statistischen Methode ist eine Stabilität in der Schätzung Damit ist bspw. gemeint, dass moderate Änderungen in der Stichprobe zu keinen starken Änderungen in den Ergebnissen führen. Auch erhalten wir für die Gewichte der Kanten nur eine Punktschätzung und keine Sicherheit. In der bisher behandelten Statistik wurden diese Unsicherheiten meist durch die Standardfehler angegeben, die die Berechnung von Konfidenzintervallen ermöglichten. Diese können jedoch für die Netzwerkanalyse nicht so einfach bestimmt werden. Zum Beispiel folgen die Werte der Gewichte auf den Kanten nicht einer benötigten Normalverteilung. Die Zentralitätsindizes sind sogar mit einem Bias versehen. Epskamp et al. (2018a) schlagen als alternativen Weg Bootstrapping vor. Damit soll eine Aussage über die Genauigkeit und Stabilität der Zentralitätsindizes und der Gewichte getroffen werden können.
Beim Bootstrapping wird ein Modell häufiger mit simulierten Daten (genannt parametric) oder einer Stichprobe (genannt non-parametric) der eigentlichen Werte bestimmt. Nochmal etwas detaillierter erklärt: Beim parametrischen Bootstrapping wird die neu geschätzte Struktur als Grundlage für die Simulation von Daten genutzt und mit diesem neuen Datensatz werden die Parameter (Gewichte, Zentralitätsindizies…) noch einmal neu geschätzt. Beim nicht-parametrischen Bootstrapping werden aus dem ursprünglichen Datensatz Beobachtungen (Personen) mit Zurücklegen gezogen und mit diesen wird die Analyse nochmal durchgeführt. Man erhält in beiden Fällen beispielsweise 100 Werte für das Gewicht der Kante zwischen dem Knoten Observe und Interest. Für Netzwerkanalysen wird typischerweise das non-parameteric Bootstrapping genutzt, da die Simulation von Werten aufgrund der Bestrafung bei der Regularisierung weitere Probleme verursacht.
Ein Konfidenzintervall kann danach recht simpel dadurch gebildet werden, dass ein bestimmtes Intervall in der Reihenfolge gesucht wird. Möchte man beispielsweise ein 90%-iges Intervall berichten, liegt dieses zwischen dem 5. und 95. Wert in einer geordneten Abfolge. Dies kann in der Netzwerkanalyse für die Gewichte der Kanten durchgeführt werden. Wichtig ist, dass auch das Konfidenzintervall nicht als Testung der Signifikanz angesehen werden sollte. Bereits die Schätzung des Gewichts als ungleich von 0 während der Regularisierung wird als Zeichen für die Verschiedenheit von 0 angesehen. Die Konfidenzintervalle sollen hingegen Hinweise auf die Stabilität eines Gewichts bieten und eventuell auch für den Vergleich zwischen verschiedenen Werten nützlich sein. Bei den Zentralitätsindizes schlägt dieser einfache Ansatz jedoch aufgrund des Bias fehl und es wurde noch keine passende Methode entwickelt. Deshalb muss die Stabilität hier anders dargestellt werden. Die später auch im Paket verwendete Lösung orientiert sich an der Logik, dass stabile Schätzer auch ähnliche Werte haben sollen, wenn nur einige Beobachtungen aus dem eigentlichen Datensatz zur Verfügung stehen. Dafür werden die Werte der Stärke für alle Knoten einmal für das Netzwerk mit allen Werten und dann für das reduzierte Netzwerk berechnet. Anschließend kann zwischen diesen beiden Werten die Korrelation bestimmt werden, wobei eine hohe Korrelation für eine hohe Stabilität in der Reihenfolge der Stärke in den Daten spricht. Dieses Vorgehen wird auch als case-dropping subset bootstrapping bezeichnet. Dabei kann nun untersucht werden, wie weit der Datensatz reduziert werden kann, ohne unter einen bestimmten Wert in der Korrelation zu gelangen. Hierfür wird im Paket später 0.7 genutzt, da dieser bei Korrelationen als großer Effekt angesehen wird. Definiert wird als correlation stability coefficient (\(CS\)) die maximale Anzahl an Personen, die ausgeschlossen werden kann, ohne dass ein 95%iges Intervall der Korrelationen unter den Threshold von 0.7 fällt. Eine bisherige Simulation zeigt, dass der Koeffizient \(CS\) nicht unter 0.25 sein sollte und am besten über 0.5 - also mindestens 25% sollten ausschließbar sein ohne unter den Threshold zu kommen. Die Entwicklung der Analyse ist in diesem Bereich aber noch nicht so weit, dass diese Werte schon als feste Orientierung dienen sollten. Sie sind erstmal nur eine Orientierung.
In R ist ein solches Vorgehen anhand eines Bootstraps in bootnet integriert (daher auch der Name - Bootstrap in Networks). Der Funktionsname entspricht an dieser Stelle auch dem Paketnamen. Es gibt verschiedene Möglichkeiten, den Input zu gestalten. Wir orientieren uns hier jetzt daran, dass wir die Struktur des Netzwerks bereits durch estimateNetwork() geschätzt und in reg_net abgelegt haben. Im Argument nBoots kann festgelegt werden, wie oft ein Bootstrap gezogen werden soll. Der hier eingegebene Wert von 100 ist sehr niedrig (Standardeinstellung ist bspw. 1000), aber wir wollen erstmal Zeit in der Berechnung sparen. Wenn die Funktion ausgeführt wird, erscheint einiges in der Konsole, was aber nicht spezifisch besprochen werden muss. Um zu zeigen, dass solch eine Aktivität normal ist, lassen wir es aber auch in diesem Tutorial erscheinen. Die Ergebnisse ordnen wir zunächst dem Objekt boot1 zu und lassen uns dessen Inhalt dann grafisch ausgeben. Da es sich beim Bootstrapping auch um eine Zufallsziehung handelt, sollte zur Vergleichbarkeit ein Seed mittels set.seed() festgelegt werden. Die Funktion ist allerdings so geschrieben, dass sie auf verschiedene Kerne zur Berechnung zurückgreift, wodurch dennoch unterschiedliche Ergebnisse resultieren können, wenn man das Vorgehen nicht auf die Durchführung mit einem Kern setzt. Eine simple Lösung ist dabei das von der Funktion bereitgestellte Argument nCores - allerdings wird die Durchführung dadurch auch langsamer, weil die Arbeit nicht mehr aufgeteilt wird. Für dieses Tutorial bleiben wir aber bei dieser schnell umsetzbaren Lösung.
set.seed(2023)
boot1 <- bootnet(reg_net, nBoots = 100, nCores = 1)## Note: bootnet will store only the following statistics: edge, strength, outStrength, inStrength## Estimating sample network...## Estimating Network. Using package::function:
## - qgraph::EBICglasso for EBIC model selection
## - using glasso::glasso## Warning in EBICglassoCore(S = S, n = n, gamma = gamma, penalize.diagonal =
## penalize.diagonal, : A dense regularized network was selected (lambda < 0.1 *
## lambda.max). Recent work indicates a possible drop in specificity. Interpret the
## presence of the smallest edges with care. Setting threshold = TRUE will enforce
## higher specificity, at the cost of sensitivity.## Bootstrapping...##
|
| | 0%
|
|= | 1%
|
|= | 2%
|
|== | 3%
|
|=== | 4%
|
|==== | 5%
|
|==== | 6%
|
|===== | 7%
|
|====== | 8%
|
|====== | 9%
|
|======= | 10%
|
|======== | 11%
|
|======== | 12%
|
|========= | 13%
|
|========== | 14%
|
|========== | 15%
|
|=========== | 16%
|
|============ | 17%
|
|============= | 18%
|
|============= | 19%
|
|============== | 20%
|
|=============== | 21%
|
|=============== | 22%
|
|================ | 23%
|
|================= | 24%
|
|================== | 25%
|
|================== | 26%
|
|=================== | 27%
|
|==================== | 28%
|
|==================== | 29%
|
|===================== | 30%
|
|====================== | 31%
|
|====================== | 32%
|
|======================= | 33%
|
|======================== | 34%
|
|======================== | 35%
|
|========================= | 36%
|
|========================== | 37%
|
|=========================== | 38%
|
|=========================== | 39%
|
|============================ | 40%
|
|============================= | 41%
|
|============================= | 42%
|
|============================== | 43%
|
|=============================== | 44%
|
|================================ | 45%
|
|================================ | 46%
|
|================================= | 47%
|
|================================== | 48%
|
|================================== | 49%
|
|=================================== | 50%
|
|==================================== | 51%
|
|==================================== | 52%
|
|===================================== | 53%
|
|====================================== | 54%
|
|====================================== | 55%
|
|======================================= | 56%
|
|======================================== | 57%
|
|========================================= | 58%
|
|========================================= | 59%
|
|========================================== | 60%
|
|=========================================== | 61%
|
|=========================================== | 62%
|
|============================================ | 63%
|
|============================================= | 64%
|
|============================================== | 65%
|
|============================================== | 66%
|
|=============================================== | 67%
|
|================================================ | 68%
|
|================================================ | 69%
|
|================================================= | 70%
|
|================================================== | 71%
|
|================================================== | 72%
|
|=================================================== | 73%
|
|==================================================== | 74%
|
|==================================================== | 75%
|
|===================================================== | 76%
|
|====================================================== | 77%
|
|======================================================= | 78%
|
|======================================================= | 79%
|
|======================================================== | 80%
|
|========================================================= | 81%
|
|========================================================= | 82%
|
|========================================================== | 83%
|
|=========================================================== | 84%
|
|============================================================ | 85%
|
|============================================================ | 86%
|
|============================================================= | 87%
|
|============================================================== | 88%
|
|============================================================== | 89%
|
|=============================================================== | 90%
|
|================================================================ | 91%
|
|================================================================ | 92%
|
|================================================================= | 93%
|
|================================================================== | 94%
|
|================================================================== | 95%
|
|=================================================================== | 96%
|
|==================================================================== | 97%
|
|===================================================================== | 98%
|
|===================================================================== | 99%
|
|======================================================================| 100%## Computing statistics...## Warning: `tbl_df()` was deprecated in dplyr 1.0.0.
## ℹ Please use `tibble::as_tibble()` instead.
## ℹ The deprecated feature was likely used in the bootnet package.
## Please report the issue to the authors.##
|
| | 0%
|
|= | 1%
|
|= | 2%
|
|== | 3%
|
|=== | 4%
|
|==== | 5%
|
|==== | 6%
|
|===== | 7%
|
|====== | 8%
|
|====== | 9%
|
|======= | 10%
|
|======== | 11%
|
|======== | 12%
|
|========= | 13%
|
|========== | 14%
|
|========== | 15%
|
|=========== | 16%
|
|============ | 17%
|
|============= | 18%
|
|============= | 19%
|
|============== | 20%
|
|=============== | 21%
|
|=============== | 22%
|
|================ | 23%
|
|================= | 24%
|
|================== | 25%
|
|================== | 26%
|
|=================== | 27%
|
|==================== | 28%
|
|==================== | 29%
|
|===================== | 30%
|
|====================== | 31%
|
|====================== | 32%
|
|======================= | 33%
|
|======================== | 34%
|
|======================== | 35%
|
|========================= | 36%
|
|========================== | 37%
|
|=========================== | 38%
|
|=========================== | 39%
|
|============================ | 40%
|
|============================= | 41%
|
|============================= | 42%
|
|============================== | 43%
|
|=============================== | 44%
|
|================================ | 45%
|
|================================ | 46%
|
|================================= | 47%
|
|================================== | 48%
|
|================================== | 49%
|
|=================================== | 50%
|
|==================================== | 51%
|
|==================================== | 52%
|
|===================================== | 53%
|
|====================================== | 54%
|
|====================================== | 55%
|
|======================================= | 56%
|
|======================================== | 57%
|
|========================================= | 58%
|
|========================================= | 59%
|
|========================================== | 60%
|
|=========================================== | 61%
|
|=========================================== | 62%
|
|============================================ | 63%
|
|============================================= | 64%
|
|============================================== | 65%
|
|============================================== | 66%
|
|=============================================== | 67%
|
|================================================ | 68%
|
|================================================ | 69%
|
|================================================= | 70%
|
|================================================== | 71%
|
|================================================== | 72%
|
|=================================================== | 73%
|
|==================================================== | 74%
|
|==================================================== | 75%
|
|===================================================== | 76%
|
|====================================================== | 77%
|
|======================================================= | 78%
|
|======================================================= | 79%
|
|======================================================== | 80%
|
|========================================================= | 81%
|
|========================================================= | 82%
|
|========================================================== | 83%
|
|=========================================================== | 84%
|
|============================================================ | 85%
|
|============================================================ | 86%
|
|============================================================= | 87%
|
|============================================================== | 88%
|
|============================================================== | 89%
|
|=============================================================== | 90%
|
|================================================================ | 91%
|
|================================================================ | 92%
|
|================================================================= | 93%
|
|================================================================== | 94%
|
|================================================================== | 95%
|
|=================================================================== | 96%
|
|==================================================================== | 97%
|
|===================================================================== | 98%
|
|===================================================================== | 99%
|
|======================================================================| 100%plot(boot1, order = "sample", labels = F)## Warning: `mutate_()` was deprecated in dplyr 0.7.0.
## ℹ Please use `mutate()` instead.
## ℹ See vignette('programming') for more help
## ℹ The deprecated feature was likely used in the dplyr package.
## Please report the issue at <]8;;https://github.com/tidyverse/dplyr/issueshttps://github.com/tidyverse/dplyr/issues]8;;>.## Warning: `select_()` was deprecated in dplyr 0.7.0.
## ℹ Please use `select()` instead.
## ℹ The deprecated feature was likely used in the dplyr package.
## Please report the issue at <]8;;https://github.com/tidyverse/dplyr/issueshttps://github.com/tidyverse/dplyr/issues]8;;>.## Warning: `summarise_()` was deprecated in dplyr 0.7.0.
## ℹ Please use `summarise()` instead.
## ℹ The deprecated feature was likely used in the dplyr package.
## Please report the issue at <]8;;https://github.com/tidyverse/dplyr/issueshttps://github.com/tidyverse/dplyr/issues]8;;>.## Warning: `group_by_()` was deprecated in dplyr 0.7.0.
## ℹ Please use `group_by()` instead.
## ℹ See vignette('programming') for more help
## ℹ The deprecated feature was likely used in the dplyr package.
## Please report the issue at <]8;;https://github.com/tidyverse/dplyr/issueshttps://github.com/tidyverse/dplyr/issues]8;;>.## Warning: `filter_()` was deprecated in dplyr 0.7.0.
## ℹ Please use `filter()` instead.
## ℹ See vignette('programming') for more help
## ℹ The deprecated feature was likely used in the dplyr package.
## Please report the issue at <]8;;https://github.com/tidyverse/dplyr/issueshttps://github.com/tidyverse/dplyr/issues]8;;>.## Warning: `arrange_()` was deprecated in dplyr 0.7.0.
## ℹ Please use `arrange()` instead.
## ℹ See vignette('programming') for more help
## ℹ The deprecated feature was likely used in the dplyr package.
## Please report the issue at <]8;;https://github.com/tidyverse/dplyr/issueshttps://github.com/tidyverse/dplyr/issues]8;;>.## Warning: `gather_()` was deprecated in tidyr 1.2.0.
## ℹ Please use `gather()` instead.
## ℹ The deprecated feature was likely used in the bootnet package.
## Please report the issue to the authors.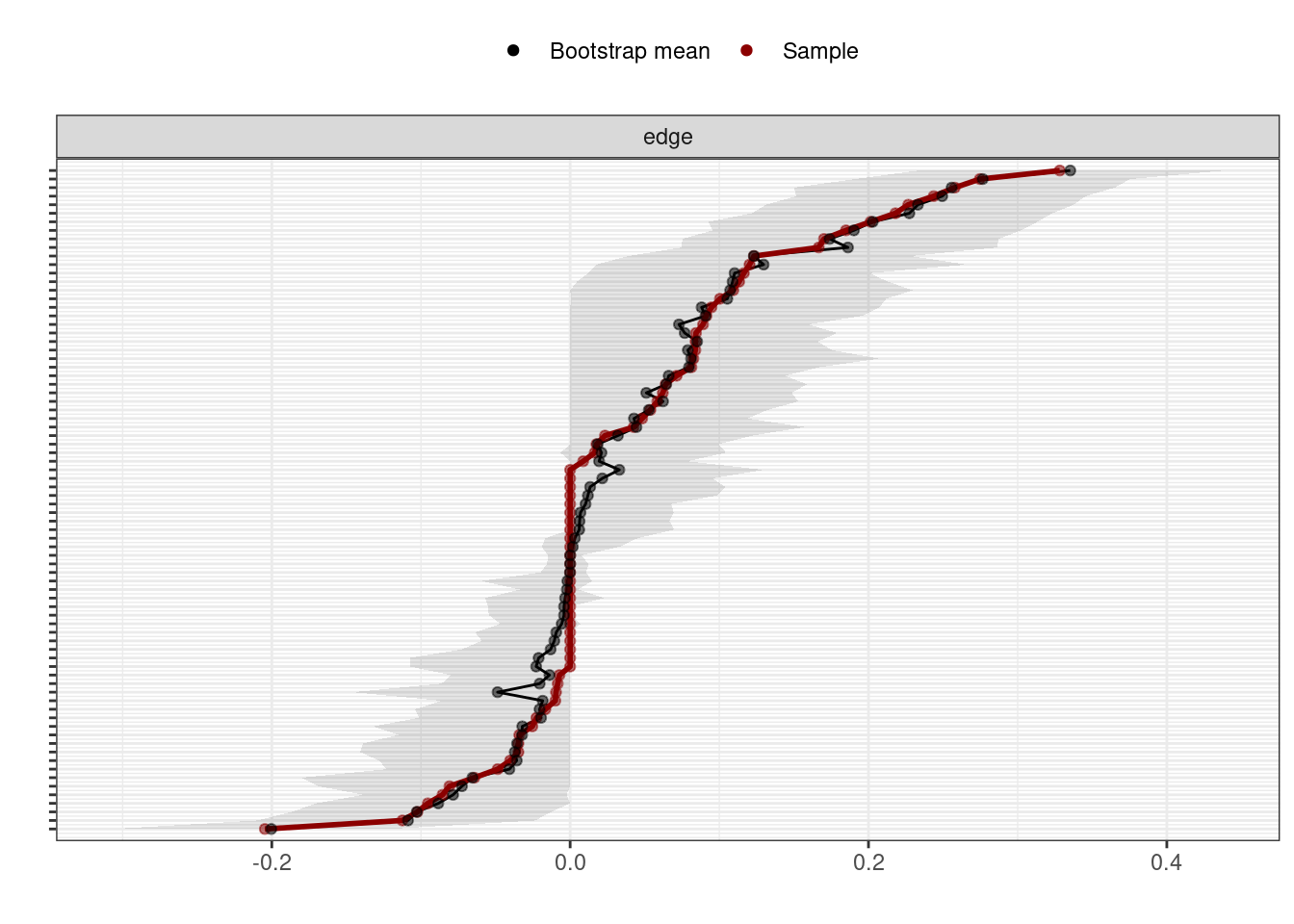
Die angegebenen Warnings betreffen eher den Code der Funktion bzw. des Paketes und können von uns nicht verändert werden. Abgebildet werden die Gewichte von allen Kanten zwischen zwei Knoten. Einmal wird die Punktschätzung angezeigt anhand der roten Linie. Weiterhin wird der Mittelwert für die berechneten Werten aus den Bootstrap durch die schwarze Linie gezeigt. Der graue Bereich gibt das Konfidenzintervall der Schätzungen an. Wir können hierbei sehen, dass die berechneten Werte gute Repräsentanten sind.
Neben der Berechnung der Konfidenzintervalle für die Gewichte der Kanten, kann auch die Stabilität der Zentrailitätsindizes über die Funktion bootnet betrachtet werden. Dafür müssen nur die Argumente angepasst werden. Für nBoot bleiben wir auch hier zunächst beim zu kleinen aber zeitsparenderem Wert von 300. In statistics können die Statistiken angegeben werden, für die die Untersuchung der Stabilität durchgeführt werden soll. Hier geben wir also "Strength" ein. Wir ordnen diese neue Operation dem Objekt boot2 zu und lassen auch dieses uns wieder durch die plot-Funktion anzeigen. In type wird festgehalten, dass wir bei der Analyse im Subset Personen ausschließen wollen. Möglich wäre auch der Ausschluss von Knoten, dieser ist aber schwieriger zu interpretieren und wird daher nicht genauer betrachtet. In caseMin wird festgehalten, wie viele Personen minimal für die Analyse entfernt werden sollen - an diesem Ort beginnt sozusagen die Suche nach dem Unterschreiten des Thresholds. Bei caseMax ist folglich die maximale Anzahl festgelegt. caseN bestimmt die Anzahl an Zwischenschritten zwischen den beiden Extremen. Zu Zwecken der Anschaulichkeit wollen wir am liebsten Schritte in 5% und erreichen das durch die Anzahl von 15. Auch bei der Durchführung dieses Codes erscheinen wieder viele Sachen in der Konsole, die auf Pandar aber augeblendet werden, um die Länge der Seite zu kürzen.
set.seed(2023)
boot2 <- bootnet(reg_net, nBoots = 300,
statistics = c("strength"),
type = "case", caseMin = 0.05,
caseMax = 0.75, caseN = 15,
nCores = 1)
plot(boot2, c("strength"))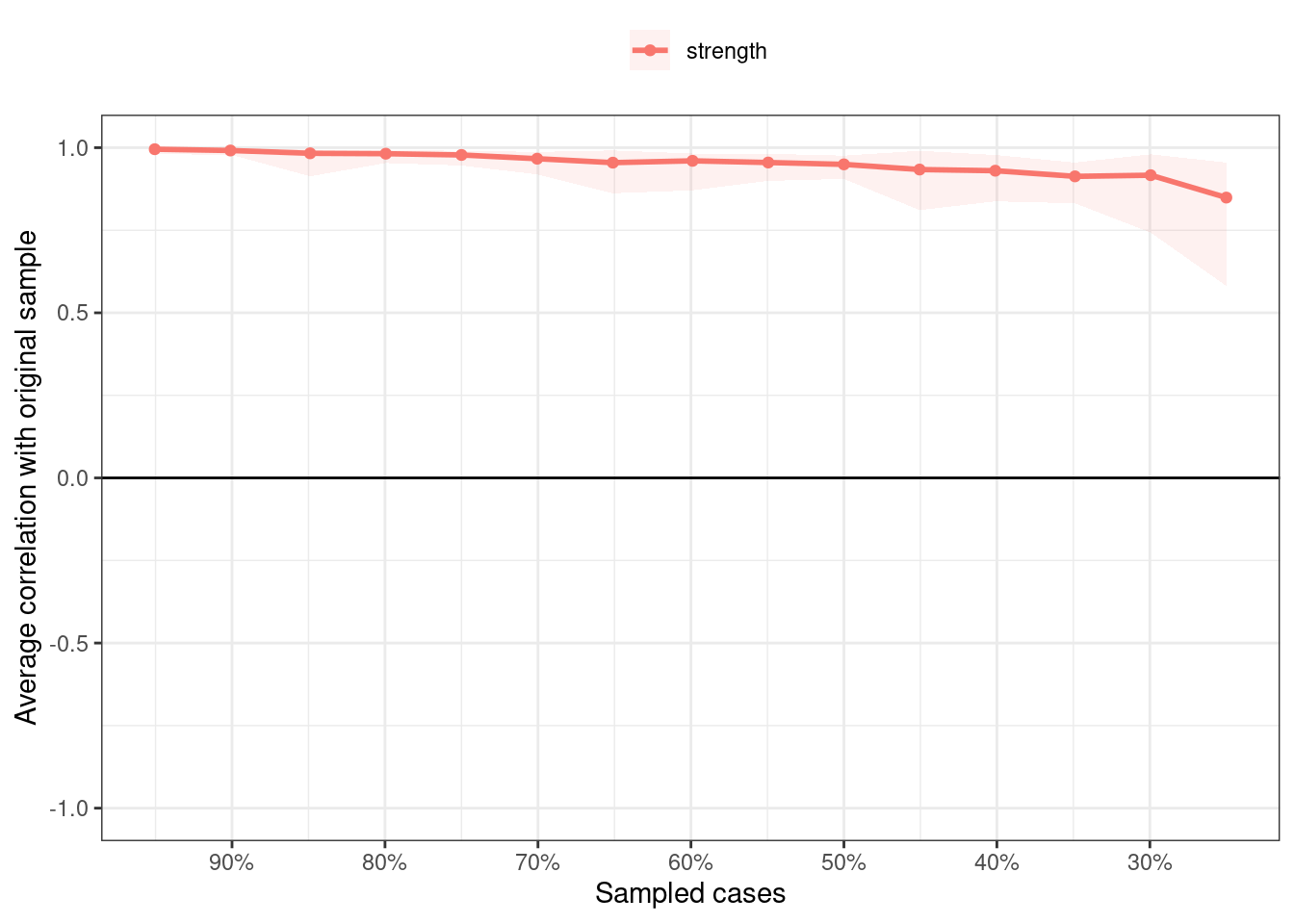
Die Stabilität sieht zunächst sehr gut aus. Um nicht mit einem Lineal die Werte prüfen zu müssen, können mit der Funktion corStability die \(CS\)-Werte bestimmt werden. Dafür müssen wir diese auf den durchgeführten Bootstrap anwenden. Ein weiteres Argument ist die Korrelation zwischen ganzem Datensatz und Subset (cor), die wir aber auf der Standardeinstellung und Empfehlung von 0.7 belassen.
corStability(boot2, cor = 0.7)## === Correlation Stability Analysis ===
##
## Sampling levels tested:
## nPerson Drop% n
## 1 96 75.0 15
## 2 115 70.1 22
## 3 134 65.1 23
## 4 154 59.9 18
## 5 173 54.9 26
## 6 192 50.0 20
## 7 211 45.1 24
## 8 230 40.1 16
## 9 250 34.9 19
## 10 269 29.9 20
## 11 288 25.0 24
## 12 307 20.1 16
## 13 326 15.1 24
## 14 346 9.9 17
## 15 365 4.9 16
##
## Maximum drop proportions to retain correlation of 0.7 in at least 95% of the samples:
##
## strength: 0.701
## - For more accuracy, run bootnet(..., caseMin = 0.651, caseMax = 0.75)
##
## Accuracy can also be increased by increasing both 'nBoots' and 'caseN'.Anhand der ausgegebenen Tabelle sehen wir zunächst, dass die Boots zufällig auf die verschiedenen Größen verteilt werden. Es wird also nicht jede prozentuale Reduzierung 300 mal durchgeführt. Dies ist ein deutliches Zeichen, dass eine höhere Anzahl in nBoots auf jeden Fall nötig wäre, damit die Ergebnisse für jede einzelne prozentuale Reduzierung weniger abhängig vom Zufall wäre und auch gleichmäßigere Verteilung in der Anzahl an Bootstraps zwischen den Cases ermöglicht wird. Strength unterschreitet selbst bei der von uns maximal eingestellten Reduktion um 75% nicht den Threshold. Werte der Strength können demnach als sehr stabil betrachtet und interpretiert werden. Gleichzeitig gibt die Funktion auch nochmal eine Empfehlung, wie ein noch spezifischerer Wert gefunden werden könnte anhand der Anpassung von caseMin und caseMax.
Fazit
Die Netzwerkanalyse für psychologische Konstrukte ist ein sich noch entwickelndes Gebiet. Sie wird kein Ersatz der typischen latenten Modelle sein können, für die Visualisierung und spezifischere Betrachtung der Dynamik zwischen Symptomen aber in jedem Fall hilfreich sein. Die genaue Vorgehensweise der Schätzung und Interpretation sind aktuell ein Thema der methodischen Forschung. Dabei ist auch in der Diskussion, welche Fragestellungen beantwortet werden können (vor allem im querschnittlichen Ansatz), da eine kausale Untersuchung mit ungericheteten Kanten natürlich nicht zulässig ist. Die Anwendungen konzentrieren sich deshalb vor allem auf die Untersuchung der Topografie eines Netzwerks für eine Störung, die Betrachtung von verbindenden Knoten und Kanten bei Netzwerken, die zwei verschiedene Konstrukte erhalten, und den Vergleich der Netzwerkstruktur zwischen zwei Gruppen (bspw. Gesunde und Kranke). In der nächsten Sitzung beschäftigen wir uns mit einem Ansatz, der längsschnittliche Daten mit der Netzwerkanalyse betrachtet.
Literatur
Epskamp, S., Borsboom, D., & Fried, E. I. (20181). Estimating psychological networks and their accuracy: A tutorial paper. Behav Res, 50, 195-212. https://doi.org/10.3758/s13428-017-0862-1
Epskamp, S., & Fried, E. I. (2018b). A tutorial on regularized partial correlation networks. Psychological Methods, 23(4), 617-634. https://doi.org/10.1037/met0000167
Foygel, R., & Drton, M. (2010). Extended Bayesian information criteria for Gaussian graphical models. Advances in Neural Information Processing Systems, 23, 604–612.
Friedman, J., Hastie, T., & Tibshirani, R. (2008). Sparse inverse covariance estimation with the graphical lasso. Biostatistics, 9(3), 432-441. https://doi.org/10.1093/biostatistics/kxm045
- Blau hinterlegte Autor:innenangaben führen Sie direkt zur universitätsinternen Ressource.
Appendix A: Weitere (veraltete) Zentralitätsindizes
Wie im Haupttext des Tutorials angesprochen, wurden auch andere Kennwerte für die Zentralität aus den technischen Netzwerken in die Psychologie übernommen. Es konnte allerdings gezeigt werden, dass die Stabilität von diesen sehr schlecht ist und auch ihre theoretische Fundierung wurde im Psychologischen Kontext in Frage gestellt. Wir wollen mit diesem Abschnitt nicht ihre Nutzung empfehlen, sondern über die Hintergründe aufklären (und auch nochmal die Instabilität aufzeigen).
Die Verbundenheit (eng: closeness) von Knoten quantifiziert ihre Beziehungen im Netzwerk anhand ihrer indirekten Verbindungen mit anderen Knoten. Hohe Verbundenheit charakterisiert im Mittel eine kurze Distanz von einem Knoten zu allen anderen Knoten. Knoten mit hoher Verbundenheit sind leicht von Veränderungen in einem beliebigen Part des Netzwerks betroffen und beeinflussen im Gegenzug leicht andere Knoten.
centrality_indices$Closeness## observe describe awaren. nonjudg. nonreact. interest
## 0.005309487 0.004851783 0.006077910 0.006195131 0.003997788 0.007024477
## emotions sleep tired appetite selfim. concentr.
## 0.006462039 0.005168103 0.006378376 0.005771059 0.007100752 0.006762420
## speed
## 0.006590195Insgesamt bitet sich ein sehr homogenes Bild in der Verbundenheit. Einige Knoten haben starke Verbindungen zu allen anderen Knoten. Das Maximum ist bei Selfimage zu finden.
Die Dazwischenheit (eng: betweenness) eines Knoten gibt Informationen über die Wichtigkeit eines Knotens im Rahmen der kürzesten Verbindungen zwischen zwei anderen Knoten. Dafür wird für jede Kombination an zwei Knoten der kürzeste Weg zwischen ihnen berechnet (also die stärkste Verbindung). Anschließend bekommt jeder Knoten, der auf diesem kürzesten Weg ist (ausgenommen der beiden Punkte, um die es geht), “einen Punkt” in Dazwischenheit. Durch einen Knoten mit hoher Dazwischenheit gehen also viele kürzeste Wege zwischen zwei anderen Knoten.
centrality_indices$Betweenness## observe describe awaren. nonjudg. nonreact. interest emotions sleep
## 16 12 8 12 0 12 6 0
## tired appetite selfim. concentr. speed
## 26 12 26 14 22In Dazwischenheit ist es üblich, dass die Werte stärker fluktuieren. In dem hier abgebildeten Netzwerk sind wieder die Knoten für Müdigkeit und Selfimage mit den höchsten Werten zu finden.
Wie im Tutorial berichtet, kann mit der Funktion centralityPlot() eine Übersicht über die Parameter erstellt werden. Im Argument include können also auch mehrere Parameter aufgeführt werden.
centralityPlot(reg_net, include = c("Closeness", "Betweenness"))## Note: z-scores are shown on x-axis rather than raw centrality indices.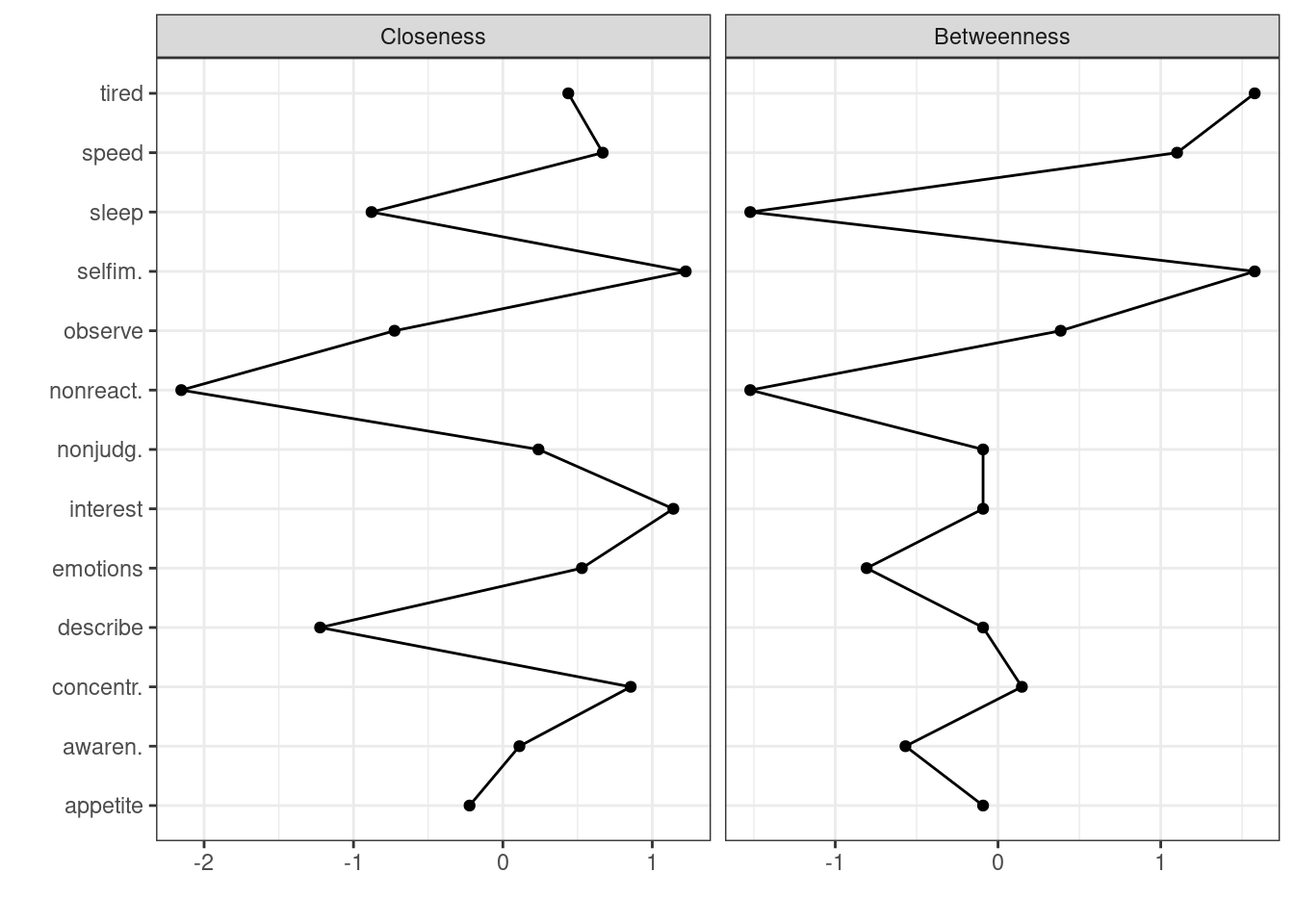
Auch der besprochene Parameter \(CS\) kann nicht nur für Strength, sondern auch für die Zentralitätsindizes bestimmt werden. Dafür nutzen wir im Tutorial beschrieben erstmal die Funktion bootnet(), um in statistics jetzt die beiden interessierende Indizes einzutragen. Die anderen Einstellungen lassen wir gleich.
set.seed(2023)
boot3 <- bootnet(reg_net, nBoots = 300,
statistics = c("betweenness", "closeness"),
type = "case", caseMin = 0.05,
caseMax = 0.75, caseN = 15,
nCores = 1)
plot(boot3, c("betweenness","closeness"))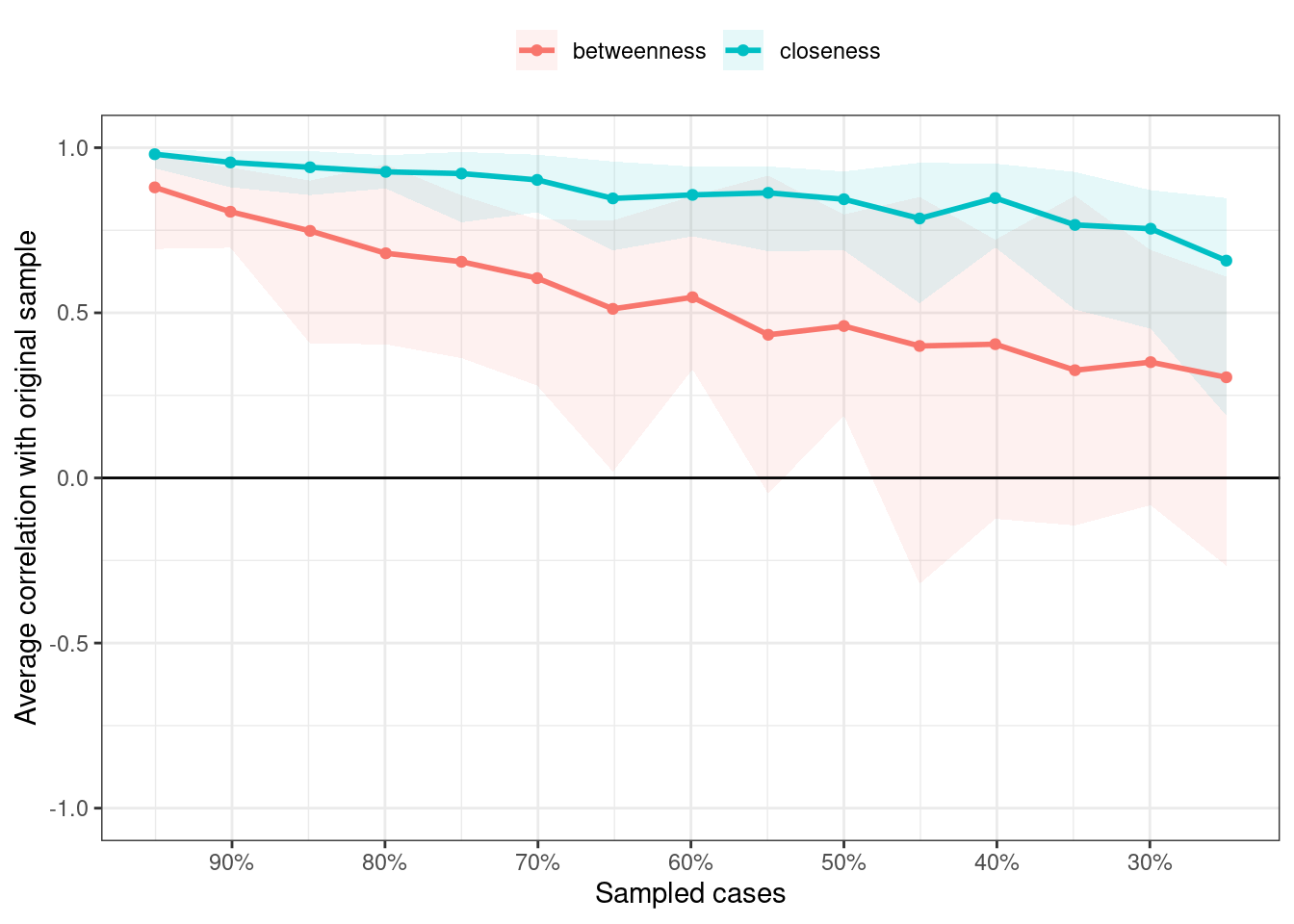
Aus der Grafik lässt sich bereits erschließen, dass Betweenness die Ansprüche an die Stabilität nicht erfüllt. Daher sollte man die Interpretation der Betweenness-Werte der Knoten nicht durchführen. Closeness ist hingegen ein wenig stabiler. Wir nutzen auch nochmal die Funktion corStability() auf unser neues Objekt boot3.
corStability(boot3, cor = 0.7)## === Correlation Stability Analysis ===
##
## Sampling levels tested:
## nPerson Drop% n
## 1 96 75.0 15
## 2 115 70.1 22
## 3 134 65.1 23
## 4 154 59.9 18
## 5 173 54.9 26
## 6 192 50.0 20
## 7 211 45.1 24
## 8 230 40.1 16
## 9 250 34.9 19
## 10 269 29.9 20
## 11 288 25.0 24
## 12 307 20.1 16
## 13 326 15.1 24
## 14 346 9.9 17
## 15 365 4.9 16
##
## Maximum drop proportions to retain correlation of 0.7 in at least 95% of the samples:
##
## betweenness: 0
## - For more accuracy, run bootnet(..., caseMin = 0, caseMax = 0.049)
##
## closeness: 0.451
## - For more accuracy, run bootnet(..., caseMin = 0.401, caseMax = 0.5)
##
## Accuracy can also be increased by increasing both 'nBoots' and 'caseN'.Bezüglich der \(CS\)-Werte wird deutlich, dass Betweenness direkt beim ersten Test mit einer Reduzierung von 5% unter die Ansprüche in der Korrelation kommt. Deshalb wird hier ein Wert von 0 ausgegeben. Für Closeness ist die Unterschreitung auch früher gegeben. Insgeamt sollten diese Werte also nicht interpretiert werden.