Deskriptivstatistik für Intervallskalen
Kernfragen dieser Lehreinheit
- Was ist der Befehl um den Mittelwert zu bestimmen?
- Wie kann die empirische Varianz bestimmt werden? Wie unterscheidet sich diese von der mit
var()bestimmten Varianz? - Wie können Variablen zentriert und standardisiert werden?
- Welche Möglichkeiten gibt es, negativ formulierte Items zu rekodieren?
- Mit welchen Befehlen können in R Skalenwerte für Fragebögenitems erstellt werden?
Wiederholung aus der Vorlesung: Skalenniveaus
| Skala | Aussage | Transformation | Zentrale Lage | Dispersion |
|---|---|---|---|---|
| Nominal | Äquivalenz | eineindeutig | Modus | Relativer Informationsgehalt |
| Ordinal | Ordnung | monoton | Median | Interquartilsbereich |
| Intervall | Verhältnis von Differenzen | positiv linear | Mittelwert | Standardabweichung, Varianz |
| Verhältnis | Verhältnisse | Ähnlichkeit | … | … |
| Absolut | absoluter Wert | Identität | … | … |
Vorbereitende Schritte
Den Datensatz haben wir bereits über diesen Link heruntergeladen und können ihn über den lokalen Speicherort einladen oder Sie können Ihn direkt mittels des folgenden Befehls aus dem Internet in das Environment bekommen. Im letzten Tutorial und den dazugehörigen Aufgaben haben wir bereits Änderungen am Datensatz durchgeführt, die hier nochmal aufgeführt sind, um den Datensatz auf dem aktuellen Stand zu haben:
#### Was bisher geschah: ----
# Daten laden
load(url('https://pandar.netlify.app/post/fb22.rda'))
# Nominalskalierte Variablen in Faktoren verwandeln
fb22$geschl_faktor <- factor(fb22$geschl,
levels = 1:3,
labels = c("weiblich", "männlich", "anderes"))
fb22$fach <- factor(fb22$fach,
levels = 1:5,
labels = c('Allgemeine', 'Biologische', 'Entwicklung', 'Klinische', 'Diag./Meth.'))
fb22$ziel <- factor(fb22$ziel,
levels = 1:4,
labels = c("Wirtschaft", "Therapie", "Forschung", "Andere"))
fb22$wohnen <- factor(fb22$wohnen,
levels = 1:4,
labels = c("WG", "bei Eltern", "alleine", "sonstiges"))Mindestens intervallskalierte Variablen
Klassische mindestens intervallskalierte Variablen
- Behaviorale Maße: Reaktionszeiten, Bearbeitungsdauer, Anzahl von Fehlern, …
- Biologische Maße: Hautleitfähigkeit, Stimmhöhe, Anzahl der Sakkaden, …
- Neurophysiologische Maße: EEG-Daten, Durchblutung von Hirnregionen, …
Konstruierte mindestens intervallskalierte Variablen
- Fragebogendaten werden meist ordinalskaliert erhoben (einzelne Items)
- Um Intervallskalenniveau zu erreichen, werden Items zu Skalenwerten verrechnet (Summe oder Mittelwert)
- Erzeugt viele mögliche Ausprägungen und wird als intervallskaliert behandelt
Beispiel: Lebenszufriedenheit
Der Mittelwert pro Person über alle 5 Items ist in der Spalte lz zu finden. Dies ist also der Skalenwert für die Lebenszufriedenheit jeder einzelnen Person.
fb22$lz## [1] 5.4 6.0 3.0 6.0 3.2 5.8 4.2 NA 5.4 4.6 4.8 5.4 5.0 4.8 6.6 6.0 5.0 6.0
## [19] 3.6 5.0 5.8 4.6 4.8 6.4 4.2 4.6 NA 5.8 6.4 4.0 4.2 5.8 4.2 5.0 5.2 6.2
## [37] 5.2 5.4 4.2 5.2 4.8 2.8 3.4 5.6 3.4 4.2 4.2 5.0 6.0 5.0 4.6 5.8 3.6 3.2
## [55] 4.0 4.6 4.8 4.6 4.8 5.0 5.4 4.4 5.2 2.6 3.8 6.6 4.8 3.6 5.8 5.8 4.6 6.2
## [73] 5.2 5.4 5.0 1.4 4.6 4.8 5.4 2.8 3.2 2.4 5.4 2.2 4.8 6.0 5.2 4.8 5.8 5.6
## [91] 4.6 4.4 5.4 5.4 3.8 5.6 5.6 4.2 4.6 6.2 3.8 4.2 3.8 3.8 5.4 4.6 5.2 3.6
## [109] 2.4 4.2 4.4 3.2 4.2 4.0 2.6 2.0 4.6 5.2 4.4 1.8 4.6 4.4 5.4 5.0 6.0 3.0
## [127] 4.8 6.0 3.4 6.4 3.6 5.2 5.0 4.8 5.8 4.8 5.8 5.2 5.2 6.4 4.8 3.8 4.6 2.6
## [145] 6.0 5.0 5.6 3.2 4.4 6.4 5.8 5.2 5.2 3.6 5.8 3.0 5.6 4.2 5.4Deskriptivstatistik für mindestens intervallskalierte Variablen
- Verfahren sind “rückwärtskompatibel”, d.h. alle Berechnungen, die auf nominalskalierte und ordinalskalierte Variablen anwendbar sind, lassen sich auch auf mindestens intervallskalierte Variablen anwenden
- Quantile, IQA und Median können weiterhin bestimmt werden
# Minimum & Maximum
range(fb22$lz, na.rm=T)## [1] 1.4 6.6# Quartile
quantile(fb22$lz, c(.25, .5, .75), na.rm=T)## 25% 50% 75%
## 4.2 4.8 5.4#Box-Whisker Plot
boxplot(fb22$lz)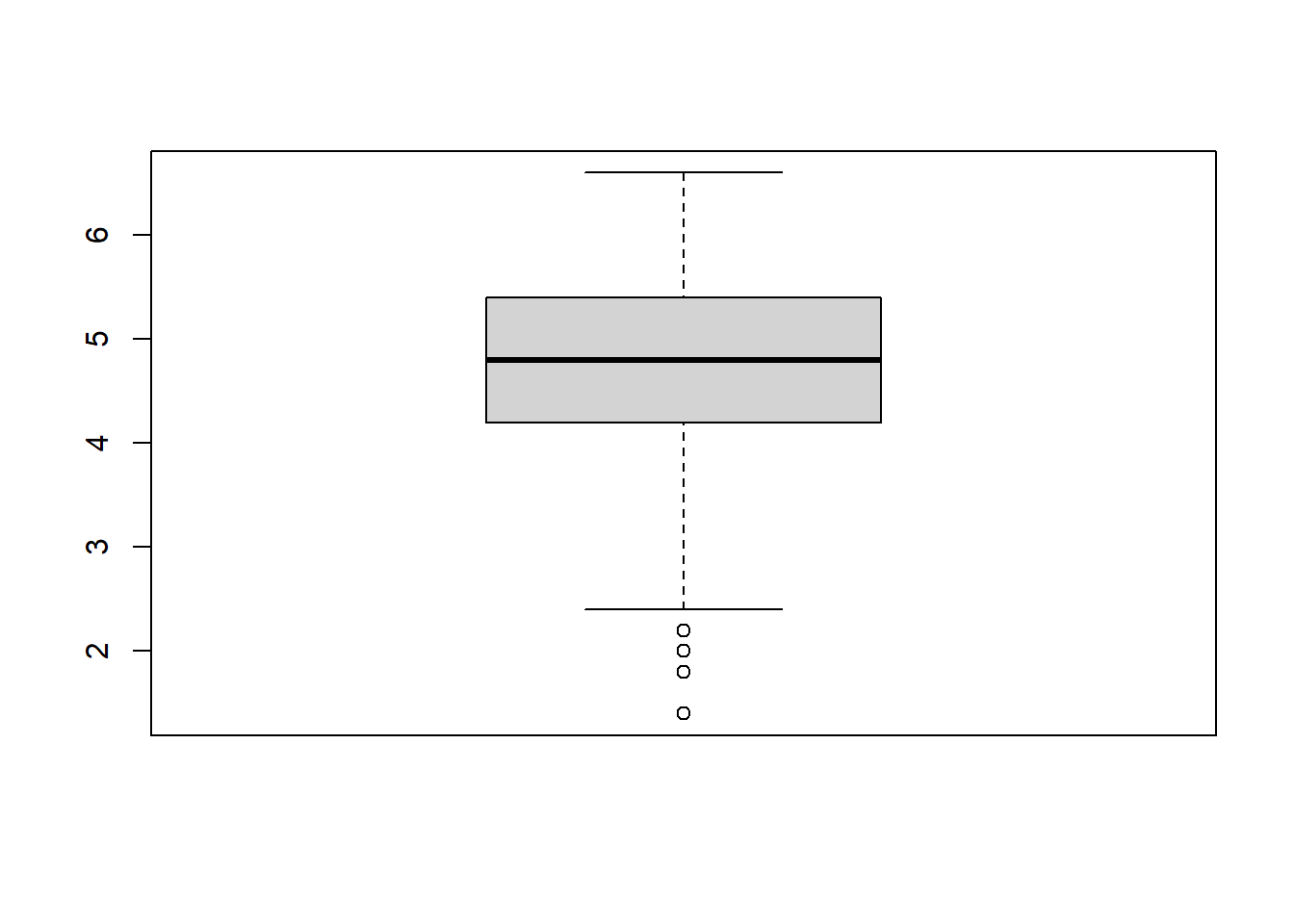
Histogramme
Für intervallskalierte Daten ist eine beliebte grafische Darstellungsform das Histogramm. Dieses fasst die kontinuierlichen Werte in Klassen (Kategorien, Intervalle) zusammen. Anschließend wird eine Häufigkeitsverteilung (ähnlich dem Barplot) für die kategorisierten Daten erstellen (sekundäre Häufigkeitsverteilung) erstellt. Grundlegend kann solch eine Grafik über den Befehl hist() angefordert werden.
# Histogramm
hist(fb22$lz)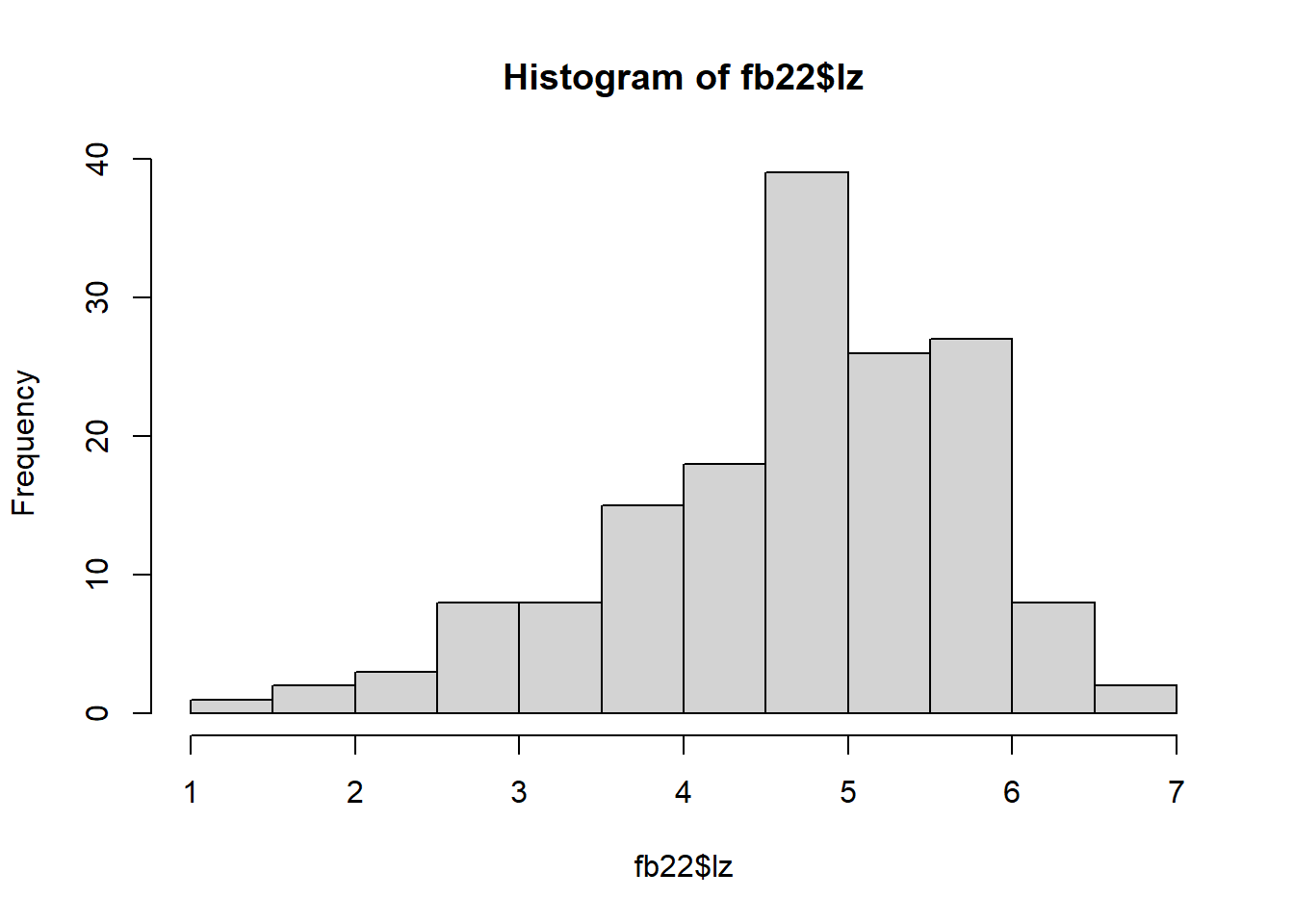
Natürlich kann man auch hier zusätzliche Argumente nutzen, die die Optik des Histogramms verändern. Dabei können beispielsweise Farbe, Achsenbeschriftungen oder auch der Titel verändert werden. Damit haben wir uns aber bereits auseinandergesetzt und wiederholen es deswegen an dieser Stelle nicht nochmal. Eine neue Bearbeitungsoption für den Plot ist aber das Argument breaks. Hierin wird beschrieben, an welchem Ort eine Kategorie anfängt und wieder aufhört. bspw. startet die erste Kategorie bei 1 und geht bis 3, die zweite dann bei 3 bis 5 und die vierte von 5 bis 7. Die Anzahl der Breakpoints wäre in diesem Beispiel 4 (c(1, 3, 5, 7)). Ohne eigenen Input bestimmt R dieses komplett selbst. Wir können aber auch einen Wert zuordnen - bspw. eine ganze Zahl.
# Histogramm (20 Breakpoints anfordern)
hist(fb22$lz,
breaks = 20)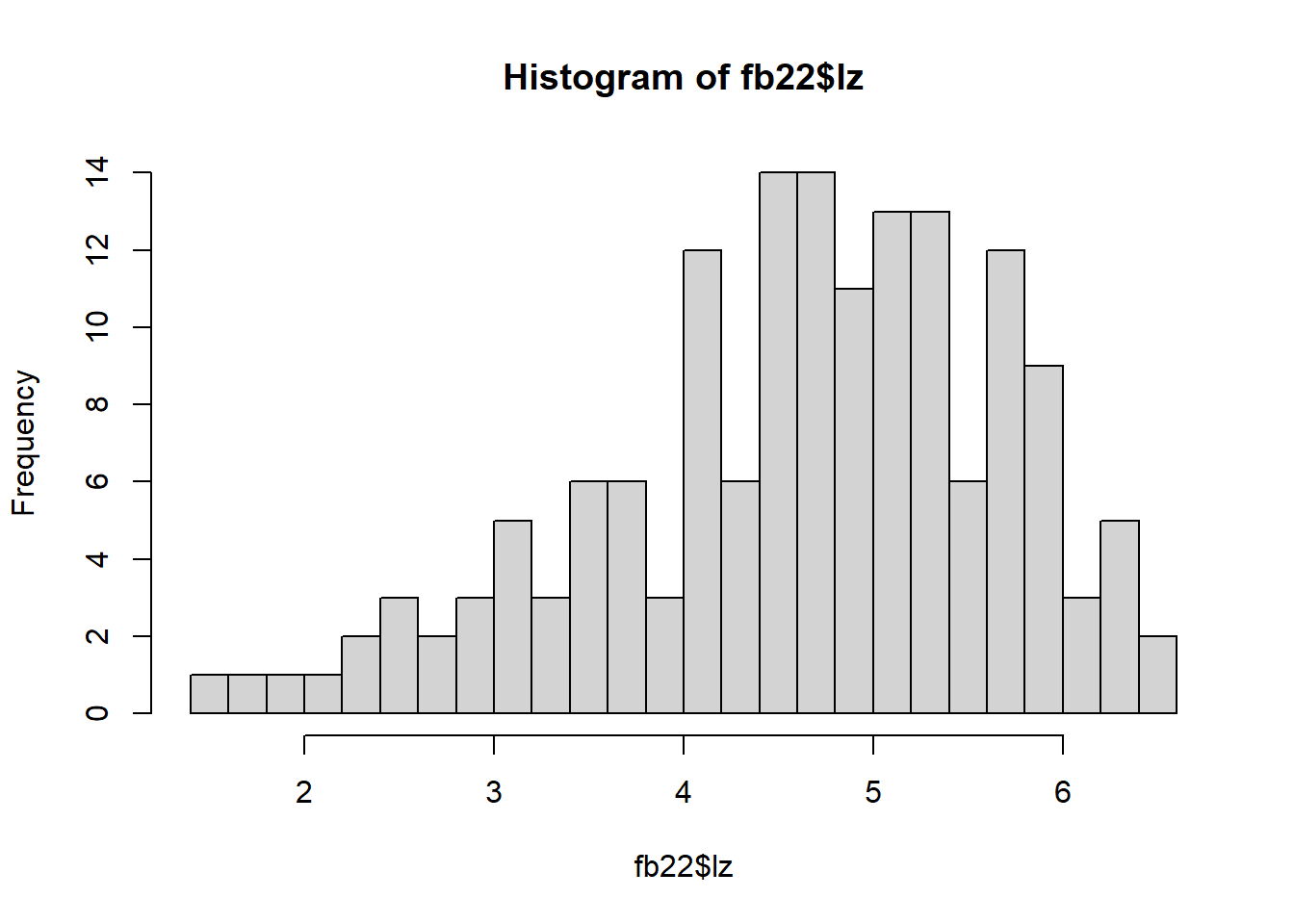
Das Argument ist eine weiche Einstellung. R weiß jetzt, dass wir 20 Kategorien bevorzugen. Im Hintergrund laufen aber Funktionen ab, die einen optisch ansprechenden Code produzieren. Deshalb erhalten wir mehr als 20 Breakpoints. Eine weiche Einstellung bedeutet also, dass R das Argument nicht als Pflicht übernimmt. Dieses Phänomen werden wir relativ selten im Verlauf des Semesters sehen. Es wird aber in der Hilfe ?hist im Unterpunkt breaks beschrieben.
Werte, die genau auf einem Break liegen, werden standardmäßig der Kategorie zugeordnet, von der sie den Abschluss bilden. Wenn die Breaks c(1, 1.5, 2) sind, wird ein Wert von 1.5 der ersten Kategorie zugeordnet. Dies gilt mit Ausnahme der untersten Kategorie - hier würde ein Wert von 1 natürlich auch der ersten Kategorie und nicht der nullten Kategorie, die es nicht gibt, zugeordnet werden.
Achtung! Die Anzahl der Kategorien kann den Eindruck der Daten beeinflussen. Hier erstellen wir ein Beispiel dafür, wie wir jeden Breakpoint selbst bestimmen können und auch den Eindruck der Daten manipulieren.
# Histogramm (ungleiche Kategorien)
hist(fb22$lz,
breaks = c(1, 3, 3.3, 3.6, 3.9, 4.5, 5, 7))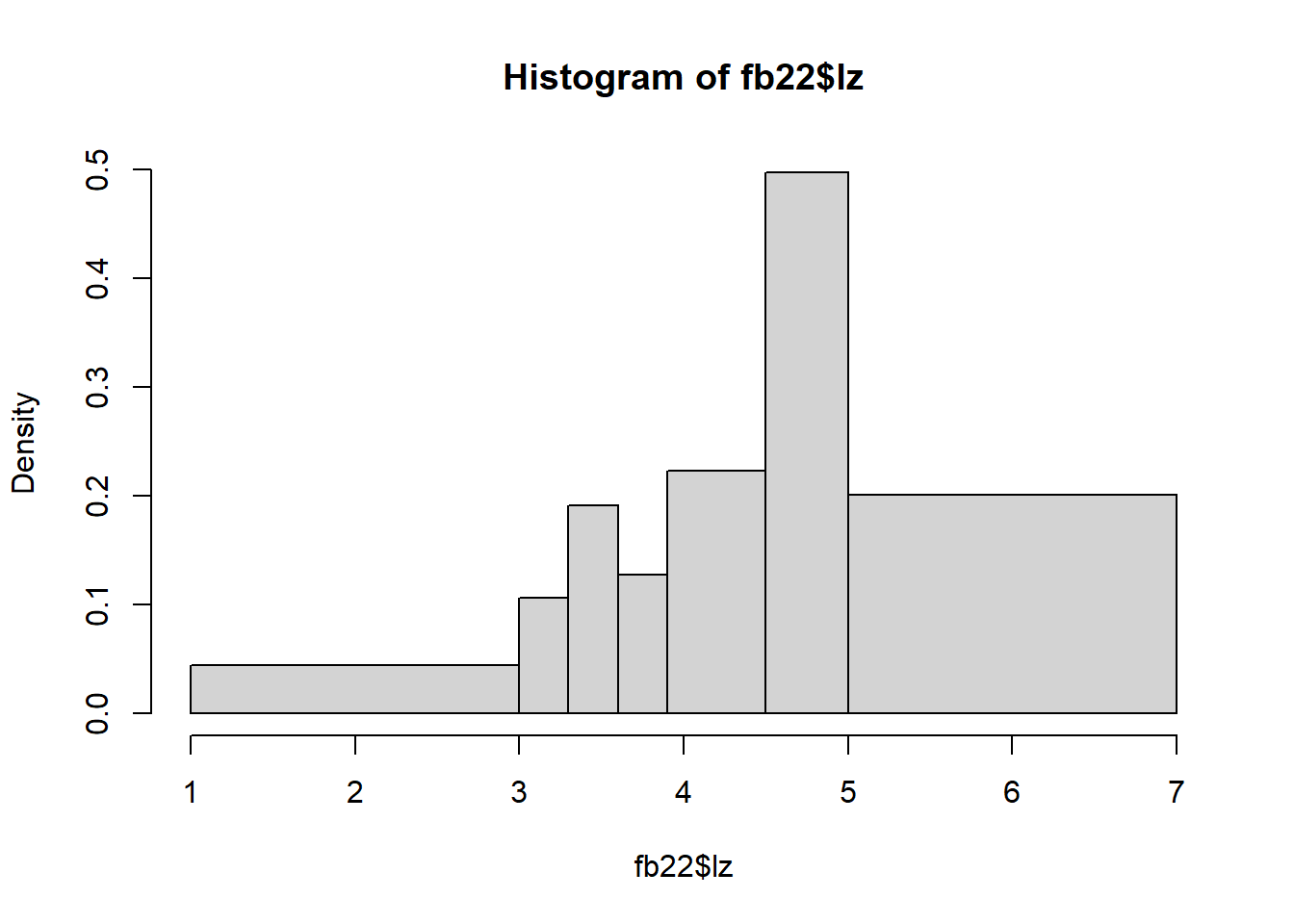
Für die eigene Bestimmung der Grenzen muss also anstatt einer ganzen Zahl dem Befehl ein Vektor c() mit allen Breakpoints übergeben werden.
Mittelwert
Betrachten wir nun, wie in R das Maß der zentralen Tendenz für mindestens intervallskalierte Daten per Funktion bestimmt werden kann. In der Vorlesung haben Sie die Formel zur Bestimmung kennen gelernt.
Formel: \({x} = \frac{\sum_{m = 1}^n x_m}{n} = \frac{1}{n} \sum_{m = 1}^n x_m\)
In R ist die Funktion zum Glück sehr intuitiv benannt. Dabei muss auch hier beachtet werden, dass fehlende Werte über na.rm = T ausgeschlossen werden
# Arithmetisches Mittel
mean(fb22$lz, na.rm = TRUE)## [1] 4.709554Varianz
Für die Varianz haben Sie in der Vorlesung folgende Formel kennen gelernt:
Formel: \(s^2_{X} = \frac{\sum_{m=1}^n (x_m - \bar{x})^2}{n}\)
Wollen wir diese nun per Hand bestimmen, könnte folgender Code das für uns erledigen:
# Händische Varianzberechnung
sum((fb22$lz - mean(fb22$lz, na.rm = TRUE))^2, na.rm = TRUE) / (nrow(fb22)-2)## [1] 1.145705Achtung! Wir benötigen für die Varianzberechnung n (s. Formel)! Wir nutzen hier nrow(fb22)-2, weil nrow(fb22) nicht das richtige n anzeigt (2 Personen haben einen fehlenden Wert, daher die Anzahl an Zeilen minus der 2 fehlenden Werte = n).
Kleiner Diskurs zu fehlenden Werten:
Um zu prüfen, ob und wie viele fehlende Werte eine Variable hat, lässt sich z. B. folgende Syntax verwenden:
is.na(fb22$lz) |> sum()## [1] 2Um die Länge einer Variablen ohne fehlende Werte (also die Anzahl an Beobachtungen auf einer Variablen) zu bestimmen, lässt sich z. B. folgende Syntax verwenden:
na.omit(fb22$lz) |> length() # mit Pipe## [1] 157length(na.omit(fb22$lz)) # ohne Pipe## [1] 157Zur händischen Varianzberechnung können wir daher auch folgende Syntax verwenden:
# Händische Varianzberechnung
sum((fb22$lz - mean(fb22$lz, na.rm = TRUE))^2, na.rm = TRUE) / (length(na.omit(fb22$lz)))## [1] 1.145705Verschiedene Varianzschätzer
Sie haben sich eventuell schon gewundert, warum wir eine so bekannten Wert wie die Varianz per Hand bestimmen müssen. Mit der ersten Intuition findet man bereits eine Funktion für die Berechnung, var(). Folgendes Ergebnis liefert R, wenn wir die R-Funktion var() zur Berechnung der Varianz verwenden:
# R-interne Varianzberechnung
var(fb22$lz, na.rm = TRUE)## [1] 1.153049Warum erhalten wir hier einen abweichenden Wert im Vergleich zu unserer händischen Varianzberechnung?
Die meisten Programme berechnen nicht die empirische Varianz, sondern einen Schätzer der Populationsvarianz: Empirische Varianz
\(s^2_{X} = \frac{\sum_{m=1}^n (x_m - \bar{x})^2}{n}\)
Schätzer der Populationsvarianz
\(\hat{\sigma}^2_{X} = \frac{\sum_{m=1}^n (x_m - \bar{x})^2}{n - 1}\)
Ein enger Zusammenhang zwischen Populationsvarianz und empirischer Varianz ist bereits nur durch Ansicht der Formeln erkenntlich. Eine Erklärung über diesen wird es erst im weiteren Verlauf der Vorlesung geben. Wir wollen uns nun darauf konzentrieren, wie wir technisch den Wert, den wir durch var() erhalten, für unsere Zwecke nutzen können.
Um in R die empirische Varianz mithilfe der var()-Funktion zu berechnen, kann man die Populationsvarianz nutzen. Multipliziert man sie mit \(\frac{n - 1}{n}\), erhält man die empirische Varianz.
# Umrechnung der Varianzen
var(fb22$lz, na.rm = TRUE) * (nrow(fb22) - 1) / nrow(fb22)## [1] 1.145797Achtung! Dies funktioniert in unserem Fall wieder nicht, da die Verwendung von nrow(fb22) - wie oben bereits angemerkt - nicht sinnvoll ist: nrow(fb22) ist nicht gleich n (es kommt NA 2 Mal vor), daher besser:
# Umrechnung der Varianzen
var(fb22$lz, na.rm = TRUE) * (length(na.omit(fb22$lz)) - 1) / (length(na.omit(fb22$lz)))## [1] 1.145705Alternativ, wenn man die fehlenden Werte händisch abzieht:
# Umrechnung der Varianzen
var(fb22$lz, na.rm = TRUE) * (157 - 1) / 157## [1] 1.145705Standardabweichung
Auch bei der Standardabweichung bestimmt R den Populationsschätzer \(\hat{\sigma}_{X}\).
\(\hat{\sigma}_{X} = \sqrt{\hat{\sigma}^2_{X}} = \sqrt{\frac{\sum_{m=1}^n (x_m - \bar{x})^2}{n - 1}}\)
# Standardabweichung in R
sd(fb22$lz, na.rm = TRUE) # Populationsschaetzer## [1] 1.073801In der Vorlesung hingegen haben Sie die empirische Standardabweichung kennen gelernt.
\(s_{X} = \sqrt{s^2_{X}} = \sqrt{\frac{\sum_{m=1}^n (x_m - \bar{x})^2}{n}}\)
Wir müssten das Ergebnis also wieder mit einem Faktor (\(\sqrt{\frac{n - 1}{n}}\)) multiplizieren, um die emprische Standardabweichung zu erhalten.
# Umrechnung der Standardabweichung
sd(fb22$lz, na.rm = TRUE) * sqrt((157 - 1) / 157)## [1] 1.070376Alternativ kann diese natürlich auch komplett händisch berechnet werden. Dafür können wir einfach den bereits geschriebenen Code für die empirische Varianz nehmen und aus dem Ergebnis die Wurzel ziehen.
# Händische Berechnung der empirischen Standardabweichung
(sum((fb22$lz - mean(fb22$lz, na.rm = TRUE))^2,
na.rm = TRUE) / (length(na.omit(fb22$lz)))) |> sqrt()## [1] 1.070376Zentrierung und Standardisierung
In der Vorlesung haben Sie gelernt, dass eine Variable zentriert oder standardisiert werden kann. Die Zentrierung sorgt für einen Mittelwert von 0, während die Standardisierung zusätzlich die Varianz auf 1 setzt. Die Variablenzentrierung und -standardisierung lässt sich in R per Hand berechnen.
# Zentrierung
lz_c <- fb22$lz - mean(fb22$lz, na.rm = TRUE)
head(lz_c) # erste 6 zentrierte Werte## [1] 0.6904459 1.2904459 -1.7095541 1.2904459 -1.5095541 1.0904459# Standardisierung
lz_z <- lz_c / sd(fb22$lz, na.rm = TRUE)
head(lz_z) # erste 6 standardisierte Werte## [1] 0.6429922 1.2017548 -1.5920582 1.2017548 -1.4058040 1.0155006…oder mit Hilfe bereits existierender Funktionen:
## Befehl zum Standardisieren
lz_z <- scale(fb22$lz)
## Befehl zum Zentrieren (ohne Standardisierung)
lz_c <- scale(fb22$lz,
scale = FALSE) # unterbindet StandardisierungItems Rekodieren
Wiederholung: Konstruierte mindestens intervallskalierte Variablen
- Fragebogendaten werden meist ordinalskaliert erhoben (einzelne Items)
- Um Intervallskalenniveau zu erreichen werden Items zu Skalenwerten verrechnet (Summe oder Mittelwert)
- Erzeugt viele mögliche Ausprägungen und wird als intervallskaliert behandelt
Positive & Negative Items
Viele Fragebögen enthalten sowohl positiv als auch negativ formulierte Items,
- …um die Befragung abwechslungsreich zu gestalten
- …um das psychologische Konstrukt umfassender zu erheben
- …um Antworttendenzen leichter identifizieren zu können
Vor der Skalenbildung müssen alle Items in eine Richtung gebracht werden: Das wird auch als Rekodierung bezeichnet.
Beispiel: Fragebogen zur Prokrastionationstendenz
- Skala soll bei hohen Werten höhere Prokrastinationstendenz darstellen
- Negativ formulierte Items müssen invertiert werden
- Invertierte Items sind 2, 3, 5, 7 und 8
- Mögliche Werte von 1 bis 4
- Hierzu kennen Sie bereits zwei Möglichkeiten (mit den Befehlen und R-Kenntnissen aus den bisherigen Sitzungen…)
Variante 1: Lineare Transformation
fb22$prok2_r <- -1 * (fb22$prok2 - 5)
head(fb22$prok2) # erste 6 Werte ohne Transformation## [1] 3 3 3 3 1 4head(fb22$prok2_r) # erste 6 Werte mit Transformation## [1] 2 2 2 2 4 1- Allgemeine Form: \(-1 \cdot (x_m - x_{\max} - 1)\)
- Vorteil: schnell und einfach umsetzbar
- Nachteil: nur für Invertierung sinnvoll, nicht allgemeiner anwendbar
Quizfrage: Ist dies eine zulässige Transformation für ordinalskalierte Variablen (wie Items)?
Antwort: Ja, denn die Ordnungsrelation bleibt hierbei erhalten!
Variante 2: Logische Filter
Mit Hilfe von logischen Filtern, die wir auch schon im R-Intro kennen gelernt haben, können wir uns auch alle Antworten einer Ausprägung (z.B. 1) anzeigen lassen und diesen dann den transformierten Wert zuweisen. Durch die Invertierung wissen wir, dass dem Wert 1 der Wert 4 zugeordnet werden muss. Also können wir eine Abfrage nach allen Teilnehmenden machen, die die Antwort 1 gegeben haben.
head(fb22$prok3 == 1, 15) #Zeige die ersten 15 Antworten## [1] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [13] TRUE FALSE TRUEWir erhalten einen booleschen Vektor, der uns sagt, wo der Wert 1 auftaucht (TRUE) und wo nicht (FALSE).
Mit Hilfe dieses booleschen Vektors können wir die Stellen ansteuern bzw. indizieren, in denen im transformierten Vektor dann eine 4 statt einer 1 stehen soll. Dies passiert für all die Stellen, an denen TRUE steht.
fb22$prok3_r[fb22$prok3 == 1] <- 4
fb22$prok3_r[fb22$prok3 == 2] <- 3
fb22$prok3_r[fb22$prok3 == 3] <- 2
fb22$prok3_r[fb22$prok3 == 4] <- 1
head(fb22$prok3)## [1] 4 2 2 4 4 2head(fb22$prok3_r)## [1] 1 3 3 1 1 3- Durch logische Filter Personen auswählen, die auf Originalvariable den relevanten Wert haben
- Auf rekodierter Variable neuen Wert zuweisen
- Vorteil: extrem flexibel, jede Transformation möglich
- Nachteil: umständlich zu schreiben
Um Code zu sparen, invertieren wir also die restlichen Items mittels der linearen Transformation.
fb22$prok5_r <- -1 * (fb22$prok5 - 5)
fb22$prok7_r <- -1 * (fb22$prok7 - 5)
fb22$prok8_r <- -1 * (fb22$prok8 - 5)Skalenwerte erstellen
Skalenwerte werden zumeist als Summen oder Mittelwerte der Items erstellt. Dafür kann man sich beispielsweise alle Daten, die der Skala zugrunde liegen, in einem eigenen kleinen Datensatz ablegen. Dieser Datensatz kann genutzt werden, um den Skalenwert wieder im Original abzulegen. Jede Person repräsentiert eine Zeile - rowMeans() berechnet den Mittelwert der Zeilen. Somit erhält jede Person einen eigenen Mittelwert über die Einträge. Führen wir das ganze beispielsweise für den Skalenwert zur Prokrastinationstendenz durch, die mit den 10 Items erhoben wurde. Wichtig ist hier auch, dass wir die rekodierten Items nehmen, da diese ja die “korrekte Richtung” aufweisen.
# Datensatz der relevanten Variablen
prokrastination <- fb22[, c('prok1', 'prok2_r', 'prok3_r',
'prok4', 'prok5_r', 'prok6',
'prok7_r', 'prok8_r', 'prok9',
'prok10')]
# Skalenwert in Originaldatensatz erstellen
fb22$prok_ges <- rowMeans(prokrastination)
head(fb22$prok_ges)## [1] 2.0 3.3 3.1 NA 2.0 2.1Natürlich kann die Erstellung auch in einem Befehl passieren - beispielsweise durch Verwendung der Pipe. Es gibt aber auch noch viele andere Optionen zur Skalenbildung - es wird (wie eigentlich fast immer) nur ein Ausschnitt der Möglichkeiten gezeigt.
# Direkter Befehle
fb22$prok_ges <- fb22[, c('prok1', 'prok2_r', 'prok3_r',
'prok4', 'prok5_r', 'prok6',
'prok7_r', 'prok8_r', 'prok9',
'prok10')] |> rowMeans()
head(fb22$prok_ges)## [1] 2.0 3.3 3.1 NA 2.0 2.1Quizfrage: Was bedeutet NA in fb22$prok_ges?
Antwort: NA bedeutet in diesem Fall, dass eine teilnehmende Person mindestens ein Item nicht beantwortet hat. Da rowMeans() im Hintergrund auch nur mean() auf jeder Zeile aufruft, gibt es bei fehlenden Werten die Ausgabe NA. Wenn man das vermeiden möchte, kann man wieder das Argument na.rm = TRUE hinzufügen. Dabei muss man sich aber im Klaren sein, dass der Mittelwert dann auch für Personen berechnet wird, die nicht alle Items ausgefüllt haben. Im schlimmsten Fall sogar nur ein einziges von 10. Daher sollte solche Entscheidungen immer mit Bedacht getroffen werden.Nützliche Funktionen in diesem Zusammenhang:
rowMeans()Mittelwert für jede Zeile (über Variablen)colMeans()Mittelwert für jede Spalte (über Personen)rowSums()Summe für jede Zeile (über Variablen)colSums()Summe für jede Spalte (über Personen)
