Exploratorische Faktorenanalyse
EFA
Forscher:innen der Psychologie oder anderer Natur-, Sozial- und Geisteswissenschaften interessieren sich häufig dafür, wie sich Daten auf einige wenige entscheidende Faktoren herunterbrechen lassen, welche ein theoretisches Erklärungsmodell für die Variation in einem Datensatz liefern. Die Annahme ist hierbei, dass die beobachtbaren Messungen eine Linearkombination (also eine Summe) aus einem systematischen (wahren) und einem unsystematischen (Fehler-)Anteil bilden. Die dahinterliegenden Faktoren sind nicht messbare (latente) Variablen, auf welche, unter gewissen Annahmen, nur anhand der Kovariation zwischen den beobachtbaren Items geschlossen werden kann. Durch diese Zusammenhänge zwischen den Messungen können schließlich Hypothesen für die latenten Variablen untersucht werden. Ein theoriegenerierendes Verfahren, das hierzu häufig verwendet wird, ist die exploratorische Faktorenanalyse (im Folgenden EFA, engl. Exploratory Factor Analysis, vgl. Eid, Gollwitzer & Schmitt, 2017, Kapitel 25. Außerdem können Sie sich Brandt, 2020, Kapitel 23 genauer ansehen, wenn Sie weitere Informationen, bzw. eine zusätzliche Erklärung wünschen).
Wir wollen die EFA zur Auswertung von Beziehungen zwischen Variablen in R näher kennenlernen. Die EFA ist manchen Gesichtspunkten, sowie im Output in R, recht verwandt mit der Hauptkomponentenanalyse (PCA) aus dem vergangenen Semester. Allerdings konnten wir bei der PCA kein Erklärungsmodell aufstellen (“wir konnten den Hauptkomponenten nicht so einfach eine inhaltliche Bedeutung zuschreiben”) und auch keine Messfehler (unsystematische Fehleranteile) mitmodellieren. Zudem waren die Hauptkomponenten der PCA Linearkombinationen (also Zusammensetzungen) aus den beobachteten Variablen, bei der EFA hingegen sind die Messungen (beobachteten Variablen) Linearkombinationen aus systematischen (latenten) Variablen sowie Messfehlern.
Bevor wir mit den Analysen beginnen können, laden wir zunächst alle Pakete, welche wir im Folgenden benötigen werden.
library(corrplot) # Korrelationsmatrix grafisch darstellen
library(psych) # EFA durchführen
library(GPArotation) # EFA Lösung rotierenDatensatz
Wir wollen uns die Faktorenstruktur der Big-5 eines entsprechenden Fragebogens ansehen. Der Originaldatensatz ist ein Onlinedatensatz, wird seit 2012 erfasst und ist auf openpsychometrics.org als .zip downloadbar. Bisher haben über 19700 Proband:innen aus der ganzen Welt daran teilgenommen. Zu jeder der fünf Facetten gibt es 10 Fragen. Der Fragebogen ist auf personality-testing.info einzusehen. Um das Ganze etwas übersichtlicher zu gestalten, betrachten wir einen gekürzten Datensatz. Wir kennen diesen Datensatz, allerdings in anderer Zusammensetzung, bereits aus den Übungen zum vergangenen Semester zum Themenblock MANOVA, weswegen wir hier das Kürzel “EFA” angehängt haben. Im Datensatz Big5_EFA.rda befinden sich 15 Items aus dem Big-5 Persönlichkeitsfragebogen. Hier werden von diesen 10 Items jeweils die ersten drei verwendet. Der Itemwortlaut der verwendeten Items ist wie folgt:
| Itemwortlaut | |
| Item Nr. | Item |
|---|---|
| E1 | I am the life of the party. |
| E2 | I don’t talk a lot. |
| E3 | I feel comfortable around people. |
| N1 | I get stressed out easily. |
| N2 | I am relaxed most of the time. |
| N3 | I worry about things. |
| A1 | I feel little concern for others. |
| A2 | I am interested in people. |
| A3 | I insult people. |
| C1 | I am always prepared. |
| C2 | I leave my belongings around. |
| C3 | I pay attention to details. |
| O1 | I have a rich vocabulary. |
| O2 | I have difficulty understanding abstract ideas. |
| O3 | I have a vivid imagination. |
Die Kürzung des vollen Datensatzes lässt sich im Appendix A nachvollziehen. Zusätzlich zu den Persönlichkeitsitems wurden demografische Daten, die mögliche Unterschiede zwischen Personen beschreiben, erfasst.
Daten laden
Wir laden zunächst die Daten: entweder lokal von Ihrem Rechner:
load("C:/Users/Musterfrau/Desktop/Big5_EFA.rda")oder wir laden sie direkt über die Website:
load(url("https://pandar.netlify.app/post/Big5_EFA.rda"))Nun sollte in R-Studio oben rechts in dem Fenster unter der Rubrik “Data” unser Datensatz mit dem Namen “Big5” erscheinen. Der Datensatz heißt also genauso wie der Datensatz für die MANOVA, enthält aber andere Variablen (also Achtung!).
Übersicht über die Daten
head(Big5, n = 10) # gebe die ersten 10 Zeilen aus## age engnat gender country E1 E2 E3 N1 N2 N3 A1 A2 A3 C1 C2 C3 O1 O2 O3
## 1 53 1 1 US 4 2 5 1 5 2 1 5 1 4 1 5 4 1 3
## 2 46 1 2 US 2 2 3 2 3 4 1 3 3 4 1 3 3 3 3
## 3 14 2 2 PK 5 1 1 5 1 5 5 1 5 4 1 5 4 5 5
## 4 19 2 2 RO 2 5 2 5 4 4 2 5 4 3 3 4 4 3 5
## 5 25 2 2 US 3 1 3 3 3 3 5 5 3 3 1 5 3 1 1
## 6 31 1 2 US 1 5 2 1 5 4 2 2 3 2 5 4 4 2 1
## 7 20 1 2 US 5 1 5 2 4 2 5 5 1 2 4 3 3 1 5
## 8 23 2 1 IN 4 3 5 1 4 4 2 5 1 4 2 5 3 1 5
## 9 39 1 2 US 3 1 5 2 4 5 1 5 1 4 3 5 3 3 5
## 10 18 1 2 US 1 4 2 5 2 5 2 3 1 5 2 4 4 2 5Wir sehen, dass in den ersten 4 Spalten die demografischen Daten wie etwa Alter (“age”), Englisch als Muttersprache (“engant”, 1=yes, 2=no, 0=missed), Geschlecht (“gender”, 1=Male, 2=Female, 3=Other, 0=missed) und Herkunftsland (“country”, ISO-kodiert, bspw. “DE” = Deutschland, “FR” = Frankreich, “EM” = Vereinigte Arabische Emirate, “US” = Vereinigten Staaten von Amerika) eingetragen wurden. In den darauf folgenden Spalten sind die Items der Extraversion (engl. extraversion, Items: E1, E2, E3), des Neurotizismus (engl. neuroticism, Items: N1, N2, N3), der Verträglichkeit (engl. agreeableness, Items: A1, A2, A3), der Gewissenhaftigkeit (engl. conscientiousness, Items: C1, C2, C3) und der Offenheit für Erfahrungen (engl. openness, Items: O1, O2, O3) eingetragen. Beispielsweise ist die erste Person des Datensatzes ein 53-jähriger Mann, der Englisch als Muttersprache spricht und in den USA lebt.
Da wir uns in der Praxis nur sehr selten in der glücklichen Lage befinden, einen solch riesigen Datensatz zu haben, wollen wir uns innerhalb des Datensatzes auf Subgruppen beschränken: wir wollen uns zunächst nur Daten von Personen aus Frankreich ansehen. Dazu wählen wir nur diejenigen Zeilen aus, in denen country == "FR" gilt. Das erreichen wir wie folgt: Mit Big5$country haben wir Zugriff auf die “Country”-Spalte im Datensatz und können mit == "FR" prüfen, an welchen Stellen hier “FR” steht, also Personen, die in Frankreich leben. dim gibt die Dimensionen des Datensatzes wieder.
dim(Big5)## [1] 19711 19data_France <- Big5[Big5$country == "FR", ]
dim(data_France)## [1] 129 19Dem Output sollte zu entnehmen sein, dass data_France 129 Zeilen (also Proband:innnen, die in Frankreich leben) und 19 Spalten (also Variablen) enthält. Für die weiteren Analysen brauchen wir die demografischen Variablen in dem Datensatz der in Frankreich lebenden Teilnehmer:innen nicht mehr. Aus diesem Grund speichern wir den Datensatz noch einmal ohne die ersten 4 Spalten ab. Anschließend stellen wir die Korrelationsmatrix dieser Daten grafisch dar (den Befehl corrplot aus dem gleichnamigen Paket kennen wir bereits aus der PCA Sitzung des vergangenen Semesters).
dataFR <- data_France[, -c(1:4)] # entferne demografische Daten und speichere als "dataFR"
#### Visualisierte Korrelationsmatrix in dataFR
corrplot(corr = cor(dataFR), # Korrelationsmatrix (Datengrundlage)
method = "color", # zeichne die Ausprägung der Korrelation farblich kodiert
addCoef.col = "black", # schreibe die Korrelationskoeffizienten in schwarz in die Grafik
number.cex = 0.7) # stelle die Schriftgröße der Koeffizienten ein
Auf den ersten Blick scheinen die Items der gleichen Skala (ausgedrückt durch gleiche Buchstaben pro Item) stärker (betragsmäßig höher) miteinander zu korrelieren. Allerdings sind hier sehr viele Korrelationen abgetragen. Wir wollen uns zunächst nur auf Extraversion und Neurotizismus beschränken.
dataFR2 <- dataFR[,1:6] # Zunächst wählen wir die ersten 6 Items: E1 bis E3 und N1 bis N3
head(dataFR2)## E1 E2 E3 N1 N2 N3
## 17 1 3 2 4 2 3
## 398 3 3 3 4 3 4
## 488 1 5 2 4 4 5
## 545 1 2 1 4 1 5
## 551 1 4 1 5 1 5
## 656 1 4 2 5 1 5# zum gleichen Ergebnis würde auch Folgendes kommen (besonders von Relevanz,
# wenn wir bspw. nicht die Position sondern nur die Namen der Variablen kennen!):
head(dataFR[, c("E1", "E2", "E3", "N1", "N2", "N3")])## E1 E2 E3 N1 N2 N3
## 17 1 3 2 4 2 3
## 398 3 3 3 4 3 4
## 488 1 5 2 4 4 5
## 545 1 2 1 4 1 5
## 551 1 4 1 5 1 5
## 656 1 4 2 5 1 5Wenn wir uns die Korrelationmatrix des gekürzten Datensatzes dataFR2 ansehen…
# Visualisierte Korrelationsmatrix
corrplot(corr = cor(dataFR2), # Korrelationsmatrix (Datengrundlage)
method = "color", # Zeichne die Ausprägung der Korrelation farblich kodiert
addCoef.col = "black", # schreibe die Korrelationskoeffizienten in schwarz in die Grafik
number.cex = 1) # Stelle die Schriftgröße der Koeffizienten ein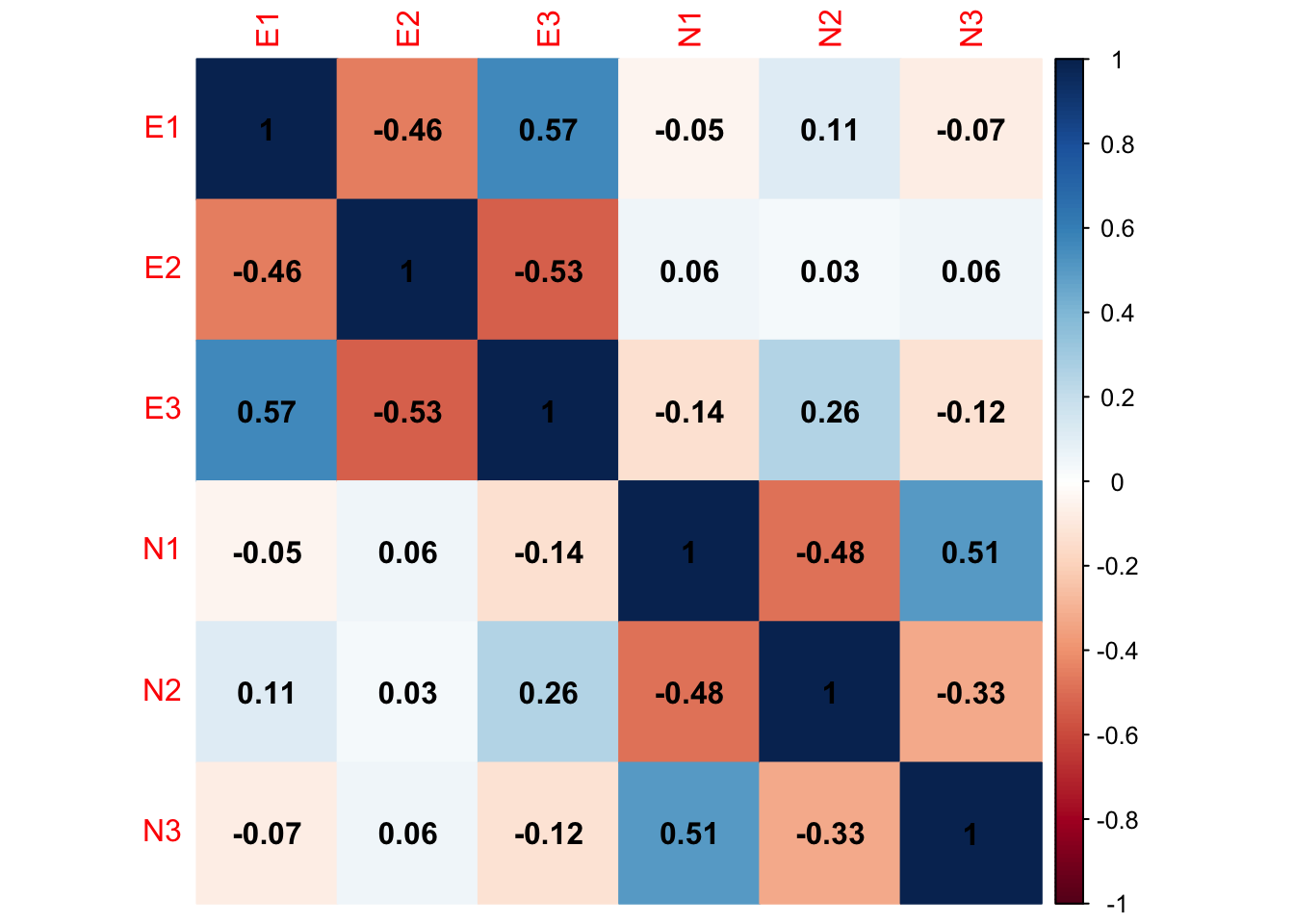
…erkennen wir deutlich, dass die Extraversionsitems und die Neurotizismusitems untereinander jeweils stärker zusammenhängen als zwischen den Konstrukten. Dennoch ist der Grafik zu entnehmen, dass die beiden Konstrukte nicht unabhängig voneinander sind (es gibt Beziehungen zwischen Items der beiden Konstrukte).
Ziel: EFA
Unser Ziel ist es, mit den gegebenen Items eine exploratorische Faktorenanalyse durchzuführen. Wir wollen hierbei die Anzahl der Faktoren mittels einer Parallelanalyse bestimmen und anschließend dieses Modell mit dem \(\chi^2\)-Test (Likelihood-Quotiententest (Likelihood-Ratio-Test)/ Likelihood-Differenzentest/ \(\chi^2\)-Differenzentest) gegen konkurrierende Modelle testen. Hierbei wollen wir die oblique rotierte und die orthogonal rotierte Lösung vergleichen und hinsichtlich unserer Daten interpretieren. Das Modell, was wir an unsere Daten anpassen wollen, sieht für 6 Variablen (\(V_1,\dots,V_6\)) im Allgemeinen erst einmal so aus (hier sind nur die Beziehungen, nicht aber die Stärken der Beziehungen zwischen den Variablen abgetragen), wobei hier schon die implizite Annahme drin steckt, dass es nur zwei zugrundeliegende latente Variablen gibt:
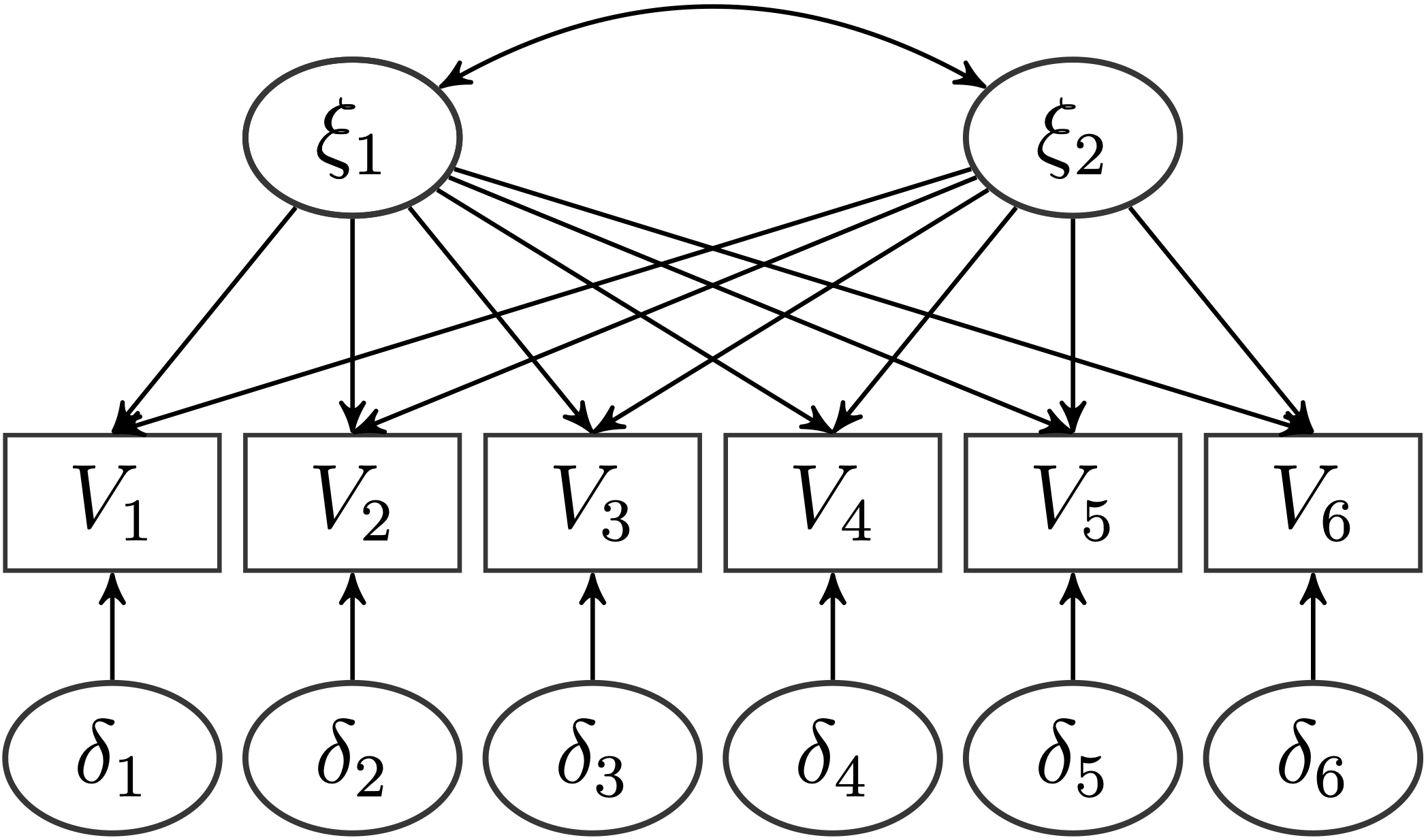
Auf unseren Datensatz angepasst, wollen wir folgendes Modell anpassen:
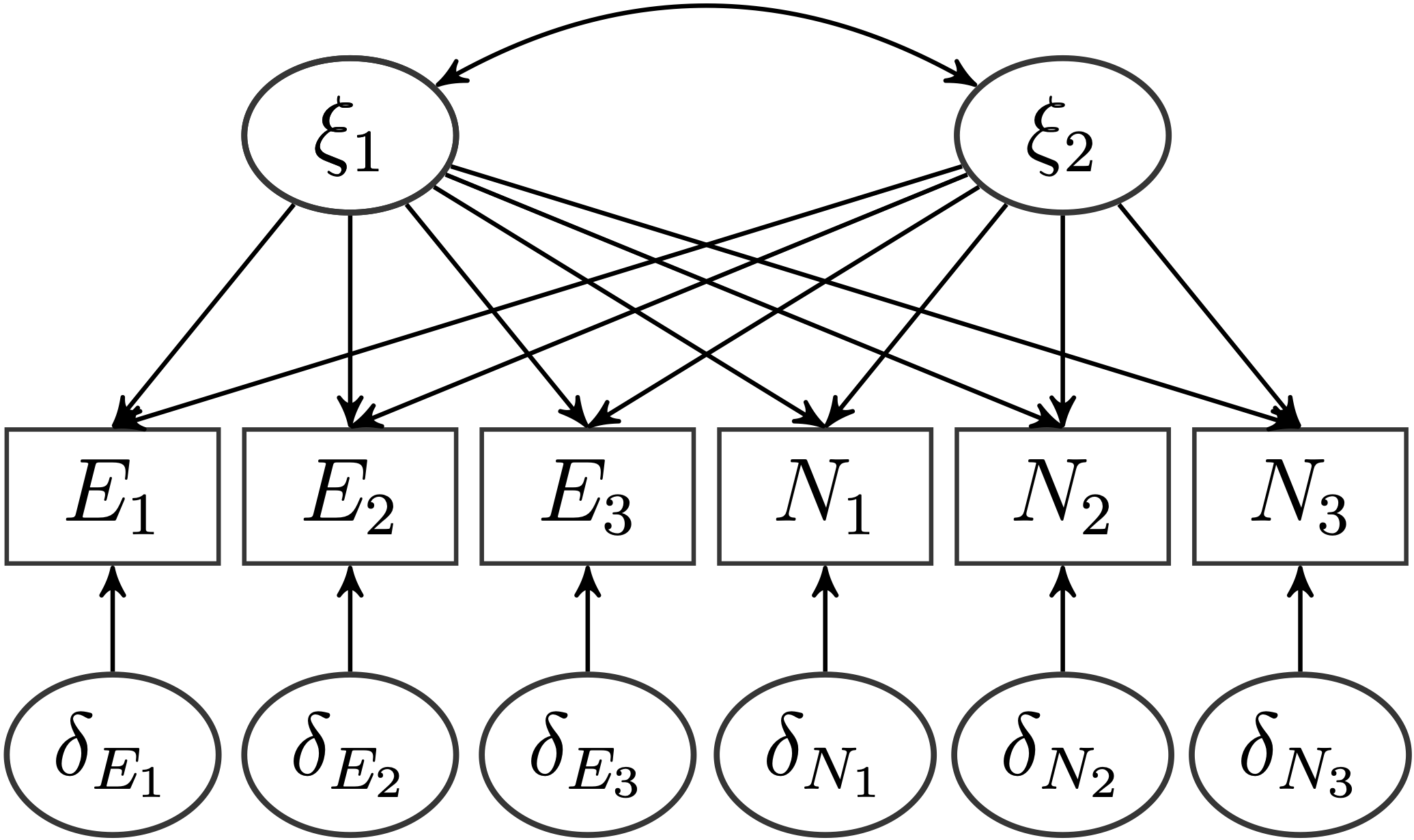
Natürlich erwarten wir, dass insgesamt 2 Faktoren die Daten am besten beschreiben und dass die konstruktkongruenten Items jeweils auf dem gleichen Faktor am stärksten laden. Aber stützen die Daten diese Hypothese?
Wir wollen im Folgenden
- eine Parallelanalyse durchführen, um in Erfahrung zu bringen, wie viele Faktoren sinnvoll zu den Daten passen
- eine Hauptachsenanalyse mit orthogonaler und obliquer Rotation durchführen
- eine exploratorische Maximum-Likelihood-Faktorenanalyse durchführen und die Passung zu den Daten untersuchen
- im Rahmen der exploratorischen Maximum-Likelihood-Faktorenanalyse die Passung zu den Daten im Vergleich zu konkurrierenden Modellen untersuchen.
Parallelanalyse und Auswahl an Faktoren
Zur Auswahl der Anzahl an Faktoren in der EFA kann auf die Eigenwerte zurückgegriffen werden. Diese Eigenwerte entstehen beispielsweise durch Lösen des Eigenwerteproblems und entsprechen den Varianzen der Faktoren. Hier gilt es, nur solche Faktoren zu wählen, die auch große Varianzen haben. Die Parallelanalyse hatten wir im Zusammenhang mit der Hauptkomponentenanalyse kennengelernt. Hier werden vielfach (z.B. 1000 Mal, für Vergleichbarkeit sogar besser mehr!) unabhängige Daten in dem gleichen Format des ursprünglichen Datensatzes gezogen und eine PCA oder EFA durchgeführt. Die entstehenden Eigenwerte werden der Größe nach sortiert und dann über die Wiederholungen gemittelt. So entsteht ein auf die Stichprobe und Anzahl der Variablen genormter, zufälliger, durchschnittlicher Eigenwerteverlauf. Sind Eigenwerte der tatsächlich beobachteten Daten größer als die der Parallelanalyse, so spricht dies für eine/n bedeutsame/n Komponente/Faktor. Weitere Kriterien zur Auswahl von zu extrahierenden Faktoren im Rahmen der PCA waren das Eigenwerte-größer-1 Kriterium (Kaiser-Guttman-Kriterium) sowie der Scree-Test (Elbow-Criterion, Knick im Eigenwerteverlauf). Weitere Informationen zur EFA sowie zu Wiederholungen der PCA und der Auswahlkriterien können beispielsweise in Eid, Gollwitzer und Schmitt (2017) in Kapitel 25 (Seite 919 und folgend) nachgelesen werden.
Der wesentliche Unterschied zwischen einer EFA und einer PCA ist, dass bei der EFA angenommen wird, dass die beobachteten Variablen systematische (wahre) und unsystematische (Fehler-) Anteile enthalten. Es wird somit ein Erklärungsmodell, welches die Variation zwischen den Variablen erzeugt, postuliert. Bei der PCA werden die beobachteten Variablen als messfehlerfrei angenommen. Eine wichtige Folge aus der (Nicht-) Modellierung der Fehler ist, dass in der Regel die Faktorladungen bei der PCA höher ausfallen als bei der EFA. Dies liegt daran, dass bei der PCA die Variablen mit ihren eigenen Messfehlern, aus welchen auch die Hauptkomponenten unter anderem zusammengesetzt sind, korrelieren. Die Faktorladungen/ Komponentenladungen stehen hierbei (im orthogonalen Fall) für die Korrelation zwischen Item und Faktor/ Komponente; im obliquen Fall sind die Faktorladungen als Regressionkoeffizienten zu interpretieren. Wird eine ML-EFA an die Daten angepasst, so wird zusätzlich noch ein Erklärungsmodell basierend auf Verteilungsannahmen (multivariate Normalverteilung der Faktoren und Fehler — und als Konsequenz daraus auch der Items) herangezogen. Bei der PCA sind die Hauptkomponenten lediglich Linearkombinationen aus den beobachteten Variablen ohne jegliche Verteilungsannahmen (die Hauptkomponenten bestehen aus gewichteten Summen der beobachteten Variablen). Entsprechend ist es bei der PCA auch nicht möglich, konkurierende Modelle gegeneinander zu testen. Es bleiben dort nur die deskriptiven und recht subjektiven Auswahlkriterien für die Anzahl der Komponenten.
Mit Hilfe des fa.parallel-Befehls aus dem psych-Paket, welchen wir im Rahmen der PCA bereits kennengelernt hatten, lässt sich ganz einfach der Eigenwerteverlauf inklusive Parallelanalyse grafisch darstellen.
fa.parallel(dataFR2)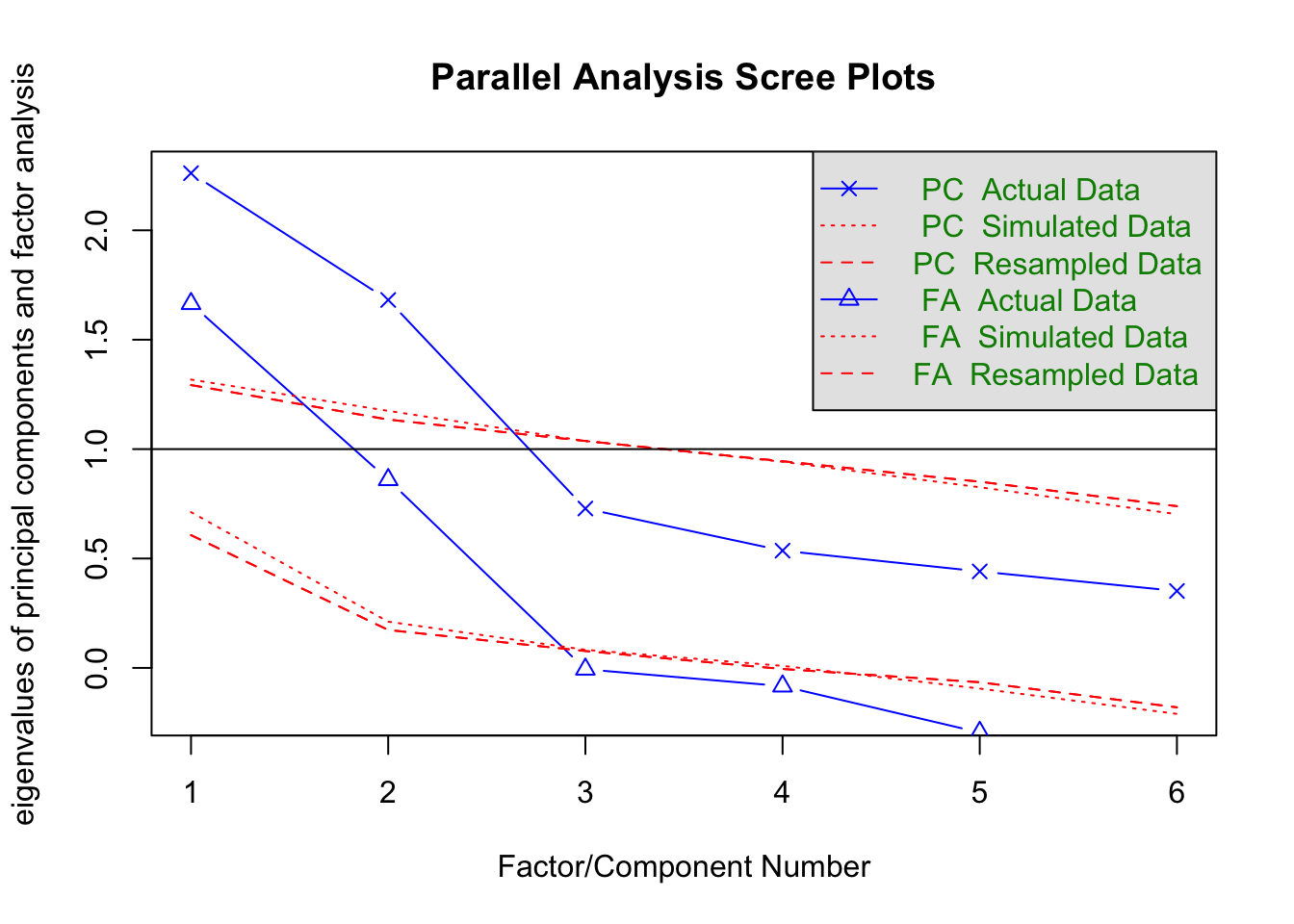
## Parallel analysis suggests that the number of factors = 2 and the number of components = 2Ohne weitere Einstellungen wird der Eigenwerteverlauf der PCA und der EFA ausgegeben. Deutlich zu sehen ist, dass die Eigenwerte der PCA größer ausfallen als die der EFA. Dies liegt erneut daran, dass die Faktoren der EFA lediglich die systematischen Anteile der Variablen enthalten, während die Komponenten der PCA Kompositionen sind - also Zusammensetzungen aus den Variablen; inklusive der Messfehler. Wählen wir fa = "fa", so wird uns nur der Verlauf der Eigenwerte auf Basis einer EFA aufgeführt.
fa.parallel(dataFR2, fa = "fa")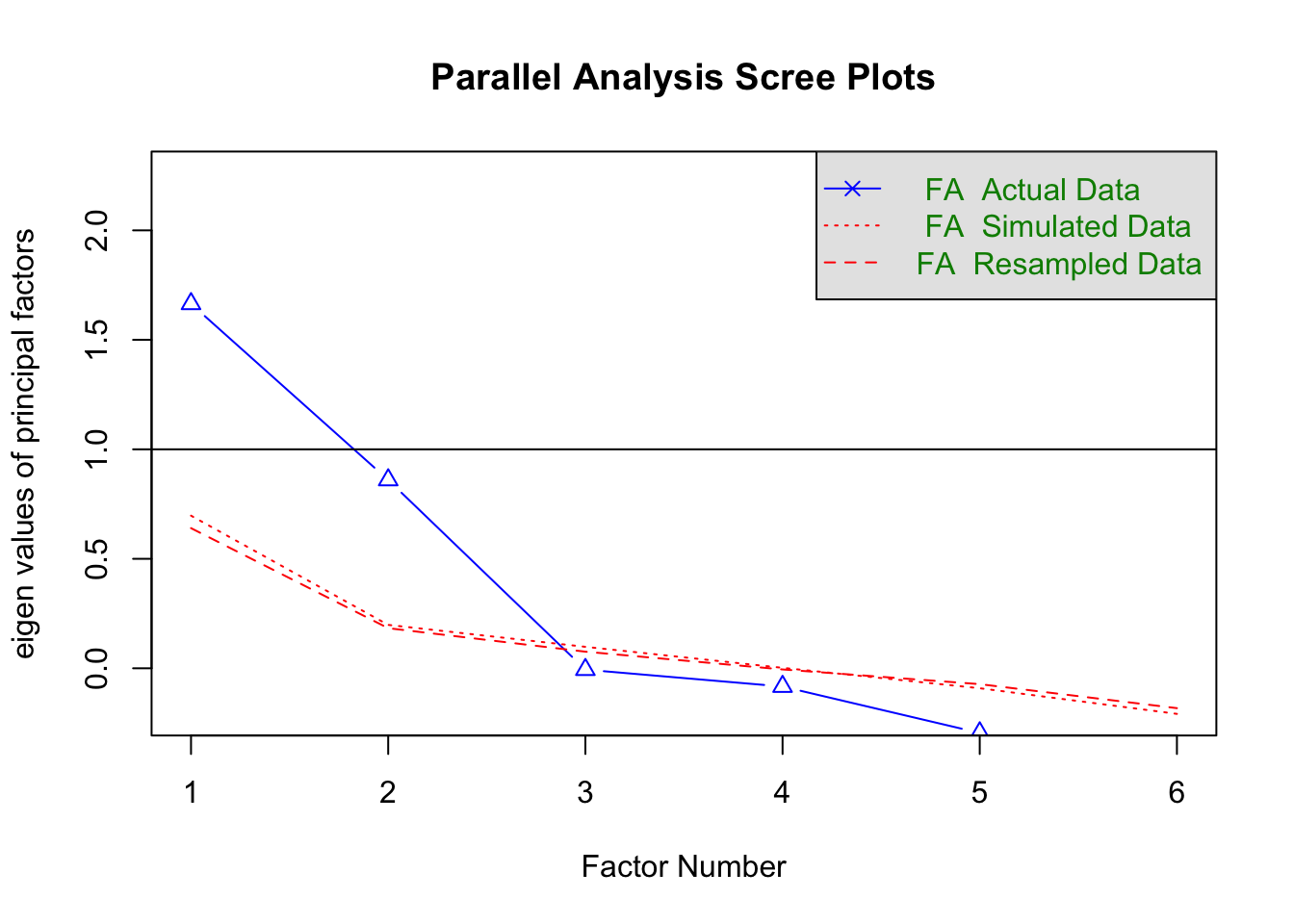
## Parallel analysis suggests that the number of factors = 2 and the number of components = NADie Grafik zeigt drei Eigenwerteverläufe. FA Actual Data ist der Eigenwerteverlauf unseres Datensatzes. FA Simulated Data ist der Eigenwerteverlauf basierend auf den 1000 simulierten Datensätzen. FA Resampled Data ist der Eigenwerteverlauf von Datensätzen, der durch Resampling, also neues Verteilen unseres Datensatzes entsteht (das ist im Grunde Bootstrapping, was im Rahmen der Sitzung zu SEM näher erläutert wird).
Der Parallelanalyse der EFA ist zu entnehmen, dass voraussichtlich 2 Faktoren genügen, um die Variation im Datensatz zu erklären. Auch die Parallelanalyse der PCA (Grafik zuvor) lässt dies vermuten. Des Weiteren sprechen beide Scree-Tests für einen Knick um den 3. Faktor/die 3. Komponente, was auch für eine Dimensionalität von 2 spricht. Zu guter Letzt zeigt auch das Kaiser-Guttman-Kriterium kein anderes Ergebnis. Allerdings ist dieses Kriterium nur sinnvoll auf den Eigenwerteverlauf der PCA anwendbar, weswegen wir es auch nur im Bezug auf den PCA-Eigenwerteverlauf interpretieren.
Orthogonale und oblique Hauptachsenanalyse
Da unsere Auswahlkriterien einstimmig für 2 Faktoren sprechen und dies auch unsere Hypothese war, modellieren wir zunächst eine orthogonale Hauptachsenanalyse. Dazu nutzen wir den fa (Factor Analysis) Befehl des psych-Paketes. Mit Hilfe der Argumente nfactors und rotate lässt sich die Anzahl an Faktoren sowie die Rotation auswählen (genauso wie bei der pca Funktion für die PCA!). Wir wollen hier orthogonal varianzmaximierend (also varimax) rotieren.
fa(dataFR2, nfactors = 2, rotate = "varimax")## Factor Analysis using method = minres
## Call: fa(r = dataFR2, nfactors = 2, rotate = "varimax")
## Standardized loadings (pattern matrix) based upon correlation matrix
## MR1 MR2 h2 u2 com
## E1 0.69 -0.06 0.48 0.52 1.0
## E2 -0.65 0.00 0.42 0.58 1.0
## E3 0.82 -0.19 0.70 0.30 1.1
## N1 -0.01 0.84 0.70 0.30 1.0
## N2 0.10 -0.58 0.35 0.65 1.1
## N3 -0.05 0.59 0.34 0.66 1.0
##
## MR1 MR2
## SS loadings 1.58 1.42
## Proportion Var 0.26 0.24
## Cumulative Var 0.26 0.50
## Proportion Explained 0.53 0.47
## Cumulative Proportion 0.53 1.00
##
## Mean item complexity = 1
## Test of the hypothesis that 2 factors are sufficient.
##
## The degrees of freedom for the null model are 15 and the objective function was 1.47 with Chi Square of 183.82
## The degrees of freedom for the model are 4 and the objective function was 0.07
##
## The root mean square of the residuals (RMSR) is 0.04
## The df corrected root mean square of the residuals is 0.07
##
## The harmonic number of observations is 129 with the empirical chi square 4.98 with prob < 0.29
## The total number of observations was 129 with Likelihood Chi Square = 9.06 with prob < 0.06
##
## Tucker Lewis Index of factoring reliability = 0.886
## RMSEA index = 0.099 and the 90 % confidence intervals are 0 0.187
## BIC = -10.38
## Fit based upon off diagonal values = 0.99
## Measures of factor score adequacy
## MR1 MR2
## Correlation of (regression) scores with factors 0.89 0.88
## Multiple R square of scores with factors 0.79 0.77
## Minimum correlation of possible factor scores 0.58 0.55Im Output ganz oben erkennen wir die Schätzmethode (hier: minres, also Minimierung der Residuen). Aus diesem Grund heißen die Faktoren in diesem Output auch MR1 und MR2; für Minimale-Residuen-Faktor 1 und 2 (diese Benennung war uns auch bereits bei der PCA aufgefallen, wo diese je nach Rotation entweder PC1 oder RC1, etc., hießen). Die Faktorladungen zu den zugehörigen Faktoren sind unter Standardized loadings (pattern matrix) based upon correlation matrix zu sehen. h2 steht für die Kommunalität (\(h^2\)), also den Anteil an systematischer Variation, die auf die 2 Faktoren zurückzuführen ist (diese kann ähnlich der Reliabilität interpretiert werden). u2 ist die “uniqueness” (\(u^2\)), also der unerklärte Anteil. Diese wird auch oft Spezifität genannt, da sie den für dieses Item spezifischen Varianzanteil beschreibt. Offensichtlich gilt \(u^2 = 1-h^2\) oder \(h^2 + u^2 = 1\). Unter den Faktorladungen erhalten wir Informationen über die Faktoren. SS loadings steht für “Sum of Squares loadings”, also die Quadratsumme der Faktorladungen. Diese ist gleich dem Eigenwert: \(\theta_j = \Sigma_{i=1}^p\lambda_{ij}^2 = \lambda_{1j}^2+\dots+\lambda_{pj}^2\) (Spaltenquadratsumme der Faktorladungen), mit \(p=\) Anzahl an Variablen (hier \(p=6\)). Allerdings gilt dies nur für den orthogonalen Fall. Sind die Faktoren korreliert, muss diese Korrelation berücksichtigt werden. Dazu später mehr! Proportion Var betitelt den Anteil der Variation, der durch die jeweiligen Faktoren erklärt werden kann. Cumulative Var kumuliert, also summiert, diese Anteile bis zum jeweiligen Faktor auf (\(\text{CumVar}_j = \sum_{k=1}^j\theta_k = \theta_1+\dots+\theta_j\), also \(\text{CumVar}_1=\theta_1\) und \(\text{CumVar}_2=\theta_1+\theta_2\)). Proportion Explained setzt die Variation, die durch die Faktoren erklärt wird, in Relation zur gesamten erklärten Varianz (d.h. hier summiert sich die erklärte Varianz immer zu 1, während sich die proportionale Varianz nur zu 1 aufsummiert, wenn die gesamte Variation im Datensatz auf die beiden Variablen zurückzuführen ist). Cumulative Proportion beschreibt das gleiche wie Cumulative Var, nur bezieht sie sich hier auf die Proportion Explained. Bei der Interpretation dieser Kennwerte ist zu bedenken, dass bei der EFA angenommen wird, dass die beobachteten Variablen Messfehler enthalten (also die Reliabilität nicht als 1 angenommen werden kann). Folglich ist die Kommunalität \(h^2\) nicht 1 und wir können nicht unbedingt davon ausgehen, dass die Faktoren die gesamte Variation der Daten erklären. All diese Koeffizienten kennen wir bereits aus der Sitzung zur PCA, wo wir diese im Hinblick auf eine PCA interpretierten. Dabei fiel uns auch auf, dass einige Koeffizienten in dieser Übersicht nicht mit allen Dezimalstellen angezeigt werden und es ggf. zu seltsamen Rundungsverfälschungen kommen kann. Aus diesem Grund hatten wir uns entschieden, die jeweiligen Koeffizienten und Informationen dem Objekt selbst zu entlocken, um diese Rundungsverfälschungen zu umgehen.
Außerdem werden durch diesen Befehl sehr viele Informationen ausgegeben. Aus diesen Gründen speichern wir uns diese Analyse als ein Objekt ab, welchem wir dann gezielt Informationen mit Hilfe von ...$... entlocken können. Welche Argumente entlockt werden können, kann beispielsweise mit names herausgefunden werden. Wir speichern das Objekt unter dem Namen two_factor ab.
two_factor <- fa(dataFR2, nfactors = 2, rotate = "varimax")
names(two_factor) # mögliche Informationen## [1] "residual" "dof" "chi" "nh"
## [5] "rms" "EPVAL" "crms" "EBIC"
## [9] "ESABIC" "fit" "fit.off" "sd"
## [13] "factors" "complexity" "n.obs" "objective"
## [17] "criteria" "STATISTIC" "PVAL" "Call"
## [21] "null.model" "null.dof" "null.chisq" "TLI"
## [25] "RMSEA" "BIC" "SABIC" "r.scores"
## [29] "R2" "valid" "score.cor" "weights"
## [33] "rotation" "hyperplane" "communality" "communalities"
## [37] "uniquenesses" "values" "e.values" "loadings"
## [41] "model" "fm" "rot.mat" "Structure"
## [45] "method" "scores" "R2.scores" "r"
## [49] "np.obs" "fn" "Vaccounted"Beispielsweise erhalten wir mit $loadings die Faktorladungsmatrix sowie Informationen über die Eigenwerte. (Wichtig für später: Die richtigen Kommunalitäten werden mit $communality angefordert.)
two_factor$loadings##
## Loadings:
## MR1 MR2
## E1 0.692
## E2 -0.646
## E3 0.819 -0.186
## N1 0.837
## N2 -0.580
## N3 0.585
##
## MR1 MR2
## SS loadings 1.578 1.419
## Proportion Var 0.263 0.236
## Cumulative Var 0.263 0.499Hier ist relativ deutlich die Zuordnung zu den jeweiligen Faktoren zu sehen. Faktor 1 (MR1) entspräche post-hoc interpretiert (die Theorie wird also aus den Daten generiert; es sind auch andere Interpretationsansätze zulässig) der Extraversion, während der zweite Faktor (MR2) dem Neurotizismus entspräche. Indem wir hinter loadings eckige Klammern mit einem Komma setzten ([,]), bekommen wir alle Nachkommastellen ohne Runden angzeigt (hätten wir bspw. round auf die Ladungsmatrix oben angewendet, würden sich auch die Eigenwerte ändern, weswegen diese Ansicht sich nicht wirklich zur genauen Interpretation der Eigenwerte eignet! Hier hatten wir das Argument Vaccounted bereits im Rahmen der PCA kennengelernt):
two_factor$loadings[,] # ohne seltsames Runden## MR1 MR2
## E1 0.69189323 -0.058067393
## E2 -0.64577474 0.004122088
## E3 0.81858640 -0.185912523
## N1 -0.01345489 0.837407770
## N2 0.09879742 -0.580348020
## N3 -0.04734674 0.585385819Die Faktorladungsmatrix wird auch manchmal Mustermatrix genannt. Die Strukturmatrix enthält Informationen über die Korrelation der Items mit den jeweiligen Faktoren. Sie heißt Structure. Auch hier ist der Zusatz [,] sinnvoll!
two_factor$Structure[,]## MR1 MR2
## E1 0.69189323 -0.058067393
## E2 -0.64577474 0.004122088
## E3 0.81858640 -0.185912523
## N1 -0.01345489 0.837407770
## N2 0.09879742 -0.580348020
## N3 -0.04734674 0.585385819Wir sehen deutlich, dass die Strukturmatrix sich nicht von der Faktorladungsmatrix unterscheidet. Das liegt daran, dass die Faktoren noch als unkorreliert angenommen werden: somit ist die Faktorladungsmatrix gleich der Strukturmatrix. Genau aus diesem Grund hatten wir uns die Strukturmatrix auch nicht im Rahmen der PCA angesehen — dort hatten wir nur orthogonal rotiert.
Da wir nicht davon ausgehen können, dass die Faktoren unkorreliert sind, wollen wir die gleiche Analyse nun für oblique (“oblimin” in R) rotierte Faktoren durchführen.
two_factor_oblimin <- fa(dataFR2, nfactors = 2, rotate = "oblimin")Die einzig neue Information können wir unter With factor correlations of ablesen: die Korrelation zwischen den Faktoren. Im Output der obliquen Rotation ist zu erkennen, dass sich die Kommunalitäten nicht ändern. Wir können also nicht mehr Variation im Datensatz erklären. Die Varianz wird nur umverteilt, wie den veränderten Eigenwerten neben SS loadings zu entnehmen ist. Hier hat der erste Faktor einen etwas größeren Eigenwert als im orthogonalen Fall (entsprechend ist der 2. Eigenwert kleiner, da nicht mehr Variation erklärt wird):
two_factor$Vaccounted## MR1 MR2
## SS loadings 1.5780086 1.4186844
## Proportion Var 0.2630014 0.2364474
## Cumulative Var 0.2630014 0.4994488
## Proportion Explained 0.5265833 0.4734167
## Cumulative Proportion 0.5265833 1.0000000two_factor_oblimin$Vaccounted## MR1 MR2
## SS loadings 1.6065736 1.3901195
## Proportion Var 0.2677623 0.2316866
## Cumulative Var 0.2677623 0.4994488
## Proportion Explained 0.5361155 0.4638845
## Cumulative Proportion 0.5361155 1.0000000Schauen wir uns die Ladungsmatrix an, …
two_factor_oblimin$loadings[,] # Ladungsmatrix## MR1 MR2
## E1 0.70055173 0.03946625
## E2 -0.65623412 -0.08729631
## E3 0.82326401 -0.07142273
## N1 0.02609114 0.84195602
## N2 0.07286715 -0.57082957
## N3 -0.02032830 0.58319228… so ist post-hoc interpretiert anzunehmen, dass der erste Faktor die Extraversion abbildet und der zweite den Neurotizismus.
Entlocken Sie doch mal dem Objekt two_factor_oblimin die latente Kovarianzmatrix, also die Kovarianzmatrix der latenten Variablen. Tipp, der griechische Buchstabe in diesem Zusammenhang ist häufig \(\Phi\). Die resultierende Matrix sieht so aus:
## MR1 MR2
## MR1 1.0000000 -0.1852246
## MR2 -0.1852246 1.0000000Als neue Information entnehmen wir der Korrelationsmatrix der Faktoren, dass die beiden Faktoren negativ korreliert sind zu -0.19. Nun wollen wir nachschauen, ob sich tatsächlich die Strukurmatrix im oblique-rotierten Fall von der Faktorladungsmatrix unterscheidet:
two_factor_oblimin$loadings[,]## MR1 MR2
## E1 0.70055173 0.03946625
## E2 -0.65623412 -0.08729631
## E3 0.82326401 -0.07142273
## N1 0.02609114 0.84195602
## N2 0.07286715 -0.57082957
## N3 -0.02032830 0.58319228two_factor_oblimin$Structure[,]## MR1 MR2
## E1 0.6932416 -0.09029319
## E2 -0.6400647 0.03425442
## E3 0.8364933 -0.22391151
## N1 -0.1298599 0.83712330
## N2 0.1785989 -0.58432636
## N3 -0.1283499 0.58695759Sie sehen, dass sich nun die Strukturmatrix von der Faktorladungsmatrix unterscheidet. Die Unterschiede sind allerdings nicht sehr groß, da die Korrelation zwischen den beiden Faktoren mit -0.19 betragsmäßig nicht sonderlich groß ausfällt. Weitere Informationen und wie die beiden Matrizen ineinander überführbar sind, erfahren Sie im Appendix C. In Appendix D erfahren Sie, wie Sie Kommunalitäten und Eigenwerte im Rahmen der EFA nur mit Hilfe der loadings und der Faktorkorrelation Phi bestimmen. Falls Sie sich nun zu Recht wundern, dass Appendix B fehlt, dann sei gesagt, dass dieser alle Analysen am vollständigen Datensatz durchführt und es durch die Abhängigkeiten der Daten in den Appendizes Sinn macht, diesen zwar im Text später zu erwähnen aber inhaltlich vorzuziehen.
Die Frage ist nun, ob unser Modell überhaupt zu den Daten passt.
Exploratorische Maximum-Likelihood-Faktorenanalyse (ML-EFA)
Wir möchten unsere Analysen nun gegen andere konkurrierende Modelle absichern sowie untersuchen, ob unser zweifaktorielles Modell überhaupt zu den Daten passt. Hierzu müssen wir annehmen, dass unsere Daten multivariat normalverteilt sind. Wie man diese Annahme zumindest deskriptiv untersucht, hatten wir im Zusammenhang mit den Voraussetzungen von statistischen Verfahren kennengelernt (Mahalanobisdistanz sollte approximativ \(\chi^2\)-verteilt sein, siehe hierzu im Appendix E nach, auch weitere Tests sind möglich: bspw. Mardia’s Test). Mit Hilfe dieser Verteilungsannahme können wir die Maximum-Likelihood-Schätzmethode nutzen, um die Parameter in unserem Modell zu schätzen. Die Likelihood ist die Wahrscheinlichkeit unserer Daten, gegeben das Modell. Sie hängt somit von den beobachteten Daten ab (den Ausprägungen der Personen auf den Variablen), hat die Gestalt unseres Modells und wird parametrisiert durch die Parameter in unserem Modell. Die durch das Modell implizierte Kovarianz oder Korrelationsmatrix der beobacheten Variablen wird mit \(\Sigma\) betitelt und setzt sich folgendermaßen zusammen:
\[\Sigma := \Lambda\Phi \Lambda' + \Theta.\] Dabei ist \(\Lambda\) die Matrix der Faktorladungen, \(\Phi\) die Kovarianz- oder Korrelationsmatrix der Faktoren und \(\Theta\) die Kovarianzmatrix der Fehler.
Im unkorrelierten/orthogonalen Fall sähe die Matrix so aus: \(\Sigma := \Lambda \Lambda' + \Theta\), da hier \(\Phi\) die Einheitsmatrix ist und \(\Lambda\) demzufolge einfach mit 1 multipliziert wird! Diese ist somit sehr nah an der implizierten Matrix im Rahmen der PCA, welche sich durch \(\Lambda \Lambda'\) ergab. Wir erkennen erneut, dass bei der PCA die Messfehler nicht mitmodelliert werden (deren Varianzen stecken in \(\Theta\)).
Unter der Normalverteilungsannahme brauchen wir nur (Ko-)Varianzen und Mittelwerte, um unsere Variablen vollständig zu beschreiben. In der Schätzung der ML-EFA geht es uns darum, die Parameter in \(\Lambda\), \(\Phi\) und \(\Theta\) so zu bestimmen, dass sich die behauptete Kovarianzmatrix \(\Sigma\) von unserer beobachteten Kovarianzmatrix \(S\) so wenig unterscheidet wie möglich. Dazu bestimmen wir mit der Maximum-Likelihood-Schätzung die Werte für z.B. Faktorladungen, die es maximal wahrscheinlich machen, dass unsere Daten enstehen würden, wenn unsere EFA das richtige Modell wäre.
Um mit Hilfe von fa eine ML-EFA durchzuführen, muss dem Argument fm die entsprechende Bezeichnung "ml" übergeben werden.
two_factor_ML <- fa(dataFR2, nfactors = 2, rotate = "oblimin", fm = "ml")
two_factor_ML## Factor Analysis using method = ml
## Call: fa(r = dataFR2, nfactors = 2, rotate = "oblimin", fm = "ml")
## Standardized loadings (pattern matrix) based upon correlation matrix
## ML1 ML2 h2 u2 com
## E1 0.69 0.04 0.47 0.53 1.0
## E2 -0.65 -0.06 0.41 0.59 1.0
## E3 0.83 -0.06 0.71 0.29 1.0
## N1 0.03 0.84 0.70 0.30 1.0
## N2 0.10 -0.57 0.35 0.65 1.1
## N3 -0.01 0.59 0.36 0.64 1.0
##
## ML1 ML2
## SS loadings 1.61 1.39
## Proportion Var 0.27 0.23
## Cumulative Var 0.27 0.50
## Proportion Explained 0.54 0.46
## Cumulative Proportion 0.54 1.00
##
## With factor correlations of
## ML1 ML2
## ML1 1.00 -0.18
## ML2 -0.18 1.00
##
## Mean item complexity = 1
## Test of the hypothesis that 2 factors are sufficient.
##
## The degrees of freedom for the null model are 15 and the objective function was 1.47 with Chi Square of 183.82
## The degrees of freedom for the model are 4 and the objective function was 0.07
##
## The root mean square of the residuals (RMSR) is 0.04
## The df corrected root mean square of the residuals is 0.07
##
## The harmonic number of observations is 129 with the empirical chi square 5.6 with prob < 0.23
## The total number of observations was 129 with Likelihood Chi Square = 8.75 with prob < 0.068
##
## Tucker Lewis Index of factoring reliability = 0.893
## RMSEA index = 0.096 and the 90 % confidence intervals are 0 0.184
## BIC = -10.69
## Fit based upon off diagonal values = 0.99
## Measures of factor score adequacy
## ML1 ML2
## Correlation of (regression) scores with factors 0.90 0.88
## Multiple R square of scores with factors 0.80 0.77
## Minimum correlation of possible factor scores 0.61 0.55Wir sehen, dass diesmal die Schätzmethode “ml” ist. Auch die Faktoren heißen nun ML1 und ML2. Die Faktorladungen im ML-EFA Modell mit obliquer Rotation sehen den Faktorladungen aus unserer vorigen Analyse sehr ähnlich.
Uns interessiert nun die Modellpassung, also inwiefern unsere Daten von unserem behaupteten Modell abweichen. $STATISTIC und $PVAL entlocken der Analyse (abgespeichert als Objekt) den \(\chi^2\)-Wert und den zugehörigen p-Wert bei 4 Freiheitsgraden. Verwirrenderweise gibt es zusätzlich $chi, was den empirisch und nicht likelihoodbasierten \(\chi^2\)-Wert ausgibt, welcher sinnvoll ist, wenn Modellvoraussetzungen nicht erfüllt sind.
two_factor_ML$STATISTIC # Likelihood basierter Chi²-Wert## [1] 8.749298two_factor_ML$PVAL # p-Wert## [1] 0.06768059Dem ist zu entnehmen, dass auf dem Signifikanzniveau von 5% die Hypothese auf Passung der Kovarianz unserer Daten mit der modellimplizierten Kovarianz in der Population nicht verworfen wird. Die Daten widersprechen dem zweifaktoriellen Modell nicht (die untersuchte Null-Hypothese ist: \(H_0: \Sigma_{Daten}=\Sigma_{2-fakt.}\), also, dass die Datenkovarianzmatrix sich durch die Kovarianzmatrix eines 2-faktoriellen EFA-Modells darstellen lässt). Vielleicht reicht auch ein Faktor aus, um die Variation in unserem Datensatz zu beschreiben? Wir wollen unser Modell mit zwei Faktoren gegen eines mit einem und eines mit drei Faktoren absichern.
Modellvergleich: ML-EFA
Das einfaktorielle Modell erhalten wir ganz einfach via:
one_factor_ML <- fa(dataFR2, nfactors = 1, rotate = "oblimin", fm = "ml")
one_factor_ML$STATISTIC # Chi²-Wert## [1] 76.76935one_factor_ML$PVAL # p-Wert## [1] 7.063217e-13Das einfaktorielle Modell scheint nicht zu den Daten zu passen (Mit einer Irrtumswahrscheinlichkeit von 5% ist davon auszugehen, dass in der Population die Differenz zwischen der Populationskovarianzmatrix und der modellimplizierten Kovarianzmatrix, bzw. der daraus folgenden Likelihoods, nicht 0 ist.). Dennoch wollen wir dies genau wissen und vergleichen die beiden Modelle direkt miteinander. Für einen solchen Vergleich ist es notwendig, dass es sich bei den beiden Modellen um geschachtelte Modelle handelt. Das bedeutet, dass ein Modell durch Restriktionen von Modellparametern aus dem anderen Modell erzeugt werden kann. Das einfaktorielle Modell lässt sich aus dem zweifaktoriellen Modell durch die Restriktion gewinnen, dass alle Ladungen auf dem Faktor 0 sind und die Varianz dieses Faktors dementsprechend ebenfalls 0 ist.
Mit Hilfe des anova-Befehls, welchen wir schon bei einigen anderen Modellvergleichen im Rahmen der Regression, der logistischen Regression sowie der Multi-Level Modelle kennengelernt haben, lässt sich nun das einfaktorielle mit dem zweifaktoriellen Modell vergleichen.
anova(one_factor_ML, two_factor_ML)## Model 1 = fa(r = dataFR2, nfactors = 1, rotate = "oblimin", fm = "ml")
## Model 2 = fa(r = dataFR2, nfactors = 2, rotate = "oblimin", fm = "ml")| df | d.df | chiSq | d.chiSq | PR | test | empirical | d.empirical | test.echi | BIC | d.BIC | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 9 | NA | 76.77 | NA | NA | NA | 142.43 | NA | NA | 33.03 | NA |
| 2 | 4 | 5 | 8.75 | 68.02 | 0 | 13.6 | 5.60 | 136.83 | 27.37 | -10.69 | -43.72 |
Zunächst bekommen wir angezeigt, welche Modelle unter welchem Kürzel gegeneinander getestet werden. Die Modellnummer steht im ANOVA-Output entsprechend für das jeweilige Modell. In der Zeile 2 steht also der Output für das 2-faktorielle Modelle und am Ende dieser Zeile steht auch der Modellvergleich.
In der ersten Spalte stehen beispielsweise die Freiheitsgrade der Modelle (df). Daneben steht die Differenz der Freiheitsgrade (d.df) und dahinter stehen verschiedene Fit-Maße, bzw. Modellvergleiche. Wir müssen im Bereich des chiSq und nicht bei empirical (eine Näherung des \(\chi^2\) Wertes, wenn Annahmen verletzt sind) nachsehen. Der Output ist immer so aufgebaut, dass zunächst der Wert pro Modell (chiSq oder empirical) angezeigt wird und anschließend die Differenz (d.chiSq oder d.empirical) sowie die Signifikanzentscheidung berichtet werden (PR test, welche allerdings nicht bei der Näherung angezeigt wird). Außerdem wird noch eine Rubrik test, bzw. test.echi angezeigt, welche noch einmal die \(\chi^2\)-Differenz geteilt durch die Freiheitsgrade repräsentiert. Der \(\chi^2\)-Differenzwert liegt bei 68.02 mit einem zugehörigen p-Wert von de facto 0. d.df (häufig \(\Delta df\)) gibt die Anzahl an Freiheitsgraden der \(\chi^2\)-Differenz (hier: df = 5) des Differenzentests an (hier wurden die Freiheitsgrade der beiden Modelle voneinander abgezogen). Ganz hinten wird noch das Bayes Information Criterion BIC, sowie dessen Differenz d.BIC aufgeführt. Dieses Informationskriterium werden wir bei der CFA und deren Modellpassung noch einmal genauer betrachten.
Insgesamt wird die Null-Hypothese, dass beide Modell die Daten gleich gut beschreiben, verworfen. Wir entscheiden uns — Ockhams Rasiermesser folgend (siehe Eid et al., 2017, p. 787) — somit für das Modell mit mehr Parametern - das weniger restriktive Modell - welches die Daten besser beschreibt: hier das zweifaktorielle Modell. Nun ist die Frage, ob wir das Modell noch weiter verbessern können, indem wir drei anstatt zwei Faktoren verwenden, um die Kovariation zwischen den Variablen zu beschreiben.
# Passt auch eines mit 3 Faktor?
three_factor_ML <- fa(dataFR2, nfactors = 3, rotate = "oblimin", fm = "ml")
three_factor_ML$STATISTIC # Chi²-Wert## [1] 0.0328432three_factor_ML$PVAL # p-Wert## [1] NADas dreifaktorielle Modell beschreibt die Daten perfekt. Das liegt daran, dass es im dreifaktoriellen Modell genauso viele Parameter gibt, wie es empirische Informationen im Datensatz gibt. Demnach lässt sich die empirische Korrelationsmatrix perfekt durch die modelltheoretische Korrelationsmatrix (diejenige Korrelationsmatrix, die sich ergibt, wenn nur die Beziehungen zwischen den Variablen bestehen, die durch das Modell angenommen werden) darstellen. Ein Test auf Modellpassung ist in diesem Fall nicht möglich und auch nicht nötig (deshalb wird beim $PVAL nichts bzw. NA ausgegeben). Nun vergleichen wir die beiden Modelle (es ist sehr sinnvoll, das komplexere Modell rechts hin zuschreiben, da es ansonsten bei manchen Analysemethoden zu negativen \(\chi^2\)-Werten kommen kann, außerdem zeigt man damit auf, wie die Schachtelung der Modelle funktioniert [allerdings sichert dies nicht die Schachtelung, dies ist eine theoretische Überlegung, die die Software leider in den meisten Fällen nicht für uns übernehmen kann]. Hier: das 2-faktorielle Modell ist ein Spezialfall des 3-faktoriellen Modells):
anova(two_factor_ML, three_factor_ML)## Model 1 = fa(r = dataFR2, nfactors = 2, rotate = "oblimin", fm = "ml")
## Model 2 = fa(r = dataFR2, nfactors = 3, rotate = "oblimin", fm = "ml")| df | d.df | chiSq | d.chiSq | PR | test | empirical | d.empirical | test.echi | BIC | d.BIC | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 4 | NA | 8.75 | NA | NA | NA | 5.60 | NA | NA | -10.69 | NA |
| 2 | 0 | 4 | 0.03 | 8.72 | 0.07 | 2.18 | 0.02 | 5.58 | 1.4 | -10.69 | NA |
Der \(\chi^2\)-Differenzwert liegt hier bei 8.72 mit einen zugehörigen p-Wert von 0.07. d.df liegt bei 4 (\(\Delta df\) = 4). Somit wird die Null-Hypothese, dass beide Modell die Daten gleich gut beschreiben, bzw. dass das sparsamere Modell die Daten genauso gut beschreiben kann, wie das komplexere Modell (\(H_0:\Sigma_{3-Fakt.} = \Sigma_{2-Fakt.}\); im Gegensatz zum anova-Befehl, steht hier das komplexere Modell links), nicht verworfen. Aus diesem Grund entscheiden wir uns - Ockhams Rasiermesser folgend (siehe Eid et al., 2017, p. 787) - für das sparsamere Modell, also jenes, welches weniger Parameter enthält und somit restriktiver ist, hier: das zweifaktorielle Modell. Denn in der Wissenschaft streben wir danach, Modelle möglichst einfach zu halten!
Wenn Sie davon noch nicht genug haben, so können Sie in Appendix B nachlesen, wie eine EFA am gesamten (gekürzten) Datensatz durchgeführt wird. Dort stehen keine neuen Informationen zur Durchführung, Sie sollten es folglich eher als Übung ansehen, falls Sie sich entschließen, Appendix B durchzuarbeiten!
Die Zuordnung, die wir hier gefunden haben, entspringt der spezifischen Stichprobe, die wir untersucht haben. Wenn wir a priori aufgestellte Theorien über die Faktorstruktur prüfen wollen, können wir uns der konfirmatorischen Faktorenanalyse bedienen, die wir in der nächsten Sitzung betrachten.
Den gesamten R-Code, der in dieser Sitzung genutzt wird, können Sie hier herunterladen.
Appendix A
Kürzen des Datensatzes
Falls Sie die Originaldaten auf openpsychometrics.org als .zip herunterladen wollen, so können Sie diesen auf die hier verwendeten Daten wie folgt kürzen:
data_full <- read.table("BIG5/data.csv", header = T, sep = "\t") # nach entpacken des .zip liegen die Daten in einem Ordner namens Big5
### Entferne leere Zeilen und Zeilen mit Missings aus dem Datensatz
ind <- apply(data_full, 1, FUN = function(x) any(is.na(x))) # erzeuge eine Variable, welche TRUE ist, wenn mindestens ein Eintrag pro Zeile fehlt und ansonsten FALSE anzeigt
data_full <- data_full[!ind, ] # Wähle nur diejenigen Zeilen, in denen unsere Indikatorvariable "ind" NICHT TRUE anzeigt, also wo alle Einträge vorhanden sind
# !ind (Ausrufezeichen vor ind) negiert die Einträge in ind (Prüfe bspw. !FALSE == TRUE, nicht false ist gleich true)
### Shorten Data Set
Big5 <- data_full[, c(2:4,7,7+rep(1:3,5)+sort(rep(seq(0,40,10),3)))]
# Verwende nur 3 Items pro Skala plus einige demografische Items
Big5 <- data.frame(Big5) # Schreibe Datensatz als data.frame
save(list = c("Big5"), file = "Big5.rda")
# Speichere gekürzten Datensatz in .rda file (dem R-internen Datenformat)
## --> Das ist auch der Datensatz, den wir weiter verwendet haben!Appendix B
ML-EFA für den gesamten (gekürzten) Datensatz
Für den vollen Datensatz mit jeweils drei Items pro Persönlichkeitsfacette, nehmen wir zunächst an, dass es 5 Faktoren gibt. Dies wird hier allerdings nicht durch die Parallelanalyse gestützt. Wir müssen die Funktion fa.parallel diesmal auf den vollen (gekürzten) Datensatz anwenden; nämlich auf dataFR.
fa.parallel(x = dataFR,fa = "fa")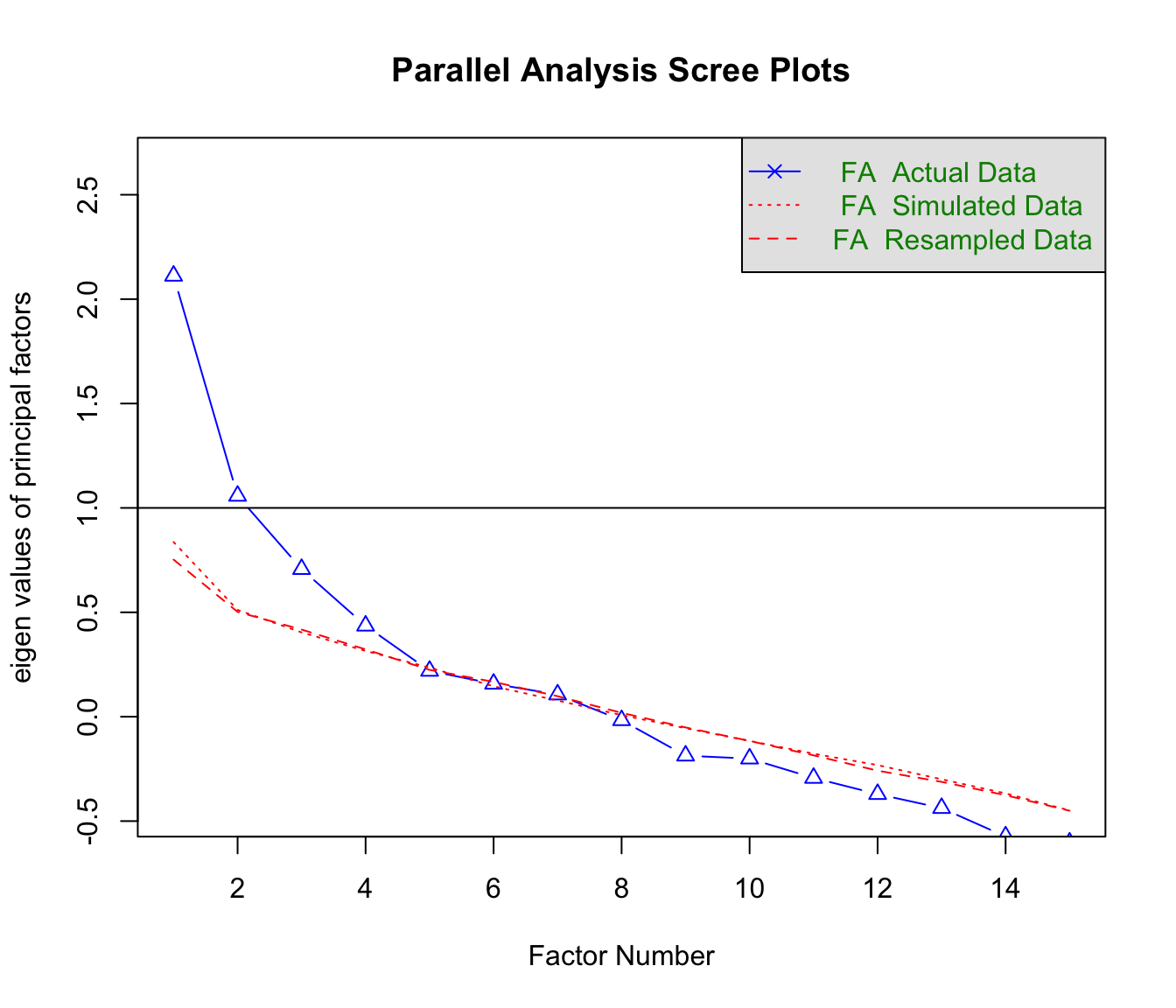
## Parallel analysis suggests that the number of factors = 4 and the number of components = NAHier scheinen eher 4 Faktoren sinnvoll. Wir prüfen dennoch erstmal unsere inhaltliche Hypothese, dass es 5 Faktoren gibt, mit Hilfe der oblique Rotierten ML-EFA.
five_factor_ML <- fa(dataFR, nfactors = 5, rotate = "oblimin", fm = "ml")
five_factor_ML$STATISTIC## [1] 44.07717five_factor_ML$PVAL # Modell wird durch die Daten nicht verworfen## [1] 0.3031972Die Daten scheinen unserem Modell mit 5 Faktoren nicht zu widersprechen. Schauen wir uns die Faktorladungen an, um die Faktoren inhaltlich zu interpretieren.
five_factor_ML$loadings # auch nochmal ohne [,] um die Ausblendehilfe von psych als Unterstützung für die Zuordnung zu nutzen##
## Loadings:
## ML4 ML3 ML1 ML2 ML5
## E1 0.688
## E2 -0.643 0.155
## E3 0.813 0.117
## N1 0.433 -0.340
## N2 0.986
## N3 0.920
## A1 -0.227 0.160 0.203 -0.276
## A2 0.655 0.242
## A3 -0.186 0.159 0.197
## C1 0.170 0.208 0.179 -0.355
## C2 0.730
## C3 0.177 0.140 0.145 -0.278
## O1 0.998
## O2 0.126 0.247 -0.214 -0.106
## O3 0.229 0.163 0.189
##
## ML4 ML3 ML1 ML2 ML5
## SS loadings 2.091 1.328 1.274 1.194 0.869
## Proportion Var 0.139 0.089 0.085 0.080 0.058
## Cumulative Var 0.139 0.228 0.313 0.392 0.450five_factor_ML$loadings[,] # alle Dezimalstellen anzeigen## ML4 ML3 ML1 ML2 ML5
## E1 0.688468319 -0.03665453 -0.012193249 0.02787857 0.071260642
## E2 -0.643272367 0.08577303 0.155240994 0.09656023 0.065735002
## E3 0.812764373 -0.05121616 0.116888237 0.01806219 -0.076129365
## N1 -0.022613674 0.43257679 -0.339987402 -0.07415779 0.069005051
## N2 0.017710987 -0.02860957 0.985613730 -0.02537580 0.026025668
## N3 -0.004230572 0.91962125 -0.026913718 -0.00657639 -0.013229825
## A1 -0.227423669 0.15957275 0.203222904 -0.08704521 -0.275728683
## A2 0.655281001 0.24198774 0.006033115 0.01175666 0.092166503
## A3 -0.186178370 0.15918711 0.095110929 0.19652141 0.097407381
## C1 0.056714149 0.16981702 0.207576065 0.17890272 -0.354809510
## C2 -0.015398173 0.01818279 0.084998138 0.01776008 0.729941525
## C3 0.014355504 0.17741965 0.140061799 0.14464044 -0.278431363
## O1 0.002352582 -0.01037494 -0.023817340 0.99812410 -0.001488256
## O2 0.125971083 0.24681060 0.029753625 -0.21358237 -0.106264287
## O3 -0.080478366 0.22862665 0.163239313 0.18923154 0.082298847Durch die Rotation sind auch hier die Faktoren anders nummeriert. Der erste Faktor ist hier ML4 (dieser Faktor ist der erste in der Liste, da hier der Eigenwerte nach Rotation maximal ist; vor Rotation hatte ML4 den viert größten Eigenwert). Die höchsten Faktorladungen mit diesem Faktor haben die Items \(E_1\), \(E_2\), \(E_3\) und \(A_2\). Somit könnte man diesen am ehesten post-hoc (die Theorie wird also aus den Daten generiert; es sind auch andere Interpretationsansätze zulässig) als Extraversion interpretieren. Allerdings scheinen die Items der Extraversion einiges mit jenen der Verträglichkeit (\(A_{...}\)) gemeinsam zu haben.
Dies könnte mit unter damit zusammen hängen, dass diese beiden Items am ehesten etwas mit sozialer Erwünschtheit zu tun haben.
Auf dem Faktor ML3 laden vor allem die Items \(N_1\) und \(N_3\). Allerdings lädt \(N_2\) besonders auf ML1.
Dies könnte durchaus daran liegen, dass \(N_1\) (“I get stressed out easily.”) und \(N_3\) (“I worry about things.”) negativ kodiert sind, während \(N_2\) (“I am relaxed most of the time.”) positiv kodiert ist und die erstgenannten Items somit mehr gemeinsam haben als die inhaltliche Zuordnung zum Neurotizismus. Somit scheint ML3 ein Faktor der Sorgen, also des Neurotizismus zu sein, während ML1 eher für einen Faktor der Gelassenheit spricht; beispielsweise laden hier auch positiv Items der Extraversion und Verträglichkeit. Das die Items des Neurotizismus auf unterschiedlichen Faktoren laden und unterschiedliche Vorzeichen aufweisen, kann für Methodeneffekte sprechen (Unterschiede die zustande kommen, da unterschiedliche Methoden, hier: Itemformulierungen [positiv vs. negativ], verwendet werden.). Auch auf ML2 und ML5 laden jeweils nur ein Item besonders stark: \(O_1\) auf ML2 und \(C_2\) auf ML5. Insgesamt muss geschlussfolgert werden, dass zwar die fünffaktorielle Struktur durch die Daten nicht verworfen wird, aber dass die oblique rotierte Lösung keine eindeutige Zuordnung der Items aufweist. Allerdings bringt auch eine varimax-rotierte Lösung keine Verbesserung der Interpretierbarkeit, da diese neben der Einfachstruktur in der Faktorladungsmatrix noch die Unkorreliertheit der Faktoren berücksichtigen muss (in der varimax-rotierten Lösung sind dafür die Konstrukte nicht überlappend, was allerdings auch eine strenge Annahme ist):
fa(dataFR, nfactors = 5, rotate = "varimax", fm = "ml")$loadings[,]## ML4 ML3 ML1 ML2 ML5
## E1 0.679741350 -0.0298612003 0.04717727 -0.06209588 -0.025294029
## E2 -0.616269745 -0.0009785951 0.07502041 0.24020664 -0.043100326
## E3 0.812929628 -0.0734949752 0.16420656 -0.12171911 0.134579147
## N1 -0.060232149 0.5043444919 -0.37548744 0.06060518 -0.063964536
## N2 0.101251528 -0.2329637937 0.95295799 0.10457873 0.106824247
## N3 -0.016430443 0.8479850127 -0.18607020 0.29295427 0.151708177
## A1 -0.213443248 0.1199149173 0.13194526 -0.04987855 0.278471636
## A2 0.644794316 0.2278750098 0.01990198 0.03032774 -0.004249186
## A3 -0.165880085 0.0456542742 0.02042712 0.28908281 -0.018069436
## C1 0.081940401 0.0183155255 0.08750067 0.11679630 0.435079003
## C2 -0.006651558 0.0264955123 0.16832618 0.26419496 -0.667066743
## C3 0.032388740 0.0576353789 0.03621164 0.11108025 0.344258937
## O1 0.056711714 -0.4160253195 -0.23367971 0.84296969 0.231306357
## O2 0.112086056 0.3032964635 0.02602280 -0.14672358 0.100453282
## O3 -0.056937114 0.0975755222 0.08029510 0.29567696 0.021600591was wahrscheinlich daran liegt, dass die Kovariation zwischen den Faktoren nicht sehr groß ist:
round(five_factor_ML$Phi, 2) # runde auf 2 Nachkommastellen## ML4 ML3 ML1 ML2 ML5
## ML4 1.00 -0.05 0.14 -0.07 -0.09
## ML3 -0.05 1.00 -0.30 -0.02 -0.02
## ML1 0.14 -0.30 1.00 0.04 0.02
## ML2 -0.07 -0.02 0.04 1.00 0.00
## ML5 -0.09 -0.02 0.02 0.00 1.00fa(dataFR, nfactors = 5, rotate = "varimax", fm = "ml")$Phi## NULLNULL zeigt hierbei an, dass es das $Phi -Objekt nicht gibt. Tatsächlich ist die Kovarianzmatrix im orthogonalen Fall die Einheitsmatrix der Dimension \(5\times5\):
\[\begin{pmatrix} 1& 0&0&0&0 \\ 0& 1&0&0&0 \\ 0& 0&1&0&0\\ 0& 0&0&1&0 \\ 0& 0&0&0&1 \end{pmatrix}\]
In R:
diag(5) # Einheitsmatrix der Dimension 5x5.## [,1] [,2] [,3] [,4] [,5]
## [1,] 1 0 0 0 0
## [2,] 0 1 0 0 0
## [3,] 0 0 1 0 0
## [4,] 0 0 0 1 0
## [5,] 0 0 0 0 1Modellvergleich: ML-EFA
Wir schauen uns nun die Passung unseres Modells im Vergleich zu einem vier- und einem sechsfaktoriellen Modell an.
four_factor_ML <- fa(dataFR, nfactors = 4, rotate = "oblimin", fm = "ml")
four_factor_ML$STATISTIC## [1] 73.04596four_factor_ML$PVAL## [1] 0.023097Das vierfaktorielle Modell wird durch die Daten verworfen (\(p<0.05\)). Nun zum Modellvergleich:
anova(four_factor_ML, five_factor_ML)## Model 1 = fa(r = dataFR, nfactors = 4, rotate = "oblimin", fm = "ml")
## Model 2 = fa(r = dataFR, nfactors = 5, rotate = "oblimin", fm = "ml")| df | d.df | chiSq | d.chiSq | PR | test | empirical | d.empirical | test.echi | BIC | d.BIC | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 51 | NA | 73.05 | NA | NA | NA | 105.81 | NA | NA | -174.80 | NA |
| 2 | 40 | 11 | 44.08 | 28.97 | 0 | 2.63 | 47.94 | 57.87 | 5.26 | -150.32 | 24.49 |
Wir entscheiden uns hier nun für das fünffaktorielle Modell. Nun wollen wir uns das fünffaktorielle Modell noch im Vergleich zum sechsfaktoriellen Modell ansehen.
six_factor_ML <- fa(dataFR, nfactors = 6, rotate = "oblimin", fm = "ml")
six_factor_ML$STATISTIC## [1] 29.19415six_factor_ML$PVAL # Modell wird durch die Daten nicht verworfen## [1] 0.5074152Dem sechsfaktoriellen Modell widersprechen die Daten genauso wenig, wie dem fünffakoriellen (beide \(p>0.05\)). Dies war zu erwarten, da wir durch Hinzunahme des sechsten Faktors die Komplexität des Modell erhöht haben, wodurch sich das Modell stärker der konkreten Datenlage annähern kann. Mehr Faktoren bedeuten immer eine detailgetreuere Abbildung der ursprünglichen Datenlage (siehe auch Eid et al., 2017, Kapitel 25).
anova(five_factor_ML, six_factor_ML)## Model 1 = fa(r = dataFR, nfactors = 5, rotate = "oblimin", fm = "ml")
## Model 2 = fa(r = dataFR, nfactors = 6, rotate = "oblimin", fm = "ml")| df | d.df | chiSq | d.chiSq | PR | test | empirical | d.empirical | test.echi | BIC | d.BIC | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 40 | NA | 44.08 | NA | NA | NA | 47.94 | NA | NA | -150.32 | NA |
| 2 | 30 | 10 | 29.19 | 14.88 | 0.14 | 1.49 | 28.63 | 19.31 | 1.93 | -116.60 | 33.72 |
Der \(\chi^2\)-Differenzwert liegt hier bei 14.88 mit einen zugehörigen p-Wert von 0.14 mit \(\Delta df\) = 10. Mit diesem Test wird geprüft, ob das sparsamere Modell die Daten schlechter abbildet. Die Nullhypothese ist also, dass das sparsamere Modell die Daten genauso gut beschreiben kann, wie das komplexere Modell (\(H_0:\Sigma_{6-Fakt.} = \Sigma_{5-Fakt.}\)). Da in diesem Fall der p-Wert größer als \(.05\) ist, wird diese Nullhypothese nicht verworfen und wir entscheiden uns — Ockhams Rasiermesser folgend (siehe Eid et al., 2017, p. 787) — für das sparsamere Modell.
Wir hätten auch mehrere Tests gleichzeitig durchführen können. Allerdings sollten nicht beliebig konkurriende Theorien getestet werden — Stichwort Alpha-Inflation!
anova(four_factor_ML, five_factor_ML, six_factor_ML)## Model 1 = fa(r = dataFR, nfactors = 4, rotate = "oblimin", fm = "ml")
## Model 2 = fa(r = dataFR, nfactors = 5, rotate = "oblimin", fm = "ml")
## Model 3 = fa(r = dataFR, nfactors = 6, rotate = "oblimin", fm = "ml")| df | d.df | chiSq | d.chiSq | PR | test | empirical | d.empirical | test.echi | BIC | d.BIC | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 51 | NA | 73.05 | NA | NA | NA | 105.81 | NA | NA | -174.80 | NA |
| 2 | 40 | 11 | 44.08 | 28.97 | 0.00 | 2.63 | 47.94 | 57.87 | 5.26 | -150.32 | 24.49 |
| 3 | 30 | 10 | 29.19 | 14.88 | 0.14 | 1.49 | 28.63 | 19.31 | 1.93 | -116.60 | 33.72 |
Appendix C
Faktorladungsmatrix vs. Strukturmatrix
Um die Beziehung zwischen der Faktorladungsmatrix und der Strukturmatrix genauer zu verstehen, schauen wir uns das zweifaktorielle Modell für den (standardisierten) Datensatz dataFR2 genauer an (standardisiert ist hier wichtig, da dies bedeutet, dass die Mittelwerte alle \(0\) sind und wir somit diese ignorieren können):
\[\begin{pmatrix}E_1\\E_2\\E_3\\N_1\\N_2\\N_3 \end{pmatrix} = \begin{pmatrix}
\lambda_{11} & \lambda_{12}\\
\lambda_{21} & \lambda_{22}\\
\lambda_{31} & \lambda_{32}\\
\lambda_{41} & \lambda_{42}\\
\lambda_{51} & \lambda_{52}\\
\lambda_{61} & \lambda_{62} \end{pmatrix} \begin{pmatrix}\xi_1\\\xi_2 \end{pmatrix} + \begin{pmatrix}\varepsilon_{E_1}\\\varepsilon_{E_2}\\\varepsilon_{E_3}\\\varepsilon_{N_1}\\\varepsilon_{N_2}\\\varepsilon_{N_3} \end{pmatrix}\]
Dies ist die Messmodellsgleichung, welche die Beziehung zwischen den latenten Variablen und den Messfehlern mit den beobachtbaren Variablen beschreibt. Die Faktorladungsmatrix \(\Lambda\) enthält hier die Gewichtung der latenten Variablen und bestimmt somit, wie groß der Anteil jeder latenten Variable an der Messung ist (dies ist ähnlich der Reliabilität zu bewerten). Die Strukturmatrix beschreibt die Korrelation/Kovariation zwischen Messung und latenter Variable und enthält somit zusätzliche Informationen über die Beziehungen der latenten Variablen untereinander.
Im Abschnitt zur Hauptachsenanalyse hatten wir erkannt, dass der erste Faktor wahrscheinlich der Extraversion und der zweite wahrscheinlich dem Neurotizismus entspricht. Demnach könnten wir \(\xi_1=\xi_\text{Extraversion}\) und \(\xi_2=\xi_\text{Neurotizismus}\) nennen. Bennen wir nun die Faktorladungsmatrix als \(\Lambda\) und die Korrelationsmatrix der latenten Variablen \(\Phi\) (die Diagonaleinträge sind \(1\)).
Die Kovarianz zwischen dem ersten Extraversionsitem und dem Extraversionsfaktor ist folgendermaßen zu berechnen (wir rechnen hier mit Kovarianzen, da dies im Allgemeinen deutlich einfacher ist, als mit Korrelationen zu rechen. Außerdem sind hier alle Variablen standardisiert und somit sind Korrelation und Kovarianz identisch; über die Rechenregeln und die Beziehungen zwischen Korrelation und Kovarianz können sie in Eid, et al. (2017) S. 195-196 und folgend und S.570-571 und folgend nachlesen):
\[\begin{align}\mathbf{C}ov[E_1, &\xi_1]\\&= \mathbf{C}ov[\lambda_{11}\xi_1 + \lambda_{12}\xi_2+\varepsilon_{E_1}, \xi_1]\\ &= \lambda_{11}\mathbf{C}ov[\xi_1, \xi_1] + \lambda_{12}\mathbf{C}ov[\xi_2, \xi_1] +\mathbf{C}ov[\varepsilon_{E_1}, \xi_1]\\ &= \lambda_{11}\mathbb{V}ar[\xi_1] + \lambda_{12}\mathbf{C}ov[\xi_2, \xi_1]\\ &= \lambda_{11}\phi_{11} + \lambda_{12}\phi_{21}\\&= \lambda_{11} + \lambda_{12}\phi_{21}\end{align}\]
\(\mathbf{C}ov[\varepsilon_{E_1}, \xi_1]=0\) gilt, da die Fehler als unabhängig von allen weiteren Variablen im Modell angenommen werden. Außerdem sind \(\phi_{11}=1\) und \(\mathbb{C}ov[\xi_1,\xi_2]=\phi_{21}=\phi_{12}=\mathbb{C}ov[\xi_2,\xi_1]\) die Varianz von \(\xi_1\) und die Kovarianz/Korrelation zwischen \(\xi_1\) und \(\xi_2\) und entsprechend Einträge von \(\Phi\). Aus dieser Rechnung folgt, dass der erste Eintrag in der Strukturmatrix (an der Stelle 1. Zeile, 1. Spalte) \(\lambda_{11} + \lambda_{12}\phi_{21}\) sein muss. Hier ist zu erkennen, dass falls die Korrelation zwischen den latenten Variablen als \(0\) angenommen wird (im orthogonalen Fall gilt dann \(\phi_{21}=\phi_{12}=0\)), dann ist die Strukurmatrix gleich der Faktorladungsmatrix und der erste Eintrag lautet \(\lambda_{11}\). Wir schauen uns dies empirisch für das orthogonale Modell (bereits geschätzt in two_factor) und das oblique-rotiert geschätzte Modell (bereits geschätzt in two_factor_oblimin) an.
Im orthogonalen Fall ist dies etwas unspannend:
two_factor$loadings[1, 1] # volle Formel für ersten Eintrag in Strukutrmatrix, da Kovarianz der Faktoren = 0## [1] 0.6918932two_factor$Structure[1, 1] # erster Eintrag in der Strukturmatrix## [1] 0.6918932Offensichtlich sind beide Einträge gleich, was daran liegt, dass die Faktoren als unkorreliert angenommen werden. Nun zum oblique rotierten Fall:
two_factor_oblimin$loadings[1, 1] # erste Faktorladung im obliquen Modell (unterscheidet sich von dem ersten Eintrag der Strukturmatrix)## [1] 0.7005517two_factor_oblimin$loadings[1, 1] + two_factor_oblimin$loadings[1, 2]*two_factor_oblimin$Phi[2, 1] # volle Formel für ersten Eintrag in Strukutrmatrix## [1] 0.6932416two_factor_oblimin$Structure[1, 1] # erster Eintrag in der Strukturmatrix## [1] 0.6932416Hier ist zu sehen, dass sich Faktorladungsmatrix und Strukturmatrix unterscheiden. Der Unterschied ist nicht sehr hoch, da die Korrelation zwischen den beiden Faktoren lediglich bei \(\hat{\phi}_{21}\)=-0.1852 liegt und somit \(\hat{\lambda}_{12}\hat{\phi}_{21}=\) -0.0073 keine große Veränderung zu \(\hat{\lambda}_{11}\) mit sich bringt. In Matrixschreibweise lässt sich die Strukturmatrix unkompliziert bestimmen. Sie wird durch folgenden Ausdruck berechnet:
\[\Lambda\Phi\]
Dies können wir in R leicht empirisch überprüfen. Einen Überblick über die Befehle für Matrix-Algebra in R finden Sie auf der Quick-R Website, auf welche bereits in der Sitzung zu Einführung in lavaan aufmerksam gemacht wurde. Außerdem ist im Appendix B der Einführungssitzung zu PsyMSc1 bereits eine Einführung in Matrixalgebra gegeben worden. Wir berechnen nun das Matrixprodukt für den oblique rotieren Fall:
two_factor_oblimin$loadings[,] %*% two_factor_oblimin$Phi[,] # Matrixprodukt## MR1 MR2
## E1 0.6932416 -0.09029319
## E2 -0.6400647 0.03425442
## E3 0.8364933 -0.22391151
## N1 -0.1298599 0.83712330
## N2 0.1785989 -0.58432636
## N3 -0.1283499 0.58695759two_factor_oblimin$Structure[,] # Strukturmatrix## MR1 MR2
## E1 0.6932416 -0.09029319
## E2 -0.6400647 0.03425442
## E3 0.8364933 -0.22391151
## N1 -0.1298599 0.83712330
## N2 0.1785989 -0.58432636
## N3 -0.1283499 0.58695759%*% signalisiert R, dass ein Matrixprodukt und keine komponentenweise Mulitplikation durchzuführen ist. [,] sorgt dafür, dass nur die Matrizen verwendet werden und nicht der zusätzliche Output, der ggf. durch das psych-Paket mit ausgegeben wird.
Das ganze funktioniert selbstverständlich auch für den fünffaktoriellen oblique rotierten ML-EFA Fall, den wir uns später angesehen haben, als es darum ging, den gesamten (gekürzten) Datensatz mit Hilfe der ML-EFA zu untersuchen. Das zugehörige Objekt, welches das geschätzte Modell enthält, heißt five_factor_ML:
five_factor_ML$loadings[,] %*% five_factor_ML$Phi[,] # Matrixprodukt## ML4 ML3 ML1 ML2 ML5
## E1 0.68012693 -0.06717103 0.09828653 -0.01822411 0.009260453
## E2 -0.63791259 0.06552915 0.04403530 0.14413074 0.125484598
## E3 0.83728352 -0.12337423 0.24576500 -0.03084187 -0.146382973
## N1 -0.09189974 0.53663293 -0.47561225 -0.09483930 0.055041769
## N2 0.15694831 -0.32787315 0.99631061 0.01289071 0.045752916
## N3 -0.04934588 0.92837355 -0.30647378 -0.02583979 -0.032437499
## A1 -0.17544108 0.11612973 0.11370804 -0.06663641 -0.254026633
## A2 0.63566748 0.20739547 0.02728767 -0.03702446 0.027811781
## A3 -0.20229561 0.13312175 0.03054772 0.20947982 0.112785431
## C1 0.09812869 0.10806476 0.16374057 0.18026600 -0.359308148
## C2 -0.07172742 -0.02229676 0.09337011 0.02096820 0.732728884
## C3 0.04129630 0.13719615 0.08822234 0.14594730 -0.280624296
## O1 -0.06746981 -0.02332237 0.01902778 0.99723607 -0.003104410
## O2 0.14261965 0.23841159 -0.03792795 -0.22572173 -0.121938771
## O3 -0.08840219 0.17745445 0.09190619 0.19639438 0.088088488five_factor_ML$Structure[,] # Strukturmatrix## ML4 ML3 ML1 ML2 ML5
## E1 0.68012693 -0.06717103 0.09828653 -0.01822411 0.009260453
## E2 -0.63791259 0.06552915 0.04403530 0.14413074 0.125484598
## E3 0.83728352 -0.12337423 0.24576500 -0.03084187 -0.146382973
## N1 -0.09189974 0.53663293 -0.47561225 -0.09483930 0.055041769
## N2 0.15694831 -0.32787315 0.99631061 0.01289071 0.045752916
## N3 -0.04934588 0.92837355 -0.30647378 -0.02583979 -0.032437499
## A1 -0.17544108 0.11612973 0.11370804 -0.06663641 -0.254026633
## A2 0.63566748 0.20739547 0.02728767 -0.03702446 0.027811781
## A3 -0.20229561 0.13312175 0.03054772 0.20947982 0.112785431
## C1 0.09812869 0.10806476 0.16374057 0.18026600 -0.359308148
## C2 -0.07172742 -0.02229676 0.09337011 0.02096820 0.732728884
## C3 0.04129630 0.13719615 0.08822234 0.14594730 -0.280624296
## O1 -0.06746981 -0.02332237 0.01902778 0.99723607 -0.003104410
## O2 0.14261965 0.23841159 -0.03792795 -0.22572173 -0.121938771
## O3 -0.08840219 0.17745445 0.09190619 0.19639438 0.088088488Hier alle Einträge auf Gleichheit zu untersuchen, ist sehr mühsam. Wir können dies viel einfacher mit einer Differenz tun:
five_factor_ML$loadings[,] %*% five_factor_ML$Phi[,] - five_factor_ML$Structure[,]## ML4 ML3 ML1 ML2 ML5
## E1 0 0 0 0 0
## E2 0 0 0 0 0
## E3 0 0 0 0 0
## N1 0 0 0 0 0
## N2 0 0 0 0 0
## N3 0 0 0 0 0
## A1 0 0 0 0 0
## A2 0 0 0 0 0
## A3 0 0 0 0 0
## C1 0 0 0 0 0
## C2 0 0 0 0 0
## C3 0 0 0 0 0
## O1 0 0 0 0 0
## O2 0 0 0 0 0
## O3 0 0 0 0 0Da hier nur Nullen herauskommen, scheinen die Ausdrücke identisch zu sein!
Appendix D
Berechnen von Eigenwerten und Kommunalitäten mit Hilfe von \(\Lambda\) und \(\Phi\)
Im vorigen Abschnitt hatten wir bemerkt, wie leicht die Strukturmatrix aus der Faktorladungsmatrix \(\Lambda\) hervorgeht, indem einfach nur die Beziehung der latenten Variablen untereinander berücksichtigt wird. Es ist folglich nur logisch, dass bei der Bestimmung der Eigenwerte und der Kommunalitäten diese Beziehung ebenfalls eine Rolle spielt. Im Rahmen der PCA hatten wir uns bereits die Beziehungen dieser Größen untereinander angesehen. Dort war es so, dass die Diagonalelemente von \(\Lambda\Lambda'\) gerade die Kommunalitäten waren und die Diagonalelemente von \(\Lambda'\Lambda\) gerade die Eigenwerte der rotierten Lösung. Es kam also lediglich darauf an, in welcher Reihenfolge \(\Lambda\) und transponiertes \(\Lambda\) miteinander verrechnet werden! Für oblique rotierte EFAs müssen wir nun noch die Korrelation der Faktoren untereinander berücksichtigen. Die implizierte Korrelationsmatrix war einfach \[\Lambda\Phi\Lambda' + \Theta,\] wobei die Elemente von \(\Theta\) im Grunde nur dafür sorgen, dass die Hauptdiagonale wieder bei 1 landet. Lassen wir \(\Theta\) weg, erhalten wir die Korrelationsmatrix mit den Kommunalitäten auf der Hauptdiagonale. Damit ist klar, dass \[\text{diag}(\Lambda\Phi\Lambda') = \text{Kommunalitäten}\] gilt. Da wir bereits wissen, dass \(\Lambda\Phi\) die Strukturmatrix ist, könnten wir auch einfach sagen, dass das Matrixprodukt Strukturmatrix Faktorladungsmatrix’ die Kommunalitäten auf der Hauptdiagonale enthält. Probieren wir dies doch einmal aus:
two_factor_ML$communality## E1 E2 E3 N1 N2 N3
## 0.4715292 0.4068085 0.7128628 0.6964745 0.3520527 0.3565427diag(two_factor_ML$loadings[,] %*% two_factor_ML$Phi[,] %*% t(two_factor_ML$loadings[,]))## E1 E2 E3 N1 N2 N3
## 0.4715292 0.4068085 0.7128628 0.6964745 0.3520527 0.3565427diag(two_factor_ML$Structure[,] %*% t(two_factor_ML$loadings[,]))## E1 E2 E3 N1 N2 N3
## 0.4715292 0.4068085 0.7128628 0.6964745 0.3520527 0.3565427In allen 3 Fällen kommen die Kommunalitäten heraus. diag fordert hierbei die Diagonalelemente einer quadratischen Matrix an. Um nun die Eigenwerte zu erhalten, müssen wir das Matrixprodukt nur umdrehen: Faktorladungsmatrix’ Strukturmatrix, bzw. das Transponierungszeichen tauschen (Strukturmatrix’ Faktorladungsmatrix ginge auch!):
\[\text{diag}(\Phi\Lambda'\Lambda) = \text{Eigenwerte}\] Wer genau aufpasst, fragt sich jetzt vielleicht, wieso \(\Phi\) kein Transponierungszeichen trägt. Das liegt daran, dass eine Kovarianz/Korrelationsmatrix immer symmetrisch ist — die Definition einer symmetrischen quadratischen Matrix \(A\) ist: \(A = A'\).
two_factor_ML$Vaccounted # Eigenwerte nach Rotation und Extraktion in SS loadings## ML1 ML2
## SS loadings 1.6053881 1.3908823
## Proportion Var 0.2675647 0.2318137
## Cumulative Var 0.2675647 0.4993784
## Proportion Explained 0.5357955 0.4642045
## Cumulative Proportion 0.5357955 1.0000000diag(two_factor_ML$Phi[,] %*% t(two_factor_ML$loadings[,]) %*% two_factor_ML$loadings[,])## ML1 ML2
## 1.605388 1.390882diag(t(two_factor_ML$Structure[,]) %*% two_factor_ML$loadings[,])## ML1 ML2
## 1.605388 1.390882In der ersten Zeile von two_factor_ML$Vaccounted stehen die Eigenwerte nach Rotation und Extraktion. Diese sind identisch zur Diagonale der beiden Matrixprodukte!
Appendix E
Prüfen der Voraussetzungen mit der Mahalanobisdistanz und Mardia’s Test
Auf multivariate Normalverteilung können wir beispeilsweise deskriptiv prüfen, indem wir die Mahalanobisdistanz (die Distanz vom gemeinsame Zentroiden; dem Mittelwert über alle Variablen; unter Berücksichtigung der Kovariation im Datensatz) plotten und sie mit einer \(\chi^2\)-Verteilung vergleichen; wobei \(df=p\) und \(p=\) Anzahl an Variablen (hier \(df=p=15\)).
Mahalanobis_Distanz <- mahalanobis(x = dataFR, cov = cov(dataFR), center = colMeans(dataFR)) # Berechnen der Mahalanobisdistanz
hist(Mahalanobis_Distanz, col = "skyblue", border = "blue", freq = F, breaks = 15) # Histogramm
lines(x = seq(0, max(Mahalanobis_Distanz), 0.01), y = dchisq(x = seq(0, max(Mahalanobis_Distanz), 0.01), df = 15), col = "darkblue", lwd = 4) # Einzeichnen der Dichte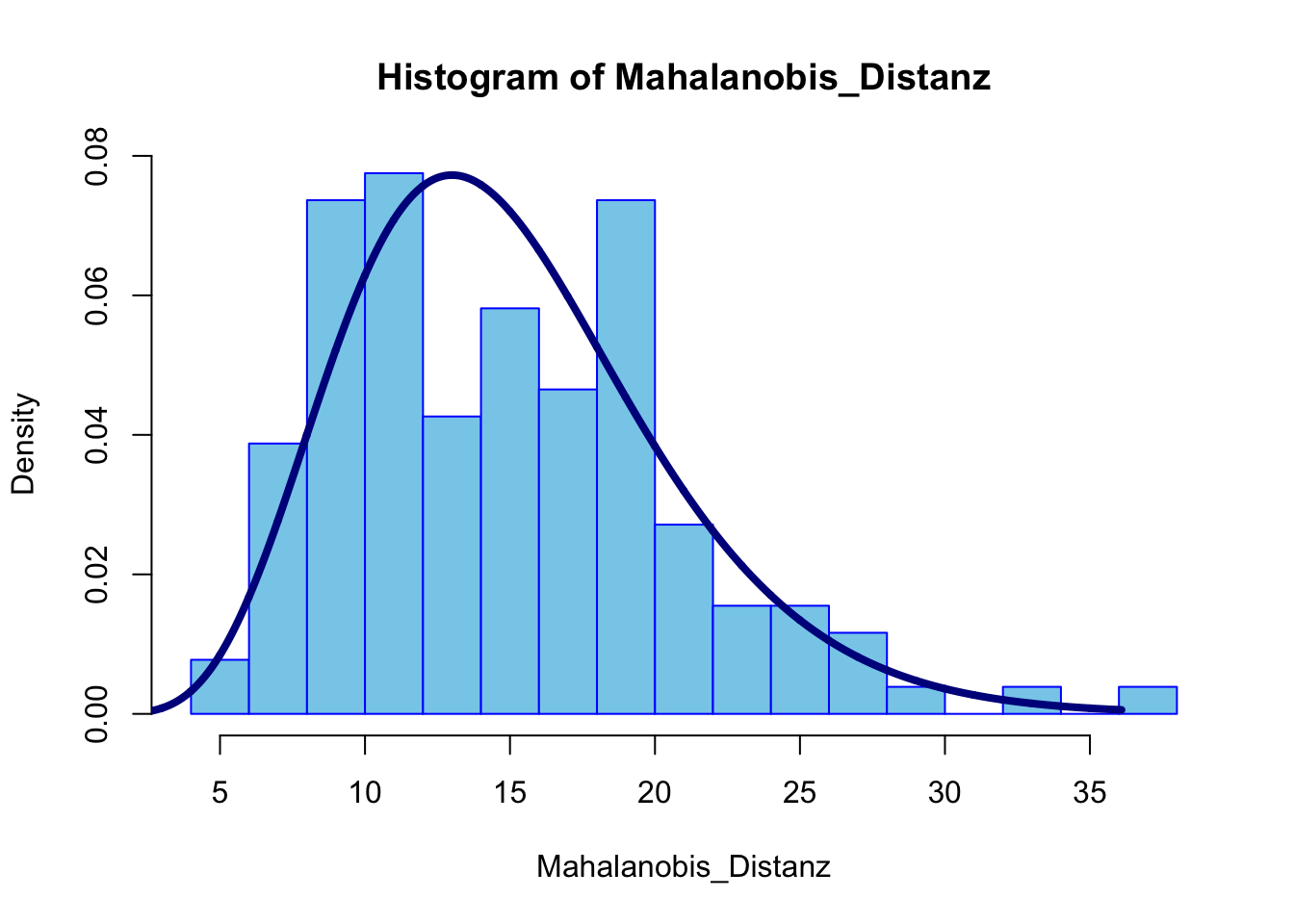
Sie können ja mal Einstellungen verändern und sich deren Konsequenz für die Grafik ansehen!
Das Histogramm scheint nicht perfekt zur \(\chi^2\)-Verteilung zu passen. Allerdings sind die Abweichungen auch nicht enorm. Wir verwerfen auf Basis des Histogramms die Normalverteilungsannahme nicht, sollten die Ergebnisse aber trotzdem unter Vorbehalt interpretiert werden.
Die Funktion mahalanobis berechnet die Mahalanobisdistanz pro Proband:in. Als Datenargument braucht sie eine Matrix x. Die Mahalanobisdistanz ist ein Distanzmaß, welches die korrelative Struktur in den Daten berücksichtigt. Wir übergeben daher mit cov = cov(dataFR) der Funktion mahalanobis die empirische Kovarianzmatrix unserer Daten (cov(dataFR)), um diese Struktur mit zuberücksichtigen. Außerdem müssen die Variablen und deren Variation relativ zu einem Zentroiden angegeben werden. Der Zentroid wird dem center-Argument übergeben. Wir brauchen also für jede Variable deren Mittelwert. Dies machen wir mit colMeans.
colMeans(dataFR)## E1 E2 E3 N1 N2 N3 A1 A2
## 2.558140 2.968992 3.217054 3.372093 3.131783 3.852713 2.620155 3.596899
## A3 C1 C2 C3 O1 O2 O3
## 2.286822 3.100775 3.131783 4.000000 3.945736 2.077519 4.240310Der hist-Befehl erzeugt schließlich ein Histogramm der Mahalanobisdistanzen. Mit den Argumenten col = "skyblue" und border = "blue" setzten wir die Farben des Histogramms fest. Mit freq = F sagen wir, dass wir nicht die absoluten sondern die relativen Häufigkeiten angezeigt haben wollen (dies brauchen wir um anschließend die Dichte der \(\chi^2\)-Verteilung einzuzeichnen). Mit breaks = 15 beschließen wir, dass insgesamt ca. 15 Balken gezeichnet werden sollen.
Schließlich zeichnen wir mit lines eine Line, welche als x-Argument x = seq(0, max(Mahalanobis_Distanz), 0.01) eine Sequenz von Zahlen von 0 bis zur maximalen Mahalanobisdistanz erhält und in 0.01 Schritten wächst. Gegen diese x-Werte zeichnen wir die Dichte der \(\chi^2(df=15)\)-Verteilung ein: y = dchisq(x = seq(0, max(Mahalanobis_Distanz), 0.01), df = 15). col = "darkblue" und lwd = 4 setzten jeweils die Linienfarbe und Liniendicke fest. Weitere Informationen zu Verteilungen und wie man diese in R umsetzt, können im R-Wiki zu Verteilungen, in Wikipedia zu Verteilungen und Dichten oder in einer Kurzzusammenfassung auf statmethods nachgelesen werden. Grundlagen hierzu können außerdem in Eid et al. (2017) in Kapitel 7 ab Seite 171 gefunden werden.
Außerdem können wir auch noch Mardia’s Test auf multivariate Normalverteilung verwenden. Diesen gibt es bspw. im R-Paket MVN (für Multi-Variate Normal-distribution). In diesem Paket verwenden wir die mvn-Funktion, um Mardia’s Test zu verwenden:
library(MVN)
mvn(data = dataFR, mvnTest = "mardia")## $multivariateNormality
## Test Statistic p value Result
## 1 Mardia Skewness 814.236119391994 0.000288124299329737 NO
## 2 Mardia Kurtosis 1.53049602635342 0.125893996300673 YES
## 3 MVN <NA> <NA> NO
##
## $univariateNormality
## Test Variable Statistic p value Normality
## 1 Anderson-Darling E1 4.9942 <0.001 NO
## 2 Anderson-Darling E2 4.0628 <0.001 NO
## 3 Anderson-Darling E3 4.0445 <0.001 NO
## 4 Anderson-Darling N1 5.1846 <0.001 NO
## 5 Anderson-Darling N2 4.5090 <0.001 NO
## 6 Anderson-Darling N3 8.7268 <0.001 NO
## 7 Anderson-Darling A1 5.2696 <0.001 NO
## 8 Anderson-Darling A2 5.8351 <0.001 NO
## 9 Anderson-Darling A3 9.9801 <0.001 NO
## 10 Anderson-Darling C1 4.7848 <0.001 NO
## 11 Anderson-Darling C2 4.0206 <0.001 NO
## 12 Anderson-Darling C3 8.3567 <0.001 NO
## 13 Anderson-Darling O1 7.4239 <0.001 NO
## 14 Anderson-Darling O2 7.7934 <0.001 NO
## 15 Anderson-Darling O3 11.2213 <0.001 NO
##
## $Descriptives
## n Mean Std.Dev Median Min Max 25th 75th Skew Kurtosis
## E1 129 2.558140 1.3044813 3 1 5 1 3 0.32427985 -1.03222800
## E2 129 2.968992 1.2433447 3 1 5 2 4 0.13071545 -0.98604106
## E3 129 3.217054 1.2683727 3 1 5 2 4 -0.20289793 -0.99959701
## N1 129 3.372093 1.3232876 4 1 5 2 4 -0.31730421 -1.14311645
## N2 129 3.131783 1.1550152 3 1 5 2 4 -0.01411112 -0.95870960
## N3 129 3.852713 1.0975881 4 1 5 3 5 -0.87031995 -0.10813842
## A1 129 2.620155 1.3761007 2 1 5 1 4 0.33995849 -1.17089544
## A2 129 3.596899 1.1693974 4 1 5 3 5 -0.37750788 -0.99209594
## A3 129 2.286822 1.3761007 2 1 5 1 4 0.55150074 -1.20186405
## C1 129 3.100775 1.1239228 3 1 5 2 4 -0.16388511 -0.85645458
## C2 129 3.131783 1.2770807 3 1 5 2 4 -0.17800768 -1.01121119
## C3 129 4.000000 1.0231691 4 1 5 3 5 -0.86845894 -0.01507734
## O1 129 3.945736 1.0178875 4 1 5 3 5 -0.90696625 0.43639201
## O2 129 2.077519 1.1012238 2 1 5 1 3 0.75369527 -0.39530983
## O3 129 4.240310 0.9080817 4 1 5 4 5 -1.16861246 0.88182592Hier bekommen wir einiges an Output. Der erste Block enthält den Test auf multivariate Normalität (unter $multivariateNormality). Der nächste Unterpunkt enthält Informationen zur univariate Normalität (unter $univariateNormality) sowie einen Block zu Deskriptivstatistiken (unter $Descriptives). Wir konzentrieren uns nur auf den multivariaten Test:
## ## $multivariateNormality
## ## Test Statistic p value Result
## ## 1 Mardia Skewness 814.236119391994 0.000288124299329737 NO
## ## 2 Mardia Kurtosis 1.53049602635342 0.125893996300673 YES
## ## 3 MVN <NA> <NA> NO
## ##In der ersten Spalte steht der Test Mardia Skewness oder Mardia Kurtosis, wo mit multivariater Schiefe (Skewness) und Kurtosis (Wölbung) untersucht wird, ob diese von der Normalverteilung abweichen. Statistic enthält Informationen zu Mardia’s Teststatistik, welche auch einen zugehörigen p value hat. Unter Result steht eine Entscheidung, ob die Schiefe oder Wölbung jeweils von einer Normalverteilung stammen könnte. Ganz unten steht MVN, also eine globale Entscheidung. Hier steht leider NO, also kann nicht von multivariater Normalverteilung gesprochen werden, denn die Null-Hypothese, dass die Daten die selbe multivariate Schiefe und Wölbung wie die einer Normalverteilung aufzeigen, musste auf dem \(\alpha=5\%\) Niveau verworfen werden. Dieser Test wird auch kurz in Eid et al. (2017, pp. 516-517) beschrieben. Für unsere Ergebnisse bedeutet dies, dass Parameter ggf. verzerrt sind und der Likelihood-Ratio-Test ggf. zu falschen Schlüssen kommt! Die Ergebnisse dieser Sitzung sind also nur unter Vorbehalt zu interpretieren.
Literatur
Brandt H. (2020). Exploratorische Faktorenanalyse (EFA). In Moosbrugger H., Kelava A. (eds) Testtheorie und Fragebogenkonstruktion. Berlin, Heidelberg: Springer. https://doi.org/10.1007/978-3-662-61532-4_23
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden (5. Auflage, 1. Auflage: 2010). Weinheim: Beltz.
- Blau hinterlegte Autor:innenangaben führen Sie direkt zur universitätsinternen Ressource.