Tests für abhängige Stichproben
Nachdem wir uns mit unabhängige Stichproben in der (letzten Sitzung) beschäftigt haben wollen wir diesmal mit abhängigen Stichproben beschäftigen. Anwendungen dafür in der Praxis sind beispielsweise Zwillinge, Paare oder auch Messwiederholungen.
Kernfragen der Lehreinheiten über Gruppenvergleiche
- Wie fertige ich Deskriptivstatistiken (Grafiken, Kennwerte) zur Veranschaulichung des Unterschieds zwischen zwei Gruppen an?
- Was sind Voraussetzungen des abhängigen t-Tests und wie prüfe ich sie?
- Wie führe ich einen abhängigen t-Test in R durch?
- Wie berechne ich den standardisierten Populationseffekt für abhängige Stichproben?
- Wie führe ich einen abhängigen Wilcoxon-Test in R durch?
- Wie berichte ich statistische Ergebnisse formal?
Vorbereitende Schritte
Den Datensatz haben wir bereits unter diesem Link heruntergeladen und können ihn über den lokalen Speicherort einladen oder Sie können Ihn direkt mittels des folgenden Befehls aus dem Internet in das Environment bekommen. In den vorherigen Tutorials und den dazugehörigen Aufgaben haben wir bereits Änderungen am Datensatz durchgeführt, die hier nochmal aufgeführt sind, um den Datensatz auf dem aktuellen Stand zu haben:
#### Was bisher geschah: ----
# Daten laden
load(url('https://pandar.netlify.app/post/fb22.rda'))
# Nominalskalierte Variablen in Faktoren verwandeln
fb22$geschl_faktor <- factor(fb22$geschl,
levels = 1:3,
labels = c("weiblich", "männlich", "anderes"))
fb22$fach <- factor(fb22$fach,
levels = 1:5,
labels = c('Allgemeine', 'Biologische', 'Entwicklung', 'Klinische', 'Diag./Meth.'))
fb22$ziel <- factor(fb22$ziel,
levels = 1:4,
labels = c("Wirtschaft", "Therapie", "Forschung", "Andere"))
fb22$wohnen <- factor(fb22$wohnen,
levels = 1:4,
labels = c("WG", "bei Eltern", "alleine", "sonstiges"))
fb22$ort <- factor(fb22$ort, levels=c(1,2), labels=c("FFM", "anderer"))
fb22$job <- factor(fb22$job, levels=c(1,2), labels=c("nein", "ja"))
# Skalenbildung
fb22$prok2_r <- -1 * (fb22$prok2 - 5)
fb22$prok3_r <- -1 * (fb22$prok3 - 5)
fb22$prok5_r <- -1 * (fb22$prok5 - 5)
fb22$prok7_r <- -1 * (fb22$prok7 - 5)
fb22$prok8_r <- -1 * (fb22$prok8 - 5)
# Prokrastination
fb22$prok_ges <- fb22[, c('prok1', 'prok2_r', 'prok3_r',
'prok4', 'prok5_r', 'prok6',
'prok7_r', 'prok8_r', 'prok9',
'prok10')] |> rowMeans()
# Naturverbundenheit
fb22$nr_ges <- fb22[, c('nr1', 'nr2', 'nr3', 'nr4', 'nr5', 'nr6')] |> rowMeans()
fb22$nr_ges_z <- scale(fb22$nr_ges) # Standardisiert
# Weitere Standardisierungen
fb22$nerd_std <- scale(fb22$nerd)
fb22$neuro_std <- scale(fb22$neuro)4. Fragestellung D: Haben Psychologiestudierende vergleichbare Werte auf den Skalen Neurotizismus und Extraversion?
Die Werte auf beiden Variablen sind insofern voneinander abhängig, dass jede Person die Fragen zu Neurotizismus und die Fragen zu Extraversion beantwortet hat (→ Messwiederholung). Es gibt daher Faktoren innerhalb der Person, die einen gemeinsamen Teil der Varianz erzeugen.
Anmerkung: Wir fragen hier bewusst nicht, ob Psychologiestudierende neurotischer sind als extravertiert. Dies würde voraussetzen, dass die Items der beiden Skalen vergleichbar schwierig sind.
Wir wollen im Folgenden lediglich die Frage beantworten, ob die Differenz zwischen den beiden Skalen (also die Mittelwerte für Neurotizismus und Extraversion) statistisch bedeutsam ist.
4.1. Deskriptivstatistik
Wie immer beginnen wir mit der deskriptivstatistischen Analyse unserer Daten.
4.1.1. grafisch
Mithilfe von Histogrammen
# Je ein Histogramm pro Skala, untereinander dargestellt, vertikale Linie für den jeweiligen Mittelwert
par(mfrow=c(2,1), mar=c(3,3,2,0))
hist(fb22$neuro,
xlim=c(1,5),
ylim = c(0,50),
main="Neurotizismus",
xlab="",
ylab="",
las=1)
abline(v=mean(fb22$neuro),
lty=2,
lwd=2)
hist(fb22$extra,
xlim=c(1,5),
ylim = c(0,50),
main="Extraversion",
xlab="",
ylab="",
las=1)
abline(v=mean(fb22$extra),
lty=2,
lwd=2)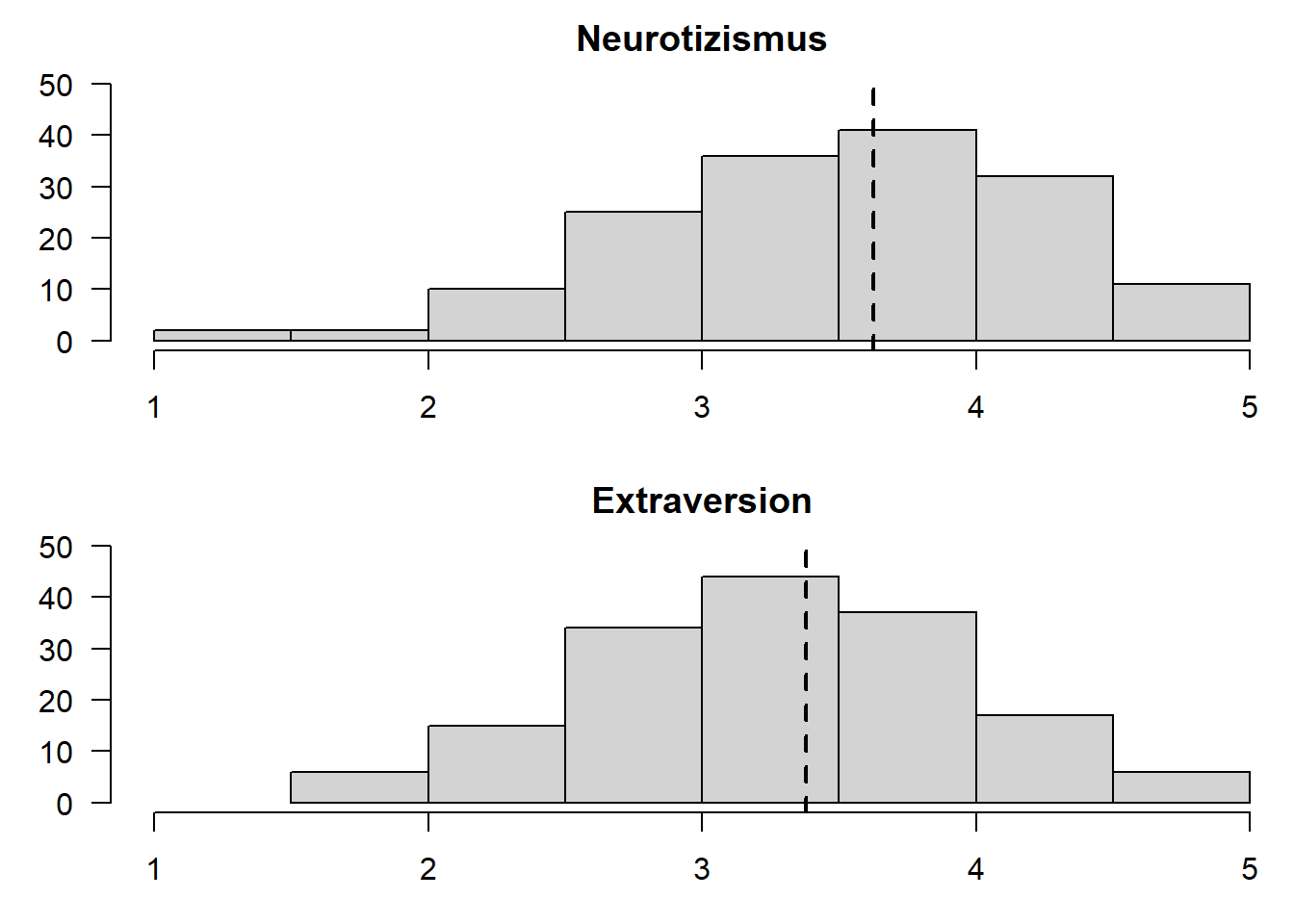
par(mfrow=c(1,1)) #Zurücksetzen des Plotfensters, zuvor hatten wir "dev.off()" kennengelerntabline() fügt eine Linie in eine Grafik ein. Mit dem Zusatzargument v geben wir eine vertikale Linie in den Plot (hier den Mittelwert). Insgesamt scheinen sich die beiden Verteilungen zu unterscheiden: Der Mittelwert von Neurotizismus liegt höher als der von Extraversion.
4.1.2. statistisch
Deskriptivstatistisch sehen die Ergebnisse so aus:
summary(fb22$neuro)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.250 3.250 3.750 3.626 4.250 5.000summary(fb22$extra)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.500 3.000 3.250 3.379 3.750 5.000#alternativ
library(psych)
describe(fb22$neuro)## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 159 3.63 0.72 3.75 3.65 0.74 1.25 5 3.75 -0.43 0.09 0.06describe(fb22$extra)## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 159 3.38 0.71 3.25 3.39 0.74 1.5 5 3.5 -0.06 -0.31 0.06Achtung: Bei den hier berichteten SD handelt es sich (wie immer in R) um den Populationsschätzer. Die Mittelwerte der beiden Gruppen unterscheiden sich. Die Frage ist nun, ob sich dieser Unterschied auf die Population verallgemeinern lässt.
4.2. Voraussetzungsprüfung
Um den Ergebnissen eines \(t\)-Test für abhängige Stichproben vertrauen zu können, müssen dessen Voraussetzungen erfüllt sein:
Voraussetzungen für die Durchführung des t-Tests für abhängige Stichproben:
- Die abhängige Variable ist intervallskaliert \(\rightarrow\) ok
- Die Messwerte innerhalb der Paare dürfen sich gegenseitig beeinflussen/voneinander abhängig sein; keine Abhängigkeiten zwischen den Messwertpaaren \(\rightarrow\) ok
- Die Differenzvariable d muss in der Population normalverteilt sein \(\rightarrow\) ab \(n \ge 30\) meist gegeben (s. zentraler Grenzwertsatz), ggf. grafische Prüfung oder Hintergrundwissen
zu 3. Normalverteilung von d
Da wir hier die Differenzvariable betrachten müssen, müssen wir diese zunächst erstellen. Anschließend schauen wir uns das Histogramm der Differenzvariable und den QQ-Plot an:
difference <- fb22$neuro-fb22$extra
hist(difference,
xlim=c(-3,3),
ylim = c(0,1),
main="Verteilung der Differenzen",
xlab="Differenzen",
ylab="",
las=1,
probability = T)
curve(dnorm(x, mean=mean(difference), sd=sd(difference)),
col="blue",
lwd=2,
add=T)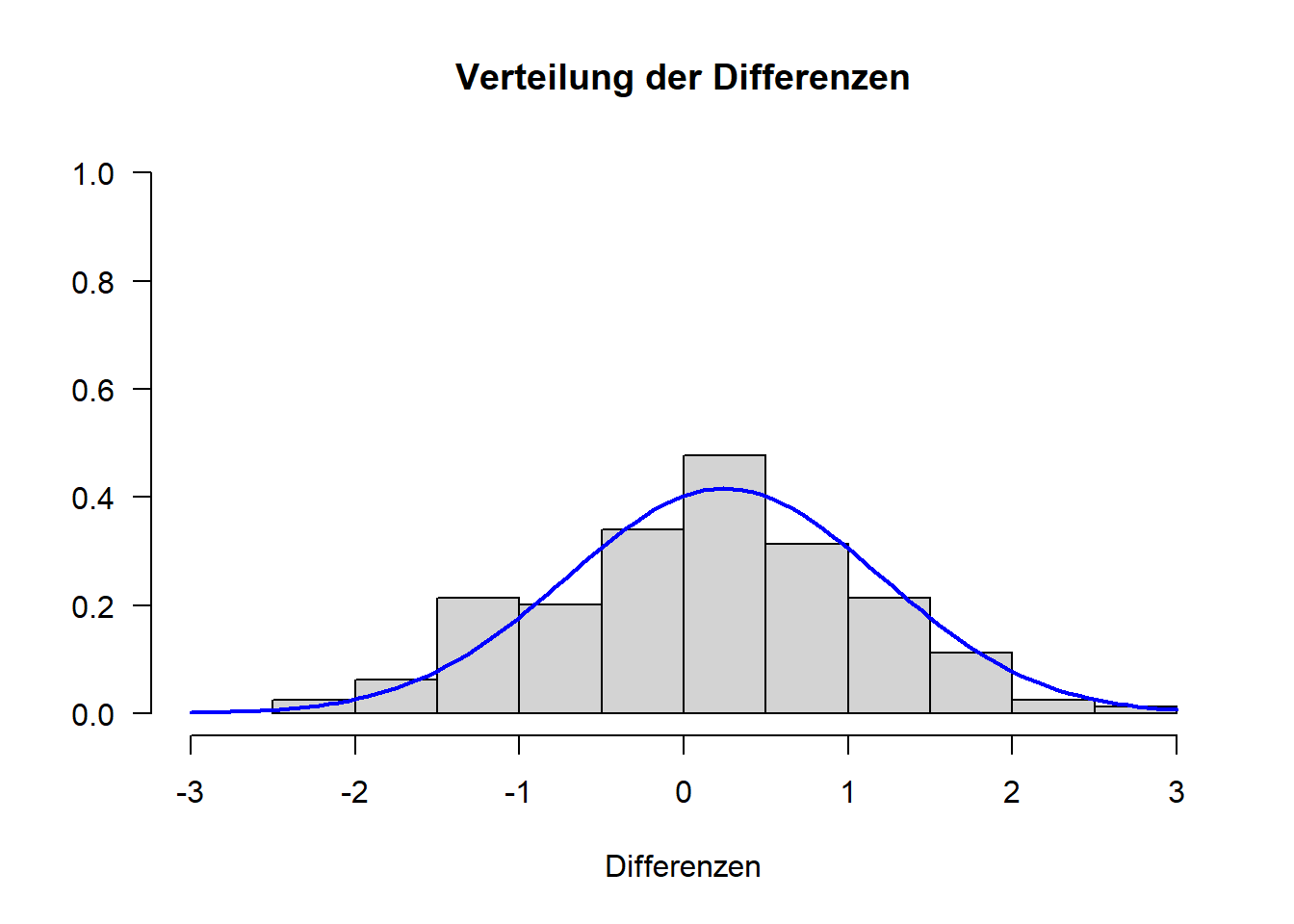
qqnorm(difference)
qqline(difference, col="blue")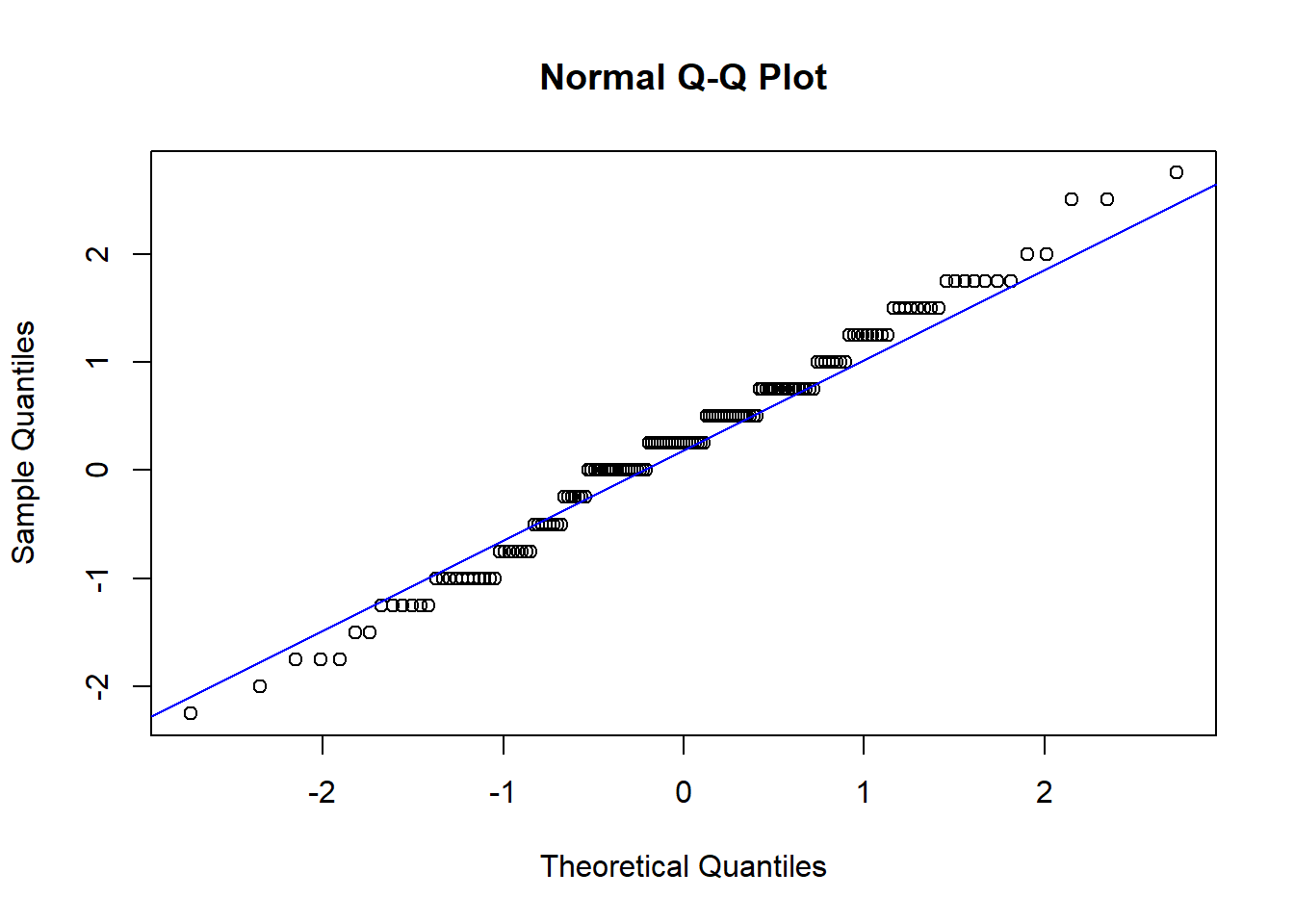
\(\Rightarrow\) Differenzen sehen normalverteilt aus, es wird also Normalverteilung angenommen. Somit sind alle drei Voraussetzungen für die Durchführung des t-Tests für abhängige Stichproben erfüllt.
4.3. Inferenzstatistik: t-Test für abhängige Stichproben
Zur Erinnerung:
Fragestellung D: “Haben Psychologiestudierende vergleichbare Werte auf den Skalen Neurotizismus und Extraversion?”
Hypothesen:
- Art des Effekts: Unterschiedshypothese
- Richtung des Effekts: Ungerichtet
- Grösse des Effekts: Unspezifisch
Hyothesenpaar (inhaltlich):
- H0: Psychologiestudierende haben vergleichbare Werte auf den Skalen Neurotizismus und Extraversion.
- H1: Bei Psychologiestudierende unterscheiden sich die Werte auf den Skalen Neurotizismus und Extraversion.
Hypothesenpaar (statistisch):
- H0: \(\mu_\text{neuro} = \mu_\text{extra}\) bzw. \(\mu_{d} = 0\)
- H1: \(\mu_\text{neuro} \ne \mu_\text{extra}\) bzw. \(\mu_{d} \ne 0\)
Signifikanzniveau
Das Signifikanzniveau muss vor der Untersuchung festgelegt werden. Es soll hier 5% betragen. \(\rightarrow\) \(\alpha=.05\) Durchführung des abhängigen t-Tests in R:
Wir verwenden hier die Funktion t.test(). Diesmal müssen wir allerdings die beiden Variablen einzeln der Funktion übergeben. Dies geschieht über die Argumente x und y. Das Argument paired = T führt dazu, dass der t-Test für abhängige (gepaarte) Stichproben durchgeführt wird.
t.test(x = fb22$extra, y = fb22$neuro, # die beiden abhaengigen Variablen
paired = T, # Stichproben sind abhaengig
conf.level = .95) ##
## Paired t-test
##
## data: fb22$extra and fb22$neuro
## t = -3.2465, df = 158, p-value = 0.001427
## alternative hypothesis: true mean difference is not equal to 0
## 95 percent confidence interval:
## -0.39703668 -0.09667401
## sample estimates:
## mean difference
## -0.2468553\(\rightarrow\) t(158) = 3.25, p < .01 \(\rightarrow\) signifikant, H0 wird verworfen.
4.4. Schätzung des standardisierten Populationseffekts
Formel: \[d_2'' = \frac{\bar{d}} {\hat{sd}_{d}}\]
wobei
- \(\bar{d}\): Mittelwert der Differenz aller Wertepaare
- \(\hat{sd}_{d}\): geschätzte SD der Differenzen
Wir führen die Berechnung von Cohen’s d für abhängige Stichproben zunächst von Hand durch. Dafür speichern wir uns die nötigen Größen ab und wenden dann die präsentierte Formel an:
mean_d <- mean(difference)
sd.d.est <- sd(difference)
d_Wert <- mean_d/sd.d.est
d_Wert## [1] 0.2574633Berechnung mit Funktion cohen.d()
#alternativ:
#install.packages("effsize")
library("effsize")d2 <- cohen.d(fb22$neuro, fb22$extra,
paired = T, #paired steht fuer 'abhaengig'
within = F) #wir brauchen nicht die Varianz innerhalb
d2##
## Cohen's d
##
## d estimate: 0.2574633 (small)
## 95 percent confidence interval:
## lower upper
## 0.09886578 0.41606085Mit dem Argument within = T, was der Default ist, wird für die Varianzberechnung die Varianz innerhalb der Gruppen herangezogen (vergleiche Formel Cohen’s d für unanghängige Stichproben).
Konventionen nach Cohen (1988) für t-Test für abhängige Stichproben (Achtung: Werte unterscheiden sich zw. abhängigem und unabhängigem t-Test):
| d’’ | Interpretation |
|---|---|
| ~ .14 | kleiner Effekt |
| ~ .35 | mittlerer Effekt |
| ~ .57 | großer Effekt |
\(\Rightarrow\) der standardisierte Populationseffekt beträgt \(d_2''\) = 0.26 und ist laut Konventionen klein bis mittel.
4.5. Ergebnisinterpretation
Es wurde an Psychologiestudierenden untersucht, ob sie vergleichbare Werte auf den Skalen Neurotizismus und Extraversion aufweisen. Zunächst findet sich deskriptiv ein Unterschied: Psychologiestudierende weisen einen durchschnittlichen Neurotizismus-Wert von 3.63 (SD = 0.72) auf, während der durchschnittliche Extraversions-Wert 3.38 (SD = 0.71) beträgt. Zur Beantwortung der Fragestellung wurde ein ungerichteter t-Test für abhängige Stichproben durchgeführt. Der Gruppenunterschied ist signifikant (t(158) = 3.25, p < .01), somit wird die Nullhypothese verworfen. Psychologiestudierende weisen einen höheren Wert auf der Skala Neurotizismus als auf der Skala Extraversion auf. Dieser Unterschied ist nach dem standardisierten Populationseffekt von \(d_2''\) = 0.26 klein bis mittel.
5. Fragestellung E: Sind jüngere Geschwister kooperativer als ältere? \(\rightarrow\) Wilcoxon-Test
In unserem fb22 Datensatz findet sich kein schönes Beispiel zur Illustration des Wilcoxon-Tests für abhängige Stichproben. Aus diesem Grund verwenden wir einen anderen Datensatz. Der Datensatz stammt aus Eid, Gollwitzer & Schmitt: “Statistik und Forschungsmethoden” (4. Auflage, S. 370).
- Abhängige Variable (AV): Kooperationsbereitschaft (stetige Variable mit Werten von 0 [nicht kooperativ] bis 1 [maximal kooperativ])
- Gruppen: das jeweils ältere Geschwisterteil (Gruppe “Älter”) vs. das jeweils jüngere Geschwisterteil (Gruppe “Jünger”)
# Datensatz generieren
dataKooperation <- data.frame(Paar = 1:10, Juenger = c(0.49,0.25,0.51,0.55,0.35,0.54,0.24,0.49,0.38,0.50), Aelter = c(0.4,0.25,0.31,0.44,0.25,0.33,0.26,0.38,0.23,0.35))
dataKooperation # überprüfen, ob alles geklappt hat## Paar Juenger Aelter
## 1 1 0.49 0.40
## 2 2 0.25 0.25
## 3 3 0.51 0.31
## 4 4 0.55 0.44
## 5 5 0.35 0.25
## 6 6 0.54 0.33
## 7 7 0.24 0.26
## 8 8 0.49 0.38
## 9 9 0.38 0.23
## 10 10 0.50 0.35Ein Blick auf die Messwertpaare lässt bereits erkennen, dass die Stichproben (also die Messwerte in den beiden experimentellen Bedingungen) voneinander abhängig sind. Die Geschwisterpaare ähneln sich hinsichtlich ihrer kooperativen Verhaltenstendenzen. Auch inhaltlich sind sie von einander abhängig, da die meisten Geschwister miteinander verwandt sind, also ähnliche Gene aufweisen, und in der Regel im gleichen Zuhause aufwachsen und somit gleiche/sehr ähnliche Umwelteinflüsse genießen.
Relevant ist nun die Frage, ob die Differenz zwischen den beiden Mittelwerten (also zwischen jüngeren und älteren Geschwistern) statistisch bedeutsam ist - also ob die mittlere Differenz zwischen den Paaren von Null verschieden ist.
5.1. Deskriptivstatistik
Wie immer beginnen wir mit der deskriptivstatistischen Analyse unserer Daten.
5.1.1. grafisch
Mithilfe von Histogrammen
# Je ein Histogramm pro Gruppe, untereinander dargestellt, vertikale Linie für den jeweiligen Mittelwert
par(mfrow=c(2,1), mar=c(3,3,2,0))
hist(dataKooperation[, "Juenger"],
xlim=c(0,1),
main="Kooperationsbereitschaft jüngeres Geschwisterteil",
xlab="",
ylab="",
las=1)
abline(v=mean(dataKooperation[, "Juenger"]),
lty=2,
lwd=2)
hist(dataKooperation[, "Aelter"],
xlim=c(0,1),
main="Kooperationsbereitschaft älteres Geschwisterteil",
xlab="",
ylab="",
las=1)
abline(v=mean(dataKooperation[, "Aelter"]),
lty=2,
lwd=2)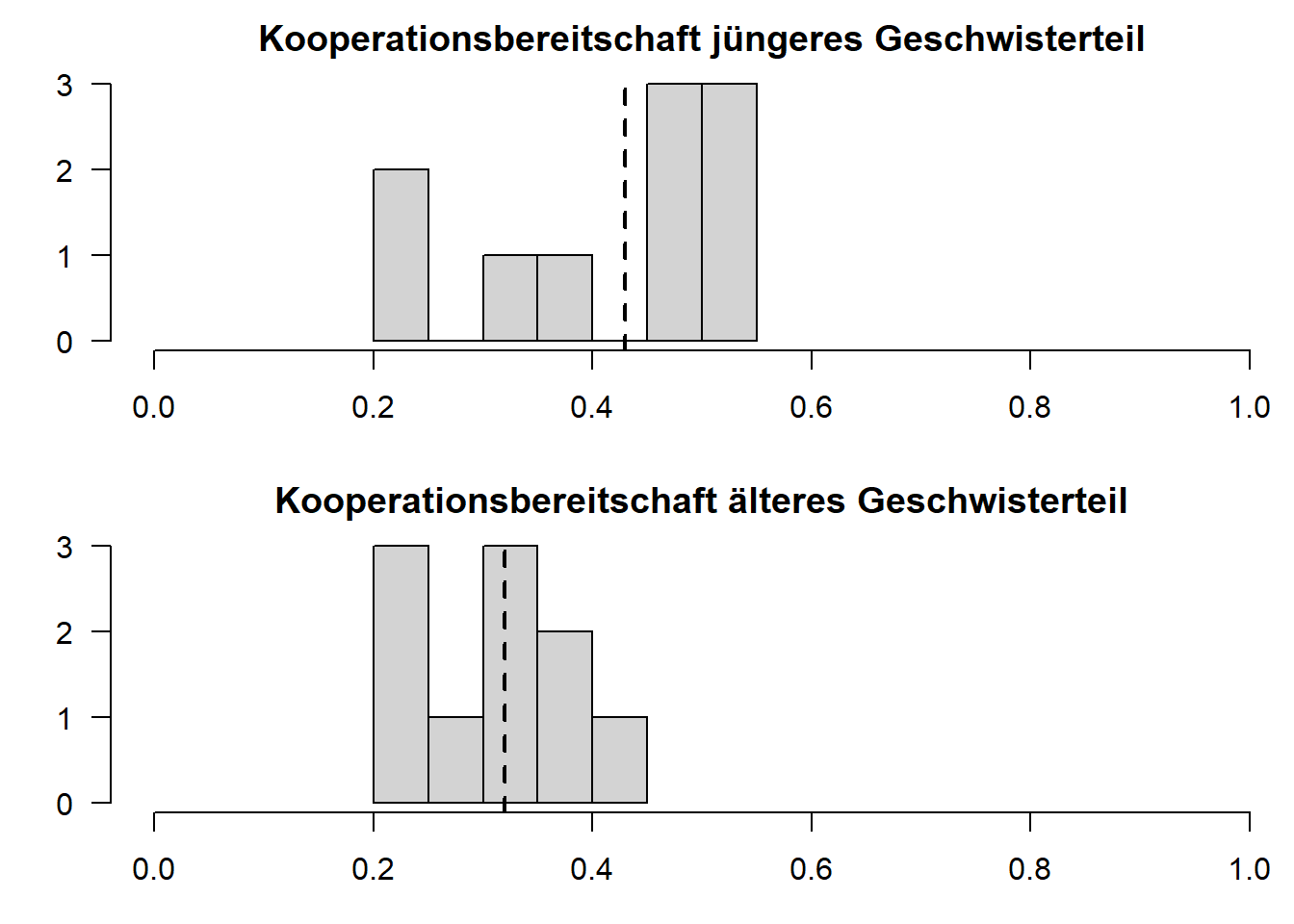
par(mfrow=c(1,1)) #Zurücksetzen des PlotfenstersDie Histogramme sind via xlim so gewählt, dass sie die gleiche x-Achse aufweisen und somit ausgesprochen gut vergleichbar sind. abline() fügt eine Linie in eine Grafik ein. Mit dem Zusatzargument v geben wir eine vertikale Linie in den Plot (hier den Mittelwert). Insgesamt scheinen sich die beiden Verteilungen etwas zu unterscheiden!
5.1.2. statistisch
Deskriptivstatistisch sehen die Ergebnisse so aus:
summary(dataKooperation[, "Juenger"])## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.2400 0.3575 0.4900 0.4300 0.5075 0.5500summary(dataKooperation[, "Aelter"])## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.2300 0.2525 0.3200 0.3200 0.3725 0.4400#alternativ
library(psych)
describe(dataKooperation[, "Juenger"])## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 10 0.43 0.12 0.49 0.44 0.08 0.24 0.55 0.31 -0.57 -1.46 0.04describe(dataKooperation[, "Aelter"])## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 10 0.32 0.07 0.32 0.32 0.1 0.23 0.44 0.21 0.23 -1.57 0.02Achtung: Bei den hier berichteten SD handelt es sich (wie immer in R) um den Populationsschätzer.
Die Mittelwerte der beiden Gruppen unterscheiden sich leicht. Die Frage ist nun, ob sich dieser Unterschied auf die Population verallgemeinern lässt.
5.2. Voraussetzungsprüfung
Zunächst prüfen wir, ob wir zur Beantwortung der Fragestellung einen \(t\)-Test für abhängige Stichproben verwenden können:
Voraussetzungen für die Durchführung des t-Tests für abhängige Stichproben:
- Die abhängige Variable ist intervallskaliert \(\rightarrow\) ok
- Die Messwerte innerhalb der Paare dürfen sich gegenseitig beeinflussen/voneinander abhängig sein; keine Abhängigkeiten zwischen den Messwertpaaren \(\rightarrow\) ok
- Die Differenzvariable d muss in der Population normalverteilt sein \(\rightarrow\) ab \(n \ge 30\) meist gegeben (s. zentraler Grenzwertsatz), ggf. grafische Prüfung oder Hintergrundwissen
zu 3. Normalverteilung von d
Da wir die Differenzvariable betrachten müssen, erstellen wir diese zunächst. Das passiert vektorwertig. Anschließend schauen wir uns wie immer das Histogramm und den QQ-Plot an:
difference <- dataKooperation[, "Juenger"]-dataKooperation[, "Aelter"]
hist(difference,
xlim=c(-.3,.3),
ylim = c(0,5.5),
main="Verteilung der Differenzen",
xlab="Differenzen",
ylab="",
las=1)
curve(dnorm(x, mean=mean(difference), sd=sd(difference)),
col="blue",
lwd=2,
add=T)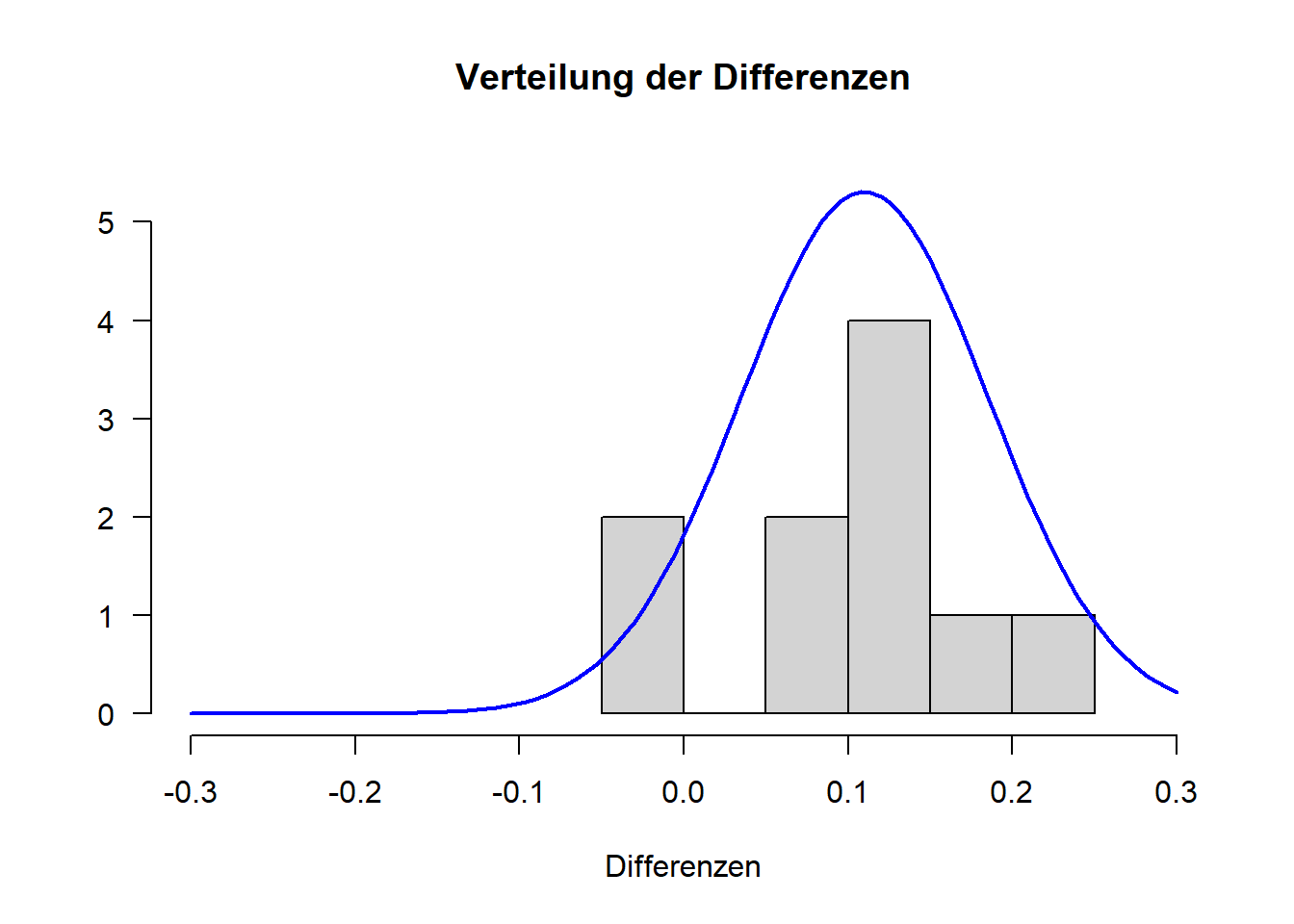
qqnorm(difference)
qqline(difference, col="blue")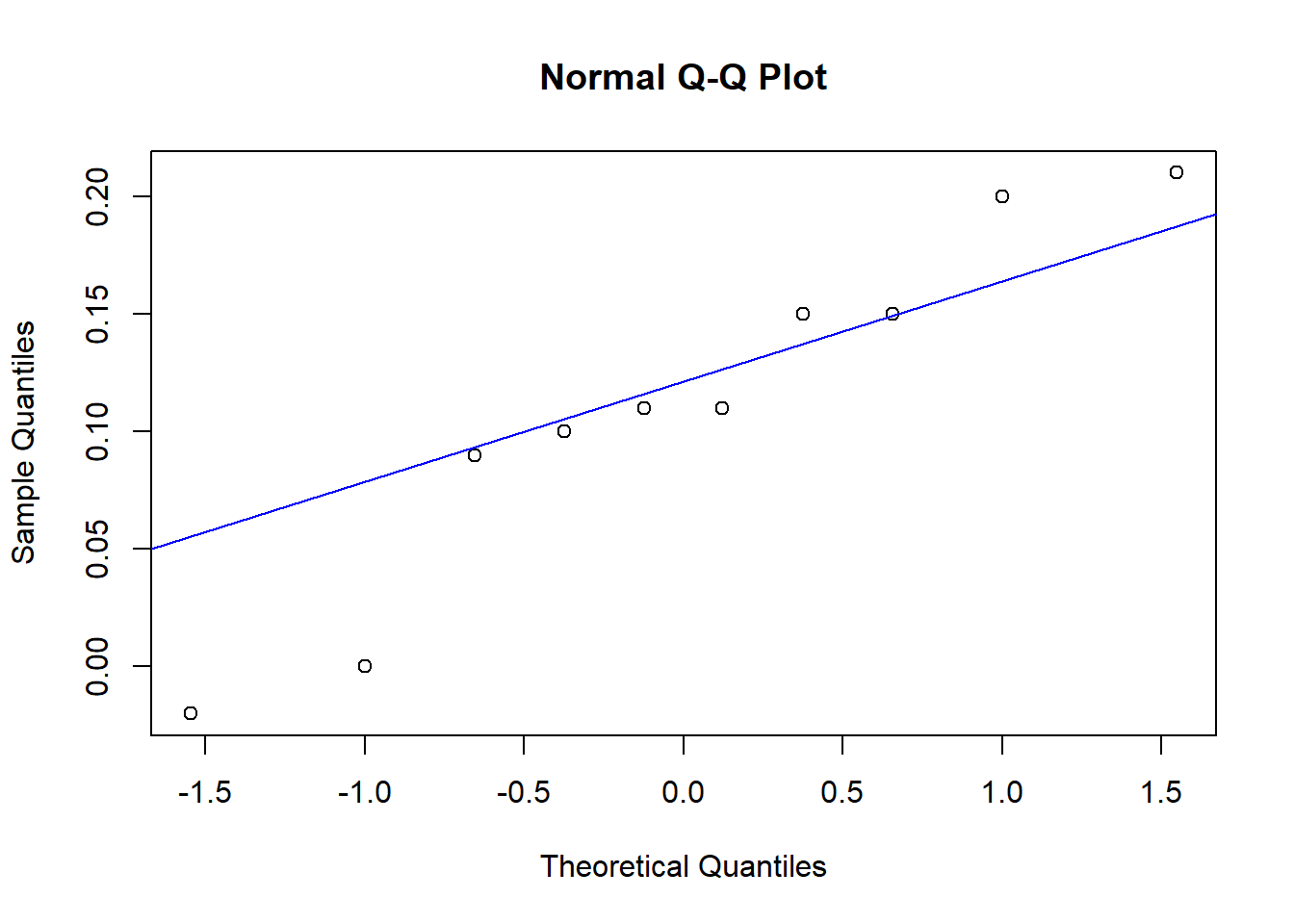
\(\Rightarrow\) Differenzen sehen nicht normalverteilt aus.
Da die letzte Voraussetzung nicht erfüllt ist, führen wir einen Wilcoxon-Test (für abhängige Stichproben) durch.
Auch für diesen Test gilt es, Voraussetzungen zu untersuchen:
Voraussetzungen für die Durchführung des Wilcoxon-Tests (für abhängige Stichproben):
- die Differenzvariable ist in der Population stetig (zumindest singulär ordinal) \(\rightarrow\) ok
- die Messwerte innerhalb der Paare dürfen sich gegenseitig beeinflussen/voneinander abhängig sein; keine Abhängigkeiten zwischen den Messwertpaaren \(\rightarrow\) ok
- die Differenzvariable ist symmetrisch verteilt (nicht notwendigerweise normalverteilt) \(\rightarrow\) ok
5.3. Inferenzstatistik: Wilcoxon-Test für abhängige Stichproben
Zur Erinnerung:
Fragestellung E: “Sind jüngere Geschwister kooperativer als ältere?”
Hypothesen:
- Art des Effekts: Unterschiedshypothese
- Richtung des Effekts: Gerichtet - positiver Effekt
- Grösse des Effekts: Unspezifisch
Hyothesenpaar (inhaltlich):
- H0: Jüngere Geschwister sind genau so oder weniger kooperativ wie ältere Geschwister.
- H1: Jüngere Geschwister sind kooperativer als ältere Geschwister.
Hypothesenpaar (statistisch):
- H0: \(\mu_\text{jünger} \le \mu_\text{älter}\) bzw. \(\mu_{d} \le 0\)
- H1: \(\mu_\text{jünger} > \mu_\text{älter}\) bzw. \(\mu_{d} > 0\)
Signifikanzniveau
Das Signifikanzniveau muss vor der Untersuchung festgelegt werden. Es soll hier 5% betragen. \(\rightarrow\) \(\alpha=.05\) Durchführung des Wilcoxon-Tests für abhängige Stichproben in R:
Die Funktion für den Wilcoxon-Test für abhängige Stichproben sieht dem des t-Tests für abhängige Stichproben sehr ähnlich.
wilcox.test(x = dataKooperation[, "Juenger"],
y = dataKooperation[, "Aelter"], # die beiden abhängigen Gruppen
paired = T, # Stichproben sind abhängig
alternative = "greater", # gerichtete Hypothese
conf.level = .95) # alpha = .05##
## Wilcoxon signed rank test with continuity correction
##
## data: dataKooperation[, "Juenger"] and dataKooperation[, "Aelter"]
## V = 44, p-value = 0.006426
## alternative hypothesis: true location shift is greater than 0V = 44, p < .01 \(\rightarrow\) H0 wird verworfen.
5.4 Ergebnisinterpretation
Es wurde an Geschwisterpaaren untersucht, ob jüngere Geschwister kooperativer sind als ältere Geschwister. Zunächst findet sich deskriptiv ein Unterschied: Jüngere Geschwister weisen einen durchschnittlichen Wert (Median) von 0.49 (IQR = 0.15) auf, während die älteren Geschwister einen Wert (Median) von 0.32 (IQR = 0.12) aufweisen [IQR ist die Interquartil-Range also die Distanz vom Prozentrang 25% bis zum Prozentrang 75%]. Da die Differenzen nicht normalverteilt waren, wurde ein Wilcoxon-Test für abhängige Stichproben durchgeführt. Der Unterschied wurde bei einem Signifikanzniveau von alpha = .05 signifikant (V = 44, p < .01). Somit wird die Nullhypothese verworfen. Der Befund deutet darauf hin, dass jüngere Geschwister kooperativer sind als ihr jeweils älteres Geschwisterteil.
