Hierarchische Regression
Pakete laden
# Benötigte Pakete --> Installieren, falls nicht schon vorhanden
library(lme4) # Für die Mehrebenen-Regression
library(dplyr) # Komfort-Funktionen für die Datentransformationen
library(ICC) # Für die einfache Berechung von ICCs
library(ggplot2) # Für Grafiken
library(interactions) # Zur Veranschaulichung von Moderator-EffektenEinleitung und Datenbeispiel
Daten in der klinisch-psychologischen Forschung haben häufig eine sogenannte hierarchische Struktur oder Mehrebenen-Struktur, in der Beobachtungen auf einer ersten Ebene in Beobachtungseinheiten auf einer übergeordneten Ebene gruppiert sind. Typische Strukturen sind Individuen in Gruppen (z. B. Patient*innen in Therapiepraxen oder in Kliniken) oder Messzeitpunkte in Personen (z. B. Befragungszeitpunkte im Verlauf einer Therapiestudie).
Unser Datenbeispiel stammt aus einer Studie zum psychischen Wohlbefinden von Individuen während des pandemie-bedingten Lockdowns in Frankreich. Es handelt sich um hierarchische Daten mit Messzeitpunkten auf Ebene 1 und Individuen auf Ebene 2. Zunächst laden wir diesen Datensatz aus dem OSF und nehmen ein paar Schritte zur Vorbereitung vor:
# Daten einlesen und vorbereiten
lockdown <- read.csv(url("https://osf.io/dc6me/download"))
# Entfernen der Personen, für die weniger als zwei Messpunkte vorhanden sind
# (Auschluss von Fällen, deren ID nur einmal vorkommt)
lockdown <- lockdown[-which(lockdown$ID %in% names(which(table(lockdown$ID)==1))),]
# Daten aufbereiten, Variablen auswählen extrahieren und in Nummern umwandeln
# Entfernen von Minderjährigen & unbestimmtes Gender mit den Funktionen filter() und select () aus dplyr.
lockdown <- lockdown %>%
filter((Age >= 18) & (Gender == 1 | Gender == 2)) %>%
select(c("ID", "Wave", "Age", "Gender", "Income", "EWB","PWB","SWB",
"IWB","E.threat","H.threat", "Optimism",
"Self.efficacy","Hope","P.Wisdom","ST.Wisdom","Grat.being",
"Grat.world","PD","Acc","Time","EWB.baseline","PWB.baseline",
"SWB.baseline","IWB.baseline"))
# Standardisieren der AVs
lockdown[,c("EWB", "PWB", "SWB", "IWB")] <- scale(lockdown[,c("EWB", "PWB", "SWB", "IWB")])
# Standardisieren möglicher Prädiktoren
lockdown[,c("E.threat", "H.threat", "Optimism", "Self.efficacy", "Hope", "P.Wisdom",
"ST.Wisdom", "Grat.being", "Grat.world")] <-
scale(lockdown[,c("E.threat", "H.threat", "Optimism", "Self.efficacy", "Hope", "P.Wisdom",
"ST.Wisdom", "Grat.being", "Grat.world")])
# ID in Faktor Umwandeln
lockdown$ID <- as.factor(lockdown$ID)Variablen im Datensatz
In diesem Datensatz stehen die Daten eines Messzeitpunktes in je einer Zeile, d.h. die Daten einer Person stehen in mehreren Zeilen (diese Struktur wird oft auch als long format bezeichtet - im Kontrast zum wide format, bei dem die Daten jeder Person in einer Zeile in verschiedenen Variablen stehen). Die Variable ID markiert, welche Daten zur selben Person gehören.
Die Variable Wave kennzeichnet mit Werten von 0 bis 5 die Erhebungswelle, zu der die Befragung erfolgt ist. Eine Person, die zu allen Zeitpunkten teilgenommen hat, hat sechs Zeilen mit den Wellen von 0 bis 5. Die Variable Time gibt die Zeit in Wochen an, die die befragte Person zum jeweiligen Zeitpunkt schon im Lockdown war.
Die abhängigen Variablen sind verschiedene Konstrukte, die Aspekte des Wohlbefindens (well being) einer Person beinhalten. In diesem Beispiel beschränken wir uns auf die wesentlichen Konstrukte des Papers, nämlich dem drei-dimensionalen Model of positive mental health (Keyes, 2002) und inner harmony (Dambrun at al., 2012). Die folgenden abhängigen Variablen wurden zu jedem Messzeitpunkt erfasst:
- EWB: Emotional Well-Being ist definiert als ein hohes Maß an positivem Affekt, ein geringes Maß an negativem Affekt und ein hohes Maß an Zufriedenheit mit dem eigenen Leben.
- PWB: Psychological Well-Being wurde als eine Kombination aus Selbstakzeptanz, Autonomie, Lebenssinn, positiven Beziehungen zu anderen, Umweltbewältigung und persönlichem Wachstum operationalisiert.
- SWB: Social Well-Being bewertet das positive soziale Funktionieren anhand von fünf Aspekten: soziale Kohärenz, soziale Verwirklichung, soziale Integration, soziale Akzeptanz und sozialer Beitrag.
- IWB: Inner Well-Being kann als ein Gefühl des Seelenfriedens mit geringer Erregung verstanden werden, von dem angenommen wird, dass es stabiler und weniger abhängig von äußeren Reizen ist als positive Gefühle mit hoher Erregung.
Als Prädiktoren können Variablen verwendet werden, die auf Personenebene (Ebene 2) angesiedelt sind - diese wurden nur zum ersten Zeitpunkt erfasst und dann als über die Zeit stabil betrachtet. Dies sind Personenvariablen wie Alter und Geschlecht, zudem verschiedene psychologischen Ressourcen wie Optimismus (Optimism), Selbstwirksamkeit (Self-efficacy), Hoffnung (Hope), Weisheit (P.Wisdom & ST.Wisdom), Dankbarkeit gegenüber der eigenen Existenz und der Welt (Grat.being & Grat.world) und Akzeptanz (Acceptance). Eine genauere Beschreibung dieser Variablen im Kontext der Studie finden Sie im Paper auf den Seiten 2 bis 5.
Als Prädiktoren auf Ebene 1 können Variablen verwendet werden, die mehrfach erfragt wurden und über die Zeit variieren. Dies ist die o.g. im Lockdown verbrachte Zeit (Time) sowie die wahrgenommene ökonomische Bedrohung, also Jobgefahr, Geldnot, etc. (E.threat) und die wahrgenommene gesundheitliche Bedrohung, also die Wahrscheinlichkeit einer Erkrankung und deren Folgen (H.threat).
Fragestellungen
Bezogen auf die AV Psychological Well-Being (PWB) werden hier die Folgenden Fragestellungen untersucht:
- Wie groß sind die Unterschiede im Niveau des Wohlbefindens zwischen Personen in Relation zu den Schwankungen innerhalb von Personen?
- Wie wirkt sich die Zeit im Lockdown auf das Wohlbefinden aus?
- Hat das Alter der befragten Personen einen Effekt auf das Wohlbefinden?
- Hat das Alter der befragten Personen einen Effekt auf den Effekt des Lockdowns?
1. Unterschiede zwischen und innerhalb von Personen
Intraklassenkorrelation
Die Intraklassenkorrelation (ICC, \(\rho_{ICC}\)) gibt den Varianzanteil einer Variablen an, der auf Unterschiede in den Beobachtungseinheiten zurückgeht.
\[\rho_{ICC}=\frac{\sigma^2_{between}}{\sigma^2_{between}+\sigma^2_{within}}\]
In unserem Fall ist das die Varianz \(\sigma^2_{between}\) in der Befindlichkeit zwischen Personen (= Ebene-2-Einheiten). Die Varianz \(\sigma^2_{within}\) innerhalb der Beobachtungseinheiten entspricht den Schwankungen der individuellen Befindlichkeiten zwischen den Zeitpunkten (= Ebene-1-Einheiten). Die ICC ist hier ein Maß dafür, wie groß interindividuell stabile Unterschiede im Befindlichkeitsniveau in Relation zur Gesamtstreuung einschließlich der intraindividuellen Schwankungen sind.
Eine einfache Methode zur Berechnung der ICC kann auf Basis der Varianzkomponenten (Inner- und Zwischengruppenvarianzen) einer einfaktoriellen ANOVA erfolgen. Mit der Funktion ICCest des Pakets ICC ermitteln wir die ICCs für die vier Befindlichkeitsvariablen:
# ICCs auf Basis der Varianzkomponenten mit der Funktion ICCbare
ICCbare(ID, EWB, data = lockdown)## [1] 0.7210427ICCbare(ID, PWB, data = lockdown)## [1] 0.7922163ICCbare(ID, SWB, data = lockdown)## [1] 0.7744171ICCbare(ID, IWB, data = lockdown)## [1] 0.7116098Wir erhalten für die Befindlichkeitsvariablen die folgenden ICCs:
- Emotional Wellbeing (EWB): \(\rho_{ICC} = 0.721\)
- Psychological Well-being (PWB): \(\rho_{ICC} = 0.792\)
- Social Well-Being (SWB): \(\rho_{ICC} = 0.774\)
- Inner well-being (IWB): \(\rho_{ICC} = 0.712\)
Die Unterschiede zwischen Personen sind also durchweg größer als die Schwankungen innerhalb der Personen. Mehr als 70% der Varianz in den Variablen lässt sich auf stabile Unterschiede zwischen Personen zurückführen.
Grafische Veranschaulischung der inter- und intraindividuellen Unterschiede
Um ein Gefühl für die Unterschiede zwischen und innerhalb von Personen zu bekommen, werden die individuellen Verläufe über die Zeit (Trajektorien) häufig als Liniendiagramme veranschaulicht. Bei einem großen Datensatz ist die Darstellung aller Fälle jedoch oft nicht mehr anschaulich:
# Individuelle Verläufe für Psychological Well Being
ggplot(lockdown, aes(x=Wave, y=PWB, color=ID)) +
theme_bw() + guides(color="none") +
geom_line()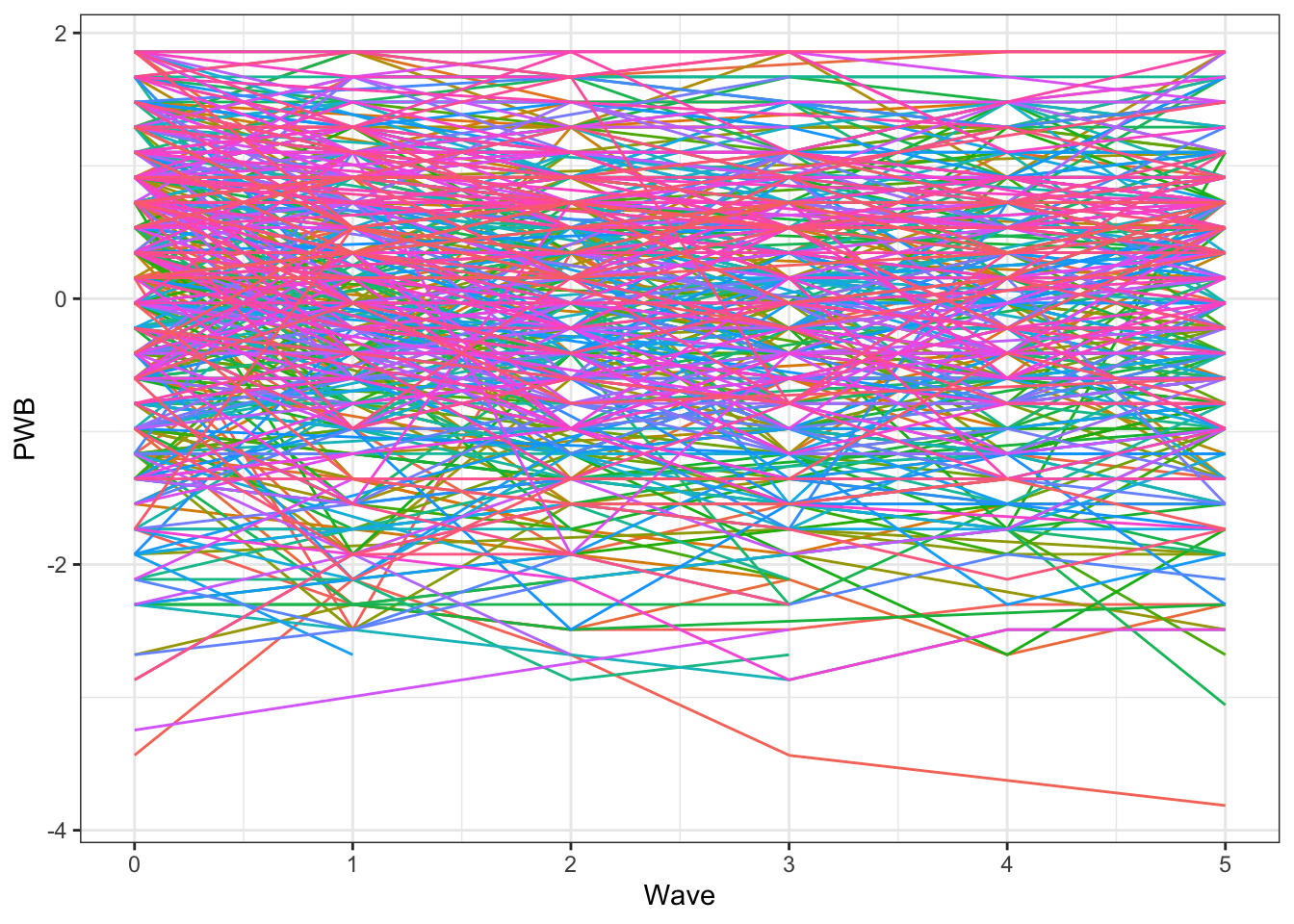
Für die grafische Veranschaulichung wählen wir hier daher eine kleine Zahl von Fällen, die zudem Daten zu allen sechs Zeitpunkten haben:
IDs.subset <- c("03858ebe", "ddf85cd4", "fab6bb4d", "c7b6e168", "c0661f6a", "f005ee8d", "f037053f", "166a701e",
"3ff1ffae", "486d63a8", "4b6a0366", "ba2ccd92", "cdbfa68a", "f43569d8", "c0c3cb43")
# Grafik mit dem Subset
ggplot(lockdown[lockdown$ID %in% IDs.subset,], aes(x=Wave, y=PWB, color=ID)) +
theme_bw() + guides(color="none") +
geom_line()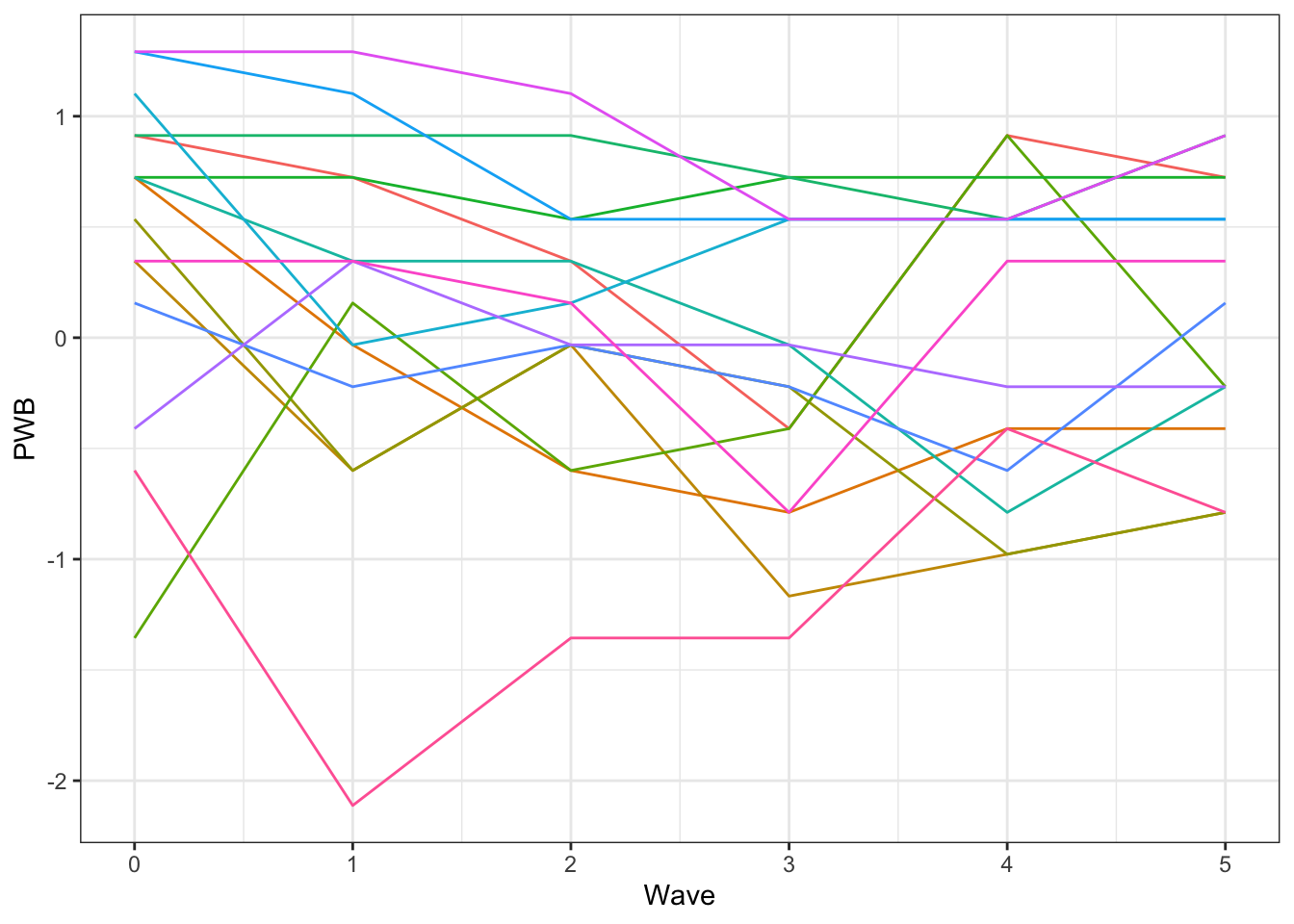
Die Grafik veranschaulicht, dass die Unterschiede zwischen dem Niveau der Linien, also zwischen Personen, stärker sind als die Schwankungen innerhalb der Linien über die Zeit (also innerhalb von Personen).
Die unterschiedliche Bedeutung der beiden Variablen Wave (Messzeitpunkt) und Time (Zeit im Lockdown in Wochen) können wir durch eine Grafik anschaulich machen, in der wir statt des Messzeitpunkts die Zeit nehmen. Man sieht, dass die Linien hier unterschiedlich lang sind, da die befragten Personen zum Zeitpunkt der Beantwortung unterschiedlich lang im Lockdown waren:
# Grafik mit dem Subset, Zeit als UV
ggplot(lockdown[lockdown$ID %in% IDs.subset,], aes(x=Time, y=PWB, color=ID)) +
theme_bw() + guides(color="none") +
geom_line()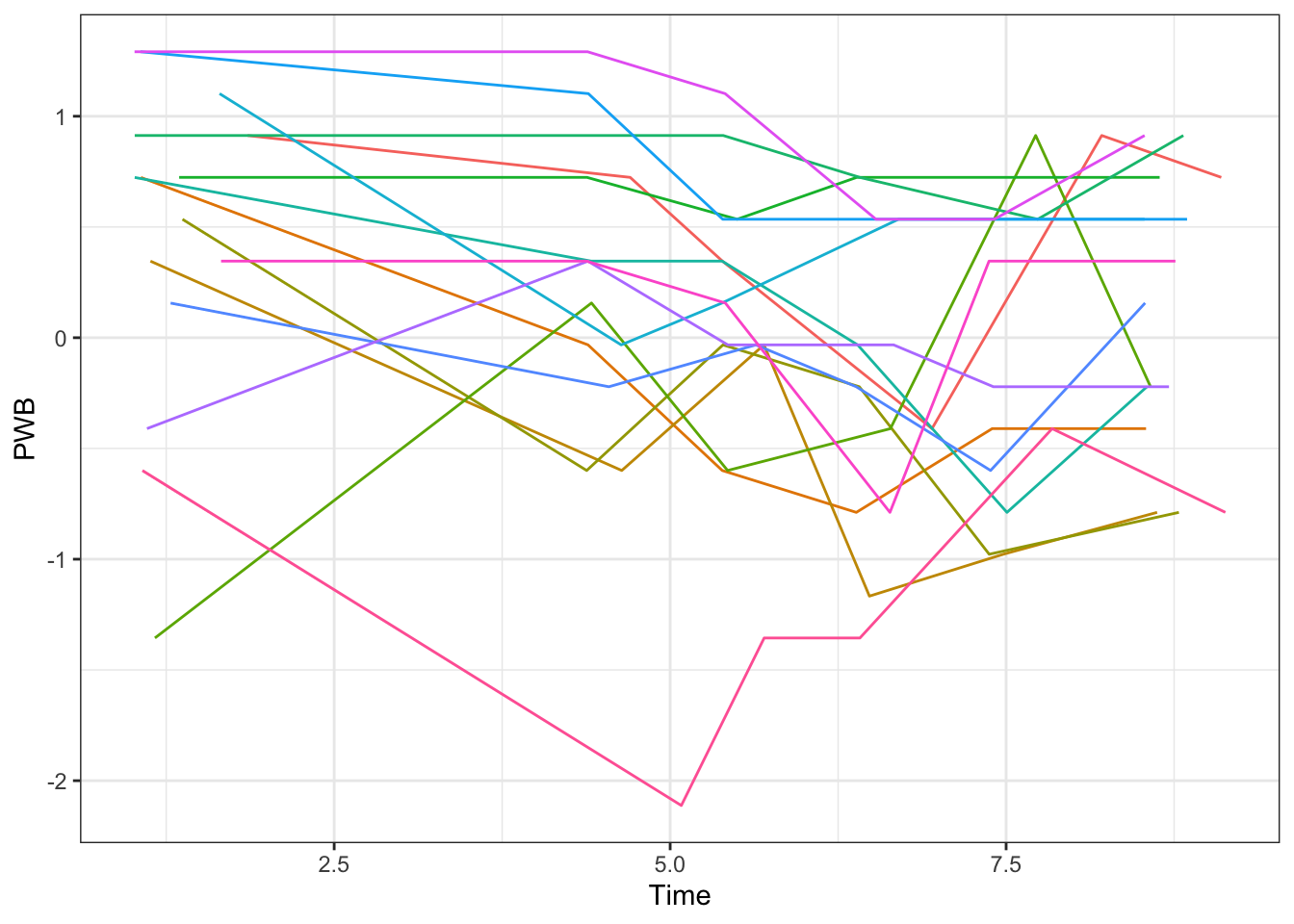
Nullmodell
Als erstes Modell berechnen wir für Psychological Wellbeing das Nullmodell ohne Prädiktoren. Dieses Modell kann für Modelle mit Prädiktoren als Referenz für Modellvergleiche dienen. Außerdem können wir auf dessen Basis auch eine Schätzung für die Intraklassenkorrelation bilden. Beide benötigten Varianzkomponenten \(\sigma^2_{between}\) und \(\sigma^2_{within}\) werden im Modell geschätzt.
Der Ausgabe für das Nullmodell können wir entnehmen, dass die Varianz des Intercepts \(\sigma^2_{between}=0.802\) beträgt, die Residualvarianz, die hier der Innerpersonen-Varianz entspricht, \(\sigma^2_{within}=0.208\). Hieraus resultiert eine ICC von \(\rho_{ICC}=0.794\). Geringfügige Abweichungen durch die oben mit der Funktion ICCbareermittelten Ergebnisse können durch die unterschiedlichen Schätzmethoden (Kleinstquadrate vs. ML) zustande kommen.
# Nulllmodell für PWB
m0 <- lmer(PWB ~ 1 + (1 | ID), data = lockdown)
summary(m0)## Linear mixed model fit by REML ['lmerMod']
## Formula: PWB ~ 1 + (1 | ID)
## Data: lockdown
##
## REML criterion at convergence: 4160
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -4.4421 -0.5184 0.0177 0.5274 3.6005
##
## Random effects:
## Groups Name Variance Std.Dev.
## ID (Intercept) 0.8019 0.8955
## Residual 0.2081 0.4562
## Number of obs: 2188, groups: ID, 485
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) -0.006756 0.041994 -0.1612. Effekte der Zeit
Im Folgenden werden wir untersuchen, ob die Zeit (Time) im Lockdown sich auf das Wohlbefinden auswirkt. Zeit ist ein Ebene-1-Prädiktor, dessen Effekt wir entweder “nur” als festen Effekt modellieren können, oder als Zufallseffekt (random slope), hinsichtlich dessen sich Personen unterscheiden können. Wir werden beide Varianten analysieren und vergleichen.
Fester Effekt
Den Effekt über alle Personen hinweg können wir in einem Modell schätzen, in dem die Zeit als fester Effekt enthalten ist:
- Gleichung auf Ebene 1: \(Y_{ij}=\beta_{0j}+\beta_{1j}X_{ij}+r_{ij}\)
- Interzept auf Ebene 2: \(\beta_{0j}=\gamma_{00}+u_{0j}\)
- Slope auf Ebene 2: \(\beta_{1j}=\gamma_{10}\)
- Gesamtmodell: \(Y_{ij}=\gamma_{00} + \gamma_{01}X_{ij} + u_{0j} + r_{ij}\)
- Als Formel für
lmer:Y ~ 1 + X + (1 | ID)
In der Anwendung auf die abhängige Variable Psychological Wellbeing (PWB) in R sehen wir, dass Zeit einen signifikanten Effekt hat.
Bei mehr als einem Parameter für feste Effekte gibt die lmer-Funktion eine Ausgabe zur “Correlation of Fixed Effects”. Diese ist kurz gesagt inhaltlich in aller Regel irrelevant und kann ignoriert werden. Sie hat nichts mit der Korrelation von Variablen im Modell zu tun, sondern sagt etwas über Abhängigkeiten der Parameterschätzungen. Eine von null verschiedene Korrelation bedeutet, dass sich die Effekte bei einer Replikation der Studie nicht unabhängig voneinander verändern würden.
PWB.time.fixed <- lmer(PWB ~ 1 + Time + (1 | ID), data = lockdown)
summary(PWB.time.fixed)## Linear mixed model fit by REML ['lmerMod']
## Formula: PWB ~ 1 + Time + (1 | ID)
## Data: lockdown
##
## REML criterion at convergence: 4086.7
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -4.5922 -0.5053 0.0394 0.5292 3.6011
##
## Random effects:
## Groups Name Variance Std.Dev.
## ID (Intercept) 0.8073 0.8985
## Residual 0.1982 0.4452
## Number of obs: 2188, groups: ID, 485
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 0.176279 0.046532 3.788
## Time -0.035775 0.003889 -9.199
##
## Correlation of Fixed Effects:
## (Intr)
## Time -0.428Da wir die AV standardisiert haben und die Zeit in Wochen angegeben ist, können wir den Effekt dahingehend interpretieren, dass sich PWB mit jeder Woche im Lockdown um \(0.036\) Standardabweichungen verschlechtert.
Die folgende Grafik veranschaulicht die Vorhersage aus dem Modell anhand der Teilmenge von Fällen, die für die Darstellung der Rohdaten oben verwendet wurde. Man sieht, dass für alle Fälle dieselbe Steigung für die Zeit angenommen wird.
# Vorhergesagte Werte im Datensatz speichern
lockdown$pred <- predict(PWB.time.fixed)
# Grafik mit dem Subset
ggplot(lockdown[lockdown$ID %in% IDs.subset,], aes(x=Time, y=pred, color=ID)) +
theme_bw() + guides(color="none") +
geom_line()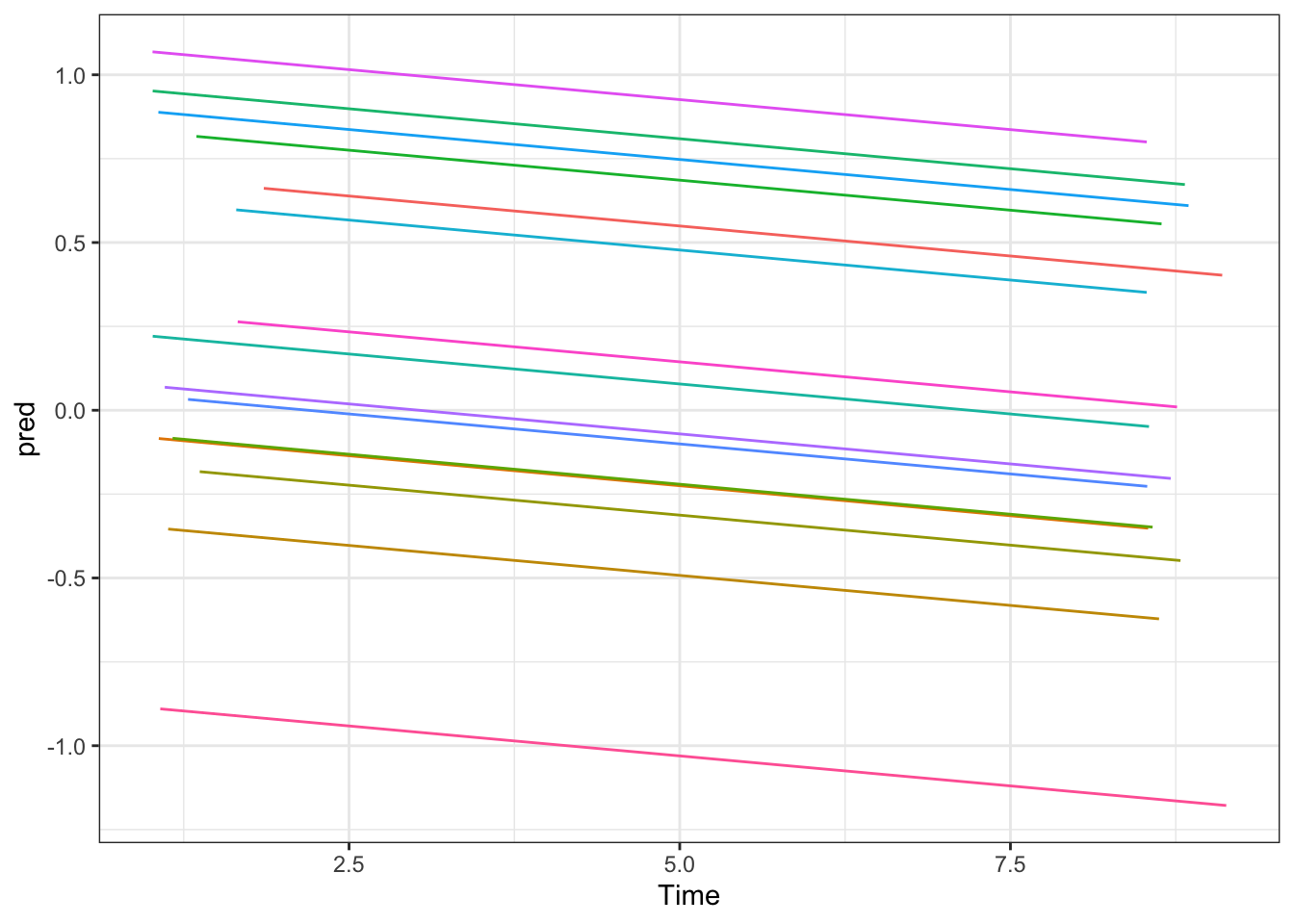
Zufallseffekt (random slope)
In einem nächsten Schritt untersuchen wir nun, ob sich der Effekt der Zeit auf das Wohlbefinden zwischen Personen unterscheidet. Hierzu wird der Effekt von Zeit als Zufallseffekt (random slope) modelliert:
- Gleichung auf Ebene 1: \(Y_{ij}=\beta_{0j}+\beta_{1j}X_{ij}+r_{ij}\)
- Interzept auf Ebene 2: \(\beta_{0j}=\gamma_{00}+u_{0j}\)
- Slope auf Ebene 2: \(\beta_{1j}=\gamma_{10}+u_{1j}\)
- Gesamtmodell: \(Y_{ij}=\gamma_{00} + \gamma_{01}X_{ij} + u_{0j}X_{ij} + u_{0j} + r_{ij}\)
- Als Formel für
lmer:Y ~ 1 + X + (1 + X | ID)
PWB.time.random <- lmer(PWB ~ 1 + Time + (1 + Time | ID), data = lockdown)## Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
## Model failed to converge with max|grad| = 0.00460588 (tol = 0.002, component 1)summary(PWB.time.random)## Linear mixed model fit by REML ['lmerMod']
## Formula: PWB ~ 1 + Time + (1 + Time | ID)
## Data: lockdown
##
## REML criterion at convergence: 4039.4
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -4.7802 -0.4633 0.0390 0.4982 3.8931
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## ID (Intercept) 0.865618 0.93039
## Time 0.003932 0.06271 -0.26
## Residual 0.168726 0.41076
## Number of obs: 2188, groups: ID, 485
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 0.177654 0.047118 3.770
## Time -0.036000 0.004693 -7.671
##
## Correlation of Fixed Effects:
## (Intr)
## Time -0.454
## optimizer (nloptwrap) convergence code: 0 (OK)
## Model failed to converge with max|grad| = 0.00460588 (tol = 0.002, component 1)Nun sind wir in eine etwas ungünstige Lage gekommen. Wir bekommen nämlich eine Warning ausgegeben, die wir nicht ignorieren sollten. Diese wird sowohl beim Schätzen ausgegeben und steht auch in der Summary ganz unten:
## optimizer (nloptwrap) convergence code: 0 (OK)
## Model failed to converge with max|grad| = 0.00460588 (tol = 0.002, component 1)Die Konvergenz bezieht sich auf den numerischen Algorithmus der im Hintergrund die Likelihood maximiert: Es handelt sich hierbei um ein iteratives Verfahren, bei welchem in jedem Schritt geschaut wird, wie stark sich die Likelihood noch verändert. Ist diese Veränderung klein, so spricht dies für Konvergenz. Hier wird nun gesagt, dass die letzte Änderung ca. .004 war, die Toleranz (also die größte akzeptierte Änderung) aber bei tol = .002 liegt. Durch diese Diskrepanz wird die Warnung ausgelöst. Weitere Evaluationsmechanismen der Lösungen zeigen jedoch an, dass die Lösung prinzipiell "OK" ist. Wir wollen es aber “richtig” machen und ändern deshalb den Optimierungsalgorithmus:
PWB.time.random <- lmer(PWB ~ 1 + Time + (1 + Time | ID), data = lockdown,
control = lmerControl(optimizer ="Nelder_Mead"))
summary(PWB.time.random)## Linear mixed model fit by REML ['lmerMod']
## Formula: PWB ~ 1 + Time + (1 + Time | ID)
## Data: lockdown
## Control: lmerControl(optimizer = "Nelder_Mead")
##
## REML criterion at convergence: 4039.4
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -4.7802 -0.4633 0.0390 0.4983 3.8932
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## ID (Intercept) 0.865730 0.93045
## Time 0.003933 0.06271 -0.26
## Residual 0.168721 0.41076
## Number of obs: 2188, groups: ID, 485
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 0.177654 0.047121 3.770
## Time -0.035999 0.004693 -7.671
##
## Correlation of Fixed Effects:
## (Intr)
## Time -0.454Nun erhalten wir keine Warnung mehr, die Lösung scheint gutartig in dem Sinne zu sein, dass alle Evaluationsmechanismen sagen, dass die numerische Lösung konvergiert ist und damit interpretiert werden kann. Wenn wir die beiden Summaries vergleichen erkennen wir, dass die Unterschiede nur marginal sind (ab der 3. Nachkommastelle gibt es Koeffizienten und Standardfehler, die sich unterscheiden). Somit scheint der optische Hinweis, die Lösung sei "OK" also nicht fehlgeleitet zu sein. Dennoch sollte bei solchen Warnungen immer genauer nachgeschaut werden! Nun zur Interpretation der Ergebnisse:
Mit mehr als einem Zufallseffekt im Modell enthält die Ausgabe nicht nur deren Varianzen, sondern auch deren Korrelation. In unserem Fall beträgt die Korrelation zwischen dem Intercept \(\beta_0\) und dem Regressionskoeffizienten \(\beta_1\) für ‘Time’ \(r=-0.26\). Das Intercept \(\beta_{0j}\) ist das erwartete Wohlbefinden einer Person \(j\) zu Beginn des Lockdowns (null Wochen im Lockdown). Die Steigung \(\beta_{1j}\) ist die erwartete Veränderung des individuellen Wohlbefindens mit jeder weiteren Woche im Lockdown. Die leicht negative Korrelation bedeutet, dass das Wohlbefinden von Personen mit einem zu Beginn höheren Niveau etwas stärker negativ entwickelt.
Der Ausgabe können wir entnehmen, dass die Varianz des Zeiteffekts \(var(u_1)=\) 0.0039 beträgt. Ob dieser auf den ersten Blick kleine Effekt signifikant ist, können wir durch den Vergleich des Modells mit und ohne Zufallseffekt testen. Die anova-Funktion schätzt die Modelle standardmäßig für den Modellvergleich neu, und zwar mit Maximum Likelihood (ML) statt der Standardmethode Restricted Maximum Likelihood (REML). Dies muss hier mit der Option refit=FALSE unterdrückt werden, da der Test von Zufallseffekten auf der REML-Schätzung basieren sollte.
anova(PWB.time.fixed, PWB.time.random, refit=FALSE)## Data: lockdown
## Models:
## PWB.time.fixed: PWB ~ 1 + Time + (1 | ID)
## PWB.time.random: PWB ~ 1 + Time + (1 + Time | ID)
## npar AIC BIC logLik deviance Chisq Df Pr(>Chisq)
## PWB.time.fixed 4 4094.7 4117.5 -2043.4 4086.7
## PWB.time.random 6 4051.4 4085.6 -2019.7 4039.4 47.334 2 5.267e-11 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Der Modellvergleich zeigt, dass die Varianz des Zeiteffekts signifikant ist (\(\chi^2=47.33\), \(df=2\)). Dennoch bleibt dieser Wert noch wenig anschaulich. Eine Möglichkeit zur grafischen Veranschaulichung ist die Darstellung der vorhergesagten individuellen Verläufe, auch hier wieder mit der oben verwendeten Teilmenge von Fällen. Die geschätzen Trajektorien unterscheiden sich nun in ihren Steigungen, manche zeigen eine deutliche Abnahme des Wohlbefindens, andere bleiben eher auf einem konstanten Niveau oder zeigen sogar einen Anstieg.
# Vorhergesagte Werte im Datensatz speichern
lockdown$pred <- predict(PWB.time.random)
# Grafik mit dem Subset
ggplot(lockdown[lockdown$ID %in% IDs.subset,], aes(x=Time, y=pred, color=ID)) +
theme_bw() + guides(color="none") +
geom_line()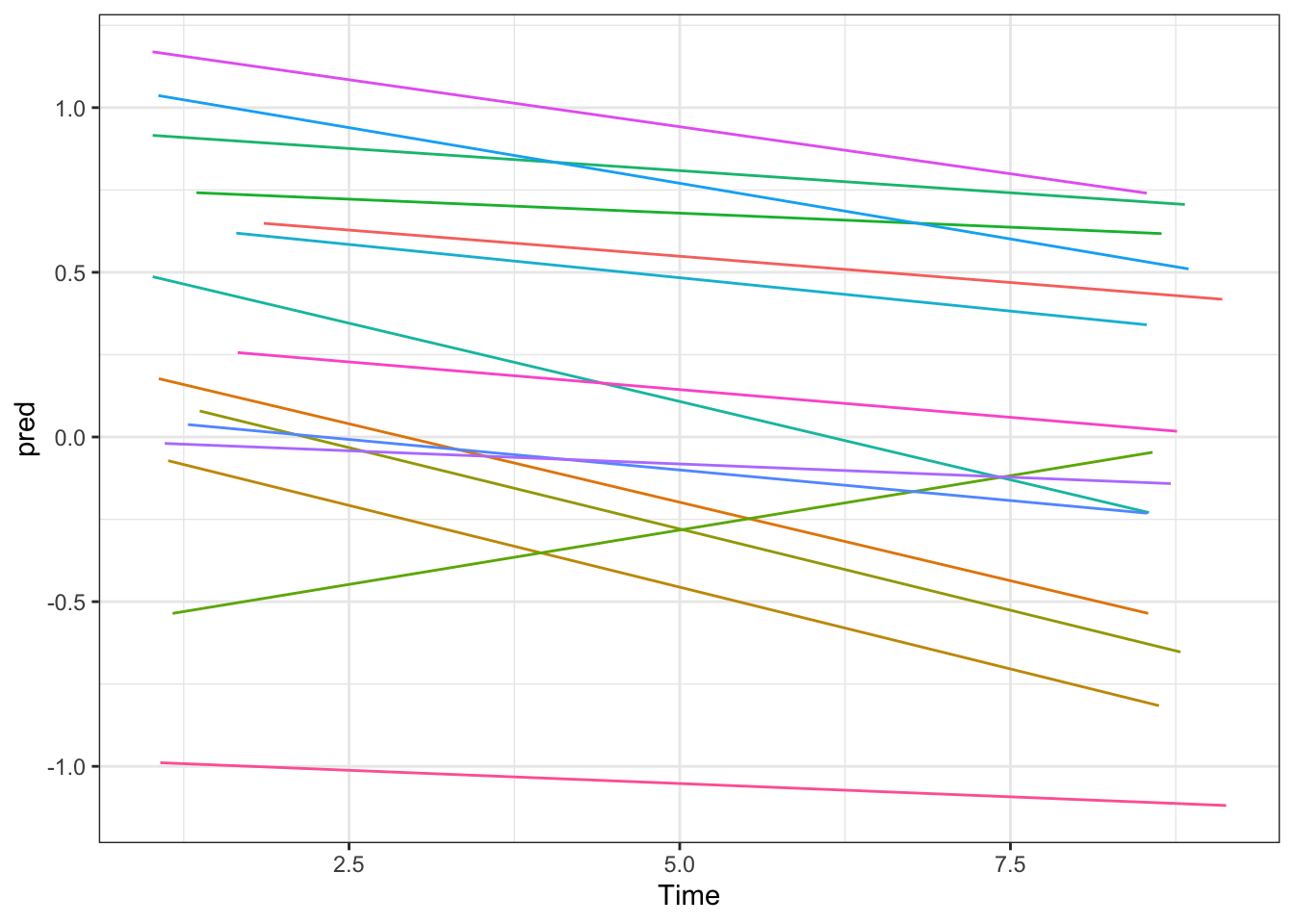
Eine weitere Art, sich die Streuung des Zufallseffekts grafisch zu veranschaulichen, ist ein Histogramm. Mit der Funktion fixef lassen sich die festen Effekte des Modells auslesen, mit randef die Zufallseffekte für jede Ebene-2-Einheit, hier also Personen. Die Verteilung der geschätzen individuellen Zeiteffekte \(\beta_{1j}\) ergibt sich aus der Verteilung des festen Effekts plus den Ebene-2-Residuen: \(\gamma_{10}+u_{1j}\). Wir sehen, dass ein großer Teil der Slopes im negativen Bereich liegt, einige jedoch auch im positiven, was einer leichten Verbesserung des Wohlbefindens mit zunehmender Zeit im Lockdown entsprechen würde.
# Histogramm der individuellen Slopes als Summe aus festem Effekt und Residuen
hist(fixef(PWB.time.random)["Time"] + ranef(PWB.time.random)$ID$Time,
main="Histogramm des Zeiteffekts", xlab = expression(beta[1]),
breaks = seq(-0.2,0.2,0.025))
abline(v=fixef(PWB.time.random)["Time"], col="blue") # Lage des festen Effektes kennzeichnen
3. Effekte des Alters als Prädiktor auf Personen-Ebene
Im Datensatz sind eine Reihe von Variablen enthalten, die für jede Person einmal erhoben wurden und als über die Zeit stabil angenommen werden - diese können als Ebene-2-Prädiktoren verwendet werden. Exemplarisch analysieren wir den Effekt des Alters auf das Wohlbefinden. Das Modell enthält einen festen Effekt für den Ebene-2-Prädiktor und (wie immer) einen Zufallseffekt für den random slope:
- Gleichung auf Ebene 1: \(Y_{ij}=\beta_{0j}+r_{ij}\)
- Interzept auf Ebene 2: \(\beta_{0j}=\gamma_{00}+\gamma_{01}Z_j+u_{0j}\)
- Gesamtmodell: \(Y_{ij}=\gamma_{00} + \gamma_{10}Z_j + u_{0j} + r_{ij}\)
- Als Formel für
lmer:Y ~ 1 + Z + (1 | ID)
Um die Modellparameter besser interpretieren zu können, zentrieren wir die Variabe zunächst um ihren Mittelwert (\(M(Age)=43.32\)).
Im Ergebnis sehen wir, dass Alter einen positiven Effekt auf das Psychische Wohlbefinden hat. Mit einem Jahr höherem Alter ändert sich das Niveau des Wohlbefindens um 0.013 Standardabweichungen. Das sieht numerisch wenig aus, bedeutet aber z. B. schon zwischen Zwanzigjährigen und Vierzigjährigen einen erwarteten Unterschied von 0.254 Standardabweichungen.
PWB.Age <- lmer(PWB ~ 1 + Age + (1 | ID), data = lockdown)
summary(PWB.Age)## Linear mixed model fit by REML ['lmerMod']
## Formula: PWB ~ 1 + Age + (1 | ID)
## Data: lockdown
##
## REML criterion at convergence: 4152.2
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -4.4343 -0.5185 0.0266 0.5245 3.5588
##
## Random effects:
## Groups Name Variance Std.Dev.
## ID (Intercept) 0.7732 0.8793
## Residual 0.2081 0.4562
## Number of obs: 2188, groups: ID, 485
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 0.0008183 0.0413217 0.020
## Age 0.0126956 0.0030009 4.231
##
## Correlation of Fixed Effects:
## (Intr)
## Age 0.0434. Interaktion zwischen Personen- und Zeitebene
Schließlich schätzen wir ein gemeinsames Modell mit Zeit und Alter. In diesem lassen wir für die Zeit wieder einen random slope zu, darüber hinaus eine Wechselwirkung (Cross-Level-Interaktion) zwischen Alter und Zeit. Inhaltlich bedeutet diese Wechselwirkung, dass der Effekt der Zeit im Lockdown auf das Wohlbefinden sich mit dem Alter verändern kann.
- Gleichung auf Ebene 1: \(Y_{ij}=\beta_{0j}+\beta_{1j}X_{ij}+r_{ij}\)
- Interzept auf Ebene 2: \(\beta_{0j}=\gamma_{00}+\gamma_{01}Z_j+u_{0j}\)
- Slope auf Ebene 2: \(\beta_{1j}=\gamma_{10}+\gamma_{11}Z_j+u_{1j}\)
- Gesamtmodell: \(Y_{ij}=\gamma_{00} + \gamma_{10}Z_j + \gamma_{01}X_{ij} + \gamma_{11}Z_jX_{ij} + u_{0j}X_{ij} + u_{0j} + r_{ij}\)
- Als Formel für
lmer:Y ~ 1 + X + (1 + X | ID)
Für dieses Modell zentrieren wie auch die Zeit-Variable. Deren Nullpunkt ist zwar ohne Zentrierung anschaulicher, aber für die Interpretation des Moderatoreffekts sollten die beteiligten Prädiktoren zentriert sein. In den festen Effekten sehen wir, dass
- der signifikante Alterseffekt bestehen bleibt,
- der negative Zeiteffekt bestehen bleibt und
- die Wechselwirkung ebenfalls nicht signifikant ist.
Der Effekt der Zeit im Lockdown hängt demzufolge nicht vom Alter der Betroffenen ab. Trotzdem zur Interpretation: Ein negativer Moderatoreffekt würde bedeuten, dass der negative Effekt des Lockdowns mit zunehmendem Alter noch stärker negativ wird.
mean(lockdown$Time)## [1] 5.355251lockdown$Time <- scale(lockdown$Time, scale = FALSE)
PWB.Age.Time <- lmer(PWB ~ 1 + Age + Time + Age:Time + (1 + Time | ID), data = lockdown)## Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
## Model failed to converge with max|grad| = 0.00644566 (tol = 0.002, component 1)summary(PWB.Age.Time)## Linear mixed model fit by REML ['lmerMod']
## Formula: PWB ~ 1 + Age + Time + Age:Time + (1 + Time | ID)
## Data: lockdown
##
## REML criterion at convergence: 4043.3
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -4.7743 -0.4747 0.0452 0.4968 3.8921
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## ID (Intercept) 0.784388 0.88566
## Time 0.003936 0.06274 0.12
## Residual 0.168728 0.41076
## Number of obs: 2188, groups: ID, 485
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) -0.0067297 0.0414505 -0.162
## Age 0.0130309 0.0030103 4.329
## Time -0.0361607 0.0046951 -7.702
## Age:Time -0.0002951 0.0003412 -0.865
##
## Correlation of Fixed Effects:
## (Intr) Age Time
## Age 0.042
## Time 0.098 -0.011
## Age:Time -0.012 0.096 -0.014
## optimizer (nloptwrap) convergence code: 0 (OK)
## Model failed to converge with max|grad| = 0.00644566 (tol = 0.002, component 1)Da wir wieder eine Warnung über Konvergenzprobleme bekommen, ändern wir wieder den Maximierungsalgorithmus:
PWB.Age.Time <- lmer(PWB ~ 1 + Age + Time + Age:Time + (1 + Time | ID), data = lockdown,
control = lmerControl(optimizer ="Nelder_Mead"))
summary(PWB.Age.Time)## Linear mixed model fit by REML ['lmerMod']
## Formula: PWB ~ 1 + Age + Time + Age:Time + (1 + Time | ID)
## Data: lockdown
## Control: lmerControl(optimizer = "Nelder_Mead")
##
## REML criterion at convergence: 4043.3
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -4.7741 -0.4747 0.0451 0.4968 3.8920
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## ID (Intercept) 0.784318 0.88562
## Time 0.003934 0.06272 0.12
## Residual 0.168739 0.41078
## Number of obs: 2188, groups: ID, 485
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) -0.0067297 0.0414488 -0.162
## Age 0.0130309 0.0030101 4.329
## Time -0.0361606 0.0046948 -7.702
## Age:Time -0.0002951 0.0003412 -0.865
##
## Correlation of Fixed Effects:
## (Intr) Age Time
## Age 0.042
## Time 0.098 -0.011
## Age:Time -0.012 0.096 -0.014Die Warnung verschwindet und die Ergebnisse der beiden Summaries stimmen wie oben auch sehr stark überein!
Zur grafischen Veranschaulichung der Wechselwirkung kann wie bei der moderierten Regression im linearen Modell auch hier die Funktion interact_plot verwendet werden. Die Lage der Linien zeigt gut den positiven Haupteffekt des Alters auf das Wohlbefinden. Zugleich veranschaulichen die fast parallelen Geraden das Nicht-Vorliegen einer Wechselwirkung.
interact_plot(model = PWB.Age.Time, pred = Time, modx = Age)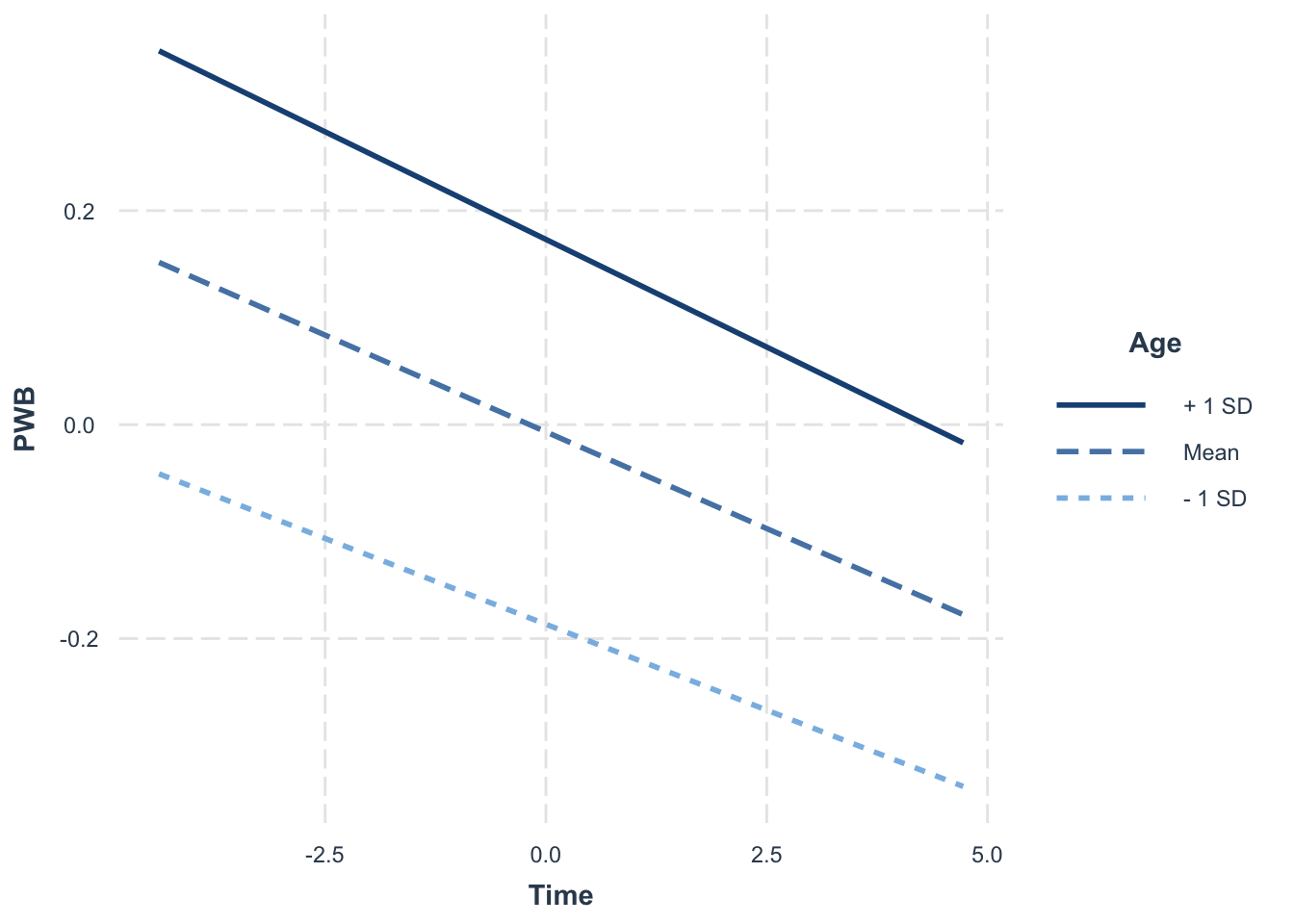
R-Skript
Den gesamten R-Code, der in dieser Sitzung genutzt wird, können Sie hier herunterladen.
