Korrelation

Balkendiagramme

Grafisch kann eine solche Kreuztabelle durch gruppierte Balkendiagramme dargestellt werden. Das Argument beside sorgt für die Anordnung der Balken (bei TRUE nebeneinander, bei FALSE übereinander). Das Argument legend nimmt einen Vektor für die Beschriftung entgegen. Die Zeilen des Datensatzes bilden dabei stets eigene Balken, während die Spalten die Gruppierungsvariable bilden. Deshalb müssen als Legende die Namen der Reihen rownames() unserer Tabelle tab ausgewählt werden.

barplot (tab,
         beside = TRUE,
         col = c('mintcream','olivedrab','peachpuff','steelblue','maroon'),
         legend = rownames(tab))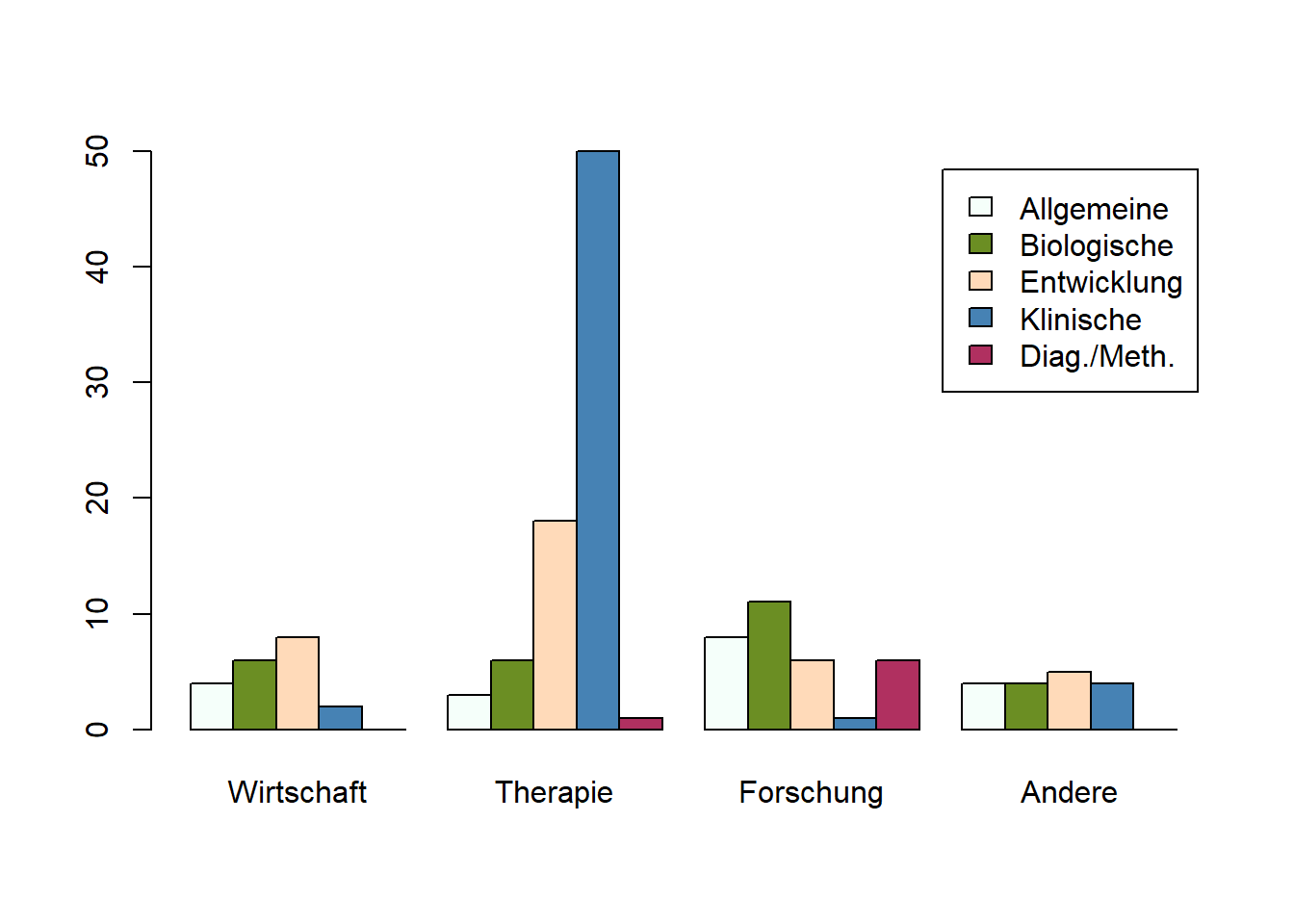

Varianz, Kovarianz und Korrelation

In der Vorlesungen haben Sie gelernt, dass es für Kovarianzen und Varianzen empirische und geschätzte Werte gibt. R berechnet standardmäßig für die Varianz und Kovarianz die Populationsschätzer, verwendet also folgende Formeln für Varianz

\[\hat{\sigma}^2_{X} = \frac{\sum_{m=1}^n (y_m - \bar{y})^2}{n-1}\]

und Kovarianz.

\[\hat{\sigma}_{XY} = \frac{\sum_{m=1}^n (x_m - \bar{x}) \cdot (y_m - \bar{y})}{n-1}\]

Die Funktionen für die Varianz ist dabei var(). Im Folgenden wird diese für die Variablen vertr (Verträglichkeit) und gewis (Gewissenhaftigkeit) aus dem Datensatz bestimmt. Als Argumente müssen jeweils die Variablennamen verwendet werden. Wie bereits in vergangenen Sitzungen gesehen, führen fehlende Werte zu der Ausgabe NA. Um dies vorzubeugen, wird im univariaten Fall na.rm = TRUE zum Ausschluss verwendet.

var(fb22$vertr, na.rm = TRUE)            #Varianz Verträglichkeit

## [1] 0.3337015

var(fb22$gewis, na.rm = TRUE)            #Varianz Gewissenhaftigkeit

## [1] 0.4389081

Die Funktion cov() wird für die Kovarianz verwendet und benötigt als Argumente die Variablen.

cov(fb22$vertr, fb22$gewis)              #Kovarianz Verträglichkeit und Gewissenhaftigkeit

## [1] 0.07689475

Da Kovarianzen unstandardisierte Kennzahlen sind, können wir Kovarianzen nicht pauschal nach ihrer Höhe beurteilen. Die Höhe hängt beispielsweise von der Antwortskala ab.

Natürlich können auch bei der Kovarianzberechnung fehlende Werte zu einem Problem werden. Zur Bewältigung des Problems gibt es das Argument use. Bei Zusammenhangsmaßen gibt es in R mehrere Möglichkeiten für den Umgang mit fehlenden Werten, die sich nur unterscheiden, wenn mehr als zwei Variablen korreliert werden:

• Paarweiser Fallausschluss: Personen, die auf (mindestens) einer von zwei Variablen NA haben, werden von der Berechnung ausgeschlossen.
• Listenweiser Fallausschluss: Personen, die auf (mindestens) einer von allen Variablen NA haben, werden von der Berechnung ausgeschlossen.
• na.or.complete: Zeilen, die einen fehlenden Wert (NA) enthalten, werden bei den Berechnungen ignoriert. Das entspricht der Angabe von na.rm = TRUE bei der Betrachtung von lediglich zwei Variablen.

Am besten lässt sich der Unterschied in einer Kovarianzmatrix veranschaulichen. Hier werden alle Varianzen und Kovarianzen von einer Menge an Variablen berechnet und in einer Tabelle darstellt. Dafür muss ein Datensatz erstellt werden, der nur die interessierenden Variablen enthält. Zu unseren beiden Variablen nehmen wir als drittes noch die Lebenszufriedenheit (lz) auf.

drei <- fb22[, c('vertr','gewis','lz')]         #Datensatzreduktion
cov(drei)                                       #Kovarianzmatrix   

##            vertr      gewis lz
## vertr 0.33370154 0.07689475 NA
## gewis 0.07689475 0.43890813 NA
## lz            NA         NA NA

Da die fehlenden Werte nicht entfernt wurden, gibt R NA aus. Nun folgt die Gegenüberstellung der beiden betrachteten Möglichkeiten zum Ausschluss.

Zu Illustrationszwecken setzen wir nun den Wert in Verträglichkeit in Zeilen 50 und 72 auf fehlend:

fb22$vertr_neu <- fb22$vertr                     # erstelle neue Variable vertr_neu
fb22[c(50,72), 'vertr_neu'] <- NA               # setze vertr_neu in den Zeilen 50 und 72 auf fehlend
drei_neu <- fb22[, c('vertr_neu','gewis','lz')]         #Datensatzreduktion
cov(drei_neu)                                       #Kovarianzmatrix   

##           vertr_neu     gewis lz
## vertr_neu        NA        NA NA
## gewis            NA 0.4389081 NA
## lz               NA        NA NA

Vergleichen wir nun dieses Ergebnis mit dem Ergebnis nach paarweisem Fallausschluss und listenweisem Fallausschluss:

cov(drei_neu, use = 'pairwise')             #Paarweiser Fallausschluss

##            vertr_neu      gewis         lz
## vertr_neu 0.33465519 0.07675721 0.08361123
## gewis     0.07675721 0.43890813 0.21902866
## lz        0.08361123 0.21902866 1.15304916

cov(drei_neu, use = 'complete')             #Listenweiser Fallausschluss

##            vertr_neu      gewis         lz
## vertr_neu 0.33083892 0.06784667 0.08361123
## gewis     0.06784667 0.43618035 0.22378090
## lz        0.08361123 0.22378090 1.15291831

Wie wir sehen, unterscheiden sich die Werte voneinander, da beim listenweisen Fallausschluss noch mehr Personen von Beginn an von der Berechnung ausgeschlossen werden (es werden hier auch die Personen in Zeilen 50 und 72 für die Berechnung der Kovarianz von Gewissenhaftigkeit und Lebenszufriedenheit ausgeschlossen - obwohl diese beiden Personen auf diesen beiden Variablen eigentlich gültige Werte besitzen). Anmerkung: Die Kovarianz einer Variablen mit sich selbst (zu finden in der Hauptdiagonalen) entspricht ihrer Varianz.

Der Zusammenhang zwischen zwei Variablen kann in einem Scatterplot bzw. Streupunktdiagramm dargestellt werden. Dafür kann man die plot() Funktion nutzen. Als Argumente können dabei x für die Variable auf der x-Achse, y für die Variable auf der y-Achse, xlim, ylim für eventuelle Begrenzungen der Achsen und pch für die Punktart angegeben werden.

plot(x = fb22$vertr, y = fb22$gewis, xlim = c(1,5) , ylim = c(1,5))

Wie in der Vorlesung besprochen, sind für verschiedene Skalenniveaus verschiedene Zusammenhangsmaße verfügbar, die im Gegensatz zur Kovarianz auch eine Vergleichbarkeit zwischen zwei Zusammenhangswerten sicherstellen. Für zwei metrisch skalierte Variablen gibt es dabei die Produkt-Moment-Korrelation. In der Funktion cor() werden dabei die Argumente x und y für die beiden betrachteten Variablen benötigt. use beschreibt weiterhin den Umgang mit fehlenden Werten.

cor(x = fb22$vertr, y = fb22$gewis, use = 'pairwise')

## [1] 0.2009235

Bei einer positiven Korrelation gilt „je mehr Variable x… desto mehr Variable y” bzw. umgekehrt, bei einer negativen Korrelation „je mehr Variable x… desto weniger Variable y” bzw. umgekehrt. Korrelationen sind immer ungerichtet, das heißt, sie enthalten keine Information darüber, welche Variable eine andere vorhersagt - beide Variablen sind gleichberechtigt. Korrelationen (und Regressionen, die wir später in einem Tutorial kennen lernen werden) liefern keine Hinweise auf Kausalitäten. Sie sagen beide etwas über den (linearen) Zusammenhang zweier Variablen aus.

In R können wir uns auch eine Korrelationsmatrix ausgeben lassen. Dies geschieht äquivalent zu der Kovarianzmatrix mit dem Datensatz als Argument in der cor() Funktion. In der Diagonale stehen die Korrelationen der Variable mit sich selbst - also 1 - und in den restlichen Feldern die Korrelationen der Variablen untereinander.

cor(drei, use = 'pairwise')

##           vertr     gewis        lz
## vertr 1.0000000 0.2009235 0.1384518
## gewis 0.2009235 1.0000000 0.3104911
## lz    0.1384518 0.3104911 1.0000000

Die Stärke des korrelativen Zusammenhangs wird mit dem Korrelationskoeffizienten ausgedrückt, der zwischen -1 und +1 liegt. Die default-Einstellung bei cor()ist die Produkt-Moment-Korrelation, also die Pearson-Korrelation.

cor(fb22$vertr, fb22$gewis, use = "pairwise", method = "pearson")

## [1] 0.2009235

Achtung! Die inferenzstatistische Testung der Pearson-Korrelation hat gewisse Voraussetzungen, die vor der Durchführung überprüft werden sollten!

Voraussetzungen Pearson-Korrelation:

1. Skalenniveau: intervallskalierte Daten \(\rightarrow\) ok (Ratingskalen werden meist als intervallskaliert aufgefasst, auch wenn das nicht 100% korrekt ist)
   
2. Linearität: Zusammenhang muss linear sein \(\rightarrow\) grafische Überprüfung (siehe Scatterplot)
   
3. Normalverteilung: Variablen müssen normalverteilt sein \(\rightarrow\) QQ-Plot, Histogramm oder Shapiro-Wilk-Test

zu 3. Normalverteilung

\(\rightarrow\) QQ-Plot, Histogramm & Shapiro-Wilk-Test

#QQ
qqnorm(fb22$vertr)
qqline(fb22$vertr)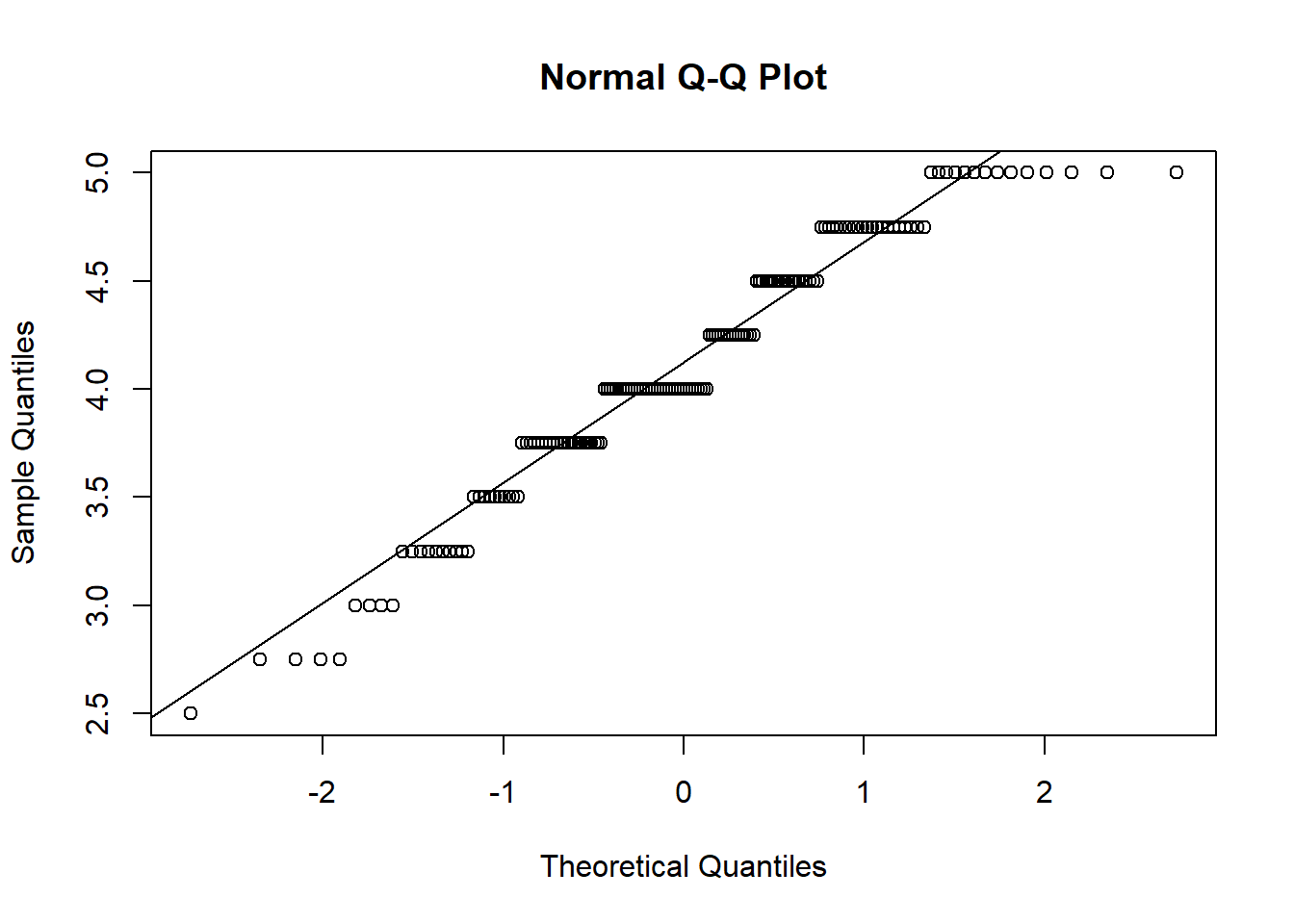

qqnorm(fb22$gewis)
qqline(fb22$gewis)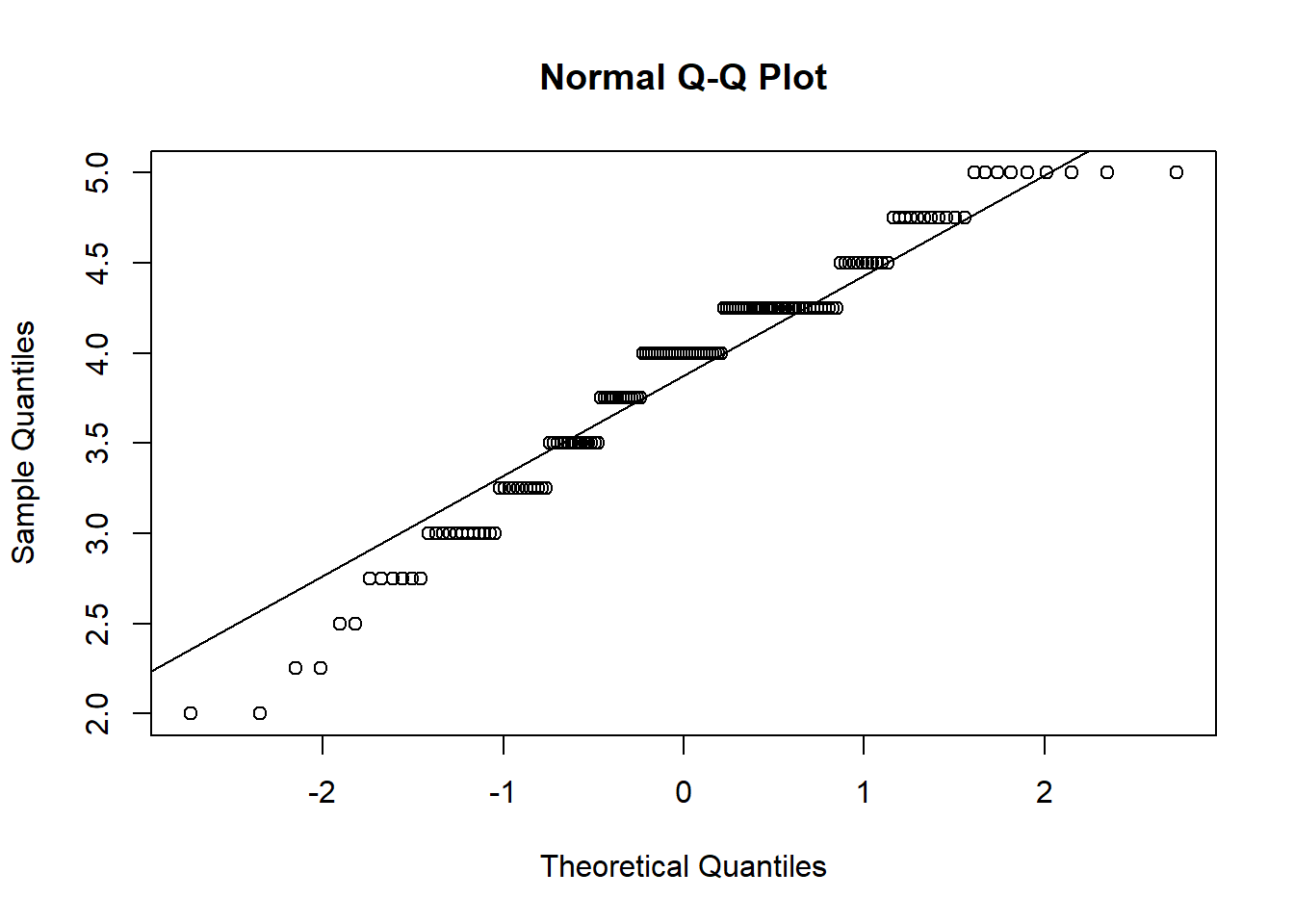

#Histogramm

hist(fb22$vertr, prob = T, ylim = c(0, 1))
curve(dnorm(x, mean = mean(fb22$vertr, na.rm = T), sd = sd(fb22$vertr, na.rm = T)), col = "blue", add = T)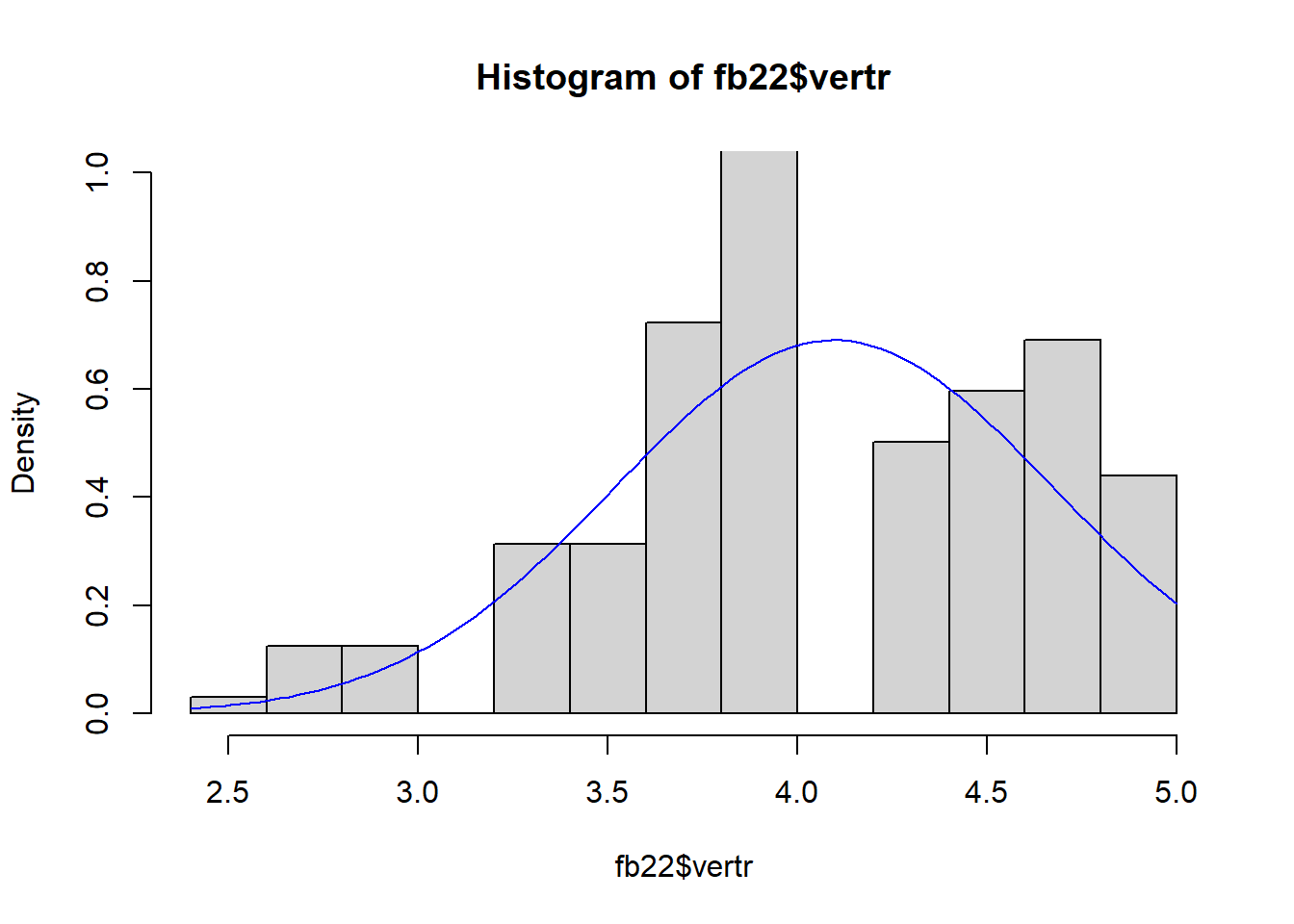  

hist(fb22$gewis, prob = T, ylim = c(0,1))
curve(dnorm(x, mean = mean(fb22$gewis, na.rm = T), sd = sd(fb22$gewis, na.rm = T)), col = "blue", add = T)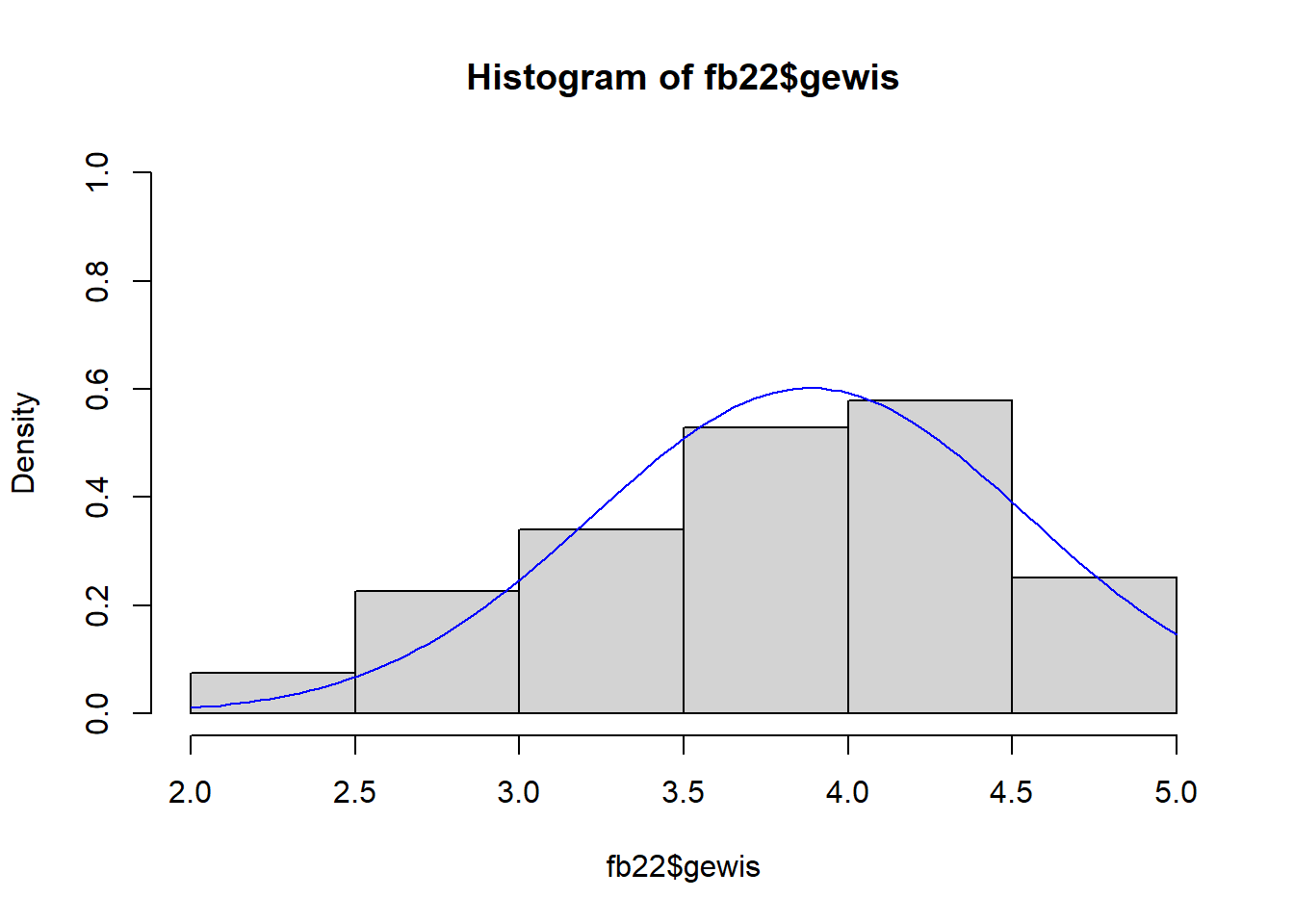

#Shapiro
shapiro.test(fb22$vertr)

## 
## 	Shapiro-Wilk normality test
## 
## data:  fb22$vertr
## W = 0.95611, p-value = 6.624e-05

shapiro.test(fb22$gewis)

## 
## 	Shapiro-Wilk normality test
## 
## data:  fb22$gewis
## W = 0.95665, p-value = 7.423e-05

\(p < \alpha\) \(\rightarrow\) H1: Normalverteilung kann nicht angenommen werden. Somit ist diese Voraussetzung verletzt. Eine Möglichkeit damit umzugehen, ist die Rangkorrelation nach Spearman. Diese ist nicht an die Voraussetzung der Normalverteilung gebunden. Das Verfahren kann über method = "spearman" angewendet werden.

Rangkorrelation in R

r1 <- cor(fb22$vertr,fb22$gewis,
          method = "spearman",     #Pearson ist default
          use = "complete") 

r1

## [1] 0.2477728

Interpretation des deskriptiven Zusammenhangs:
Es handelt sich um eine positive Korrelation von r = 0.25. Der Effekt ist nach Cohens (1988) Konvention als schwach bis mittelstark zu bewerten. Je höher die Ausprägung in Verträglichkeit, desto höher ist die Ausprägung in der Gewissenhaftigkeit und anders herum.

Cohens (1988) Konvention zur Interpretation von \(|r|\):

• ~ .10: schwacher Effekt
  
• ~ .30: mittlerer Effekt
  
• ~ .50: starker Effekt

Als weitere Variante der Rangkorrelation gibt es noch Kendalls \(\tau\). Diese kann man mit method = "kendall" angesprochen werden.

cor(fb22$vertr, fb22$gewis, use = 'complete', method = 'kendall')

## [1] 0.1882259

Die Interpretation erfolgt wie bei Spearman’s Rangkorrelation.

Signifikanztestung des Korrelationskoeffizienten: Nachdem der Korrelationskoeffizient berechnet wurde, kann dieser noch auf Signifikanz geprüft werden. Dazu verwenden wir die cor.test()-Funktion.

• H0: \(\rho = 0\) \(\rightarrow\) es gibt keinen Zusammenhang zwischen Verträglichkeit und Gewissenhaftigkeit
• H1: \(\rho \neq 0\) \(\rightarrow\) es gibt einen Zusammenhang zwischen Verträglichkeit und Gewissenhaftigkeit

cor <- cor.test(fb22$vertr, fb22$gewis, 
         alternative = "two.sided", 
         method = "spearman",      #Da Voraussetzungen für Pearson verletzt
         use = "complete")

## Warning in cor.test.default(fb22$vertr, fb22$gewis, alternative = "two.sided", :
## Kann exakten p-Wert bei Bindungen nicht berechnen

cor$p.value      #Gibt den p-Wert aus

## [1] 0.001638895

Anmerkung: Bei der Rangkorrelation kann der exakte p-Wert nicht berechnet werden, da gebundene Ränge vorliegen. Das Ergebnis ist allerdings sehr eindeutig: \(p > \alpha\) \(\rightarrow\) H1. Die Korrelation ist mit einer Irrtumswahrscheinlichkeit von 5% signifikant von 0 verschieden. Daraus würde sich die folgende Interpretation ergeben:

Ergebnisinterpretation: Es wurde untersucht, ob Verträglichkeit und Gewissenhaftigkeit miteinander zusammenhängen. Der spearman-Korrelationskoeffizient beträgt 0.25 und ist statistisch signifikant (p = 0.002). Folglich wird die Nullhypothese hier verworfen: Verträglichkeit und Gewissenhaftigkeit weisen einen signifikanten Zusammenhang auf.

Modifikation Wir haben in der Funktion cor.test() als Argument method = "spearman" eingegeben, da die Voraussetzungen für die Pearson-Korrelation nicht erfüllt waren. Wenn dies der Fall gewesen wäre, müsste man stattdessen method = "pearson" angeben:

cor.test(fb22$vertr, fb22$gewis, 
         alternative = "two.sided", 
         method = "pearson",       
         use = "complete")

## 
## 	Pearson's product-moment correlation
## 
## data:  fb22$vertr and fb22$gewis
## t = 2.57, df = 157, p-value = 0.0111
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.04673796 0.34575779
## sample estimates:
##       cor 
## 0.2009235