Logistische Regression
Generalisiertes lineares Modell: dichotome abhängige Variablen
Einleitung
In dieser Sitzung wollen wir dichotome abhängige Variablen mit der logistischen Regression (vgl. bspw. Eid, Gollwitzer & Schmitt, 2017, Kapitel 22 und Pituch und Stevens, 2016, Kapitel 11) analysieren. Diese Daten sind dahingehend speziell, dass die abhängige Variable nur zwei Ausprägungen hat, welche in der Regel mit \(0\) und \(1\) kodiert werden. Dies führt zu verschiedenen Problemen in der linearen Regression, die wir gleich betrachten wollen. Wir wollen uns ein reales Datenbeispiel ansehen, in welchem die Wahrscheinlichkeit der Drogenabhängigkeit durch einen Depressionsscore und das Geschlecht vorhergesagt werden soll. Der Datensatz ist öffentlich zugänglich auf dem Open-Science-Framework zu finden.
Daten laden
Wir laden zunächst die Daten. Dies können Sie lokal von Ihrem Rechner machen. Falls Sie den Datensatz lokal einladen wollen, müssen Sie ihn natürlich zunächst von der bereits angegebenen Seite herunterladen. Beachten Sie, dass es sich bei dem Datensatz um einen im Format von SPSS handelt. Um diesen in R einzulesen, kann das Paket haven installiert und die Funktion read_sav genutzt werden. Der Rest des verwendeten Codes entspricht dem Code, den wir auch bei load verwendet haben. Wir weisen den Datensatz aber direkt einem Objekt zu, da er sonst nur in der Konsole angezeigt werden würde.
install.packages("haven")
library(haven)
osf <- read_sav("C:/Users/Musterfrau/Desktop/Raw SubdataSet.sav")Sie können den Datensatz aber auch direkt über die Website in das Environment einladen. Dafür verwenden Sie den folgendenen Befehl:
library(haven)
osf <- read_sav(file = url("https://osf.io/prc92/download"))Nun sollte in R-Studio oben rechts in dem Fenster unter der Rubrik “Data” unser Datensatz mit dem Namen “osf” erscheinen.
.
Übersicht über die Daten
Wir wollen uns einen Überblick über die Daten verschaffen:
names(osf) # Variablennamen im Datensatz## [1] "CASEID" "QUESTID" "GENDER_R" "WHITENH"
## [5] "BLACKNH" "NATAMNH" "PACISL" "ASIAN"
## [9] "MIXED" "HISPANIC" "TOTFAMINCOME" "MJANDCOKE"
## [13] "MDELASTYR" "MARJLTYR" "COCCRKLY" "FEMALE"
## [17] "COCINDEX" "MRJINDEX" "ANYINDEX" "COCDUMMY"
## [21] "MRJDUMMY" "ANYDUMMY" "DEPRESSIONINDEX" "DEPRESSIONINDEX2"
## [25] "Sex" "EverUse_MarCoc" "LY_MDE" "LY_Marijuana"
## [29] "LY_CocaineCrack" "Deplvl_Cocaine" "Deplvl_Marijuana" "Deplvl_Anydrug"
## [33] "CocaineDep" "MarijuanaDep" "AnydrugDeg" "Depression_lvl1"
## [37] "Depression_lvl" "AnydrugDep"dim(osf) # Dimensionen des Datensatzes## [1] 55602 38Es gibt insgesamt 38 Variablen. Viele Variablen sind hier auch doppelt in verschiedener Kodierung enthalten. Wir wollen uns auf 3 Variablen fokussieren. Die Variable ANYDUMMY gibt dabei an, ob eine Person irgendeine Drogenabhängigkeit hat. Diese Fälle sind mit 1 kodiert. Die Variable Gender_R enthält eine Dummykodierung für das Geschlecht (in diesem Fall dichotom aufgeführt), wobei 0 für weiblich und 1 für männlich steht. Die Variablen Depression_lvl enthält eine Likert-Skala, auf der zwischen 0 und 9 die Depressionswerte der Personen abgetragen sind.
Auch in diesem Datensatz gibt es natürlich fehlende Werte. Zur Illustration werden wir Personen entfernen, wenn sie auf einer der relevanten Variable einen fehlenden Wert haben. Beachten Sie, dass dieses Vorgehen in einer normalen Analyse weitreichende Probleme mit sich bringen würde und nur zur Vereinfachung für Lehrzwecke eingesetzt wird.
missings_id <- which(is.na(osf$ANYDUMMY) |
is.na(osf$GENDER_R) |
is.na(osf$Depression_lvl))
length(missings_id)## [1] 18659Durch die Kombination aus which und is.na werden alle Zeilennummern identifiziert, in denen eine der drei Variablen fehlend ist. Der vertikale Strich steht dabei für eine Verknüpfung mit “oder”. Es reicht also ein fehlender Wert auf einer der Variablen, um in dem Objekt missings_id getracked zu werden. Insgesamt sind von unserem Ausschluss 18659 Personen betroffen. Nun müssen wir die Fälle noch ausschließen:
osf <- osf[-missings_id, ]
dim(osf) # nach Fallauschluss## [1] 36943 38Die Menge an Personen hat sich drastische reduziert. Dennoch können wir mit der vorhanden Stichprobe, die Funktionsweise der logistischen Regression gut erläutern. Für diese wollen wir auch noch das Geschlecht als Variable des Typs factor hinterlegen. Dabei steht 0 für weiblich und 1 für männlich.
osf$GENDER_R <- as.factor(osf$GENDER_R)
levels(osf$GENDER_R) <- c("weiblich", "maennlich")Fragestellungen
Für unser Beispiel wollen wir die Drogenabhängigkeit als abhängige Variable benutzen. Dabei wollen wir untersuchen, ob der Depressionswert oder das Geschlecht eine Vorhersage leisten können.
Warum keine lineare Regression?
Um die Drogenabhängigkeit zu modellieren, könnten wir eine Regressionsanalyse heranziehen und die Drogenabhängigkeit (ANYDUMMY) durch bspw. den Depressionswert (Depression_lvl) vorhersagen. Wir nennen unser Modell zur Modellierung der Drogenabhängigkeit reg_model.
reg_model <- lm(ANYDUMMY ~ 1 + Depression_lvl, data = osf)
summary(reg_model)##
## Call:
## lm(formula = ANYDUMMY ~ 1 + Depression_lvl, data = osf)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.09351 -0.02512 -0.02512 -0.02512 0.97488
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.0251208 0.0010294 24.40 <2e-16 ***
## Depression_lvl 0.0075993 0.0003446 22.05 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1809 on 36941 degrees of freedom
## Multiple R-squared: 0.01299, Adjusted R-squared: 0.01297
## F-statistic: 486.3 on 1 and 36941 DF, p-value: < 2.2e-16Laut der einfachen Regressionsanalyse scheint es, dass der Depressionsscore sehr gering mit dem Drogenkonsum zusammenhängt. Lassen Sie sich dabei von der Signifikanz nicht täuschen. Der Zusammenhang würde zwar für die Population angenommen werden, aber das heißt nicht, dass es ein starker Zusammenhang ist. Die erklärte Varianz wäre aber bei einem Prozent.
Betrachten wir nun exemplarisch zwei Voraussetzungen der Regression. Der Code für die Grafiken ist in Appendix B zu finden.
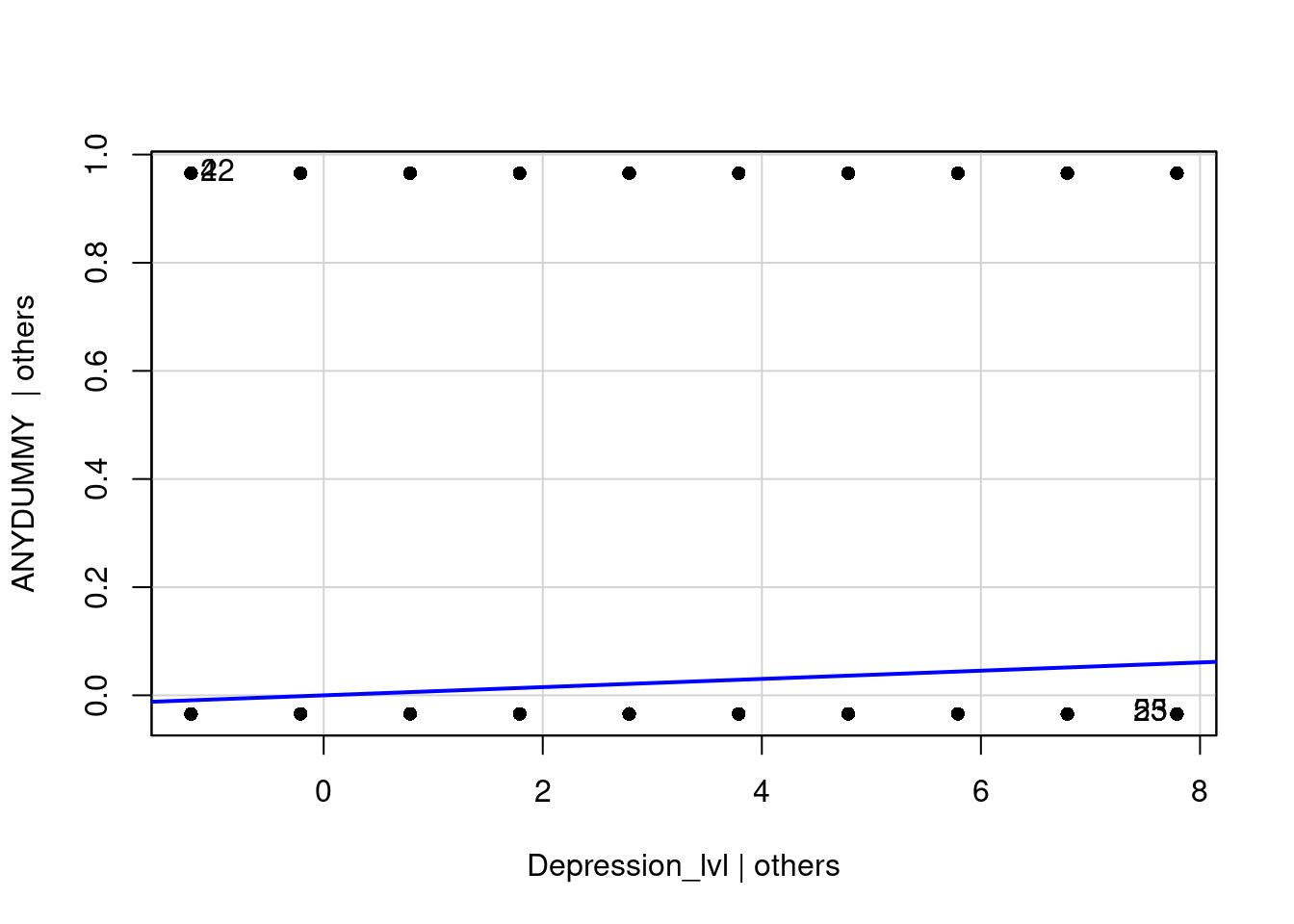
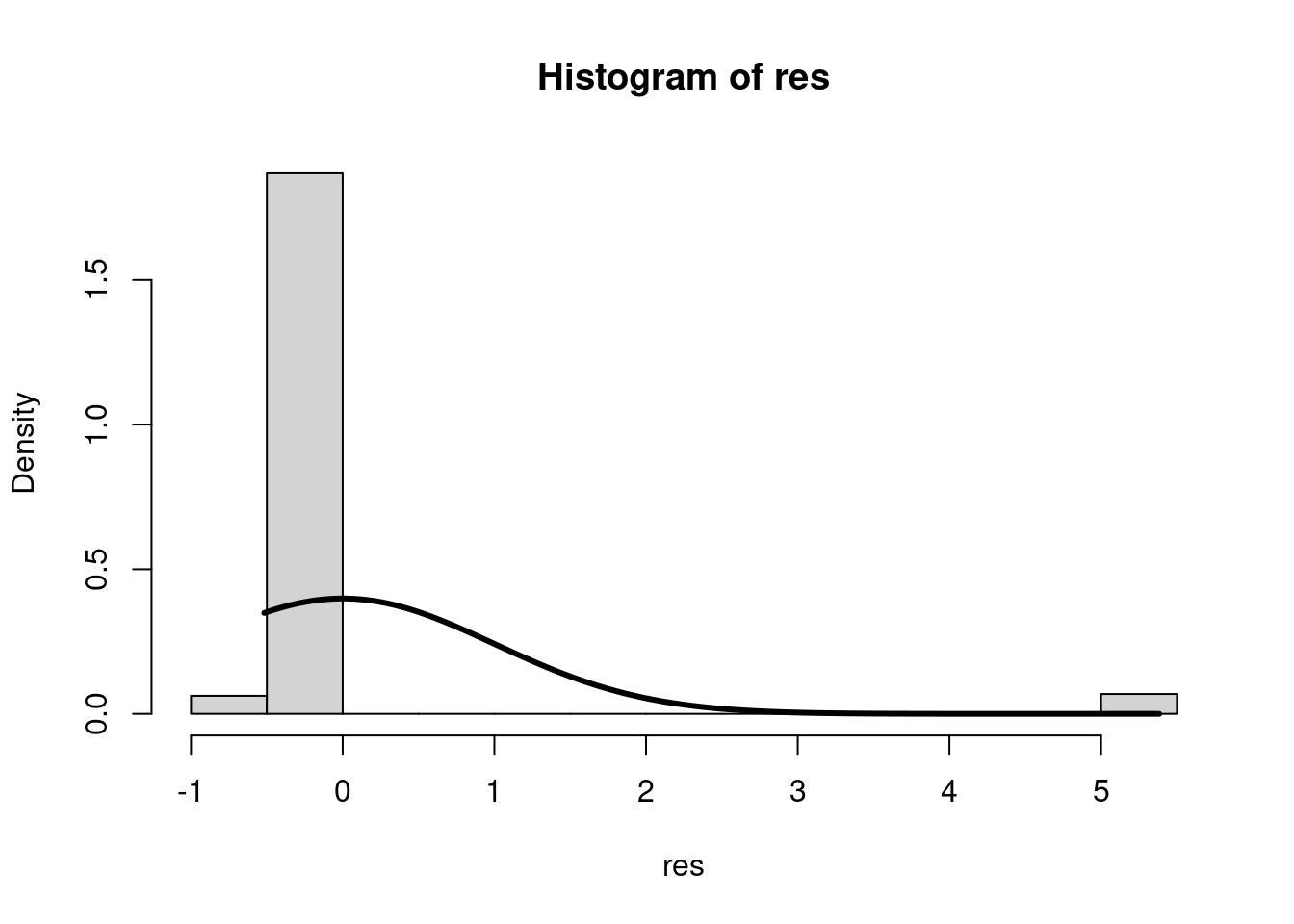
In dieser Analyse sind einige Annahmen der Regressionsanalyse verletzt: Normalverteilung der Residuen, Homoskedastizität und auch Unabhängigkeit der Residuen. Den Verteilungen der Residuen können wir deutlich entnehmen, dass diese systematisch ausfallen (mit steigender Depression steigen die Residuen linear an) und auch die Normalverteilungsannahme ist deutlich verletzt. Eine Regression erscheint nicht sinnvoll. Den Ergebnisse der Signifikanzentscheidungen kann nicht getraut werden. Zusätzlich würde eine Vorhersage der abhängigen Variable viele Werte außerhalb der beiden sinnvollen Ausprägungen 0 und 1 ergeben. Wir müssen uns also irgendwie anders mit den Daten auseinandersetzen! Aus diesem Grund wollen wir die logistische Regression heranziehen.
Im Grunde wird bei der logistischen Regression die Wahrscheinlichkeit des “Erfolgs” (was auch immer der Erfolg ist: erkrankt ja/nein, genesen ja/nein etc.) modelliert. Der Trick dabei ist, dass sich diese Wahrscheinlichkeit auf unterschiedlichen Ausprägungen der Prädiktoren unterschiedlich verhalten kann. Sie wird also durch die Prädiktoren bedingt. Die Funktion in R hierzu heißt glm, was für Generalized Linear Model steht. Um den Wertebereich der AV einzuhalten, wird die Erfolgswahrscheinlichkeit so transformiert, dass sie linear durch die UVs vorhergesagt werden kann, aber die Wahrscheinlichkeit trotzdem zwischen 0 und 1 liegt. Gehen wir bspw. von zwei Prädiktoren \(X_1\) und \(X_2\) aus:
\[\begin{align*} p &= \mathbb{P}(Y = 1 | X_1 = x_1, X_2 = x_2) = \frac{e^{\beta_0 + \beta_1x_1 + \beta_2x_2}}{1 + e^{\beta_0 + \beta_1x_1 + \beta_2x_2}}\\[2ex] odds(p) & = \frac{\mathbb{P}(Y = 1 | X_1 = x_1, X_2 = x_2)}{1-\mathbb{P}(Y = 1 | X_1 = x_1, X_2 = x_2)} = e^{\beta_0 + \beta_1x_1 + \beta_2x_2}\\[2ex] logit(p) & = \ln\left(\frac{\mathbb{P}(Y = 1 | X_1 = x_1, X_2 = x_2)}{1-\mathbb{P}(Y = 1 | X_1 = x_1, X_2 = x_2)}\right) = \beta_0 + \beta_1x_1 + \beta_2x_2 \end{align*}\]
Hier ist \(\ln\) der natürliche Logarithmus zur Basis \(e\) (\(e\) ist die Eulersche Zahl \(\approx 2.718282\)). Der \(logit\) stellt hierbei die Link-Funktion dar, die eine transformierte Version der interessanten Wahrscheinlichkeit, linear durch die Prädiktoren darstellen lässt. Die \(odds\) und \(p\) sind dann nur Retransformationen, die aus der Link-Funktion resultieren. Einige Wiederholungen zu Exponenten- oder Logarithmusregeln können Sie am Anfang der Sitzung zu exponentiellem Wachstum aus dem Bachelor nachlesen.
Generalisiertes Lineares Modell: Logistische Regressionsanalyse
Fragestellung 1: Depression als Prädiktor
Für die erste Hypothese müssen wir den Einfluss des Depressionsscores auf die Wahrscheinlichkeit der Drogenabhängigkeit bestimmen. Dafür wollen wir eine logistische Regressionsanlyse durchführen. In dieser werden die Residuen nicht länger als normalverteilt angenommen, sondern die AV wird als (bedingt) binomialverteilt modelliert. Wir nennen das Modell glm_model, da wir uns im Generalisierten Linearen Model bewegen. Die Funktion glm übernimmt für uns die richtige Transformation, nämlich den Logit als Link-Funktion, indem wir noch das Zusatzargument family = "binomial" festlegen. Die Binomialverteilung ist gerade jene Verteilung, die beschreibt, wie häufig bei \(n\) Versuchen Erfolg eintritt (also genau die richtige Verteilung für unser Modell!).
glm_model <- glm(ANYDUMMY ~ 1 + Depression_lvl, family = "binomial", data = osf)
summary(glm_model)##
## Call:
## glm(formula = ANYDUMMY ~ 1 + Depression_lvl, family = "binomial",
## data = osf)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.4615 -0.2268 -0.2268 -0.2268 2.7106
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -3.648086 0.035940 -101.50 <2e-16 ***
## Depression_lvl 0.162463 0.007836 20.73 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 11043 on 36942 degrees of freedom
## Residual deviance: 10671 on 36941 degrees of freedom
## AIC: 10675
##
## Number of Fisher Scoring iterations: 6Der Output der Summary unterscheidet sich geringfügig von der der normalen Regressionsanalyse:
##
## Call:
## glm(formula = ANYDUMMY ~ 1 + Depression_lvl, family = "binomial",
## data = osf)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.4615 -0.2268 -0.2268 -0.2268 2.7106Er zeigt uns, dass wir kein lm-Objekt sondern ein glm-Objekt vor uns haben. Außerdem werden uns dieses Mal Deviance Residuals angezeigt anstatt normale Residuen. Mit der Bedeutung dieser Residuen werden wir uns im Rahmen des Seminars nicht auseinandersetzen. Das Schätzverfahren ist ein anderes. Es wird nicht das Kleinste-Quadrate-Verfahren angewandt, sondern die Maximum-Likelihood-Schätzmethode (ML).
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -3.648086 0.035940 -101.50 <2e-16 ***
## Depression_lvl 0.162463 0.007836 20.73 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)Der Überblick über die (ML-)Parameterschätzung unterscheidet sich kaum von der normalen Regression. Lediglich die \(t\)-Werte werden durch \(z\)-Werte ersetzt. Die Idee hinter der Signifikanzentscheidung ist aber komplett identisch (außerdem geht die \(t\)-Verteilung für große \(n\) in die \(z\)-(Standardnormal-)Verteilung über). Hier scheint sich ein signifikanter Effekt des Depressionsscores zu zeigen.
## Null deviance: 11043 on 36942 degrees of freedom
## Residual deviance: 10671 on 36941 degrees of freedom
## AIC: 10675
##
## Number of Fisher Scoring iterations: 6In diesem Abschnitt werden die Devianzen angezeigt. Die Gleichung haben wir im theoretischen Teil schon kennen gelernt:
\[D_{model} = -2[ln(l_{model}) - ln(l_{perfekt})]\]
Die Devianz beschreibt die Log-Likelihooddifferenz eines beliebigen Modells zum saturierten Modell (einem Modell, das genau perfekt zu den Daten passt). Diese Logik werden wir bei mehreren Verfahren sehen, die mittels ML-Schätzung bestimmt werden. Bei der logistischen Regression kann ein saturiertes Modell die Daten perfekt vorhersagen, weshalb die likelihood (\(l_{perfekt}\)) 1 und dessen Logarithmus (\(ln(l_{perfekt})\)) dann 0 ist. De facto beschreibt die Devianz für ein spezifisches Modell also die Abweichung zu den wirklichen Daten. Die Null deviance beschreibt hier den Unterschied eines Modells ohne Prädiktoren zu den Daten. Dieses hat hier 36942 Freiheitsgrade. Unter Residual deviance wird nun die Devianz unseres angenommenen Modells verstanden. Da wir in unserem interessierenden Modell einen Prädiktor aufgenommen haben (Depressionsscore), geht ein Freiheitsgrad für diesen Parameter verloren, weswegen die Residualdevianz hier 36941 Freiheitsgrade hat (siehe bspw. Eid, et al., 2017, Kapitel 22.8 und insbesondere Seiten 823-824). Der AIC (Akaike’s Information Criterion) unseres Modells liegt bei 10675. Mit Hilfe dieses AICs können auch nicht geschachtelte Modelle sowie Modelle mit unterschiedlichen Annahmen verglichen werden. Eine Signifikanzentscheidung ist allerdings nicht möglich (siehe bspw. Eid, et al., 2017, Seite 750). Die letzte Zeile gibt an, wie lange der Fisher-Scoring-Algorithmus gebraucht hat, um die Standardfehler zu bestimmen. Dies kann Auskunft über mögliche Konvergenzschwierigkeiten liefern , also Schwierigkeiten des Algorithmus damit, bei einer guten Lösung anzukommen. Hier ist ein Wert von 6 aber sehr niedrig!
Wir haben bereits anhand des Tests des Steigungsparameters gesehen, dass ein signifikanter Einfluss des Depressionsscores auf die Wahrscheinlichkeit der Drogenabhängigkeit für die Population angenommen werden kann. Trotzdem wollen wir uns nochmal damit auseinandersetzen, wie ein gesamtes Modell (mit allen Prädiktoren) gegen das Nullmodell (also ohne jeglichen Prädiktor) getestet werden kann. Natürlich könnte man sich diese Funktion schnell selbst schreiben und den kritischen Wert raus suchen, aber es gibt ein Paket, welches diese Arbeit für uns übernhemen kann. Dafür müssen wir lmtest installieren. Bei der Installation sollte auch die Abhängigkeit zoo mit installiert werden.
install.packages("lmtest")
library(lmtest)Im theoretischen Teil haben wir gelernt, dass für den Modellvergleich der Likelihood-Ratio-Test verwendet wird, in dem die Likelihood des Modells mit Prädiktoren in Verhältnis zu der Likelihood des Modells ohne Prädiktoren gesetzt wird. Ist der Gewinn in der Likelihood durch die Prädiktoren groß genug, resultiert ein signifikantes Ergebnis. Die zugehörige Funktion in R heißt lrtest. Diese braucht als einziges Argument jenes mit Prädiktoren und kann dieses mit dem Modell ohne Prädiktoren vergleichen.
lrtest(glm_model)## Likelihood ratio test
##
## Model 1: ANYDUMMY ~ 1 + Depression_lvl
## Model 2: ANYDUMMY ~ 1
## #Df LogLik Df Chisq Pr(>Chisq)
## 1 2 -5335.4
## 2 1 -5521.6 -1 372.43 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Der Output zeigt uns zunächst nochmal an, welche Modelle verglichen werden. In Model 1 ist die Variable Depression_lvl als Prädiktor enthalten, während bei Model 2 kein Prädiktor vorhanden ist. In der kleinen Tabelle sehen wir dann die Likelihoods der beiden Modelle, ihren Unterschied in Freiheitsgraden und den empirischen \(\chi^2\)-Wert. Dabei wird auch angezeigt, dass der Test signifikant ausfällt - das Modell leistet einen signifikanten Beitrag zur Vorhersage über das Null-Modell hinaus. Beachten Sie, dass die Funktion automatisch das leere Modell als zweites Modell in die Testung aufnimmt. Daraus resultiert, ein negativer Wert in der Spalte der Freiheitsgrade für den Test. Da dieser Wert nur von der Reihenfolge der Modelle in der Funktion abhängig ist, hat das auf unsere Interpretation keinen Einfluss.
Fazit der Analyse
Der Effekt des Despressionsscores ist statistisch signifikant. Wir haben dieses Mal ein sinnvolleres Modell eingesetzt, was bedeutet, dass wir den Ergebnissen eher trauen können. Insgesamt stützen die Daten unsere erste Hypothese. Allerdings ist dieser Effekt sehr klein (dazu später mehr, wenn wir zur Ergebnisinterpretation und zur Einordnung der Koeffizienten kommen). Wenn wir den Wertebereich entlang der x-Achse sehr/unrealistisch groß wählen und den Depressionsscore von -20 bis 60 laufen lassen, so können wir uns die linearen und nichtlinearen Beziehungen zwischen Depressionsscore - Logit, Depressionsscore - Odds und Depressionsscore - Wahrscheinlichkeit ansehen, andernfalls ist der Effekt so klein, dass wir kaum etwas erkennen. glm_model$coefficients[1] + glm_model$coefficients[2]*Depressionswerte ist hierbei die Formel für den Logit, da die Parameterschätzungen einfach die \(\beta\)-Koeffizienten sind, welche linear verknüpft den Logit ergeben.
Depressionswerte <- seq(-20, 60, 0.1)
logit <- glm_model$coefficients[1] + glm_model$coefficients[2]*Depressionswerte
plot(x = Depressionswerte, y = logit, type = "l", col = "blue", lwd = 3)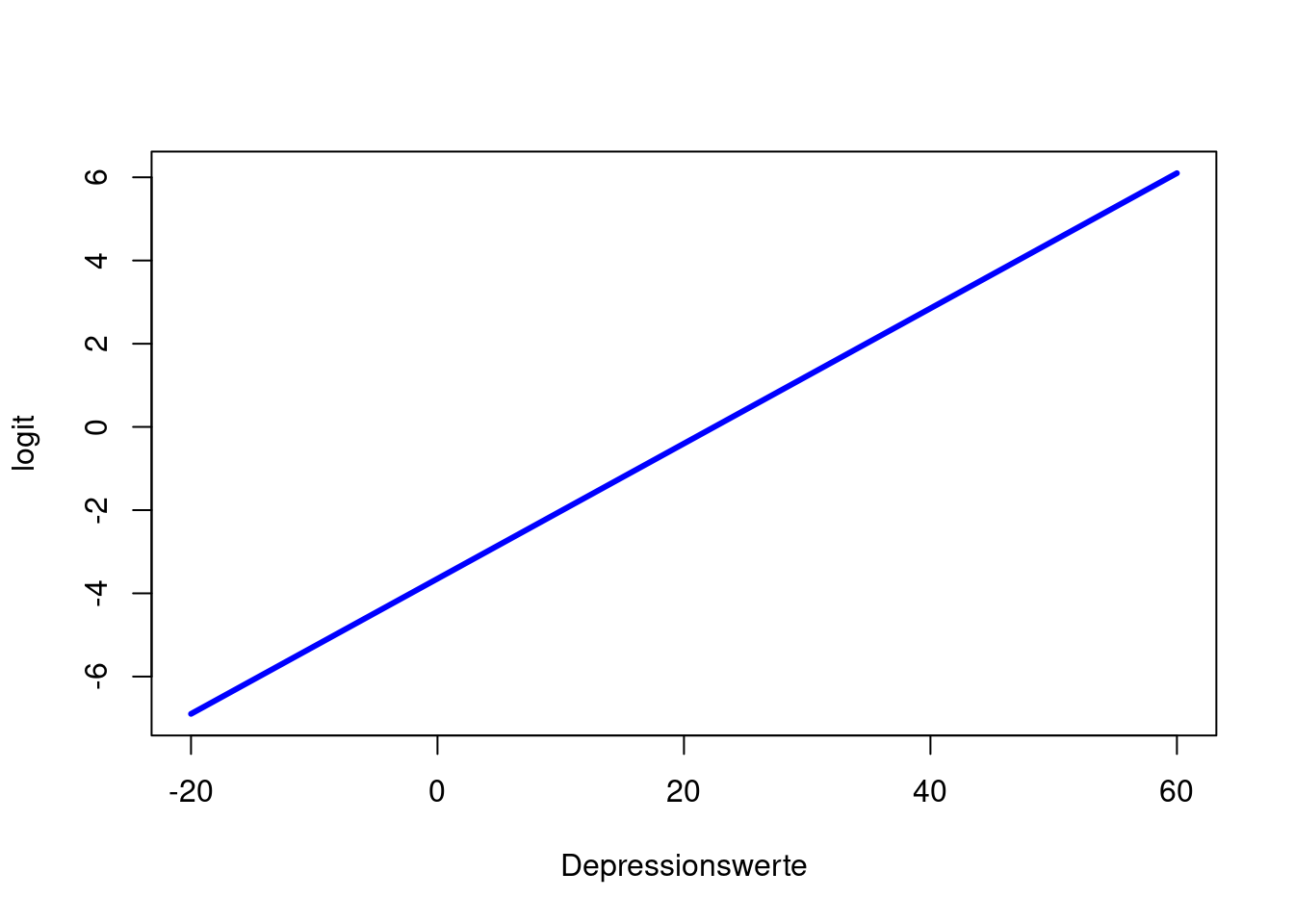
type = "l" fordert eine Linie anstatt von Punkten an, lwd = 3 sagt, dass diese Linie dreimal so dick wie der Default sein soll und col = "blue" sagt, dass die Linie blau sein soll.
Glücklicherweise sind Logit, Odds und Wahrscheinlichkeit sehr leicht ineinander überführbar. Für die Berechnung der Odds muss nur die Funktion exp auf die Logit-Werte angewendet werden, während die Wahrscheinlichkeit die Odds geteilt durch eins plus Odds ist.
odds <- exp(logit)
plot(x = Depressionswerte, y = odds, type = "l", col = "blue", lwd = 3)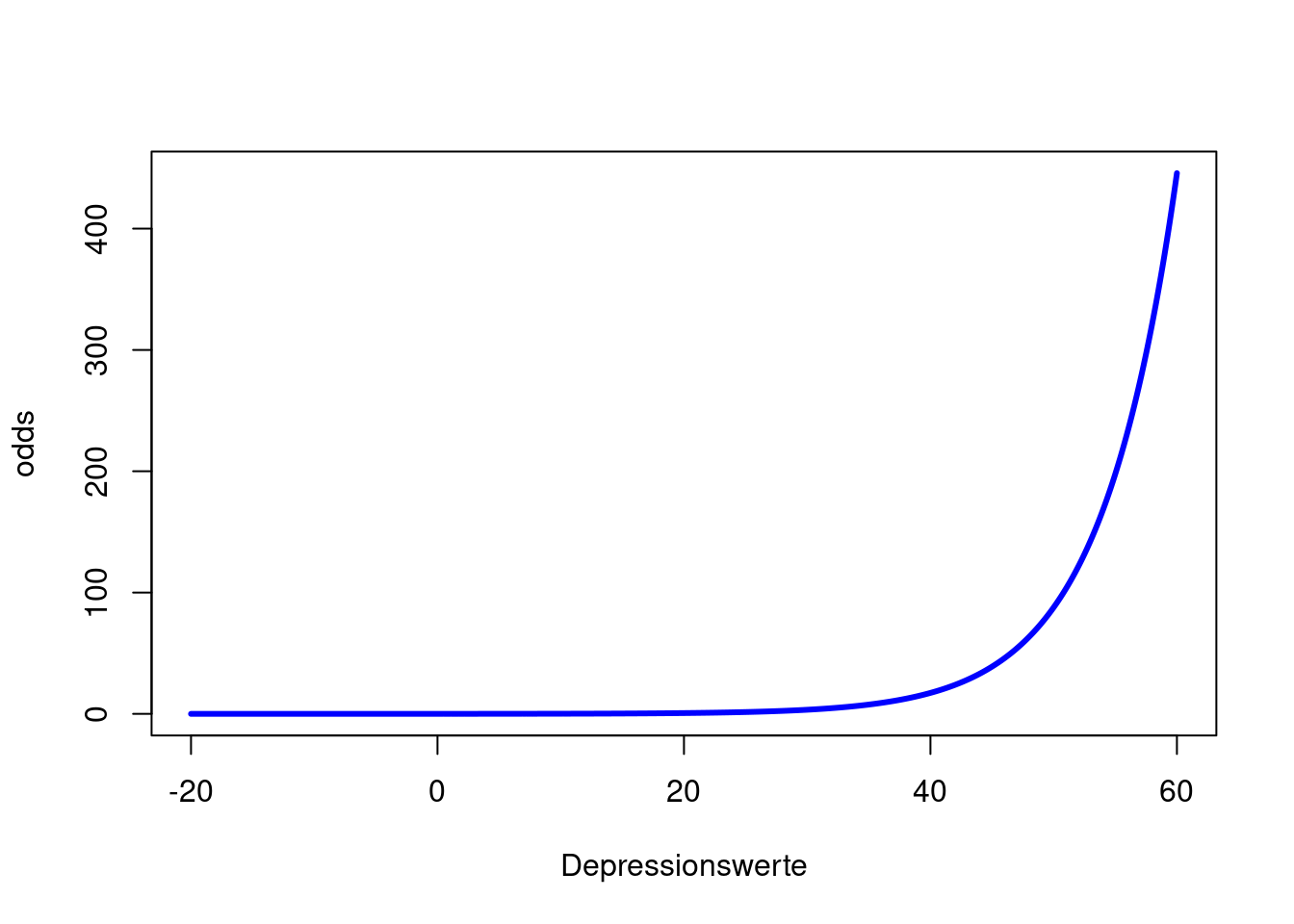
p <- odds/(1 + odds)
plot(x = Depressionswerte, y = p, type = "l", col = "blue", lwd = 3)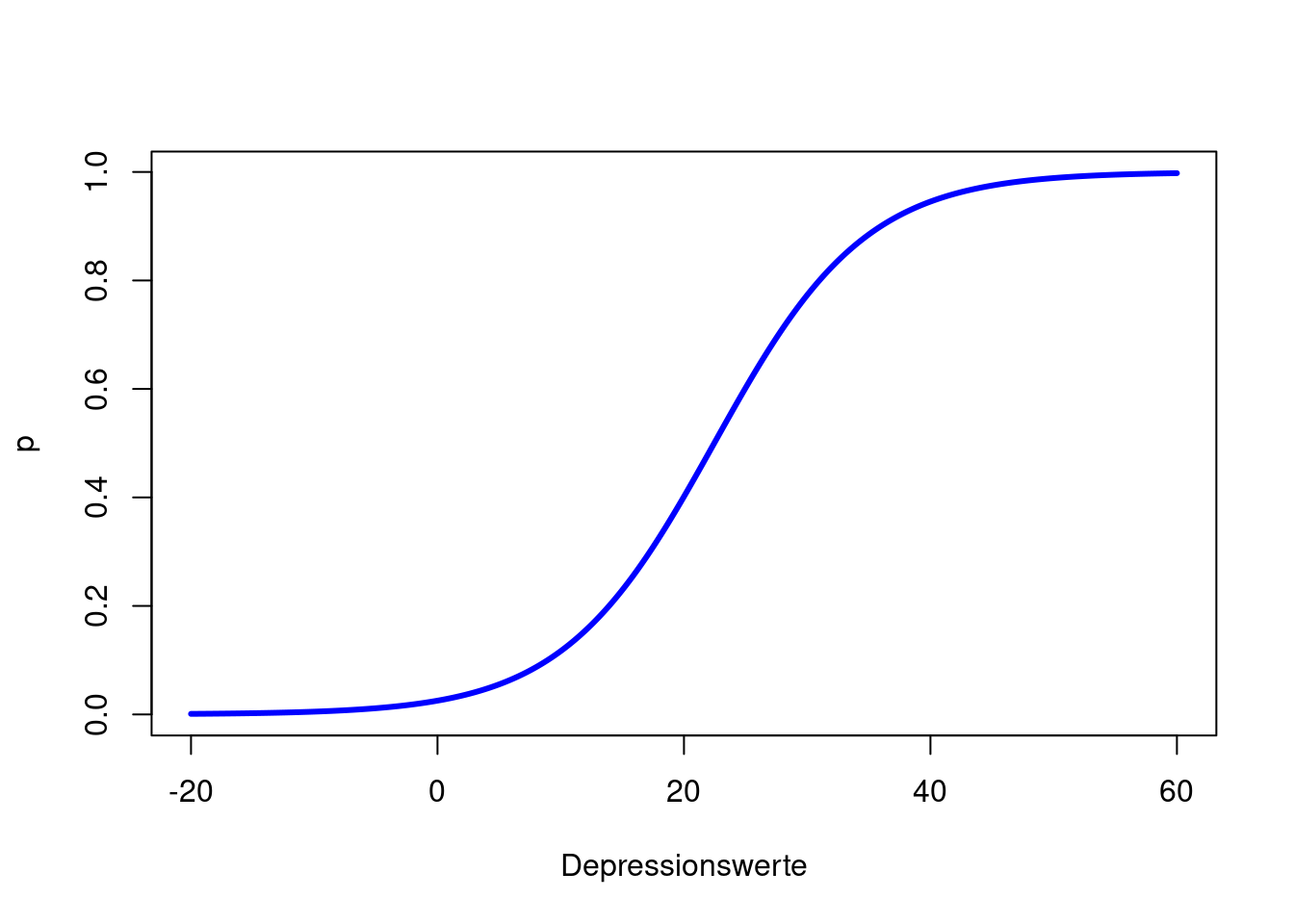
Wir erkennen in allen drei Plots die positive Beziehung zwischen Drogenabhängigkeit und Depressionsscore. Der Logit ist eine lineare Funktion (Wertebereich [\(-\infty\),\(\infty\)]). Somit steigt (bzw. sinkt) der Logit um \(\beta_1\), wenn der Prädiktor (hier Depressionsscore) um eine Einheit erhöht wird. Die Odds sind eine Exponentialfunktion (Wertebereich [0,\(\infty\)]) und bei der Wahrscheinlichkeit handelt es sich um eine sogenannte Ogive (Wertebereich [0,1]). Die Odds steigen (bzw. sinken) um den Faktor \(e^{\beta_1}\) (auch Odds-Ratio genannt), wenn der Prädiktor (hier Depressionsscore) um eine Einheit erhöht wird - die Beziehung zwischen Odds und Prädiktor ist somit multiplikativ! Wir schauen uns die Parameterinterpretation der Odds im nächsten Abschnitt genauer an. Wie sich die Wahrscheinlichkeit verändert, ist nicht pauschal zu sagen. Diese Veränderung hängt von der Ausprägung des Prädiktors ab und lässt sich nicht durch eine einzige Zahl quantifizieren. Wir erkennen aber, dass die Ogive erst nach einem Depressionsscore von Null nach links laufend flacher gegen 0 geht. Im Intervall von 0 bis 9 (also möglichen Depressionsscores) ist die Wahrscheinlichkeit der Drogenabhängigkeit kleiner als 20% und steigend mit dem Depressionsscore. In Appendix A haben Sie die Möglichkeit, spielerisch die Einflüsse der Parameter in der logistischen Regression kennen zu lernen.
Fragestellung 2: Geschlecht als Prädiktor
Nun wollen wir das Geschlecht mit in unser Modell aufnehmen und somit Hypothese 2 untersuchen. Da das Geschlecht hier auch nur 2 Ausprägungen hat, kann dieser Effekt als Vergleich zwischen Gruppen verstanden werden. Diese Dummy-Variable haben wir zu Beginn schon als Faktor festgelegt. Mit der Funktion table erhalten wir einen Überblick über die Kombination an Drogenabhängigkeit und dem Geschlecht.
table(osf$GENDER_R, osf$ANYDUMMY)##
## 0 1
## weiblich 18381 600
## maennlich 17294 668In der Tabelle wird entlang der Spalten die Drogenabhängigkeit vs. das Geschlecht in den Zeilen abgetragen. Dieser Tabelle ist zu entnehmen, dass der relative Anteil an Männerr, die unter einer Abhängigkeit leiden, höher ist als der der Frauen: 668 vs. 17294 für die Männer und 600 vs. 18381 für die Frauen. Auch absolut gesehen leiden mehr Männer unter einer Abhängigkeit. Da die Unterschiede aber recht klein sind, ist ein Geschlechtereffekt erstmal fraglich. Diese 4-Feldertafel könnten wir auch heranziehen, um einen \(\chi^2\)-Unabhängigkeitstest durchzuführen. Wir wollen aber den Effekt des Geschlechts über den Depressionsscore hinaus auf die Wahrscheinlichkeit der Drogenabhängigkeit modellieren:
glm_model2 <- glm(ANYDUMMY ~ 1 + Depression_lvl + GENDER_R, family = "binomial", data = osf)
summary(glm_model2)##
## Call:
## glm(formula = ANYDUMMY ~ 1 + Depression_lvl + GENDER_R, family = "binomial",
## data = osf)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.5225 -0.2460 -0.2460 -0.2040 2.7867
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -3.862029 0.050888 -75.893 < 2e-16 ***
## Depression_lvl 0.173445 0.008049 21.549 < 2e-16 ***
## GENDER_Rmaennlich 0.378801 0.059125 6.407 1.49e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 11043 on 36942 degrees of freedom
## Residual deviance: 10630 on 36940 degrees of freedom
## AIC: 10636
##
## Number of Fisher Scoring iterations: 6Das Besondere an diesem Output ist, dass bei der Variable Geschlecht noch maennlich dahinter steht:
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -3.862029 0.050888 -75.893 < 2e-16 ***
## Depression_lvl 0.173445 0.008049 21.549 < 2e-16 ***
## GENDER_Rmaennlich 0.378801 0.059125 6.407 1.49e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)Dies gibt an, dass hier dummy-kodiert wurde und der Effekt von 1 (maennlich) im Vergleich zur Referenzgruppe (also 0, weiblich) dargestellt ist. Bei der Betrachtung der Signifikanztestung der einzelnen Prädiktoren erhalten wir für beide signifikante Ergebnisse.
Ergebnisinterpretation
Die \(\beta\)-Gewichte zu interpretieren, hat wenig inhaltliche Aussagekraft. Wir könnten bspw. für das Geschlecht lediglich die Aussage treffen, dass (unter Konstanthaltung aller weiteren Prädiktoren im Modell), wenn Männer im Vergleich zu Frauen betrachtet werden, der Logit (der Wahrscheinlichkeit der Drogenabhängigkeit) um 0.379 steigt. Wenn wir allerdings anstatt des Logits die Odds heranziehen, so können wir mit Hilfe des Odds-Ratio doch eine Aussage über die Wahrscheinlichkeit der Drogenabhängigkeit treffen. Dazu müssen wir die \(\beta\)-Gewichte transformieren via \(e^\beta\):
exp(glm_model2$coefficients) # Odds-Ratios## (Intercept) Depression_lvl GENDER_Rmaennlich
## 0.02102529 1.18939523 1.46053194Nun können wir die Ergebnisse (einigermaßen) sinnvoll interpretieren. Das Interzept wird an der Stelle interpretiert, wo alle Prädiktoren den Wert 0 annehmen. Für den Depressionsscore würde das natürlich eine Person ohne Punkte im Fragebogen darstellen. Außerdem ist noch die Variable GENDER_R im Modell. Dies ist eine Dummy-Variable, die den Wert 1 annimmt, wenn das Geschlecht den Wert 1 (im Vergleich zu 0; der Referenzkategorie) annimmt; also wenn wir einen Mann im Vergleich zu einer Frau betrachten. Folglich hat diese Dummy-Variable gerade den Wert 0, wenn eine Frau betrachtet wird. Wir interpretieren das Interzept bzgl. der Odds wie folgt: Eine weibliche Person mit einem Depressionsscore von 0 Person hat Drogenabahängigkeits-Odds von 0.021. Dies bedeutet, dass es für sie 0.021-mal so wahrscheinlich eine Drogenabhängigkeit zu haben als sie nicht zu haben.
Der Effekt der Depression lässt sich wie folgt interpretieren: Steigt der Depressionsscore um 1 an (unter Konstanthaltung aller weiteren Prädiktoren im Modell), so verändern sich die Odds zur Drogenabhängigkeit um den Faktor (multiplikativ) 1.189. Insgesamt steigen die Odds und damit die Wahrscheinlichkeit einer Drogenabhängigkeit mit dem Depressionsscore, denn das Odds-Ratio ist genau dann größer 1, wenn der \(\beta\)-Koeffizient des Logit größer als 0 ist und es sich somit um eine positive/steigende Beziehung handelt!
Beschäftigen wir uns nun mit der Geschlechtervariable: Wird ein Mann im Vergleich zu einem Frau betrachtet, so steigen die Odds für eine Drogenabhängigkeit um den Faktor 1.461. Somit haben (unter Konstanthaltung aller weiteren Prädiktoren im Modell) Männer eine 1.461 mal so hohe Wahrscheinlichkeit für eine Drogenabhängigkeit wie die Frauen. Hier ist extrem wichtig, zu beachten, dass die Odds sich multiplikativ ändern und nicht additiv, wie wir es von der linearen Regression (und im Übrigen auch vom Logit) gewohnt sind.
Grafische Veranschaulichung
Wir können uns dieses Modell auch grafisch ansehen und damit die oben aufgezeigten Effekte verdeutlichen. Den Code können Sie im Appendix B finden. Dieser geht über den Inhalt des Moduls hinaus.
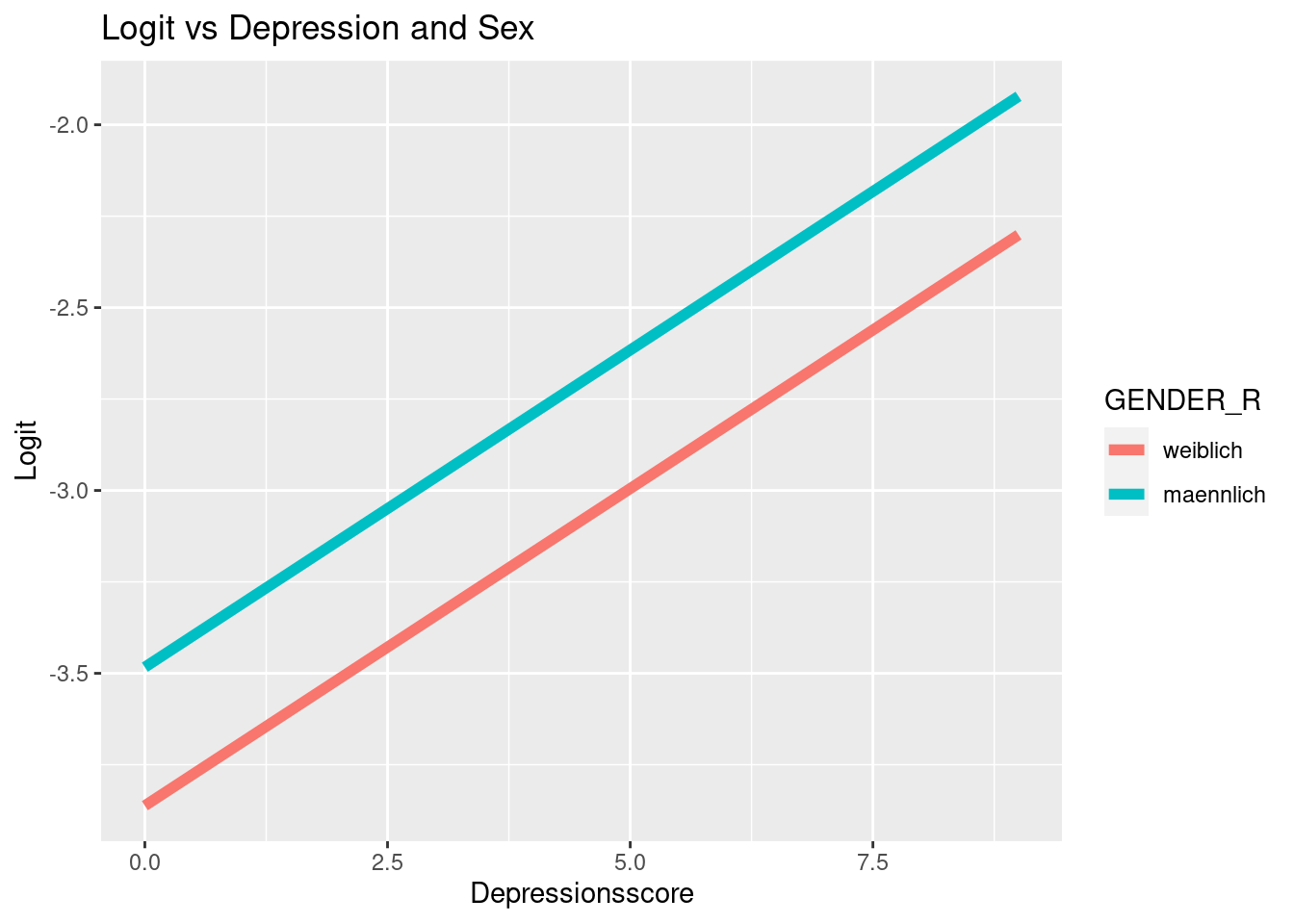
In dem Plot sind die vorhergesagten Logits für alle Personen im Datensatz zu sehen. Dabei ist der Logit natürlich vom Depressionsscore abhängig und das Geschlecht wird als Gruppierungsvariable für zwei verschiedene Geraden verwendet. Die Logik lässt sich auch auf die Odds und die Wahrscheinlichkeit der Drogenabhängigkeit übertragen.
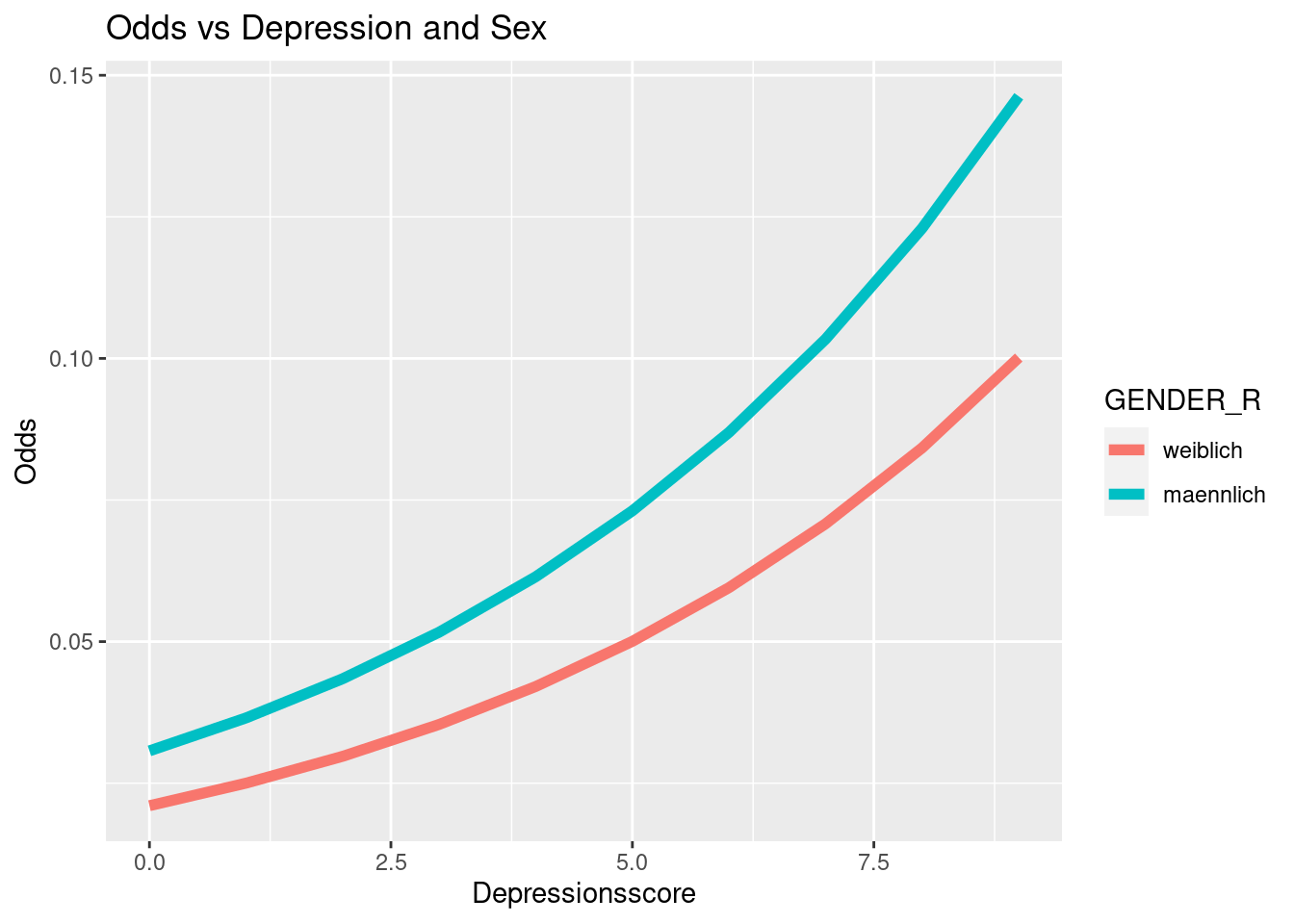
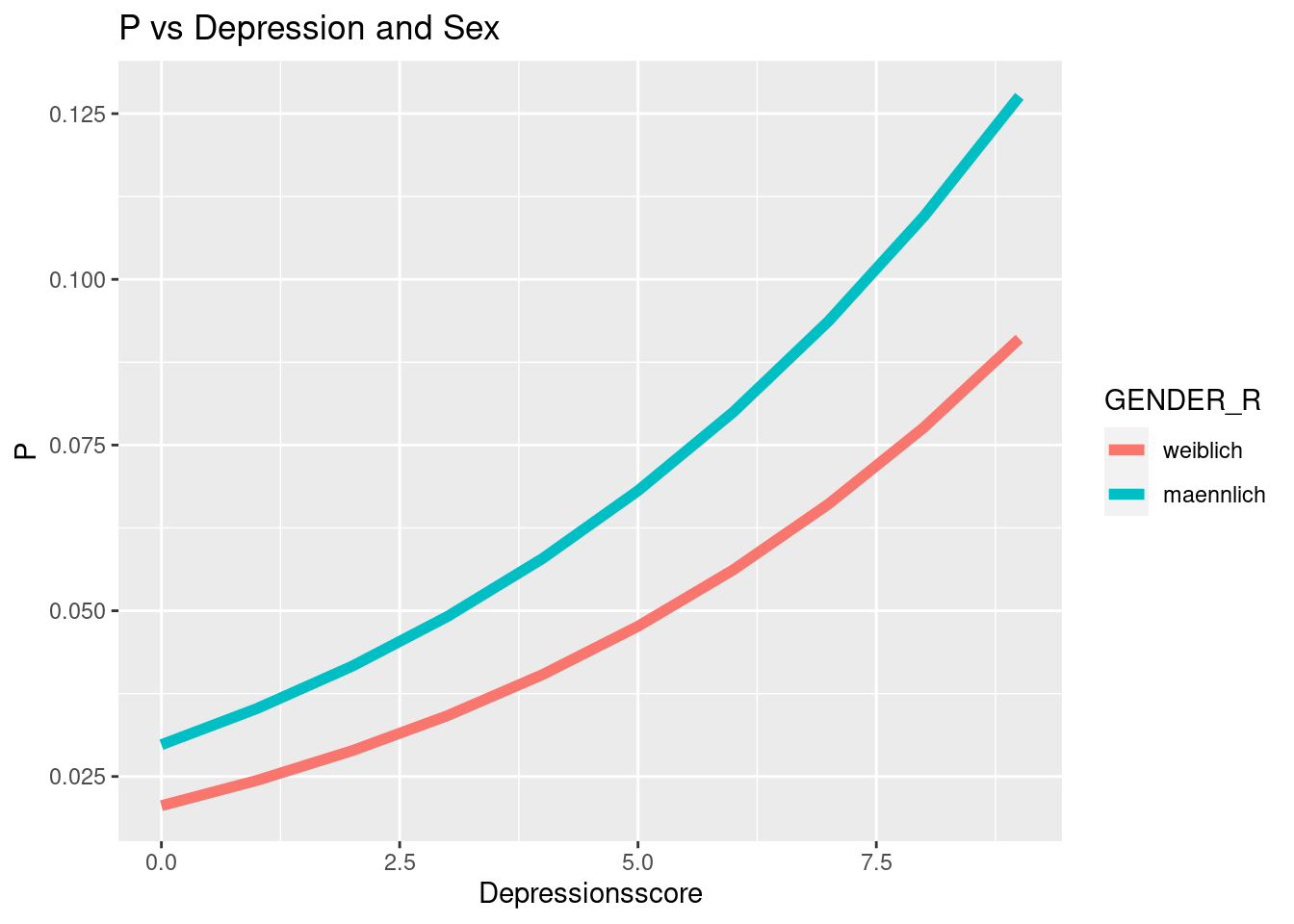
Der Verlauf der Odds und der Wahrscheinlichkeit sieht in diesem Beispiel recht ähnlich aus. Das liegt daran, dass wir nun den realistischen Bereich der Daten betrachten. Wenn wir den Bereich der x-Achse erweitern würden, würden die Odds gegen \(\infty\) gehen, während die Wahrscheinlichkeit die ogive Form zeigen und sich damit der 1 annähern würde.
Wie bereits in der ersten Analyse festgestellt, scheint ein höherer Depressionscore mit einer erhöhten Wahrscheinlichkeit des Drogenkonsums einherzugehen. Auch das Geschlecht scheint einen Einfluss auf diese Wahrscheinlichkeit zu haben.
Modellvergleich
Zum Abschluss wollen wir uns jetzt mittels Modellvergleichen nochmal der Frage widmen, ob das Geschlecht über den Depressionsscore hinaus einen signifikanten Beitrag zur Vorhersage leistet.
Zunächst testen wir das neu erstellte Gesamtmodell gegen das Null-Modell, wie wir es bereits mit dem glm_model getan haben.
lrtest(glm_model2)## Likelihood ratio test
##
## Model 1: ANYDUMMY ~ 1 + Depression_lvl + GENDER_R
## Model 2: ANYDUMMY ~ 1
## #Df LogLik Df Chisq Pr(>Chisq)
## 1 3 -5314.8
## 2 1 -5521.6 -2 413.66 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Wenig überraschend erzeugt auch dieser Test ein signifikantes Ergebnis. Spannender ist jetzt, ob die Hinzunahme des Geschlechts auch einen signifikanten Mehrwert bringt. Wie immer in R gibt es für den Vergleich zwischen zwei Modellen mehrere Wege, wir bleiben aber bei der verwendeten lrtest Funktion. Diese kann nämlich auch zwei Modelle als Argumente annehmen und vegleichen.
lrtest(glm_model, glm_model2)## Likelihood ratio test
##
## Model 1: ANYDUMMY ~ 1 + Depression_lvl
## Model 2: ANYDUMMY ~ 1 + Depression_lvl + GENDER_R
## #Df LogLik Df Chisq Pr(>Chisq)
## 1 2 -5335.4
## 2 3 -5314.8 1 41.232 1.352e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Der Output ist für uns nicht mehr neu. Statt dem Nullmodell sind jetzt zwei Modelle mit Prädiktoren aufgeführt. Model 1 enthält allerdings nur einen Prädiktor und wird deshalb auch als eingeschränkt bezeichnet. Model 2 hingegen ist das uneingeschränkte Modell. Da wir ein signifikantes Ergebnis erhalten, würden wir uns für das uneingeschränkte Modell entscheiden.
Fazit
Final können wir festhalten, dass sowohl der Depressionsscore als auch das Geschlecht als Prädiktoren für die Wahrscheinlichkeit der Drogenabhängigkeit fungieren können.
Appendix
Appendix A
Parametereinflüsse
Die folgende Funktion stellt vier Grafiken dar: den Logit, die Odds, die Wahrscheinlichkeit und die Wahrscheinlichkeit vs. eine Zufallserhebung. Sie können \(\beta_0\) und \(\beta_1\) dieses Modells so einstellen, wie Sie wünschen und können sich den Effekt auf die verschiedenen Darstellungsformen der logistischen Regression ansehen. In hellblau wird jeweils die Funktion mit \(\beta_0 = 0\) und \(\beta_1 = 1\) als Referenz dargestellt. Die gestrichelten Linien stellen jeweils die x- und die y-Achse dar. In roten Punkten werden Realisierungen von \(Y=0,1\) dargestellt, die mit der angezeigten Wahrscheinlichkeit gezogen wurden. Um die Ergebnisse vergleichbar zu machen, wird set.seed(1234) verwendet (vgl. Simulation).
Logistic_functions <- function(beta0 = 0, beta1 = 1)
{
par(mfrow=c(2,2)) # 4 Grafiken in einer
xWerte <- seq(-5, 5, 0.1)
logit <- beta0 + beta1*xWerte
plot(x = xWerte, y = logit, type = "l", col = "blue", lwd = 3, main = "Logit vs X", xlab = "X")
lines(xWerte, xWerte, col = "skyblue")
abline(h = 0, lty = 3); abline(v = 0, lty = 3)
odds <- exp(logit)
plot(x = xWerte, y = odds, type = "l", col = "blue", lwd = 3, main = "Odds vs X", xlab = "X")
abline(h = 0, lty = 3); abline(v = 0, lty = 3)
lines(xWerte, exp(xWerte), col = "skyblue")
p <- odds/(1 + odds)
plot(x = xWerte, y = p, type = "l", col = "blue", lwd = 3, main = "P vs X", ylim = c(0,1), xlab = "X")
lines(xWerte, exp(xWerte)/(1 + exp(xWerte)), col = "skyblue")
abline(h = 0, lty = 3); abline(v = 0, lty = 3)
set.seed(1234) # Vergleichbarkeit
Y <- rbinom(n = length(xWerte), size = 1, prob = p)
plot(x = xWerte, y = p, type = "l", col = "blue", lwd = 3, main = "P vs X und zufällige Realisierungen",
ylim = c(0,1), xlab = "X", ylab = "P und Y")
abline(h = 0, lty = 3); abline(v = 0, lty = 3)
points(x = xWerte, y = Y, pch = 16, cex = .5, col = "red")
}Sie führen diese Funktion aus, indem Sie alles von Logistic_functions <- function(beta0 = 0, beta1 = 1){ bis } kopieren und in Ihrem R-Studio Fenster ausführen, sodass in der Rubrik oben rechts (dort wo auch immer Data erscheint) unter Functions Logistic_functions als Funktion aufgeführt wird. Sie können sich bspw. die Konstellation für \(\beta_0 = 1\) und \(\beta_1 = -0.5\) im Vergleich zu \(\beta_0 = 0\) und \(\beta_1 = 1\) ansehen:
Logistic_functions(beta0 = 1, beta1 = -.5)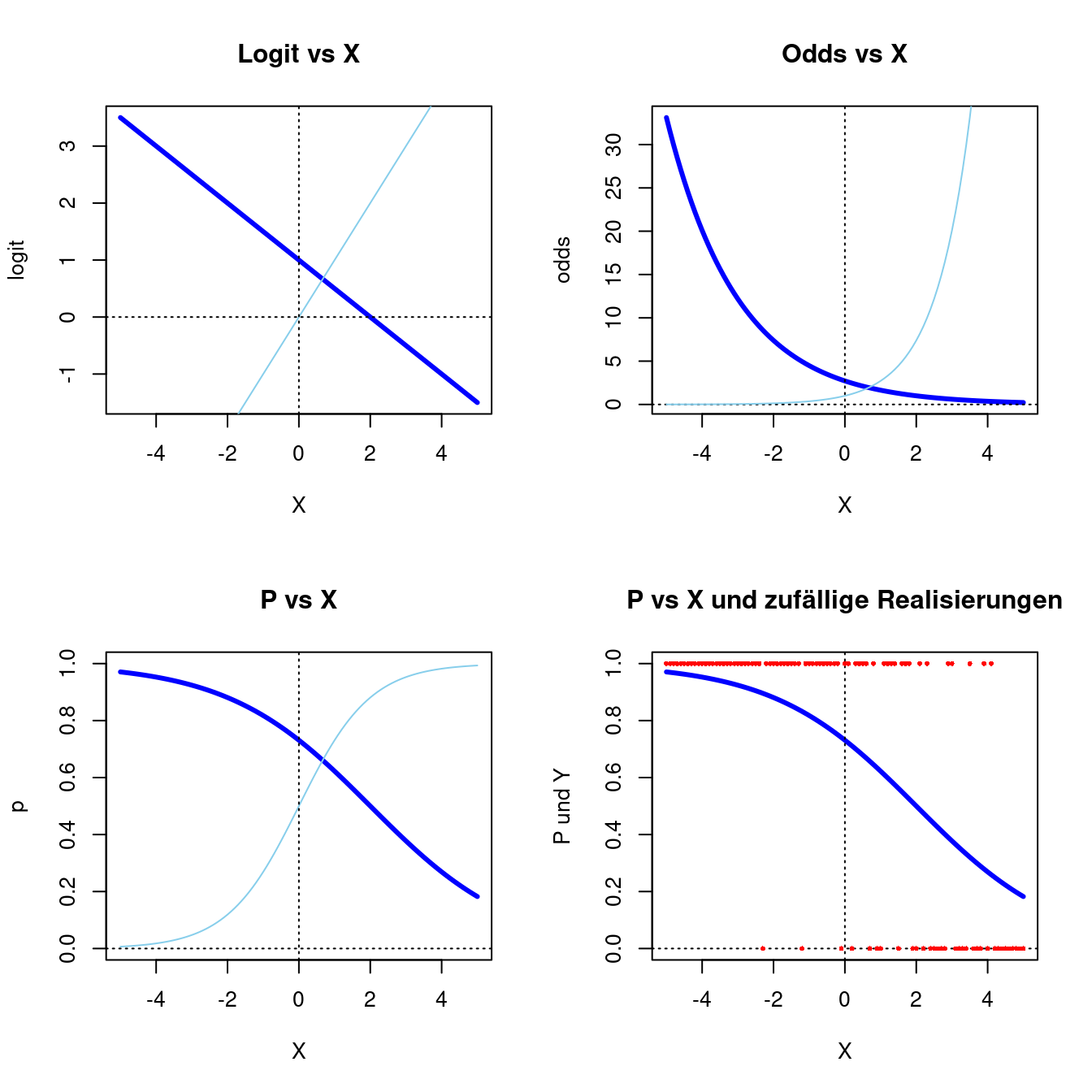
Appendix B
Fortgeschrittene Grafiken
Zunächst beschäftigen wir uns mit den beiden Grafiken, die die Residuen der linearen Regression zwischen Depressionsscore und Drogenabhängigkeit betrachten. Für den ersten Plot benötigen wir das Paket car.
library(car) # nötiges Paket laden
avPlots(model = reg_model, pch = 16)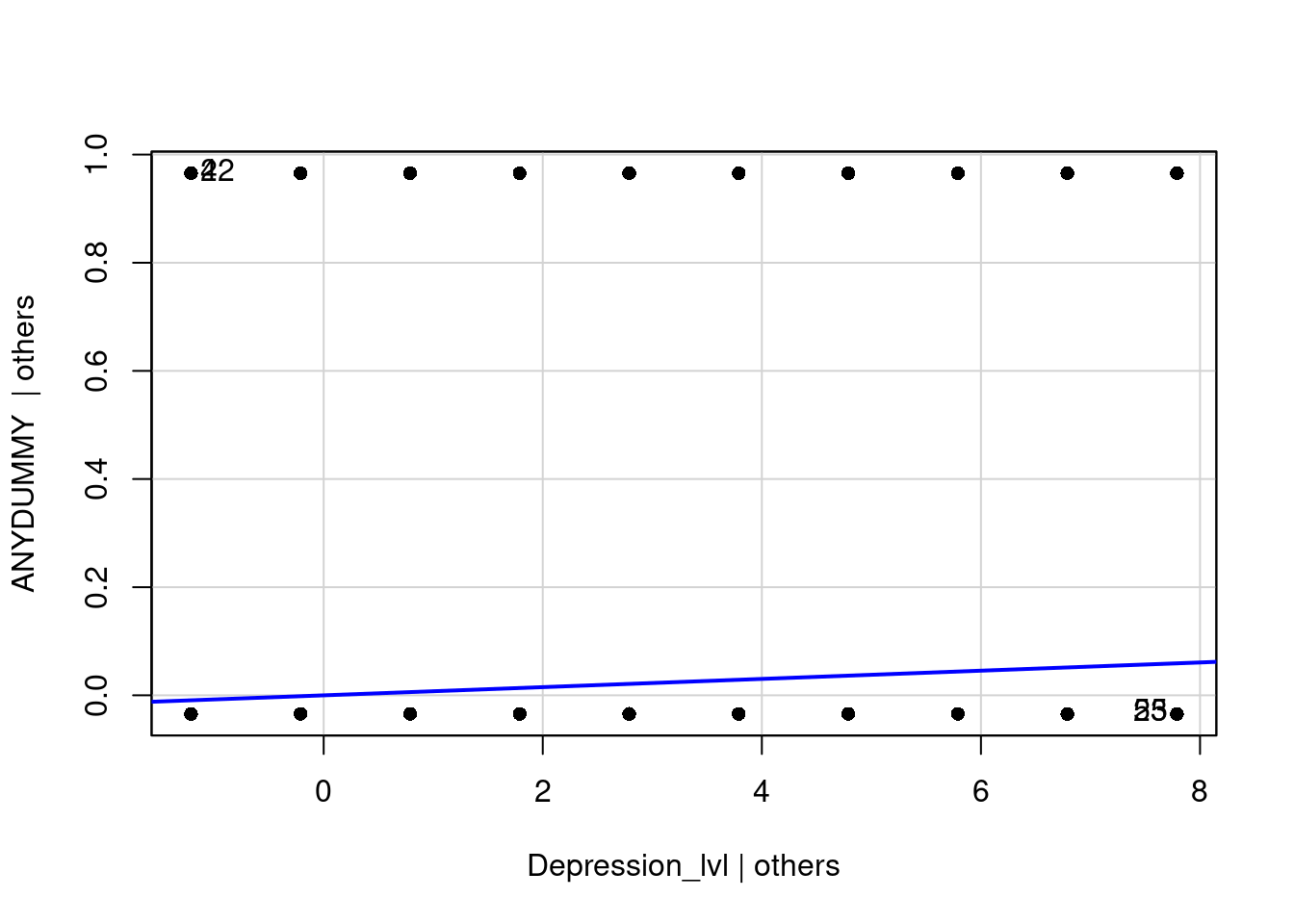
Für die Erstellung des zweiten Plots muss das Paket MASS aktiviert sein. Zunächst werden die studentisierten Residuen als Objekt abgelegt. Dafür kann die Funktion studres verwendet werden. Diese werden in einem Histogramm abgebildet.
library(MASS)# nötiges Paket laden
res <- studres(reg_model) # Studentisierte Residuen als Objekt speichern
hist(res, freq = F)
xWerte <- seq(from = min(res), to = max(res), by = 0.01)
lines(x = xWerte, y = dnorm(x = xWerte, mean = mean(res), sd = sd(res)), lwd = 3)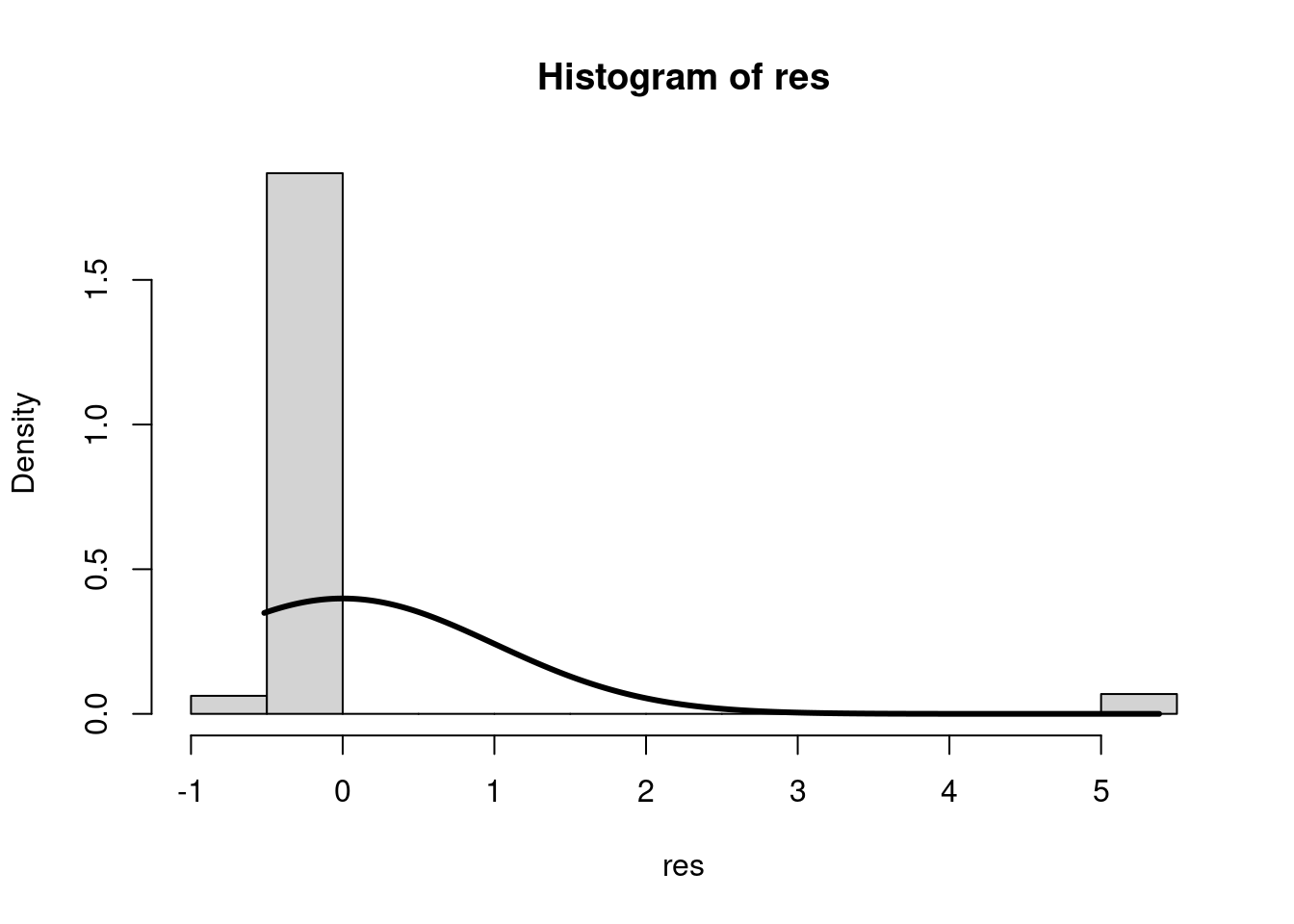
Um die Normalverteilunskurve auch noch einzuzeichnen erstellen wir einen Vektor mit x Variablen vom Minimum bis zum Maximum der Residuen-Werte. Anschließend legen wir über lines und dnorm die Kurve auf unser Histogramm. dnorm bestimmt dabei die Werte, die die Normalverteilung an der Stelle x mit dem Mittelwert und der Standardabweichung der Residuen hätte.
Die beschriebenen Plots sind mit einem Paket und einer Basis-Funktion von R erstellt. Für die Erstellung von individuellen Plots ist ggplot2 das richtige Paket. Dieses wurde bereits häufiger im Appendix als Möglichkeit zum Erzeugen von Plots beschrieben. Weitere Informationen zu ggplot2 erhalten Sie bspw. auf Tidyverse. Außerdem können Sie sich auch eine Einführung in ggplot2 auf dieser Website ansehen.
library(ggplot2)Wir können hier sehr leicht Gruppierungen in Grafiken darstellen. Zunächst müssen wir allerdings die Prädiktionen unseres Modells bestimmen, denn wir wollen uns die Vorhersage/Erwartung unseres Modells ansehen. Die Funktion, mit der wir dies machen können, heißt genauso wie die Funktion die sie ausführt: predict. Wir sagen damit den Logit für alle Konstellationen von Depressionsscore und Geschlecht in unseren Daten vorher, indem wir der Funktion das Modell übergeben. Wir bestimmen also für jede Personen die erwartete Wahrscheinlichkeit der Drogenabhängigkeit unter diesem Modell (der Prädiktion durch Geschlecht und Depressionsscore). Anschließend können wir den Logit so transformieren, dass wir die Odds oder die Wahrscheinlichkeit erhalten. Um dies leichter nachvollziehbar zu machen, führen wir die Transformationen mit neu erstellten Variablen durch, ehe wir diese dem Datensatz anhängen (denn ggplot hat es am liebsten, wenn wir mit data.frames, also ganzen Datensätzen arbeiten).
logit_glm2 <- predict(glm_model2) # Logit unter Modell glm2 bestimmen
odds_glm2 <- exp(logit_glm2) # Logit unter Modell glm2 in Odds transformieren
p_glm2 <- odds_glm2/(1 + odds_glm2) # Odds in Wahrscheinlichkeiten transformieren
# dem Datensatz anhängen:
osf$logit_glm2 <- logit_glm2
osf$odds_glm2 <- odds_glm2
osf$p_glm2 <- p_glm2Eine Grafik erhalten wir nun mit ggplot sehr einfach:
ggplot(data = osf, mapping = aes(x =
as.numeric(Depression_lvl),
y = logit_glm2, col =
GENDER_R)) +
geom_line(lwd = 2) +
ggtitle("Logit vs Depression and Sex") +
xlab("Depressionsscore") +
ylab("Logit")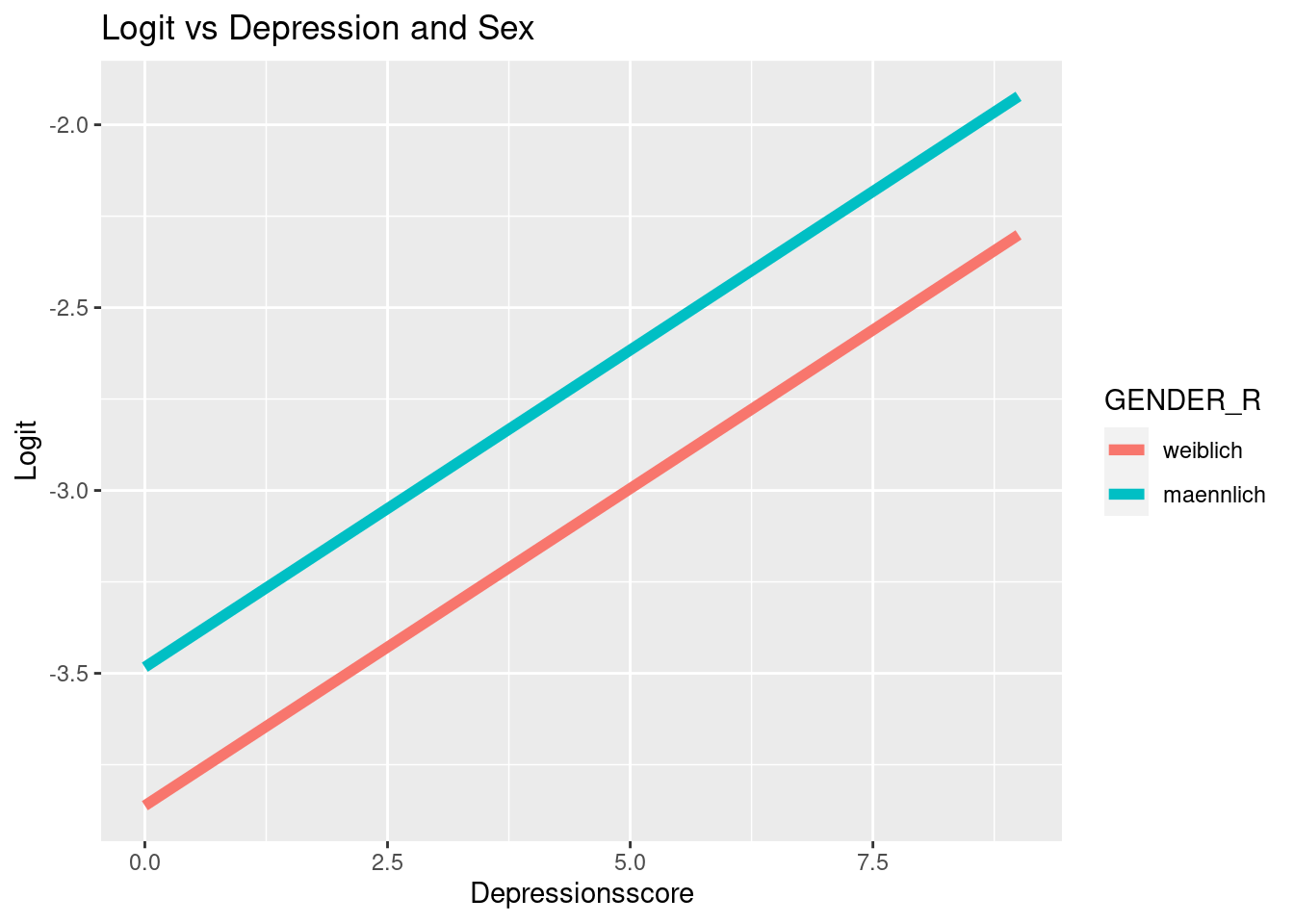
ggplot arbeitet etwas anders als die Basisfunktion plot. Zunächst übergeben wir ihr die Daten data = osf. Dem mapping übergeben wir sozusagen das Achsenkreuz und Gruppenzugehörigkeiten und Farbkodierungen innerhalb von aes(x = Depression_lvl, y = logit_glm2, col = GENDER_R). Hier wird gesagt, dass der Depressionsscore auf die x-Achse soll und wir den Logit entlang der y-Achse plotten wollen. Außerdem soll für das Geschlecht eine separate Linie eingezeichnet werden und diese soll farblich kodiert sein. Damit dies funktioniert, müssen natürlich die Variablen im richtigen Format vorliegen. Bspw. müssen Gruppierungen, wie etwa das Geschlecht, als Faktor vorliegen. Anschließend fügen wir mit + hinzu, was genau geplottet werden soll. In diesem Beispiel wollen wir Linien haben. Deshalb verwenden wir die Funktion geom_line mit dem Argument lwd = 2 für zweifache Liniendicke. Würden wir hier bspw. geom_point verwenden, so würden Punkte gezeichnet werden. Wieder mit dem + fügen wir außerdem einen Titel hinzu mit der Funktion ggtitle. xlab und ylab lassen uns die Achsentitel modifizieren. Gleiches können wir auch für die Odds oder die Wahrscheinlichkeit durchführen:
ggplot(data = osf, mapping = aes(x = Depression_lvl,
y = odds_glm2,
col = GENDER_R)) +
geom_line(lwd = 2) +
ggtitle("Odds vs Depression and Sex")+
xlab("Depressionsscore") +
ylab("Odds")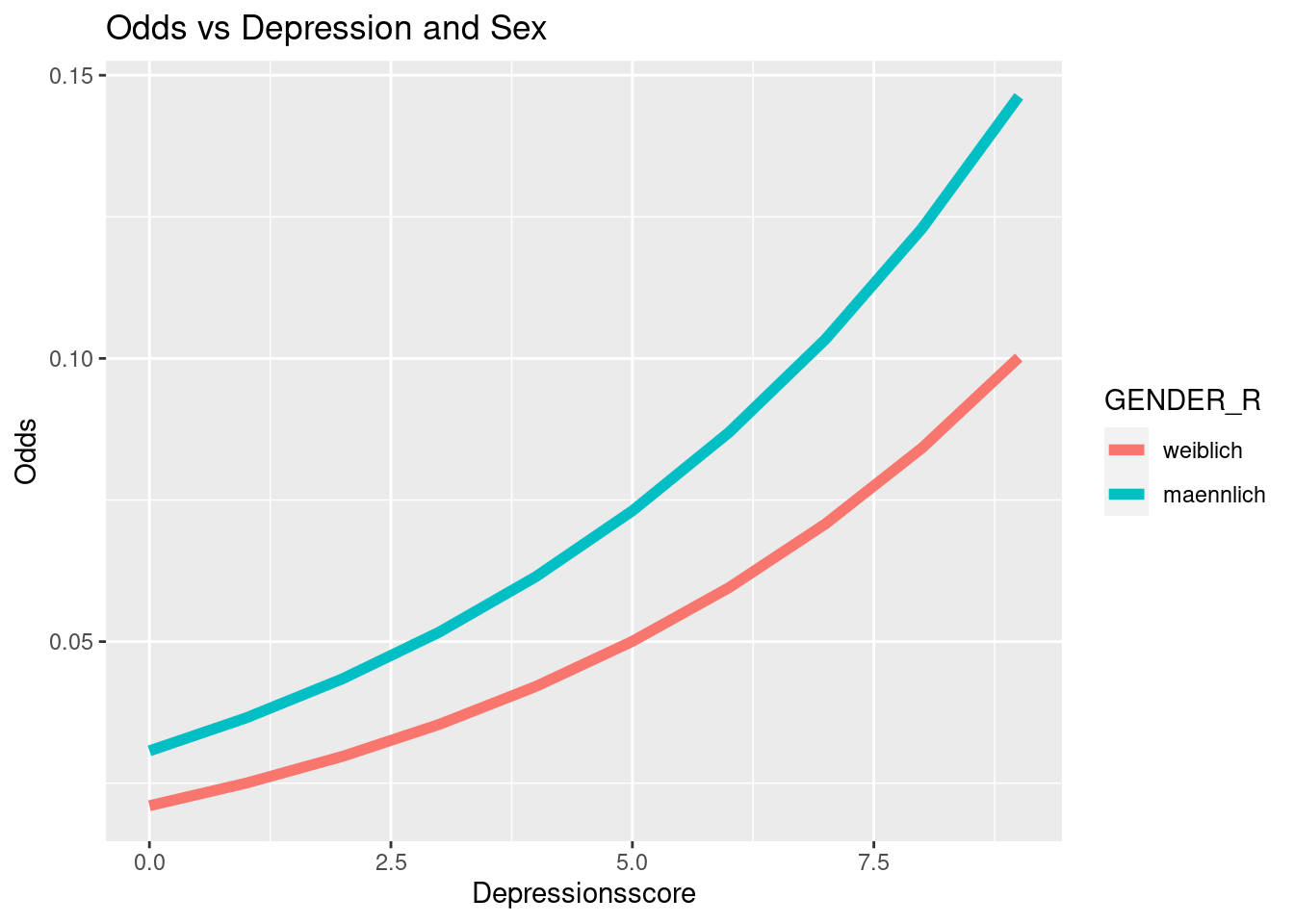
ggplot(data = osf, mapping = aes(x = Depression_lvl,
y = p_glm2,
col = GENDER_R)) +
geom_line(lwd = 2) +
ggtitle("P vs Depression and Sex") +
xlab("Depressionsscore") +
ylab("Logit")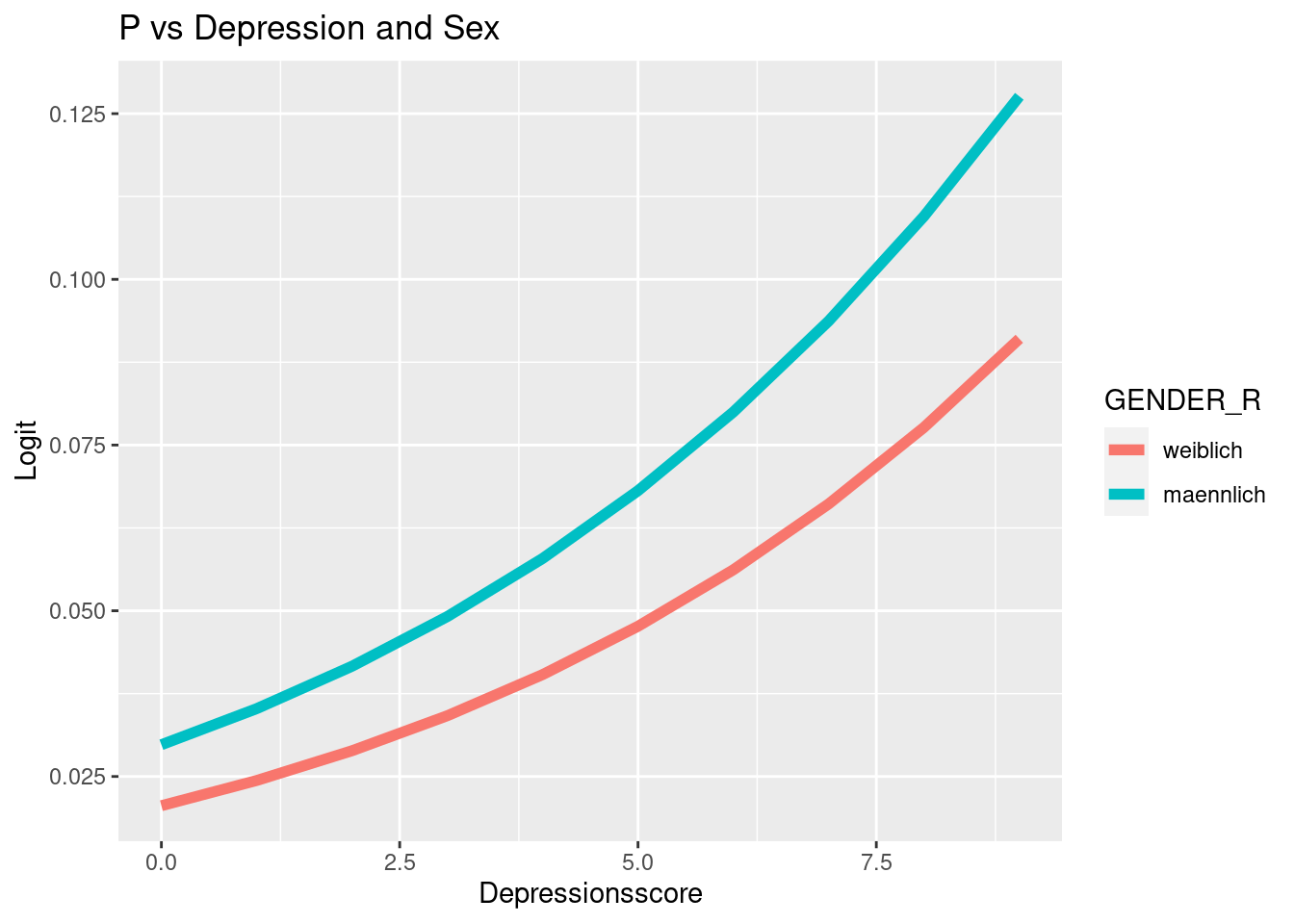
Literatur
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden (5. Auflage, 1. Auflage: 2010). Weinheim: Beltz.
Pituch, K. A. & Stevens, J. P. (2016). Applied Multivariate Statistics for the Social Sciences (6th ed.). New York: Taylor & Francis.
- Blau hinterlegte Autor:innenangaben führen Sie direkt zur universitätsinternen Ressource.
