Hierarchische Regression
Multi-Level Modeling
Einleitung
In dieser Sitzung wollen wir hierarchische Daten mit der Multi-Level-Regression (auch hierarchische Regression, Multi-Level-Modeling, Linear Mixed-Effects Modeling, Random Coefficient Regression vgl. bspw. Eid, Gollwitzer & Schmitt, 2017, Kapitel 20 und Pituch und Stevens (2016) Kapitel 13) analysieren. Diese Daten sind dahingehend speziell, dass es in ihnen Clusterungen von Datenpunkten gibt, die zueinander ähnlicher sind als zu den übrigen. Dies verletzt die Annahme der Unabhängigkeit in der typischen Regressionsanalyse, was zu erheblichen Fehlschlüssen führen kann. Wir wollen uns ein fiktives Datenbeispiel (Datensatz StudentsInClasses aus dem gleichnamigen .rda File StudentsInClasses.rda) mit Schüler/innen (Ebene 1) in Schulklassen (Eben 2) anschauen. Sie können den Datensatz “StudentsInClasses.rda” hier herunterladen.
Daten laden
Dazu laden wir mit load die Daten (bspw. auf dem Desktop von Frau “Musterfrau”) Tipp: Verwenden Sie unbedingt die automatische Vervollständigung von R-Studio, wie in den letzten Sitzung beschrieben.
load("C:/Users/Musterfrau/Desktop/StudentsInClasses.rda")Genauso können Sie die Daten direkt von der Website laden:
load(url("https://pandar.netlify.app/post/StudentsInClasses.rda"))Nun sollte in R-Studio oben rechts in dem Fenster unter der Rubrik “Data” unser Datensatz mit dem Namen “StudentsInClasses” erscheinen.
Übersicht über die Daten
In Multilevel-Daten gibt es, wie der Name schon andeutet, mehrere Level. In unserem Datensatz gibt es zwei: Level 1 enthält die Individualdaten (within) und Level 2 enthält die clusterspezifischen Daten (between). Wir verwenden wieder head, um zu schauen, welche Variablen wohl auf welchem Level liegen:
head(StudentsInClasses)## MatheL Motivation KFT KlassenG schulklasse
## 1 48.76 4 98 26 1
## 2 46.01 3 96 26 1
## 3 65.96 5 112 26 1
## 4 42.08 4 94 26 1
## 5 0.00 2 78 26 1
## 6 56.52 5 104 26 1Aus dieser Übersicht ergibt sich folgende Aufteilung:
Ebene 1 (within-level)
- Mathematikleistung als AV:
MatheL - Motivation der Schüler/innen als Prädiktor:
Motivation - Intelligenz der Schüler/innen als Prädiktor:
KFT(Kognitiver Fähigkeitstest)
Ebene 2 (between-level)
- Klassengröße als Prädiktor:
KlassenG - Klassenzugehörigkeit als Gruppierungsvariable:
schulklasse
Die Daten liegen hier im “Long”-Format vor, was bedeutet, dass Schüler aus einer Klasse untereinander stehen und es eine Clustervariable gibt, die die Schüler jeweils einer Klasse zuordnet. In diesem Fall ist dies die Level 2 Variable schulklasse (hierbei ist es wichtig, dass jedes Schulkind nur einer Schulklasse zugeordnet werden kann und dass unterschiedliche Schulklassen auch unterschiedliche Bezeichnungen haben müssen - die Level 2 Variable KlassenG kann für unterschiedliche Schulklassen die selbe Ausprägung aufweisen, sie ist nämlich nur eine Variable, die das Cluster näher beschreibt). Wir schauen uns noch schnell die Mittelwerte der Variablen an:
colMeans(StudentsInClasses)## MatheL Motivation KFT KlassenG schulklasse
## 53.616047 4.285882 100.001176 27.090588 20.280000Bei Multi-Level-Analysen ist darauf zu achten, dass für bessere Interpretierbarkeit unabhängige Variablen zentriert werden sollten. Wir können zwischen Grand-Mean-Centering und Group-Mean-Centering unterscheiden. Beim Grand-Mean-Centering wird am Stichprobenmittelwert der jeweiligen Variable zentriert. Somit spricht ein Wert von Null auf der zentrierten Variable für den Mittelwert über alle Erhebungen (hier: Schulkinder). Beim Group-Mean-Centering wird am Mittelwert des jeweiligen Clusters zentriert. Somit entspricht ein Mittelwert von 0 auf der zentrierten Variable für einen durchschnittlichen Wert innerhalb dieses Clusters (hier: für einen durchschnittlichen Wert innerhalb dieser Schulklasse). Beim Group-Mean-Centering können die Ergebnisse gut in Hinsicht auf die Schulklasse interpretiert werden, allerdings geht die Unterschiedlichkeit zwischen Klassen verloren, weswegen häufig zusätzlich zur zentrierten Variable auch der Mittelwert pro Cluster als L2 Variable mit in das Modell aufgenommen wird. Wir schauen uns dies später im Abschnitt Datenzentrierung genauer an.
Hypothesen
Wir wollen folgende Hypothesen untersuchen:
- Mathematikleistung hängt von der Lernmotivation ab
- Der Effekt der Motivation unterscheidet sich zwischen Klassen
- Mathematikleistung hängt von der Klassengröße ab
- Es gibt eine Wechselwirkung (Cross-Level-Interaktion) zwischen Motivation und Klassengröße
Pakete laden
Wir werden im Folgenden wieder neue R-Pakete benötigen. Diese müssen zunächst installiert werden (install.packages) und anschließend geladen werden: Das wichtigste Paket ist lme4 (linear mixed effects 4, wobei wir annehmen können, dass die 4 hier für four steht, was sich wie “for r” spricht), welches für die Multi-Level Analysen von Nöten ist. lmerTest verwenden wir, um Modellvergleiche sinnvoll auch für Varianzen durchführen zu können. lme4 und lmerTest sollten immer gemeinsam geladen werden (auch wenn in den meisten Fällen lmerTest erzwingt, dass lme4 auch geladen wird), denn lmerTest erweitert lediglich das Paket lme4 um einige wichtige Funktionen. robutmeta verwenden wir, um Daten gruppenspezifisch zu zentrieren.
library(lme4) # für das Durchführen von Multi-Level Regressionen
library(lmerTest) # lmerTest markiert in der Ausgabe signifikante Koeffizienten und korrigiert Modellvergleiche für Varianzen
library(robumeta) # Datensatzmanipulation## Warning: Paket 'robumeta' wurde unter R Version 4.1.1 erstelltlibrary(ggplot2) # ggplot2 und dplyr werden nur für Grafiken benötigt## Warning: Paket 'ggplot2' wurde unter R Version 4.1.2 erstelltlibrary(dplyr) # für DatensatzmanipulationenModellspezifikation
Wir verwenden die Funktion lmer des Pakets lme4 (bzw. des Pakets lmerTest), um Multi-Level-Modelle zu schätzen. Die allgemeine Syntax ähnelt sehr der Syntax der lm-Funktion für lineare Modelle. Diese Syntax sah so aus:
lm(Y ~ 1 + X, data = StudentsInClasses)
Die Syntax für lmer wird nun erweitert, um die Clusterung zu enthalten: wir nehmen für einen Augenblick an, dass X eine L1-Variable ist, Z eine L2 Variable und gruppe die Clusterungsvariable. In der Modellgleichung werden wie im linearen Modell die Prädiktoren aufgeführt, deren Effekte als feste Effekte geschätzt werden. Zusätzlich werden mit dem senkrechten Strich | Zufallseffekte spezifiziert, welche Variationen beschreiben, die auf das Cluster (hier die Zugehörigkeit zu einer Schulklasse) zurückzuführen sind. Vor dem | stehen die Effekte, die als zufällig behandelt werden sollen, danach die Gruppierungsvariable, durch die die Ebene definiert ist:
Y ~ 1 + (1 | gruppe): Random Intercept für Y auf Ebene der Gruppen (dies wird auch das Nullmodell genannt, da keine Prädiktoren enthalten sind)Y ~ 1 + X + (1 | gruppe): Random Intercept und fester Effekt für XY ~ 1 + X + (1 + X | gruppe): Random Intercept und Random Slope für XY ~ 1 + X + Z + (1 + X | gruppe): Random Intercept und Random Slope für X und Prädiktor Z auf L2 (Aufklärung der Interzeptvariation durchZ)Y ~ 1 + X + Z + Z:X + (1 + X | gruppe): Random Intercept und Random Slope für X und Prädiktor Z auf L2, sowie Cross-Level-Interaktion (Aufklärung der Interzept- und Slopevariation durchZ)
Wir erkennen, wie oben schon angedeutet, L2-Variablen nur daran, dass sie über eine Clustereinheit nicht variieren. In unserem Beispiel sehen wir dies daran, dass die Klassengröße für jedes Schulkind aus der selben Schulklasse identisch ist. Dies ist auch in der Modellgleichung so: hier wird Z analog zu X in die Modellgleichung aufgenommen, an welcher wir nicht erkennen, ob es sich hierbei um einen L2-Effekt handelt - dies können wir nur wissen, wenn wir wissen in welchem Format die Daten vorliegen. : steht für das Produkt zwischen Variablen in Regressionsmodellen. Oft wird auch * verwendet, welches dann sowohl die einzelnen Haupteffekte, als auch die Interaktion repräsentiert: also Z*X = Z + X + Z:X.
Die zugehörigen Gleichungen zu den Modellen sehen so aus (siehe auch Eid, et al., 2017, Kapitel 20.2):
Y ~ 1 + (1 | gruppe)- \(Y_{ij} = \beta_{0j} + \varepsilon_{ij}\)
- \(\beta_{0j}=\gamma_{00} + u_{0j}\)
- \(\Longrightarrow Y_{ij} = \gamma_{00} + u_{0j} + \varepsilon_{ij}\)
Y ~ 1 + X + (1 | gruppe)- \(Y_{ij} = \beta_{0j} + \beta_{1j}X_{ij} + \varepsilon_{ij}\)
- \(\beta_{0j}=\gamma_{00} + u_{0j}\)
- \(\beta_{1j}=\gamma_{10}\) [\(\beta_{1j}\) ist konstant/ gleich für alle \(j\)]
- \(\Longrightarrow Y_{ij} = \gamma_{00} + u_{0j} + \gamma_{10}X_{ij} + \varepsilon_{ij}\)
Y ~ 1 + X + (1 + X | gruppe)- \(Y_{ij} = \beta_{0j} + \beta_{1j}X_{ij} + \varepsilon_{ij}\)
- \(\beta_{0j}=\gamma_{00} + u_{0j}\)
- \(\beta_{1j}=\gamma_{10} + u_{1j}\)
- \(\Longrightarrow Y_{ij} = \gamma_{00} + u_{0j} + \gamma_{10}X_{ij} + u_{1j}X_{ij} + \varepsilon_{ij}\)
Y ~ 1 + X + Z + (1 + X | gruppe)- \(Y_{ij} = \beta_{0j} + \beta_{1j}X_{ij} + \varepsilon_{ij}\)
- \(\beta_{0j}=\gamma_{00} + \gamma_{01}Z_j + u_{0j}\)
- \(\beta_{1j}=\gamma_{10} + u_{1j}\)
- \(\Longrightarrow Y_{ij} = \gamma_{00} + \gamma_{01}Z_j + u_{0j} + \gamma_{10}X_{ij} + u_{1j}X_{ij} + \varepsilon_{ij}\)
Y ~ 1 + X + Z + Z:X + (1 + X | gruppe)- \(Y_{ij} = \beta_{0j} + \beta_{1j}X_{ij} + \varepsilon_{ij}\)
- \(\beta_{0j}=\gamma_{00} + \gamma_{01}Z_j + u_{0j}\)
- \(\beta_{1j}=\gamma_{10} + \gamma_{11}Z_j+ u_{1j}\)
- \(\Longrightarrow Y_{ij} = \gamma_{00} + \gamma_{01}Z_j + u_{0j} + \gamma_{10}X_{ij} + \gamma_{11}Z_jX_{ij} + u_{1j}X_{ij} + \varepsilon_{ij}\)
Hierbei ist zu beachten, dass natürlich auch nur eine L2 Variable in das Modell aufgenommen werden könnte oder die Interzeptvariation durch die L2-Variable erklärt werden könnte, ohne, dass eine Random Slope spezifiziert wird, etc. Dies hängt von den Hypothesen ab.
Außerdem können wir den Gleichungen die Unabhängigkeitsverletzung einer einfachen Regression entnehmen. Dies erkennen wir bereits am Nullmodell, dass in eingesetzter Form wie folgt aussieht:
\[ Y_{ij} = \gamma_{00} + \underbrace{u_{0j} + \varepsilon_{ij}}_{e_i}\] In einer einfachen Regression würde \(e_i:=u_{0j}+\varepsilon_{ij}\) als Residuum angesehen werden. Damit haben alle Erhebungen aus der gleichen Clustereinheit \(j\) etwas gemeinsam (nämlich \(u_{0j}\)) und sind somit korreliert. Dies widerspricht der \(i.i.d.\)-Annahme in der Regression (vgl. Regressionssitzung).
Analysen mit dem Beispieldatensatz
Bevor wir mit den Analysen beginnen, müssen wir prüfen, ob eine Multi-Level-Analyse überhaupt nötig ist. Dazu wollen wir uns die Intraklassenkorrelation ansehen. Diese erhalten wir durch Schätzen des sogenannten Nullmodells ohne weiteren Prädiktoren.
Preliminary Analyses: Nullmodell und Intraklassenkorrelation (ICC)
Wir nennen das Nullmodell-Objekt einfach mal m0 (für Modell 0).
m0 <- lmer(MatheL ~ 1 + (1 | schulklasse), data = StudentsInClasses)
summary(m0)## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: MatheL ~ 1 + (1 | schulklasse)
## Data: StudentsInClasses
##
## REML criterion at convergence: 6565.3
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -4.5448 -0.5642 -0.0015 0.5695 3.5476
##
## Random effects:
## Groups Name Variance Std.Dev.
## schulklasse (Intercept) 23.87 4.885
## Residual 123.12 11.096
## Number of obs: 850, groups: schulklasse, 40
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) 54.0235 0.8658 37.0961 62.4 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Die Summary sieht der der normalen linearen Regression sehr ähnlich. Wir schauen uns diese im Detail an.
## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: MatheL ~ 1 + (1 | schulklasse)
## Data: StudentsInClasseszeigt uns, dass es sich um ein Linear mixed model handelt (also ein Multi-Level-Modell/hierarchische Regression), welches mit der REstricted Maximum Likelihood Methode geschätzt wurde. Bei REML werden zunächst die Random Effects geschätzt und anschließend werden erst die fixed Effects bestimmt. Damit ist das Verfahren stabiler und oft auch statistisch effizienter (kleinere SE). Außerdem wird unsere Modellgleichung nochmals wiederholt.
##
## REML criterion at convergence: 6565.3
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -4.5448 -0.5642 -0.0015 0.5695 3.5476gibt uns Informationen über die Konvergenz (sozusagen den Log-Likelihood-Wert), sowie Auskunft über die Verteilung de Residuen (ähnlich wie bei der Regression). Diese scheinen hier recht symmetrisch verteilt zu sein.
##
## Random effects:
## Groups Name Variance Std.Dev.
## schulklasse (Intercept) 23.87 4.885
## Residual 123.12 11.096
## Number of obs: 850, groups: schulklasse, 40zeigt uns die Schätzungen der Random effects, also der Varianzen (und Kovarianzen) von \(u\) (dem zufälligen Anteil des Interzept und der Slope, falls vorhanden) sowie von \(\varepsilon\) (dem Residuum). Eine Signifikanzentscheidung wird nicht mit ausgegeben. Wir müssen diese via einem Modellvergleich, dem Likelihood-Differenzen-Test (LRT) untersuchen - dazu später mehr! Wir erkennen, dass uns sowohl die Varianzen des Interzepts und des Residuums, sowie die Standardabweichung (Std.Dev.) ausgegeben werden, wobei dies einfach nur die Wurzel aus Variance ist. Die Varianz zwischen Klassen beträgt 23.868 und die (Residual-) Varianz innerhalb der Klassen 123.117. Mit Hilfe dieser Informationen können wir den Intraklassenkorrelationskoeffizienten bestimmen. Außerdem entnehmen wir diesem Output, dass insgesamt 850 Schulkinder untersucht wurden in 40 Klassen.
Berechnung der Intraklassenkorrelation (ICC)
Wir wollen uns noch schnell den ICC ansehen. Entweder machen wir dies per Hand und tippen die Varianzen aus dem Output ab, oder wir entlocken sie dem m0 Objekt. Der ICC ergibt sich als
\[ICC := \frac{\mathbb{V}ar[u_0]}{\mathbb{V}ar[u_0]+\mathbb{V}ar[\varepsilon]}.\]
# Per Hand
23.87 / (23.87 + 123.12)## [1] 0.162392# Mit Zugriff auf das Nullmodell-Objekt
VarCorr(m0)$schulklasse[1] / (VarCorr(m0)$schulklasse[1] + summary(m0)$sigma^2)## [1] 0.1623841Achtung: Unterschiede kommen durch Runden zustande - die Ergebnisse abgelesen aus dem Output sind nur auf 2 Nachkommastellen genau.
Die Funktion VarCorr gibt die Varianz, die Standardabweichung, sowie die Korrelationen zwischen mehreren Random Effekten (z.B. die Korrelation zwischen Interzept und Slope) aus. Wir müssen dann das Interzept via $schulklasse[1] auswählen, weil es der erste zufällige Effekt ist, der auf das Cluster zurückgeführt werden kann.
VarCorr(m0) # nur die Standardabweichungen (also Wurzel aus den Varianzen) werden angezeigt## Groups Name Std.Dev.
## schulklasse (Intercept) 4.8855
## Residual 11.0958VarCorr(m0)$schulklasse # auch Varianzen werden angezeigt## (Intercept)
## (Intercept) 23.86806
## attr(,"stddev")
## (Intercept)
## 4.885495
## attr(,"correlation")
## (Intercept)
## (Intercept) 1VarCorr(m0)$schulklasse[1] # das erste Element ist die Varianz des Interzepts## [1] 23.86806Dem Summary Objekt (also summary(m0)) können wir via $sigma die Standardabweichung der Residuen entlocken, welche quadriert die Varianz von \(\varepsilon\) ist.
summary(m0)$sigma # Residualstandardabweichung## [1] 11.09581summary(m0)$sigma^2 # Residualvarianz## [1] 123.1171names(summary(m0)) # alle Informationen, die wir der Summary entlocken können## [1] "methTitle" "objClass" "devcomp" "isLmer" "useScale"
## [6] "logLik" "family" "link" "ngrps" "coefficients"
## [11] "sigma" "vcov" "varcor" "AICtab" "call"
## [16] "residuals" "fitMsgs" "optinfo"Inhaltliche Interpretation: 16.2% der Varianz in der Mathematikleistung können durch die Klassenzugehörigkeit erklärt werden. Die Multi-Level-Struktur in den Daten muss somit unbedingt berücksichtigt werden.
Nun weiter im Output:
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) 54.0235 0.8658 37.0961 62.4 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1enthält die Fixed effects (also die \(\gamma\)s aus den Gleichungen zuvor). Im Nullmodell gibt es nur \(\gamma_{00}\), das globale Interzept. Es liegt bei 54.0236, was bedeutet, dass die durchschnittliche Matheleistung über alle Schulklassen und -kinder hinweg bei ca 54 liegt. Das Interzept ist zudem signifikant von 0 verschieden: \(t\)-Wert = 62.4 mit \(p < .001\) (<2e-16 = \(<2*10^{-16}\)). Somit können wir mit einer Irrtumswahrscheinlichkeit von 5% davon ausgehen, dass die durchschnittliche Matheleistung von Null abweicht. Diese Information ist hier nicht spannend, da die Matheleistung gerade von 0 bis 100 geht und somit ein Mittelwert von 0 sehr unwahrscheinlich erscheint.
Nun wollen wir prüfen, ob sich die Matheleistung durch die Motivation zu Lernen vorhersagen lässt.
Hypothese 1: Motivation als Prädiktor
Bevor wir den Effekt der Motivation auf die Matheleistung untersuchen, zentrieren wir die Lernmotivation am Stichprobenmittelwert und nennen die Variable $Motivation_c (durch das Dollarzeichen wird sie dem Datensatz angehängt):
StudentsInClasses$Motivation_c <- StudentsInClasses$Motivation - mean(StudentsInClasses$Motivation)
round(colMeans(StudentsInClasses), 10) # Spaltenmittelwerte gerundet auf 10 Nachkommastellen## MatheL Motivation KFT KlassenG schulklasse Motivation_c
## 53.616047 4.285882 100.001176 27.090588 20.280000 0.000000Den Spaltenmittelwerten entnehmen wir, dass Motivation_c nun einen Mittelwert von 0 hat (gerundet mit round auf 10 Nachkommastellen). Nun nehmen wir diese Variable in das Multi-Level-Modell mit auf. Das Modell nennen wir entsprechend der 1. Hypothese m1.
m1 <- lmer(MatheL ~ 1 + Motivation_c + (1 | schulklasse), data = StudentsInClasses)
summary(m1)## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: MatheL ~ 1 + Motivation_c + (1 | schulklasse)
## Data: StudentsInClasses
##
## REML criterion at convergence: 6231.1
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.9343 -0.5597 0.0146 0.6001 4.7018
##
## Random effects:
## Groups Name Variance Std.Dev.
## schulklasse (Intercept) 26.57 5.154
## Residual 81.46 9.026
## Number of obs: 850, groups: schulklasse, 40
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) 54.0708 0.8751 37.7353 61.79 <2e-16 ***
## Motivation_c 6.0879 0.2991 808.6683 20.35 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr)
## Motivatin_c 0.000Im Output hat sich nun der Abschnitt Fixed effects erweitert um den Effekt der Motivation. Das Regressionsgewicht für (die am Stichprobenmittelwert zentrierte) Motivation beträgt 6.088 und ist mit p < .001 signifikant. Somit wird die Nullhypothese verworfen: “Mit einer Irrtumswahrscheinlichkeit von 5% ist der Zusammenhang (Steigungskoeffizient, \(\gamma_{10}\)) zwischen Motivation und Mathematikleistung in der Population aller Schüler von Null verschieden.” Durch die Zentrierung können wir weiterhin das Interzept (\(\gamma_{00}\)) sinnvoll interpretieren. Ein durchschnittlich motiviertes Kind hat im Mittel eine Matheleistung von 54.071.
Correlation of Fixed Effects: gibt an, wie stark die festen Efffekte (hier Interzept und Steigungskoeffizient von Motivation_c) korreliert sind. Dies ist ein Maß für die Stabilität der Schätzung. Sind diese Korrelationen sehr groß, dann hat dies negative Auswirkungen auf die Standardfehler. Diese sind dann zu groß. An den Schätzungen der Parameter ändert dies allerdings nichts. Jedoch kann die Signifikanzentscheidung negativ beeinflusst sein. Diese Korrelationen können reduziert werden, durch Verringerungen der Komplexität im Modell (Multikollinearität), aber auch durch Zentrierung!
Insgesamt ist zu sagen, dass unsere Hypothese 1 durch die Daten gestützt wird. Es stellt sich allerdings die Frage, ob die signifikante lineare Beziehung der Variable auch inhaltlich bedeutsam ist. Um dies besser beurteilen zu können, wollen wir ein Pseudo-\(R^2\) bestimmen - es ist sehr dem Determinationskoeffizienten der Regression verwandt, kann aber Fehlschätzungen unterliegen, weswegen es nicht für bare Münze genommen werden sollte. Es kann uns allerdings helfen, besser einschätzen zu können, wie groß denn die Varianzaufklärung des Prädiktors ist, auch wenn wir im Hinterkopf behalten sollten, dass mit Pseudo-\(R^2\) auch Probleme auftreten können (die es in der Regel mit dem Determinationskoeffizienten nicht gibt). Für mehr Informationen hierzu schaue bspw. in Eid, et al. (2017) Kapitel 20.3.4 ab Seite 750.
Pseudo \(R^2\): within
Die Varianz unseres Kriteriums \(Y\) haben wir im Null-Modell in Varianz des Cluster (Interzeptvarianz) und (within) Residualvarianz aufgeteilt: \(\mathbb{V}ar[Y] = \mathbb{V}ar[u_0]+\mathbb{V}ar[\varepsilon]\). Die Variation von \(u_0\) beschreibt somit die between-Variation, die auf Unterschiede zwischen Klassen (und somit Unterschiede, die auf die Clusterung zurückzuführen sind), während die Variation von \(\varepsilon\) gerade die within-Variation ist. Unter ideellen Bedingungen sollte nun ein L1-Prädiktor nur die within-Residualvariation verringern (dies ist dann gegeben, wenn ein L1 Prädiktor sich nicht systematisch zwischen Klassen unterscheidet, es also keine Mittelwertsunterschiede über Klassen hinweg auf dieser L1 Variable gibt!): für den Prädiktor Motivation (\(X_1\)) ergibt sich die Variation von \(Y\) als \[\mathbb{V}ar[Y] = \mathbb{V}ar[u_0]+\underbrace{\gamma_{10}^2\mathbb{V}ar[X_1]+\mathbb{V}ar[\varepsilon^*]}_{\mathbb{V}ar[\varepsilon]}.\] Für mehr Informationen zu Varianzrechenregeln siehe im Appendix B nach. Wir schreiben hier \(\varepsilon^*\), da es sich um ein anderes Residuum handelt, als im leeren Modell (\(X_1\) ist ja mit von der Partie). Dieser ideellen Gleichung ist zu entnehmen, dass die Varianz von \(\varepsilon^*\) kleiner ausfällt, also die von \(\varepsilon\), wenn \(\gamma_{10}\neq 0\) und \(X_1\) nicht konstant ist, also wenn \(X_1\) zur Vorhersage vom Kriterium beiträgt (also folgt \(\mathbb{V}ar[\varepsilon^*]<\mathbb{V}ar[\varepsilon]\)). Wir machen uns diese Gegebenheit zu nutze und quantifizieren die relative Veränderung in der Varianz des Residuums und nennen diese Pseudo-\(R^2\): \[R^2_\text{pseudo:within}=\frac{\mathbb{V}ar[\varepsilon]-\mathbb{V}ar[\varepsilon^*]}{\mathbb{V}ar[\varepsilon]}=1-\frac{\mathbb{V}ar[\varepsilon^*]}{\mathbb{V}ar[\varepsilon]}.\]
In der Realität ist es so, dass Prädiktoren je nach Zentrierung auch within und between Variation von \(Y\) erklären, da der Mittelwert eines Clusters between-Information enthält und die Abweichungen von diesem Mittelwert within-Informationen. Somit ist es so, dass ein nicht-zentrierter Prädiktor sowohl within als auch between Variation am Kriterium erklärt. Hinzu kommt dann noch die Schätzungenauigkeit.
Um Pseudo-\(R^2\) in R umzusetzen, müssen wir lediglich die Residualvarianzen der beiden Modelle abgreifen und verrechnen:
VarE0 <- summary(m0)$sigma^2 # Varianz des Residuums im Nullmodell
VarE1 <- summary(m1)$sigma^2 # Varianz des Residuums im Modell mit Motivation als Prädiktor
1- VarE1/VarE0## [1] 0.3383368# oder kurz:
1 - summary(m1)$sigma^2/summary(m0)$sigma^2## [1] 0.3383368Insgesamt können also 33.83% der Variation der Matheleistung innerhalb einer Klasse erklärt werden. Die Motivation scheint substantielle Anteile zu erklären. Die Residualvarianz im Modell mit der Motivation als Prädiktor ist um 33% geringer als im Nullmodell.
Pseudo \(R^2\): between
Genauso wie wir soeben die relative Veränderung der (within) Residualvarianz quantifiziert haben, können wir auch die relative Veränderung der Interzeptvariation (between Variation, Variation, die auf Unterschiede des Clusters/zwischen Klassen zurückzuführen sind) bestimmen. Da wir die Motivation am Gesamtmittelwert zentriert haben, sind einige Unterschiede zwischen den Klassen immer noch in der Variable Motivation_c enthalten (dazu später mehr im Abschnitt zur Datenzentrierung). Diesen Varianzanteil wollen wir nun quantifizieren und vergleichen dazu die beiden Modelle m0 und m1:
\[\begin{align}
\texttt{m0}:&\quad \mathbb{V}ar[Y] = \mathbb{V}ar[u_0]+\mathbb{V}ar[\varepsilon]\\
\texttt{m1}:&\quad \mathbb{V}ar[Y] = \mathbb{V}ar[u_0^*]+\gamma_{10}^2\mathbb{V}ar[X_1]+\mathbb{V}ar[\varepsilon^*]
\end{align}\]
Falls der Prädiktor der Motivation (Grand-Mean zentriert) auch noch Unterschiede zwischen den Klassen enthält, dann sollten gelten: \(\mathbb{V}ar[u_0^*]<\mathbb{V}ar[u_0]\); also sollte die Interzeptvariation von m0 zu m1 kleiner werden. Analog zum Pseudo-\(R^2\) zuvor wird Pseudo-\(R^2\) für die between Ebene (L2) definiert:
\[R^2_\text{pseudo:between}=\frac{\mathbb{V}ar[u_0]-\mathbb{V}ar[u_0^*]}{\mathbb{V}ar[u_0]}=1-\frac{\mathbb{V}ar[u_0^*]}{\mathbb{V}ar[u_0]}.\]
Wie wir die Interzeptvarianz erhalten, hatten wir uns schon angesehen, als es um den ICC ging. Folglich berechnen wir \(R^2_\text{pseudo:between}\) so:
VarU0 <- VarCorr(m0)$schulklasse[1] # Varianz des Interzepts im Nullmodell
VarU1 <- VarCorr(m1)$schulklasse[1] # Varianz des Interzepts im Modell mit Motivation als Prädiktor
1- VarU1/VarU0## [1] -0.1130776# oder kurz:
1 - VarCorr(m1)$schulklasse[1]/VarCorr(m0)$schulklasse[1]## [1] -0.1130776Am Ergebnis erkennen wir auch, wieso es sich hierbei nur um ein Pseudo-\(R^2\) handelt, denn die Varianz des Interzepts steigt tatsächlich von m0 zu m1. Dies kann auf die simultane Schätzung der beiden Varianzen mit Hilfe von (restricted) Maximum Likelihood zurückgeführt werden, welche nicht nur von den Varianzen der Mittelwerte abhängt, sondern auch vom Stichprobenfehler (vgl. Eid, et al., 2017, S. 752). In so einem Fall wird Pseudo-\(R^2\) auf 0 gesetzt. Folglich gehen wir davon aus, dass der erklärte between Varianzanteil der Matheleistung durch die Motivation 0 ist. Diesem Problem kann durch die zusätzliche Gewichtung der Varianzen durch die Anzahl der Level 1 und Level 2 Einheiten entgegengewirkt werden, was Sie vielleicht beim Schreiben Ihrer Masterarbeit dann durchführen könnten (vgl. Eid, et al., 2017, S. 752 und folgend).
Pseudo \(R^2\): between and within
Zum Schluss bestimmen wir nun noch den Anteil der Variation des Kriteriums der insgesamt (between und within) durch den Prädiktor erklärt werden kann. Dazu schauen wir uns die gemeinsame Veränderung der Varianzen auf Level 1 (within) und Level 2 (between) an. Erklärt der Prädiktor substantielle Anteile, so sollte gelten: \(\mathbb{V}ar[u_0^*]+\mathbb{V}ar[\varepsilon^*]<\mathbb{V}ar[u_0]+\mathbb{V}ar[\varepsilon]\); also sollte die gesamte nicht erklärte Varianz vom Kriterium von m0 zu m1 kleiner werden! Die relative Veränderung quantifizieren wir mit Hilfe von Pseudo-\(R^2\) für between und within:
\[\begin{align*}
R^2_\text{pseudo:bw}&=\frac{(\mathbb{V}ar[u_0]+\mathbb{V}ar[\varepsilon])-(\mathbb{V}ar[u_0^*]+\mathbb{V}ar[\varepsilon^*])}{\mathbb{V}ar[u_0]+\mathbb{V}ar[\varepsilon]}\\
&=1-\frac{\mathbb{V}ar[u_0^*]+\mathbb{V}ar[\varepsilon^*]}{\mathbb{V}ar[u_0]+\mathbb{V}ar[\varepsilon]}.
\end{align*}\]
Folglich berechnen wir \(R^2_\text{pseudo:bw}\) so:
VarE0 <- summary(m0)$sigma^2 # Varianz des Residuums im Nullmodell
VarE1 <- summary(m1)$sigma^2 # Varianz des Residuums im Modell mit Motivation als Prädiktor
VarU0 <- VarCorr(m0)$schulklasse[1] # Varianz des Interzepts im Nullmodell
VarU1 <- VarCorr(m1)$schulklasse[1] # Varianz des Interzepts im Modell mit Motivation als Prädiktor
1- (VarU1 + VarE1)/(VarU0 + VarE0)## [1] 0.2650343# oder kurz:
1 - (VarCorr(m1)$schulklasse[1] + summary(m1)$sigma^2)/(VarCorr(m0)$schulklasse[1] + summary(m0)$sigma^2)## [1] 0.2650343Insgesamt lassen sich also 26.5% der Variation der Matheleistung durch die Motivation erklären. Hierbei ist zu beachten, dass \(R^2_\text{pseudo:bw}\) nicht einfach der Mittelwert von \(R^2_\text{pseudo:between}\) und \(R^2_\text{pseudo:within}\) ist, sondern tatsächlich das gewichtete Mittel der beiden, wobei die Varianzen die Gewichte darstellen, denn ist die Residualvarianz sehr groß, dann fällt diese auch insgesamt bei der Gesamtvarianz vom Kriterium stärker ins Gewicht! Lassen wir zusätzlich unterschiedliche Steigungen zu (Random Slope), so müssen wir auch diese Varianzquelle in die Berechnung mit einbeziehen.
Hypothese 2: Modell mit zufälligem Motivations-Effekt
Um Unterschiede in der Beziehung zwischen Matheleistung und Motivation über die Klassen hinweg zu untersuchen, erweitern wir unser Modell um eine Random Slope. So lassen wir zu, dass die Beziehung zwischen der Motivation und der Matheleistung über die Klassen hinweg variiert (\(\beta_{1j}=\gamma_{10} + u_{1j}\)).
m2 <- lmer(MatheL ~ 1 + Motivation_c + (1 + Motivation_c | schulklasse), data = StudentsInClasses)
summary(m2)## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: MatheL ~ 1 + Motivation_c + (1 + Motivation_c | schulklasse)
## Data: StudentsInClasses
##
## REML criterion at convergence: 5769.6
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.2170 -0.6311 0.0160 0.6304 2.8758
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## schulklasse (Intercept) 29.38 5.420
## Motivation_c 37.73 6.143 0.31
## Residual 39.85 6.313
## Number of obs: 850, groups: schulklasse, 40
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) 54.0572 0.8858 38.3681 61.025 < 2e-16 ***
## Motivation_c 5.8938 0.9960 39.0897 5.918 6.69e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr)
## Motivatin_c 0.291Diesmal wird der Abschnitt Random effects erweitert um die Varianz des Effekts der (zentrierten) Motivation sowie die Korrelation zwischen der Motivation und dem Interzept. Die Korrelation (zwischen \(u_{0j}\) und \(u_{1j}\), also zwischen der Variation des Interzepts und der Slope) ist .31 und damit substanziell.
Interpretation: Der Motivationseffekt hat eine Varianz von 37.73 zwischen Klassen. Außerdem fällt auf, dass sich die Residualvarianz drastisch reduziert hat (von 81.46 in m1 zu 39.85 in m2). Allerdings können wir noch keine Aussage über die Signifikanz dieses Unterschieds treffen.
Test des Zufallseffekts
Um zu testen, ob die Varianz des Motivationseffekts signifikant wird, wird das Modell m1 ohne random slope mit dem Modell m2 mit random slope verglichen. Dies machen wir mit Hilfe der anova Funktion, welche in R dazu genutzt wird, um Modelle zu vergleichen. Hierbei ist es essentiell, dass wir zuvor das Paket lmerTest geladen haben. Der anova-Funktion müssen wir zunächst das restriktivere Modell (mit weniger \(df\)) übergeben und als zweites Argument das weniger restriktive Modell. Außerdem wählen wir explizit die Methode, mit welcher die Modelle verglichen werden sollen via test = "LRT". Somit verwenden wir den Likelihood-Ratio-Test. Allerdings sei an dieser Stelle erwähnt, dass dieser LRT nur eine Näherung darstellt. Um mögliche Fehlschlüsse zu reduzieren, sollten große Stichproben verwendet werden. Hierbei ist die Clusteranzahl die entscheidende Größe. Es sollten so viele Clustereinheiten wie möglich verwendet werden. Das wir Varianzen gegen Null testen stellt auch generelles Problem dar. Dies liegt daran, dass Varianzen nicht negativ sein können, wir daher eine gerichtete Hypothese formulieren müssten. Dies gilt allerdings ausschließlich für Varianzen (vgl Eid, et al., 2017, Seite 749 und folgend).
Da wir hier zunächst nur Random Effects auf Signifikanz prüfen wollen, sollten wir mit REML Schätzungen rechnen. Dazu müssen wir refit = F wählen und so der anova-Funktion zu sagen, dass REML-Schätzungen verwendet werden sollen. Würden wir fixed Effects auf Signifikanz via LRTs prüfen wollen, so müssten wir das Modell “refitten” – und zwar mit der vollen Likelihood. Wir würden dann ML verwenden.
anova(m1, m2, test = "LRT", refit = F) ## Data: StudentsInClasses
## Models:
## m1: MatheL ~ 1 + Motivation_c + (1 | schulklasse)
## m2: MatheL ~ 1 + Motivation_c + (1 + Motivation_c | schulklasse)
## npar AIC BIC logLik deviance Chisq Df Pr(>Chisq)
## m1 4 6239.1 6258.1 -3115.6 6231.1
## m2 6 5781.6 5810.1 -2884.8 5769.6 461.51 2 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Die LRT-Teststatistik (empirischer \(\chi^2\)-Wert) liegt bei \(\chi^2(df=2)=461.51\). Der Modellvergleichsoutput enthält folgende Informationen (dieser ist annähernd identisch aufgebaut und enthält jeweils unterschiedliche Teststatistiken, je nach dem welchen Test wir anfordern - bspw. bei der Regression würde Omnibustest/F-Test verwendet werden, entsprechend stünde dort die \(F\)-Statistik).
## Data: StudentsInClasses
## Models:
## m1: MatheL ~ 1 + Motivation_c + (1 | schulklasse)
## m2: MatheL ~ 1 + Motivation_c + (1 + Motivation_c | schulklasse)gibt uns an, welche Daten verwendet werden und welche Modelle verglichen werden. Hier sollte das komplexere Modell an 2. Stelle stehen, da sonst die Likelihood-Differenz negativ sein könnte.
## npar AIC BIC logLik deviance Chisq Df Pr(>Chisq)
## m1 4 6239.1 6258.1 -3115.6 6231.1
## m2 6 5781.6 5810.1 -2884.8 5769.6 461.51 2 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1gibt uns Kennwerte zum Modellvergleich an. Ganz vorne stehen die Namen der Modelle (der Objekte), die verglichen werden. npar gibt die zu schätzenden Parameter an. Für das Modell m1 ist dies \(\gamma_{00},\gamma_{10}\) (fixed) und \(\mathbb{V}ar[u_0],\mathbb{V}ar[\varepsilon]\) (random), während für m2 \(\gamma_{00},\gamma_{10}\) (fixed) und \(\mathbb{V}ar[u_0], \mathbb{V}ar[u_1], \mathbb{C}ov[u_0,u_1],\mathbb{V}ar[\varepsilon]\) (random) geschätzt werden müssen. Es kommen also die Varianz von \(u_1\) sowie die Kovarianz zwischen \(u_0\) und \(u_1\) hinzu. Der AIC (Akaike’s Information Criterion) sowie der BIC (Bayes’ Information Criterion) sind Informationskriterien, die die Komplexität des Modells sowie die Stichprobengröße mit einbeziehen. Kleinere Werte stehen für besseren Modell-Fit. Allerdings kann keine Aussage über die Signifikanz einer möglichen Differenzen in diesen getroffen werden. logLik gibt die Loglikelihood (hier restricted Loglikelihood) der Modelle an. Größere Werte sind wünschenswert. deviance ist hier einfach \(-2*\)logLik und entspricht quasi der Abweichung der Daten vom Modell (kleine Werte sind zu bevorzugen). Chisq ist die Likelihood-Differenz \(\chi^2_{emp}=-2(LL_{m_1}-LL_{m_2})=D_{m_1}-D_{m_2}\), die sich entweder über -2 mal der Loglikelihood (\(LL\)) Differenz bestimmen lässt oder via der Differenz der Devianzen (\(D\)). Df gibt die Freiheitsgrade der Likelihood-Differenz an. Dies ist hier gerade die Differenz der Anzahl der Parameter der beiden Modelle (siehe npar). Pr(>Chisq) ist der zugehörige \(p\)-Wert.
Interpretation: Modell m1 passt signifikant schlechter zu den Daten, \(\chi^2(df=2)=461.51; p<.001\), also ist die Varianz des Effekts signifikant von Null verschieden. Wir entscheiden uns somit für ein Modell inklusive Random Slope für die Motivation! Hypothese 2 wird somit durch die Daten gestützt. Dies bedeutet, dass sich die Beziehung zwischen Motivation und Matheleistung über die Klassen hinweg unterscheidet (in manchen Klassen hängt die Matheleistung somit stärker von der Lernmotivation eines Kindes ab als in anderen Schulklassen).
Grafische Veranschaulichung des Zufallseffekts
Diese Heterogenität lässt sich über ein Streudiagramm der klassenspezifischen Koeffizienten \(\beta_{1j}\) veranschaulichen. Den Code zu den hier aufgeführten Grafiken können Interessierte in Appendix A einsehen.
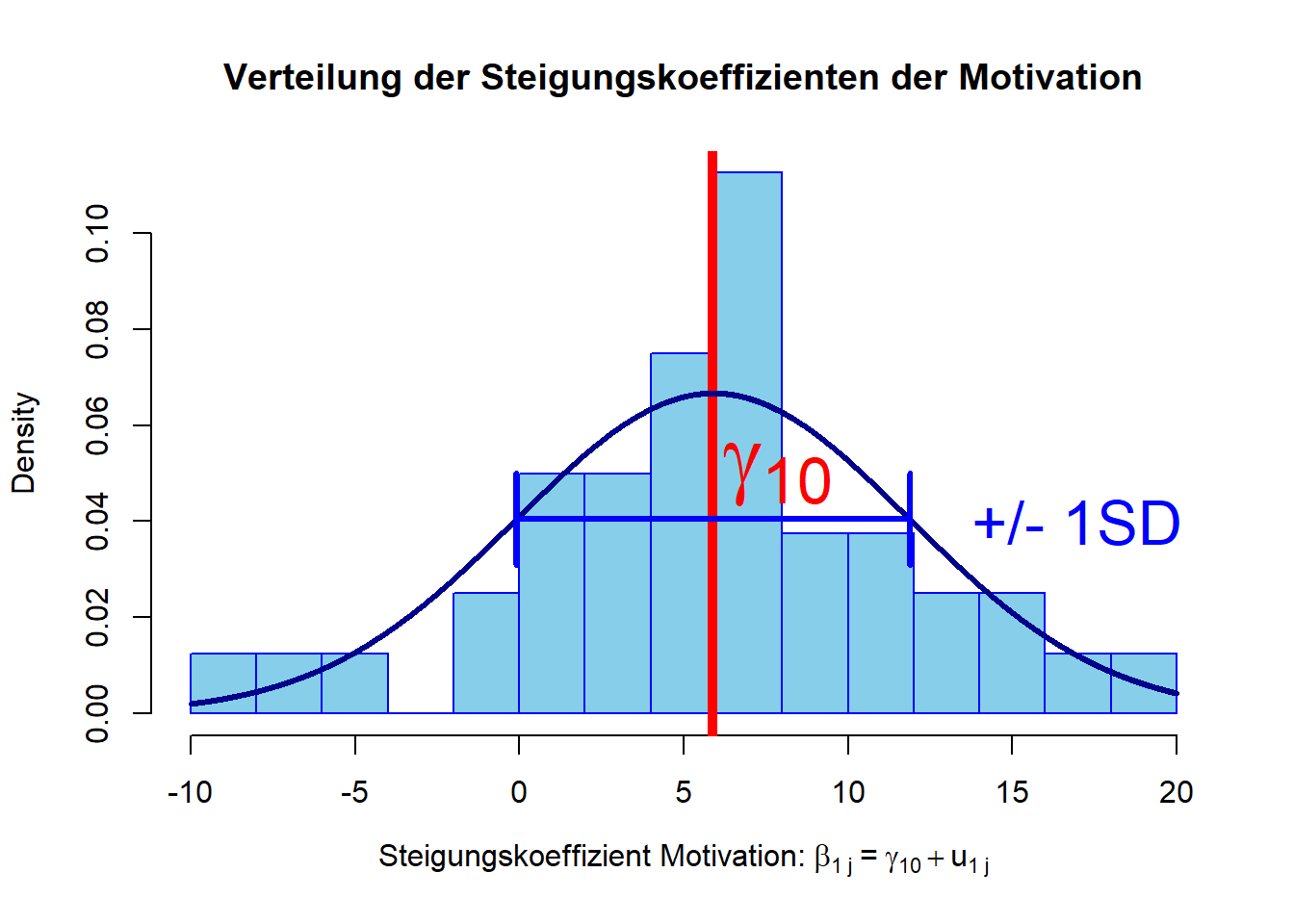
Dem Histogramm ist deutlich zu entnehmen, dass die Steigungskoeffizienten annähernd normalverteilt sind (dies ist eine wichtige Annahme, die in die Modellierung einfließt). Außerdem können wir die Heterogenität der Steigungskoeffizienten erkennen.
Eine alternative Visualisierung ist der Plot der klassenspezifischen Regresssionsgeraden, wobei \(\beta_{0j}\) und \(\beta_{1j}\) klassenspezifisch variieren. Die blaue Linie stellt hierbei den durchschnittliche (fixed) Effekt dar, welcher auch als Formel nochmals in die Grafik geschrieben wurde. Auch entnehmen wir der Grafik, dass die Motivation kategoriell ist (vertikale Ansammlung der Punkte).
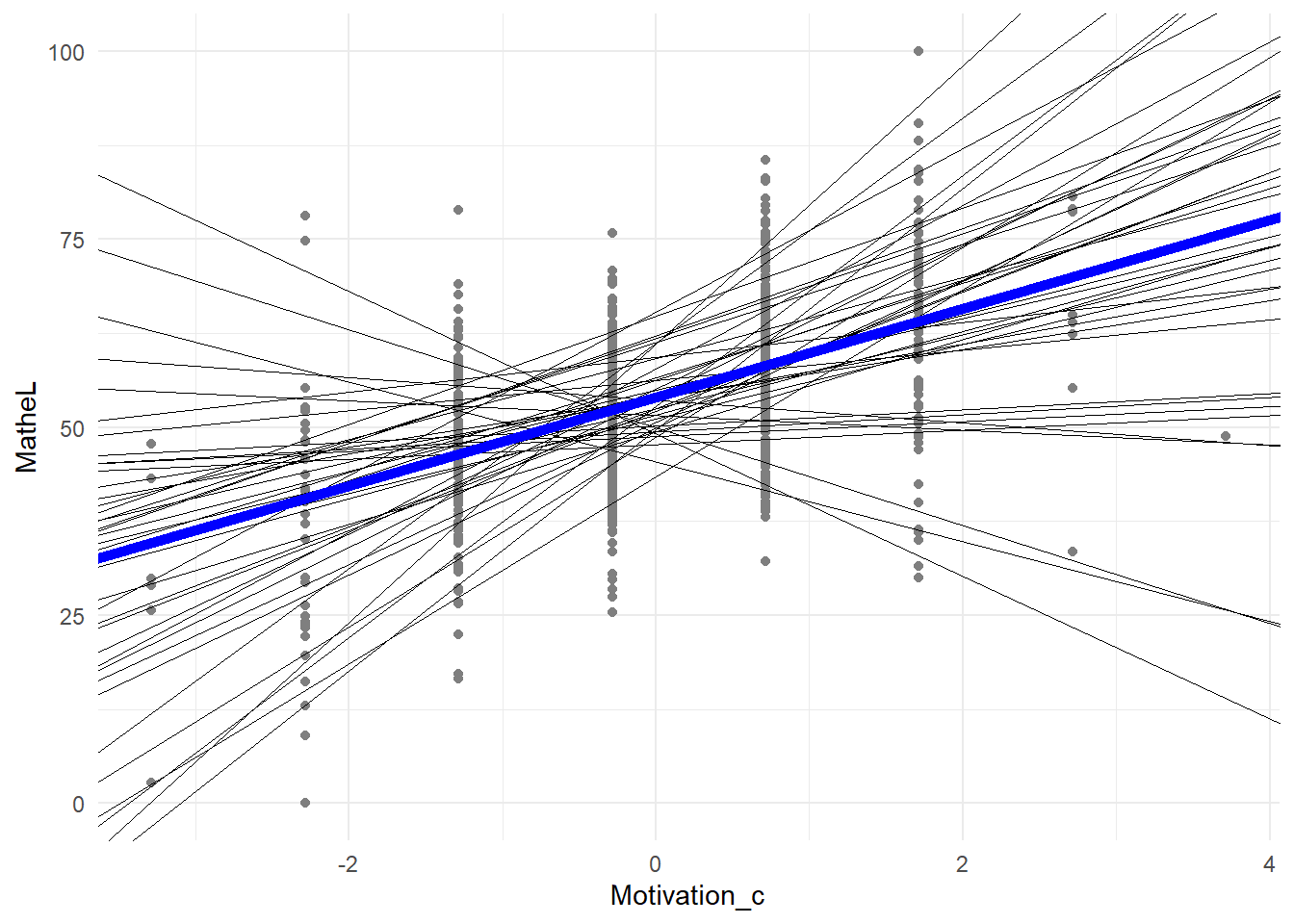
Außerdem können wir diesem Plot die Korrelation des Interzepts und der Steigung entnehmen, welche bei .31 lag. Hierbei müssen wir genau aufpassen, wo wir diese Korrelation ablesen. Die Aussage ist nämlich, dass je größer der Interzept, desto stärker der Zusammenhang zwischen Motivation und Matheleistung. Dies müssen wir entlang der y-Achse (vertikale gestrichelte Linie) untersuchen - an der Stelle, wo die Motivation durchschnittlich ausgeprägt ist und die zentrierte Variable somit den Wert 0 annimmt. Wenn wir genau hinsehen, ist es so, dass je größer der Schnittpunkt mit der y-Achse, desto größer die Steigung!
Einen reinen ML-LRT können wir beispielsweise benutzen, um den fixed Effect der Motivation auf Signifikanz zu prüfen. Dies können wir zwar auch mit dem ausgegebenen t-Wert machen. Wir wollen es uns dennoch der Vollständigkeit halber ansehen. Zur Erinnerung: Werden nur Random Effects untersucht, dann sollte REML verwendet werden, wird allerdings mindestens ein fixed Effect untersucht, so muss ML verwendet werden.
anova(m0, m1) # KEIN refit## refitting model(s) with ML (instead of REML)## Data: StudentsInClasses
## Models:
## m0: MatheL ~ 1 + (1 | schulklasse)
## m1: MatheL ~ 1 + Motivation_c + (1 | schulklasse)
## npar AIC BIC logLik deviance Chisq Df Pr(>Chisq)
## m0 3 6572.8 6587.1 -3283.4 6566.8
## m1 4 6240.1 6259.1 -3116.1 6232.1 334.7 1 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Hier sehen wir nun, dass das Modell “gerefitted” wurde. Wir haben also die ML-Schätzung verwendet, um die Likelihooddifferenz zu bestimmen. Das Ergebnis ist signifikant. Dies ist wenig überraschend. Wir hatten zuvor schon bemerkt, dass die Motivation sich auf die Matheleistung auswirkt (mit einer Irrtumswahrscheinlichkeit von \(5\%\)).
Hypothese 3: Klassengröße als Prädiktor
Nun nehmen wir die Klassengröße mit in das Modell auf. Um das Modell nicht zu komplex zu machen, lassen wir im Folgenden die Random Slope wieder weg.
Bspw. könnte angenommen werden, dass in größeren Klassen die Lehrkraft weniger Zeit pro Schüler/in aufwenden kann und somit es systematische Unterschiede zwischen Klassen mit großer und kleiner Klassengröße gibt (Hypothese 3), bzw. es mehr auf die jeweilige Motivation des Individuums ankommt (Hypothese 4). Die Klassengröße wird als fester Effekt (für eine Ebene-2-Variable ist ein Zufallseffekt auch gar nicht möglich) zusätzlich im Modell aufgenommen - mit einer L2 Variable erhofft man sich Unterschiede zwischen Clustereinheiten (hier Klassen) zu erklären (also die Interzeptvariation zu reduzieren):
m3 <- lmer(MatheL ~ 1 + KlassenG + Motivation_c + (1 | schulklasse), data=StudentsInClasses)
summary(m3)## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: MatheL ~ 1 + KlassenG + Motivation_c + (1 | schulklasse)
## Data: StudentsInClasses
##
## REML criterion at convergence: 6230.7
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.9364 -0.5567 0.0190 0.6018 4.6944
##
## Random effects:
## Groups Name Variance Std.Dev.
## schulklasse (Intercept) 25.38 5.038
## Residual 81.45 9.025
## Number of obs: 850, groups: schulklasse, 40
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) 59.7531 3.5953 38.6351 16.620 <2e-16 ***
## KlassenG -0.2198 0.1350 37.5172 -1.628 0.112
## Motivation_c 6.0893 0.2991 808.8593 20.358 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr) KlssnG
## KlassenG -0.971
## Motivatin_c 0.003 -0.003Der Output wird erweitert um den Effekt der Klassengröße \(\gamma_{01}\). Außerdem wird uns noch die Korrelation zwischen den festen Effekte ausgegeben (zwischen \(\gamma_{00},\gamma_{11},\gamma_{01}\)):
## Correlation of Fixed Effects:
## (Intr) KlssnG
## KlassenG -0.971
## Motivatin_c 0.003 -0.003Diese Informationen sollten nicht inhaltlich interpretiert werden, sondern geben Auskunft über die Schätzung der Parameter. Die Schätzung des Interzepts korreliert sehr hoch negativ mit der Schätzung des Koeffizienten der Klassengröße. Dies senkt die Stabilität der Parameterschätzungen und führt dazu, dass die Standardfehler größer werden (Stichwort: Multikollinearität).
Interpretation: Bei gleichzeitiger Berücksichtigung der Motivation ist der Effekt der Klassengröße nicht signifikant, bzw. über die Motivation hinaus ist der Effekt der Klassengröße nicht bedeutsam.
Nun wollen wir die Klassengröße noch als zentrierte Variable in das Modell aufnehmen. Wir definieren die am Stichprobenmittelwert zentrierte Klassengröße und fügen sie dem Datensatz folgendermaßen hinzu:
StudentsInClasses$KlassenG_c <- StudentsInClasses$KlassenG - mean(StudentsInClasses$KlassenG)
m3b <- lmer(MatheL ~ 1 + KlassenG_c + Motivation_c + (1 | schulklasse), data=StudentsInClasses)
summary(m3b)## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: MatheL ~ 1 + KlassenG_c + Motivation_c + (1 | schulklasse)
## Data: StudentsInClasses
##
## REML criterion at convergence: 6230.7
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.9364 -0.5567 0.0190 0.6018 4.6944
##
## Random effects:
## Groups Name Variance Std.Dev.
## schulklasse (Intercept) 25.38 5.038
## Residual 81.45 9.025
## Number of obs: 850, groups: schulklasse, 40
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) 53.7974 0.8739 36.0551 61.562 <2e-16 ***
## KlassenG_c -0.2198 0.1350 37.5172 -1.628 0.112
## Motivation_c 6.0893 0.2991 808.8593 20.358 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr) KlssG_
## KlassenG_c 0.190
## Motivatin_c 0.000 -0.003Interpretation: Die Zentrierung hat keinerlei Auswirkungen auf die Signifikanzentscheidung bzgl. der Klassengröße. Die Schätzung des durchschnittlichen Interzepts (\(\gamma_{00}\)) ändert sich. Insgesamt findet Hypothese 3 keine Evidenz in den Daten. Da der Effekt nicht signifikant ist, schauen wir uns auch nicht die erklärte between-Variation an.
Wir erkennen auch, dass die Zentrierung der Klassengröße sich positiv auf die Korrelation der fixed effects auswirkt. Damit verbunden fällt der Standardfehler des Interzepts etwas geringer aus.
Hypothese 4: Wechselwirkung zwischen Klassengröße und Motivation
Eine Wechselwirkung (also eigentlich ein Produkt von Prädiktoren) zwischen zwei Prädiktoren kann mit der Syntax X1:X2 in das Modell aufgenommen werden: Y ~ X1 + X2 + X1:X2. Eine Kurzschreibweise hier für ist Y ~ X1*X2. Insbesondere für dieses Modell empfiehlt es sich, die Klassengröße zu zentrieren, da eine Klassengröße von Null wenig sinnvoll ist und Wechselwirkungen von den Mittelwerten der Variablen abhängen (das haben wir im Abschnitt zuvor schon erledigt!). Wir ergänzen das Modell m3b um die Wechselwirkung zwischen (zentrierter) Klassengröße und (zentrierter) Motivation:
m4 <- lmer(MatheL ~ 1 + KlassenG_c + Motivation_c + KlassenG_c:Motivation_c + (1 | schulklasse),
data=StudentsInClasses)
summary(m4)## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: MatheL ~ 1 + KlassenG_c + Motivation_c + KlassenG_c:Motivation_c +
## (1 | schulklasse)
## Data: StudentsInClasses
##
## REML criterion at convergence: 6200.9
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -4.0830 -0.5785 0.0163 0.6004 4.5850
##
## Random effects:
## Groups Name Variance Std.Dev.
## schulklasse (Intercept) 25.5 5.050
## Residual 78.2 8.843
## Number of obs: 850, groups: schulklasse, 40
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) 53.79131 0.87354 36.11427 61.579 < 2e-16 ***
## KlassenG_c -0.21300 0.13491 37.53996 -1.579 0.123
## Motivation_c 6.13299 0.29316 807.83209 20.920 < 2e-16 ***
## KlassenG_c:Motivation_c 0.27575 0.04679 808.15014 5.893 5.56e-09 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr) KlssG_ Mtvtn_
## KlassenG_c 0.191
## Motivatin_c 0.000 -0.003
## KlssnG_c:M_ -0.001 0.009 0.025Dieses Modell kommt zum selben Ergebnis wie:
m4b <- lmer(MatheL ~ 1 + KlassenG_c*Motivation_c + (1 | schulklasse), data=StudentsInClasses)
summary(m4b)Interpretation: Der Koeffizient des Wechselwirkungsterms (\(\gamma_{11}\)) ist statistisch signifikant. Er beträgt 0.27575, d.h. mit jedem Kind mehr in der Klasse steigt der Motivationseffekt um ca. 0.28 Punkte. Hypothese 4 wird somit durch die Daten gestützt.
Grafische Veranschaulichung
Die Wechselwirkung kann veranschaulicht werden, indem die Regressionsgeraden nach Klassengröße unterschieden werden (hier: über die Farbe). Die in der folgenden Grafik goldene/gelbe Geraden repräsentieren (überdurchschnittlich) große Klassen, die blauen kleine (unterdurchschnittlich große/ überdurchschnittlich kleine) Klassen. Die goldenen/gelben Linien sind steiler als die blauen Linien.
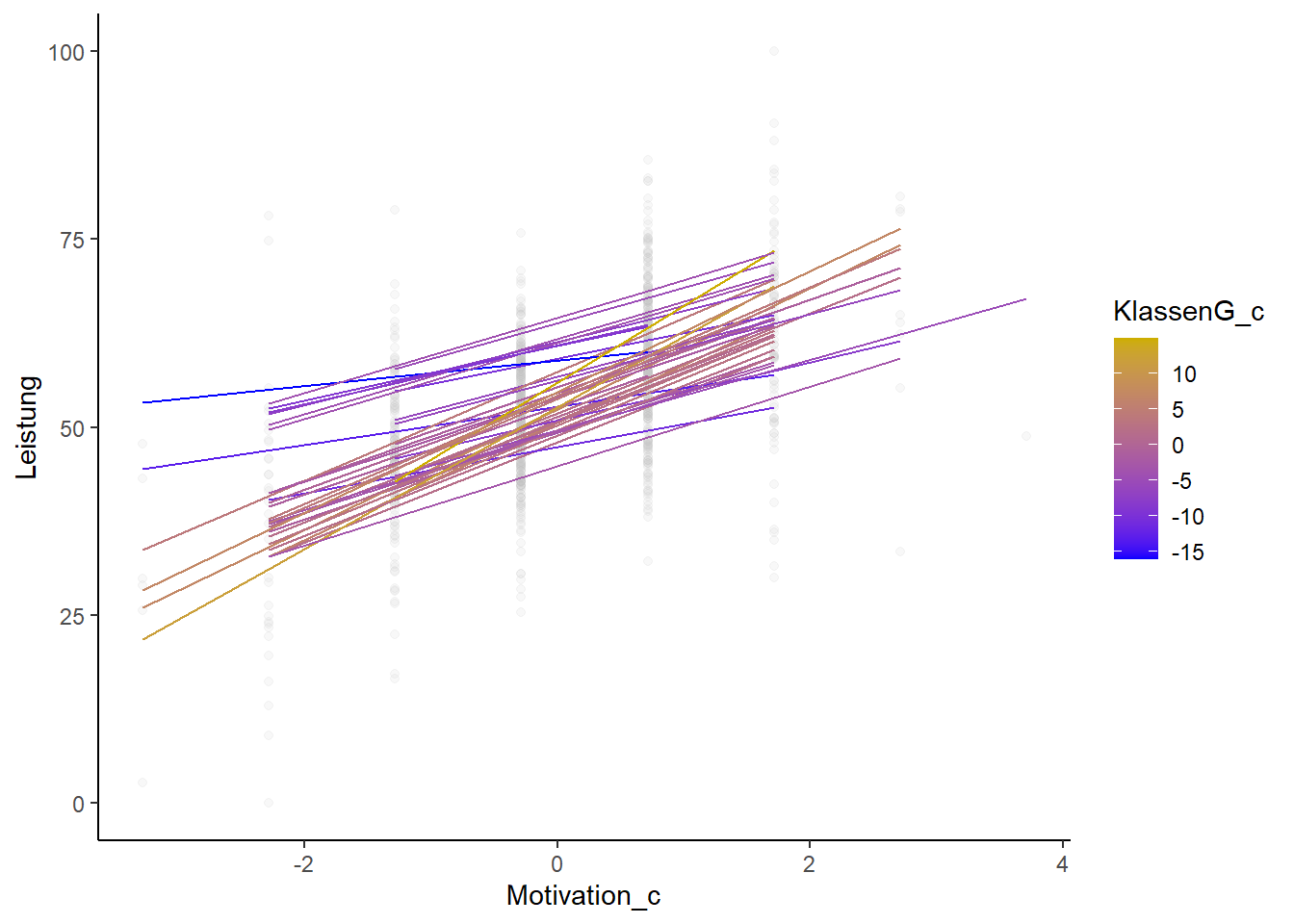
Der Grafik ist dieser Effekt deutlich zu entnehmen. Final können wir sagen, dass die individuelle Matheleistung in Schulklassen mit mehr Schülerinnen und Schülern stärker von der Lernmotivation der/des Einzelnen abhängt als in kleinen Schulklassen.
Eigentlich würde eine Cross-Level-Interaktion vor allem dann in ein Modell aufgenommen werden, wenn wir die Random Slope Variation durch eine L2 Variable erklären wollen. Wenn wir ein Modell mit ebenfalls Random Intercept Random Slope untersuchen, erkennen wir allerdings, dass die Wechselwirkung und der Haupteffekt der Klassengröße nun keinen Effekt mehr haben:
m4c <- lmer(MatheL ~ 1 + KlassenG_c + Motivation_c + KlassenG_c:Motivation_c +
(1 + Motivation_c | schulklasse),
data=StudentsInClasses)
summary(m4c)## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: MatheL ~ 1 + KlassenG_c + Motivation_c + KlassenG_c:Motivation_c +
## (1 + Motivation_c | schulklasse)
## Data: StudentsInClasses
##
## REML criterion at convergence: 5767.3
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.2062 -0.6242 0.0259 0.6379 2.8811
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## schulklasse (Intercept) 28.26 5.316
## Motivation_c 36.74 6.062 0.39
## Residual 39.85 6.313
## Number of obs: 850, groups: schulklasse, 40
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) 53.7744 0.8889 36.9895 60.495 < 2e-16 ***
## KlassenG_c -0.2158 0.1366 37.8116 -1.580 0.122
## Motivation_c 6.1883 1.0062 37.6948 6.150 3.65e-07 ***
## KlassenG_c:Motivation_c 0.2148 0.1542 38.1319 1.394 0.171
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr) KlssG_ Mtvtn_
## KlassenG_c 0.206
## Motivatin_c 0.367 0.080
## KlssnG_c:M_ 0.080 0.365 0.211anova(m4, m4c, test = "LRT", refit = F)## Data: StudentsInClasses
## Models:
## m4: MatheL ~ 1 + KlassenG_c + Motivation_c + KlassenG_c:Motivation_c + (1 | schulklasse)
## m4c: MatheL ~ 1 + KlassenG_c + Motivation_c + KlassenG_c:Motivation_c + (1 + Motivation_c | schulklasse)
## npar AIC BIC logLik deviance Chisq Df Pr(>Chisq)
## m4 6 6212.9 6241.4 -3100.5 6200.9
## m4c 8 5783.3 5821.2 -2883.6 5767.3 433.66 2 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Der Modellvergleich zeigt, dass ein Modell nur mit Klassengröße, Motivation und Interaktion zwischen Klassengröße und Motivation signifikant schlechter zu den Daten passt als ein Modell mit zusätzlicher Random Slope. Final würden wir uns also für ein Modell mit Random Intercept und Random Slope entscheiden, allerdings die Klassengröße als Prädiktor (und Cross-Level Interaktion) herauslassen.
Datenzentrierung
Wir wollen uns noch kurz ansehen, wie denn anders zentriert werden hätte können. Dazu müssen wir uns kurz klar machen, was bei der Zentrierung passiert. Dazu sei \(X_{ij}\) eine Variable der Person \(i\) aus Cluster \(j\), die wir zentrieren wollen.
Grand-Mean-Centering
Beim Grand-Mean-Centering, also der Zentrierung am Stichprobenmittelwert, ziehen wir einfach den globalen Mittelwert der Variable über alle Erhebungen und Cluster ab (das haben wir oben ja schon gemacht!): \[X^*_{ij}=X_{ij}-\bar{X}_{\cdot\cdot}\] Ein Wert von 0 auf \(X_{ij}^*\) bedeutet, dass diese Messung gerade genau dem Mittelwert der gesamten Stichprobe (über alle Personen \(i\) und alle Clustereinheiten \(j\)) entspricht.
Group-Mean-Centering
Bei der gruppenspezifischen (auch clusterspezifischen) Zentrierung (Group-Mean-Centering), ziehen wir von jeder Messung \(X_{ij}\) den Mittelwert des \(j\) Clusters auf dieser Variable ab (also bspw. den Mittelwert der Matheleistung einer Klasse ziehen wir von den individuellen Matheleistungen aller Schüler dieser Klasse ab):
\[X_{ij}^{**}=X_{ij}-\bar{X}_{\cdot j}\] Ein Wert von 0 auf \(X_{ij}^{**}\) entspricht nun dem Durchschnitt in Cluster/Gruppe \(j\). Die Variable \(X_{ij}^{**}\) sollte somit within Variation erklären (im Beispiel also die Variation innerhalb einer Klasse), was dafür spricht, dass es sinnvoll ist, diese Varianzaufklärung mit \(R^2_\text{pseudo:within}\) zu quantifizieren. Außerdem ist es sinnvoll anschließend die Variable \(\bar{X}_{\cdot j}\) mit in die Analysen aufzunehmen, da sie between-Variation enthält (also Variation, die Unterschiede zwischen Clustern darstellt). Die Varianzaufklärung von \(\bar{X}_{\cdot j}\) kann somit mit \(R^2_\text{pseudo:between}\) quantifiziert werden. Die gemeinsame Varianzaufklärung (quasi den Gesamtanteil between und within) können wir mit \(R^2_\text{pseudo:bw}\) quantifizieren.
Um diese Variablen anschließend auch noch sinnvoll hinsichtlich (z.B. Cross-Level-) Interaktionen interpretieren zu können, sollte die Gruppenmittelwertsvariable idealerweise auch noch am zentralen Mittelwert zentriert sein (der zentrale Mittelwert ist gerade auch der Mittelwert dieser Gruppenmittelwertsvariable): \[\bar{X}_{\cdot j}^*=\bar{X}_{\cdot j} - \bar{X}_{\cdot \cdot}\] Somit entspricht ein Wert von 0 auf dieser Variable gerade einer Erhebung, die dem durchschnittlichen Mittelwert über alle Cluster entspricht. Demnach können wir auch sinnvoll beide zentrierten Variablen auf einmal interpretieren. Wenn eine Person auf der Variable \(X_{ij}^{**}\) und auf der Variable \(\bar{X}_{\cdot j}^*\) einen Wert von Null aufweist, so bedeutet dies, dass die Ausprägung auf dieser Variable durchschnittlich im Bezug auf das Cluster ist und auch auf die Gesamtstichprobe (wir landen also wieder beim gesamten Durchschnitt über die Stichprobe, können aber Effekte nun im Bezug auf Unterschiede zwischen den einzelnen Gruppe und innerhalb der Gruppen auseinanderdröseln). Folgende Aussagen sind möglich: (Kinder aus) Schulklassen mit durchschnittlich höherer Motivation zeigen insgesamt im Durchschnitt eine höhere Matheleistung (quasi: wenn der Durchschnitt der Motivation höher liegt in einer Klasse, so liegt auch der Mittelwert der Matheleistung in dieser Klasse im Mittel höher) und Kinder, die im Vergleich zu ihrer Schulklasse motivierter sind, zeigen ebenfalls eine im Schnitt eine höhere Matheleistung als andere Kinder ihrer Schulklasse. Auch Interaktionen können weitere Einblicke in die Daten bringen. Natürlich könnten diese Effekte auch gegenläufig sein.
Umsetzung in R: Group-Mean-Centering
In R sieht das Ganze so aus:
# group-mean-centering:
StudentsInClasses$Motivation_groupc <- group.center(var = StudentsInClasses$Motivation,
grp = StudentsInClasses$schulklasse)
# bestimmen der gruppenspezifischen Mittelwerte (durch Umstellen der Gleichung)
StudentsInClasses$Mot_groupmeans <- group.mean(var = StudentsInClasses$Motivation,
grp = StudentsInClasses$schulklasse)
# Zentrieren der Gruppenmittelwertsvariable
StudentsInClasses$Mot_groupmeans_c <- StudentsInClasses$Mot_groupmeans -
mean(StudentsInClasses$Motivation)
head(StudentsInClasses)## MatheL Motivation KFT KlassenG schulklasse Motivation_c KlassenG_c
## 1 48.76 4 98 26 1 -0.2858824 -1.090588
## 2 46.01 3 96 26 1 -1.2858824 -1.090588
## 3 65.96 5 112 26 1 0.7141176 -1.090588
## 4 42.08 4 94 26 1 -0.2858824 -1.090588
## 5 0.00 2 78 26 1 -2.2858824 -1.090588
## 6 56.52 5 104 26 1 0.7141176 -1.090588
## Motivation_groupc Mot_groupmeans Mot_groupmeans_c
## 1 -0.36 4.36 0.07411765
## 2 -1.36 4.36 0.07411765
## 3 0.64 4.36 0.07411765
## 4 -0.36 4.36 0.07411765
## 5 -2.36 4.36 0.07411765
## 6 0.64 4.36 0.07411765# (Spalten-)Mittelwerte (gerundet auf 10 Nachkommastellen)
round(colMeans(StudentsInClasses), 10)## MatheL Motivation KFT KlassenG
## 53.616047 4.285882 100.001176 27.090588
## schulklasse Motivation_c KlassenG_c Motivation_groupc
## 20.280000 0.000000 0.000000 0.000000
## Mot_groupmeans Mot_groupmeans_c
## 4.285882 0.000000Die Funktion group.center aus dem robumeta-Paket nimmt uns die Arbeit ab, die Daten händisch an den Gruppenmittelwerten zu zentrieren (\(X_{ij}^{**}\)). Sie nimmt 2 Argumente entgegen: var die Variable, die zentriert werden soll (hier die Motivation), und grp die Gruppierungsvariable (hier die Schulklasse). Die Funktion group.mean funktioniert analog zu group.center und gibt uns gruppenspezifische Mittelwerte aus. Zum Schluss wird noch die Gruppierungsvariable zentriert am Gesamtmittelwert: \(\bar{X}_{\cdot j}^*=\bar{X}_{\cdot j} - \bar{X}_{\cdot \cdot}\). Den Spaltenmittelwerten entnehmen wir, dass die gruppenzentrierte Variable einen Mittelwert von 0 hat und die zentrierte Gruppenmittelwertsvariable ebenfalls. Außerdem sehen wir hier nochmals, dass der Mittelwert der Motivation gleich dem Mittelwert der Gruppenmittelwertsmotivation ist (Motivation vs. Mot_groupmeans).
Diese Art der Zentrierung spielt insbesondere in Multi-Level-Analyse mit Messwiederholung von Personen (die Person ist die Clusterung und die L1 Variable sind die Messungen einer Person) eine wichtige Rolle (siehe auch Eid, et al., 2017, Kapitel 20.4).
In Appendix C wird eine Funktion präsentiert, mit welcher wir uns leicht Effekte in Multi-Level-Modellen ansehen können und so bspw. erkennen, wie unterschiedliche within und between Effekte ausfallen können - z.B. dass sie komplett gegenläufig sein können, was gleichzeitig einen wichtigen Vorteil dieser Analysemethode aufzeigt! Es wird auch das Big-Fish Little-Pond Prinzip daran erläutert.
Appendix
Appendix A
Grafische Veranschaulichung des Zufallseffekts
In den folgenden 2 Grafiken müssen Sie für die eigenen Analysen lediglich m2 durch Ihr Modell austauschen und anschließend die Gruppierungsvariable (hier schulklasse) durch Ihre Clusterungsvariable ersetzen. Zudem sollten Sie anschließend die Grafikgrenzen bearbeiten.
# Histogramm der Klassenspezifischen Koeffizienten
model <- m2
beta <- coef(model)$schulklasse # Übergeben der Koeffizienten pro Klasse (Interzept und Steigungskoeffizent)
hist(beta[,2], breaks = 10, freq = F, col = "skyblue", border = "blue",
main = "Verteilung der Steigungskoeffizienten der Motivation",
xlab = expression("Steigungskoeffizient Motivation:"~beta[1~"j"]~"="~gamma[10]+u[1~"j"])) # Histogramm
gamma10 <- mean(beta[,2]) # Mittlere Steigung
VarU1 <- var(beta[,2]) # Varianz der Steigung
abline(v=gamma10, col = "red", lwd = 5) # Mittlere Steigung in der Grafik
text(x = gamma10+2, y = 0.05, labels = expression(gamma[10]), cex = 3, col = "red") # Bennenung gamma01
lines(x=seq(-10,20,0.01), dnorm(x = seq(-10,20,0.01), mean = gamma10,
sd = sqrt(VarU1)), col = "darkblue", lwd = 3) # Normalverteilung als Vergleich
arrows(y0 = dnorm(x = gamma10+sqrt(VarU1), mean = gamma10,
sd = sqrt(VarU1)), y1 = dnorm(x = gamma10+sqrt(VarU1), mean = gamma10,sd = sqrt(VarU1)),
x0 = gamma10-sqrt(VarU1), x1 = gamma10+sqrt(VarU1),
code = 3, col = "blue", lwd = 3, angle = 90) # +/- 1 SD in der Grafik
text(x = 17, y= 0.04, labels = "+/- 1SD", col = "blue", cex = 2) # Text in Grafik einfügen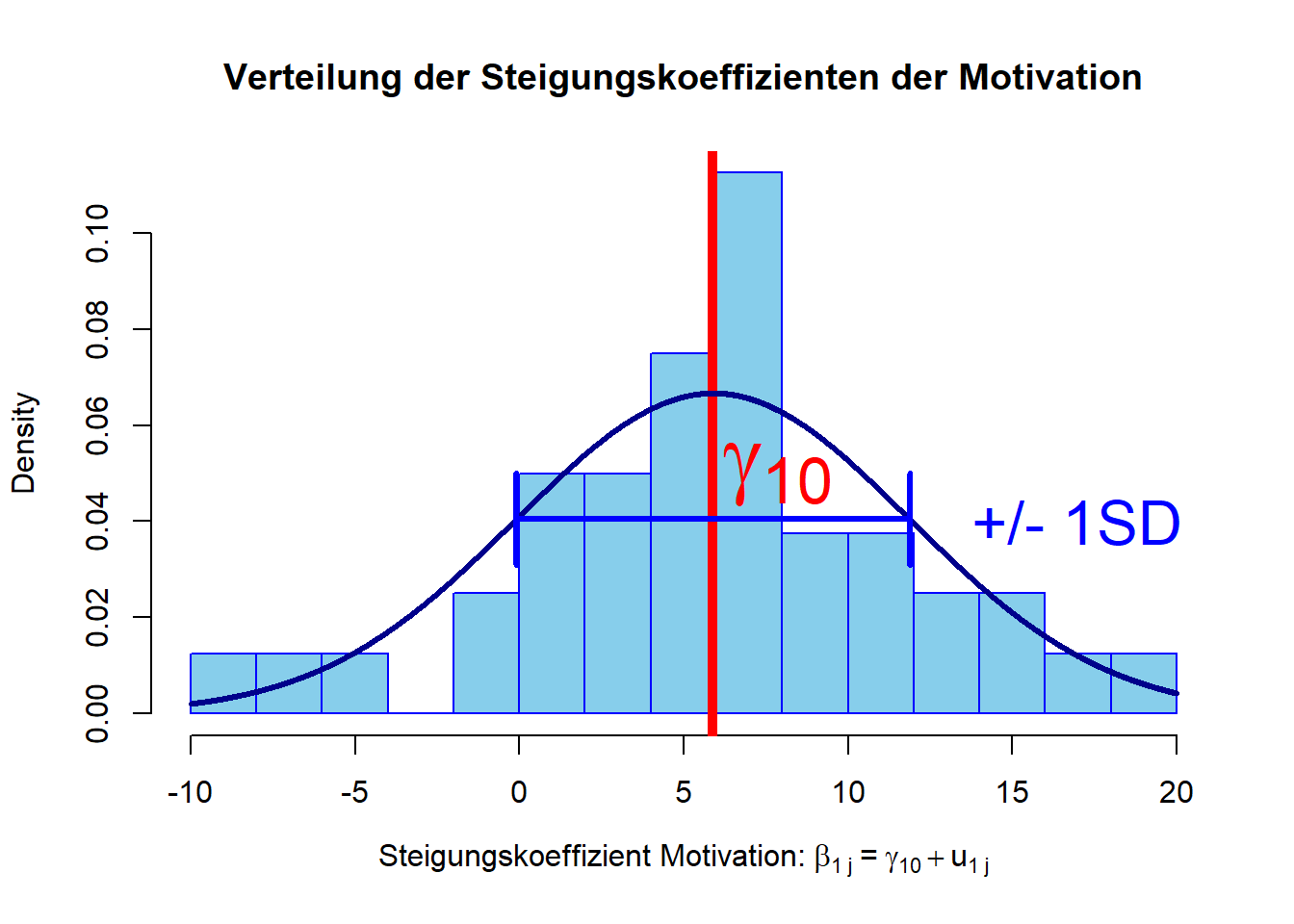
#### Das Modell zeichnen!
model <- m2
beta <- coef(model)$schulklasse # Übergeben der Koeffizienten pro Klasse (Interzept und Steigungskoeffizent)
summary_model <- summary(model)
library(ggplot2)
ggplot(data = StudentsInClasses, aes(x=Motivation_c, y = MatheL))+geom_point(col = "grey50")+
theme_minimal() + geom_abline(intercept =beta$`(Intercept)`, # Interzepts
slope = beta$Motivation_c, lwd = .2) + # und Slopes für Grafiken verwenden
geom_abline(intercept = summary_model$coefficients[1,1], # Interzepts und Slope von Durchschnitt nehmen
slope = summary_model$coefficients[2,1], lwd = 2, col = "blue")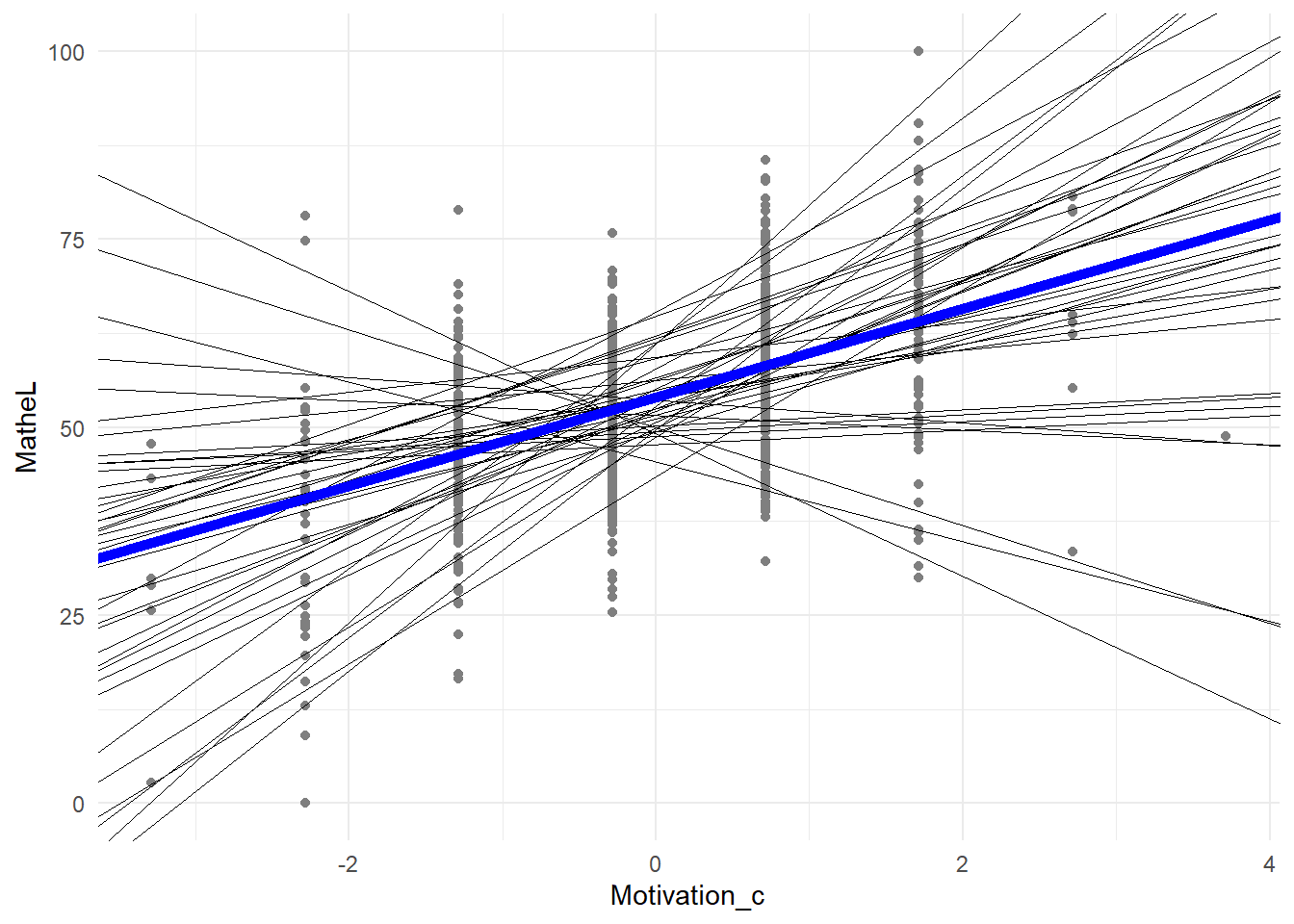
Die folgende Grafik können Sie für Ihr Modell replizieren, indem Sie m4 durch Ihr Modell ersetzen und anschließend die Clustervariable durch Ihre ersetzen (in group = schulklasse) und die L2 Variable ebenfalls durch Ihre L2 Variable ersetzen (in color = KlassenG_c). In y = MatheL muss Ihre AV rein und x = Motivation_c ist die (zentrierte) UV.
library(ggplot2) # Lade ggplot2
library(dplyr) # Lade dplyr, um Datensätze zu manipulieren (via "mutate" und "%>%")
StudentsInClasses %>% # Datensatz wird manipuliert
mutate(Leistung = fitted(m4)) %>% # Vorhergesagte Werte in den Datensatz via Funktion fitted(), nenne diese Variable Leistung
ggplot(aes(x = Motivation_c, Leistung, group = schulklasse, color = KlassenG_c)) +
scale_color_gradient(low="blue", high = "gold3") + # von blau bis gold skalieren
theme_classic() + # klassisches Thema wählen, sodass der Hintergrund nicht grau ist
geom_point(aes(y = MatheL), alpha = 0.1, color="grey")+ # beobachtete Werte als Punkte
geom_line(size=0.5) # Vorhergesagte Werte als Linien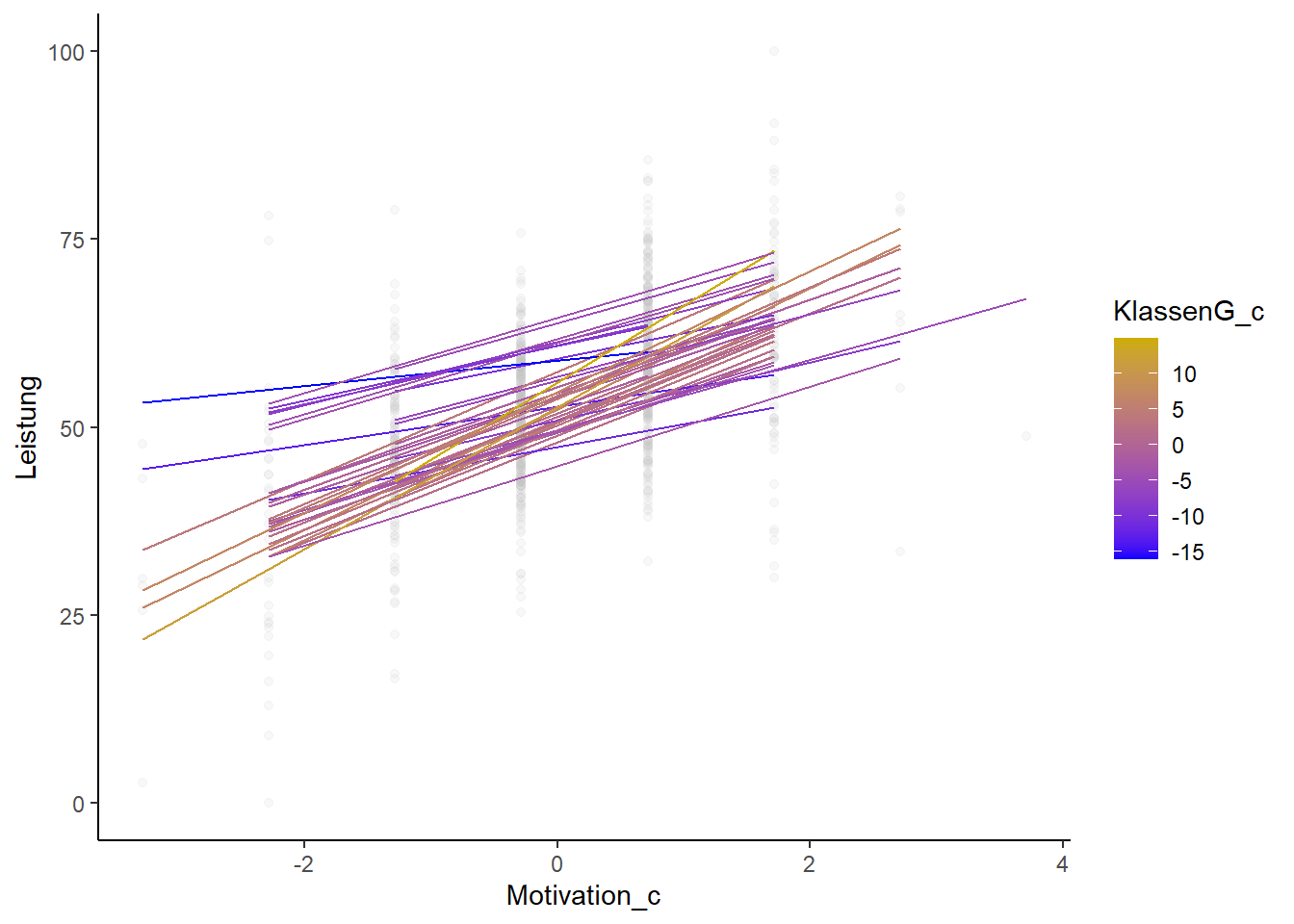
Appendix B
Varianzrechenregeln
Wenn Sie sich nun fragen, wieso wir \(\gamma_{10}\) in \(\mathbb{V}ar[Y] = \mathbb{V}ar[u_0]+\underbrace{\gamma_{10}^2\mathbb{V}ar[X_1]+\mathbb{V}ar[\varepsilon^*]}_{\mathbb{V}ar[\varepsilon]}\) quadrieren mussten, dann überlegen Sie sich folgendes Beispiel anhand der empirischen Stichprobenvarianz von einer Variable \(Y\). Diese berechnen wir so:
\[\hat{\mathbb{V}ar}[Y] = \frac{1}{n}\sum_{i=1}^n(Y_i-\bar{Y})^2,\]
wobei \(\bar{Y}\) der Mittelwert von \(Y\) ist. Wenn wir nun alle Einträge von \(Y\) mit einer Konstanten multiplizieren, also für jede Person \(i\) das Produkt \(aY_i\) berechnen (z.B. \(a=10\) oder \(a=\gamma_{10}\)) und die Varianz bestimmen (der Mittelwert von \(aY\) ist einfach \(a\bar{Y}\)), dann ergibt sich: \[\begin{align*} \hat{\mathbb{V}ar}[aY] &= \frac{1}{n}\sum_{i=1}^n(aY_i-a\bar{Y})^2\\ &=\frac{1}{n}\sum_{i=1}^n\big(a(Y_i-\bar{Y})\big)^2\\ &=\frac{1}{n}\sum_{i=1}^na^2(Y_i-\bar{Y})^2\\ &=a^2\frac{1}{n}\sum_{i=1}^n(Y_i-\bar{Y})^2\\ &=a^2\hat{\mathbb{V}ar}[Y], \end{align*}\]
Da \(a\) in der Klammer steht, die quadriert wird, muss natürlich \(a\) quadriert werden. Da auch \(a^2\) eine Konstante ist, kann sie vor die Summe gezogen werden. Daraus wird dann ersichtlich, dass die Varianz des Produktes einer Variablen mit einer Konstanten gleich der Konstanten zum Quadrat multipliziert mit der Varianz der Variablen ist. Das Ganze kann auch als Beweis durchgeführt werden - wir müssten lediglich mit Integralen und Dichten (Wahrscheinlichkeitsverteilungen) rechnen. Weitere wichtige Rechenvorschriften sind (für \(A\) und \(B\) Zufallsvariablen und \(\alpha\) und \(\beta\) Konstanten):
\[\begin{align} \mathbb{V}ar[\alpha] &= 0\\ \mathbb{V}ar[A]&=\mathbb{C}ov[A,A] \\ \mathbb{C}ov[A,B]&= \mathbb{C}ov[B,A]\\ \mathbb{C}ov[\alpha A,\beta B]&=\alpha \beta \mathbb{C}ov[A,B]\\ \mathbb{V}ar[A+B]&= \mathbb{V}ar[A] + 2\mathbb{C}ov[A,B] + \mathbb{V}ar[B]\\ \mathbb{V}ar[\alpha A+\beta B]&= \alpha^2\mathbb{V}ar[A] + 2\alpha \beta \mathbb{C}ov[A,B] + \beta^2\mathbb{V}ar[B] \end{align}\]
Außerdem ist es so, dass wenn \(A\) und \(B\) unabhängig sind so folgt, dass \(\mathbb{C}ov[A,B]=0\) (aber nicht umgekehrt!). Eine Konstante ist unabhängig von allen Variablen und hat eine Varianz von 0. Somit können wir die Variation von \(Y\) im Modell mit Motivation \(X_1\) als Prädiktor wie folgt berechnen:
\[\begin{align} \mathbb{V}ar[Y_{ij}]&=\mathbb{V}ar[\gamma_{00} + u_{0j} + \gamma_{10}X_{1,ij} + \varepsilon_{ij}^*]\\ &= \mathbb{V}ar[u_{0j}] + 2\gamma_{10}\mathbb{C}ov[u_{0j},X_{1,ij}] +\mathbb{C}ov[u_{0j},\varepsilon_{ij}^*] + 2\gamma_{10}\mathbb{C}ov[X_{1,ij},\varepsilon_{ij}^*] + \gamma_{10}^2\mathbb{V}ar[X_{1,ij}] + \mathbb{V}ar[\varepsilon_{ij}^*] \\ &= \mathbb{V}ar[u_0]+\gamma_{10}^2\mathbb{V}ar[X_1]+\mathbb{V}ar[\varepsilon^*], \end{align}\]
da \(u_0\) und \(\varepsilon^*\) unabhängig von einander und vom Prädiktor sind (somit ihre Kovarianzen jeweils 0 sind).
Außerdem siehe Eid, et al. (2017) S. 195-196 und folgend und S.570-571 und folgend, um weitere Informationen über die Rechenregeln und die Beziehungen zwischen Korrelation und Kovarianz zu wiederholen.
Appendix C
Effekte in Multi-Level-Modellen
Die angegebene Funktion kann einfache Multi-Level-Modelle plotten, in welcher es eine Variable gibt, die einen within und einen between Effekt aufweist. Somit können wir dies so interpretieren, wie eine Group-Mean-gecenterte Variable (ggplot2 muss dafür installiert sein):
plot_within_between_effects <- function(nb = 50, nw = 50, between_effect = 1, within_effect = 1)
{
# Wiederholungsfunktion
reps <- function(X, r)
{
out <- c()
for(x in X)
{
out <- c(out, rep(x, r))
}
out
}
# Daten generieren (Normalverteilt)
Xb <- rnorm(nb, mean = 0)
Yb <- between_effect*Xb + rnorm(nb)
# between Effekte
between <- cbind(Xb, Yb)
between <- apply(between, 2, FUN = function(x) reps(X = x, r = nw))
# Within Effekte
Xw <- .1*rnorm(dim(between)[1])
Yw <- within_effect*Xw + .1*rnorm(dim(between)[1])
within <- cbind(Xw, Yw)
# Gesamteffekte
total <- between + within
Cluster <- rep(1:nb, nw); Cluster <- sort(Cluster)
total <- cbind(total, Cluster)
total <- data.frame(total)
names(total) <- c("X", "Y", "Cluster")
total$Cluster <- as.factor(total$Cluster)
# Grafik erstellen
library(ggplot2)
ggplot(data = total, mapping = aes(x = X, y = Y, col = Cluster))+geom_point()+
theme_minimal()
}Die Funktion nimmt 4 Argumente entgegen. nb die Anzahl an Clustern (Default ist 50), nw Anzahl an Erhebungen innerhalb eines Clusters (Default ist 50), between_effect Effekt zwischen den Clustern (Default ist 1, hier ist es sinnvoll nur Werte zwischen -1 und 1 zu nehmen) und within_effect ist der within Gruppeneffekt (Default ist 1, hier ist es sinnvoll nur Werte zwischen -1 und 1 zu nehmen). Bspw. können wir nun ganz einfach eine Grafik für das Simpson Paradoxon (oder auch den Ökologischen Fehlschluss) erstellen (siehe auch Eid, et al., 2017, S. 729-730). Hier wird global betrachtet ein anderer Effekt gefunden, wie innerhalb der Gruppen. Wir können dies verstehen, indem wir den Between-Effekt bspw. auf -1 setzen und den Within-Effekt auf 1:
plot_within_between_effects(nb = 50, nw = 50, between_effect = -1, within_effect = 1)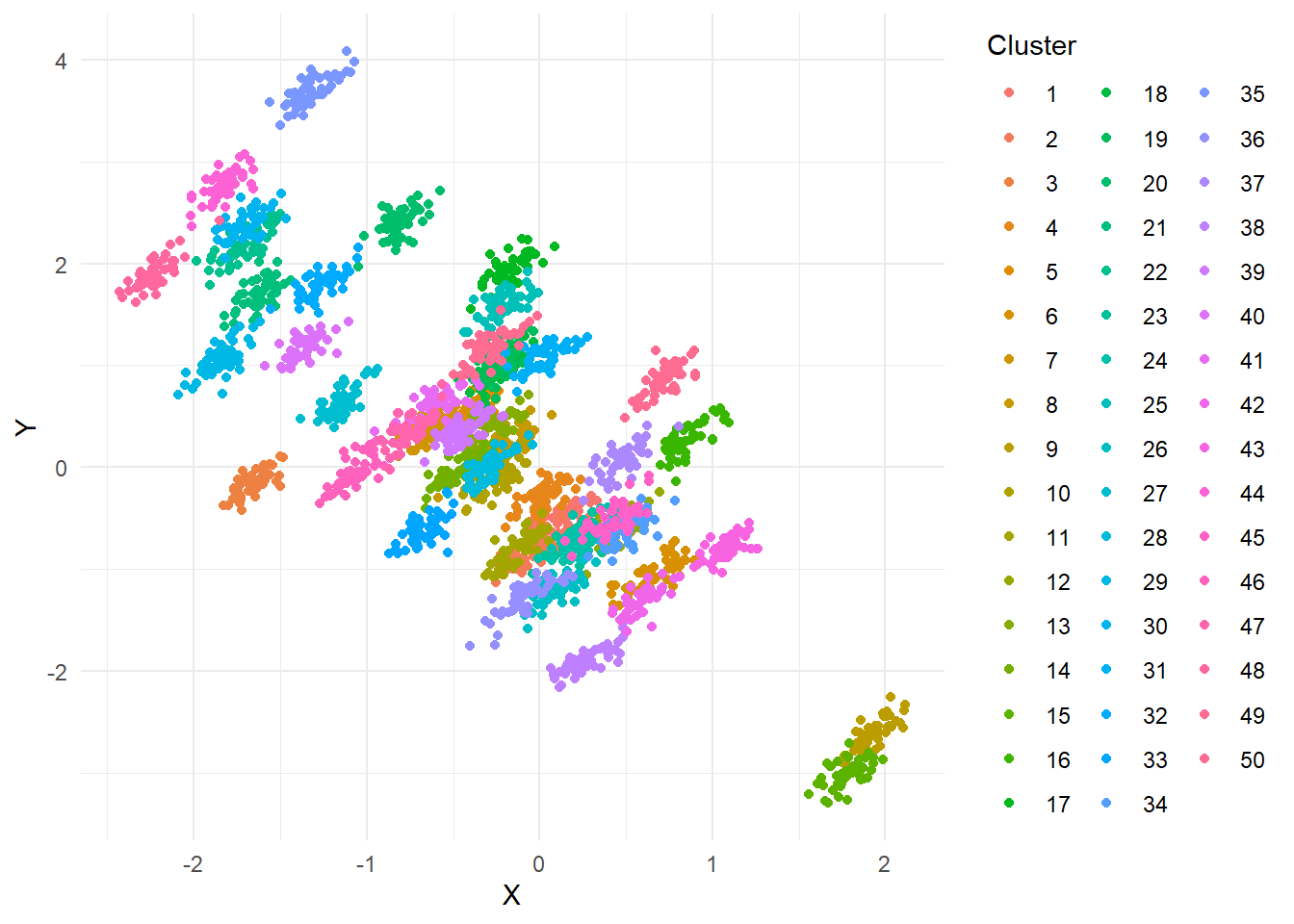
Die gesamte Punktewolke sinkt in Y für steigendes X, aber innerhalb einer Gruppe (Cluster) steigt Y für steigendes X. Falls wir hier also die Multi-Level-Struktur ignorieren, so würden wir falsche Schlüsse im Hinblick auf die Beziehung zwischen X und Y ziehen. Dieser Effekt wird manchmal auch Big-Fish-Little-Pond Effekt (siehe auch Eid, et al., 2017 S. 740; auch Kapitel 20.2.5 behandelt diese Kontexteffekt etwas ausführlicher) genannt: wenn wir beispielsweise annehmen, dass Y das Leistungsselbstkonzept ist und X ist die Begabung. In bspw. Schulklassen mit niedriger Begabung sollten Kinder mit vergleichsweise hoher Begabung ein höheres Leistungsselbstkonzept haben. Dies gilt auch für Schulklassen mit begabteren Kindern. Allerdings ist in Klassen mit durchschnittlich begabteren Kindern insgesamt das Leistungsselbstkonzept etwas niedriger, da diese sich nur mit ebenfalls sehr begabten Kindern vergleichen können.
Probieren Sie doch einmal verschiedene Effekte aus, indem Sie den Code der Funktion plot_within_between_effects <- function ... kopieren (bis hin zur letzte geschwungenen Klammer }), bei sich ausführen (dann sollte die Funktion oben rechts in Ihrem R-Studiofenser unter der Rubrik Functions zu finden sein) und anschließend verschiedene Kombinationen ausführen.
Literatur
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden (5. Auflage, 1. Auflage: 2010). Weinheim: Beltz.
Pituch, K. A. & Stevens, J. P. (2016). Applied Multivariate Statistics for the Social Sciences (6th ed.). New York: Taylor & Francis.
- Blau hinterlegte Autor:innenangaben führen Sie direkt zur universitätsinternen Ressource.
