Problemstellung

Vorgehen für dieses Projekt

Das Ziel dieses Projektes ist es, mit einer selbstgeschriebenen Funktion ein lösbares Sudoku zu erstellen. Es ist dir selbst überlassen, wie du an dieses Projekt herangehst. Wie du vielleicht auch schon hier auf Wikipedia gelesen hast, gibt es viele verschiedene Wege, um ein Sudoku zu erstellen. Aus diesem Grund kannst du entweder den hier vorgeschlagenen Weg gehen und die hier gewählte Methode mit unserer Hilfe selbstständig umsetzen oder deinen ganz eigenen Weg gehen.

Unser Vorgehen gliedert sich dabei in drei verschiedene Schritte:

1. Das Erstellen einer Lösungsfunktion: Zuerst schreiben wir eine Funktion, die bereits bestehende Sudokus lösen kann. Wie wir dabei im Detail vorgehen, erklären wir dir in Teil 1. Diese Funktion soll am Ende dazu dienen, das erstellte Sudoku auf seine Lösbarkeit zu überprüfen.
2. Das Erstellen eines vollständig ausgefüllten Gitters: Im zweiten Schritt wollen wir eine Funktion schreiben, die ein 9x9-Gitter nach den Sudoku-Prinzipien mit den Zahlen von 1 bis 9 füllt.
3. Das Generieren von eigenen Sudokus: Ausgehend von diesen beiden Funktionen werden wir dann ein Gitter vollständig befüllen, um es zur Erstellung eines Sudokus zu nutzen. Die hier erstellte Funktion soll nun von diesem Gitter eine bestimmte Anzahl an Zahlen entfernen. Hat die Funktion das gemacht, so soll sie das entstandene Sudoku auf Lösbarkeit überprüfen. Dieser Vorgang soll so lange wiederholt werden, bis wir ein lösbares Sudoku erstellt haben.

Wenn du das geschafft hast, hast du den schwierigen Teil erledigt. Nun kannst du dich darum bemühen, eine verschönerte Abbildung des Sudokus in R zu erstellen, indem du die Sudoku-Matrix als Plot darstellst. Dann kannst du dir das Sudoku als Bild speichern und mit dem Lösen deines ersten eigenen Sudokus beginnen!

Aufgabe 1: Lösungsfunktion

Erstelle eine Lösungsfunktion, mit der du ein Sudoku lösen kannst. Hierfür ist es besonders wichtig, dass du dich mit verschiedenen Lösungsstrategien vertraut machst. Diese kannst du hier auf Wikipedia finden. Wenn du bereits eine Idee hast oder eine eigene Strategie, versuch diese in R umzusetzen.

Um deine Funktion zu überprüfen, kannst du hier und hier zwei Sudokus herunterladen, um sie von deiner Funktion lösen zu lassen. Geh dabei auf Nummer sicher und schau dir auf jeden Fall an, wie häufig jede Zahl am Ende im Gitter vorhanden ist. Sind alle Zahlen 9 Mal vorhanden, kannst du relativ sicher sein, dass das Sudoku korrekt gelöst wurde.

Aufgabe 2: Ausgefülltes 9x9-Gitter erstellen

Im zweiten Schritt sollst du nun ein ganzes Sudoku erstellen. Dafür brauchst du zunächst das Gitter mit neun Zeilen und neun Spalten. Hierfür lernst du eine neue Art kennen, Daten zu speichern: die Matrix. Falls du mehr über den Umgang mit Matrizen erfahren willst, kannst du hier vorbeischauen. Im Allgemeinen ähnelt der Umgang mit Matrizen jedoch stark dem Umgang mit einem Dataframe.

Um die neun 3x3-Boxen zu definieren, die ein Sudoku typischerweise hat, kannst du für jede Box ein eigenes Objekt erstellen. Dafür wählst du die entsprechenden Felder durch Zeilen- und Spaltenbegrenzungen aus dem gesamten Sudoku aus.

Damit ist die Grundlage schon mal geschafft und das Ziel ist jetzt, dieses Gitter zu befüllen. Dafür brauchst du eine Funktion, die mithilfe von einer Zeilen- und einer Spaltenvariable von Zeile 1 bis Zeile 9 und von Spalte 1 bis Spalte 9 jedes Feld durchgeht und eine Zahl einsetzt. Überlege dir, mit welcher Art von Schleife das am besten umgesetzt werden kann. Wenn du nicht weiter weißt, kannst du dir Tipp 2 zu dieser Teilaufgabe anschauen.

Die Zahl, die eingefüllt wird, sollte eine Zufallszahl zwischen 1 und 9 sein, da sonst immer das gleiche Sudoku erzeugt werden würde. Diese Zufallszahl muss darauf überprüft werden, ob sie in der Zeile, Spalte oder in der Box bereits vorkommt. Dafür muss zunächst bestimmt werden, in welcher der neun Boxen das betrachtete Feld liegt. Kleiner Tipp: Das muss für jede Box einzeln getestet werden. Nun kannst du testen, ob die Zahl nicht in der Spalte, nicht in der Zeile und auch nicht in der Box enthalten ist. Wenn dies der Fall ist, kann die Zahl im betrachteten Feld eingesetzt werden.

Vor allem wenn das Befüllen des Sudokus weiter fortgeschritten ist, werden diese drei Bedingungen immer häufiger im ersten Versuch nicht erfüllt sein. Dann muss das Ganze erneut versucht werden. Diesmal benötigst du aber eine Zufallszahl zwischen eins und neun unter Ausschluss der bereits getesteten Zahl. Die neue Zufallszahl sollte nun auf die gleiche Weise wie zuvor auf ihr Vorkommen in der Zeile, der Spalte oder der Box überprüft werden. Falls es nun zu einem Fall kommt, bei dem ein Feld nicht nach den Sudoku-Regeln mit einer Zahl besetzt werden kann, dann sollte die Funktion an dieser Stelle abgebrochen werden und ein neues, komplett leeres Sudoku befüllen.

Denk immer daran, dass du aus jeder Schleife auch einen Ausweg brauchst. Vor allem wenn du repeat benutzt, musst du an den richtigen Stellen break einbauen. Außerdem kannst du in der Entwicklungsphase deines Sudokus zum Beispiel eine Variable einbauen, die die Durchgänge zählt. Damit, und auch durch andere Befehle, die kleine Nachrichten ausgeben, kannst du deinen Fortschritt überprüfen und gegebenenfalls fehlerhafte Stellen aufdecken. Das letzte break kannst du mit der Frage verknüpfen, ob das Sudoku voll ist bzw. ob 81 Zahlen eingesetzt wurden.

Aufgabe 3: Letzte Schritte zum eigenen Sudoku

Nutze jetzt deine beiden erstellten Funktionen, um dein eigenes, lösbares Sudoku zu erstellen. Dafür erzeugst du zuerst ein vollständig ausgefülltes 9x9-Gitter. Aus diesem Gitter lässt du so lange Zahlen löschen, bis eine bestimmte Anzahl (X) übrig bleibt. Du könntest zum Beispiel mit X = 30 anfangen. Dann überprüfst du mit deiner Lösungsfunktion, ob das erstellte Sudoku lösbar ist oder nicht. Auch hier solltest du geduldig sein und davon ausgehen, dass der Vorgang mehrere Versuche brauchen wird. Implementiere hier jeweils eine Schleife:

• Eine, die so lange läuft, bis ein lösbares Sudoku entstanden ist und
• eine, die die Lösungsfunktion abbricht, wenn das Sudoku nicht lösbar ist.

Außerdem solltest du dir das jeweils ausgearbeitete Sudoku abspeichern, bevor du versuchst, es zu lösen. Ansonsten würdest du nicht mehr nachvollziehen können, wie dein erstelltes Sudoku vor dem Lösen durch die Lösungsfunktion ausgesehen hat.

Aufgabe 4: Sudokuausgabe in R verschönern

Herzlichen Glückwunsch! Zu diesem Zeitpunkt solltest du dein erstes eigenes Sudoku erstellt haben. Um es dir anzuschauen, kannst du z.B. View('Sudoku') benutzen. Wie dir vielleicht auffällt, ist der Anblick davon nicht ganz so schön. Außerdem ist durch die Tabellendarstellung das Lösen deutlich erschwert, da auch die Begrenzungen der 3x3-Quadrate nicht deutlich werden. Aus diesem Grund möchten wir jetzt auch noch am Aussehen des Endergebnisses schrauben, um dem Ganzen den letzten Schliff zu verpassen.

Diese R-Seite und weitere Informationen zu Plots in R (wie z.B. dieses Dokument über Grafiken in R) können dir dabei eine Hilfe sein. Um die Gitterlinien zu bearbeiten, könnte dir folgende Website helfen.

Wir möchten dir in deiner Kreativität natürlich freien Lauf lassen, aber damit du eine ungefähre Vorstellung hast, wie das am Ende aussehen könnte, siehst du hier unser Endergebnis:

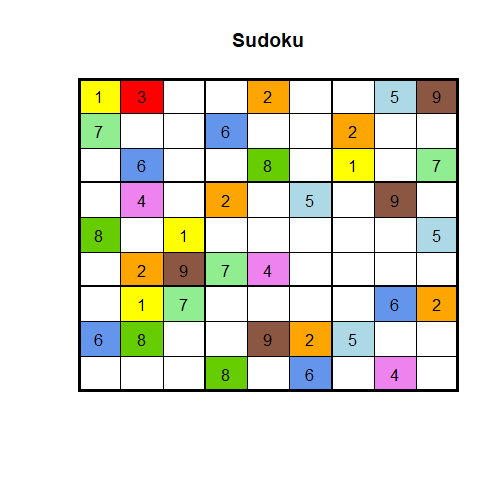
Hilfe und Lösungen

Falls du nicht weiterkommst, kannst du dir kleine Denkanstöße bei unseren Tipps holen. Probiere aber am Besten zunächst aus, ob du das Problem selbstständig mithilfe der dir gegebenen Informationen lösen kannst. Wenn du fertig bist, kannst du deine Lösung mit unseren Lösungen vergleichen. Du musst auch nicht immer den gleichen Code haben, da es oft viele Wege zum Ziel gibt.