Regressionsanalyse III
Voraussetzungsprüfung
Übersicht und Vorbereitung
In den letzten Sitzungen haben wir gesehen, wie wir ein Modell für eine Multiple Regression in R aufstellen und verschiedene Modelle gegeneinander testen können. Besonders bei der Nutzung von Inferenzstatistik wissen wir aber auch, dass genutzte statistische Verfahren häufig Voraussetzungen an die Daten mitbringen. Das Thema der heutigen Sitzung ist daher die Überprüfung von Voraussetzungen im Rahmen der Regressionsdiagnostik. Einige der aufgeführten Punkte könnten noch aus der einfachen linearen Regression bekannt sein, aber wir betrachten sie auch im Übertrag auf den hier vorliegenden multivariaten Fall. Im speziellen werden wir uns in dem Tutorial mit folgenden Aspekten beschäftigen:
- Korrekte Spezifikation des Modells - bspw. Linearität
- Homoskedastizität
- Normalverteilung der Residuen
- Multikollinearität
- Identifikation von Ausreißern und einflussreichen Datenpunkten
Über diese Aspekte hinaus, gibt es noch zwei Voraussetzungen, die wir nur kurz beschreiben und nicht mit R in diesem Tutorial analysieren werden.
Anmerkung: Im Sinne der einer sehr präzisen Benennung handelt es sich bei der Multikollinearität und der Identifikation von Ausreißern / einflussreichen Datenpunkten nicht um Voraussetzungen sondern problematische Datensituationen, die aber ähnliche Auswirkungen auf die Analysen haben können.
Übungs-Datensatz
Diese Sitzung basiert auf dem gleichen Datensatz, der auch in der Sitzung zu Regression I und II verwendet wurde. Nochmal zur Erinnerung: Eine Stichprobe von 100 Schülerinnen und Schülern hat einen Lese- und einen Mathematiktest bearbeitet, und zusätzlich dazu einen allgemeinen Intelligenztest absolviert. Im Datensatz enthalten ist zudem das Geschlecht (Variable: female, 0 = m, 1 = w). Die abhängige Variable ist die Matheleistung, die durch die anderen Variablen im Datensatz vorhergesagt werden soll.
Den Datensatz und die benötigten Pakete laden Sie wie folgt:
# Datensatz laden
load(url("https://pandar.netlify.app/post/Schulleistungen.rda"))Modell aufstellen
Wir wollen in einem ersten Schritt das Modell betrachten, um das es heute bei der Testung der Voraussetzungen gehen soll. Dabei soll Leseleistung durch das Geschlecht und die Intelligenz vorhergesagt werden. Das Modell wird unter dem Namen mod gespeichert und wir sehen uns die Ergebnisse mit Hilfe von summary() an.
mod <- lm(reading ~ female + IQ, data = Schulleistungen)
summary(mod)##
## Call:
## lm(formula = reading ~ female + IQ, data = Schulleistungen)
##
## Residuals:
## Min 1Q Median 3Q Max
## -208.779 -64.215 -0.211 58.652 174.254
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 88.2093 56.5061 1.561 0.1218
## female 38.4705 17.3863 2.213 0.0293 *
## IQ 3.9444 0.5529 7.134 1.77e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 86.34 on 97 degrees of freedom
## Multiple R-squared: 0.3555, Adjusted R-squared: 0.3422
## F-statistic: 26.75 on 2 and 97 DF, p-value: 5.594e-10Im Output sehen wir die Parameterschätzungen unseres Regressionsmodells: \[\text{reading}_i=b_0+b_1\text{female}_i+b_2\text{IQ}_i+\varepsilon_i,\] für \(i=1,\dots,100=:n\).
Den Koeffizienten entnehmen wir, dass die Prädiktoren female und IQ signifikante Anteile am Kriterium erklären (Mit einer Irrtumswahrscheinlichkeit von 5% ist der Regressionkoeffizent und damit die lineare Beziehung zwischen dem jeweiligen Prädiktor (z.B. IQ) und der Leseleistung in der Population nicht 0). Insgesamt werden 35.55% der Variation der Leseleistung durch die beiden Prädiktoren erklärt.
Die Regressionskoeffizienten \(b_j\) beziehen sich auf die Maßeinheiten der Variablen im Datensatz (um wie viele Einheiten nimmt \(y\) zu, wenn \(x_j\) um eine Einheit zunimmt). Wie wir bereits gelernt haben, sind diese unstandardisierten Regressionskoeffizienten verschiedener Prädiktoren nicht vergleichbar. So lässt sich nicht einfach sagen, dass das Geschlecht einen stärkeren Einfluss auf die Leseleistung hätte als Intelligenz, nur weil das Regressionsgewicht für Geschlecht (\(b_1=\) 38.5) größer ist als das für Intelligenz (\(b_2=\) 3.9). Aus diesem Grund werden oft standardisierte Regressionskoeffizienten berechnet und berichtet. Diese können wir mithilfe der Funktion lm.beta() aus dem Paket lm.beta ermitteln, welches wir bereits installiert haben und nur noch aktivieren müssen.
library(lm.beta)
summary(lm.beta(mod))##
## Call:
## lm(formula = reading ~ female + IQ, data = Schulleistungen)
##
## Residuals:
## Min 1Q Median 3Q Max
## -208.779 -64.215 -0.211 58.652 174.254
##
## Coefficients:
## Estimate Standardized Std. Error t value Pr(>|t|)
## (Intercept) 88.2093 NA 56.5061 1.561 0.1218
## female 38.4705 0.1810 17.3863 2.213 0.0293 *
## IQ 3.9444 0.5836 0.5529 7.134 1.77e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 86.34 on 97 degrees of freedom
## Multiple R-squared: 0.3555, Adjusted R-squared: 0.3422
## F-statistic: 26.75 on 2 and 97 DF, p-value: 5.594e-10Die standardisierten Regressionsgewichte für die Prädiktoren geben an, um wieviele Standardabweichungen sich \(y\) verändert, wenn sich \(x\) um eine Standardabweichung verändert.
Der standardisierte Koeffizient des IQ ist hierbei deutlich größer (\(\hat{\beta}_2=\) 0.58) als der vom Geschlecht (\(\hat{\beta}_1=\) 0.18). Hierdurch wird sichtbar, dass der IQ mehr Variation am Kriterium Leseleistung erklärt. Diese Information ist den unstandardisierten Koeffizienten nicht zu entnehmen (das unstandardierte Regressionsgewicht für Geschlecht ist ja sogar größer als das für Intelligenz, s.o.). Der Unterschied zwischen den unstandardisierten und standardisierten Koeffizienten kommt im Beispiel dadurch zustande, dass der Prädiktor IQ eine wesentlich größere Streuung (\(\sigma_{IQ}^2\)=248.11) aufweist als die dummykodierte Variable female (\(\sigma_{female}^2\)=0.25). Für den Fall eines intervallskalierten Prädiktors wie IQ ist der standardisierte Koeffizient auch einfacher zu interpretieren, da man die Skala Verteilung der Variablen nicht berücksichtigen muss: Wenn sich IQ um eine Standardabweichung ändert, ändert sich die Leseleistung um 0.58 Standardabweichungen. Für dummykodierte Variablen wie Geschlecht ist diese Interpretation nicht so anschaulich, da hier “eine Einheit in \(x\)” schon aussagekräftig ist - sie entspricht nämlich dem Unterschied zwischen den mit null und eins kodierten Gruppen. Der unstandardisierte Koeffizient \(b_1=\) 38.5 lässt sich als Unterschied zwischen Jungen und Mädchen in Maßeinheiten der Lesefähigkeit interpretieren. “Eine Standardabweichung im Geschlecht” ist hingegen weniger anschaulich. Daher ist es hilfreich, beide Angaben (unstandardisierte und standardisierte Regressionsgewichte) zu kennen.
Messfehlerfreiheit der unabhängigen Variablen und Unabhängigkeit der Residuen
Die beiden Voraussetzungen werden wir im Tutorial wie schon beschrieben nicht genauer analysieren, sondern hier nur zum Start die Bedeutung und Auswirkung kurz zusammenfassen. Messfehlerfreiheit der unabhängigen Variable umfasst, dass die Ausprägung der Variablen ohne Fehler gemessen werden können. Messfehler können zur Unterschätzung oder Überschätzung der Regressionsgewichte führen. Eine vielleicht aus der Diagnostik bekannte Größe, die den Grad an Messfehlerabhängigkeit bestimmen kann, ist die Reliabilität. Messinstrumente mit hoher Reliabilität sind demnach zu bevorzugen und resultieren in weniger Fehlern. Bei der Unabhängigkeit der Residuen geht es darum, dass die Residuen untereinander voneinander unabhängig sind. Verletzt wird dies bspw. bei Klumpenstichproben (Schüler:innen aus 4 verschiedenen Klassen werden erhoben - jede Klasse bildet einen Klumpen). Hier wird davon ausgegangen, dass sich Personen innerhalb eines Klumpens ähnlicher sind und damit die Fehler dieser Personen voneinander abhängen. Dies führt typischerweise zu einer Unterschätzung der Standardfehler und damit einem niedrigeren Irrtumsniveau, als wir eigentlich festgelegt haben. Ein anderes Beispiel wäre serielle Abhängigkeit, die bei Messwiederholungen auftreten kann.
Korrekte Spezifikation des Modells - bspw. Linearität
In die korrekte Spezifikation des Modells fällt, dass keine als Prädiktor relevanten Variablen aus der Population ausgelassen werden und auch keine Variablen eingeschlossen werden, die nicht zur Erklärung beitragen. Ein Aspekt davon ist, dass der Zusammenhang zwischen den Prädiktoren und dem Kriterium auch so sein soll, wie von uns in der Regressionsgleichung postuliert. Bisher nutzen wir nur lineare Zusammenhänge, weshalb eine Voraussetzung hier sein sollte, dass in der Population auch wirklich ein linearer Zusammenhang zwischen den Prädiktoren und dem Kriterium besteht.
Eine grafische Prüfung der partiellen Linearität zwischen den einzelnen Prädiktorvariablen und dem Kriterium kann durch partielle Regressionsplots (engl. Partialplots) erfolgen. Dafür sagen wir in einem Zwischenschritt einen einzelnen Prädiktor durch alle anderen Prädiktoren im Modell vorher und speichern die Residuen, die sich aus dieser Regression ergeben. Diese kennzeichnen den eigenständigen Anteil, den ein Prädiktor nicht mit den anderen Prädiktoren gemein hat. Dann werden die Residuen aus dieser Vorhersage gegen die Residuen des Kriteriums bei Vorhersage durch alle Prädiktor bis auf den betrachteten Prädiktor dargestellt. Bspw. im Block reading | others vs. IQ | others ist die lineare Beziehung zwischen der Leseleistung, wobei alle Varianzanteile der “anderen Prädiktoren” bereits herausgezogen wurden (à la Partial-/Semipartialkorrelation). Hier gibt es nur noch das Geschlecht im Modell, wodurch ersichtlich wird, dass hier die Leseleistung unter Kontrolle des Geschlechts abgebildet wird gegen die Intelligenz unter Kontrolle des Geschlecht. Mit “unter Kontrolle” meinen wir hier “gegeben die jeweiligen Prädiktoren”. Das ist im Grunde eine sehr komplizierte Ausdrucksweise, um tatsächlich einfach die Residuen einer Regression zu meinen. Wir tragen also die Residuen der Regression der Leseleistung durch das Geschlecht vs. die Residuen der Intelligenz gegeben das Geschlecht ab. Diese Grafiken können Hinweise auf systematische nicht-lineare Zusammenhänge geben, die in der Modellspezifikation nicht berücksichtigt wurden. Die zugehörige R-Funktion des car Pakets, das wir bereits installiert haben, heißt avPlots() und braucht als Argument lediglich das Regressionsmodell mod.
library(car) # Paket mit einigen Funktionen zur Regressionsdiagnostik## Loading required package: carData# partielle Regressionsplots
avPlots(model = mod, pch = 16, lwd = 4)
Mit Hilfe der Argumente pch=16 und lwd=4 werden die Darstellung der Punkte (ausgefüllt anstatt leer) sowie die Dicke der Linie (vierfache Dicke) manipuliert. Den Achsenbeschriftungen ist zu entnehmen, dass auf der y-Achse jeweils reading | others dargestellt ist. Die vertikale Linie | steht hierbei für den mathematischen Ausdruck gegeben. Others steht hierbei für alle weiteren (anderen) Prädiktoren im Modell. Dies bedeutet, dass es sich hierbei um die Residuen aus der Regression von reading auf alle anderen Prädiktoren handelt. Bei den unabhängigen Variablen (UV, also female und IQ) steht UV | others also jeweils für die jeweilige UV gegeben der anderen UVs im Modell. Somit beschreiben die beiden Plots jeweils die Beziehungen, die die UVs über die anderen UVs im Modell hinaus mit dem Kriterium (AV, abhängige Variable) haben. Wir sehen, dass die Prüfung der Linearität für die dummykodierte Variable Geschlecht wenig sinnvoll ist. Für die intervallskalierte Variable IQ ist die Prüfung sinnvoll - hier zeigt die Grafik, dass die lineare Funktion der Verteilung der Daten gut gerecht wird.
Verteilung der Residuen
Homoskedastizität
Die Varianz der Residuen sollte unabhängig von den Ausprägungen der Prädiktoren sein. Dies wird i.d.R. grafisch geprüft, indem die Residuen \(e_i\) gegen die vorhergesagten Werte \(\hat{y}_i\) geplottet werden: der sogenannte Residuenplot (engl.: residual plot). In diesem Streudiagramm sollten die Residuen gleichmäßig über \(\hat{y}_i\) streuen und keine systematischen Trends (linear, quadratisch, auffächernd, o.ä.) erkennbar sein. Die Funktion residualPlots des Pakets car erzeugt separate Streudiagramme für die Residuen in Abhängigkeit von jedem einzelnen Prädiktor \(x_j\) und von den vorhergesagten Werten \(\hat{y}_i\) (“Fitted Values”); als Input braucht sie das Modell mod. Zusätzlich wird für jeden Plot ein quadratischer Trend eingezeichnet und auf Signifikanz getestet, wodurch eine zusätzliche Prüfung auf nicht-lineare Effekte erfolgt. Sind diese Test nicht signifikant, ist davon auszugehen, dass diese Effekte nicht vorliegen und die Voraussetzungen in dieser Hinsicht nicht verletzt sind.
# Residuenplots (+ Test auf Nicht-Linearität)
residualPlots(mod, pch = 16)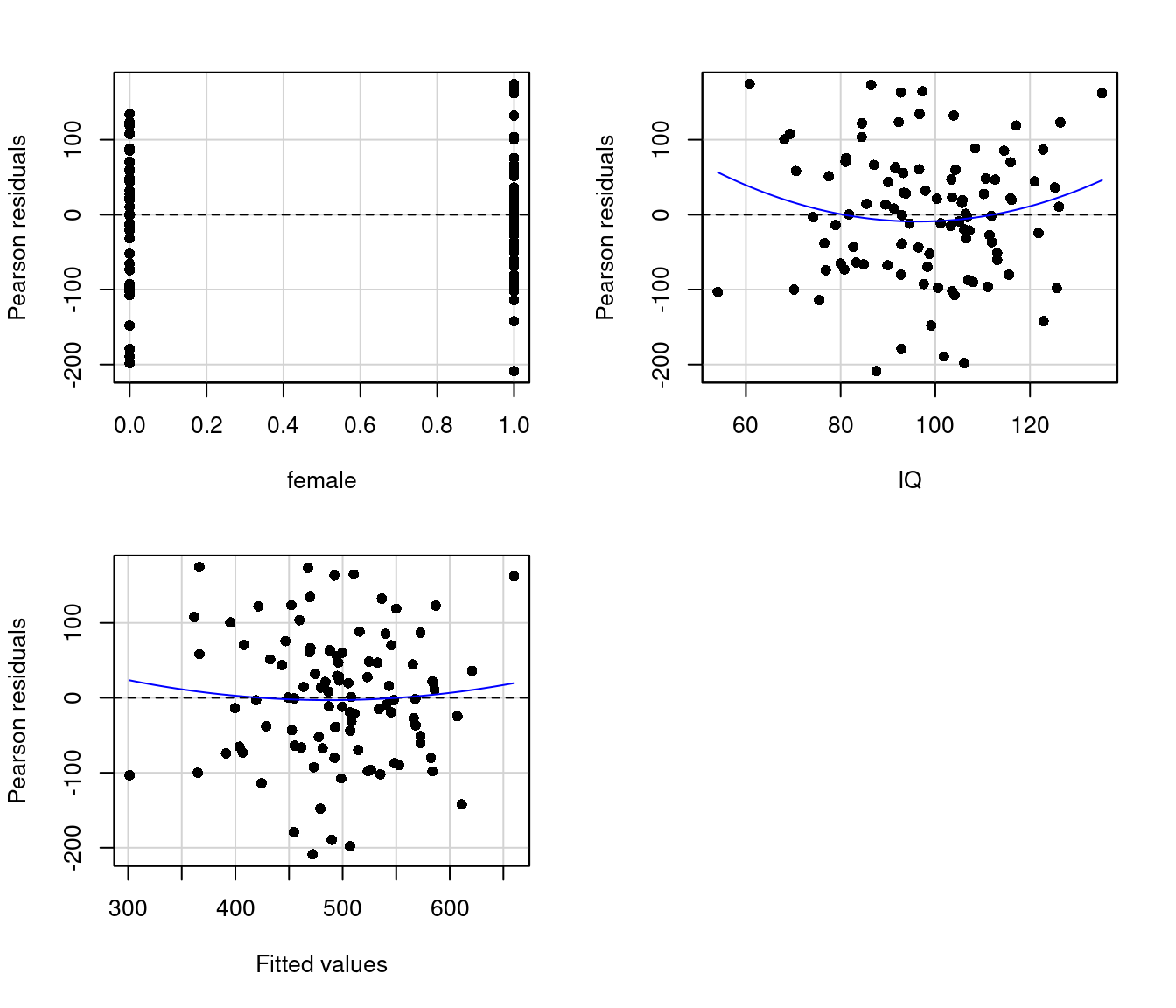
## Test stat Pr(>|Test stat|)
## female 0.0207 0.9835
## IQ 1.4015 0.1643
## Tukey test 0.5234 0.6007Die Funktion ncvTest (Test For Non-Constant Error Variance) prüft, ob die Varianz der Residuen signifikant linear (!) mit den vorhergesagten Werten zusammenhängt. Wird dieser Test signifikant, ist die Annahme der Homoskedaszidität verletzt (siehe Breusch-Pagan-Test auf Wikipedia). Wird er nicht signifikant, kann dennoch eine Verletzung vorliegen, z.B. ein nicht-linearer Zusammenhang.
# Test For Non-Constant Error Variance
ncvTest(mod)## Non-constant Variance Score Test
## Variance formula: ~ fitted.values
## Chisquare = 0.6481475, Df = 1, p = 0.42078Sowohl die grafischen Darstellungen als auch die Ergebnisse der Tests lassen keine Verletzung der Homoskedastizität erkennen.
Normalverteilung
Voraussetzung für die Signifikanztests im Kontext der linearen Regression ist die Normalverteilung der Residuen (nicht, wie oft irrtürmlich angenommen wird, der in die Analyse einbezogenen Variablen). Diese Annahme wird i.d.R. grafisch geprüft. Hierfür bietet sich zum einen ein Histogramm der Residuen an, zum anderen ein Q-Q-Diagramm (oder “Quantile-Quantile-Plot”). Zusätzlich zur grafischen Darstellung erlaubt z.B. der Shapiro-Wilk-Test auf Normalität (shapiro.test) einen Signifkanztest der Nullhypothese, dass die Residuen normalverteilt sind. Auch der Kolmogorov-Smirnov (ks.test) Test, welcher eine deskriptive mit einer theoretischen Verteilung vergleicht, wäre denkbar.
Wir beginnen mit der Vorbereitung der Daten. Wir wollen die studentisierten Residuen grafisch mit dem R-Paket ggplot2darstellen. Studentisierte Residuen sind wie standardisierten Residuen, bei denen zusätzlich eine Gewichtung der geschätzten Standardabweichung an der Stelle \(x_j\) mit einfließt, was eine präziseren Schätzung der normierten Residuen zur Folge hat. Normiert bedeutet hier, dass der Mittelwert der studentisierten Residuen 0 beträgt und die Varianz 1 ist (somit lassen sich solche Plots immer gleich interpretieren). Für mehr Informationen zu standardisierten und studentisierten Residuen schaue doch im Appendix B vorbei. Der Befehl studres aus dem MASS Paket speichert die Residuen aus einem lm Objekt, also aus dem definierten Modell mod, und studentisiert diese. Speichern Sie die Residuen aus mod als res ab und erzeugen Sie daraus einen data.frame, den Sie unter dem Namen df_res speichern. Diesen wollen wir später in den Grafiken mit ggplot2 verwenden.
library(MASS)
res <- studres(mod) # Studentisierte Residuen als Objekt speichern
df_res <- data.frame(res) # als Data.Frame für ggplot
head(df_res) # Kurzer Blick in den Datensatz## res
## 1 0.00392582
## 2 -0.03417459
## 3 -1.75038305
## 4 -0.42786749
## 5 0.23030077
## 6 -2.37718507Im Folgenden erzeugen wir ein Histogramm und ein Q-Q-Diagramm aus dem Datensatz — die Kommentare im Code erläutern diesen.
library(ggplot2)
# Histogramm der Residuen mit Normalverteilungs-Kurve
ggplot(data = df_res, aes(x = res)) +
geom_histogram(aes(y = after_stat(density)),
bins = 20, # Wie viele Balken sollen gezeichnet werden?
colour = "blue", # Welche Farbe sollen die Linien der Balken haben?
fill = "skyblue") + # Wie sollen die Balken gefüllt sein?
stat_function(fun = dnorm, args = list(mean = mean(res), sd = sd(res)), col = "darkblue") + # Füge die Normalverteilungsdiche "dnorm" hinzu und nutze den empirischen Mittelwert und die empirische Standardabweichung "args = list(mean = mean(res), sd = sd(res))", wähle dunkelblau als Linienfarbe
labs(title = "Histogramm der Residuen mit Normalverteilungsdichte", x = "Residuen") # Füge eigenen Titel und Achsenbeschriftung hinzu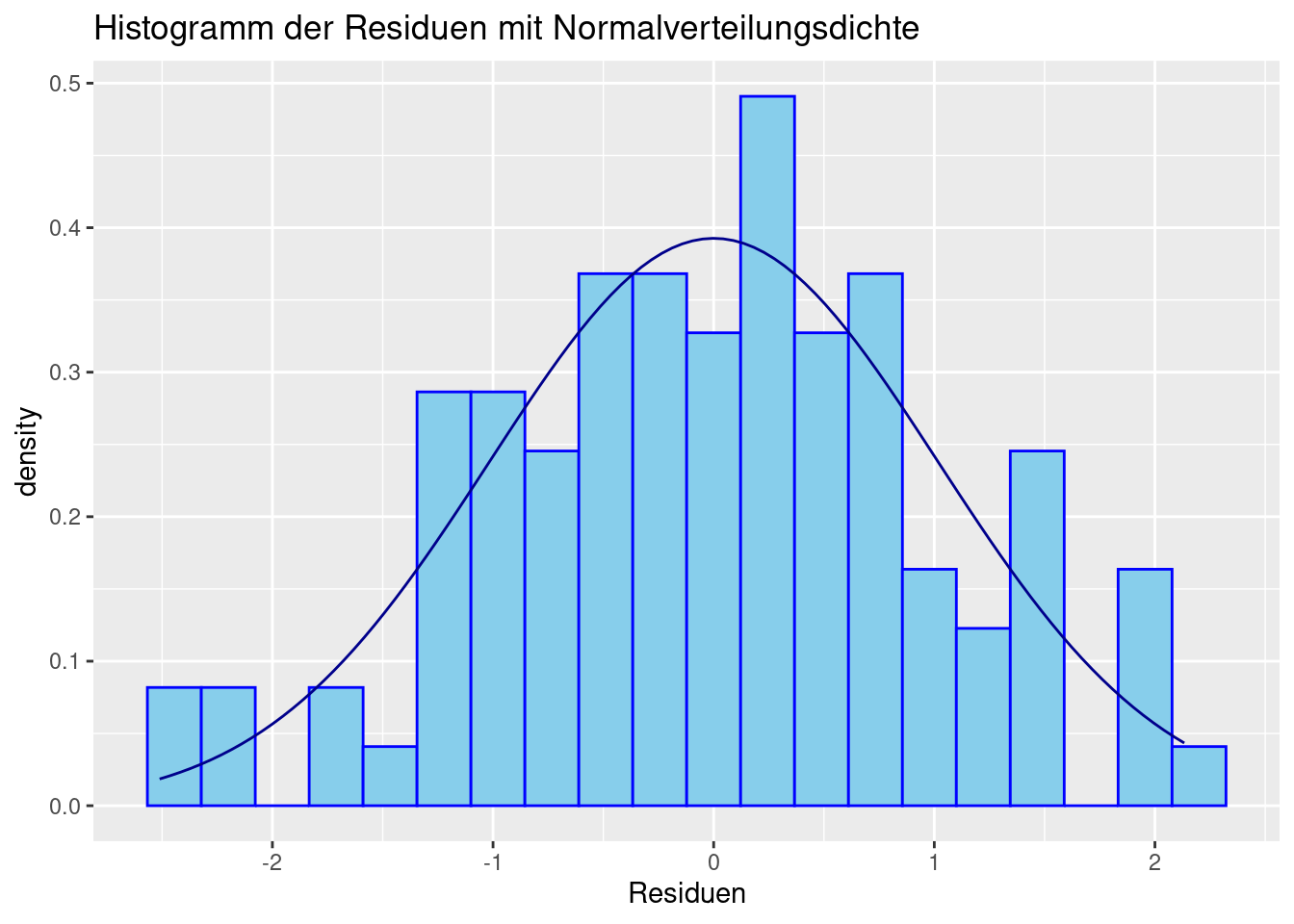
# Grafisch: Q-Q-Diagramm mit der Funktion qqPlot aus dem Paket car
qqPlot(mod, pch = 16, distribution = "norm") 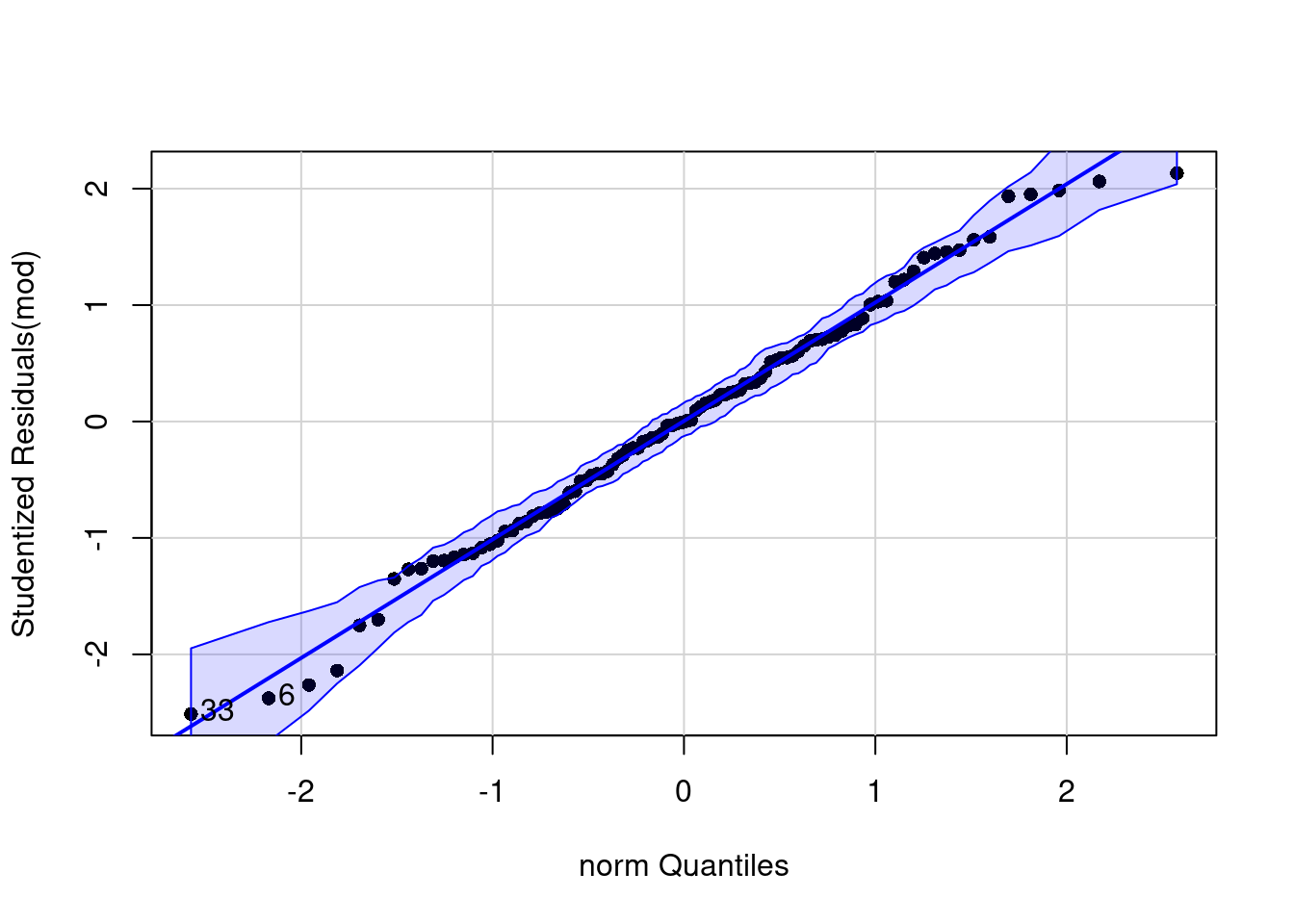
## [1] 6 33Die in der Konsole von der Funktion qqplot() ausgegebenen Werte geben die Zeilen im Datensatz an, welche Ausreißer darstellen, diese sind auch in der Grafik beschriftet.
Zusätzlich zur grafischen Darstellung können wir die Hypothese auf Normalverteilung der Residuen natürlich auch inferenzstatistisch prüfen - mit dem Shapiro-Wilk-Test oder dem Kolmogorov-Smirnov-Test prüfen. Dieses Vorgehen kann als problemtisch angesehen werden, da wir im Endeffekt auf die H0 (Verteilung der Residuen weicht nicht von Normalverteilung ab) testen wollen, was wir aber nicht können. Wir haben für unsere Überprüfung demnach keine Irrtumswahrscheinlichkeit (das wäre \(beta\)), sondern verwerfen die Normalverteilung nur bei einer extremen Verletzung (gefundene Verteilung ist seltener als 5\(%\) unter der Annahme, dass eigentlich Normalverteilung vorliegt). Die Durchführung der Inferenzstatistik ist daher als vorsichtige Ergänzung anzusehen.
# Test auf Abweichung von der Normalverteilung mit dem Shapiro-Test
shapiro.test(res)##
## Shapiro-Wilk normality test
##
## data: res
## W = 0.99015, p-value = 0.6764# Test auf Abwweichung von der Normalverteilung mit dem Kolmogorov-Smirnov Test
ks.test(res, "pnorm", mean(res), sd(res))##
## Asymptotic one-sample Kolmogorov-Smirnov test
##
## data: res
## D = 0.035584, p-value = 0.9996
## alternative hypothesis: two-sidedBeide Grafiken zeigen keine deutlichen Abweichungen von der Normalverteilung. Auch beide Tests sind nicht signifikant. Zusammenfassend können wir die Annahme normalverteilter Residuen beibehalten.
Multikollinearität
Multikollinearität ist ein potenzielles Problem der multiplen Regressionsanalyse und liegt vor, wenn zwei oder mehrere Prädiktoren hoch miteinander korrelieren. Hohe Multikollinearität
- schränkt die mögliche multiple Korrelation ein, da die Prädiktoren redundant sind und überlappende Varianzanteile in \(y\) erklären.
- erschwert die Identifikation von bedeutsamen Prädiktoren, da deren Effekte untereinander konfundiert sind (die Effekte können schwer voneinander getrennt werden).
- bewirkt eine Erhöung der Standardfehler der Regressionkoeffizienten (der Standardfehler ist die Standardabweichung zu der Varianz der Regressionskoeffizienten bei wiederholter Stichprobenziehung und Schätzung). Dies bedeutet, dass die Schätzungen der Regressionsparameter instabil, und damit weniger verlässlich, werden. Für weiterführende Informationen zur Instabilität und Standardfehlern siehe Appendix A.
Multikollinearität kann durch Inspektion der bivariaten Zusammenhänge (Korrelationsmatrix) der Prädiktoren \(x_j\) untersucht werden, dies kann aber nicht alle Formen von Multikollinearität aufdecken. Darüber hinaus ist die Berechung der sogennanten Toleranz und des Varianzinflationsfaktors (VIF) für jeden Prädiktor möglich. Hierfür wird für jeden Prädiktor \(x_j\) der Varianzanteil \(R_j^2\) berechnet, der durch Vorhersage von \(x_j\) durch alle anderen Prädiktoren in der Regression erklärt wird. Toleranz und VIF sind wie folgt definiert:
- \(T_j = 1-R^2_j = \frac{1}{VIF_j}\)
- \(VIF = \frac{1}{1-R^2_j} = \frac{1}{T_j}\)
Offensichtlich genügt eine der beiden Statistiken, da sie vollständig ineinander überführbar und damit redundant sind. Empfehlungen als Grenzwert für Kollinearitätsprobleme sind z. B. \(VIF_j>10\) (\(T_j<0.1\)) (siehe Eid, Gollwitzer, & Schmitt, 2017, S. 712 und folgend). Die Varianzinflationsfaktoren der Prädiktoren im Modell können mit der Funktion vif des car-Paktes bestimmt werden, der Toleranzwert als Kehrwert des VIFs.
# Korrelation der Prädiktoren
cor(Schulleistungen$female, Schulleistungen$IQ)## [1] -0.08467395Die beiden Prädiktoren sind nur schwach negativ korreliert. Wir schauen uns trotzdem den VIF und die Toleranz an. Dazu übergeben wir wieder das definierte Regressionsmodell an vif.
# Varianzinflationsfaktor:
vif(mod)## female IQ
## 1.007221 1.007221# Toleranzwerte als Kehrwerte
1 / vif(mod)## female IQ
## 0.9928303 0.9928303Für unser Modell wird ersichtlich, dass die Prädiktoren praktisch unkorreliert sind und dementsprechend kein Multikollinearitätsproblem vorliegt. Unabhängigkeit folgt hieraus allerdings nicht, da nichtlineare Beziehungen zwischen den Variablen bestehen könnten, die durch diese Indizes nicht abgebildet werden.
Identifikation von Ausreißern und einflussreichen Datenpunkten
Die Plausibilität unserer Daten ist enorm wichtig. Aus diesem Grund sollten Aureißer oder einflussreiche Datenpunkte analysiert werden. Diese können bspw. durch Eingabefehler entstehen (Alter von 211 Jahren anstatt 21) oder es sind seltene Fälle (hochintelligentes Kind in einer Normstichprobe), welche so in natürlicher Weise (aber mit sehr geringer Häufigkeit) auftreten können. Es muss dann entschieden werden, ob Ausreißer die Repräsentativität der Stichprobe gefährden und ob diese besser ausgeschlossen werden sollten.
Hebelwerte \(h_j\) erlauben die Identifikation von Ausreißern aus der gemeinsamen Verteilung der unabhängigen Variablen, d.h. einzelne Fälle, die weit entfernt vom Mittelwert der gemeinsamen Verteilung der unabhängigen Variablen liegen und somit einen starken Einfluss auf die Regressionsgewichte haben können. Diese werden mit der Funktion hatvalues ermittelt (die Hebelwerte spielen auch bei der Bestimmung standardisierter und studentisierter Residuen eine wichtige Rolle, sodass interessierte Lesende gerne im Appendix B mehr Informationen dazu finden). Kriterien zur Beurteilung der Hebelwerte variieren, so werden von Eid et al. (2017, S. 707 und folgend) Grenzen von \(2\cdot k / n\) für große und \(3\cdot k / n\) für kleine Stichproben vorgeschlagen, in den Vorlesungsfolien werden Werte von \(4/n\) als auffällig eingestuft (hierbei ist \(k\) die Anzahl an Prädiktoren und \(n\) die Anzahl der Beobachtungen). Alternativ zu einem festen Cut-Off-Kriterium kann die Verteilung der Hebelwerte inspiziert und diejenigen Werte kritisch betrachtet werden, die aus der Verteilung ausreißen. Die Funktion hatvalues erzeugt die Hebelwerte aus einem Regression-Objekt. Wir wollen diese als Histogramm darstellen.
n <- length(residuals(mod)) # n für Berechnung der Cut-Off-Werte
h <- hatvalues(mod) # Hebelwerte
df_h <- data.frame(h) # als Data.Frame für ggplot
# Erzeugung der Grafik
ggplot(data = df_h, aes(x = h)) +
geom_histogram(aes(y =after_stat(density)), bins = 15, fill="skyblue", colour = "blue") +
geom_vline(xintercept = 4/n, col = "red") # Cut-off bei 4/n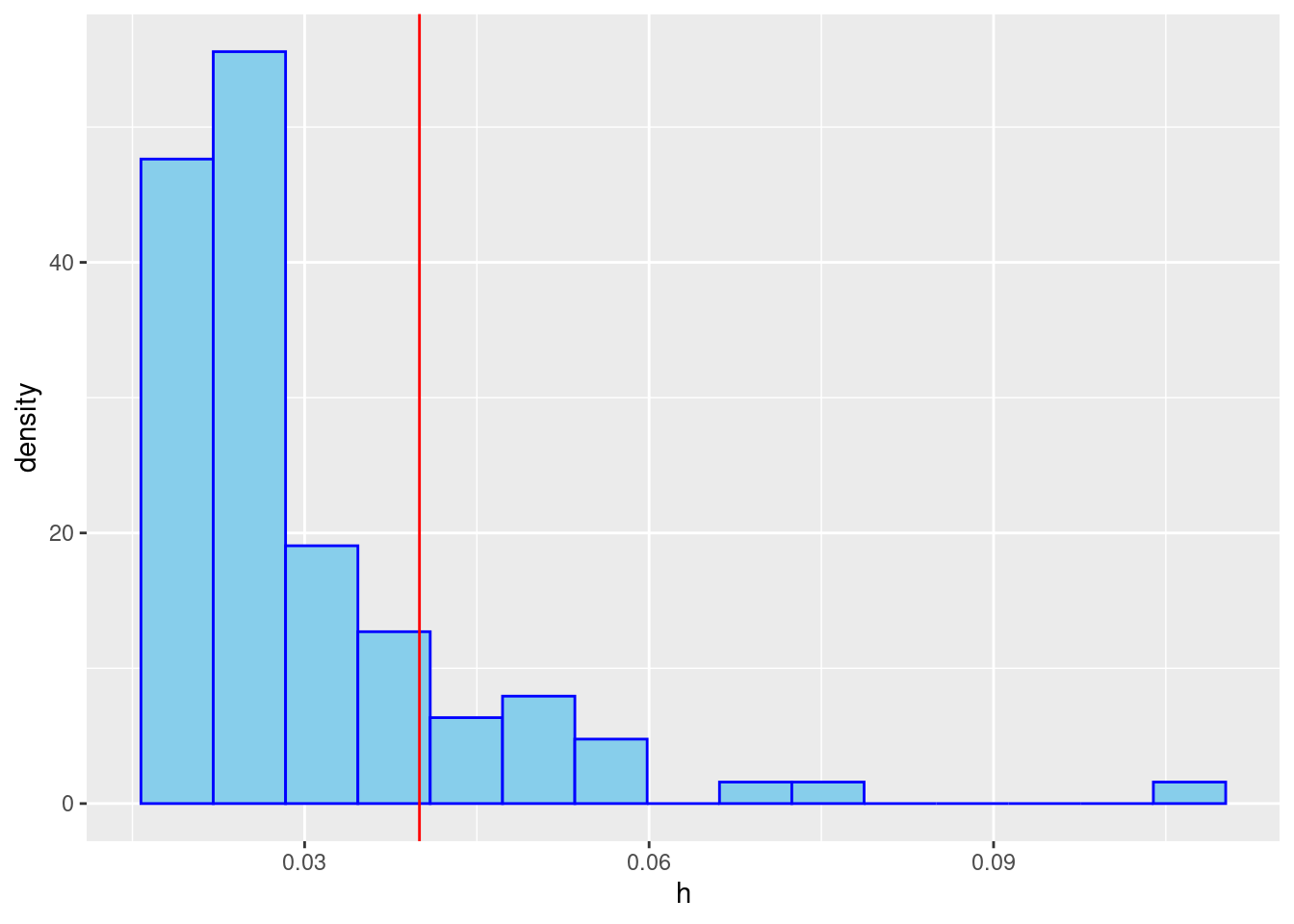
Cook’s Distanz \(CD_i\) gibt eine Schätzung, wie stark sich die Regressionsgewichte verändern, wenn eine Person \(i\) aus dem Datensatz entfernt wird. Fälle, deren Elimination zu einer deutlichen Veränderung der Ergebnisse führen würden, sollten kritisch geprüft werden. Als einfache Daumenregel gilt, dass \(CD_i>1\) auf einen einflussreichen Datenpunkt hinweist. Cook’s Distanz kann mit der Funktion cooks.distance ermittelt werden.
# Cooks Distanz
CD <- cooks.distance(mod) # Cooks Distanz
df_CD <- data.frame(CD) # als Data.Frame für ggplot
# Erzeugung der Grafik
ggplot(data = df_CD, aes(x = CD)) +
geom_histogram(aes(y =after_stat(density)), bins = 15, fill="skyblue", colour = "blue") +
geom_vline(xintercept = 1, col = "red") # Cut-Off bei 1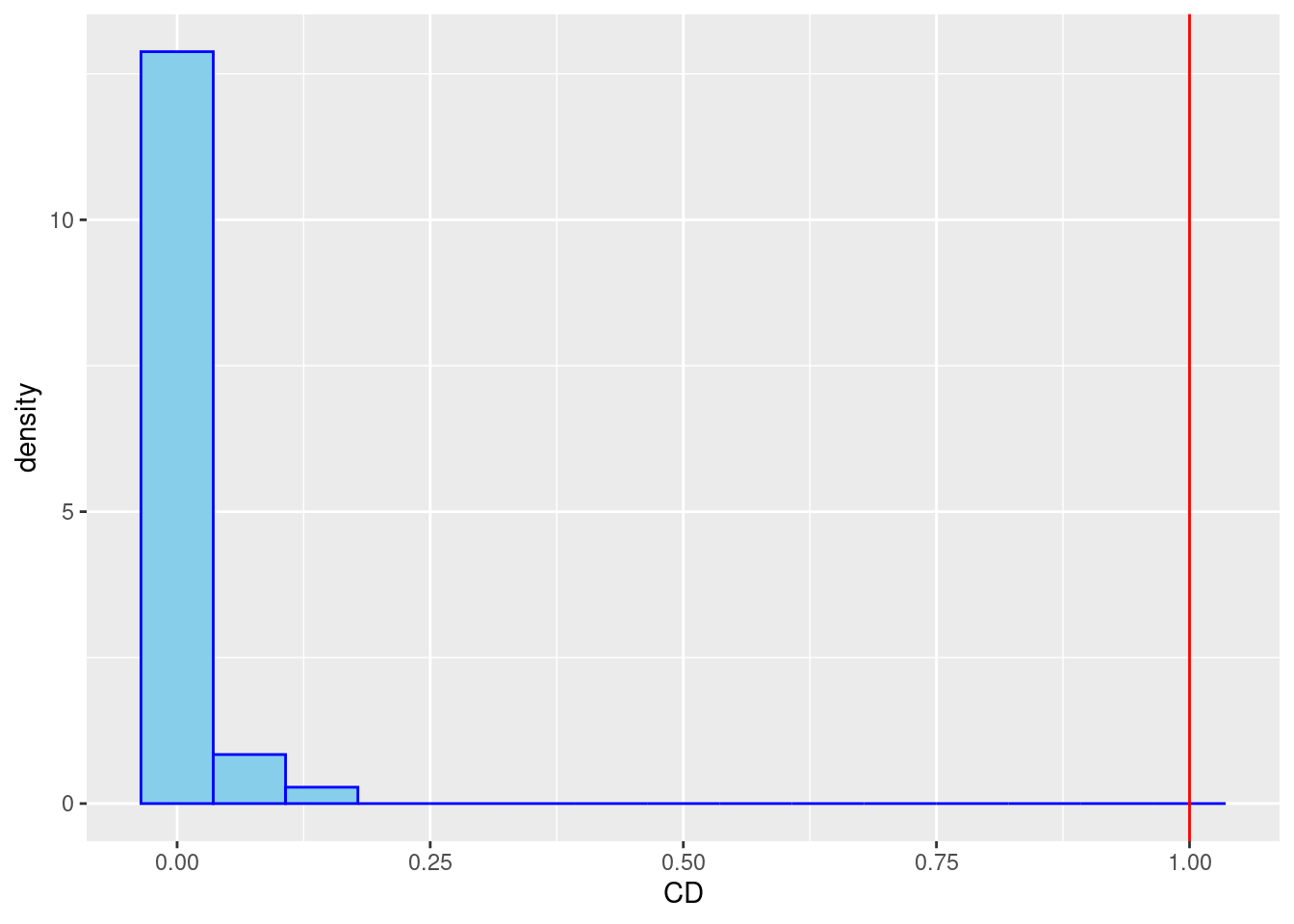
Die Funktion influencePlot des car-Paktes erzeugt ein “Blasendiagramm” zur simultanen grafischen Darstellung von Hebelwerten (auf der x-Achse), studentisierten Residuen (auf der y-Achse) und Cooks Distanz (als Größe der Blasen). Vertikale Bezugslinien markieren das Doppelte und Dreifache des durchschnittlichen Hebelwertes, horizontale Bezugslinien die Werte -2, 0 und 2 auf der Skala der studentisierten Residuen. Fälle, die nach einem der drei Kriterien als Ausreißer identifiziert werden, werden im Streudiagramm durch ihre Zeilennummer gekennzeichnet. Diese Zeilennummern können verwendet werden, um sich die Daten der auffälligen Fälle anzeigen zu lassen. Sie werden durch InfPlot ausgegeben werden. Auf diese kann durch as.numeric(row.names(InfPlot)) zugegriffen werden.
InfPlot <- influencePlot(mod)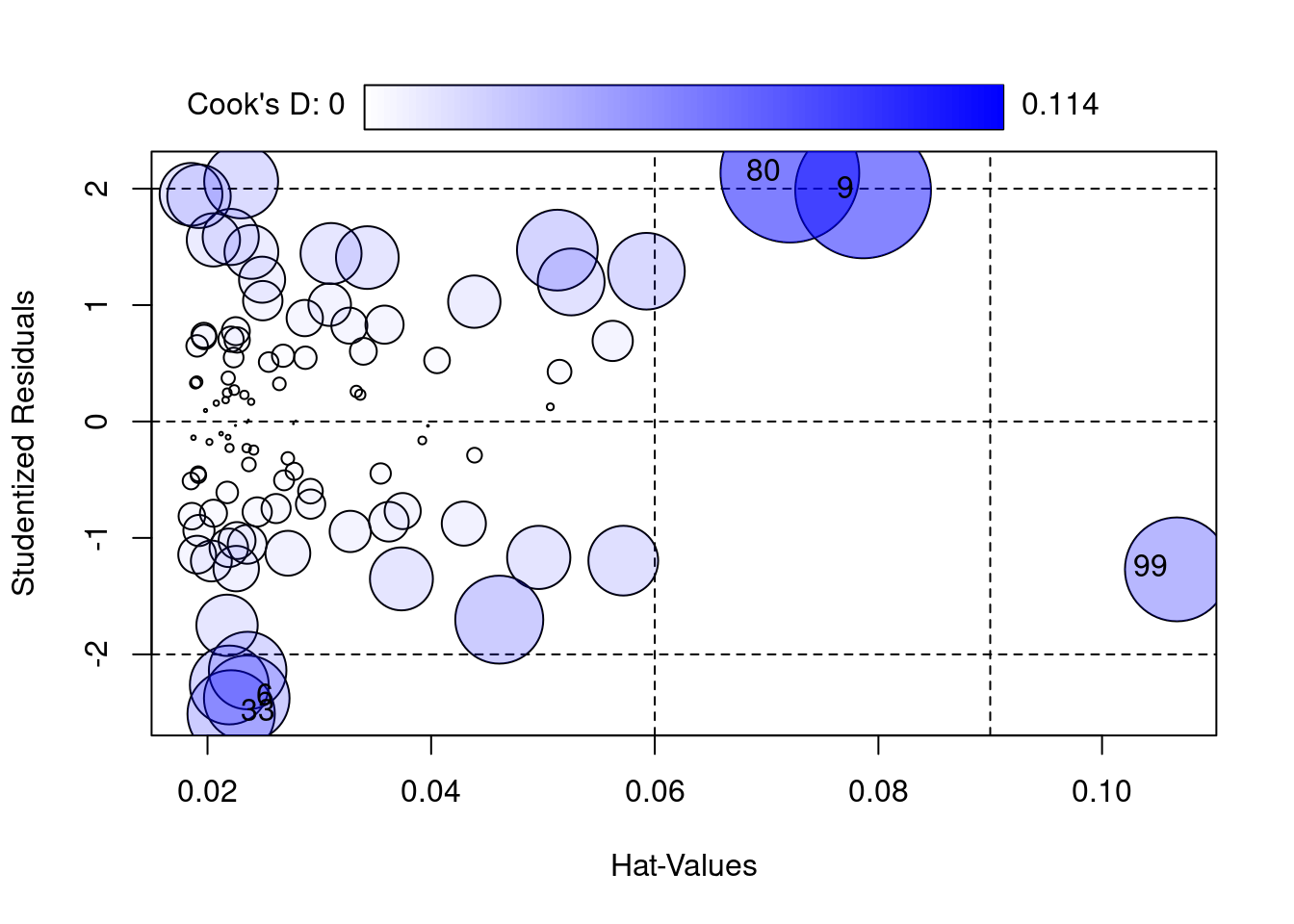
IDs <- as.numeric(row.names(InfPlot))Schauen wir uns die möglichen Ausreißer an und standardisieren die Ergebnisse für eine bessere Interpretierbarkeit.
# Rohdaten der auffälligen Fälle (gerundet für bessere Übersichtlichkeit)
round(Schulleistungen[IDs,],2)## female IQ reading math
## 6 0 106.14 308.75 602.86
## 9 1 135.20 822.01 749.56
## 33 1 87.55 263.23 494.10
## 80 1 60.77 540.63 366.73
## 99 0 54.05 198.11 367.98# z-Standardisierte Werte der auffälligen Fälle
round(scale(Schulleistungen)[IDs,],2) ## female IQ reading math
## [1,] -1.08 0.51 -1.76 0.35
## [2,] 0.92 2.35 3.06 1.61
## [3,] 0.92 -0.67 -2.19 -0.58
## [4,] 0.92 -2.37 0.42 -1.67
## [5,] -1.08 -2.80 -2.80 -1.66Die Funktion scale z-standardisiert den Datensatz, mit Hilfe von [IDs,], werden die entsprechenden Zeilen der Ausreißer aus dem Datensatz ausgegeben und anschließend auf 2 Nachkommastellen gerundet. Mit Hilfe der z-standardisieren Ergebnisse lassen sich Ausreißer hinsichtlich ihrer Ausprägungen einordnen:
Interpretation
Was ist an den fünf identifizierten Fällen konkret auffällig?
- Fall 6: recht niedrige Lesekompetenz bei gleichzeitig durchschnittlichem bis überdurchschnittlichem IQ
- Fall 9: Sehr hohe Werte in IQ, Lesen & Mathe
- Fall 33: Unterdurchschnittliche Leseleistung “trotz” eher durchschnittlicher Intelligenz
- Fall 80: Sehr niedriger IQ, gleichzeitig durchschnittliche bis überdurchschnittliche Lesekompetenz
- Fall 99: Sehr niedrige Werte in IQ, Lesekompetenz und Mathematik
Die Entscheidung, ob Ausreißer oder auffällige Datenpunkte aus Analysen ausgeschlossen werden, ist schwierig und kann nicht pauschal beantwortet werden. Im vorliegenden Fall wäre z.B. zu überlegen, ob die Intelligenztestwerte der Fälle 80 und 99, die im Bereich von Lernbehinderung oder sogar geistiger Behinderung liegen, in einer Stichprobe von Schüler:innen aus Regelschulen als glaubwürdige Messungen interpretiert werden können oder als Hinweise auf mangelndes Commitment bei der Beantwortung. Sollte Unschlüssigkeit über den Ausschluss von Datenpunkten bestehen, bietet es sich an, die Ergebnisse einmal mit und einmal ohne die Ausreißer zu berechnen und zu vergleichen. Sollte sich ein robustes Effektmuster zeigen, ist die Entschiedung ob Ausschluss oder nicht, nicht essentiell.
Appendix A
Multikollinearität und Standardfehler
Disclaimer: Dieser Block ist als Zusatz anzusehen und für Interessierte bestimmt.
Im Folgenden stehen \(\beta\)s für unstandardisierte Regressionskoeffizienten.
Für eine einfache Regressionsgleichung mit \[Y_i=\beta_0 + \beta_1x_{i1} + \beta_2x_{i2} + \varepsilon_i\] kann die selbe Gleichung auch in Matrixnotation formuliert werden \[Y = X\beta + \varepsilon.\] Hier ist \(X\) die Systemmatrix, welche die Zeilenvektoren \(X_i=(1, x_{i1}, x_{i2})\) enthält. Die Standardfehler, welche die Streuung der Parameter \(\beta:=(\beta_0,\beta_1,\beta_2)\) beschreiben, lassen sich wie folgt ermitteln. Wir bestimmen zunächst die Matrix \(I\) wie folgt \[I:=(X'X)^{-1}\hat{\sigma}^2_e,\] wobei \(\hat{\sigma}^2_e\) die Residualvarianz unserer Regressionanalyse ist (also der nicht-erklärte Anteil an der Varianz von \(Y\)). Aus der Matrix \(I\) erhalten wir die Standardfehler sehr einfach: Sie stehen im Quadrat auf der Diagonale. Das heißt, die Standardfehler sind \(SE(\beta)=\sqrt{\text{diag}(I)}\) (Wir nehmen mit \(\text{diag}\) die Diagonalelemente aus \(I\) und ziehen aus diesen jeweils die Wurzel: der erste Eintrag ist der \(SE\) von \(\beta_0\); also \(SE(\beta_0)=\sqrt{I_{11}}\); der zweite von \(\beta_1\);\(SE(\beta_1)=\sqrt{I_{22}}\); usw.). Was hat das nun mit der Kollinearität zu tun? Wir wissen, dass in \(X'X\) die Information über die Kovariation im Datensatz steckt (dafür muss nur noch durch die Stichprobengröße geteilt werden und das Vektorprodukt der Mittelwerte abgezogen werden; damit wir eine Zentrierung um die Mittelwert sowie eine Normierung an der Stichprobengröße vorgenommen). Beispielsweise lässt sich die empirische Kovarianzmatrix \(S\) zweier Variablen \(z_1\) und \(z_2\) sehr einfach bestimmen mit \(Z:=(z_1, z_2)\): \[ S=\frac{1}{n}Z'Z - \begin{pmatrix}\overline{z}_1\\\overline{z}_2 \end{pmatrix}\begin{pmatrix}\overline{z}_1&\overline{z}_2 \end{pmatrix}.\] Weitere Informationen hierzu (Kovarianzmatrix und Standardfehler) können bei Eid et al. (2017) Unterpunkt 5.2-5.4 bzw. ab Seite 1058) nachgelesen werden.
Insgesamt bedeutet dies, dass die Standardfehler von der Inversen der Kovarianzmatrix unserer Daten sowie von der Residualvarianz abhängen. Sie sind also groß, wenn die Residualvarianz groß ist (damit ist die Vorhersage von \(Y\) schlecht) oder wenn die Inverse der Kovarianzmatrix groß ist (also wenn die Variablen stark redundant sind und somit hoch mit einander korrelieren). Nehmen wir dazu der Einfachheit halber an, dass \(\hat{\sigma}_e^2=1\) (es geht hier nur um eine numerische Präsentation der Effekte, nicht um ein sinnvolles Modell) sowie \(n = 100\) (Stichprobengröße). Zusätzlich gehen wir von zentrierten Variablen (Mittelwert von 0) aus. Dann lässt sich aus \(X'X\) durch Division durch \(100\) die Kovarianzmatrix der Variablen bestimmen. Wir gucken uns drei Fälle an mit
Fall 1: \(X'X=\begin{pmatrix}100&0&0\\0&100&0\\0&0&100\end{pmatrix},\qquad\)
Fall 2: \(X'X=\begin{pmatrix}100&0&0\\0&100&99\\0&99&100\end{pmatrix} \quad\) und
Fall 3: \(X'X=\begin{pmatrix}100&0&0\\0&100&100\\0&100&100\end{pmatrix}\).
Hierbei ist zu beachten, dass \(X\) die Systemmatrix ist, welche auch die \(1\) des Interzepts enthält. Natürlich ist eine Variable von einer Konstanten unabhängig, weswegen die erste Zeile und Spalte von \(X'X\) jeweils der Vektor \((100, 0, 0)\) ist. Die zugehörigen Korrelationsmatrizen können durch Divison durch 100 berechnet werden (da wir zentrierte Variablen haben, die Stichprobengröße gleich 100 ist und die Varianzen der Variablen gerade 100 sind!). Wir betrachten nur die Minormatrizen, aus welchen die 1. Zeile und die 1. Spalte gestrichen wurden. Diese teilen wir durch 100 und erhalten die Korrelationsmatrix der Variablen:
Fall 1: \(\Sigma_1=\begin{pmatrix}1&0\\0&1\end{pmatrix},\qquad\)
Fall 2: \(\Sigma_2=\begin{pmatrix}1&.99\\.99&1\end{pmatrix} \quad\) und
Fall 3: \(\Sigma_3=\begin{pmatrix}1&1\\1&1\end{pmatrix}\).
Im Fall 1 sind die zwei Variablen unkorreliert. Die Inverse ist leicht zu bilden.
XX_1 <- matrix(c(100,0,0,
0,100,0,
0,0,100),3,3)
XX_1 # Die Matrix X'X im Fall 1## [,1] [,2] [,3]
## [1,] 100 0 0
## [2,] 0 100 0
## [3,] 0 0 100I_1 <- solve(XX_1)*1 # I (*1 wegen Residualvarianz = 1)
I_1## [,1] [,2] [,3]
## [1,] 0.01 0.00 0.00
## [2,] 0.00 0.01 0.00
## [3,] 0.00 0.00 0.01sqrt(diag(I_1)) # Wurzel aus den Diagonalelementen der Inverse = SE, wenn sigma_e^2=1## [1] 0.1 0.1 0.1Die Standardfehler sind nicht sehr groß: alle liegen bei \(0.1\).
Im Fall 2 sind die zwei Variablen fast perfekt (zu \(.99\)) korreliert - es liegt hohe Multikollinearität vor. Die Inverse ist noch zu bilden. Die Standardfehler sind deutlich erhöht im Vergleich zu Fall 1.
XX_2 <- matrix(c(100,0,0,
0,100,99,
0,99,100),3,3)
XX_2 # Die Matrix X'X im Fall 2## [,1] [,2] [,3]
## [1,] 100 0 0
## [2,] 0 100 99
## [3,] 0 99 100I_2 <- solve(XX_2)*1 # I (*1 wegen Residualvarianz = 1)
I_2## [,1] [,2] [,3]
## [1,] 0.01 0.0000000 0.0000000
## [2,] 0.00 0.5025126 -0.4974874
## [3,] 0.00 -0.4974874 0.5025126sqrt(diag(I_2)) # SEs im Fall 2## [1] 0.1000000 0.7088812 0.7088812sqrt(diag(I_1)) # SEs im Fall 1## [1] 0.1 0.1 0.1Die Standardfehler des Fall 2 sind sehr groß im Vergleich zu Fall 1 (mehr als sieben Mal so groß); nur der Standardfehler des Interzept bleibt gleich. Die Determinante von \(X'X\) in Fall 2 liegt deutlich näher an \(0\) im Vergleich zu Fall 1; hier: \(10^6\).
det(XX_2) # Determinante Fall 2## [1] 19900det(XX_1) # Determinante Fall 1## [1] 1e+06Im Fall 3 sind die zwei Variablen perfekt korreliert - es liegt perfekte Multikollinearität vor. Die Inverse kann nicht gebildet werden (da \(\text{det}(X'X) = 0\)). Die Standardfehler können nicht berechnet werden. Eine Fehlermeldung wird ausgegeben.
XX_3 <- matrix(c(100,0,0,
0,100,100,
0,100,100),3,3)
XX_3 # Die Matrix X'X im Fall 3## [,1] [,2] [,3]
## [1,] 100 0 0
## [2,] 0 100 100
## [3,] 0 100 100det(XX_3) # Determinante on X'X im Fall 3## [1] 0I_3 <- solve(XX_3)*1 # I (*1 wegen Residualvarianz = 1)
I_3
sqrt(diag(I_3)) # Wurzel aus den Diagonalelementen der Inverse = SE, wenn sigma_e^2=1
# hier wird eine Fehlermeldung ausgegeben, wodurch der Code nicht ausführbar ist und I_3 nicht gebildet werden kann:
# Error in solve.default(XX_3) :
# Lapack routine dgesv: system is exactly singular: U[2,2] = 0Der VIF bzw. die Toleranz quantifizieren die Korrelation zwischen den beiden Variablen. Der VIF wäre in diesen Analysen im 1. Fall für beide Variablen 1, im 2. Fall für beide Variabeln 50.25 und im 3. Fall nicht berechenbar (bzw. \(\infty\)). Entsprechend wäre die Toleranz im 1. Fall 1 und 1, im 2. Fall 0.02 und 0.02 sowie im 3. Fall 0 und 0.
Dieser Exkurs zeigt, wie sich die Multikolinearität auf die Standardfehler und damit auf die Präzision der Parameterschätzung auswirkt. Inhaltlich bedeutet dies, dass die Prädiktoren redundant sind und nicht klar ist, welchem Prädiktor die Effekte zugeschrieben werden können.
Die Matrix \(I\) ist im Zusammenhang mit der Maximum-Likelihood-Schätzung die Inverse der Fischer-Information und enthält die Informationen der Kovariationen der Parameterschätzer (diese Informationen enthält sie hier im Übrigen auch!).
Appendix B
Standardisierte und Studentisierte Residuen
Disclaimer: Dieser Block ist als Zusatz anzusehen und für Interessierte bestimmt.
Wir wollen uns in diesem Abschnitt verschiedene “normierte” Residuen ansehen, welche dafür genutzt werden, einflussreiche Datenpunkte und Ausreißer zu bestimmen. Diese können dann aus der Analyse ausgeschlossen werden oder zumindest genauer betrachtet werden. Normiert bedeutet hier, dass diese Residuen über Studien hinweg vergleichbar gemacht werden sollen. Der Vorteil ist somit, dass bspw. Grafiken, die auf diesen normierten Residuen beruhen, immer gleich interpretiert werden können.
Der Einfluss der Position entlang der Regressiongerade (oder Hyperebene, wenn es mehrere Prädiktoren sind) in “x”-Richtung kann mit unter enorm sein. Weit vom (gemeinsamen) Mittelwert entfernt liegende Punkte in den Prädiktoren sind hinsichtlich der Vorhersage von \(Y\) mit wesentlich größerer Unsicherheit behaftet, als diejenigen, die nah am (gemeinsamen) Mittelwert liegen. Eben jene Unsicherheit gilt es bei standardisierten und studentisierten Residuen einzupreisen. Zunächst schauen wir uns diese Unsicherheit an: Dazu simulieren wir geschwind ein paar Daten - so ähnlich wie wir dies im vergangenen Semester bereits kennengelernt haben. Wir benötigen einen Prädiktor \(X\), der beispielsweise gamma-verteilt sein soll (das ist eine recht schiefe Verteilung). Anschließend brauchen wir für eine Regressionsgleichung noch ein Residuum \(\varepsilon\), welches wir als normalverteilt annehmen, sowie ein Interzept \(\beta_0\) und einen Steigungskoeffizienten \(\beta_1\):
# Vergleichbarkeit
set.seed(1)
# simuliere X~gamma
n <- 20
X <- rgamma(n = n, shape = .7, rate = 1)
hist(X) # recht schief
# simuliere eps~norm
eps <- rnorm(n = n, mean = 0, sd = 2)
# setzte Y zusammen
beta0 <- .5; beta1 <- .6
Y <- beta0 + beta1*X + eps
# füge X und Y in einen data.frame
df <- data.frame(X, Y)
# fitte ein Regressionsmodell
reg <- lm(Y~X, data = df)
summary(reg)##
## Call:
## lm(formula = Y ~ X, data = df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.2530 -1.5084 -0.2787 1.2584 5.0920
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.2648 0.6378 0.415 0.683
## X 0.7395 0.5209 1.420 0.173
##
## Residual standard error: 2.283 on 18 degrees of freedom
## Multiple R-squared: 0.1007, Adjusted R-squared: 0.05076
## F-statistic: 2.016 on 1 and 18 DF, p-value: 0.1727Wir sehen, dass die Populationsparameter, die wir vorgegeben haben, nicht exakt getroffen werden. Das Interzept ist mit \(\hat{\beta_0}\) = 0.265 und der Steigungskoeffizent mit \(\hat{\beta_1}\) = 0.74 recht nah an den wahren Werten 0.5 und 0.6 dran, aber eben nicht exakt. Diese Unsicherheit gilt es in der Statistik zu beschreiben und einzuordnen. Ist der Effekt relativ zur Unsicherheit groß, dann sprechen wir von Signifikanz. Wir können diese Daten sehr leicht mit ggplot veranschaulichen und einen Regressionstrend hinzu zufügen. Per Default wird dann auch direkt ein Konfidenzintervall für die Regressionsgerade eingezeichnet:
library(ggplot2)
ggplot(data = df, mapping = aes(x = X, y = Y)) + geom_point() +
geom_smooth(method = "lm", formula = "y~x") +
theme_minimal()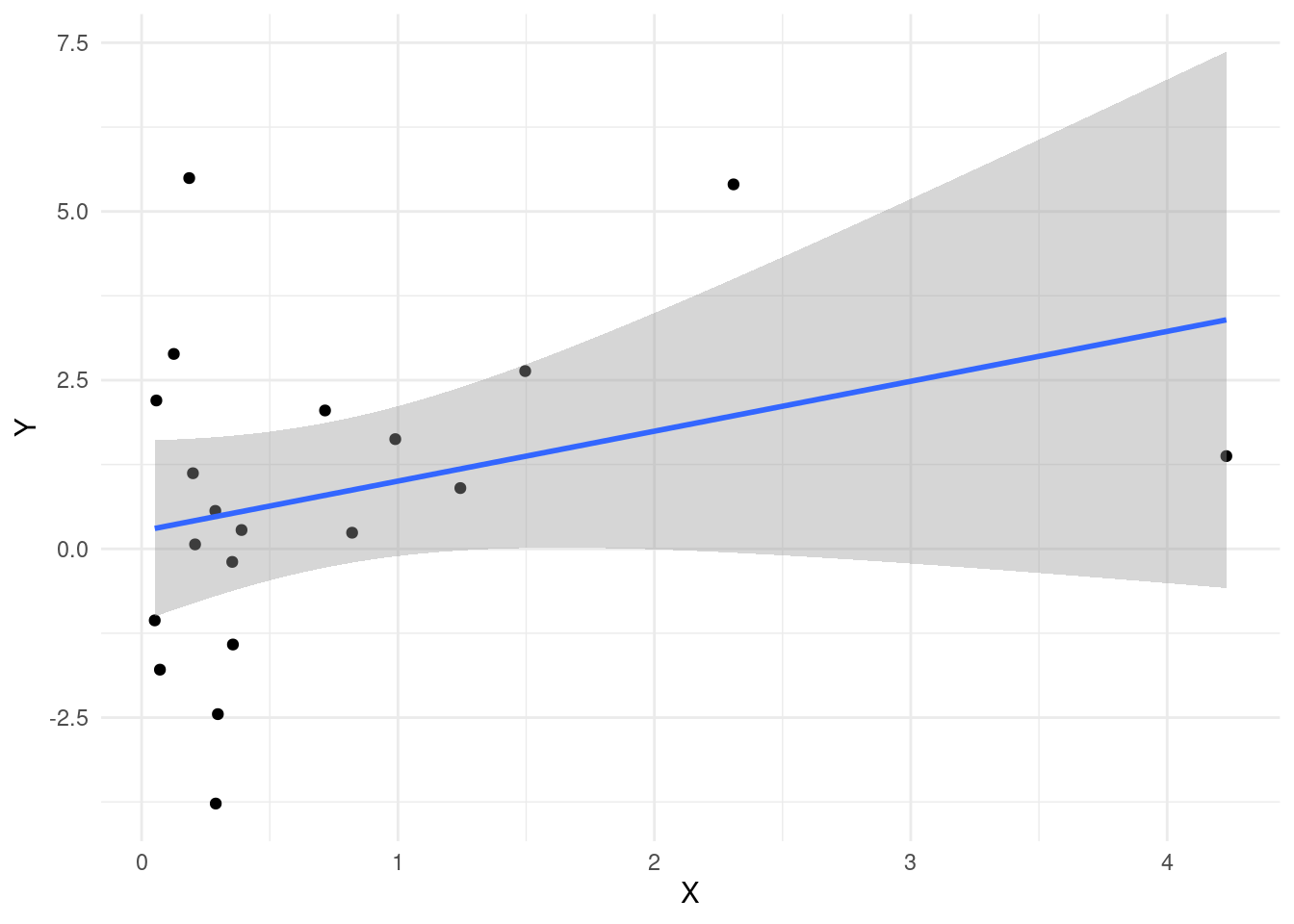
Diesem Plot entnehmen wir sehr deutlich, dass die Unsicherheit bezüglich der Vorhersage von \(Y\) (nämlich \(\hat{Y}\)) für große \(X\) viel größer ausfällt, als für mittlere (oder kleine) \(X\). Um den Fehler der Vorhersage genauer zu untersuchen, benötigen wir den Vorhersagefehler, also das Residuum. Um dieses über Studien hinweg immer gleich interpretieren zu können, muss dieses normiert werden. Wir wollen, dass es eine Varianz von 1 hat. Wenn Sie in Eid et al. (2017) die Seiten 709 bis 710 durcharbeiten, lernen Sie standardisierte und studentisierte Residuen kennen. Diese Definition weicht etwas von der Definition der standardisierten und studentisierten Residuen aus dem MASS-Paket ab. In Eid et al. (2017) wird das standardisierte Residuum so definiert, dass das Residuum einfach durch seine Standardabweichung geteilt wird:
\[\hat{\varepsilon}_{i,\text{std}} := \frac{\hat{\varepsilon}_{i}}{\hat{\sigma}},\]
wobei \(\hat{\sigma}\) der geschätze Regressionsfehler (also die Standardabweichung der Residuen) ist.
So haben wir die Standardisierung auch schon vorher kennengelernt. Da bei einem Residuum der Mittelwert eh bei 0 liegt, müssen wir den Mittelwert des Residuums auch vorher nicht mehr abziehen, sondern es reicht das Residuum durch die Standardabweichung zu teilen. Gleichzeitig wird in Eid et al. (2017) das studentisierte Residuum so definiert, dass wir uns das Wissen über den Regressionzusammenhang zwischen den unabhängigen Variablen und der abhängigen Variable zu Nutze machen und einpreisen, dass wir für Punkte, die weit vom Mittelwert der Prädiktoren entfernt liegen, größere Residuen erwarten können. Das hatten wir auch in dem Plot gesehen, dass an den Rändern das Konfidenzintervall viel breiter ausfällt.
Wir bestimmen nun das standardisierte Residuum und das studentisierte Residuum für den größten \(X\)-Wert. Diesen müssen wir vorher erst noch einmal finden und nennen ihn dann Xmax:
# größtes X finden
ind_Xmax <- which.max(X)
Xmax <- X[ind_Xmax]
Xmax## [1] 4.230831# zugehörigen Y-Wert finden
Y_Xmax <- Y[ind_Xmax]
Y_Xmax## [1] 1.374412# sd_eps bestimmen
sd_eps <- summary(reg)$sigma
sd_eps## [1] 2.282814# vorhergesaten y-Wert bestimmen
Y_pred_Xmax <- predict(reg, newdata = data.frame("X" = Xmax))
Y_pred_Xmax## 1
## 3.39369In ind_Xmax steht einfach nur die Position innerhalb des Vektors, an der das Maximum angenommen wird - also quasi die Personennummer - hier ist das die 5. Wenn wir diese auf \(X\) und \(Y\) anwenden, erhalten wir die jeweiligen Werte, die zu dieser Person gehören.
Um zu prüfen, ob wir uns verrechnet haben, zeichnen wir den vorhergesagten \(Y\)-Wert für den größten \(X\)-Wert von 4.231 in unsere Grafik ein:
ggplot(data = df, mapping = aes(x = X, y = Y)) + geom_point() +
geom_smooth(method = "lm", formula = "y~x") +
theme_minimal()+
geom_point(mapping = aes(x = Xmax, y = Y_pred_Xmax), cex = 4, col = "gold3")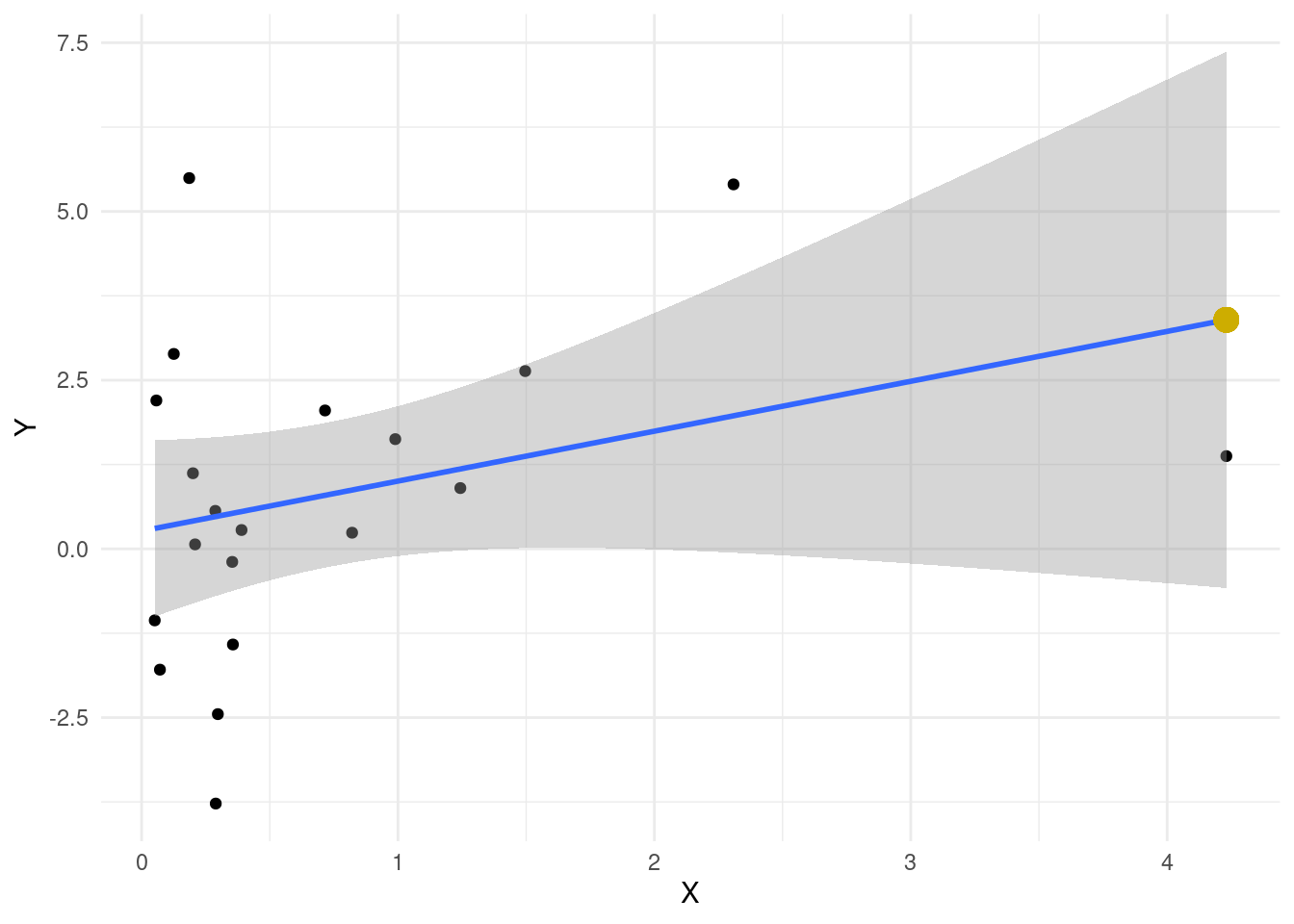
Der gelbe Punkt liegt genau auf der Gerade - super!
Das standardisierte Residuum nach Eid et al. (2017) bekommen wir nun, indem wir das Residuum durch den Standardfehler der Regression teilen. Dazu brauchen wir zunächst das Residuum:
# Residuum bestimmen
resid_Xmax <- resid(reg)[ind_Xmax]
resid_Xmax## 5
## -2.019278# std Residuum (nach Eid et al., 2017)
resid_Xmax_std <- resid_Xmax / sd_eps
resid_Xmax_std## 5
## -0.8845566Jetzt müssen wir noch die Unsicherheit einpreisen, die dadurch resultiert, dass die \(X\)-Werte weit entfernt von ihrem Mittelwert liegen. Wir haben dazu bereits ein Maß kennengelernt - nämlich die Hebelwerte. Diese berechnen sich wie folgt:
\[h = \text{diag}\left[X(X'X)^{-1}X'\right]\]
Sie sind die Diagonalelemente der sogenannten Hut-Matrix. \(\text{diag}[\cdot]\) bestimmt hier die Diagonalelemente der Matrix \(X(X'X)^{-1}X'\), welche oft auch als Hutmatrix bezeichnet iwrd. Wir berechnen diese und vergleichen Sie mit der jeweiligen Funktion, welche wir oben schon kennengelernt haben:
X_mat <- cbind(1, X)
h <- diag(X_mat %*% solve(t(X_mat) %*% X_mat) %*% t(X_mat))
round(h-hatvalues(reg), digits = 10)## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
## 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0Super, die hatvalues haben wir schon mal ausgerechnet. Nun kommen wir zu den studentisierten Residuen, welche diese Werte mit einbeziehen. Wir bestimmen hier zwei Varianten des studentisierten Residuums (Eid et al., 2017); das internal studentisierte Residuum und das external studentisierte Residuum. Internal und external bezieht sich hierbei auf dem Umstand, ob die Standardabweichung der Residuen unter einbezug (internal) oder unter Auschluss (external) der betrachteten Person bestimmt wird:
\[\hat{\varepsilon}_{i,\text{stud, internal}} := \frac{\hat{\varepsilon}_{i}}{\hat{\sigma}\sqrt{1-h_i}}\]
\[\hat{\varepsilon}_{i,\text{stud, external}} := \frac{\hat{\varepsilon}_{i}}{\hat{\sigma}_{(-i)}\sqrt{1-h_i}}\]
Die beiden Residuen werden also bestimmt, indem das eigentliche Residuum der Person \(i\), nämlich \(\hat{\varepsilon}_i = Y_i - \hat{Y}_i\) durch den Standardfehler \(\hat{\sigma}\) multipliziert mit \(\sqrt{1-h_i}\) geteilt wird: \(\hat{\sigma}\sqrt{1-h_i}\). \(h_i\) ist der Hebelwert der Person \(i\). Für das external studentisierte Residuum wird nun zur Bestimmung des Standardfehlers die Analyse wiederholt, nur das Person \(i\) aus dem Datensatz ausgeschlossen wird. Dies ist Ähnlich zu der Cooks-Distanz von oben. Nun führen wir das Ganze mal empirisch durch. Hier muss nun gesagt werden, dass innerhalb des MASS-Pakets internal-studentisierte Residuen mit dem stdres und external-studentisierte Residuen mit dem studres-Befehl bestimmt werden und es so zu einer Vermischung der Termologien kommt:
# hatvalue für Xmax bestimmen
h_Xmax <- h[ind_Xmax]
h_Xmax## [1] 0.686591# Residuum internal studentisiert (Mittelwert abziehen und durch SD teilen)
resid_Xmax_stud_int <- resid_Xmax / (sd_eps*sqrt(1-h_Xmax))
resid_Xmax_stud_int## 5
## -1.580047# vergleich -> identisch!
stdres(reg)[ind_Xmax] # internal studentisiert nach MASS## 5
## -1.580047# studentisiertes Residuum bestimmen
reg2 <- lm(Y~X, data = df[-ind_Xmax,]) # Regression ohne Person i
sd_eps_Xmax <- summary(reg2)$sigma
resid_Xmax_stud_ext <- resid_Xmax / (sd_eps_Xmax*sqrt(1-h_Xmax))
resid_Xmax_stud_ext## 5
## -1.654551# vergleich -> identisch!
studres(reg)[ind_Xmax] # external studentisiert nach MASS## 5
## -1.654551Das Schöne ist nun, dass sich diese Residuen auch über Analysen hinweg vergleichen lassen, da sie eben normiert sind und den Abstand vom Mittelwert und damit auch den Einfluss auf die Analyse und die damit verbundenen Unsicherheit integrieren. Beide Arten der Normierung haben den Abstand zum Mittelwert von \(X\) ausgedrückt durch die Hebelwerte berücksichtigt. Würden wir dies nicht tun, würde das naiv-standardisierte Residuum so ausfallen (dies ist das standardisierte Residuum nach Eid, et al.):
resid_Xmax_std <- resid_Xmax / sd_eps
resid_Xmax_std## 5
## -0.8845566Also sehr viel kleiner! Somit würde sein Einfluss auf die Analyse unterschätzt, da signalisiert werden würde, dass der Vorhersagefehler nicht sonderlich groß ausfällt.
Literatur
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden (5. Auflage, 1. Auflage: 2010). Weinheim: Beltz.
- Blau hinterlegte Autor:innenangaben führen Sie direkt zur universitätsinternen Ressource.
