Tests und Konfidenzintervalle
Kernfragen dieser Lehreinheit
- Wie berechne ich, ob es einen Unterschied zwischen einer Stichprobe und der dazugehörigen Population gibt?
- Wann und wie rechne ich einen z-Test (Einstichproben-Gauss-Test)? Wie interpretiere ich die Ergebnisse?
- Wie bestimme ich das Konfidenzintervall des wahren Werts \(\mu\)?
- Wann und wie rechne ich einen t-Test? Welche Voraussetzungen hat dieser? Wie interpretiere ich die Ergebnisse?
- Wie gehe ich mit gerichteten vs. ungerichteten Hypothesen um?
- Was ist Cohen’s d und wie berechne ich es? Wie interpretiere ich die Ergebnisse?
Was erwartet Sie heute?
Nachdem wir uns die letzten Wochen mit Deskriptivstatistik und Verteilungen beschäftigt haben, wird unser Thema nun Gruppenunterschiede sein. Wir interessieren uns heute vor allem für den Unterschied zwischen dem Mittelwert einer Stichprobe und dem Mittelwert der dazugehörigen Population, aus der die Stichprobe stammt.
Aufbau der Sitzung
- z-Test
- Konfidenzintervalle
- t-Test
- Beispiel am Datensatz
- Effektgröße
Vorbereitende Schritte
Der Datensatz wird in diesem Tutorial nicht direkt verwendet, wird aber für das spätere Beispiel gebraucht. Wir beschäftigen uns aber wieder zu Beginn mit dem Einladen, um die Struktur der Tutorials gleich zu lassen. Den Datensatz haben wir bereits unter diesem Link heruntergeladen und können ihn über den lokalen Speicherort einladen oder Sie können Ihn direkt mittels des folgenden Befehls aus dem Internet in das Environment bekommen. In den vorherigen Tutorials und den dazugehörigen Aufgaben haben wir bereits Änderungen am Datensatz durchgeführt, die hier nochmal aufgeführt sind, um den Datensatz auf dem aktuellen Stand zu haben:
#### Was bisher geschah: ----
# Daten laden
load(url('https://pandar.netlify.app/post/fb22.rda'))
# Nominalskalierte Variablen in Faktoren verwandeln
fb22$geschl_faktor <- factor(fb22$geschl,
levels = 1:3,
labels = c("weiblich", "männlich", "anderes"))
fb22$fach <- factor(fb22$fach,
levels = 1:5,
labels = c('Allgemeine', 'Biologische', 'Entwicklung', 'Klinische', 'Diag./Meth.'))
fb22$ziel <- factor(fb22$ziel,
levels = 1:4,
labels = c("Wirtschaft", "Therapie", "Forschung", "Andere"))
fb22$wohnen <- factor(fb22$wohnen,
levels = 1:4,
labels = c("WG", "bei Eltern", "alleine", "sonstiges"))
# Skalenbildung
fb22$prok2_r <- -1 * (fb22$prok2 - 5)
fb22$prok3_r <- -1 * (fb22$prok3 - 5)
fb22$prok5_r <- -1 * (fb22$prok5 - 5)
fb22$prok7_r <- -1 * (fb22$prok7 - 5)
fb22$prok8_r <- -1 * (fb22$prok8 - 5)
# Prokrastination
fb22$prok_ges <- fb22[, c('prok1', 'prok2_r', 'prok3_r',
'prok4', 'prok5_r', 'prok6',
'prok7_r', 'prok8_r', 'prok9',
'prok10')] |> rowMeans()
# Naturverbundenheit
fb22$nr_ges <- fb22[, c('nr1', 'nr2', 'nr3', 'nr4', 'nr5', 'nr6')] |> rowMeans()
fb22$nr_ges_z <- scale(fb22$nr_ges) # Standardisiert
# Weitere Standardisierugen
fb22$nerd_std <- scale(fb22$nerd)
fb22$neuro_std <- scale(fb22$neuro)Let’s start
Der durchschnittliche IQ der Population ist \(\mu_0\) = 100 und die Standardabweichung ist 15. Eine Forschungsgruppe glaubt aber, dass dieser gestiegen sei und entscheidet, diese Vermutung an einer zufälligen Stichprobe von 75 Erwachsenen zu testen. Sie finden heraus, dass der durchschnittliche IQ der Stichprobe \(\mu_1\) = 105 (SD = 17) ist.
Was wären hier \(H_0\) und \(H_1\)?
\(\alpha\) = .05
\(H_0\): Der durchschnittliche IQ der Stichprobe ist gleich oder geringer als zuvor.
\(H_0\): \(\mu_0\) \(\geq\) \(\mu_1\)
\(H_1\): Der durchschnittliche IQ der Stichprobe ist höher als zuvor.
\(H_1\): \(\mu_0\) \(<\) \(\mu_1\)
Die Frage: Reicht dieses deskriptive Ergebnis (100 vs. 105) um daraus schlusszufolgern, dass der durchschnittliche IQ sich verändert hat?
Nein. Erst mit Hilfe des z- oder t-Tests kann herausgefunden werden, wie (un)wahrscheinlich die beobachtete Diskrepanz (100 vs. 105) ist.
ABER: ob z- oder t-Test zum Einsatz kommt, hängt davon ab, ob neben dem Mittelwert auch die Standardabweichung (SD, \(\sigma\)) der Grundgesamtheit bekannt ist.
In diesem Fall ist die SD bekannt, demnach wäre ein z-Test an dieser Stelle anzuwenden.
z-Test
Der z-Test oder Einstichproben-Gauss-Test setzt voraus, dass das Merkmal in der Population, auf die sich die Nullhypothese (\(H_0\)) bezieht, normalverteilt ist und der Mittelwert sowie die Standardabweichung bekannt sind.
Des Weiteren verwendet der Gauss-Test grundsätzlich die Standardnormalverteilung als Stichprobenkennwerteverteilung (SKV), deswegen ist er nicht für kleine Stichproben geeignet.
Der Einstichproben-Gauss-Test prüft anhand des arithmetischen Mittels einer Stichprobe, ob der Erwartungswert der zugehörigen Grundgesamtheit ungleich (bzw. kleiner oder größer) als ein vorgegebener Wert ist.
Die Formel für den empirischen z-Wert \(z_{emp}\) ist:
\[z_{emp} = |\frac{\bar{x} - {\mu}}{\sigma_{\bar{x}}}|\] wobei sich der Standardfehler (SE) des Mittelwerts wie folgt berechnet:
\[\sigma_{\bar{x}} = {\frac{{\sigma}}{\sqrt{n}}}\]
Zunächst legen wir alle für den z-Wert relevanten Informationen in unser Environment ab, wobei wir auch schon den Standardfehler des Mittelwerts (\(\sigma_{\bar{x}}\)) berechnen.
mean_IQ <- 100 #Mean Grundgesamtheit
sd_IQ <- 15 #SD der Grundgesamtheit
sample_size <- 75 #Stichprobengröße
se_IQ <- sd_IQ/sqrt(sample_size) #standard error (SE), also Standardfehler
new_mean_IQ <- 105 #Stichprobenmittelwert
new_sd_IQ <- 17 #SD der Stichprobe (Populationsschätzer)Demnach wird der empirische z-Wert \(z_{emp}\) wie folgt berechnet:
z_IQ <- abs((new_mean_IQ-mean_IQ)/(sd_IQ/sqrt(sample_size))) #abs() berechnet den Betrag des Ergebnisses
z_IQ## [1] 2.886751bzw.
z_IQ <- abs((new_mean_IQ-mean_IQ)/se_IQ)
z_IQ## [1] 2.886751Beachten Sie: es geht immer um den Betrag des Ergebnisses, weshalb wir die Funktion abs() verwenden.
Der empirische z-Wert \(z_{emp}\) ist eine Angabe, um wie viele Standardabweichungen der Mittelwerte der SKV (das heißt: um wie viele Standardfehler SE) der Mittelwert der Stichprobe vom Mittelwert der Grundgesamtheit abweicht.
Der beobachtete Stichprobenmittelwert weicht demnach um \(z_{IQ}\) = 2.89 SE (nach oben) vom Mittelwert der Grundgesamtheit ab.
Um entscheiden zu können, ob es sich um eine signifikante Abweichung handelt, muss der kritische z-Wert \(z_{krit}\) bestimmt werden.
Für eine Irrtumswahrscheinlichkeit von 5% und eine einseitige Hypothesentestung wäre dies:
z_krit <- qnorm(1-.05) #bei einer zweiseitigen Testung würden wir qnorm(1-(.05/2)) verwenden
z_krit## [1] 1.644854Der kritische z-Wert beträgt demnach \(z_{krit}\) = 1.64. Damit das Ergebnis als signifikant gewertet wird, muss der empirische z-Wert \(z_{emp}\) größer sein als der kritsiche z-Wert (\(z_{IQ}\) > \(z_{krit}\)). Hierfür können wir auch eine logische Abfrage nutzen:
z_IQ > z_krit## [1] TRUEDas Ergebnis TRUE zeigt uns, dass es sich um einen signifikanten Unterschied handelt.
Mit einer Irrtumswahrscheinlichkeit von 5% kann die \(H_0\) verworfen werden. Der durchschnittliche IQ der Stichprobe ist höher als der durchschnittliche IQ der Grundgesamtheit.
Weitere Möglichkeit: pnorm()
Wie hoch ist die Wahrscheinlichkeit angesichts der bekannten Normalverteilung diesen oder einen GRÖßEREN (einseitig) empirischen z-Wert \(z_{emp}\) zu erreichen?
p_z_IQ_oneside <- pnorm(z_IQ, lower.tail = FALSE)
p_z_IQ_oneside## [1] 0.001946209Wie hoch ist die Wahrscheinlichkeit angesichts der bekannten Normalverteilung diesen oder einen EXTREMEREN (zweiseitig) z-Wert \(z_{emp}\) zu erreichen?
p_z_IQ_twoside <- 2*pnorm(z_IQ, lower.tail = FALSE) #verdoppeln, da zweiseitig
p_z_IQ_twoside## [1] 0.003892417Wir erkennen, dass in beiden Fällen der Wert kleiner als .05 (5%) ist. Demnach ist die Wahrscheinlichkeit, diesen Wert (oder einen noch extremeren Wert) per Zufall erhalten zu haben, sehr gering, wenn die \(H_0\) gilt.
Konfidenzintervalle
Wir können auch ein Konfidenzintervall um den wahren Populationsmittelwert \(\mu\) bestimmen. Wenn wir z.B. ein 95%-Konfidenzintervall wählen und wir aus der selben Grundgesamtheit wiederholt die selbe Anzahl an Fällen ziehen (unsere Studie also sehr oft wiederholen), dann werden 95% aller Konfidenzintervalle den wahren Populationsmittelwert \(\mu\) enthalten.
Dabei gilt:
\[\mu = \bar{x} \pm z_{\frac{\alpha}{2}} * \sigma_{\bar{x}} = \bar{x} \pm z_{\frac{\alpha}{2}}*\frac{\sigma}{\sqrt{n}}\]
Ein 95%-Konfidenzintervall ist somit ein Intervall, welches in 95% der Fälle beim Ziehen aus der selben Grundgesamtheit den wahren Wert \(\mu\) enthält.
Wenn wir ein 95%-Konfidenzintervall bestimmen wollen, brauchen wir das zugehörige Quantil aus der Standardnormalverteilung - also den z-Wert für \(\frac{\alpha}{2}\). Wir müssen das \(\alpha\)-Niveau halbieren, da wir uns momentan beim Bilden eines zweiseitigen Konfidenzintervalles befinden. Wir haben bereits gelernt, dass man Quantile aus der Normalverteilung mit der Funktion qnorm() erhalten kann. Die Standardnormalverteilung mitt Mittelwert von 0 und Standardabweichung von 1 ist dabei der Default, aber wir geben die Argumente zur Übung trotzdem selbst an.
z_quantil_zweiseitig <- qnorm(p = 1-(.05/2), mean = 0, sd = 1)
z_quantil_zweiseitig## [1] 1.959964Wir sehen, dass der Wert 1.96 2.5% der Verteilung Richtung positiv unendlich abtrennt. Nun haben wir alle wichtigen Informationen, um ein zweiseitiges Konfidenzintervall um unseren Mittelwert zu legen.
positive_mean_IQ <- new_mean_IQ+((z_quantil_zweiseitig*sd_IQ)/sqrt(sample_size))
positive_mean_IQ## [1] 108.3948negative_mean_IQ <- new_mean_IQ-((z_quantil_zweiseitig*sd_IQ)/sqrt(sample_size))
negative_mean_IQ## [1] 101.6052conf_interval_IQ <- c(negative_mean_IQ, positive_mean_IQ )
conf_interval_IQ## [1] 101.6052 108.3948In diesem Fall liegt der Schätzer für den wahren IQ Wert der Grundgesamtheit \(\mu\), aus der die Stichprobe gezogen wurde, zwischen 101.61 und 108.39. Das bedeutet, dass mit einer Wahrscheinlichkeit von 95% der wahre IQ Wert der Grundgesamtheit in unserem Konfidenzinterall 101.61 und 108.39 liegt.
Das Konfidenzintervall kann auch dafür genutzt werden, um eine Aussage über die von uns angenommenen Hypothesen zu treffen. Dafür müsste untersucht werden, ob das Intervall den angenommenen Populationsmittelwert (100 enthält). Wir erinnern uns jedoch, dass in den Hypothesen eine Richtung vorgegeben wurde, weshalb hierfür auch ein einseitiges Konfidenzintervall benötigt werden würde.
Wir wollten also testen, ob der Stichprobenmittelwert größer als der Wert 100 ist. Daher müssen in unserem Konfidenzintervall um den Stichprobenmittelwert eine untere Grenze bestimmen, während wir es nach oben offen halten können (Richtung positiv unendlich). Die zugehörige Gleichung ändert sich nur geringfügig. Wir müssen den z-Wert nun einseitig bestimmen und dann eben auch nur die untere Grenze unseres Intervalls.
\[\mu = \bar{x} - z_{\alpha} * \sigma_{\bar{x}} = \bar{x} \pm z_{\alpha}*\frac{\sigma}{\sqrt{n}}\]
Wir haben bereits gesehen, dass eine Bestimmung des z-Werts durch die Funktion qnorm() möglich ist.
z_quantil_einseitig <- qnorm(p = 1-.05, mean = 0, sd = 1)
z_quantil_einseitig## [1] 1.644854Anschließend kann die untere Grenze des Intervalls sehr simpel bestimmt werden.
new_mean_IQ-((z_quantil_einseitig*sd_IQ)/sqrt(sample_size))## [1] 102.151Da das Konfidenzintervall für den Stichprobenmittelwert die 100 nicht enthält, ist die Annahme unter der \(H_0\) (\(\mu \leq 100\)) nicht haltbar. Daher würden wir die \(H_0\) in diesem Fall verwerfen. Beachten Sie: Ein einseitiger z-Test bei einer Irrtumswahrscheinlichkeit \(\alpha\) und die Besimmung über ein (1-\(\alpha\))-Konfidenzintervall kommen immer zu denselben Schlussfolgerungen.
t-Test
Die Bekanntheit des Populationsmittelwertes und der Populationsvarianz ist jedoch ein seltener Fall in der Praxis. Zunächst machen wir eine Erweiterung auf den Fall, dass die Populationsvarianz nicht bekannt ist. Trotzdem soll weiterhin ein Stichprobenmittelwert mit einem bekannten Populationsmittelwert verglichen werden. Wir werden sehen, dass dies zwar ein paar Veränderungen im Vorgehen und den Gleichungen mit sich bringt, das Prinzip aber erhalten bleibt. Bezeichnet wird das Vorgehen nun als t-Test, den wir im Einstichproben-Fall hier durchführen möchten.
Unterschiedliche Quellen geben an, dass die durchschnittliche Größe der Männer in Deutschland 180 cm beträgt (z.B. https://www.laenderdaten.info/durchschnittliche-körpergrössen.php). Eine Forschungsgruppe vermutet jedoch, dass die Männer in Deutschland eigentlich größer sind und ermittelt von zehn zufällig gezogenen Männer die Körpergröße.
Die Größe der Männer beträgt: 183, 178, 175, 186, 185, 179, 181, 179, 182, 177 (gemessen in cm).
Voraussetzungsprüfung
Der Test hat die folgenden Voraussetzungen:
- Metrisch skalierte abhängige Variable
- Bei n < 30 : Normalverteilung der abhängigen Variable in der Population.
Die erste Voraussetzung lässt sich nicht mathematisch sondern theoretisch prüfen. Im Beispiel können wir uns mit der Größe in cm aber zum Glück sehr sicher sein, dass eine metrische Variable vorliegt.
Fehlt also noch die Testung der Normalverteilung der abhängigen Variable. Dafür sollten wir zunächst unsere gemessenen Werte in einen Vektor ablegen.
men_height <- c(183, 178, 175, 186, 185, 179, 181, 179, 182, 177)In der letzten Woche haben wir bereits gelernt, dass man die Normalverteilung einer erhobenen Variable graphisch prüfen kann. In einem sog. QQ-Plot werden die unter der Normalverteilung erwarteten Quantile und die tatsächlich beobachteten Quantile in einem Streudiagramm dargestellt. Je deutlicher die Punkte auf der Geraden liegen, desto näher ist die beobachtete Verteilung an der Normalverteilung.
qqnorm(men_height)
qqline(men_height)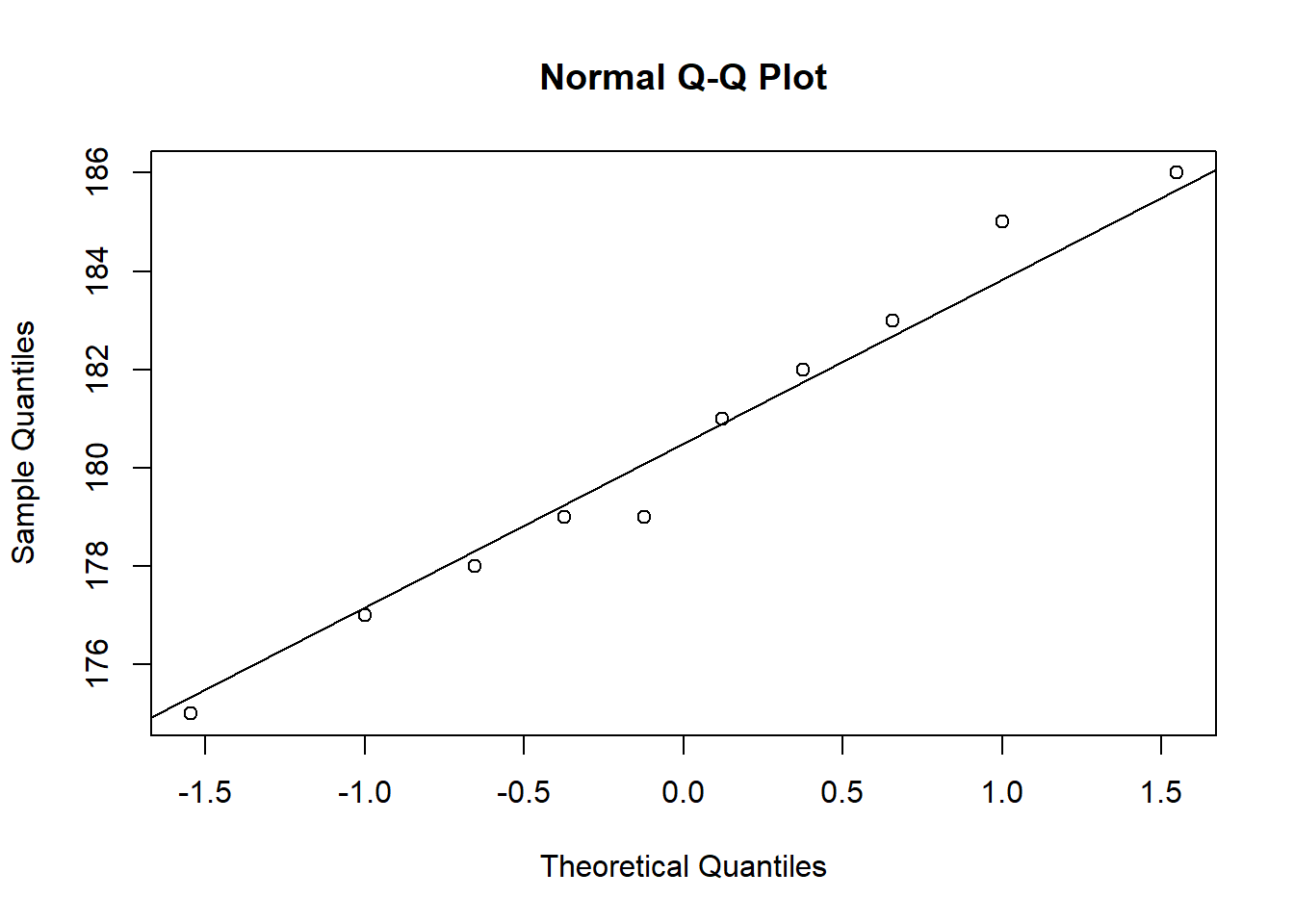
Es sind keine weiten Abweichungen zu erkennen, weshalb wir zunächst davon ausgehen, dass die Vermutung nicht verworfen werden muss.
Signifikanz bestimmen
Nun wollen wir inferenzstatistisch prüfen, ob die Vermutung der Forschungsgruppe bestätigt werden kann. Als ersten Schritt berechnen wir den Mittelwert in unserer Stichprobe. Da unsere Alternativhypothese davon handelt, dass der Wert in der Stichprobe größer sein soll, können wir zunächst betrachten, ob dies deskriptiv überhaupt der Fall ist.
mean_men_height <- mean(men_height)
mean_men_height## [1] 180.5Wir sehen, dass der Wert deskriptiv größer ist als die angegebene Größe der Population von 180cm. Der t-Test basiert auf folgender Formel:
\[t_{emp} = |\frac{\bar{x} - {\mu}}{\hat\sigma_{\bar{x}}}|\] wobei sich der Standardfehler (SE) des Mittelwerts wie folgt zusammensetzt:
\[\hat\sigma_{\bar{x}} = {\frac{{\hat\sigma}}{\sqrt{n}}}\]
Da die Varianz in der Population nicht bekannt ist, muss diese mittels Nutzung der Varianz der Stichprobe geschätzt werden. Dies funktioniert über die Funktion sd().
sd_men_height <- sd(men_height)
sd_men_height## [1] 3.535534Der Standardfehler des Mittelwerts wird anschließend auf der Basis dieses geschätzten Wertes selber geschätzt und nicht wie im z-Test bestimmt. Dafür brauchen wir als zusätzliche Information noch die Stichprobengröße, die wir beispielsweise über die length unserer Werte bestimmen können.
n_men_height <- length(men_height)
se_men_height <- sd_men_height/sqrt(n_men_height)Als letzten Bestandteil unserer Berechnungen kann man jetzt noch den gegebenen Populationsmittelwert in ein Objekt ablegen.
average_men_height <- 180Nun haben wir alle Informationen gegeben, um den empirischen t-Wert \(t_{emp}\) zu bestimmen:
t_men_height <- abs((mean_men_height-average_men_height)/se_men_height)
t_men_height## [1] 0.4472136Die empirische Prüfgröße (wie auch der Name des Tests) weist bereits darauf hin, dass wir uns bei der Hypothesenprüfung nicht mehr im Rahmen der Standardnormalverteilung bewegen. Dies liegt daran, dass sich durch das Schätzen der Populationsvarianz keine exakte Standardnormalverteilung mehr ergibt. Stattdessen wird mit einer t-Verteilung gearbeitet, deren genaue Form von der Anzahl der Freiheitsgraden abhängt. Die Unterscheidung zwischen Standardnormalverteilung und der t-Verteilung liegt besonders in den Extrembereichen. Da genau diese jedoch für die inferenzstatistische Testung von Interesse sind, ist die Nutzung der richtigen Verteilung wichtig.
Im Rahmen des t-Testes im Einstichproben-Fall bestimmen sich die Freiheitsgrade mittels \(n - 1\). Der kritische t-Wert \(t_{krit}\) für unser Beispiel kann also folgendermaßen bestimmt werden:
krit_t_men_height <- qt(0.95, df=n_men_height-1)
krit_t_men_height## [1] 1.833113Ist der empirische größer als der kritische t-Wert (\(t_{emp} > t_{krit}\))?
t_men_height > krit_t_men_height## [1] FALSEDer empirische t-Wert wird hier nicht überboten.
Alternativ: Bestimmen des \(p\)-Wertes:
p_t_men_height <- pt(t_men_height, n_men_height-1, lower.tail = F) #einseitige Testung
p_t_men_height## [1] 0.3326448Der p-Wert liegt über .05 (\(p > \alpha\)).
Die Differenz zwischen dem Mittelwert der Population \(\mu\) und dem beobachteten Mittelwert \(\bar{x}\) in der Stichprobe ist nicht signifikant. Demnach wird die \(H_0\) mit einer Irrtumswahrscheinlichkeit von 5% beibehalten.
t-test mit t.test() Funktion
Natürlich geht alles auch noch einfacher:
t.test(men_height, mu=180, alternative="greater") #alternative bestimmt, ob die Hypothese gerichtet ist oder nicht. Siehe hierzu ?t.test.##
## One Sample t-test
##
## data: men_height
## t = 0.44721, df = 9, p-value = 0.3326
## alternative hypothesis: true mean is greater than 180
## 95 percent confidence interval:
## 178.4505 Inf
## sample estimates:
## mean of x
## 180.5Hier haben wir nun alle wichtigen Informationen gebündelt.
t = \(t_{emp}\) = 0.4472136
df = Freiheitsgrade = 9
p-value = \(p\) = 0.3326448
mean of x = \(\bar{x}\) = 180.5
Wir erkennen auch hier, dass der empirische p-Wert über .05 liegt (\(p > \alpha\)). Demnach wird die \(H_0\) mit einer Irrtumswahrscheinlichkeit von 5% beibehalten.
Das 95%ige Konfidenzintervall wird uns ebenfalls ausgegeben. Beachten Sie, dass es sich aufgrund unserer Hypothese um ein einseitiges Intervall handelt (nach oben offen). Basierend auf der Stichprobe liegt der wahre Wert \(\mu\) zwischen 178.4505174 und \(\infty\). Man erkennt also, dass der Wert von 180 in diesem Konfidenzintervall liegt, was ebenso bestätigt, dass es keinen Unterschied gibt.
Beispiel mit unserem Datensatz
Unterscheidet sich unsere studentische Stichprobe in ihrem Neurotizismuswert von Studierenden im Allgemeinen? Wir nehmen an, dass der mittlere Neurotizismuswert in der Population der Studierenden bei \(\mu\) = 3.3 liegt.
- Ist die erste Voraussetzung erfüllt?
- Normalverteilungsannahme darf verletzt sein (verzerrt das Ergebnis des t-Tests nicht), wenn die Stichprobe mindestens 30 Personen umfasst. Dann gilt der zentrale Grenzwertsatz: “Die Stichprobenkennwertverteilung nähert sich einer Normalverteilung an, selbst wenn diese nicht normalverteilt ist.”
Bevor wir in die inferenzstatistische Analyse einsteigen, ist es immer gut, sich einen Überblick über die deskriptiven Werte zu verschaffen. Wir können nun natürlich einfach die bereits gelernten Funktionen zu Mittelwert, Varianz, Minimum, etc. nutzen. Doch gibt es einen schnelleren Weg? Die Basisinstallation von R bietet uns keine Alternative. Jedoch gibt es zusätzliche Pakete, die den Pool an möglichen Funktionen erweitern. Die Logik wird im Folgenden erläutert.
Wie können andere Funktionen in R genutzt werden? - Library und Pakete
R ist in einer Pakete-Logik aufgebaut. Das liegt daran, dass es immer mehr Funktionen in R gibt, die aber nie jemand alle gleichzeitig brauchen wird. Zur Schonung der Kapazität sind diese Funktionalitäten also in Pakete aufgeteilt. In Basispaketen, die standardmäßig geladen werden (also vorinstalliert sind beim Öffnen von R), sind grundlegende Befehle und Analysen implementiert (Beispiele für solche Basispakete sind base, stats, graphics). Für spezifischere Analysen (also Funktionen) müssen Zusatzpakete teilweise erst installiert, zumindest aber immer per Hand geladen werden (Beispiele sind psych, car, ggplot2). Nur die Funktionen von erst installierten und dann geladenen Paketen können in einem Skript benutzt werden.
Unter dem Reiter Packages wird die Library angezeigt. Hier sind alle Pakete enthalten, die einmal installiert wurden. Pakete müssen ab und zu (per Hand) aktualisiert werden.
Sobald Sie eigene Pakete installiert haben, gibt es in dem Reiter Packages die Einteilung in die System Library (also standardmäßig installierte Pakete) und die User Library (von Ihnen installierte Pakete).
Die folgenden Bilder verdeutlichen nochmal das Prinzip vom Installieren und Laden. Bei der Installation von R werden die Basispakete automatisch in die Library installiert. Zusatzpakete müssen mit der Funktion install.packages() mit dem Paketnamen als Argument installiert werden. Hierzu ist meist eine Internetverbindung nötig.
Beim Start von R werden die Basispakete automatisch geladen. Zusatzpakete müssen hingegen mit der Funktion library() mit dem Paketnamen als Argument geladen werden.
Gehen wir das Prinzip an dem Beispielpaket psych durch, das verschiedene Operationen enthält, die in der psychologischen Forschung häufig benötigt werden. Die Installation muss dem Laden des Paketes logischerweise vorausgestellt sein. Wenn R einmal geschlossen wird, müssen alle Zusatzpakete neu geladen, jedoch nicht neu installiert werden.
install.packages('psych') # installierenlibrary(psych) # laden## Warning: Paket 'psych' wurde unter R Version 4.2.2 erstelltWir erhalten hier als Warning Message den Hinweis, unter welcher Version das Paket erstellt wurde.
Eine kleine Suche nach Hilfe zu Pakete kann man mit ?? erhalten.
??psych # HilfeDa das Paket psych nun geladen ist, können wir Funktionen aus diesem nutzen. Für unsere Übersicht über deskriptive Maße der Variable neuro gibt es die Funktion describe().
describe(fb22$neuro)## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 159 3.63 0.72 3.75 3.65 0.74 1.25 5 3.75 -0.43 0.09 0.06Wir bekommen auf einen Schlag sehr viele relevante Informationen über unsere Variable. Der Mittelwert unserer Stichprobe liegt beispielsweise bei 3.6257862. Beachten Sie, dass auch bei describe() unter sd die geschätzte Populationsstandardabweichung angegeben wird (wie bei der Basis-Funktion sd()). Man müsste sie also umrechnen, um eine Angabe über die Stichprobe machen zu können.
Hypothesengenerierung
Variante 1:
Ungerichtete \(H_1\): “Der mittlere Neurotizismuswert unserer Stichprobe unterscheidet sich vom mittleren Neurotizismuswert der Studierenden-Population” –> zweiseitiger t-Test
Ungerichtete \(H_0\): “Der mittlere Neurotizismuswert unserer Stichprobe unterscheidet sich nicht vom mittleren Neurotizismuswert der Studierenden-Population”
Variante 2:
Gerichtete (geringer) \(H_1\): “Der mittlere Neurotizismuswert unserer Stichprobe ist niedriger als der mittlere Neurotizismuswert der Studierenden-Population.”
–> einseitiger t-Test mit alternative="less"
Gerichtete (geringer) \(H_0\): “Der mittlere Neurotizismuswert unserer Stichprobe ist gleich oder höher als der mittlere Neurotizismuswert der Studierenden-Population.”
Variante 3:
Gerichtete (höher) \(H_1\): “Der mittlere Neurotizismuswert unserer Stichprobe ist höher als der mittlere Neurotizismuswert der Studierenden-Population.”
–> einseitiger t-Test mit alternative="greater"
Gerichtete (höher) \(H_0\): “Der mittlere Neurotizismuswert unserer Stichprobe ist gleich oder niedriger als der mittlere Neurotizismuswert der Studierenden-Population.”
In der Praxis würde man sich für eine der drei Hypothesen-Varianten entscheiden. Zu Übungszwecken werden aber alle drei Varianten durchgespielt.
t.test(fb22$neuro, mu=3.3) #ungerichtet##
## One Sample t-test
##
## data: fb22$neuro
## t = 5.716, df = 158, p-value = 5.295e-08
## alternative hypothesis: true mean is not equal to 3.3
## 95 percent confidence interval:
## 3.513214 3.738358
## sample estimates:
## mean of x
## 3.625786t.test(fb22$neuro, mu=3.3, alternative="less") #gerichtet, Stichprobenmittelwert geringer##
## One Sample t-test
##
## data: fb22$neuro
## t = 5.716, df = 158, p-value = 1
## alternative hypothesis: true mean is less than 3.3
## 95 percent confidence interval:
## -Inf 3.720089
## sample estimates:
## mean of x
## 3.625786t.test(fb22$neuro, mu=3.3, alternative="greater") #gerichtet, Stichprobenmittelwert höher##
## One Sample t-test
##
## data: fb22$neuro
## t = 5.716, df = 158, p-value = 2.648e-08
## alternative hypothesis: true mean is greater than 3.3
## 95 percent confidence interval:
## 3.531484 Inf
## sample estimates:
## mean of x
## 3.625786Konfidenzintervall: Wir erkennen, dass das 95%-ige Konfidenzintervall per Standardeinstellung berechnet wird. Falls wir dieses vergrößern oder verkleinern wollen, müssen wir dies explizit formulieren im Argument conf.level:
t.test(fb22$neuro, mu=3.3, conf.level=0.99) #99%-iges Konfidenzintervall für die ungerichtete Hypothese##
## One Sample t-test
##
## data: fb22$neuro
## t = 5.716, df = 158, p-value = 5.295e-08
## alternative hypothesis: true mean is not equal to 3.3
## 99 percent confidence interval:
## 3.477181 3.774391
## sample estimates:
## mean of x
## 3.625786t.test(fb22$neuro, mu=3.3, alternative="less", conf.level=0.99) #99%-iges Konfidenzintervall für die gerichtete Hypothese (Stichprobenmittelwert geringer)##
## One Sample t-test
##
## data: fb22$neuro
## t = 5.716, df = 158, p-value = 1
## alternative hypothesis: true mean is less than 3.3
## 99 percent confidence interval:
## -Inf 3.759737
## sample estimates:
## mean of x
## 3.625786t.test(fb22$neuro, mu=3.3, alternative="greater", conf.level=0.99) #99%-iges Konfidenzintervall für die gerichtete Hypothese (Stichprobenmittelwert höher)##
## One Sample t-test
##
## data: fb22$neuro
## t = 5.716, df = 158, p-value = 2.648e-08
## alternative hypothesis: true mean is greater than 3.3
## 99 percent confidence interval:
## 3.491836 Inf
## sample estimates:
## mean of x
## 3.625786Es zeigt sich, dass der Neurotizismuswert der Studierenden sich von der Studierenden-Population signifikant auf dem 1%-Niveau unterscheidet.
Ungerichtet
Die \(H_0\) wird mit einer Irrtumswahrscheinlichkeit von 1% verworfen. Der Neurotizismuswert der Studierenden unterscheidet sich von der Studierenden-Population.
Gerichtet (geringer)
Die \(H_0\) wird beibehalten. Der Neurotizismuswert der Studierenden ist nicht kleiner als der der Studierenden-Population. Bemerke: Einen gerichteten t-Test, der \(\bar{x} < \mu\) untersucht, würde man an dieser Stelle nicht durchführen, da die deskriptiven Werte schon gegen die Hypothese sprechen (da \(\bar{x} > \mu\) und nicht \(\bar{x} < \mu\)).
Gerichtet (höher)
Die \(H_0\) wird mit einer Irrtumswahrscheinlichkeit von 1% verworfen. Der Neurotizismuswert der Studierenden ist höher als der der Studierenden-Population.
Effektgröße
Als Effektgröße für Mittelwertsunterschiede kann Cohen’s d (Cohen, 1988) verwendet werden.
Dieses statistische Effektmaß beschreibt die Relevanz von signifikanten Ergebnissen. Zudem kann es verwendet werden, um den Effekt über verschiedene Studien hinweg zu vergleichen.
\[d = |\frac{\bar{x} - {\mu}}{\sigma}|\]
mean_Neuro <- mean(fb22$neuro) #Neurotizismuswert der Stichprobe
sd_Neuro <- sd(fb22$neuro, na.rm = T) #Stichproben SD (Populationsschätzer)
mean_Popu_Neuro <- 3.3 #Neurotizismuswert der Grundgesamtheit
d <- abs((mean_Neuro-mean_Popu_Neuro)/sd_Neuro) #abs(), da Betrag
d## [1] 0.4533059Die Effektgröße ist in diesem Fall mit einem Wert von .4533 mittelstark ausgeprägt. Normalerweise sollte die Einordnung der Größe anhand vergleichbarer Studien aus dem selben Bereich durchgeführt werden. Bei völliger Ahnungslosigkeit über relevante Größen gibt es eine Übersicht zur Orientierung. Es gilt nach Cohen (1988):
d = 0.2 -> kleiner Effekt
d = 0.5 -> mittlerer Effekt
d = 0.8 -> großer Effekt
Cohen, J. (1988). Statistical power analysis for the Behavioral Sciences. Routledge.
