ANCOVA und moderierte Regression
Einleitung
In dieser Sitzung schauen wir uns die Kovarianzanalyse, auch ANalysis Of COVAriance (ANCOVA), als Erweiterung der ANOVA an und nutzen diese als Überleitung zur moderierten Regressionsanalyse. Diese Sitzung basiert auf Literatur aus Eid et al. (2017) Kapitel 19 (insbesondere 19.9-19.12).
Daten laden
Wir verwenden wieder den Datensatz von Schaeuffele et al. (2020), die den Effekt des Unified Protocol (UP) als Internetintervention für bestimmte psychische Störungen durchgeführt haben. Wir laden den Datensatz ein und kürzen diesen (für mehr Informationen zum Datensatz sowie zum Einladen und Kürzen erhalten Sie in der vorherigen Sitzung zu ANOVA vs. Regression):
osf <- read.csv(file = url("https://osf.io/zc8ut/download"))
osf <- osf[, c("ID", "group", "stratum", "bsi_post", "swls_post", "pas_post")]
# Missings ausschließen
osf <- na.omit(osf)
head(osf) # finaler Datensatz## ID group stratum bsi_post swls_post pas_post
## 1 1 Treatment DEP 2 29 1
## 2 2 Treatment ANX 11 22 7
## 3 3 Treatment ANX 22 6 1
## 4 4 Treatment DEP 2 23 3
## 7 7 Treatment DEP 14 16 3
## 8 8 Treatment SOM 2 27 5Wir beschränken uns auf einige wenige Variablen, die nach Durchführung des Treatments erhoben wurden: ID (Teilnehmendennummer), group (Gruppenzugehörigkeit: Wartelistenkontrollgruppe vs. Treatmentgruppe), stratum (Krankheitsbild: Angststörung [ANXiety], Depression [DEPression] oder somatische Belastungsstörung [SOMatic symptom disorder]), bsi_post (Symptomschwere), swls_post (Lebenszufriedenheit [Satisfaction With Life Screening]) und pas_post (Panikstörung und Agoraphobie [Panic and Agoraphobia Screening]).
Vorbereitung
Möchten wir nominalskalierte Prädiktoren (also Gruppenvariablen) in eine Regression aufnehmen, so ist es essentiell, dass diese auch als solche kodiert sind. Da manchmal Zahlen für Gruppenzugehörigkeiten verwendet werden, ist es ratsam, sich direkt anzugewöhnen, Gruppenvariablen als factor zu kodieren:
# Skalenniveaus anpassen: Factors bilden
osf$group <- factor(osf$group)
osf$stratum <- factor(osf$stratum)Da wir später auch mit Interaktionen zu tun haben werden, zentrieren wir noch alle kontinuierlichen Prädiktoren im Modell. Zentrierung bedeutet, dass der Mittelwert der Variablen auf 0 gesetzt wird, indem dieser von jeder einzelnen Beobachtung abgezogen wird (, ist die zentrierte Version von für Beobachtung ). Zum Zentrieren verwenden wir scale mit den Zusatzargumenten center = T und scale = F.
# Zentrieren
osf$swls_post <- scale(osf$swls_post, center = T, scale = F)
osf$pas_post <- scale(osf$pas_post, center = T, scale = F)Die Werte von zentrierten Variablen sind etwas anders zu interpretieren als jene in der ursprünglichen Skala. Ein Wert von 0 steht hier für den durchschnittlichen Wert auf dieser Variable.
Hätten wir auch noch scale = T gewählt, so hätten wir nicht nur zentriert, sondern ebenfalls standardisiert — also auch noch die Varianz auf 1 gesetzt, indem wir die Variablen durch die Standardabweichung geteilt hätten (, ist die standardisierte Version von ). Wir haben hier “nur” zentriert, da die Zentrierung schon ausreicht, um mögliche Multikollinearität zu vermeiden (dazu später etwas mehr). Die Standardisierung ist sozusagen nur “nice to have” und vereinfacht die Interpretation. Da wir nicht den Eindruck erwecken wollten, dass dies zwangsläufig nötig ist, haben wir nur zentriert und nicht standardisiert.
Kovarianzanalyse: ANCOVA
In der letzten Sitzung hatten wir bemerkt, dass ANOVA und Regressionsanalysen (auch in R) so gut wie identisch sind und dass nur die Art und Weise, wie Hypothesen aufgestellt werden sollen, im Endeffekt entscheiden, wie genau die Analysen ausfallen. Diese Hypothesen hatten sich in der Wahl der Quadratsummen geäußert.
Die Kovarianzanalyse kann nun sowohl in ANOVA- als auch im Regressionssetting betrachtet werden. Entscheidend ist, für welchen Effekt wir uns interessieren. Im ANOVA-Setting wird eine (oder mehrere) kontinuierliche Kovariate hinzugefügt, um deren Einfluss der Mittelwertsvergleich “bereinigt” werden soll. Damit sollen Varianzeinflüsse der Kovariate herausgerechnet werden, was die Power erhöht, einen Mittelwertsunterschied zu finden. Im Regressionssetting soll eine Kombination aus Prädiktoren unterschiedlicher Skalenniveaus untersucht werden. Hier könnte bspw. neben einem kontinuierlichem Prädiktor auch eine nominalskalierte Gruppierungsvariable aufgenommen werden. Wenn wir uns eine einfache Regression vorstellen, so hätte dies zur Folge, dass wir für jede Gruppe ein Interzept einführen würden!
Einfache ANCOVA
Wir betrachten die ANCOVA im Regressionssetting. Wir verwenden also wieder die lm-Funktion, um das Modell aufzustellen und wenden auf das resultierende Objekt wieder die Anova-Funktion aus dem car-Paket an. Wir verwenden hier nicht ezANOVA, da wir die Gleichungsnotation der Regression verwenden wollen und weil ezANOVA für ANCOVAs erstmal nur eine Betaversion enthält.
An dieser Stelle sei gesagt, dass wir im Grunde eine ANCOVA schon in der Sitzung zur Regression durchgeführt haben, ohne dies genau zu erläutern. Dort hatten wir die Depressivität durch das Geschlecht sowie die Lebenszufriedenheit vorhergesagt. Das Geschlecht war hier dichotom und die Lebenszufriedenheit wurde als kontinuierlich angesehen.
Wir möchten nun für unseren Datensatz osf wissen, ob sich die Symptomschwere durch die Lebenszufriedenheit vorhersagen lässt. Dazu hatten wir am Anfang der vergangenen Sitzung bereits eine Untersuchung vorgenommen. Allerdings hatten wir auch die Ausprägung der Panikstörung und Agoraphobie mit in das Modell aufgenommen. Beide Prädiktoren hatten signifikante Varianzanteile an der Symptomschwere erklärt. Wir beschränken uns jetzt allerdings auf die Lebenszufriedenheit:
reg_swl <- lm(bsi_post ~ 1 + swls_post, data = osf)
summary(reg_swl)##
## Call:
## lm(formula = bsi_post ~ 1 + swls_post, data = osf)
##
## Residuals:
## Min 1Q Median 3Q Max
## -16.870 -6.053 -1.305 4.327 30.266
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 18.7979 0.9393 20.012 < 2e-16 ***
## swls_post -0.7330 0.1371 -5.346 6.49e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 9.107 on 92 degrees of freedom
## Multiple R-squared: 0.237, Adjusted R-squared: 0.2288
## F-statistic: 28.58 on 1 and 92 DF, p-value: 6.494e-07Der Zusammenhang zwischen Lebenszufriedenheit und Symptomschwere ist negativ und signifikant. Das bedeutet, dass die Symptomschwere geringer ausfällt für höhere Lebenszufriedenheit. Grafisch sieht das so aus (der Code zu den Grafiken ist für unsere inhaltlichen Überlegungen nicht so relevant und kann daher bei Interesse in Appendix A nachgelesen werden):
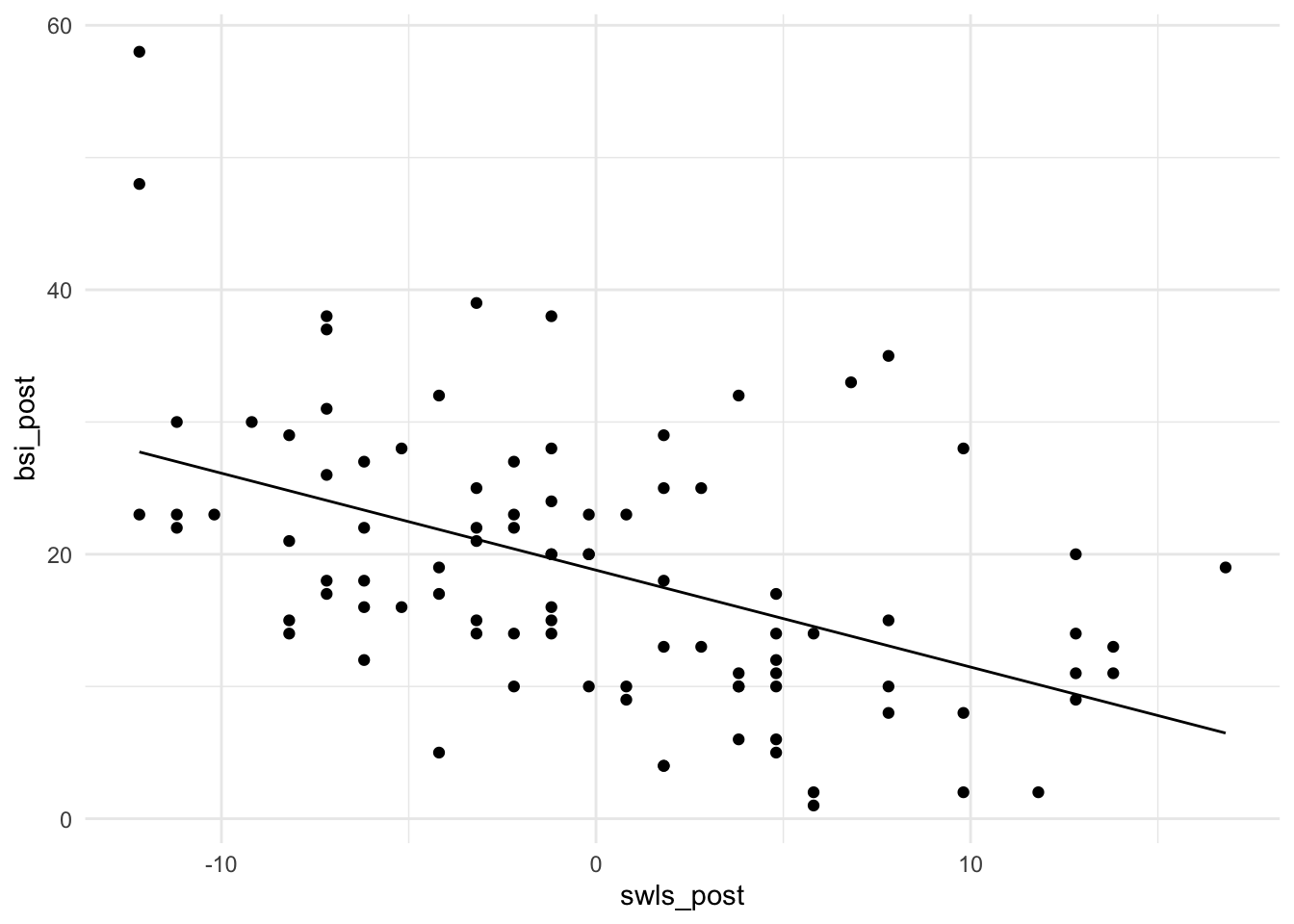
Die Zentrierung der Lebenszufriedenheit ist leicht zu erkennen. Die Werte streuen um die Null. Außerdem ist so das Interzept gut zu interpretieren. Es entspricht der durchschnittlichen Ausprägung der Symptomschwere!
Nun ist es aber so, dass einige der Proband:innen das Onlinetreatment erhalten haben. Wenn wir nun die Gruppierungsvariable mit in das Modell aufnehmen, so sehen wir mit bloßem Auge, dass sich die beiden Gruppen leicht im Mittel unterscheiden.
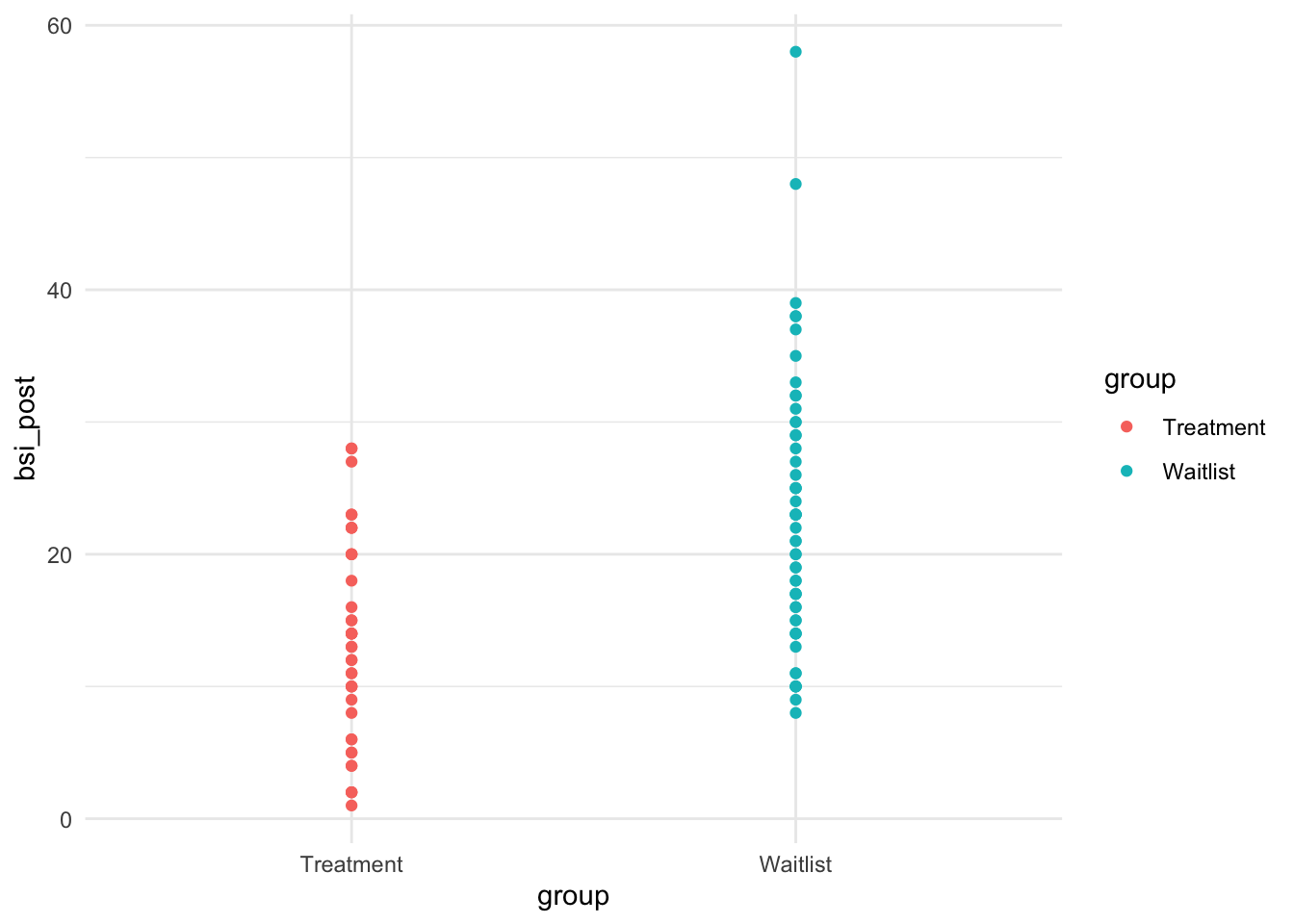
Dass sich das Treatment positiv auf die Symptomschwere auswirkt, hatten wir in der Sitzung zur ANOVA vs. Regression bereits festgestellt. Wir färben die Gruppen unterschiedlich ein und fügen so die Gruppierung in die Regression von zuvor ein:
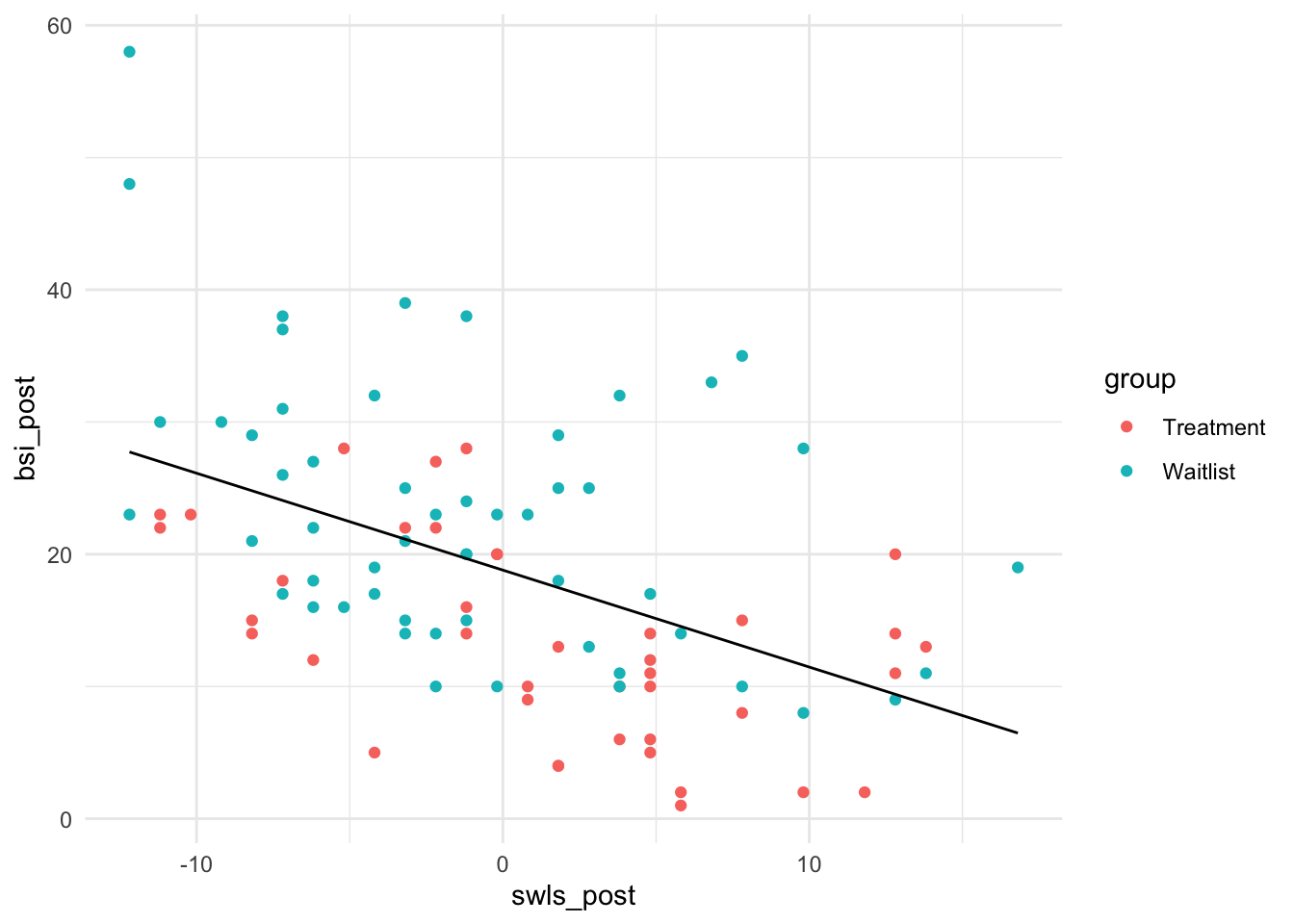 Die Frage ist nun, ob dieser Unterschied auch statistisch bedeutsam ist. Dazu nehmen wir jetzt die Gruppierungsvariable in das Regressionsmodell auf. Was wir damit erreichen ist, dass wir durchschnittliche Unterschiede zwischen den beiden Gruppen mit in das Modell aufnehmen — und zwar für eine gegebene (feste) Ausprägung. Wenn wir also die Gruppierungsvariable aufnehmen, dann fügen wir ein gruppenspezifisches Interzept hinzu. So können wir die Gruppenunterschiede bereinigt um die Kovariate Lebenszufriedenheit interpretieren und genauso können wir den Zusammenhang zwischen Lebenszufriedenheit und Symptomschwere bereinigt um Unterschiede durch die Behandlung interpretieren.
Die Frage ist nun, ob dieser Unterschied auch statistisch bedeutsam ist. Dazu nehmen wir jetzt die Gruppierungsvariable in das Regressionsmodell auf. Was wir damit erreichen ist, dass wir durchschnittliche Unterschiede zwischen den beiden Gruppen mit in das Modell aufnehmen — und zwar für eine gegebene (feste) Ausprägung. Wenn wir also die Gruppierungsvariable aufnehmen, dann fügen wir ein gruppenspezifisches Interzept hinzu. So können wir die Gruppenunterschiede bereinigt um die Kovariate Lebenszufriedenheit interpretieren und genauso können wir den Zusammenhang zwischen Lebenszufriedenheit und Symptomschwere bereinigt um Unterschiede durch die Behandlung interpretieren.
Wir nennen die Dummyvariable der Gruppierungsvariable und die Lebenszufriedenheit . Die Symptomschwere nennen wir . Somit ergibt sich folgendes Regressionsmodell (das Residuum heißt ) für Proband:innen :
Es gelten nun zwei Regressionsgleichungen in den beiden Gruppen. Für (Wartekontrollgruppe) gilt und für (Treatmentgruppe) gilt . Somit ist ersichtlich, dass wir durch Hinzunahme der Gruppierungsvariable gruppenspezifische Interzepts einführen. Das Interzept ist eine Funktion von . Diese könnten wir bspw. nennen. Dann ist das Interzept (insbesondere gilt: ). Das Modell in R sieht ganz einfach so aus (wir fügen einfach alle Prädiktoren mit + getrennt in die Regressionsgleichung ein und schleifen der Vollständigkeit halber wieder das Interzept 1 mit, welches per Default immer in der Gleichung ist):
reg_ancova <- lm(bsi_post ~ 1 + group + swls_post, data = osf)
summary(reg_ancova)##
## Call:
## lm(formula = bsi_post ~ 1 + group + swls_post, data = osf)
##
## Residuals:
## Min 1Q Median 3Q Max
## -13.5459 -6.2084 -0.8385 5.4089 28.2297
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 14.2295 1.3228 10.757 < 2e-16 ***
## groupWaitlist 7.9523 1.7592 4.520 1.85e-05 ***
## swls_post -0.6224 0.1269 -4.903 4.10e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 8.275 on 91 degrees of freedom
## Multiple R-squared: 0.377, Adjusted R-squared: 0.3633
## F-statistic: 27.53 on 2 and 91 DF, p-value: 4.473e-10Wir erkennen also, dass kein Extrapaket o.ä. benötigt wird, um eine ANCOVA zu schätzen, sondern die richtige Formatierung der Variablen, die in das Modell aufgenommen werden, entscheidet, welches Modell genau geschätzt wird.
Der Effekt der Lebenszufriedenheit () ist statistisch bedeutsam. Auch der Effekt der Gruppierungsvariable ist bedeutsam () [jeweils mit einer Irrtumswahrscheinlichkeit von ]. Hätten wir mehrere Ausprägungen pro Gruppe, könnten wir leicht gesammelte Signifikanzentscheidungen pro Variable anfordern, indem wir den Anova-Befehl aus dem car-Paket verwenden:
library(car)## Loading required package: carDataAnova(reg_ancova)## Anova Table (Type II tests)
##
## Response: bsi_post
## Sum Sq Df F value Pr(>F)
## group 1399.2 1 20.434 1.853e-05 ***
## swls_post 1646.1 1 24.040 4.099e-06 ***
## Residuals 6231.2 91
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Was wir sofort sehen ist, dass die -Werte in der summary und im Anova-Output identisch sind. Das liegt an der Verwandtschaft zwischen Regression und ANOVA (ANCOVA), welche wir in der vorangegangenen Sitzung diskutiert hatten und daran, dass wir hier nur eine Gruppierungsvariable mit zwei Gruppen verwendet haben (siehe ANOVA vs. Regression).
Grafisch sieht das so aus
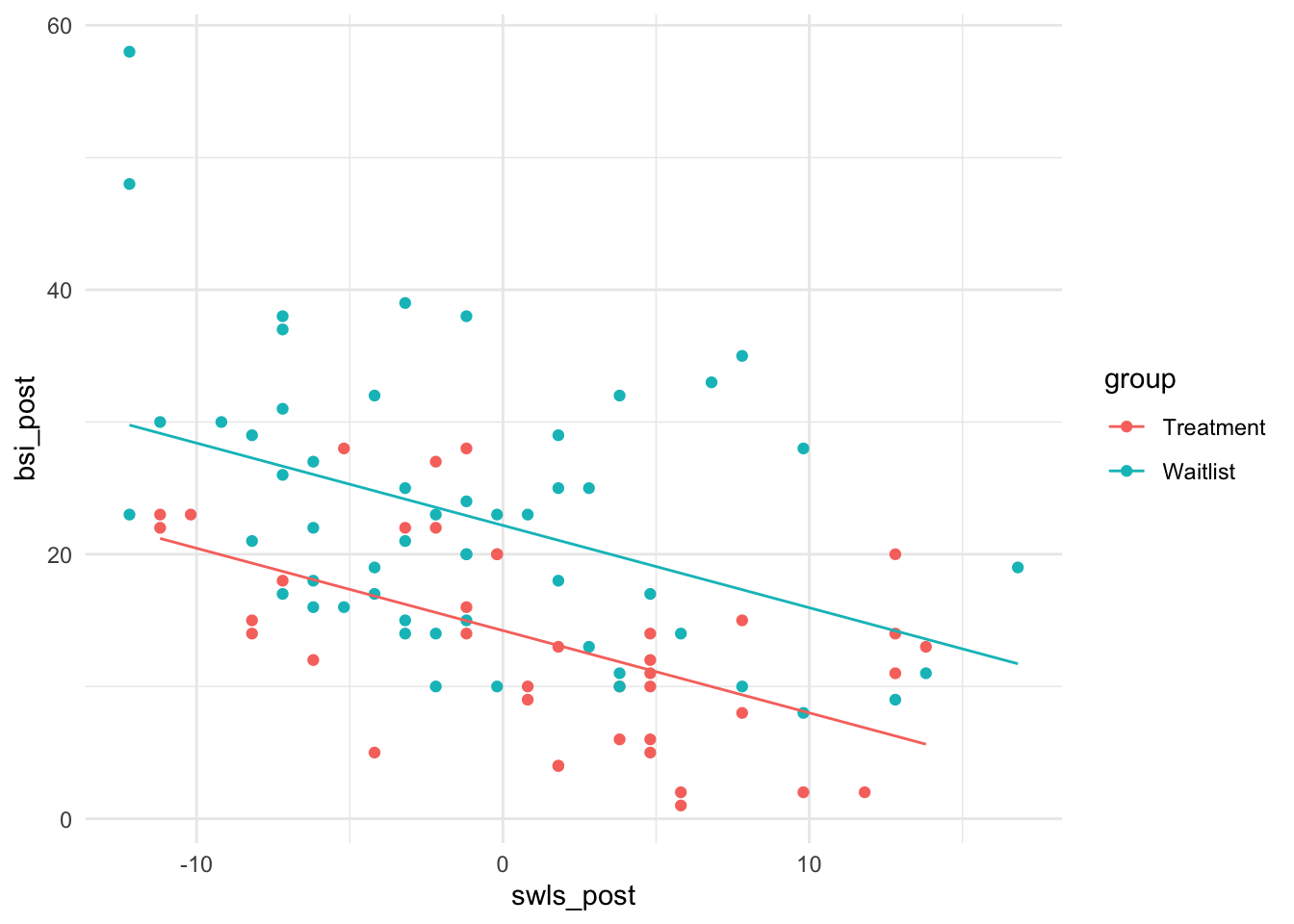
Pro Gruppe gibt es ein eigenes Interzept. Außerdem sehen wir deutlich, welche wichtige Annahme implizit in dieser Modellierungsmethode steckt: der lineare Zusammenhang zwischen Lebenszufriedenheit und Symptomschwere ist in beiden Gruppen gleich!
Generalisierte ANCOVA
Weichen wir die Annahme gleicher linearer Zusammenhänge pro Gruppe auf, landen wir bei der “generalisierten” ANCOVA. Was wir dazu tun müssen, ist für jede Gruppe eine eigene Steigung für die Lebenszufriedenheit einzuführen. Umsetzbar ist dies durch eine Interaktion zwischen der Lebenszufriedenheit und der Gruppierungsvariable. Die Interaktion ist hier etwas anders zu interpretieren als für eine zweifaktorielle ANOVA. Es sind nicht länger die Mittelwerte in den Gruppen, die von der spezifischen Kombination der Gruppenzugehörigkeiten abhängen, sondern die lineare Beziehung zwischen dem kontinuierlichen Prädiktor und dem Kriterium ist für jede Gruppe unterschiedlich! Natürlich können zusätzlich noch die Mittelwerte unterschiedlich sein. Das wird dann durch das Interzept mit abgebildet. Die Modellgleichung sieht so aus:
Wenn wir diese Gleichung nach der Variable umstellen, erhalten wir
An dieser Schreibweise ist ersichtlich, dass wir durch Hinzunahme der Interaktion eigentlich einen eigenen Steigungskoeffizienten pro Gruppe in das Modell hinzufügen. Es gelten wieder zwei Regressionsgleichungen in den beiden Gruppen. Für (Wartekontrollgruppe) gilt und für (Treatmentgruppe) gilt . Somit ist ersichtlich, dass durch Hinzunahme der Gruppierungsvariable inklusive Interaktion gruppenspezifische Interzepts und Slopes (Steigungskoeffizienten) eingeführt werden. Sowohl das Interzept als auch die Slope sind eine Funktion von . Diese könnten wir bspw. und nennen — beide sind Funktionen von . Dann ist das Interzept und die Slope (insbesondere gilt: ).
Damit die Interaktion sinnvoll interpretierbar ist, müssen wir annehmen, dass sich der kontinuierliche Prädiktor (die kontinuierliche Kovariate) im Mittel nicht über die Gruppen unterscheidet. Unterschiedliche Beziehungen mit dem Kriterium hatten wir bereits zugelassen. Diese Annahme entfällt also. Um keine artifizielle lineare Beziehung zwischen Gruppierungsvariable und kontinuierlichem Prädiktor zu erzeugen, war die Zentrierung des Prädiktors mit dem scale-Befehl von Nöten (siehe oben).
Das Modell in R sieht im Grunde so aus, wie eine zweifaktorielle ANOVA, nur das Skalenniveau von swls_post ist eben das Intervallskalenniveau (kontinuierlicher Prädiktor):
reg_gen_ancova <- lm(bsi_post ~ 1 + group + swls_post + group:swls_post,
data = osf)
summary(reg_gen_ancova)##
## Call:
## lm(formula = bsi_post ~ 1 + group + swls_post + group:swls_post,
## data = osf)
##
## Residuals:
## Min 1Q Median 3Q Max
## -13.5986 -6.5874 -0.8768 5.1062 27.6775
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 14.1293 1.3473 10.487 < 2e-16 ***
## groupWaitlist 7.9958 1.7696 4.518 1.89e-05 ***
## swls_post -0.5571 0.1938 -2.875 0.00504 **
## groupWaitlist:swls_post -0.1153 0.2573 -0.448 0.65512
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 8.312 on 90 degrees of freedom
## Multiple R-squared: 0.3783, Adjusted R-squared: 0.3576
## F-statistic: 18.26 on 3 and 90 DF, p-value: 2.449e-09Wir erkennen, dass bis auf die Interaktion () alle Effekte signfikant sind. Gleiches Ergebnis liefert uns auch die Anova
Anova(reg_gen_ancova, type = 2)## Anova Table (Type II tests)
##
## Response: bsi_post
## Sum Sq Df F value Pr(>F)
## group 1399.2 1 20.2549 2.021e-05 ***
## swls_post 1646.1 1 23.8291 4.533e-06 ***
## group:swls_post 13.9 1 0.2008 0.6551
## Residuals 6217.3 90
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Da die Interaktion nicht signifikant ist, bleiben wir bei Quadratsummen vom Typ II. Es gibt also keine gruppenspezifische Steigung der Lebenszufriedenheit. Das bedeutet, dass sich die Lebenszufriedenheit in beiden Gruppen gleich auf die Symptomschwere auswirkt. Grafisch sieht dies so aus:
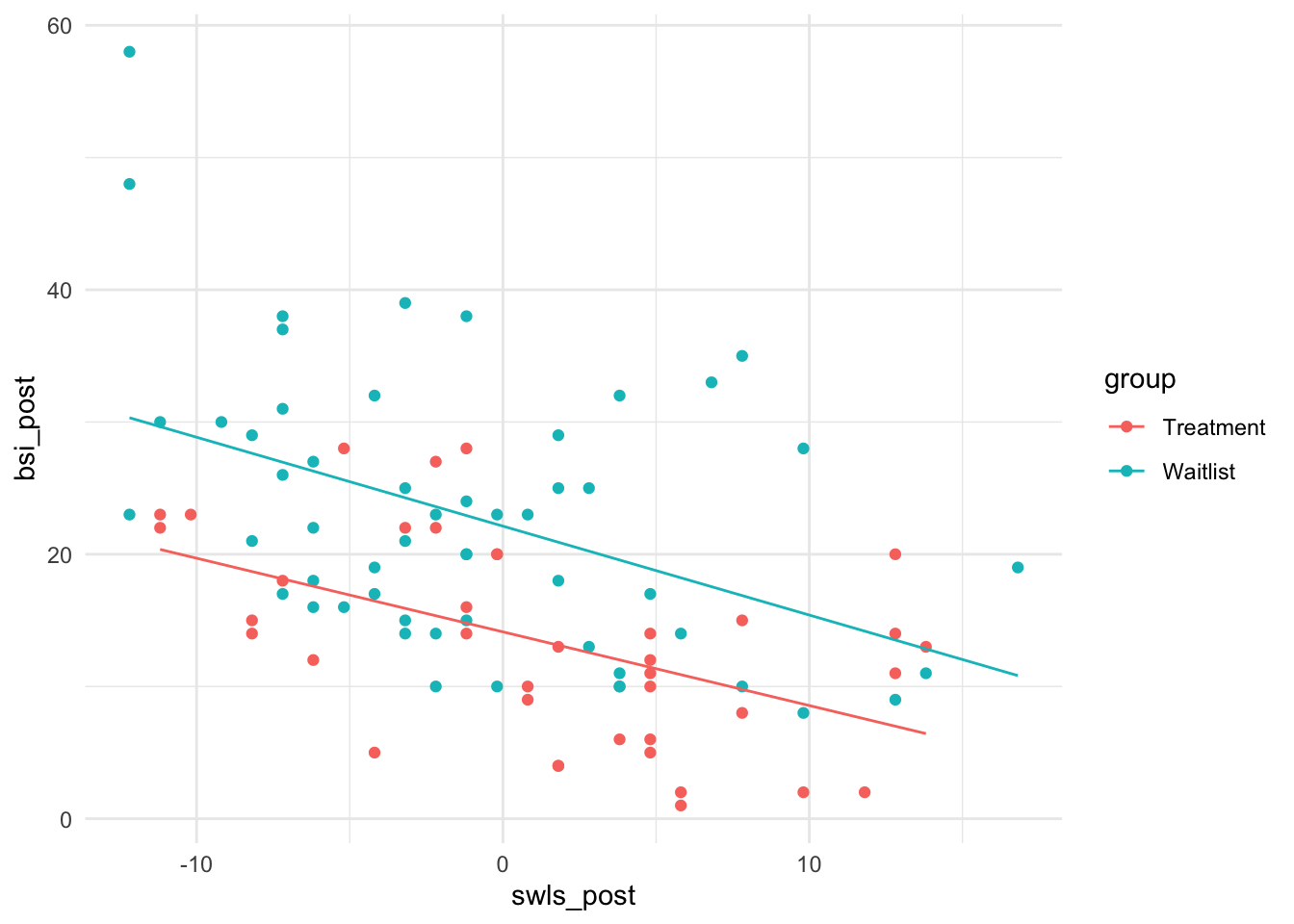 Wir erkennen nur ganz leicht einen Effekt der unterschiedlichen Steigungen (die rote Linie ist etwas weniger steil), allerdings ist dieser Unterschied nicht signifikant und lässt sich damit auch nicht auf die Population verallgemeinern.
Wir erkennen nur ganz leicht einen Effekt der unterschiedlichen Steigungen (die rote Linie ist etwas weniger steil), allerdings ist dieser Unterschied nicht signifikant und lässt sich damit auch nicht auf die Population verallgemeinern.
Wir schauen uns das Ganze nochmals für die Diagnose an und stellen das gleiche Modell wie oben auf, mit dem Unterschied, dass wir die Effekte des Treatments durch die der Diagnose austauschen:
reg_gen_ancova_s <- lm(bsi_post ~ stratum + swls_post + stratum:swls_post, data = osf)
Anova(reg_gen_ancova_s)## Anova Table (Type II tests)
##
## Response: bsi_post
## Sum Sq Df F value Pr(>F)
## stratum 151.5 2 0.9257 0.4001
## swls_post 2278.0 1 27.8449 9.345e-07 ***
## stratum:swls_post 279.5 2 1.7083 0.1871
## Residuals 7199.4 88
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Die Diagnose scheint keinen Einfluss auf die Symptomschwere zu haben. Weder die Interzept noch die Slopes unterscheiden sich über die Gruppen. Wir wollen uns trotzdem die Grafik ansehen:
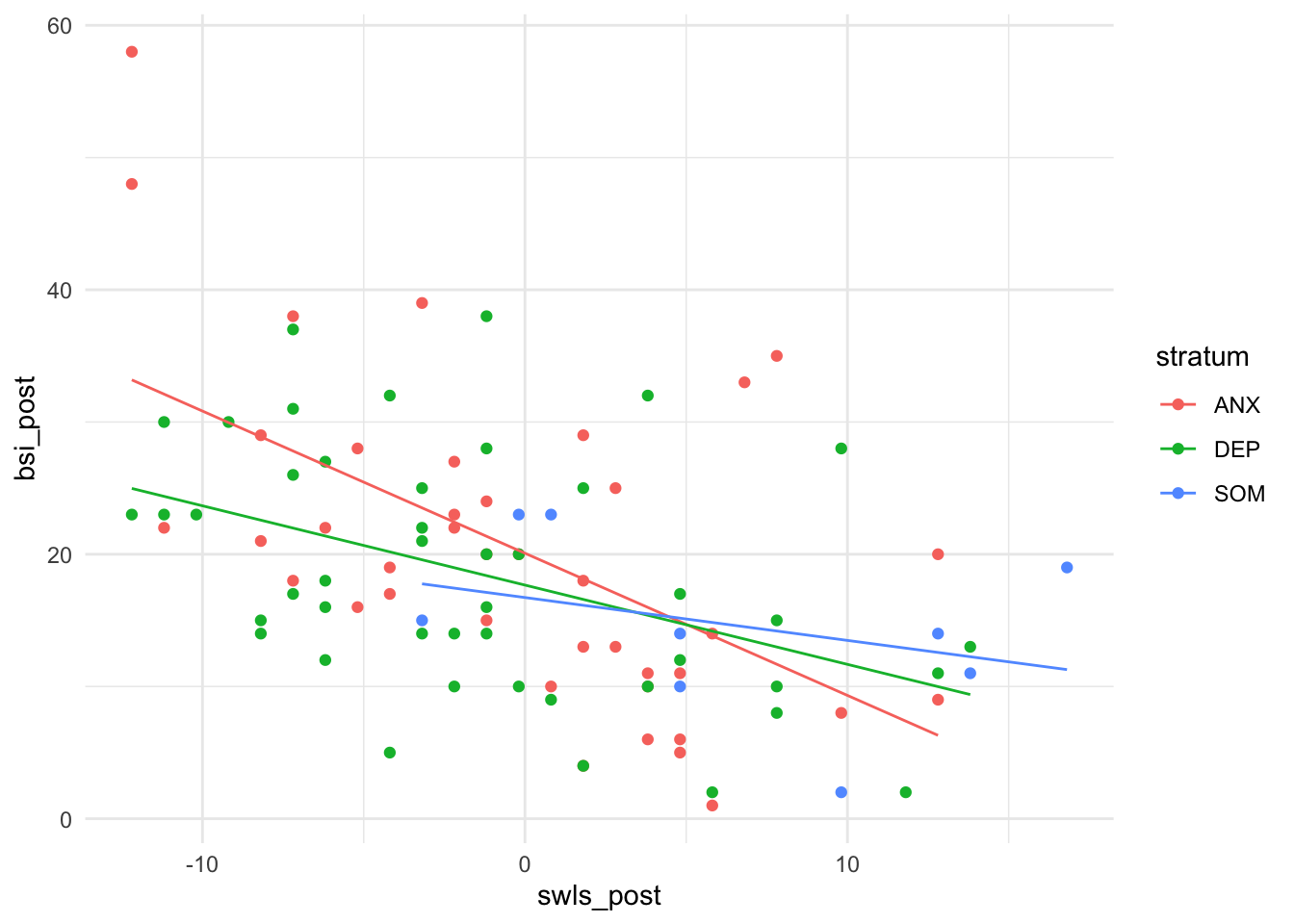
Hier erkennen wir zwar unterschiedliche Steigungen und Interzepts, allerdings sind keine der Unterschied statistisch bedeutsam.
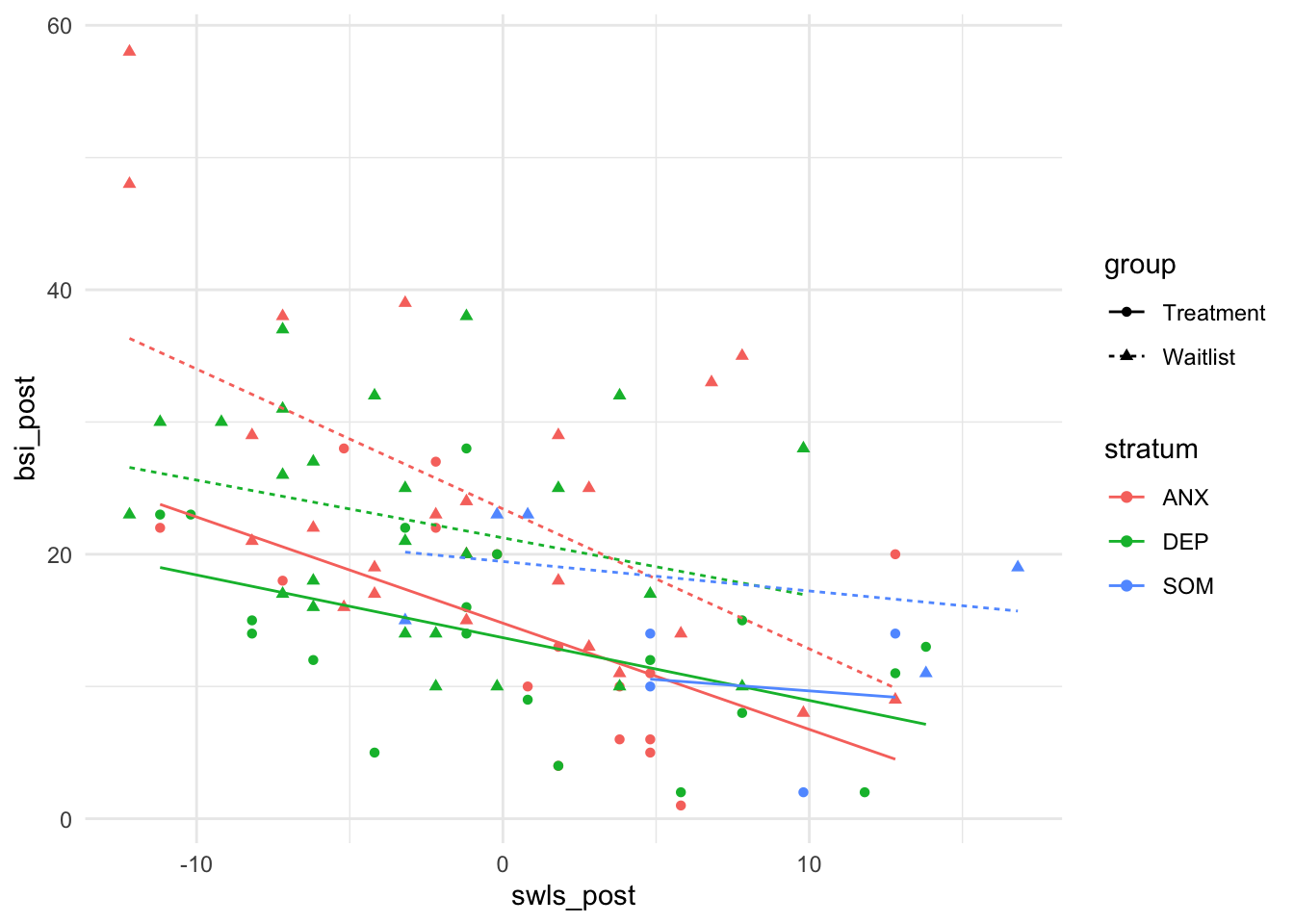
Genauso wären auch noch komplizierte Modelle möglich. Bspw. könnten wir für jede Kombination aus Gruppierung und Diagnose ein eigenes Regressionsmodell einführen. Grafisch sieht das so aus (für mehr dazu siehe Appendix B):
Moderierte Regression
Wenn wir uns nun vorstellen, dass wir unendlich viele Gruppen hätten, dann wäre es theoretisch möglich, für jede Gruppe eine Ausprägung der Slope oder des Interzepts zu finden. So ähnlich funktioniert nun die moderierte Regression. Anstatt dass wir unendlich viele Gruppen haben, nehmen wir einen kontinuierlichen Prädiktor her. Diesen Prädiktor nennen wir Moderator. Wenn wir nun eine Interaktion zwischen unserem eigentlichen (kontinuierlichen) Prädiktor und dem Moderator in die Regressionsgleichung aufnehmen, dann erhalten wir ein Regressionsmodell, welches der generalisierten ANCOVA sehr ähnlich sieht. Wir nennen den Moderator wie oben , stellen die Gleichung nach (unserem Prädiktor) um und benennen das Interzept und die Slope in Abhängigkeit von :
Wir erkennen wieder ein Interzept und eine Slope, welche jeweils abhängig von der Ausprägung des Moderators sind. Bis hierhin unterscheiden sich die Gleichungen der moderierten Regression und generalisierten ANCOVA nicht. Allerdings kann in der moderierten Regression (theoretisch) jeden beliebigen Wert annehmen. Außerdem sei an dieser Stelle gesagt, dass die Bezeichnungen für Moderator und Prädiktor nicht von den Daten abgeleitet werden können. Sie sind rein konzeptioneller Natur. Das äußert sich darin, dass wir für die moderierte Regression im Gegensatz zur ANCOVA die Rolle der beiden Prädiktoren vertauschen können. Wir können also die Gleichung einfach anders aufstellen und schon haben wir ein Interzept und eine Slope von auf , die jeweils abhängig sind von .
Um die Analyse besser interpretierbar zu machen und um möglicher Multikollinearität zwischen linearen und nichtlinearen Termen (Interaktion) vorzubeugen, sollte sowohl der Prädiktor als auch der Moderator zentriert sein. Das haben wir ganz am Anfang der Sitzung im Block Vorbereitung bereits mit dem scale-Befehl gemacht, da dies bereits für die ANCOVA von Relevanz war!
Wenn Prädiktor und Moderator zentriert sind, lässt sich der Wert , also der Mittelwert von , sehr schön interpretieren. Dann ist nämlich und . Wir erkennen also, dass und jeweils das Interzept und die Slope für ein durchschnittliches beschreiben. Die Koeffizienten und symbolisieren dann die Abweichungen vom mittleren Interzept oder der mittleren Slope in Abhängigkeit von . Die Berechnung in R laufen mit dem lm-Befehl ab. Wir fügen einfach eine Interaktion zwischen dem Prädiktor und dem Moderator ein.
Inhaltlich wollen wir nun die Beziehung zwischen der Symptomschwere als abhängiger Variable und den Prädiktoren Lebenszufriedenheit und Panikstörungs- und Agoraphobiesymptomatik untersuchen. Hierbei soll die Panikstörungs- und Agoraphobiesymptomatik der Prädiktor sein, welcher durch die Lebenszufriedenheit moderiert wird. Wir wollen also untersuchen, ob für unterschiedliche Ausprägungen der Lebenszufriedenheit auch unterschiedliche (lineare) Beziehungen zwischen Panikstörungs- und Agoraphobiesymptomatik und Symptomschwere bestehen. Wir stellen zunächst das Modell auf und interpretieren die Parameter. Das Modellobjekt nennen wir mod_reg:
mod_reg <- lm(bsi_post ~ swls_post + pas_post + swls_post:pas_post, data = osf)
summary(mod_reg)##
## Call:
## lm(formula = bsi_post ~ swls_post + pas_post + swls_post:pas_post,
## data = osf)
##
## Residuals:
## Min 1Q Median 3Q Max
## -13.7496 -4.8657 -0.8335 4.2496 19.9304
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 18.570066 0.749053 24.791 < 2e-16 ***
## swls_post -0.562248 0.109733 -5.124 1.70e-06 ***
## pas_post 0.525460 0.071774 7.321 9.98e-11 ***
## swls_post:pas_post -0.016080 0.009669 -1.663 0.0998 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 7.14 on 90 degrees of freedom
## Multiple R-squared: 0.5413, Adjusted R-squared: 0.526
## F-statistic: 35.4 on 3 and 90 DF, p-value: 3.342e-15Die Ergebnisse sind recht eindeutig. Die beiden linearen Effekte von swls_post und pas_post sind statistisch bedeutsam. Die Interaktion/Moderation allerdings nicht. Dies bedeutet, dass die Beziehung zwischen Panikstörungs- und Agoraphobiesymptomatik und Symptomschwere nicht durch die Ausprägung der Lebenszufriedenheit moderiert (beeinflusst) wird. Die linearen Effekte gehen ferner in die erwartete Richtung: die Symptomschwere steigt mit steigender Ausprägung der Panikstörungs- und Agoraphobiesymptomatik (unter Konstanthaltung der Lebenszufriedenheit). Außerdem sinkt die Symptomschwere mit steigender Lebenszufriedenheit (unter Konstanthaltung der Panikstörungs- und Agoraphobiesymptomatik). Bei all diesen Aussagen sollten Sie sich ein “mit einer Irrtumswahrscheinlichkeit von ” denken, wie das immer so ist in der Inferenzstatistik!
Wir können ein Gefühl für die Moderation bekommen, indem wir die Ergebnisse grafisch darstellen. Dazu nutzen wir sogenannte Simple-Slope Grafiken. Diese stellen für verschiedene Ausprägungen des Moderators die Beziehung zwischen Prädiktor und abhängiger Variable als Linie dar. Dazu können wir praktischerweise ein Paket benutzen. Dieses heißt interactions und muss nach Installation zunächst geladen werden. Aus diesem Paket nutzen wir die Funktion interact_plot. Dieser müssen wir 3 Argumente übergeben: model ist unser Regressionsmodell (mod_reg, welches wir zuvor geschätzt hatten), pred setzt den Prädiktor fest (hier: pas_post) und modx setzt den Moderator (hier: swls_post) fest:
library(interactions)
interact_plot(model = mod_reg, pred = pas_post, modx = swls_post)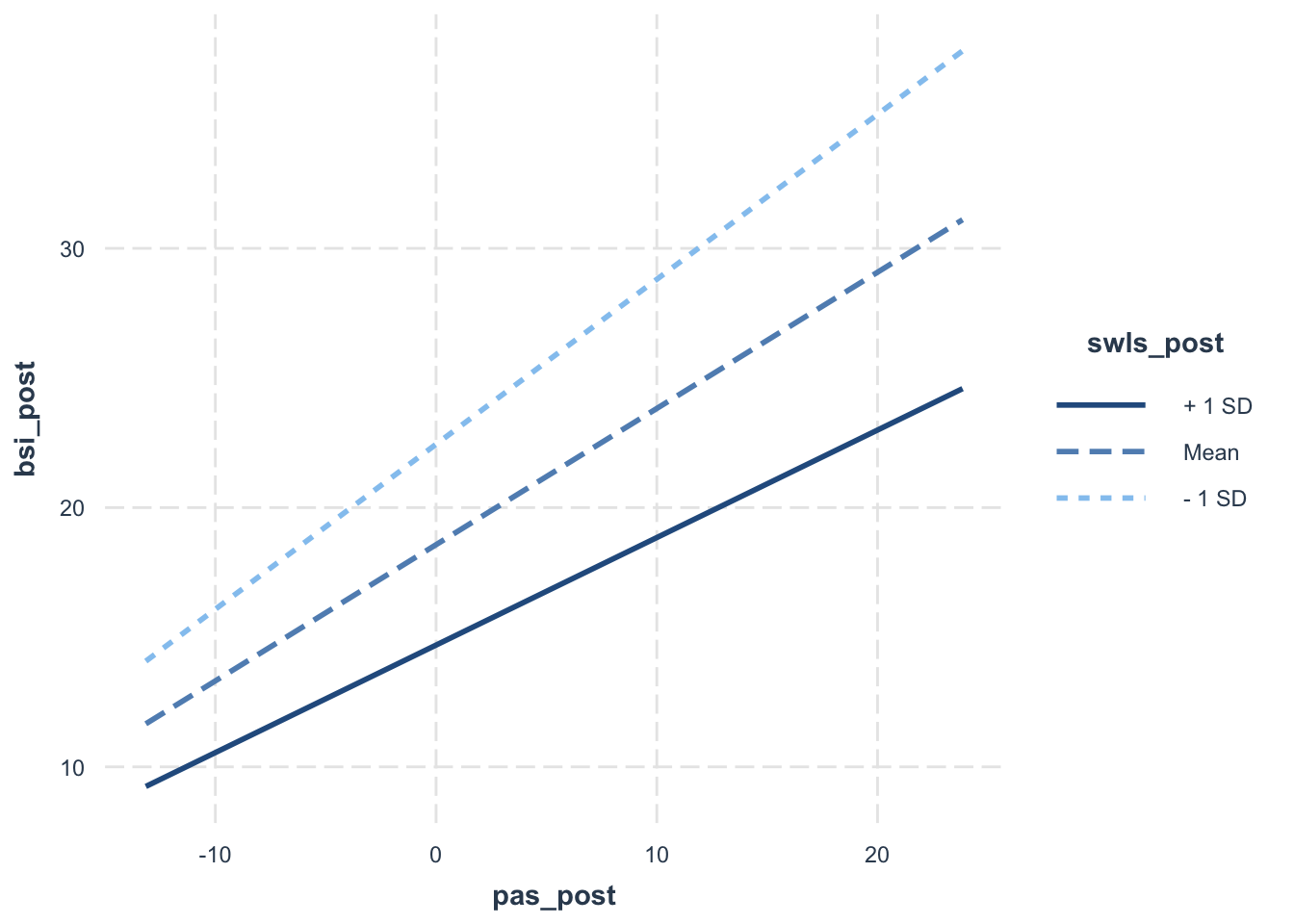
Wir bekommen eine Grafik mit Symptomschwere auf der y-Achse und Panikstörungs- und Agoraphobiesymptomatik auf der x-Achse. Es werden drei Linien für drei unterschiedliche Ausprägungen der Lebenszufriedenheit (dem Moderator) dargestellt: + 1 SD, Mean, - 1 SD. Diese Werte stehen für den durchschnittlichen Wert der Lebenszufriedenheit (Mean) sowie für zwei Werte, die eine Standardabweichung weit weg vom Mittelwert (+ 1 SD, - 1 SD) liegen. An diesem Plot lassen sich die oben beschriebenen Effekte recht gut ablesen. Da die drei Linien nicht komplett aufeinander liegen, ist ersichtlich, dass es Unterschiede in den Interzepts oder Slopes in Abhängigkeit der Lebenszufriedenheit geben muss. Die Unterschiedlichkeit der Interzepts lässt sich sehr gut sehen. Diese hatten wir oben durch den signifikanten linearen Effekt der Lebenszufriedenheit auf die Symptomschwere erkannt. Die Interaktion/Moderation ist nicht signifikant. Das erkennen wir im Plot daran, dass die drei Linien fast parallel sind (denn sind Geraden parallel, so müssen ihre Steigungskoeffizienten identisch sein!). Rein deskriptiv war der Moderationseffekt negativ. Das bedeutet, dass mit steigender Lebenszufriedenheit die Beziehung zwischen Symptomschwere und Panikstörungs- und Agoraphobiesymptomatik geringer ausfällt (in unserer Stichprobe — verallgemeinern auf die Population lässt sich diese Aussage leider nicht, auch wenn sie sehr plausibel klingt). Das können wir auch im Plot erahnen.
Im Gegensatz zur ANCOVA, die wir weiter oben kennengelernt hatten, gibt es natürlich nicht nur diese drei Linien. Der Moderator kann jede beliebige Ausprägung annehmen. Dies kann in folgender Grafik abgelesen werden (für den Code zur Grafik siehe Appendix C).
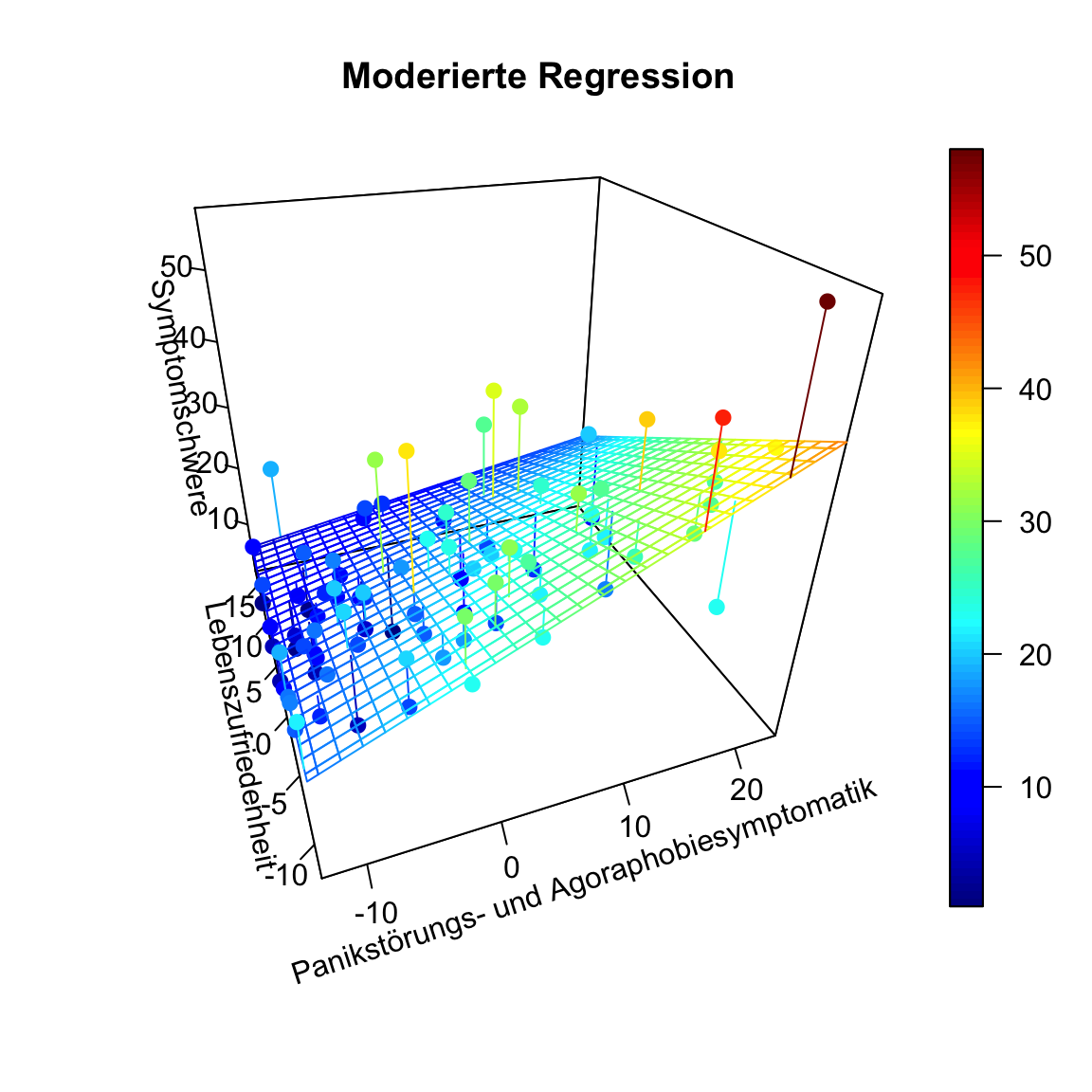
Hier ist die x-Achse () der Prädiktor Panikstörungs- und Agoraphobiesymptomatik (pas_post) und in die Tiefe wird der Moderator Lebenszufriedenheit (swls_post) dargestellt (oft z-Achse: ()). Die y-Achse (im Plot heißt diese blöderweise z-Achse) ist die Symptomschwere dargestellt (). Wir erkennen in dieser Ansicht ein wenig die Simple-Slopes von zuvor, denn die Achse der Leseleistung läuft ins negative “aus dem Bildschirm hinaus”, während sie ins positive “in den Bildschirm hinein” verläuft. Der nähere Teil der “Hyperebene” weißt eine höhere Beziehung zwischen Panikstörungs- und Agoraphobiesymptomatik und Symptomschwere auf, während der Teil, der weiter entfernt liegt, eine kleinere Beziehung aufweist. Genau das haben wir auch in den Simple-Slopes zuvor gesehen. Dort war für hohe Lebenszufriedenheit die Beziehung zwischen Panikstörungs- und Agoraphobiesymptomatik und Symptomschwere auch schwächer. Wichtig ist, dass in diesem Plot die Beziehung zwischen Panikstörungs- und Agoraphobiesymptomatik und Symptomschwere für eine fest gewählte Ausprägung der Lebenszufriedenheit tatsächlich linear verläuft. Es ist also so, dass wir quasi ganz viele Linien aneinanderkleben, um diese gewölbte Ebene zu erhalten. Allerdings war die Interaktion nicht statistisch bedeutsam, sodass dies nicht auf die Population zu verallgemeinern ist.
Absicherung gegen quadratische Effekte und Multikollinearität
Unser Moderationseffekt war nicht signifikant. Wäre er es gewesen, müssten wir noch sicherstellen, ob nicht eigentlich ein quadratischer Effekt besteht. Denn es ist so, dass der Interaktionsterm mit quadratischen Termen korreliert sein kann, wenn die zugrundeliegenden Variablen korreliert sind. So kann es zu Multikollinearität im Modell kommen und wir könnten uns fälschlicherweise für einen Interaktionseffekt entscheiden, obwohl es tatsächlich einen quadratischen Effekt gibt. Quadratische Effekte können wir in ein Regressionsmodell aufnehmen, indem wir entweder eine neue Variable mit quadrierten (aber zentrierten!) Werten erstellen, oder indem wir innerhalb des lm-Befehls die I() sogenannte as.is-Funktion verwenden, mit welcher wir einfache Transformationen an bestehenden Daten in Modellen verwenden können, ohne explizit Daten dafür erstellen zu müssen:
mod_quad_reg <- lm(bsi_post ~ swls_post + pas_post + swls_post:pas_post + I(swls_post^2) + I(pas_post^2), data = osf)
summary(mod_quad_reg)##
## Call:
## lm(formula = bsi_post ~ swls_post + pas_post + swls_post:pas_post +
## I(swls_post^2) + I(pas_post^2), data = osf)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.5320 -4.6874 -0.6398 3.9883 20.3207
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 18.161602 1.167593 15.555 < 2e-16 ***
## swls_post -0.628430 0.111957 -5.613 2.28e-07 ***
## pas_post 0.557138 0.080224 6.945 6.23e-10 ***
## I(swls_post^2) 0.028553 0.013480 2.118 0.037 *
## I(pas_post^2) -0.008184 0.006810 -1.202 0.233
## swls_post:pas_post -0.014298 0.009667 -1.479 0.143
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 7.007 on 88 degrees of freedom
## Multiple R-squared: 0.568, Adjusted R-squared: 0.5435
## F-statistic: 23.15 on 5 and 88 DF, p-value: 9.151e-15Wir erkennen, dass es einen quadratischen Effekt der Lebenszufriedenheit gibt. Die Interaktion ist allerdings wieder nicht signifikant. Grafisch sieht dies nun so aus:
interact_plot(model = mod_quad_reg, pred = pas_post, modx = swls_post)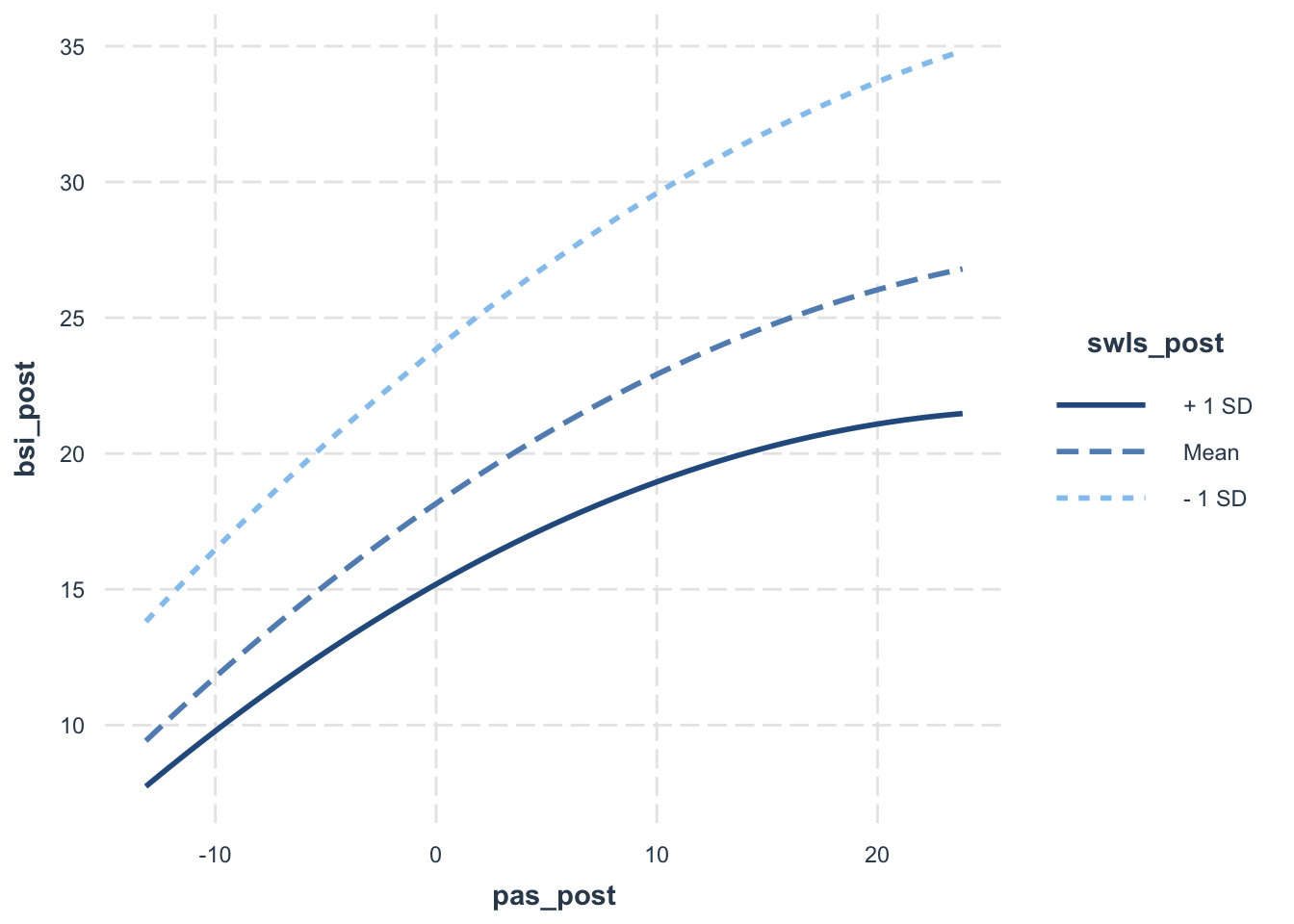
Die Simple-Slopes sind keine einfachen Steigungen mehr, sondern gleichen “einfachen” Parabeln. Die Interpretation ist immer ähnlich zu den Simple-Slopes von zuvor. Die Beziehung zwischen Symptomschwere und Panikstörungs- und Agoraphobiesymptomatik fällt geringer aus für höhere Lebenszufriedenheit. Außerdem lässt sich ein Plateau vermuten für große Panikstörungs- und Agoraphobiesymptomatik-Werte. Der 3D-Plot zeigt uns, dass es diesmal nicht aneinander geklebte Linien, sondern Parabeln sind:
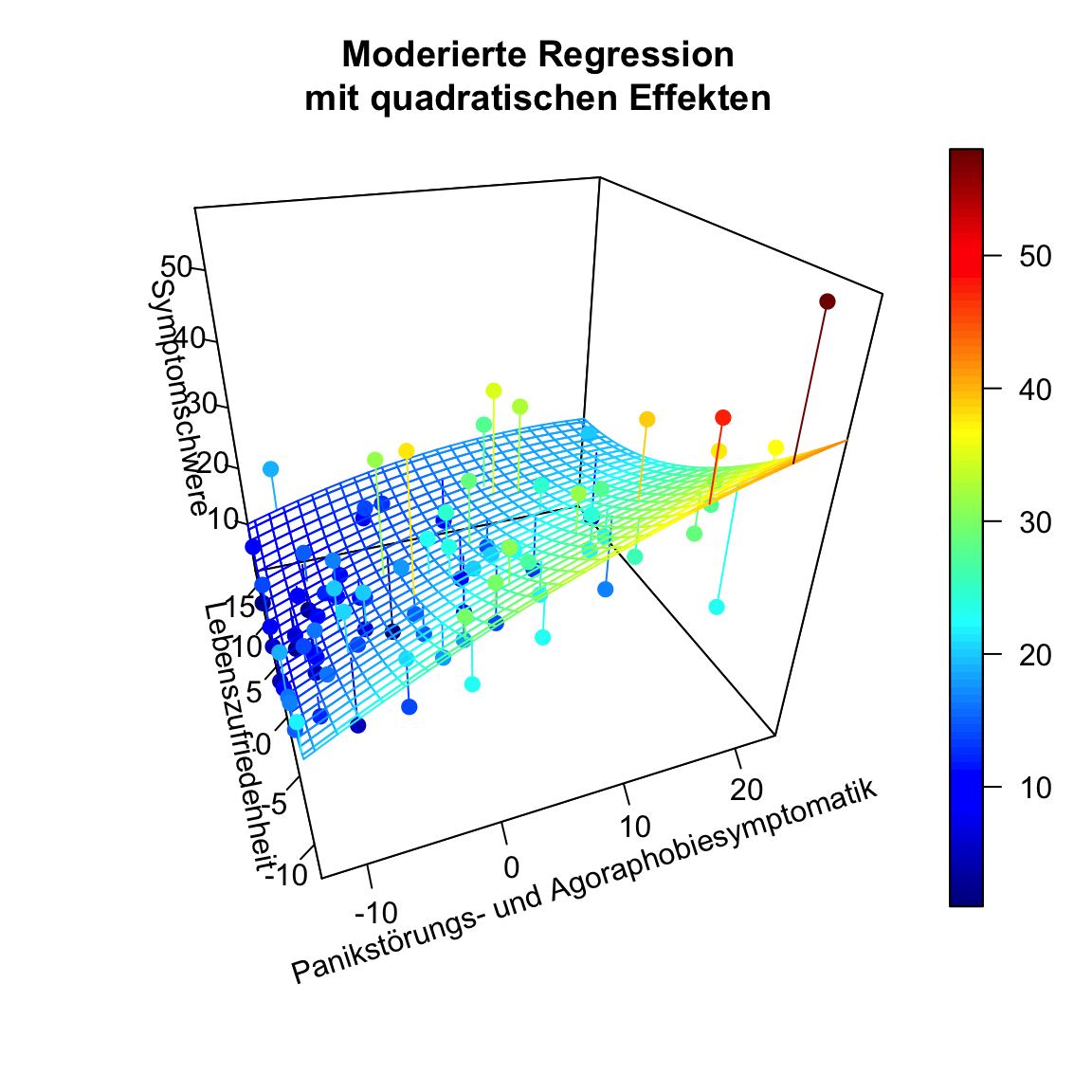
Entlang der Achse der Lebenszufriedenheit ist diese Krümmung auch statistisch bedeutsam. Wir erkennen deutlich, dass eine hohe Lebenszufriedenheit sich positiv auf die Symptomschwere auswirkt, da diese dann niedriger ausgeprägt ist. Außerdem scheint es (rein deskriptiv) so zu sein, dass dann auch die Beziehung zwischen Symptomschwere und Panikstörungs- und Agoraphobiesymptomatik geringer ausfällt. Allerdings war dieser Effekt nicht statistisch bedeutsam.
Umgang mit quadratischen und Interaktionseffekten
In der Regel interessieren sich Forschende für Interaktionseffekte, da diese Beziehungen zwischen Variablen in Abhängigkeit von Moderatoren darstellen. So können bspw. Puffer-Effekte untersucht werden. Um sicher zu gehen, dass es einen Interaktionseffekt in den Daten gibt, sollte zunächst ein rein quadratisches Modell aufgestellt werden und dieses sollte dann mit dem quadratischen moderierten Regressionsmodell verglichen werden. Ist das erklärte Varianzinkrement der Interaktion statistisch bedeutsam, kann von einer Moderation gesprochen werden. Sind quadratische Effekte auch statistisch bedeutsam, sollten sie ebenfalls in das Modell mit aufgenommen werden. Vorgehen:
quad_reg <- lm(bsi_post ~ swls_post + pas_post + I(swls_post^2) + I(pas_post^2), data = osf)
anova(quad_reg, mod_quad_reg)## Analysis of Variance Table
##
## Model 1: bsi_post ~ swls_post + pas_post + I(swls_post^2) + I(pas_post^2)
## Model 2: bsi_post ~ swls_post + pas_post + swls_post:pas_post + I(swls_post^2) +
## I(pas_post^2)
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 89 4427.4
## 2 88 4320.0 1 107.39 2.1877 0.1427Hier ist nun ersichtlich, dass die Interaktion nicht statistisch bedeutsam ist. Das hatten wir allerdings auch schon der summary von mod_quad_reg ablesen können.
Fazit
Wir haben mit der “generalisierten” ANCOVA und der moderierten Regressionsanalyse zwei Modelle kennengelernt, welche durch Interkationen aus linearen Modellen hervorgehen. Damit lassen sich lineare Beziehung in Abhängigkeit weiterer Variablen ausdrücken: entweder in Abhängigkeit von Gruppierungsvariablen (dann landen wir im generalisierten ANCOVA-Setting) oder in Abhängigkeit von kontinuierlichen Prädiktoren (Kovariaten; das ist dann die moderierte Regression).
Appendix
Appendix A
Code zu den Grafiken zur ANCOVA
Wir verwenden für diese Sitzung das ggplot2-Paket, welches nachdem es installiert wurde (install.packages) geladen werden muss. Für eine Einführung in ggplot können Sie gerne in den Unterlagen zu den Veranstaltungen im Bachelor vorbeischauen. Für noch mehr Grafiken siehe Unterlagen zu ggplotting.
library(ggplot2) # ggplot2-Paket laden
ggplot(data = osf, mapping = aes(x = swls_post, y = bsi_post))+
geom_point()+
geom_line(mapping = aes(x = swls_post, y = predict(reg_swl)))+
theme_minimal()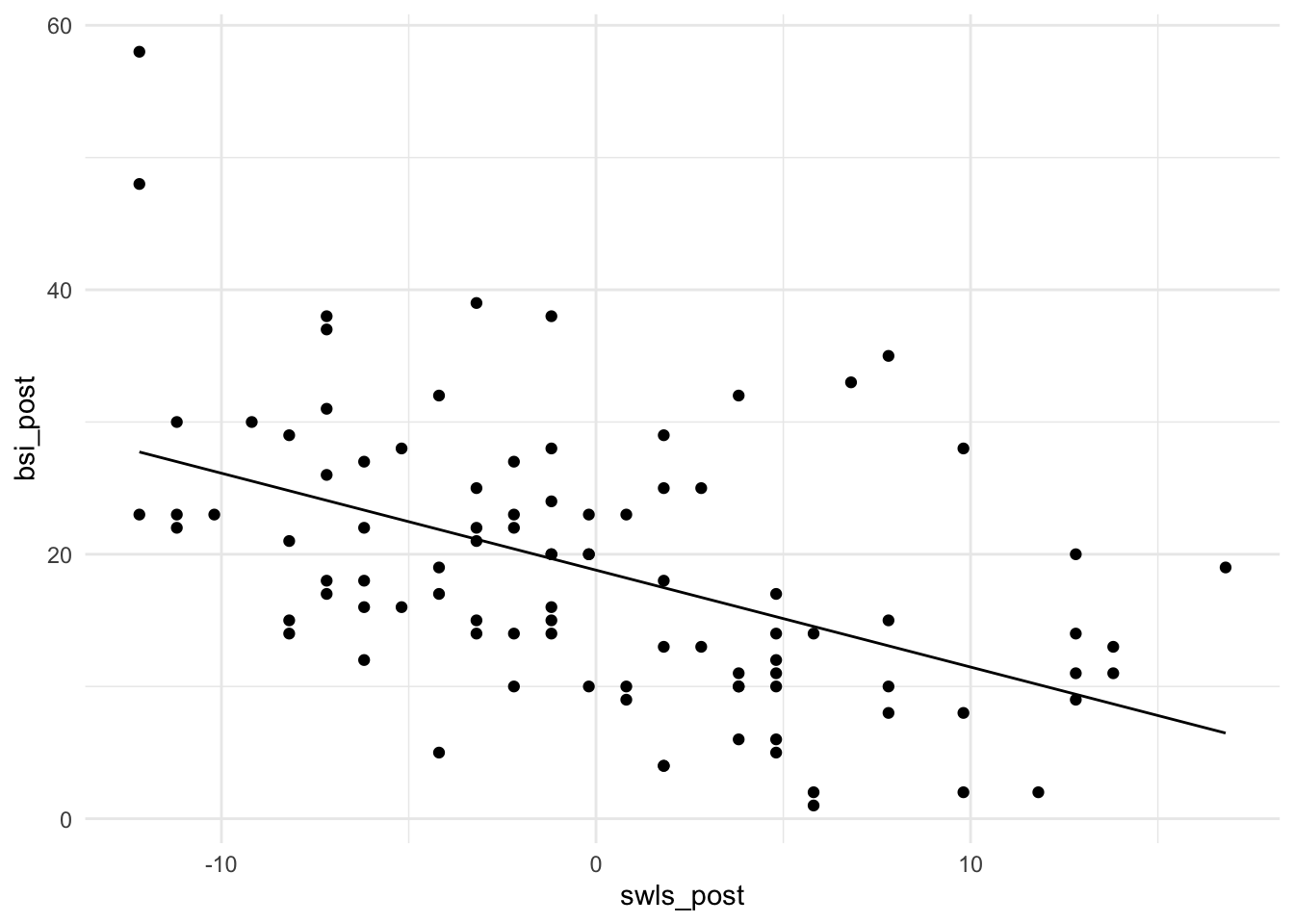
Wenn wir uns für Gruppenunterschiede über group interessieren, schauen wir uns folgenden Plot an:
ggplot(data = osf, mapping = aes(x = group, y = bsi_post, col = group, group = group))+geom_point()+
theme_minimal()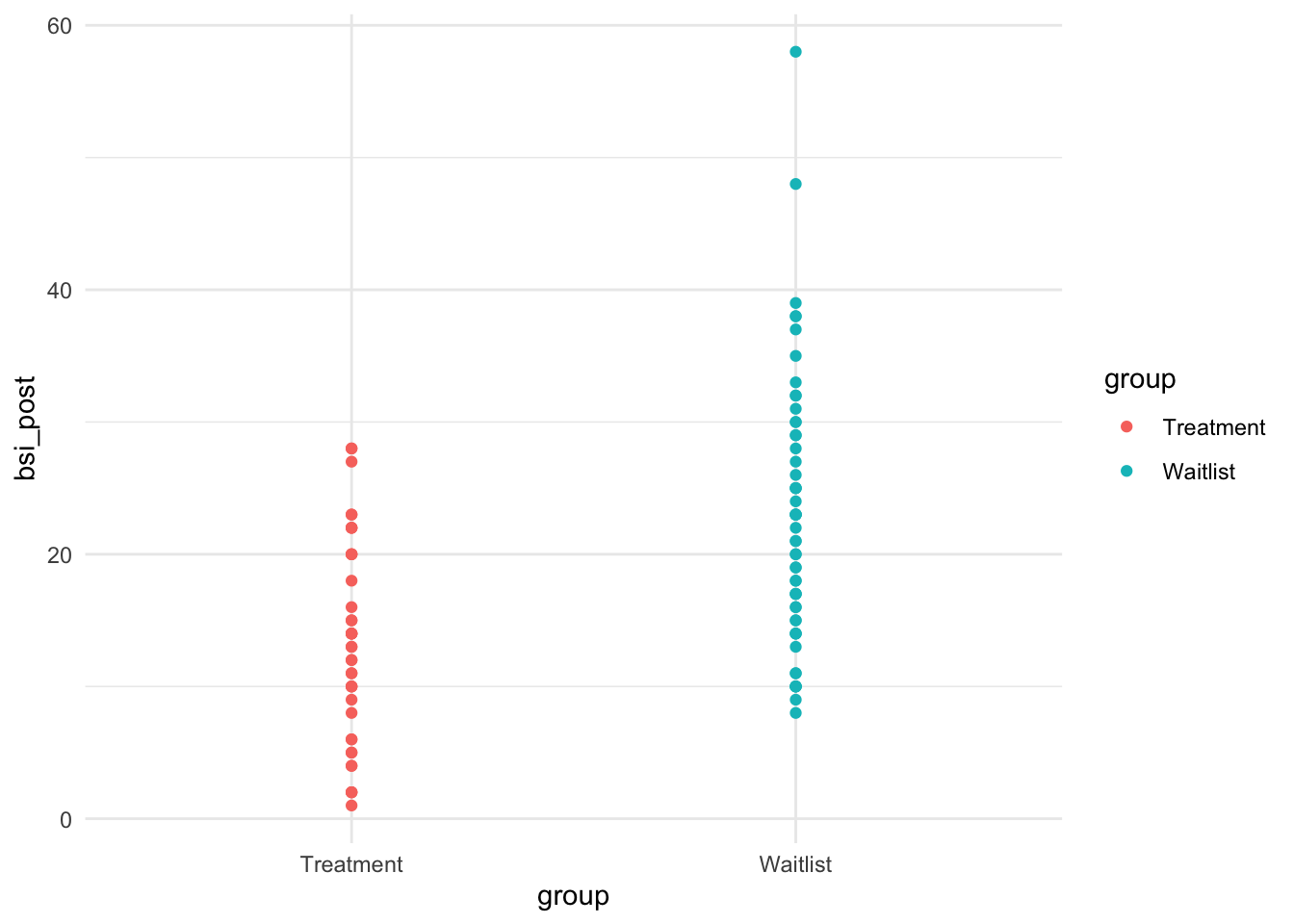
Wenn wir die Gruppierungsvariable als Farbkodierung verwenden (col = group) im Regressionsplot verwenden, erhalten wir:
ggplot(data = osf, mapping = aes(x = swls_post, y = bsi_post, col = group))+
geom_point()+
geom_line(mapping = aes(x = swls_post, y = predict(reg_swl)), col = "black")+
theme_minimal()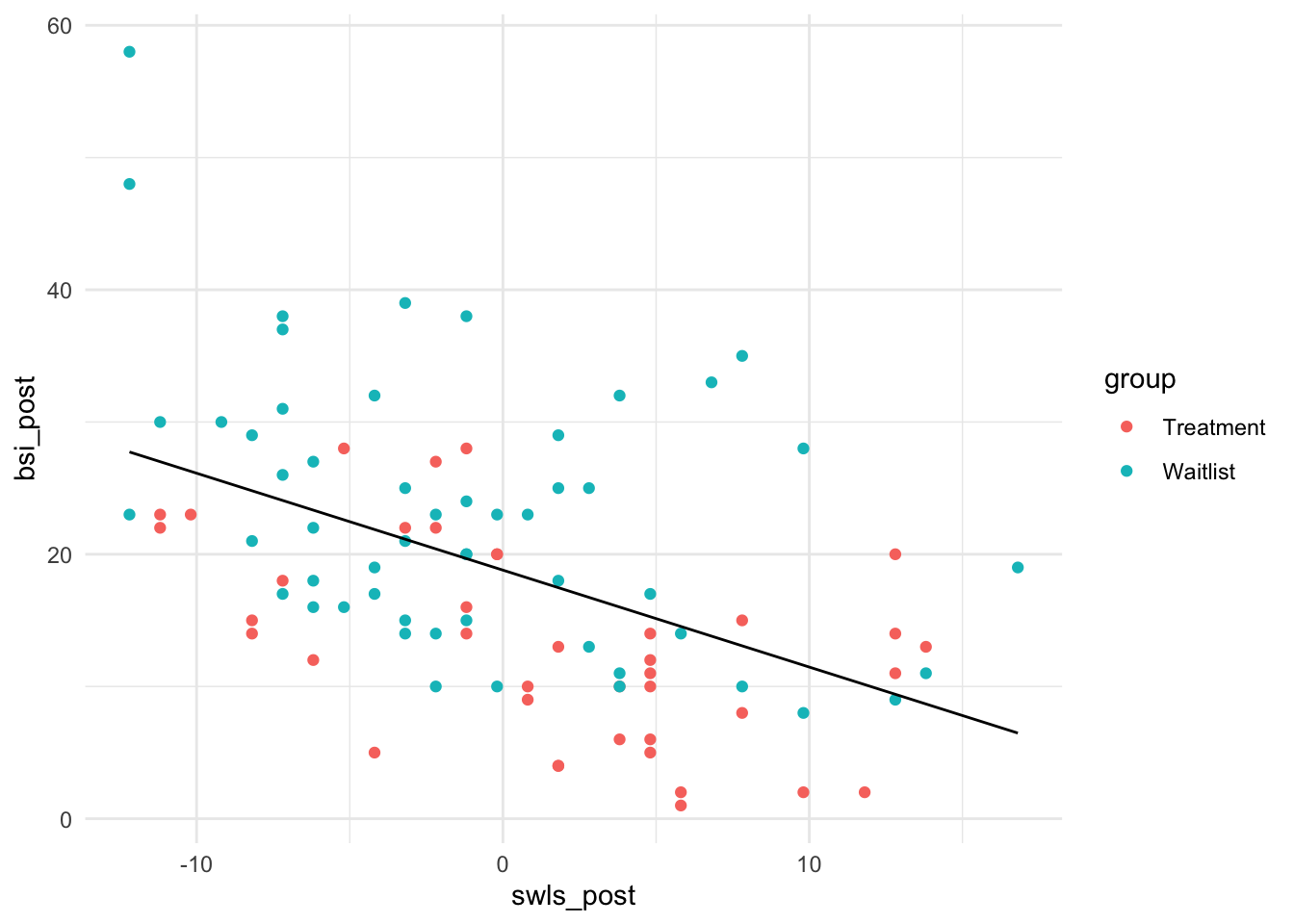
Wenn wir nun pro Gruppe ein Interzept einfügen (ANCOVA-Modell), erhalten wir:
ggplot(data = osf, mapping = aes(x = swls_post, y = bsi_post, col = group))+
geom_point()+
geom_line(mapping = aes(x = swls_post, y = predict(reg_ancova)))+
theme_minimal()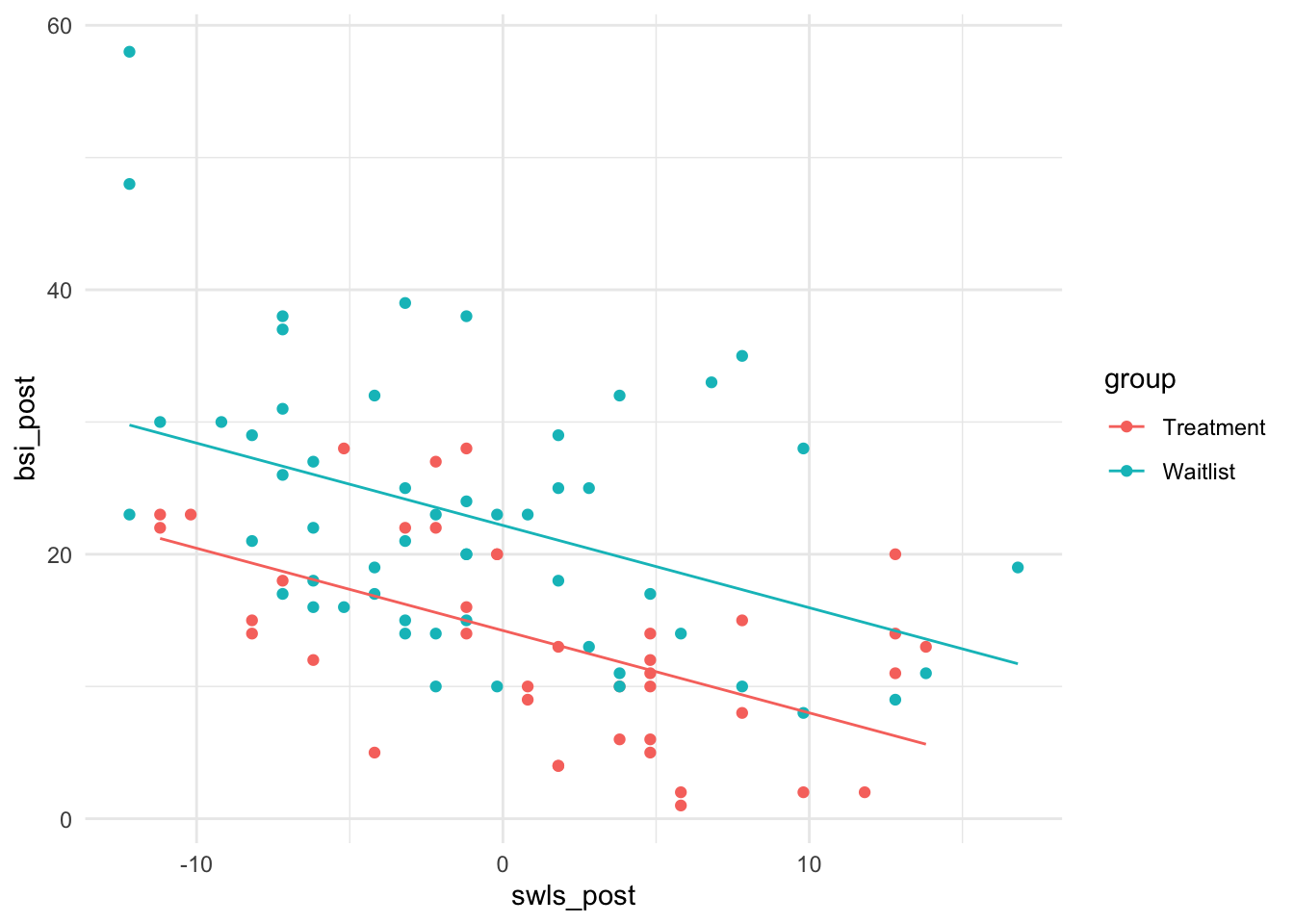
Beim generalisierten ANCOVA Modell landen wir, wenn wir auch noch jeweils einen Steigungskoeffizienten pro Gruppe einfügen:
ggplot(data = osf, mapping = aes(x = swls_post, y = bsi_post, col = group))+
geom_point()+
geom_line(mapping = aes(x = swls_post, y = predict(reg_gen_ancova)))+
theme_minimal()
Außerdem schauen wir uns auch nochmals den Effekt der Diagnose an:
ggplot(data = osf, mapping = aes(x = swls_post, y = bsi_post, col = stratum))+
geom_point()+
geom_line(mapping = aes(x = swls_post, y = predict(reg_gen_ancova_s)))+
theme_minimal()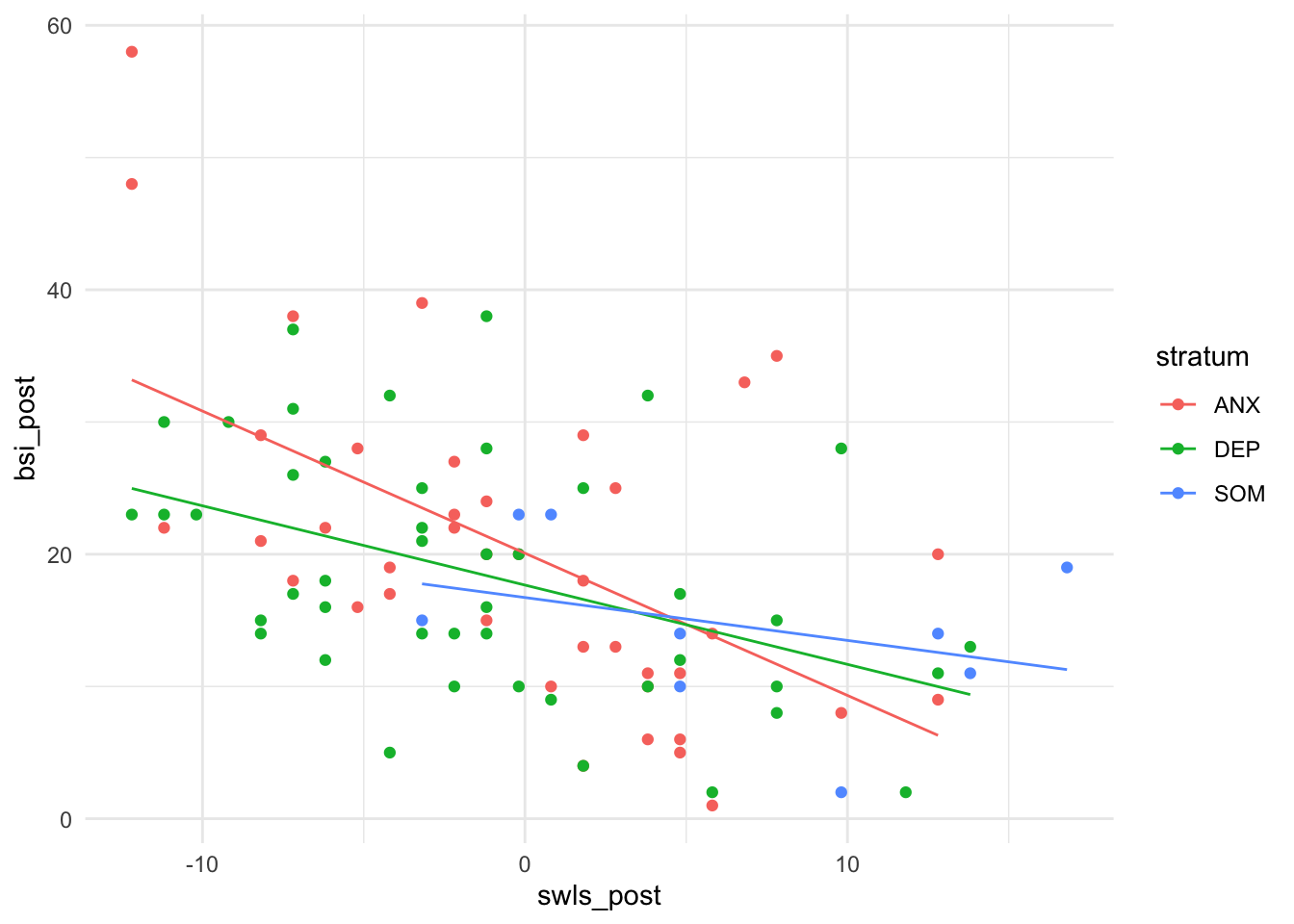
Appendix B
Weitere ANCOVA Modelle
Mit dem * können wir sowohl die Haupteffekte als auch die Interaktionseffekte in ein Modell aufnehmen.
group*stratum*swls_post steht für group + stratum + group:stratum + swls_post + group:swls_post + stratum:swls_post. Insgesamt gibt es also 6 Interzept und 6 Steigungskoeffizienten:
reg_gen_ancova_gs <- lm(bsi_post ~ group*stratum*swls_post, data = osf)
summary(reg_gen_ancova_gs)##
## Call:
## lm(formula = bsi_post ~ group * stratum * swls_post, data = osf)
##
## Residuals:
## Min 1Q Median 3Q Max
## -12.918 -5.939 -1.681 4.796 21.676
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 14.7876 2.1368 6.920 9.15e-10 ***
## groupWaitlist 8.6378 2.7487 3.143 0.00233 **
## stratumDEP -1.0989 2.8489 -0.386 0.70069
## stratumSOM -3.4086 10.9618 -0.311 0.75663
## swls_post -0.8031 0.3759 -2.136 0.03564 *
## groupWaitlist:stratumDEP -1.0886 3.8243 -0.285 0.77663
## groupWaitlist:stratumSOM -0.5674 12.0018 -0.047 0.96241
## groupWaitlist:swls_post -0.2549 0.4585 -0.556 0.57982
## stratumDEP:swls_post 0.3287 0.4531 0.725 0.47024
## stratumSOM:swls_post 0.6320 1.2845 0.492 0.62402
## groupWaitlist:stratumDEP:swls_post 0.2924 0.6054 0.483 0.63032
## groupWaitlist:stratumSOM:swls_post 0.2032 1.3909 0.146 0.88419
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 8.398 on 82 degrees of freedom
## Multiple R-squared: 0.4218, Adjusted R-squared: 0.3442
## F-statistic: 5.437 on 11 and 82 DF, p-value: 1.95e-06Die einzelnen Effekte können wir wieder mit Anova auf Signifikanz prüfen:
Anova(reg_gen_ancova_gs)## Anova Table (Type II tests)
##
## Response: bsi_post
## Sum Sq Df F value Pr(>F)
## group 1388.5 1 19.6877 2.813e-05 ***
## stratum 100.7 2 0.7142 0.4926
## swls_post 1558.1 1 22.0929 1.035e-05 ***
## group:stratum 6.9 2 0.0492 0.9521
## group:swls_post 6.0 1 0.0855 0.7707
## stratum:swls_post 286.5 2 2.0314 0.1377
## group:stratum:swls_post 16.5 2 0.1170 0.8897
## Residuals 5783.0 82
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1ggplot(data = osf, mapping = aes(x = swls_post, y = bsi_post, col = stratum, lty = group, pch = group))+
geom_point()+
geom_line(mapping = aes(x = swls_post, y = predict(reg_gen_ancova_gs)))+
theme_minimal()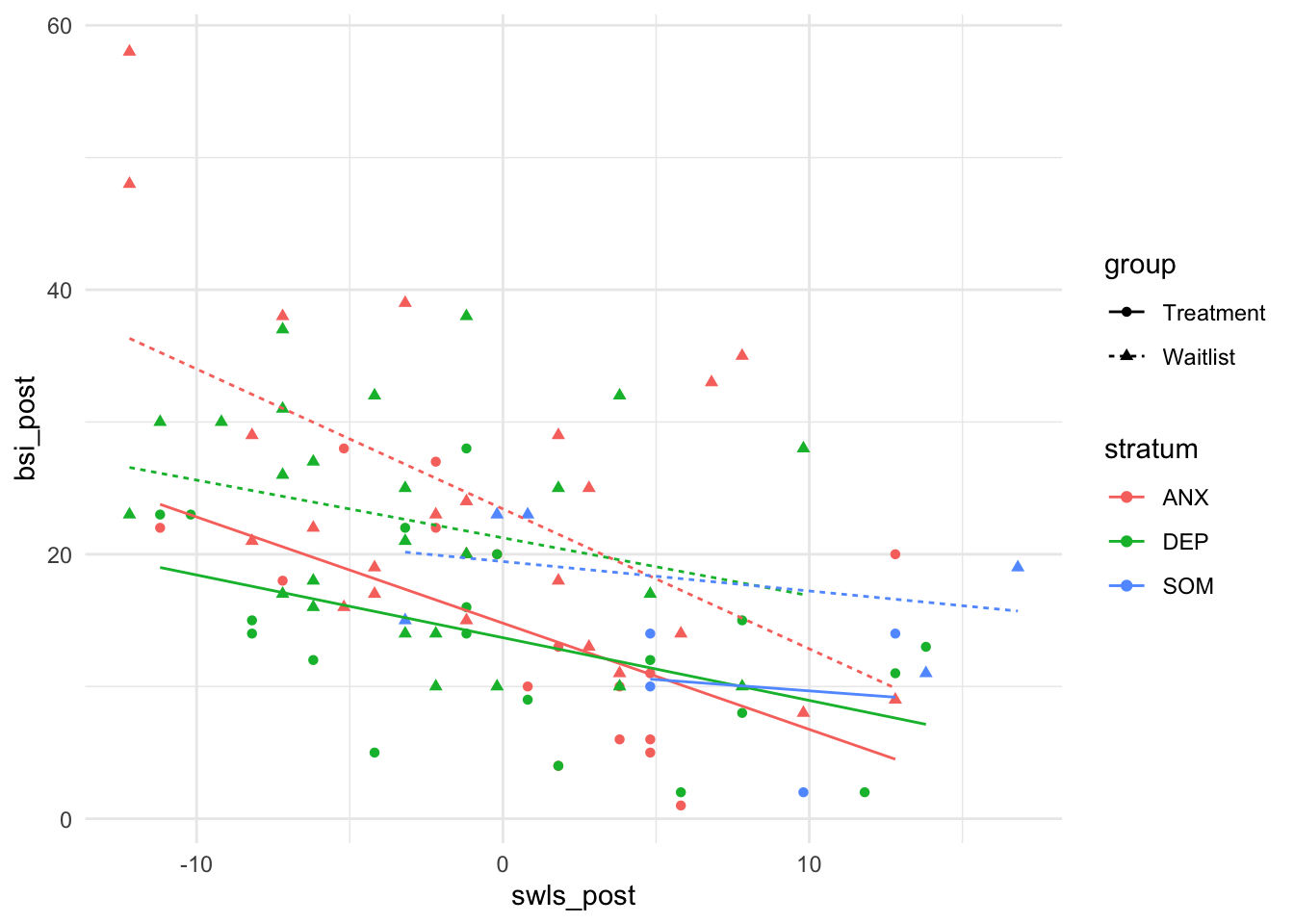
Es kommen keine neuen Effekte hinzu. Nur das Treatment und die Lebenszufriedenheit haben Vorhersagekraft für die Symptomschwere. Keine der Interaktionen ist statistisch bedeutsam!
Appendix C
Plots zur moderierten Regression
library(plot3D)
# Übersichtlicher: Vorbereitung
x <- c(osf$pas_post)
y <- c(osf$bsi_post)
z <- c(osf$swls_post)
fit <- lm(y ~ x + z + x:z)
grid.lines = 26
x.pred <- seq(min(x), max(x), length.out = grid.lines)
z.pred <- seq(min(z), max(z), length.out = grid.lines)
xz <- expand.grid(x = x.pred, z = z.pred)
y.pred <- matrix(predict(fit, newdata = data.frame(xz)),
nrow = grid.lines, ncol = grid.lines)
fitpoints <- predict(fit)
# Plot:
scatter3D(x = x, y = z, z = y, pch = 16, cex = 1.2,
theta = -30, phi = 30, ticktype = "detailed",
xlab = "Panikstörungs- und Agoraphobiesymptomatik", ylab = "Lebenszufriedenheit", zlab = "Symptomschwere",
surf = list(x = x.pred, y = z.pred, z = y.pred,
facets = NA, fit = fitpoints),
main = "Moderierte Regression")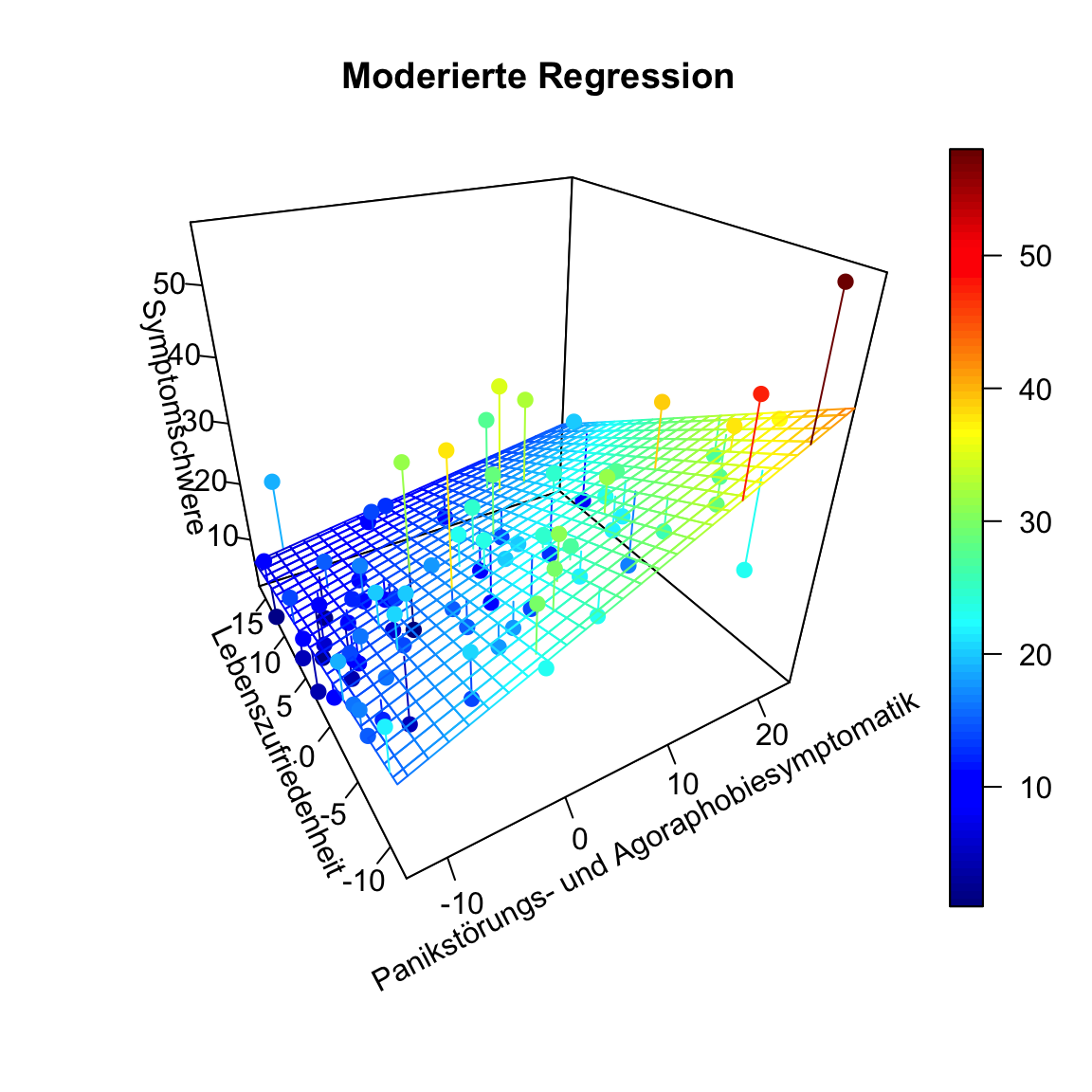
# Übersichtlicher: Vorbereitung
x <- c(osf$pas_post)
y <- c(osf$bsi_post)
z <- c(osf$swls_post)
fit <- lm(y ~ x + z + z:x + I(x^2) + I(z^2)) # Modellerweiterung um quadratische Effekte
grid.lines = 26
x.pred <- seq(min(x), max(x), length.out = grid.lines)
z.pred <- seq(min(z), max(z), length.out = grid.lines)
xz <- expand.grid(x = x.pred, z = z.pred)
y.pred <- matrix(predict(fit, newdata = data.frame(xz)),
nrow = grid.lines, ncol = grid.lines)
fitpoints <- predict(fit)
# Plot:
scatter3D(x = x, y = z, z = y, pch = 16, cex = 1.2,
theta = -20, phi = 30, ticktype = "detailed",
xlab = "Panikstörungs- und Agoraphobiesymptomatik", ylab = "Lebenszufriedenheit", zlab = "Symptomschwere",
surf = list(x = x.pred, y = z.pred, z = y.pred,
facets = NA, fit = fitpoints),
main = "Moderierte Regression\nmit quadratischen Effekten")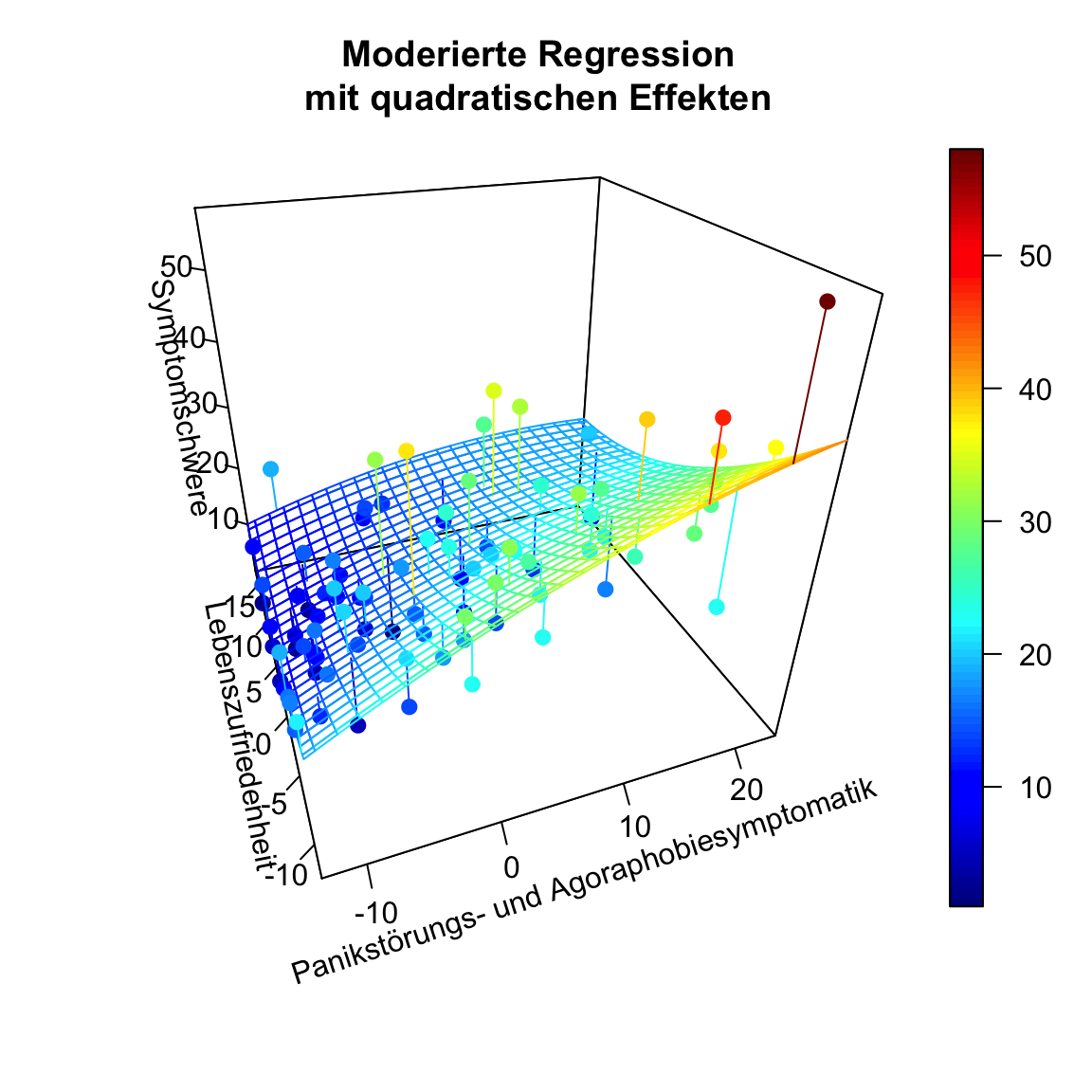
Appendix D
Exkurs: Effekte der Zentrierung
In diesem Abschnitt schauen wir uns den Effekt der Zentrierung an einem vereinfachten Beispiel an. Dieser Abschnitt fundiert auf dem Appendix A in der Sitzung zu moderierter Regression aus dem Bachelor.
Um den Sachverhalt zu vereinfachen, erstellen wir einen Vektor (also eine Variable) der die Zahlen von 0 bis 10 enthält in 0.1 Schritten:
A <- seq(0, 10, 0.1)Nun bestimmen wir zunächst die Korrelation zwischen und :
cor(A, A^2)## [1] 0.9676503Diese fällt sehr hoch aus. Nun zentrieren wir die Daten. Das geht entweder händisch oder mit der scale Funktion:
A_c <- A - mean(A)
mean(A_c)## [1] 2.639528e-16A_c2 <- scale(A, center = T, scale = F) # scale = F bewirkt, dass nicht auch noch die SD auf 1 gesetzt werden soll
mean(A_c2)## [1] 2.639528e-16Nun vergleichen wir die Korrelationen zwischen mit mit der Korrelation zwischen und :
cor(A_c, A_c^2)## [1] 1.763581e-16cor(A, A^2)## [1] 0.9676503# auf 15 Nachkommastellen gerundet:
round(cor(A_c, A_c^2), 15)## [1] 0round(cor(A, A^2), 15)## [1] 0.9676503Beide Korrelationen unterscheiden sich enorm. Die Korrelation zwischen und ist 0 und damit drastisch geringer als die Korrelation zwischen und . Was hat das Ganze nun mit Interaktionen zu tun? Im Grunde ist ja eine Interaktion ein Produkt zweier Prädiktoren: bspw. . Wenn wir für wählen, dann erhalten wir natürlich , was also einen Spezialfall einer Interaktion darstellt — nämlich die Interaktion mit sich selbst!
Wir simulieren noch schnell zwei normalverteilte Variablen und schauen uns die Korrelation mit der Interaktion an:
set.seed(1234) # Vergleichbarkeit
X <- rnorm(1000, mean = 2, sd = 1) # 1000 normalverteile Zufallsvariablen mit Mittelwert 2 und Standardabweichung = 1
Z <- X + rnorm(1000, mean = 1, sd = 0.5) # generiere Z ebenfalls normalverteilt und korreliert zu X
cor(X, Z) # Korrelation zwischen X und Z## [1] 0.9022937und sind zu 0.902 korreliert. Wir zentrieren die beiden Variablen und schauen uns jeweils die Korrelationen untereinander und mit der Interaktion an:
X_c <- scale(X, center = T, scale = F)
Z_c <- scale(Z, center = T, scale = F)
cor(X, X*Z)## [1] 0.9347276cor(X_c, X_c*Z_c)## [,1]
## [1,] 0.01993774Die Korrelation zwischen und liegt bei 0.935, während sie bei den zentrierten Varianten und bei 0.02 liegt. Damit resultiert die erste Variante in Multikollinearitätsproblemen in einem Regressionsmodell, während die zweite dies nicht tut.
Mathematische Begründung
Dieser Abschnitt ist für die “Warum ist das so?”-Fragenden bestimmt und ist als reinen Zusatz zu erkennen. Wir konzentrieren uns weider auf das Quadrat, da es einfacher zu untersuchen ist.
Wir wissen, dass die Korrelation der Bruch aus der Kovarianz zweier Variablen geteilt durch deren Standardabweichung ist. Aus diesem Grund reicht es, die Kovarianz zweier Variablen zu untersuchen, um zu schauen, wann die Korrelation 0 ist. Wir hatten oben die Variablen zentriert und bemerkt, dass dann die Korrelation zwischen und verschwindet. Warum ist das so? Dazu stellen wir in Abhängigkeit von seinem Mittelwert und , der zentrierten Version von , dar:
So kann jede Variable zerlegt werden: in seinen Mittelwert (hier: ) und die Abweichung vom Mittelwert (hier: ). Nun bestimmen wir die Kovarianz zwischen den Variablen und und setzen in diesem Prozess für ein und wenden die binomische Formel an .
An dieser Stelle pausieren wir kurz und bemerken, dass wir diese beiden Ausdrücke schon kennen . Ersteres ist die Kovarianz zwischen einer Konstanten und einer Variable, welche immer 0 ist und dass die Kovarianz zwischen und 0 ist, hatten wir oben schon bemerkt! Diese Aussage, dass die Korrelation/Kovarianz zwischen und 0 ist, gilt insbesondere für die transformierten Daten mittels poly (hier bezeichnet quasi den quadratischen Anteil, der erstellt wird, siehe dazu Sitzung aus dem Bachelor und auch für einige Verteilungen (z.B. symmetrische Verteilungen, wie die Normalverteilung) ist so, dass die linearen Anteile und die quadratischen Anteile unkorreliert sind. Im Allgemeinen gilt dies leider nicht.
Folglich können wir sagen, dass für bspw. normalverteiltes A
wobei wir hier benutzen, dass die Kovarianz mit sich selbst die Varianz ist und dass die zentrierte Variable die gleiche Varianz wie hat (im Allgemeinen, siehe weiter unten, bleibt auch noch die Kovarianz zwischen und erhalten). Dies können wir leicht prüfen:
var(A)## [1] 8.585var(A_c)## [1] 8.585# Kovarianz
cov(A, A^2)## [1] 85.852*mean(A)*var(A)## [1] 85.85# zentriert:
round(cov(A_c, A_c^2), 14)## [1] 0round(2*mean(A_c)*var(A_c), 14)## [1] 0Der zentrierte Fall ist auf 14 Nachkommastellen identisch und weicht danach nur wegen der sogenannten Maschinengenauigkeit von einander ab. Somit ist klar, dass wenn der Mittelwert = 0 ist, dann ist auch die Korrelation zwischen einer Variable und seinem Quadrat 0, solange die Variable symmetrisch verteilt ist, andernfalls ist die Korrelation zumindest kleiner, als wenn nicht zentriert wurde, was ebenfalls der Multikollinearitätsproblematik entgegben wirkt! Analoge Überlegungen können genutzt werden, um das gleiche für die Interaktion von Variablen zu sagen.
Im Allgemeinen:
Im Allgemeinen ist es dennoch sinnvoll die Daten zu zentrieren, wenn quadratische Effekte (oder Interaktionseffekte) eingesetzt werden, da zumindest immer gilt:
somit wird die Kovarianz zwischen und künstlich vergrößert, wenn die Daten nicht zentriert sind. Denn nutzen wir zentrierte Variablen ist nur noch relevant (da ). Hier ein beispiel mit stark schiefen Daten, nämlich exponentialverteilten Variablen:
A <- rexp(1000)
hist(A)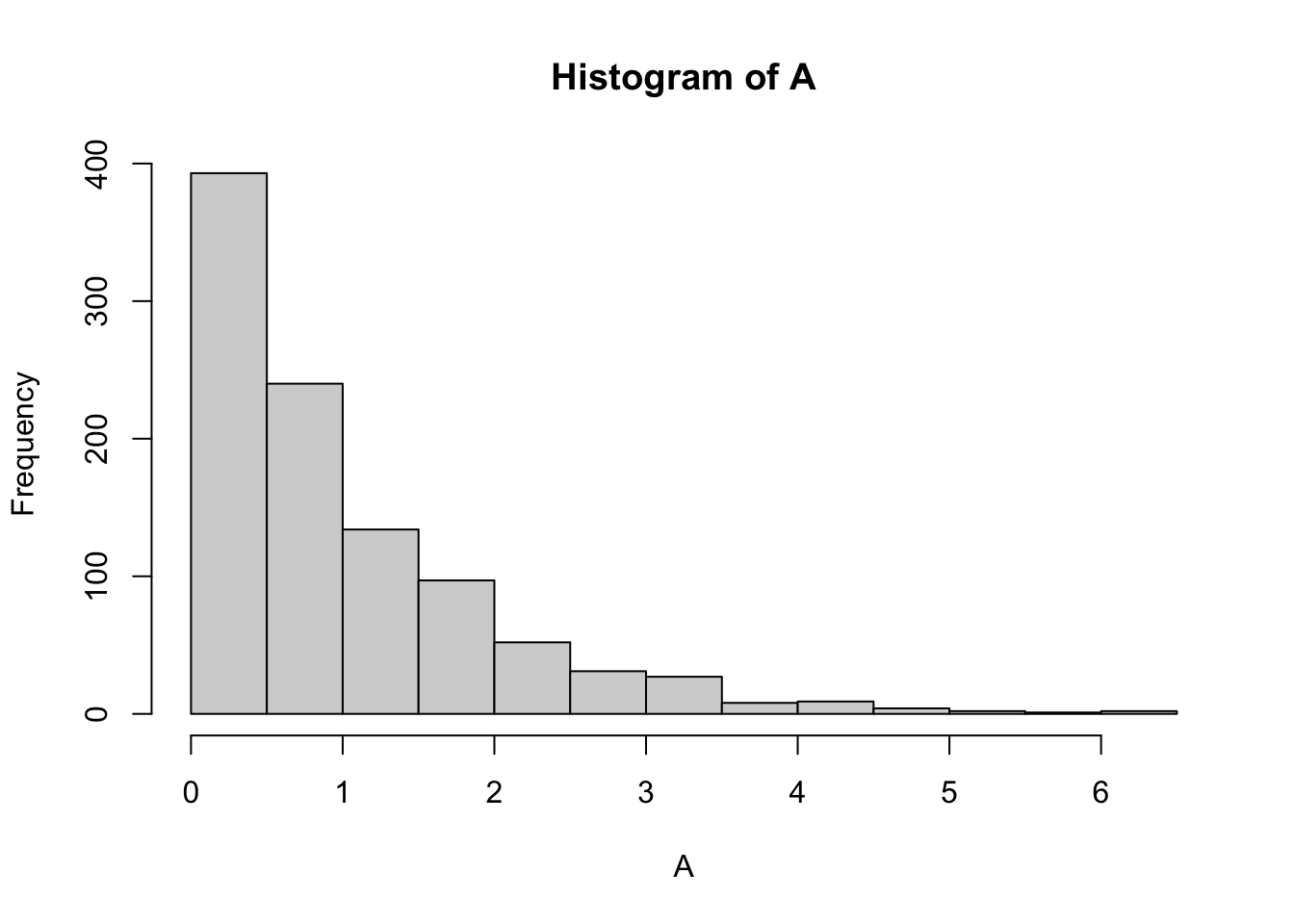
mean(A) # Mittelwert von A## [1] 1.00317sd(A) # SD(A)## [1] 0.9767583B <- (A + rexp(1000))/sqrt(2) # durch Wurzel 2 teilen für vergleichbare Varianzen von A und B
mean(B) # Mittelwert von B## [1] 1.428577sd(B) # SD(B)## [1] 0.9666604cor(A, B)## [1] 0.6761999cov(A, B)## [1] 0.6384637cor(A, A*B)## [1] 0.9091913cov(A, A*B)## [1] 3.124103cor(A, A^2)## [1] 0.9194526cov(A, A^2)## [1] 3.524668A_c <- scale(A, center = T, scale = F)
B_c <- scale(B, center = T, scale = F)
cor(A_c, A_c*B_c) # Korrelation und Kovarianz von 0 verschieden ## [,1]
## [1,] 0.6641127cov(A_c, A_c*B_c) # zwischen A_c und Interaktion, jedoch etwas kleiner als nicht-zentriert## [,1]
## [1,] 1.120672cor(A_c, A_c^2) # Korrelation und Kovarianz von 0 verschieden ## [,1]
## [1,] 0.7301108cov(A_c, A_c^2) # zwischen A_c und A_c^2, jedoch etwas kleiner als nicht-zentriert## [,1]
## [1,] 1.610506Wir sehen deutlich, dass die Kovarianzen/Korrelationen im zentrierten Fall geringer ausfallen, als im nicht zentrierten Fall! Aus diesem Grund macht es immer Sinn, Prädiktoren zu zentrieren, wenn Interaktionen vorkommen. So wird die Multikolliniearität reduziert.
Literatur
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden (5. Auflage, 1. Auflage: 2010). Weinheim: Beltz.
Datensatz
Schaeuffele, C., Homeyer, S. L., Perea, L., Scharf, L., Schulz, A., Knaevelsrud, C., … Boettcher, J. (2020, December 16). The Unified Protocol as an Internet-based Intervention for Emotional Disorders: Randomized Controlled Trial. https://doi.org/10.31234/osf.io/528tw
- Blau hinterlegte Autor:innenangaben führen Sie direkt zur universitätsinternen Ressource.
