Diskriminanzanalyse
Deskriptive lineare Diskriminanzanalyse
Einleitung
Die (deskriptive) Diskriminanzanalyse geht der entgegengesetzten Fragestellung der MANOVA auf den Grund. Mit ihr können wir (deskriptiv) untersuchen, ob Gruppenzugehörigkeiten durch die AVs der MANOVA vorhergesagt werden können (siehe bspw. Pituch und Stevens, 2016, Kapitel 10 sowie Eid, Gollwitzer & Schmitt, 2017, Kapitel 15.4). Wir wollen uns wieder das fiktive Datenbeispiel (Datensatz Therapy aus dem gleichnamigen .rda File Therapy.rda) ansehen, den wir bereits in der MANOVA-Sitzung untersucht haben. Sie können den Datensatz “Therapy.rda” hier herunterladen.
Daten laden
Wir laden zunächst die Daten: entweder lokal von Ihrem Rechner:
load("C:/Users/Musterfrau/Desktop/Therapy.rda")oder wir laden sie direkt über die Website:
load(url("https://pandar.netlify.app/post/Therapy.rda"))Nun sollte in R-Studio oben rechts in dem Fenster unter der Rubrik “Data” unser Datensatz mit dem Namen “Therapy” erscheinen.
Übersicht über die Daten
Wir wollen uns einen Überblick über die Daten verschaffen:
head(Therapy)## Lebenszufriedenheit Arbeitsbeanspruchung Depressivitaet Arbeitszufriedenheit
## 1 7 4 7 5
## 2 5 5 8 3
## 3 8 7 6 6
## 4 6 4 5 5
## 5 6 9 8 5
## 6 8 7 8 6
## Intervention Geschlecht
## 1 Kontrollgruppe 0
## 2 Kontrollgruppe 1
## 3 Kontrollgruppe 0
## 4 Kontrollgruppe 1
## 5 Kontrollgruppe 1
## 6 Kontrollgruppe 1levels(Therapy$Intervention)## [1] "Kontrollgruppe" "VT Coaching"
## [3] "VT Coaching + Gruppenuebung"levels(Therapy$Geschlecht)## [1] "0" "1"Die abhängigen Variablen sind Lebenszufriedenheit, Arbeitsbeanspruchung Depressivitaet und Arbeitszufriedenheit. Die Variable Intervention hat drei Stufen: eine Kontrollgruppe, ein verhaltenstherapiebasiertes Coaching, sowie das verhaltenstherapiebasierte Coaching inklusive einer Gruppenübung. Das Geschlecht ist 0-1 kodiert, wobei 0 für männlich und 1 für weiblich steht. Insgesamt sind die Variablennamen der AVs recht lang. Wir wollen diese kürzen:
colnames(Therapy) # Spaltennamen ansehen## [1] "Lebenszufriedenheit" "Arbeitsbeanspruchung" "Depressivitaet"
## [4] "Arbeitszufriedenheit" "Intervention" "Geschlecht"colnames(Therapy) <- c("LZ", "AB", "Dep", "AZ", "Intervention", "Geschlecht") # Spaltennamen neu zuordnen
head(Therapy)## LZ AB Dep AZ Intervention Geschlecht
## 1 7 4 7 5 Kontrollgruppe 0
## 2 5 5 8 3 Kontrollgruppe 1
## 3 8 7 6 6 Kontrollgruppe 0
## 4 6 4 5 5 Kontrollgruppe 1
## 5 6 9 8 5 Kontrollgruppe 1
## 6 8 7 8 6 Kontrollgruppe 1So - schon viel übersichtlicher!
Pakete laden
Nachdem wir neue Pakete installiert haben (install.packages), laden wir diese:
library(MASS) # für lineare Diskrimianzanalys (lda)
library(ggplot2) # GrafikenZiel der linearen Diskriminanzanalyse
Wir wollen mit der Lebenszufriedenheit, der Depression, der Arbeitsbeanspruchung und der Arbeitszufriedenheit die Zugehörigkeit zu den Therapiegruppen vorhersagen (ob dies inhaltlich sinnvoll ist, sei jetzt mal dahingestellt!). Die lineare Diskriminanzanalyse (LDA) funktioniert ähnlich wie die PCA. Die PCA maximiert die Varianz auf jeder Hauptkomponente. Die LDA maximiert die Diskrimination entlang der Achsen, also quasi die Varianz zwischen den Gruppen auf den Achsen. Somit sind beide Verfahren de facto Varianzmaximierungsverfahren.
Die LDA hat im Grunde die gleichen Annahmen wie die MANOVA. Die Kovarianzmatrizen über die Gruppen müssen homogen sein. Die Daten sollten multivariat normalverteilt sein (diese Annahme lässt sich bspw. in Fisher’s linearer Diskriminanzanalye lockern, sodass sie nicht so wichtig ist). Die Beobachtungen stammen aus einer independent and identically distributed (, deutsch: unabhängig und identisch verteilt) Population (dies bedeutet, dass alle Beobachtungen unabhängig sind und den gleichen Verteilungs- und Modellannahmen unterliegen). Die letzte Annahme können wir nicht prüfen. Sie kann nur über die sinnvolle Wahl des Designs (Randomisierung etc.) angenommen werden. Wie dies zu prüfen ist, hatten wir in der Sitzung zur MANOVA kennengelernt.
Analysen
Der Befehl in R heißt lda für lineare Diskriminanzanalyse. Ihr übergeben wir wieder eine Gleichung, ähnlich der MANOVA-Gleichung der vergangenen Sitzung. Allerdings ist diesmal die Intervention die AV und die AVs der MANOVA (LZ, Dep, AB und AZ) sind die UVs, die zur Prädiktion herangezogen werden. Mit Hilfe von $scaling können wir die Gewichtungskoeffizienten der Variablen auf den Diskriminanzachsen einsehen. Insgesamt sind bei einer linearen Diskriminanzanalyse immer maximal Diskriminanzfunktionen/achsen möglich, wobei die Anzahl an UVs ist und die Anzahl an Gruppen beschreibt. Hier sind es UVs und Gruppen. Folglich können maximal Diskriminanzfunktionen bestimmt werden:
model_DA <- lda(Intervention ~ LZ + Dep + AB + AZ, Therapy)
model_DA## Call:
## lda(Intervention ~ LZ + Dep + AB + AZ, data = Therapy)
##
## Prior probabilities of groups:
## Kontrollgruppe VT Coaching
## 0.3333333 0.3333333
## VT Coaching + Gruppenuebung
## 0.3333333
##
## Group means:
## LZ Dep AB AZ
## Kontrollgruppe 5.933333 7.133333 6.033333 5.133333
## VT Coaching 5.933333 5.066667 5.833333 6.833333
## VT Coaching + Gruppenuebung 7.333333 4.766667 6.300000 7.500000
##
## Coefficients of linear discriminants:
## LD1 LD2
## LZ 0.1618370 -0.88229519
## Dep 0.7453510 0.09824489
## AB -0.4155893 -0.35778884
## AZ -0.1519953 0.48104478
##
## Proportion of trace:
## LD1 LD2
## 0.7892 0.2108model_DA$scaling # Koeffizienten## LD1 LD2
## LZ 0.1618370 -0.88229519
## Dep 0.7453510 0.09824489
## AB -0.4155893 -0.35778884
## AZ -0.1519953 0.48104478Für die erste Achse sind besonders Dep und AB relevant, während auf der zweiten Achse AZ und LZ stärker ins Gewicht fallen. Wir können predict nutzen, um eine Vorhersage mittels dieses Modells (model_DA) zu erhalten. predict gibt hierbei 3 Listen aus: $posterior gibt die Wahrscheinlichkeit an, in die jeweilige Gruppe zu gelangen, $class gibt die Vorhersage für die Gruppenzugehörigkeit an und $x gibt die vorhergesagte Ausprägung auf der jeweiligen Diskriminanzachse an.
head(predict(model_DA)$posterior) # Wahrscheinlichkeit in der jeweiligen Gruppe zu landen## Kontrollgruppe VT Coaching VT Coaching + Gruppenuebung
## 1 0.9518348 0.02825584 0.019909382
## 2 0.9669084 0.02447494 0.008616686
## 3 0.2868306 0.08677168 0.626397717
## 4 0.4461846 0.36122866 0.192586789
## 5 0.5512585 0.12202873 0.326712765
## 6 0.8868980 0.02379371 0.089308278head(predict(model_DA)$class) # Vorhergesagte Klasse## [1] Kontrollgruppe Kontrollgruppe
## [3] VT Coaching + Gruppenuebung Kontrollgruppe
## [5] Kontrollgruppe Kontrollgruppe
## Levels: Kontrollgruppe VT Coaching VT Coaching + Gruppenuebunghead(predict(model_DA)$x) # vorhergesagte Ausprägung auf der jeweiligen Diskriminanzachse## LD1 LD2
## 1 2.1797562 -0.3780597
## 2 2.4898346 0.1648972
## 3 0.1974790 -1.9509215
## 4 0.5272172 0.3077457
## 5 0.6853238 -1.1864638
## 6 1.6881810 -1.7544317Wir wollen uns die Ausprägungen auf den beiden Diskriminanzachsen grafisch ansehen. Dazu speichern wir diese unter DA1 und DA2 jeweils für 1. und 2. Diskriminanzachse ab.
Therapy$DA1 <- predict(model_DA)$x[, 1] # erste DA
Therapy$DA2 <- predict(model_DA)$x[, 2] # zweite DAAnschließend können wir wieder ggplot verwenden, um die beiden Diskriminanzachsen gegeneinander abzutragen. Außerdem fügen wir noch die Nullpunkte auf den Diskriminanzachsen als gepunktete Linie ein:
ggplot(data = Therapy, aes(x = DA1, y = DA2, color = Intervention)) +
geom_point()+
geom_hline(yintercept = 0, lty = 3)+
geom_vline(xintercept = 0, lty = 3)+
ggtitle(label = "Diskriminanzachsen", subtitle = "mit Trennlinien")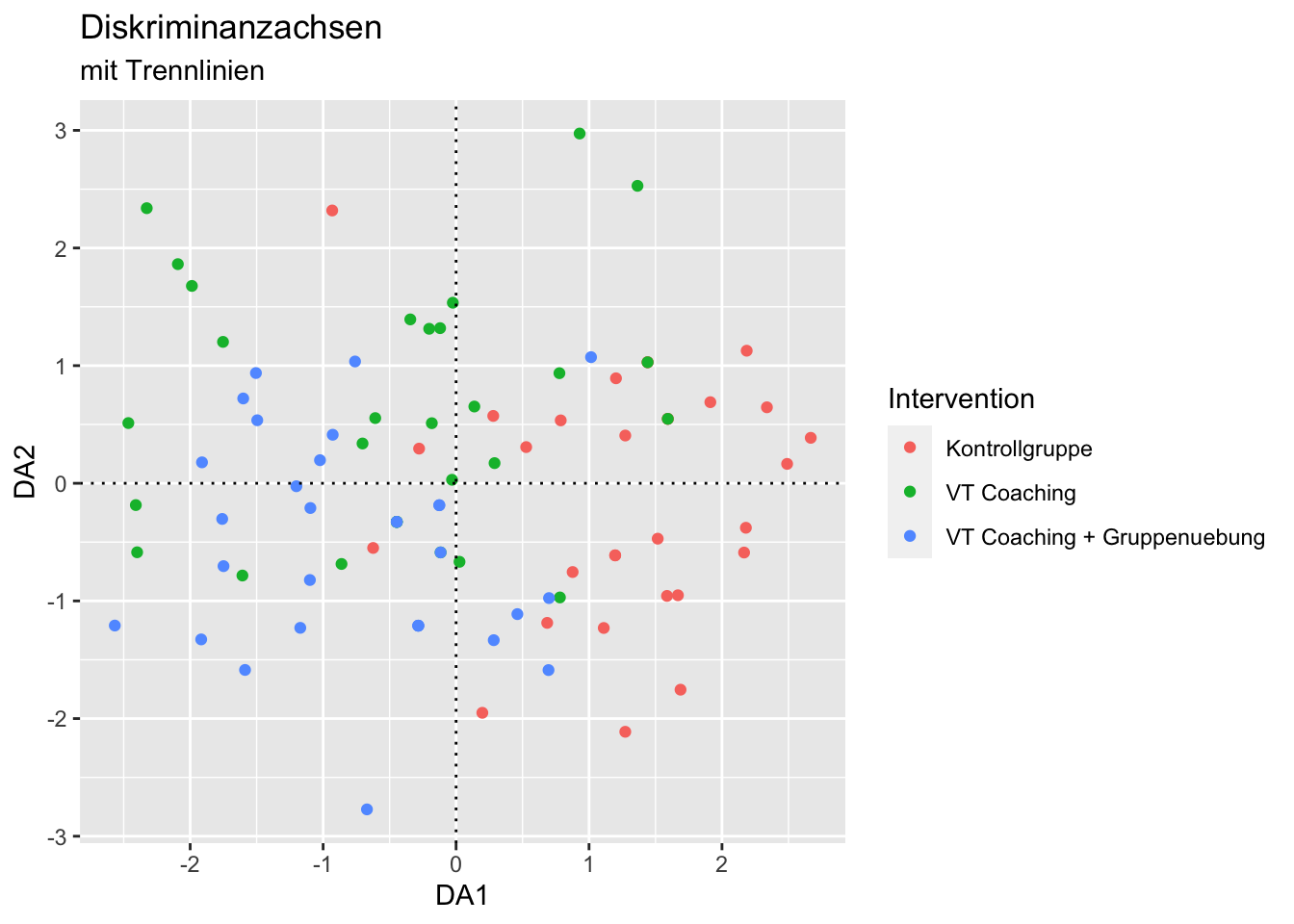
Was wir nun sehen, ist, dass entlang der x-Achse besonders zwischen blau/grün vs rot unterschieden wird. D.h. die erste Diskriminanzachse hilft uns, zwischen den Interventionsgruppen und der Kontrollgruppe zu unterscheiden. Die zweite Achse trennt eher zwischen den beiden Interventionsgruppen, wobei diese Trennung nicht sehr eindeutig ist.
Wir hätten auch einfach die plot-Funktion auf das model_DA-Objekt anwenden können:
plot(model_DA)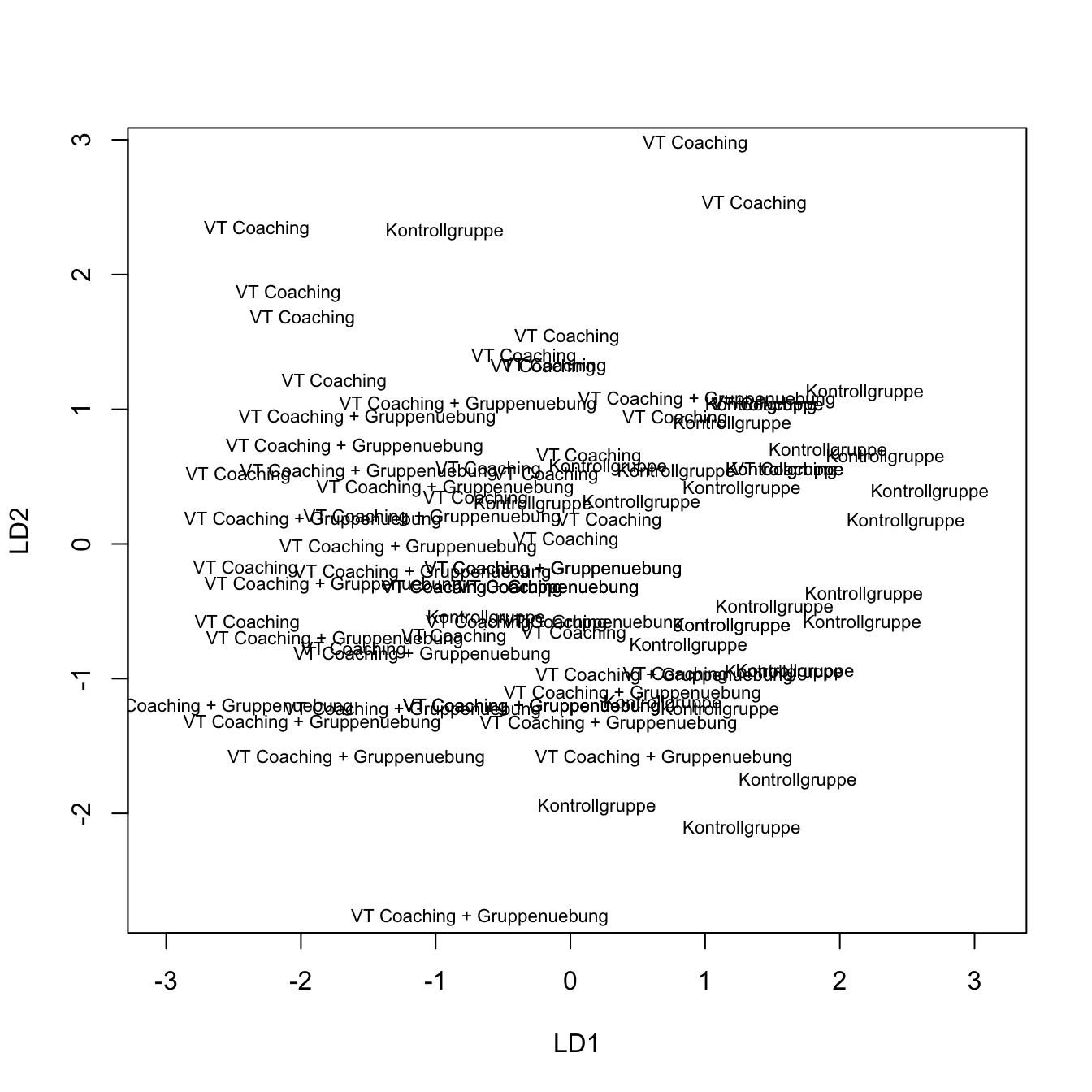
Wenn wir diesem noch Farben zuordnen (hier jeweils 30 mal die selbe Farbe, da die Gruppen so häufig hintereinander im Datensatz standen…), dann sieht diese Grafik der mit ggplot erzeugten Grafik recht ähnlich. Natürlich können wir auch hier die Nullpunkte einfügen:
plot(model_DA, col = c(rep("red", 30), rep("gold3", 30), rep("blue", 30)))
abline(v = 0, lty = 3)
abline(h = 0, lty = 3)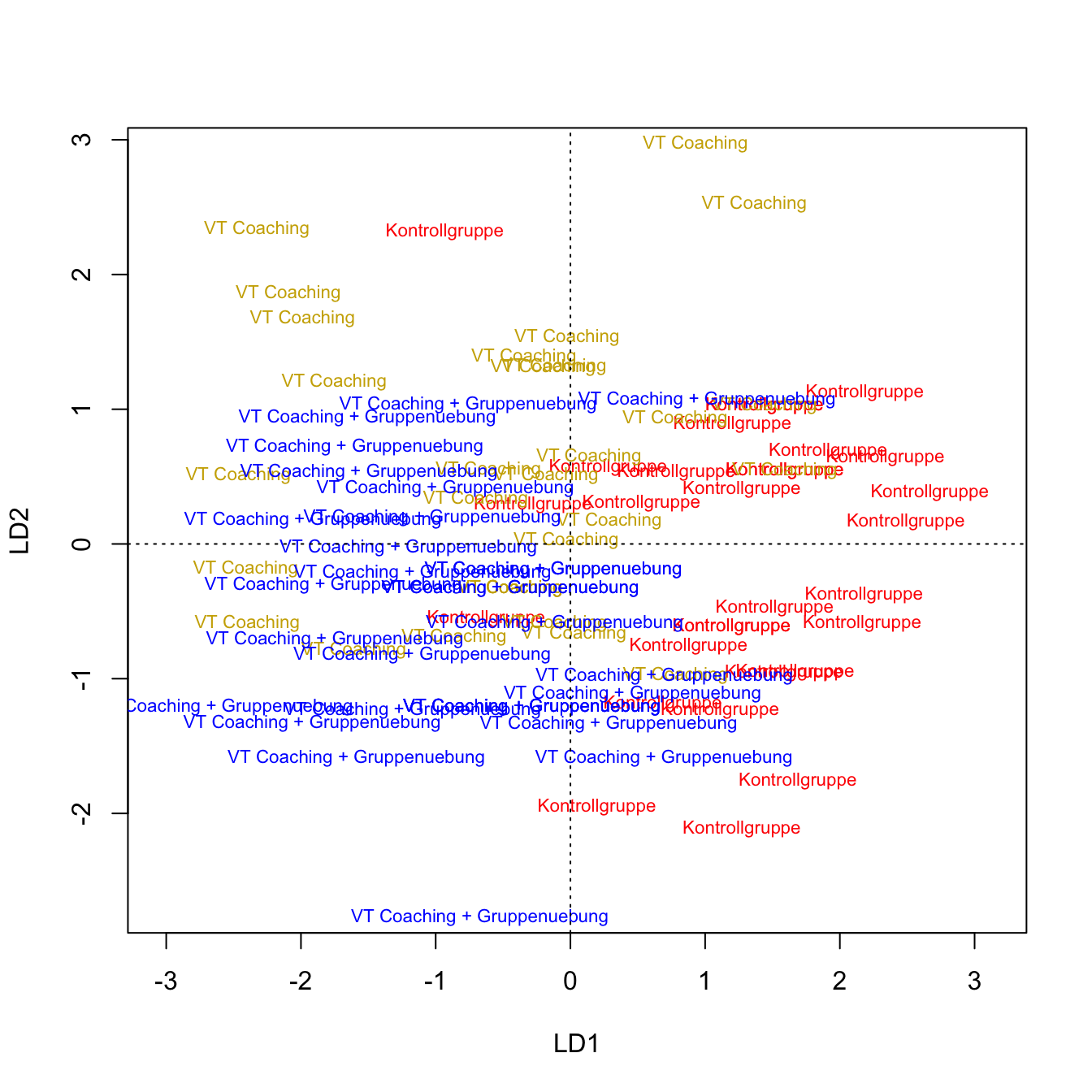
Zu guter Letzt fügen wir noch die Trennlinien, die zwischen den Gruppen unterscheiden, in die erste Grafik ein. Diese liegen immer auf halbem Weg (durchgezogenen schwarzen Linien, hier für Kontrollgruppe vs. VT-Coaching + Gruppenübung) zwischen zwei Mittelwerten pro Gruppe (gestrichelten Linien) auf den jeweiligen Achsen:
# Mittelwerte auf den DAs
Means <- aggregate(cbind(DA1, DA2) ~ Intervention, data = Therapy, FUN = mean)
# Mittelwerte auf DA1
mDA1_K <- Means[1,2] # Kontrollgruppenmittelwert auf DA1
mDA1_V <- Means[2,2] # Mittelwert VT auf DA1
mDA1_VG <- Means[3,2] # Mittelwert VT + Gruppenuebung auf DA1
# Mittelwerte auf DA2
mDA2_K <- Means[1,3] # Kontrollgruppenmittelwert auf DA2
mDA2_V <- Means[2,3] # Mittelwert VT auf DA2
mDA2_VG <- Means[3,3] # Mittelwert VT + Gruppenuebung auf DA2
ggplot(data = Therapy, aes(x = DA1, y = DA2, color = Intervention)) + geom_point()+
geom_hline(yintercept = mDA2_K, lty = 2, col = "red")+
geom_hline(yintercept = mDA2_V, lty = 2, col = "gold3")+
geom_hline(yintercept = mDA2_VG, lty = 2, col = "blue")+
geom_hline(yintercept = (mDA2_VG+mDA2_K)/2, lty = 1, col = "black", lwd = 0.2)+
geom_vline(xintercept = mDA1_K, lty = 2, col = "red")+
geom_vline(xintercept = mDA1_V, lty = 2, col = "gold3")+
geom_vline(xintercept = mDA1_VG, lty = 2, col = "blue")+
geom_vline(xintercept = (mDA1_VG+mDA1_K)/2, lty = 1, col = "black", lwd = 0.2)+
ggtitle(label = "Diskriminanzachsen", subtitle = "mit Mittelwerten pro Gruppe")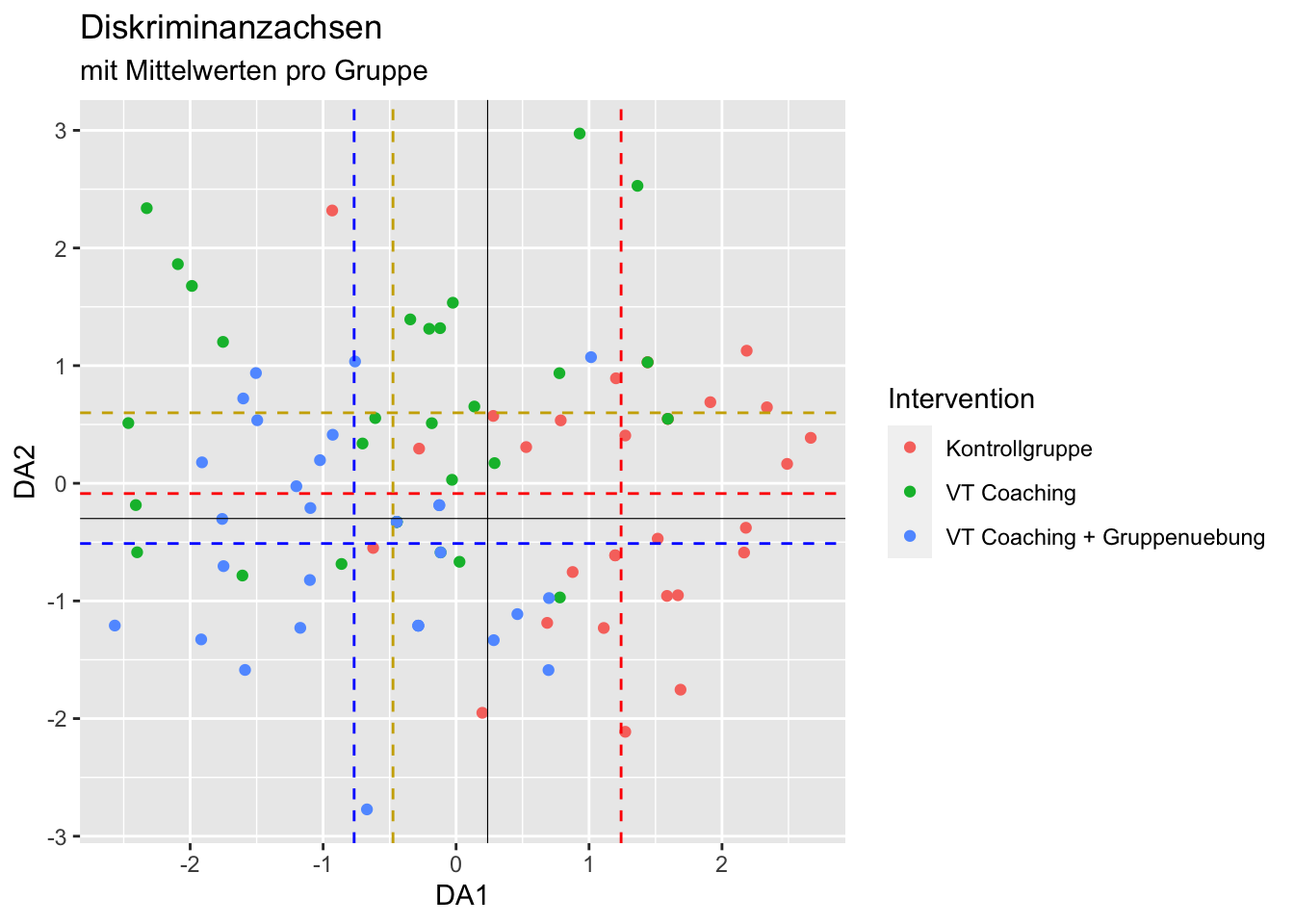
Wir sehen auch an den mit plot erstellten Grafiken, dass sich die Kontrollgruppe von den Interventionsgruppen unterscheiden lässt, während sich die Interventionsgruppen nicht stark voneinander unterscheiden. Dies hatten wir insbesondere auch in der Sitzung zur MANOVA so herausgefunden.
Wie gut ist unsere Gruppenzuordnung?
Um zu prüfen, wie gut wir die Gruppen zugeordnet haben, müssen wir untersuchen, wie häufig richtig zugeordnet wurde. Das können wir bspw. mit table machen und hier die Vorhersagen (predict(model_DA)$class) mit den Beobachtungen (Therapy$Intervention) vergleichen. Wir speichern predict(model_DA)$class zunächst als Variable ab und hängen es an den Datensatz dran:
Therapy$predict_class <- predict(model_DA)$class
table(Therapy$predict_class, Therapy$Intervention)| Kontrollgruppe | VT Coaching | VT Coaching + Gruppenuebung | |
|---|---|---|---|
| Kontrollgruppe | 25 | 5 | 4 |
| VT Coaching | 3 | 15 | 6 |
| VT Coaching + Gruppenuebung | 2 | 10 | 20 |
Die Diagonalelemente dieser Tabelle zeigen die richtig zugeordneten Werte. Wir können diese Werte auch nochmals durch 30 teilen, was die relativen Anteile erzeugt (dies funktioniert hier so einfach, da in jeder Gruppe 30 Probanden waren, normalerweise müssten wir hier die relativen Anteile pro Gruppe betrachten).
table(Therapy$predict_class, Therapy$Intervention)/30| Kontrollgruppe | VT Coaching | VT Coaching + Gruppenuebung | |
|---|---|---|---|
| Kontrollgruppe | 0.8333333 | 0.1666667 | 0.1333333 |
| VT Coaching | 0.1000000 | 0.5000000 | 0.2000000 |
| VT Coaching + Gruppenuebung | 0.0666667 | 0.3333333 | 0.6666667 |
83.33% der Kontrollgruppenprobanden wurden dieser wieder richtig zugeordnet, 50% der VT-Coaching- Gruppe wurden dieser wieder richtig zugeordnet und 66.67% der VT-Coaching + Gruppenübung- Gruppe wurden dieser wieder richtig zugeordnet. Insgesamt wurden
mean(Therapy$predict_class == Therapy$Intervention)*100## [1] 66.66667% der Probanden der richtigen Gruppe zugeordnet. Dies zeigt, dass die Prädiktion nicht perfekt war, was höchstwahrscheinlich daran liegt, dass Proband*innen aus den Interventionsgruppen sich kaum in der Lebenszufriedenheit, Arbeitszufriedenheit, Depression und Arbeitsbeanspruchung unterschieden. Ähnliches hatten wir bereits mit der MANOVA herausgefunden.
Trennlinien im ursprünglichen Variablenkoordinatensystem
Nun wollen wir die Trennlinien auch einmal in das ursprüngliche Koordinatensystem einzeichnen. Dazu führen wir eine Diskriminanzanalyse nur mit den beiden Zufriedenheitsmaßen durch.
model_DA2 <- lda(Intervention ~ LZ + AZ, data = Therapy)
model_DA2## Call:
## lda(Intervention ~ LZ + AZ, data = Therapy)
##
## Prior probabilities of groups:
## Kontrollgruppe VT Coaching
## 0.3333333 0.3333333
## VT Coaching + Gruppenuebung
## 0.3333333
##
## Group means:
## LZ AZ
## Kontrollgruppe 5.933333 5.133333
## VT Coaching 5.933333 6.833333
## VT Coaching + Gruppenuebung 7.333333 7.500000
##
## Coefficients of linear discriminants:
## LD1 LD2
## LZ -0.3160376 0.883895
## AZ 0.8736389 -0.337895
##
## Proportion of trace:
## LD1 LD2
## 0.7589 0.2411model_DA2$scaling # Koeffizienten## LD1 LD2
## LZ -0.3160376 0.883895
## AZ 0.8736389 -0.337895Wir sehen, dass jeweils eine Variable besonders stark auf einer Diskriminanzfunktion diskriminiert (großer Koeffizient). Um jetzt die Trennlinien einzeichnen zu können, brauchen wir ein Koordinatensystem, in dem für alle Kombinationen von LZ und AZ entschieden wird, in welcher Gruppe ein/e Proband*in mit dieser Ausprägung landen würde. Dies übernimmt die expand.grid Funktion für uns.
# Ein Koordinatensystem erstellen von 0 bis 12 auf den beiden Variablen
contour_data <- expand.grid(LZ = seq(0,12, 0.01), AZ = seq(0,12,0.01))
contour_data| LZ | AZ |
|---|---|
| 0.00 | 0 |
| 0.01 | 0 |
| 0.02 | 0 |
| 0.03 | 0 |
| 0.04 | 0 |
| 0.05 | 0 |
| LZ | AZ | |
|---|---|---|
| 1442395 | 11.94 | 12 |
| 1442396 | 11.95 | 12 |
| 1442397 | 11.96 | 12 |
| 1442398 | 11.97 | 12 |
| 1442399 | 11.98 | 12 |
| 1442400 | 11.99 | 12 |
| 1442401 | 12.00 | 12 |
Die predict-Funktion sagt die modellimplizierten Werte vorher. Wir können dieser Funktion auch einen Wert übergeben, der so in den Daten noch nicht vorkam, nämlich dem Argument newdata. Somit bekommen wir die Vorhersage unter unserem Modell für die neuen Datenpunkte. Als letztes kann mit stat_contour die Gruppenzugehörigkeit eingezeichnet werden. Diese übergeben wir der 3. Dimension z in der stat_contour-Funktion. Bei diesem Plot ist es von Vorteil, wenn die Gruppierungsvariable im Originaldatensatz gleich heißt wie die Prädiktion im neuen Datensatz.
# Für das Koordinatensystem für jeden Punkt die Gruppenzugehörigkeit bestimmen
contour_data$Intervention <- as.numeric(predict(object = model_DA2, newdata = contour_data)$class)
head(contour_data$Intervention)## [1] 1 1 1 1 1 1# Gruppenzugehörigkeiten in Originalkoordinatensystem einzeichnen
ggplot(data = Therapy, mapping = aes(x = LZ, y = AZ, color = Intervention))+
geom_point()+
stat_contour(aes(x = LZ, y = AZ, z = Intervention), data = contour_data)+
ggtitle("Lebenszufriedenheit vs Arbeitszufriedenheit", subtitle = "inklusive retransformierter Entscheidungslinien\nabgeleitet von den Diskriminanzachsen")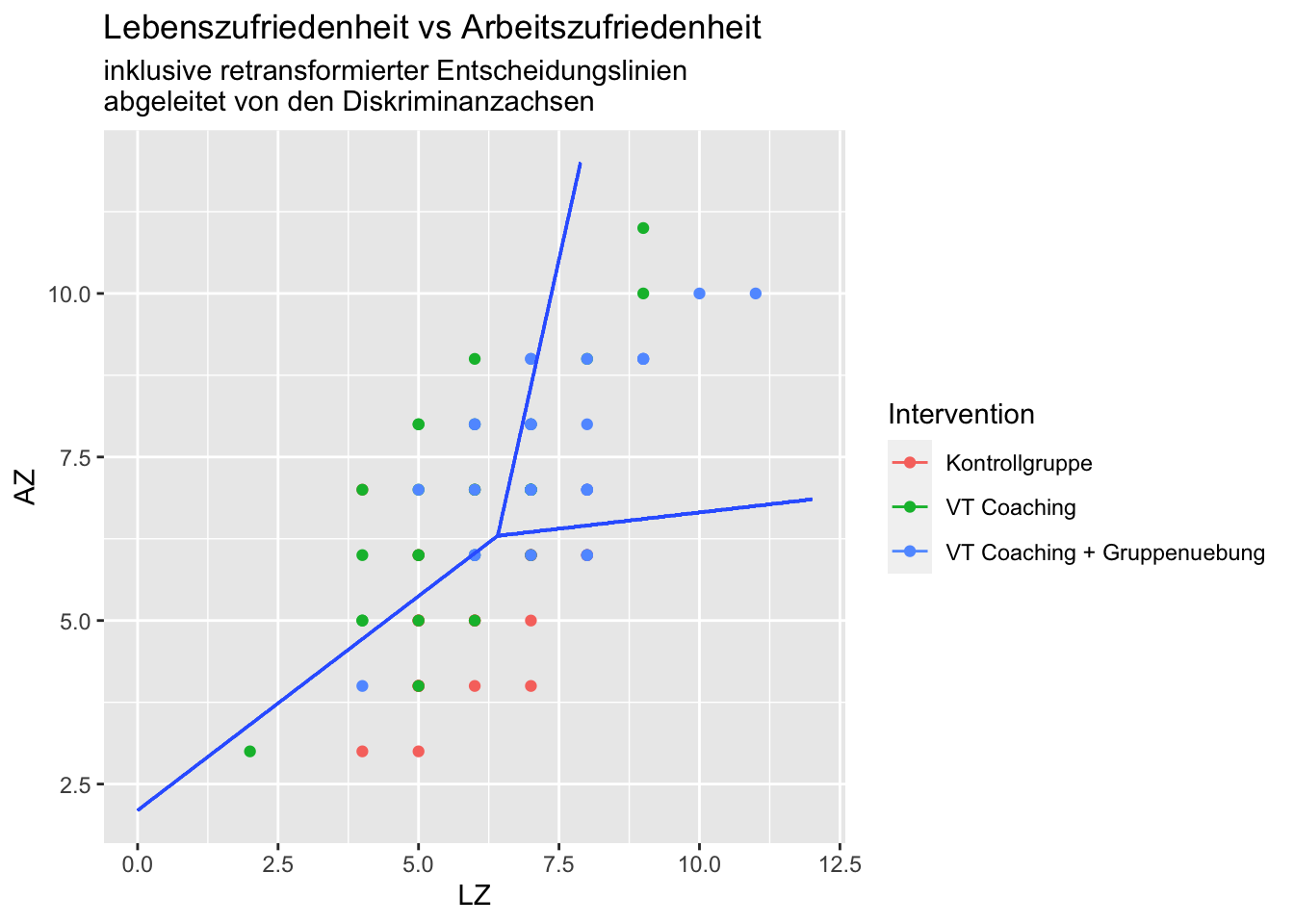
Wir sehen, dass die Trennlinien nicht rechtwinklig zueinander verlaufen. Dies liegt daran, dass die Achsen hier in die Originalskala retransformiert wurden. Die Gruppen werden wie folgt zugeordnet: oben links = VT Coaching, oben rechts = VT Coaching + Gruppenuebung und unten rechts/unten = Kontrollgruppe. Allerdings ist diese Zuordnung nicht sehr genau…
Literatur
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden (5. Auflage, 1. Auflage: 2010). Weinheim: Beltz.
Pituch, K. A. & Stevens, J. P. (2016). Applied Multivariate Statistics for the Social Sciences (6th ed.). New York: Taylor & Francis.
- Blau hinterlegte Autor:innenangaben führen Sie direkt zur universitätsinternen Ressource.
