Modell-Fit, Stichprobengröße und Fehlspezifikation
Ein Exkurs
Der Likelihood-Ratio-Test (-Differenzentest) vergleicht die Likelihoods zweier Modelle und somit implizit eigentlich die Kovarianzmatrizen (und Mittelwerte). In Lehrbüchern steht häufig der -Wert ist stichprobenabhängig und wächst mit der Stichprobengröße, was ebenfalls als Grund für die Fit-Indizes genannt wird. Das ist allerdings nur teilweise richtig, denn der -Wert ist nur für Modelle stichprobenabhängig, in welchen die -Hypothese nicht gilt. In einigen Lehrbüchern steht zudem die Formel für den -Wert wie folgt: Wir definieren zunächst die sogenannte Fit-Funktion (diese wurde bereits in der Sitzung zur CFA erwähnt), welche die Differenz zwischen der Kovarianzmatrix der Daten sowie der modellimplizierten Kovarianzmatrix quantifiziert (für die Formeln siehe gerne auch bspw. in Schermelleh-Engel, Moosbrugger & Müller, 2003): wobei die modellimplizierte Kovarianzmatrix und die Kovarianzmatrix der Daten ist und die Anzahl an beobachteten Variablen. ist die Determinante einer Matrix (bspw. ) und bezeichnet hierbei die Summe der Diagonalelemente des jeweiligen Objekts (der resultierenden quadratischen Matrix). Die Null-Hypothese besagt: Diese Null-Hypothese sagt also, dass die Kovarianzmatrix der Daten () und die modellimplizierte Kovarianzmatrix () identisch sind. Es wird also behauptet, dass interindividuelle Unterschiede und deren Zusammenhänge durch die modellierte Struktur abgebildet werden können. Der -Wert ergibt sie wie folgt: Somit wirkt es so, dass der -Wert zwangsläufig mit der Stichprobengröße wachsen muss. Allerdings ist für wachsendes () , solange die Null-Hypothese gilt. Dies liegt daran, dass gerade die Differenz zwischen den beiden Matrizen quantifiziert und diese Differenz unter der Null-Hypothese im Mittel gegen 0 konvergiert. Diese Differenz geht für steigende Stichprobengröße gegen den Wert 0, wird also kleiner mit steigender Stichprobengröße. Wenn das Modell korrekt ist, sollten Abweichungen zwischen den beiden Matrizen durch zufällige Schwankungen in der Stichprobe zustande kommen - wenn diese Stichprobe größer wird, werden diese stichprobenbedingten Schwankungen geringer.
Um eine Verteilung als Referenz verwenden zu können (hier: die kritischen Werte der -Verteilung), ist eine Art Reskalierung vonnöten. Aus diesem Grund wird mit multipliziert und die bekannte -Verteilung entsteht. Gilt nun eine Alternativ-Hypothese: dann konvergiert im Mittel nicht mehr gegen Null; es gilt also () , sondern , wobei gerade die wahre Differenz zwischen den beiden Modellen quantifiziert. Das bedeutet gleichzeitig, dass für den zugehörigen mittleren -Wert unter gilt: , der -Wert also mit der Stichprobengröße wächst (da gerade proportional zu wächst)! Wir wollen uns dies an folgendem Modell klar machen:
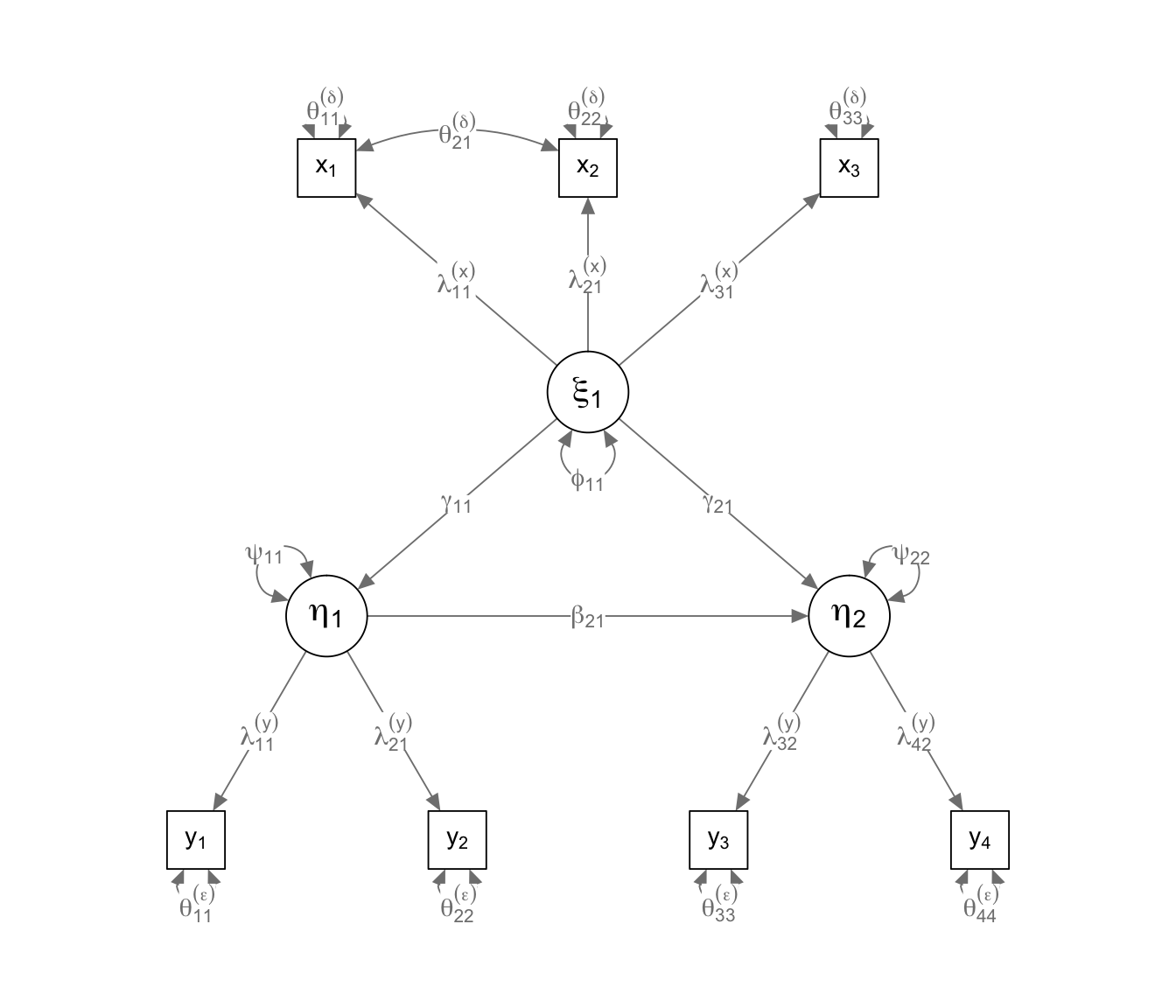
Als Populationsmodell wählen wir das Folgende:
pop_model_H0 <- '
# Messmodelle
Xi1 =~ x1 + 0.7*x2 + 0.6*x3
Eta1 =~ y1 + 0.8*y2
Eta2 =~ y3 + 0.9*y4
# Strukturmodell
Eta1 ~ 0.5*Xi1
Eta2 ~ 0.54*Xi1 + 0.4*Eta1
# Fehlerkovarianzen
x1 ~~ 0.4*x2
'
set.seed(123456)
data <- simulateData(model = pop_model_H0, meanstructure = F, sample.nobs = 200)Die Werte, die in diesem Modell stehen, symbolisieren die wahren Populationsparameter. Bspw. bedeutet Xi1 =~ x1 + 0.7*x2 + 0.6*x3, dass in der Population gilt: und (wobei auch der Skalierer ist!). Oder Eta2 ~ 0.54*Xi1 + 0.4*Eta1 steht für: in der Population. x1 ~~ 0.4*x2 symbolisert eine Fehlerkovarianz von 0.4, also .
Wenn ein Modell in dieser Form vorliegt, so kann die simulateData Funktion in lavaan verwendet werden, um dieses Modell zu simulieren. Wir übergeben der Funktion dazu das Modell model = pop_model_H0, spezifizieren mit meanstructure = F, dass alle Mittelwerte im Mittel 0 sind und legen die Stichprobengröße fest mit sample.nobs = 200. In data liegen nun die Beobachtungen der simulierten manifesten Variablen (die latenten Variablen werden nicht abgespeichert). Hierbei entscheiden die Kürzel, die wir vergeben (z.B. x1 oder y2) über die Namen in data:
head(data)## x1 x2 x3 y1 y2 y3
## 1 -0.5118338 1.11104804 -0.0729622 -2.46234468 -0.30571231 -1.2051386
## 2 0.4893225 -0.03456975 -0.2210260 -0.09834857 -0.03301419 0.7306844
## 3 -0.4599010 -0.11154386 -1.0774381 0.35941394 -0.11804480 0.3918804
## 4 -0.1563487 -1.94395700 0.5893962 0.34173255 0.32207594 0.1185581
## 5 -3.9850494 -1.34148731 -3.8810032 -0.24632514 -0.68642627 -2.3917236
## 6 -1.7981084 -0.66823365 0.6577428 1.37194245 0.25453754 -2.3033950
## y4
## 1 -0.97309774
## 2 0.42660131
## 3 2.04007846
## 4 -0.07890436
## 5 -2.65022281
## 6 -1.43756669Wir verwenden das Modell auch, um die Daten zu analysieren (dies ist das Modell von oben ohne jegliche Zahlen, also in dem Format, welches wir bereits kennen!):
model_H0 <- '
# Messmodelle
Xi1 =~ x1 + x2 + x3
Eta1 =~ y1 + y2
Eta2 =~ y3 + y4
# Strukturmodell
Eta1 ~ Xi1
Eta2 ~ Xi1 + Eta1
# Fehlerkovarianzen
x1 ~~ x2
'Das Pfaddiagramm sieht so aus (hier wurden die Zusatzeinstellungen curve = T, curvePivot = T im semPlot verwendet):
fit_H0 <- sem(model = model_H0, data = data)
semPaths(fit_H0, curve = T, curvePivot = T)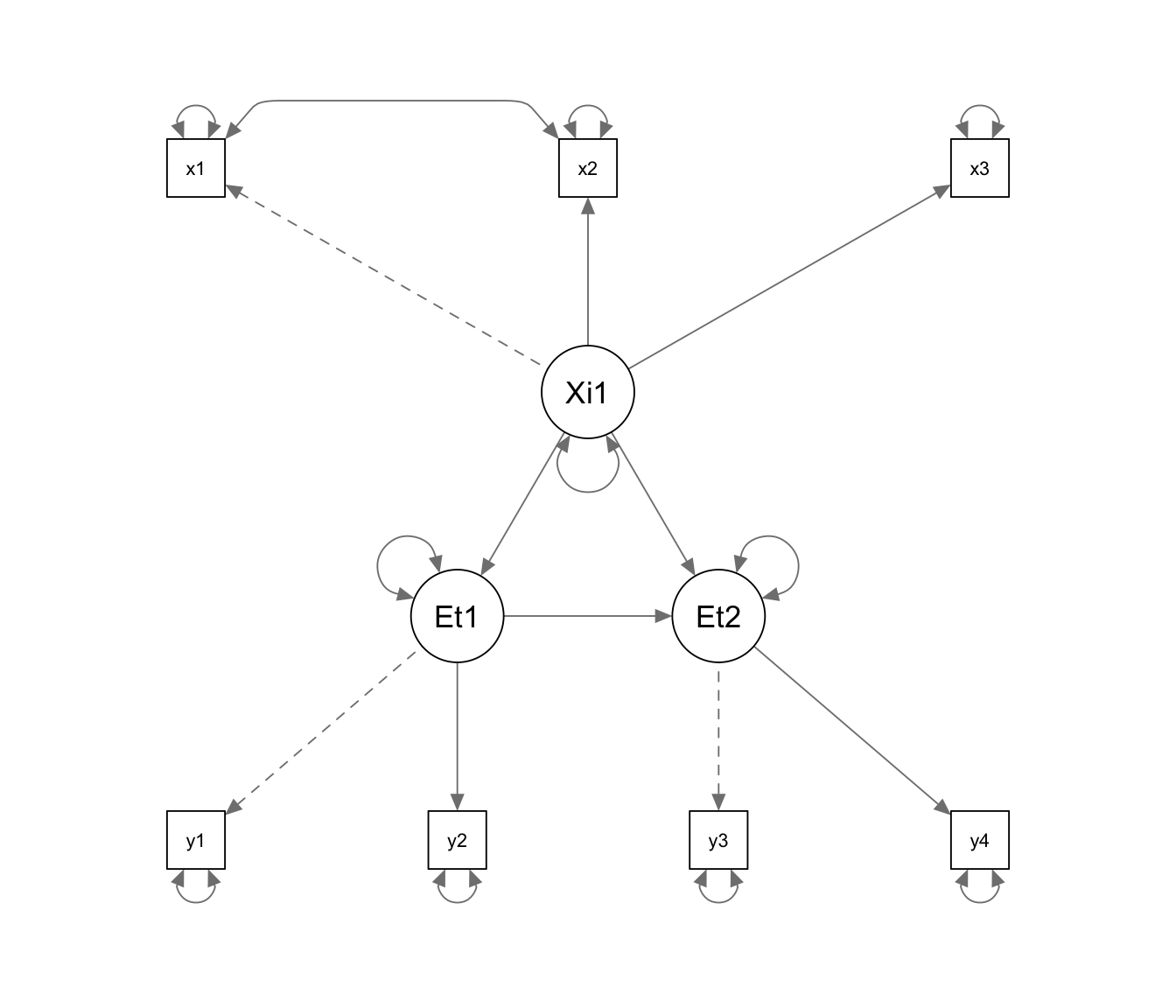
Schätzen wir nun das Modell und gucken uns den den -Wert an.
fit_H0 <- sem(model = model_H0, data = data)
fit_H0## lavaan 0.6-8 ended normally after 45 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 18
##
## Number of observations 200
##
## Model Test User Model:
##
## Test statistic 4.739
## Degrees of freedom 10
## P-value (Chi-square) 0.908Wie bereits im Beitrag zur CFA besprochen, können wir den -Wert, die und den zugehörigen -Wert auch über die fitmeasures-Funktion erhhalten:
fitmeasures(fit_H0, c("chisq", 'df', "pvalue"))## chisq df pvalue
## 4.739 10.000 0.908Außerdem wollen wir zwei fehlspezifizierte Modelle betrachten. Unter model_H1_kov speichern wir ein Modell, welches, bis auf die fehlende Fehlerkovarianz, äquivalent zu model_H0 ist.
model_H1_kov <- '
# Messmodelle
Xi1 =~ x1 + x2 + x3
Eta1 =~ y1 + y2
Eta2 =~ y3 + y4
# Strukturmodell
Eta1 ~ Xi1
Eta2 ~ Xi1 + Eta1
'semPaths(sem(model_H1_kov, data))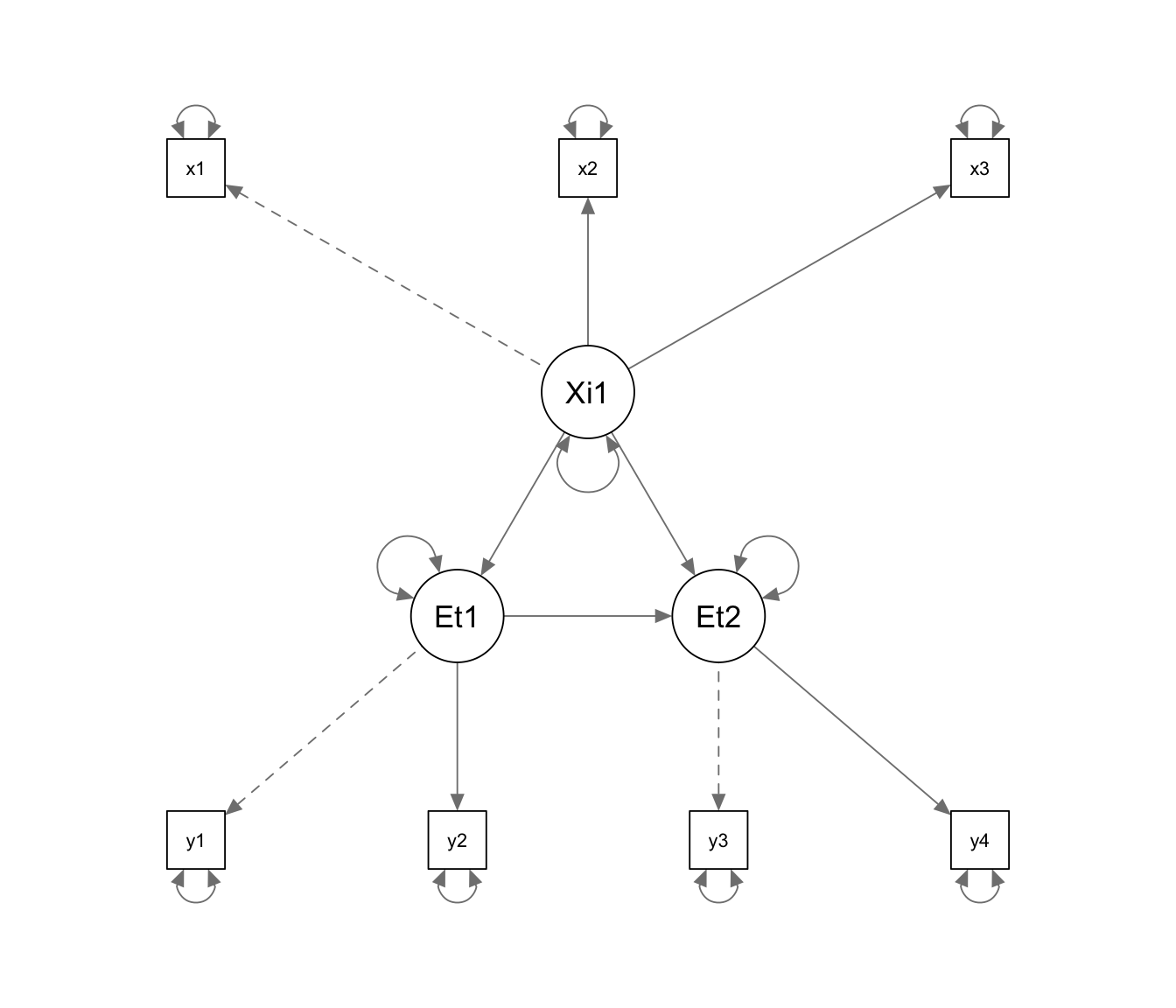
Unter model_H1_Struk speichern wir ein Modell, welches erneut äquivalent zu model_H0 ist, bis auf die fehlende gerichtete Beziehung zwischen und .
model_H1_Struk <- '
# Messmodelle
Xi1 =~ x1 + x2 + x3
Eta1 =~ y1 + y2
Eta2 =~ y3 + y4
# Strukturmodell
Eta1 ~ Xi1
Eta2 ~ Eta1
# Fehlerkovarianzen
x1 ~~ x2
'semPaths(sem(model_H1_Struk, data))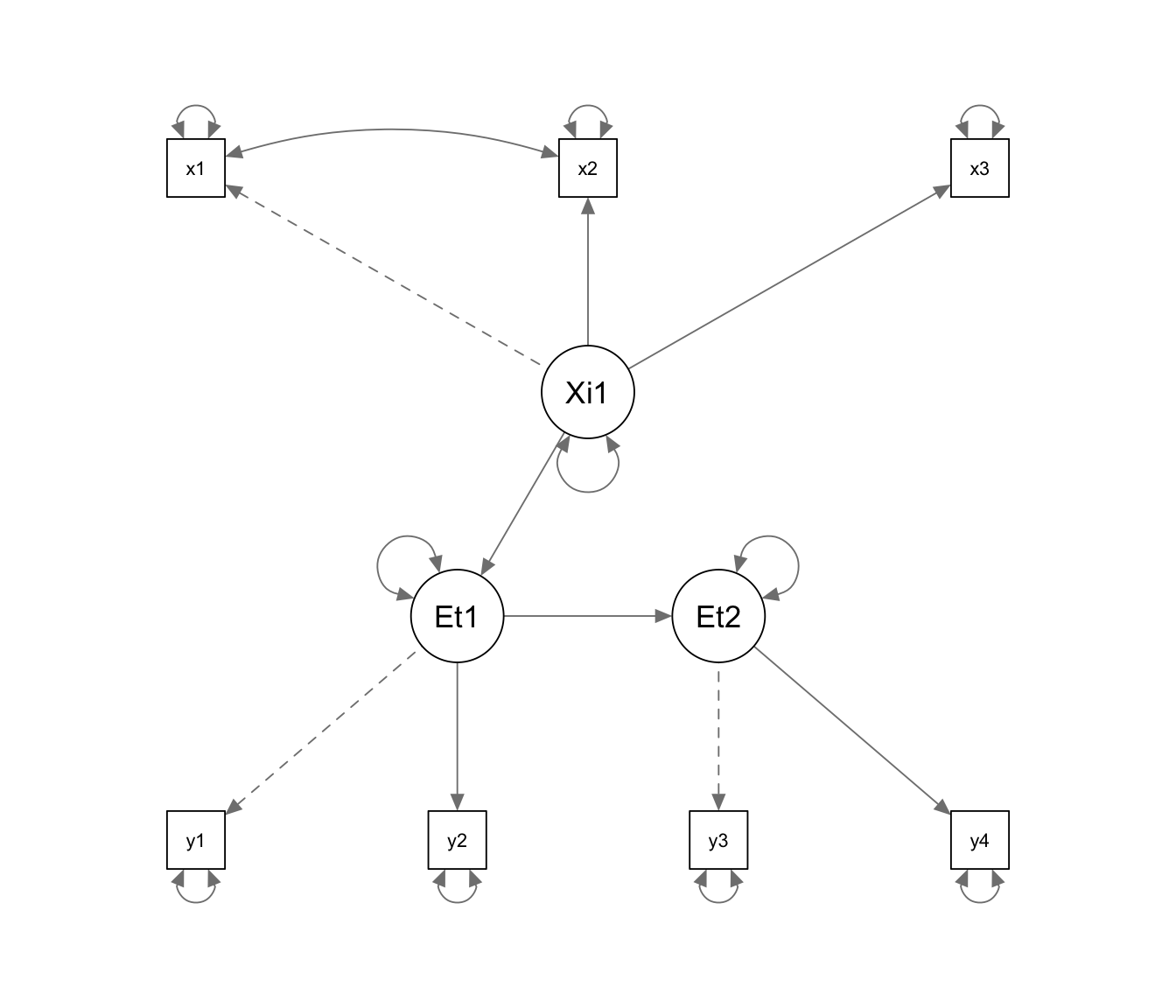
Hierbei ist das Weglassen der Fehlerkovarianz ein “kleiner” Fehler, während die Annahme einer vollständigen Mediation hier zu einem deutlichen Fehler führen sollte, da in die Fehlervarianz nur zwei Variablen involviert sind, während die gerichtete Beziehung zwischen den beiden latenten Variablen und mindestens alle manifesten Variablen, die Messungen von und sind, betrifft. Wir gucken uns den Modellfit für alle drei Modelle an:
fit_H1_kov <- sem(model_H1_kov, data)
fit_H1_Struk <- sem(model_H1_Struk, data)
fitmeasures(fit_H0, c("chisq", 'df', "pvalue"))
fitmeasures(fit_H1_kov, c("chisq", 'df', "pvalue"))
fitmeasures(fit_H1_Struk, c("chisq", 'df', "pvalue"))## H0:## chisq df pvalue
## 4.739 10.000 0.908## H1: Fehlerkovarianz## chisq df pvalue
## 9.474 11.000 0.578## H1: Vollständige Mediation## chisq df pvalue
## 23.174 11.000 0.017Nun wiederholen wir das ganze für eine größere Stichprobengröße von .
set.seed(123456)
data <- simulateData(model = pop_model_H0, meanstructure = F, sample.nobs = 1000)
fit_H0 <- sem(model = model_H0, data = data)
fit_H1_kov <- sem(model_H1_kov, data)
fit_H1_Struk <- sem(model_H1_Struk, data)fitmeasures(fit_H0, c("chisq", 'df', "pvalue"))
fitmeasures(fit_H1_kov, c("chisq", 'df', "pvalue"))
fitmeasures(fit_H1_Struk, c("chisq", 'df', "pvalue"))## H0:## chisq df pvalue
## 9.754 10.000 0.462## H1: Fehlerkovarianz## chisq df pvalue
## 22.57 11.00 0.02## H1: Vollständige Mediation## chisq df pvalue
## 58.973 11.000 0.000Wir sehen, dass das Weglassen der gerichteten Beziehung zu einem größeren mittleren Fehler führt, also zu einem größeren mittleren -Wert. Gilt die Null-Hypothese, so sollte der mittlere -Wert bei der Anzahl der liegen. Nun wollen wir uns die mittleren -Werte ansehen für verschiedene . Da diese Simulation länger dauern würde, schauen wir uns nur die Ergebnisse an:
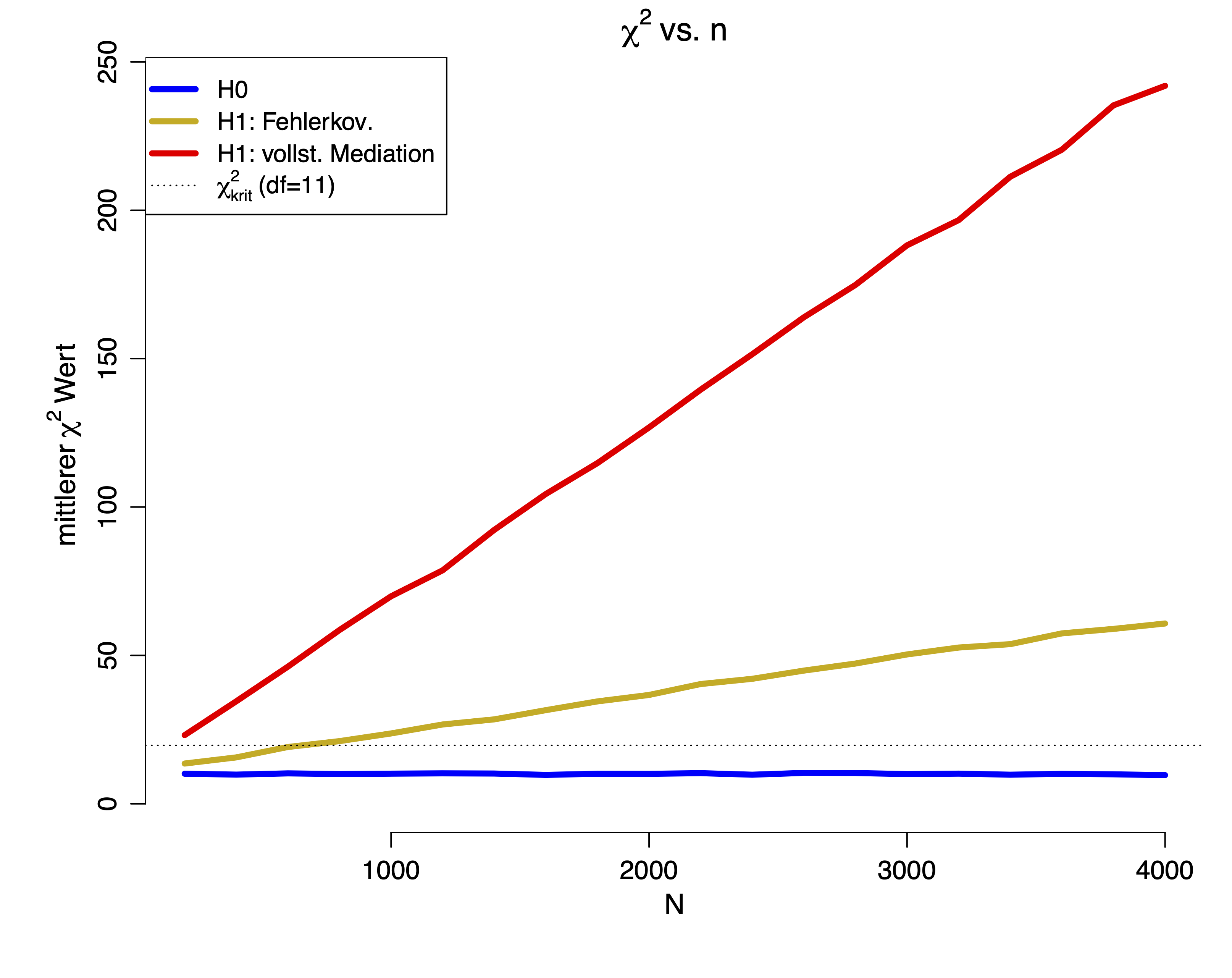
Wir sehen deutlich, dass in beiden -Bedingungen der mittlere -Wert mit der Stichprobengröße wächst. Nur in der -Bedingung pendelt sich der mittlere -Wert gerade bei den ein. Die gestrichelte Linie repräsentiert den , somit ist ersichtlich, dass beide -Modelle ab einer gewissen Stichprobengröße verworfen werden. Nun ist es aber so, dass in der Wissenschaft Daten häufig nicht perfekt vorliegen, sondern kleine Fehlspezifikationen (also Abweichungen von der Theorie, die aber an sich nicht bedeutsam sind) vorhanden sind. Aus diesem Grund wurden Fit-Indizes entwickelt, welche kleine Fehlspezifikationen relativieren sollen. Ansonsten würde das Verhalten dieses Tests die Wissenschaft dazu bringen, kleinere Stichproben zu untersuchen, was allerdings das Aufdecken von Effekten erschwert. Um diesem Dilemma aus dem Weg zu gehen, wird auf die Fit-Indizes zurückgegriffen.
Beispielhaft gucken wir uns nun das Verhalten des und des an. Die Definition des ist:
wobei die Subskripts und für das target-Modell, also unser Modell, und das independence-Modell stehen, welches keine Beziehung zwischen den manifesten Variablen annimmt (das Unabhängigkeitsmodell, also das am schlechtesten passende Modell). Einen Ausdruck wie bzw. oder einfacher bzw. lesen wir so: hier wird das Maximum zwischen 2 bzw. 3 Ausdrücken bestimmt und damit weitergerechnet; dadurch, dass einer der 2 bzw. 3 Ausdrücke gerade die 0 ist, bedeutet dies, dass dieses Maximum immer größer oder gleich 0 sein wird (). Der ist ein Vergleich zwischen dem schlechtesten und dem betrachteten Modell. Der mittlere unter der -Hypothese sollte bei 1 liegen für große , da für große der -Wert im Mittel bei den liegt und somit , also der Bruch im Mittel bei 0 liegt (somit wird von der 1 im Mittel nichts abgezogen unter der ). Dies erkennen wir in der Grafik daran, dass im -Modell der mittlere -Wert gegen 1 geht (dies bedeutet gleichzeitig, dass kleine s gerade für einen schlechten Fit sprechen!):

Der wird wie folgt definiert
und ist die mittlere Abweichung pro Freiheitsgrad kontrolliert für die Stichprobengröße. Der mittlere unter der -Hypothese sollte bei 0 liegen für große , da für große , nahe 0 liegt (das hatten wir weiter oben bereits disskutiert, als es darum ging, dass unter gilt: ) und damit also negativ ist. Das Maximum wiederum zwischen einer negativen Zahl und 0 liegt gerade bei 0. In der Grafik erkennen wir dies daran, dass der mittlere -Wert des -Modells gegen 0 geht (dies bedeutet gleichzeitig, dass große s gerade für einen schlechten Fit sprechen!):

Der sowie der pendeln sich für die -Modelle gerade bei den “wahren” Abweichungen des Modells unabhängig von der Stichprobengröße ein. Somit ist ersichtlich, dass dies nicht die tatsächlichen Modelle sind, welche den Daten zugrunde liegen, aber zumindest wird quantifiziert, wie stark diese Modelle vom wahren Modell abweichen — unabhängig von der Stichprobengröße.
Die gestrichelten Linien geben jeweils die Grenze an, ab welchem Wert nicht mehr von einem “guten” Fit gesprochen werden sollte: und (Schermelleh-Engel et al., 2003).
Die Abweichungen von 0 bzw. 1 beim sowie bei sind allerdings nur für eines der beiden Modelle “extrem”. Nur in diesem würde von keinem guten Fit mehr gesprochen werden: nämlich beim Modell, in welchem fälschlicherweise eine vollständige Mediation angenommen wird (keine gerichtete Beziehung zwischen und ). Allerdings sind diese Cut-Off-Werte, die von Schermelleh-Engel et al. (2003) postuliert wurden, keine in Stein gemeiselten Größen, sondern Richtwerte. Schermelleh-Engel et al. haben ein ganz bestimmtes SEM herangezogen und sich dann angeschaut, ab wann die Fit-Indizes so stark vom erwarteten Wert unter der -Hypothese abweichen, als das nicht mehr von einem guten Modellfit gesprochen werden kann. Auch andere Autoren wie etwa Hu und Bentler (1999) haben solche Fit-Kriterien postuliert. Allerdings haben auch diese Autoren spezielle Modelle herangezogen und an diesen Cut-Off Werte abgeleitet. Diese Kriterien mögen für viele Modelle “ganz gut” passen, allerdings besteht immer die Möglichkeit, dass sie ggf. für bestimmte Modelle oder Stichprobengröße zu konservativ oder zu liberal sind. Aus diesem Grund wurde das R-Paket ezCutoffs entwickelt, welches simulationsbasierte Cut-Kriterien speziell angepasst an das vorliegende Modell berechnet. Dieses Paket wurde in der Sitzung zu Pfadanalysen und SEM kurz vorgestellt.
Literatur
Hu, L. T., & Bentler, P. M. (1999). Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling: A Multidisciplinary Journal, 6(1), 1-55.
Schermelleh-Engel, K., Moosbrugger, H., & Müller, H. (2003). Evaluation the fit of structural equation models: tests of significance and descriptive goodness-of-fit measures. Methods of Psychological Research Online, 8(2), 23-74.
