Explorative Grafiken
Explanative und Explorative Grafiken
Mit Grafiken können unterschiedliche Ziele verfolgt werden:
- Explanative Grafiken dienen dazu, anderen einen bestimmten Sachverhalt (ein Muster in den Daten) zu kommunizieren
- Explorative Grafiken sollen dabei helfen, bestimmte Sachverhalte (Muster in den Daten) zu erkennen
Der Fokus des Workshops lag bisher stark auf explanativen Grafiken. In diesem Abschnitt wollen wir Ihnen nun einige Techniken zum Anfertigen von explorativen Grafiken vorstellen. Diese sind:
- Prinzip des “small multiple” anhand von Faceting
- Eine Serie gleicher Grafiken mit Funktion und Schleife erzeugen
- Viele bivariate Zusammenhänge mit
ggpairs() - Multivariate Daten mit
tableplot()durchkämmen
Auch in diesem Abschnitt arbeiten wir wieder mit dem edu_exp-Datensatz. Außerdem muss noch ggplot2 geladen werden.
load(url('https://pandar.netlify.com/post/edu_exp.rda'))
library(ggplot2)Prinzip des “small multiple” anhand von Faceting
Die Technik des faceting erlaubt es, Grafiken gemäß Edward Tufte‘s Prinzip des small multiple (siehe Block 3 im Foliensatz) zu erzeugen.
At the heart of quantitative reasoning is a single question: Compared to what? Small multiple designs, multivariate and data bountiful, answer directly by visually enforcing comparisons of changes, of the differences among objects, of the scope of alternatives. For a wide range of problems in data presentation, small multiples are the best design solution.
Tufte (1990). Envisioning Information. Graphics Press (p. 67).
Grafiken, die diesem Prinzip entsprechen, sind stets gleich aufgebaut und ermöglichen so einen schnellen Vergleich der dargestellten Information zwischen den einzelnen Grafiken.
In ggplot() stehen zwei Funktionen für faceting zur Vefügung:
- Mit
facet_grid()werden die Plots in Zeilen, in Spalten oder in einem Raster (grid) aus Zeilen und Spalten dargestellt - Mit
facet_wrap()werden die Plots nebeneinander, ggf. mit Zeilenumbruch (wrap) dargestellt
Die Variable, für die separate Plots erzeugt werden sollen, muss als diskrete Variable im Datensatz enthalten sein (z.B. Land, Weltregion). Im nachfolgenden Beispiel stellen wir den Zusammenhang zwischen den Variablen Wirtschaftsleistung und Lebenserwartung separat für jede der vier Weltregionen dar:
edu_exp |>
subset(Year == 2016) |>
ggplot(aes(x=Income, y=Expectancy)) +
geom_point() +
theme(axis.text.x = element_text(angle = 90, hjust = 1, vjust = .5)) +
facet_grid(. ~ Region)## Warning: Removed 8 rows containing missing values (geom_point).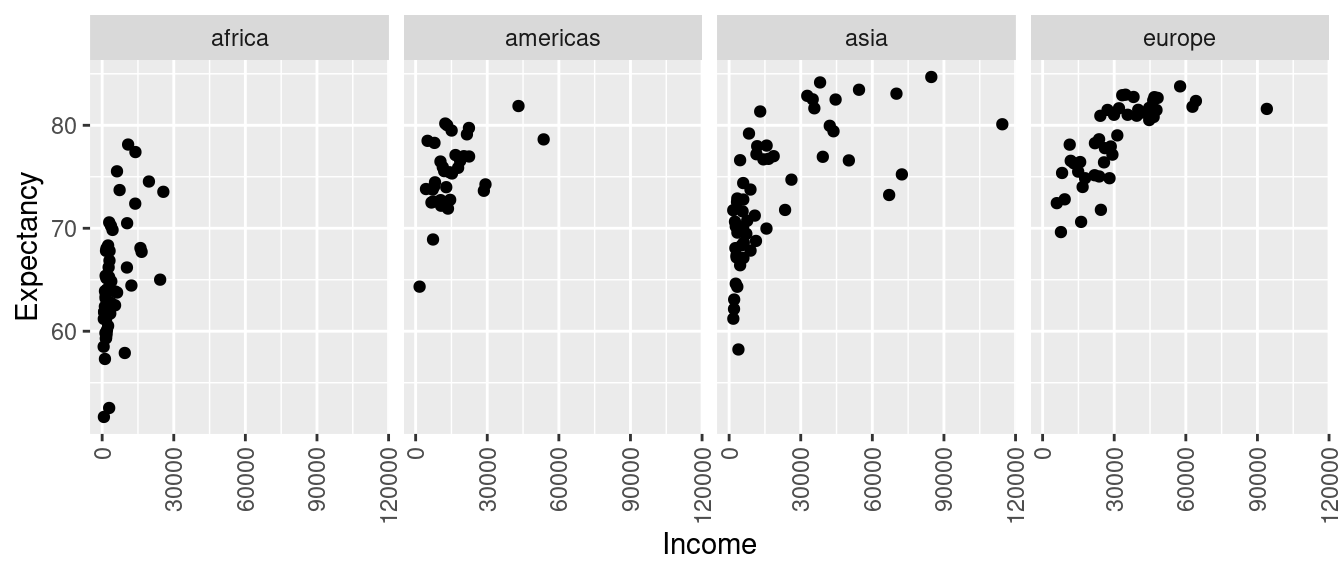
Und nun zeigen wir Ihnen noch ein weiteres Beispiel für Faceting, um die vermutlich schönste Illustration des Anscombe Quartett in diesen Materialien unterzubringen: den Datasaurus. Der Datensatz liegt im Paket datasauRus vor, welches zunächst geladen werden muss:
library(datasauRus)
names(datasaurus_dozen)## [1] "dataset" "x" "y"Der Datensatz enthält drei Variablen: x, y und dataset. Der Zusammenhang zwischen x und y ohne Berücksichtigung der zugrunde liegenden Gruppen (Variable dataset) sieht unspektakilär aus - man kann kein Muster erkennen:
ggplot(datasaurus_dozen, aes(x=x, y=y)) +
geom_point()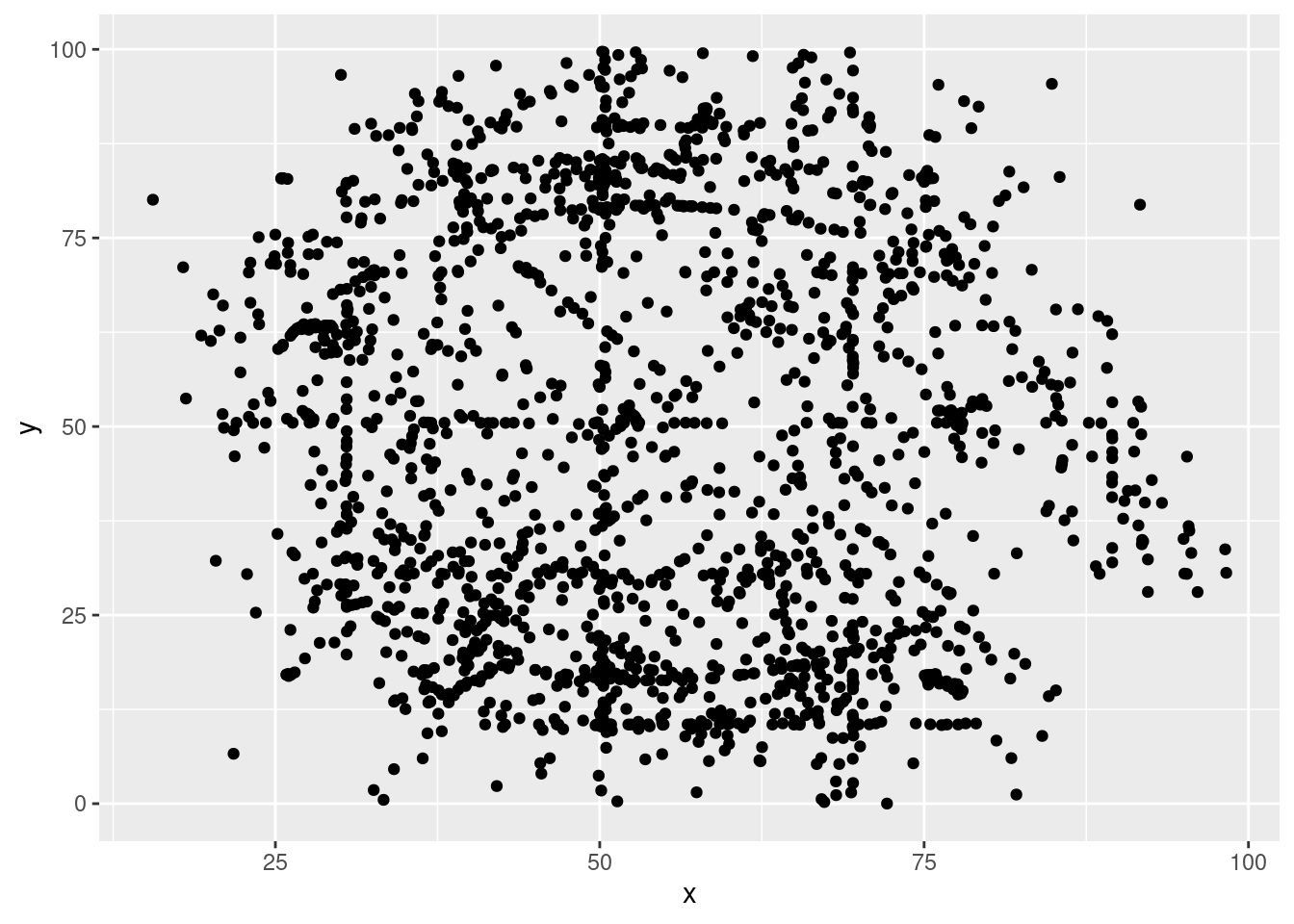
Nun wenden wir Faceting an, um small multiples für jedes der datasets anzufordern:
ggplot(datasaurus_dozen, aes(x=x, y=y)) +
geom_point() +
facet_wrap(~dataset) +
labs(x="", y="")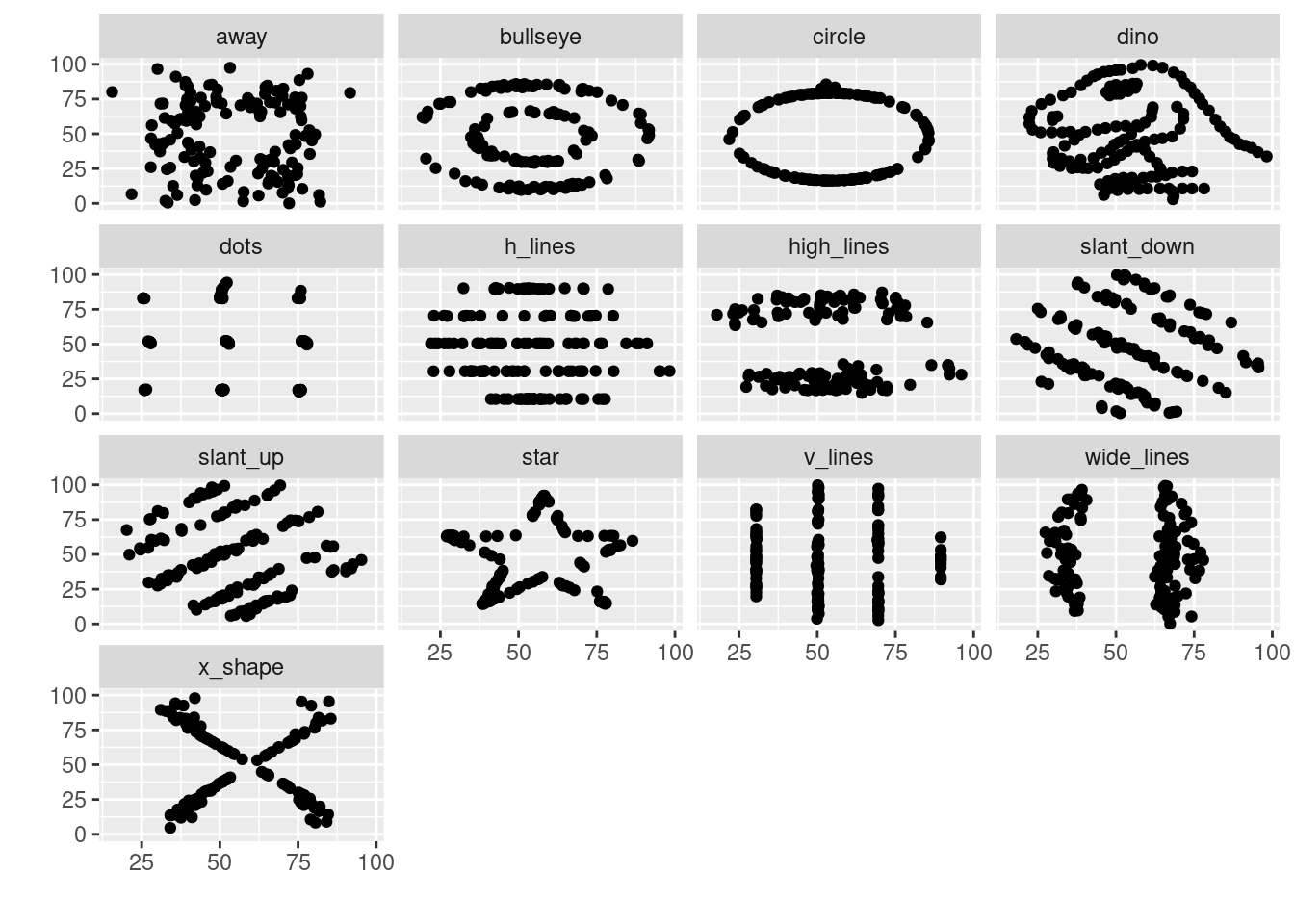
Die unterschiedlichen Zusammenhänge in jeder der Subgruppen fallen somit unmittelbar ins Auge. Zusätzlich kann auch noch eine Farb-Ästhetik zur Darstellung der Gruppenzugehörigkeit (dataset) vergeben werden. Dadurch erhält jedes Kästchen eine eigene Farbe. Diese trägt absolut keine Information bei, da die Gruppenzugehörigkeit ohnehin klar ist. Es handelt sich dabei also um ein Beispiel für Tuftes sog. “chartjunk” - aber nun ist die Grafik schön bunt. :-)
ggplot(datasaurus_dozen, aes(x=x, y=y)) +
geom_point(aes(colour=dataset), show.legend=F) +
facet_wrap(~dataset) +
labs(x="", y="")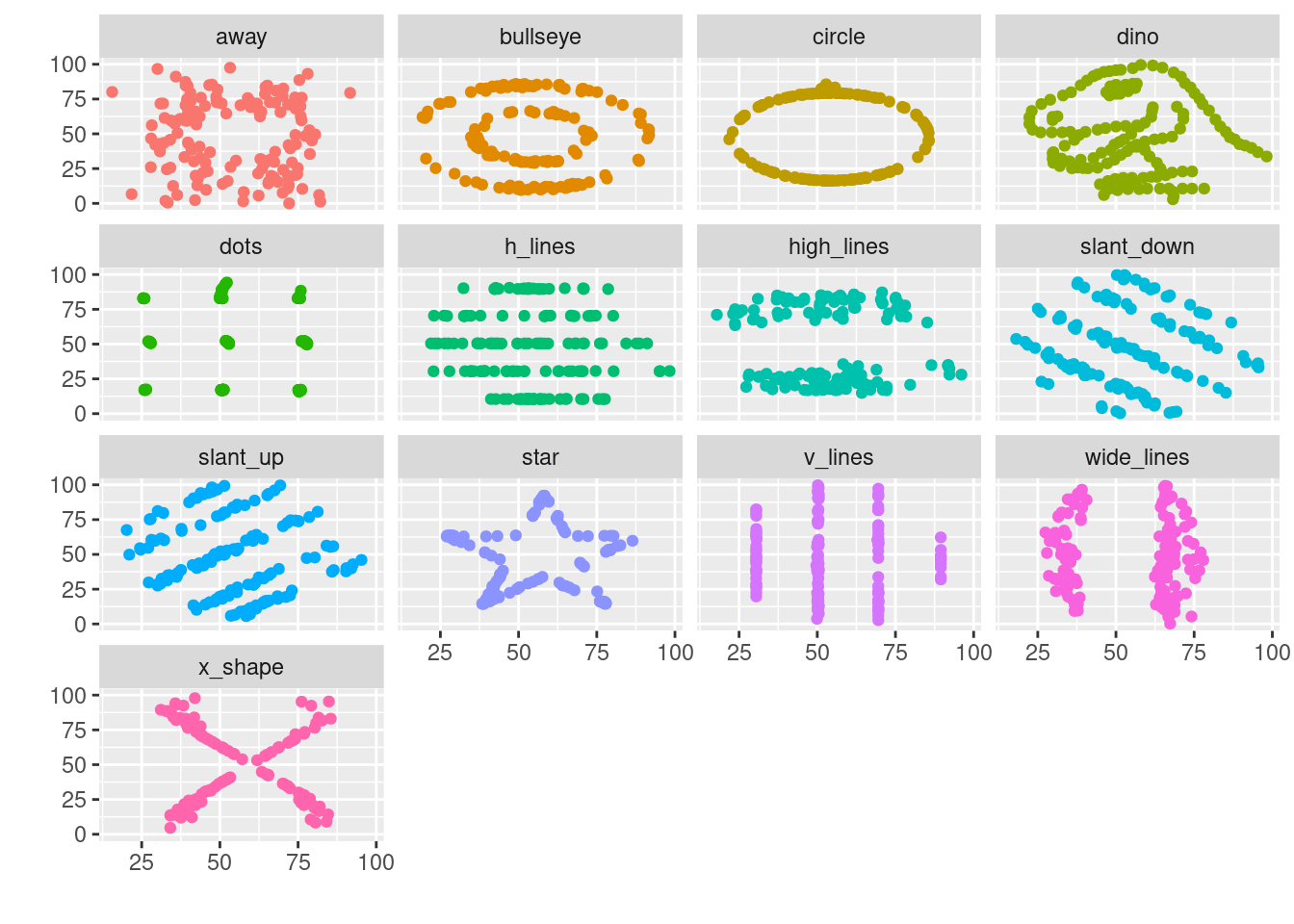
Mit der Technik des Faceting lässt sich also schnell ein Eindruck über Datenmuster in einer Vielzahl von Gruppen gewinnen. Außergewöhnliche Muster müssten so schnell auffallen.
Eine Serie gleicher Grafiken mit Funktion und Schleife erzeugen
Bisher haben wir stets Funktionen benutzt, die im Basis-R oder in den aktuell geladenen Paketen enthalten sind. Funktionen können jedoch auch selbst geschrieben und an die eigenen Bedürfnisse (z.B. eine bestimmte Grafik) angepasst werden. Mithilfe einer for()-Schleife kann diese Funktion dann auf alle Variablen oder alle Länder eines Datensatzes etc. angewendet werden. So entsteht eine Serie von Grafiken, die man schnell durchscrollen und im Hinblick auf Auffälligkeiten überprüfen kann, z.B. zur Qualitätssicherung während der Datenaufbereitung.
Sehen wir uns zunächst einmal einfache Beispiele für Funktionen und Schleifen an.
Beispiel für eine Funktion
Im nachfolgenden Text erstellen wir eine Funktion namens quadrieren(), die genau ein Argument (zahl) entgegennehmen kann. Die Funktion soll diese Zahl quadrieren und das Ergebnis zurückgeben. Der entsprechende Befehl sieht wie folgt aus:
quadrieren <- function(zahl){
ergebnis <- zahl^2
return(ergebnis)
}Testen wir nun die Funktion:
quadrieren(1)## [1] 1quadrieren(2)## [1] 4quadrieren(3)## [1] 9Beispiel für eine for()-Schleife
Anhand von Schleifen (loops) lassen sich wiederholt Aktionen für alle Elemente eines Vektors durchführen. In R gibt es for(), while() und break()-Schleifen. Wir zeigen Ihnen nachfolgend eine einfache for()-Schleife. Sie soll für alle Zahlen zwischen 4 und 6 eine Quadrierung vornehmen. Die Zahlen zwischen 4 bis 6 werden in einem Vektor abelegt, über den dann die Schleife läuft; die Elemente des Vektors werden mit z indiziert.
zahlen <- 4:6
for(z in zahlen){
print(z^2)
}## [1] 16
## [1] 25
## [1] 36Anwendung: je eine Grafik pro Land
Wir kombinieren nun eine selbstgeschriebene Funktion mit einer for()-Schleife, um je eine Grafik pro Land abzuspeichern. Mit der Funktion definieren wir, wie die Grafik aussehen soll, und mit der Schleife wenden wir diese Funktion dann auf jedes Element im Vektor mit den Ländernamen an.
Die Grafik soll die Lebenserwartung im Zeitverlauf sowie den jeweiligen Mittelwert anzeigen. Für Afghanistan sollte sie also so aussehen:
dipfblau <- rgb(102,153,204, max=255)
tmp.data <- subset(edu_exp, Country == "Afghanistan")
tmp.mw <- mean(tmp.data$Expectancy)
ggplot(tmp.data, aes(x=Year, y=Expectancy)) +
geom_line(size=2, show.legend=F) +
geom_point(size=2.5, show.legend=F) +
xlim(1997, 2017) +
ylim(20, 85) +
labs(x="Jahr", y="Lebenserwartung") +
ggtitle("Lebenserwartung in Afghanistan im Zeitverlauf", "Kontinent: Europa") +
geom_hline(aes(yintercept=tmp.mw), size=2, col=dipfblau) +
annotate("text", 2000, tmp.mw+3, fontface='italic',
label=paste0("M = ", round(tmp.mw, 2)), col=dipfblau)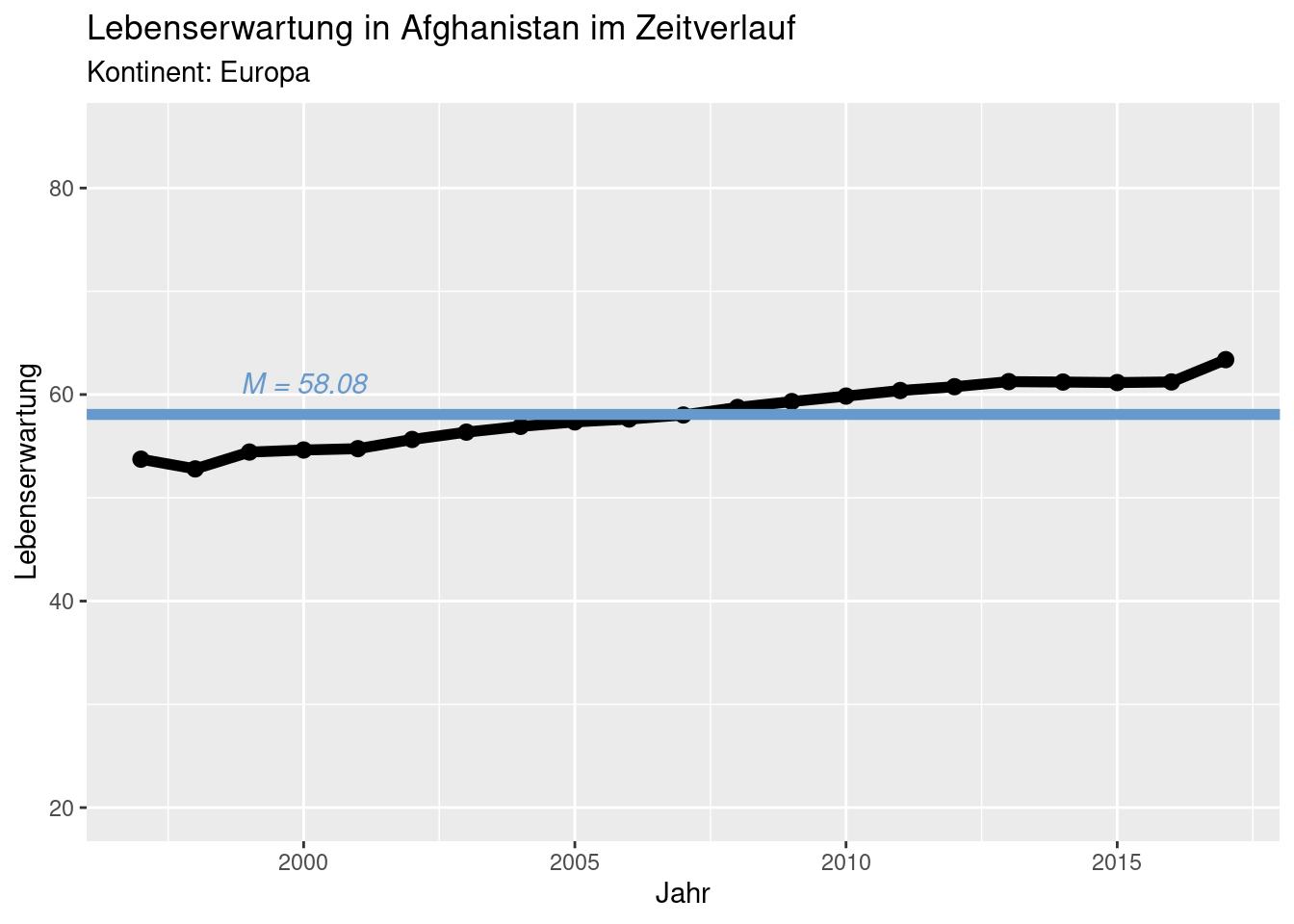
Dieser Befehl muss nun so abstrahiert werden, dass er für jedes Land funktioniert. Alles, was mit Afghanistan zu tun hat, wird nun so umgeschrieben, dass irgendein Ländername eingesetzt werden kann - nämlich den, der als Wert für das Argument which.country in der Funktion angebenen wurde. Wichtig ist, dass der Wertebereich von x- und y-Achse spezifiziert wird, um sicherzustellen, dass jedes Plot gleich aufgebaut ist. Außerdem soll die Funktion so geschrieben sein, dass man die Linie für den Mittelwert ein- und ausschalten kann. Dies hinterlegen wir als ein optionales Argument, das per Voreinstellung die Linie nicht enthält.
gm.plot <- function(which.country, show.mean=FALSE){
dipfblau <- rgb(102,153,204, max=255)
tmp.data <- subset(edu_exp, Country == which.country)
tmp.mw <- mean(tmp.data$Expectancy)
tmp.plot <- ggplot(tmp.data, aes(x=Year, y=Expectancy)) +
geom_line(size=2, show.legend=F) +
geom_point(size=2.5, show.legend=F) +
xlim(1997, 2017) +
ylim(20, 85) +
labs(x="Jahr", y="Lebenserwartung",
title=paste0("Lebenserwartung in ", which.country, " im Zeitverlauf"),
subtitle=paste0("Kontinent: ", tmp.data$Region[1]))
if(show.mean==TRUE){
tmp.plot <- tmp.plot +
geom_hline(aes(yintercept=tmp.mw), size=2, col=dipfblau) +
annotate("text", 2000, tmp.mw+3, fontface='italic',
label=paste0("M = ", round(tmp.mw, 2)), col=dipfblau)
}
return(tmp.plot)
}Prüfen wir nun die Funktion für Afghanistan - sie müsste ja genauso aussehen wie zuvor:
gm.plot("Afghanistan", TRUE)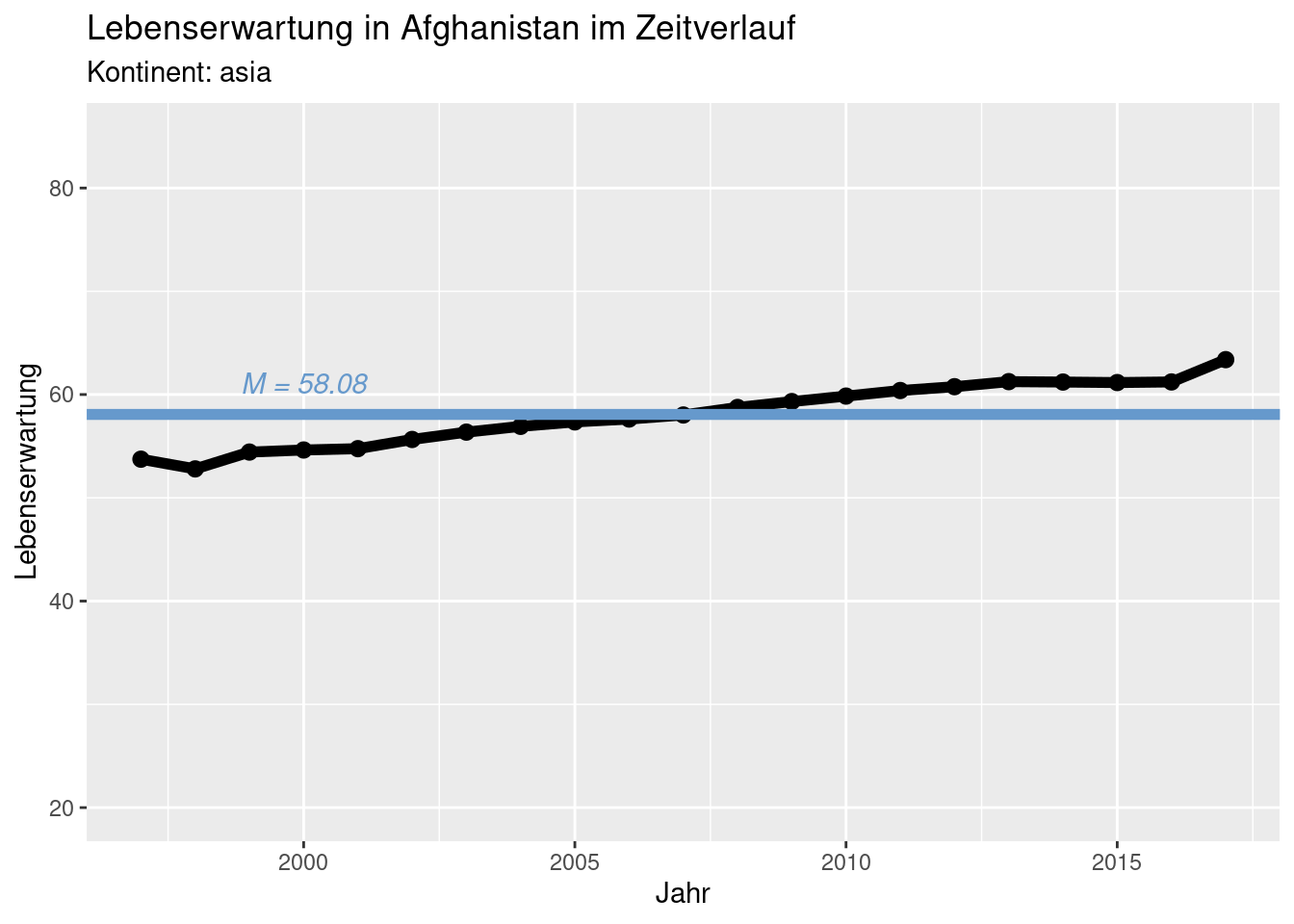
Das hat geklappt! Als nächstes erstellen wir ein Verzeichnis (“gapminder-plots”), in dem die Grafiken später gespeichert werden können. Dies kann mit dir.create() aus R heraus erfolgen:
dir.create("./gapminder-Plots")Die Funktion soll nun für jedes Land angewendet werden. Dafür benötigen wir einen Vektor, der alle Ländernamen enthält:
countries <- unique(edu_exp$Country)
head(countries)## [1] "Afghanistan" "Angola" "Albania"
## [4] "Andorra" "United Arab Emirates" "Argentina"length(countries)## [1] 197Der Vektor enthält 197 Elemente, folglich werden mit der for()-Schleife 197 Grafiken erzeugt werden. Wir erweitern die Schleife noch so, dass sie uns in die Konsole schreibt, wie weit sie ist. So können wir den Fortschritt live überwachen:
for(c in 1:length(countries)){
gm.plot(countries[c], show.mean = TRUE)
ggsave(paste0("./gapminder-Plots/Plot-", countries[c], ".png"),
width=24, height=12, units="cm", dpi=200)
print(paste0("Grafik erstellt fuer: ", countries[c], " (", c, "/", length(countries), ")"))
}
Nachdem die Schleife fertig durchgelaufen ist, liegen alle 197 Grafiken im Ordner:
Durch diese kann man sich nun durcharbeiten - auffällige Muster fallen dann schnell auf:
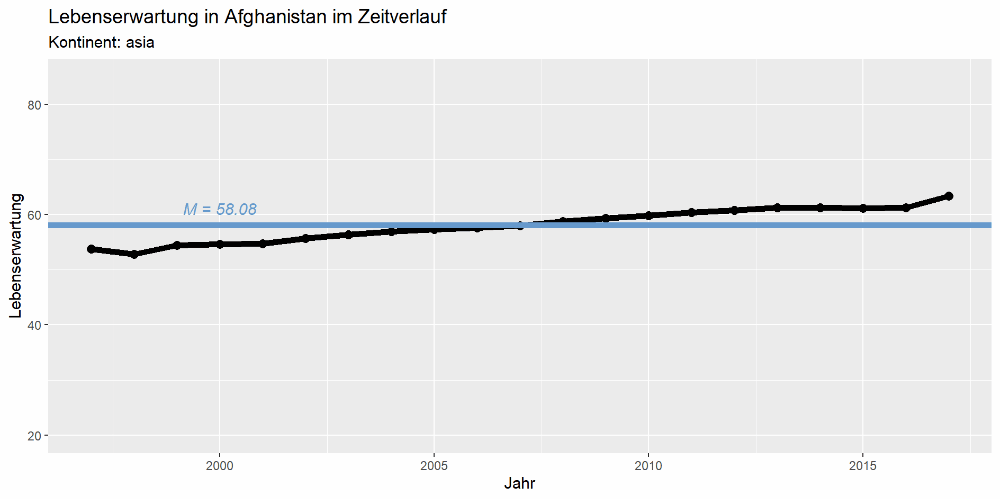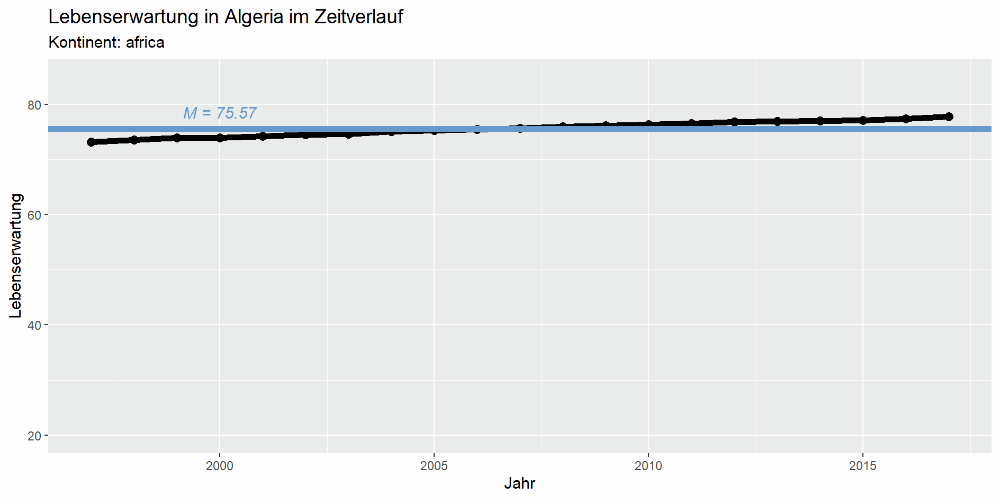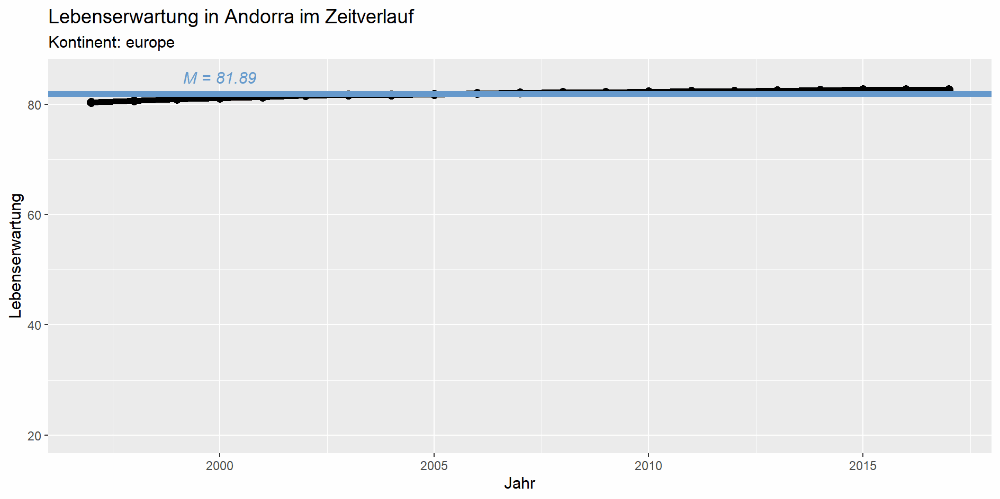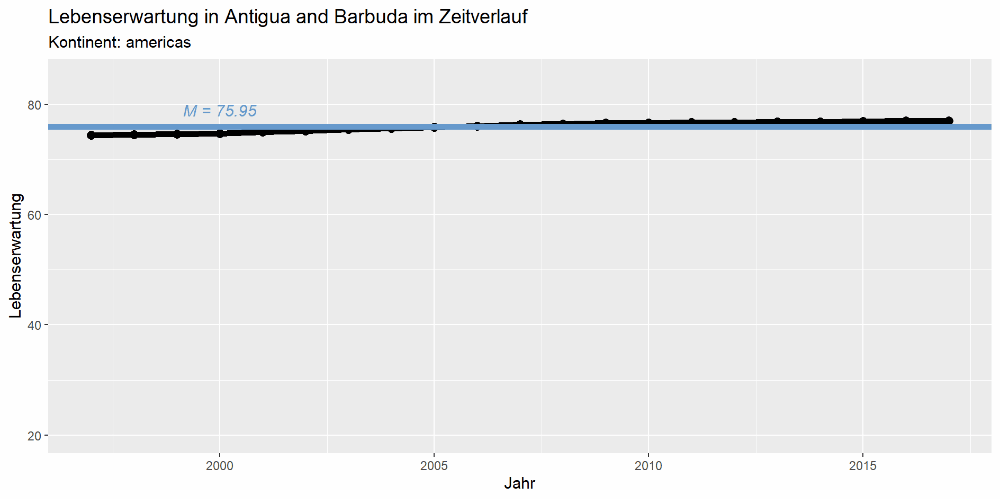
Viele bivariate Zusammenhänge mit ggpairs()
Das Paket GGally stellt die praktische Funktion ggpairs() bereit. Wir illustrieren diese anhand unseres Datensatzes für die Variablen Wirtschaftsleistung, Lebenserwartung und Bildungsindex, getrennt nach Weltregion. Dafür erstellen wir zunächst einen entsprechenden Teildatensatz:
edu_exp_sel <- edu_exp[, c("Income", "Expectancy", "Index", "Region")]ggpairs() stellt nun für jede der Variablen univariate und bivariate Deskriptivstatistiken bereit:
- univariate Verteilungen (auf der Hauptdiagonalen)
- Scatterplots und Korrelationskoeffizienten für jede Kombination von Variablen
library(GGally)## Registered S3 method overwritten by 'GGally':
## method from
## +.gg ggplot2ggpairs(edu_exp_sel, columns = 1:3)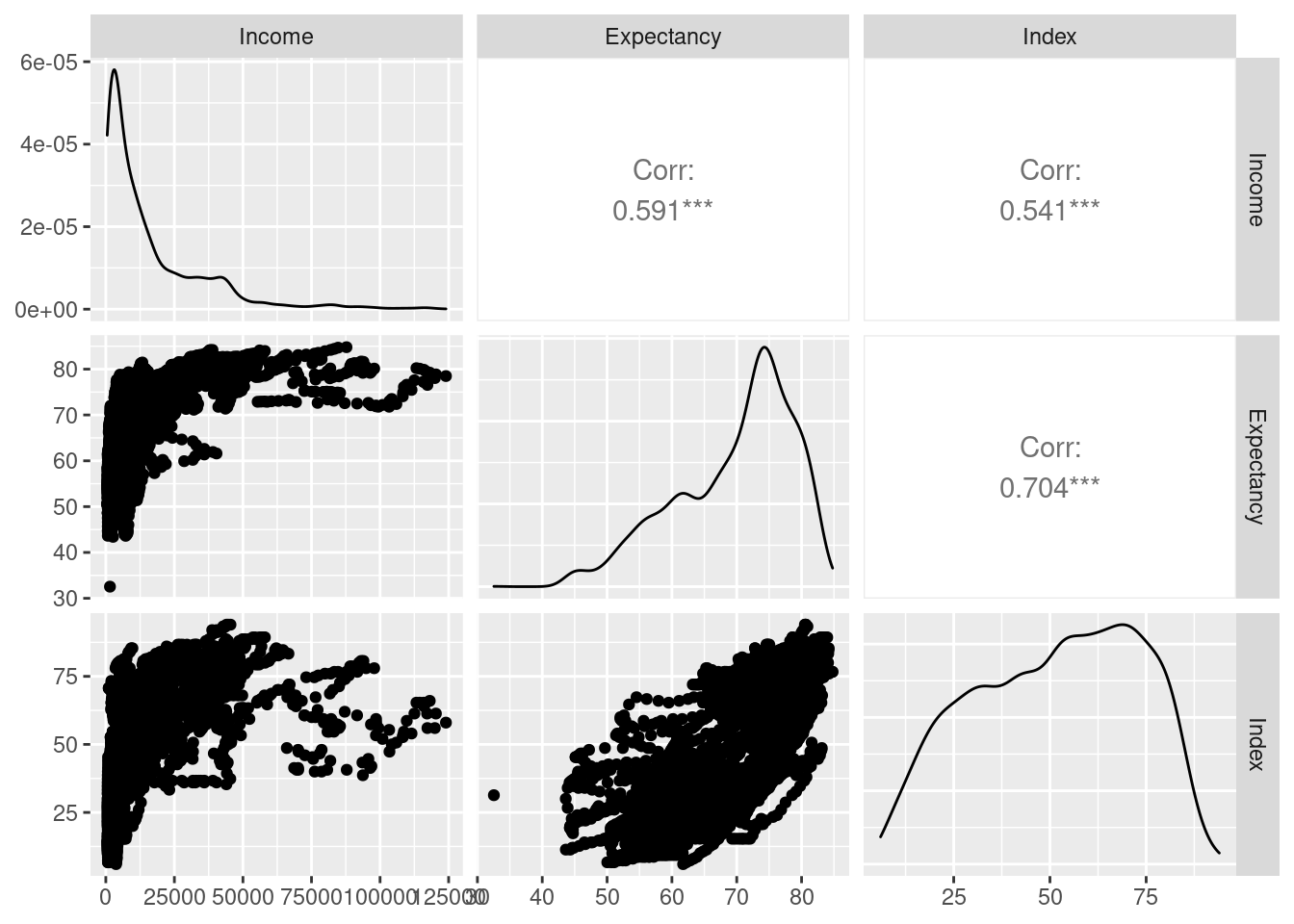
Richtig spannend wird es aber erst, wenn wir zusätzlich noch separate Verteilungen für jede der vier Weltregionen (Region) anfordern, die farblich kodiert sind:
ggpairs(edu_exp_sel, columns = 1:3, aes(color = Region, alpha = .5))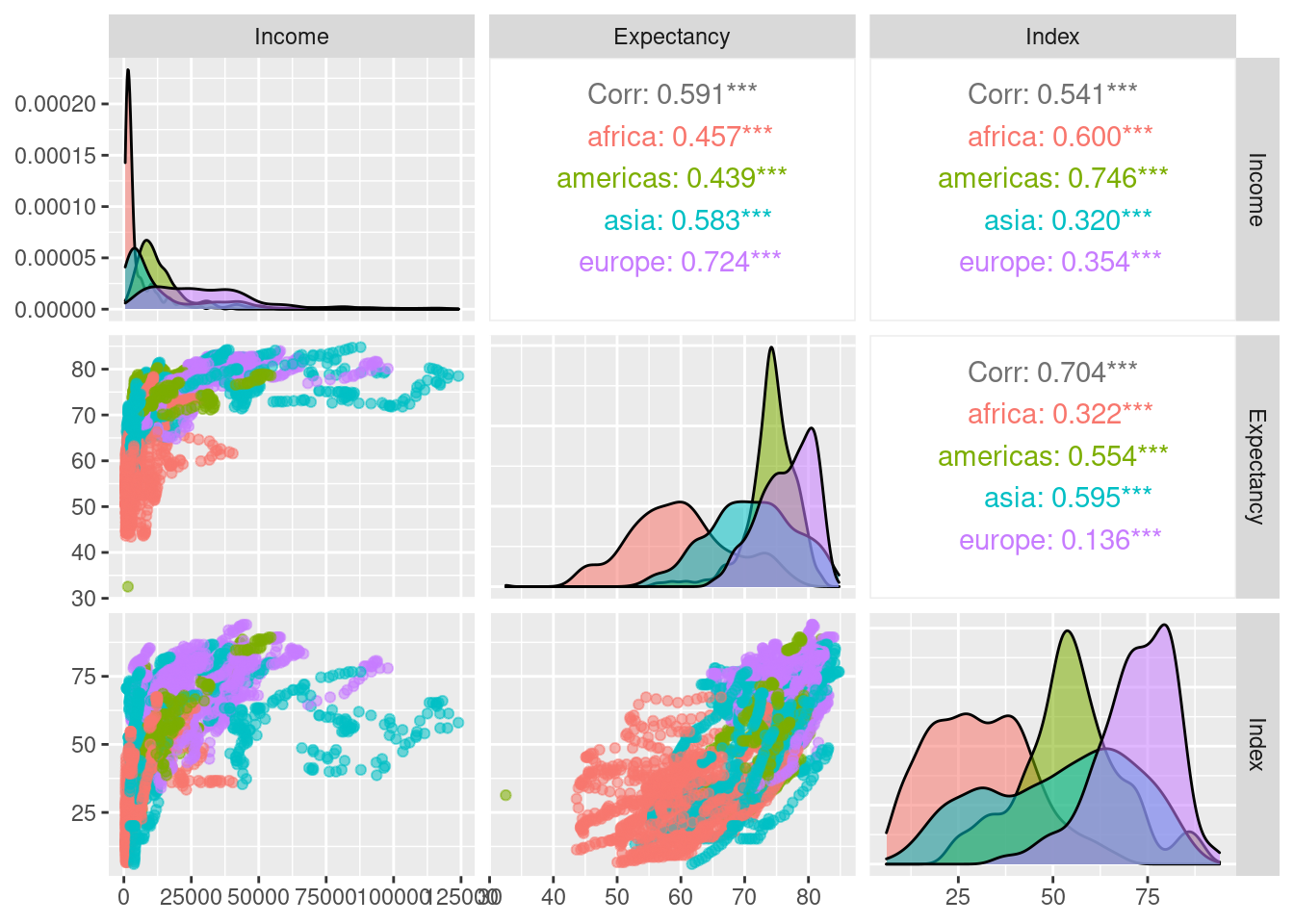
So lässt sich auch recht schnell ein Eindruck von den Daten gewinnen, um so auffällige Muster festzustellen.
Multivariate Daten mit tableplot() durchkämmen
Schließlich wollen wir Ihnen die Funktion tableplot() aus dem Paket tabplot nicht vorenthalten. Da dieses nicht auf CRAN, sondern auf github gehostet wird, installieren wir es über die devtools-Funktion install_github().
library(devtools)
install_github("mtennekes/tabplot")
library(tabplot)Das sog. Tableplot ist geeignet, um große multivariate Datensätze zu visualisieren. Für jede Subgruppe (per Default: für jedes Quantil) auf einer Variable werden Statistiken auf anderen Variablen dargestellt:
- für kontinuierliche Variablen: Balkendiagramm der Mittelwerte
- für kategoriale Variablen: Gestapeltes Balkendiagramm der Häufigkeiten einzelner Kategorien
Zunächst reduzieren wir den edu_exp-Datensatz aus didaktischen Gründen auf sechs Variablen
edu_exp_2 <- subset(edu_exp, select = c("Country", "Region", "Index", "Expectancy", "Population", "Income"))Ohne weitere Einstellungen sieht das Tableplot für diesen Teildatensatz so aus:
tableplot(edu_exp_2)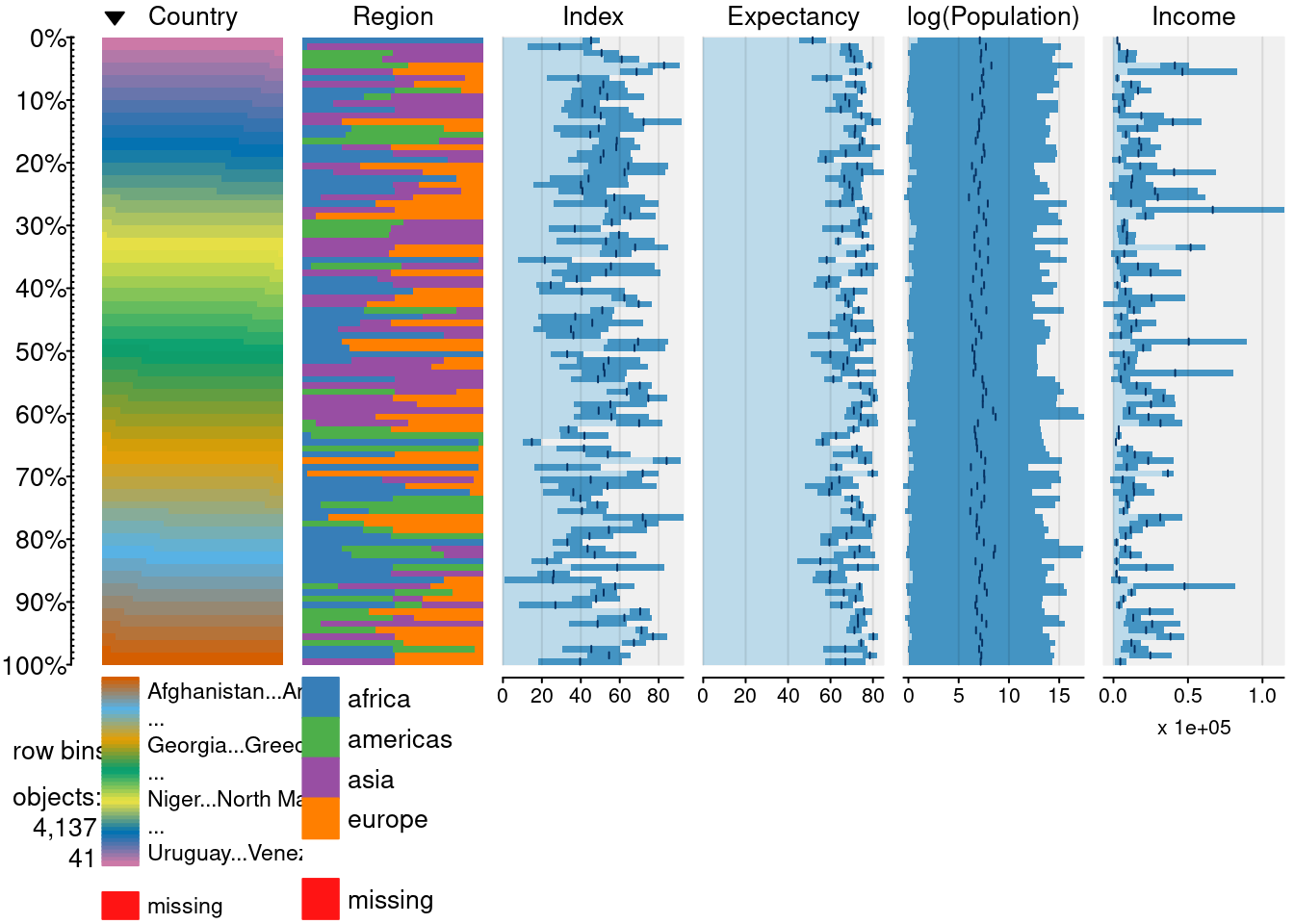
Per Voreinstellung werden die Daten nach der ersten Variable im Datensatz sortiert (Variable country; alphabetisch sortiert) - dies ist hier nicht sonderlich sinnvoll. Außerdem würden wir nicht annehmen, dass die Bevölkerungszahl oder das Jahr der Erhebung eines Landes mit den anderen Variablen in Zusammenhang steht, also schließen wir sie im nächsten Schritt aus. Außerdem sortieren wir den Datensatz diesmal nach der Ausprägung auf der Variable Income:
# Sortiert nach Income
tableplot(edu_exp_2,
select=c(Region, Index, Expectancy, Income),
sortCol = Income)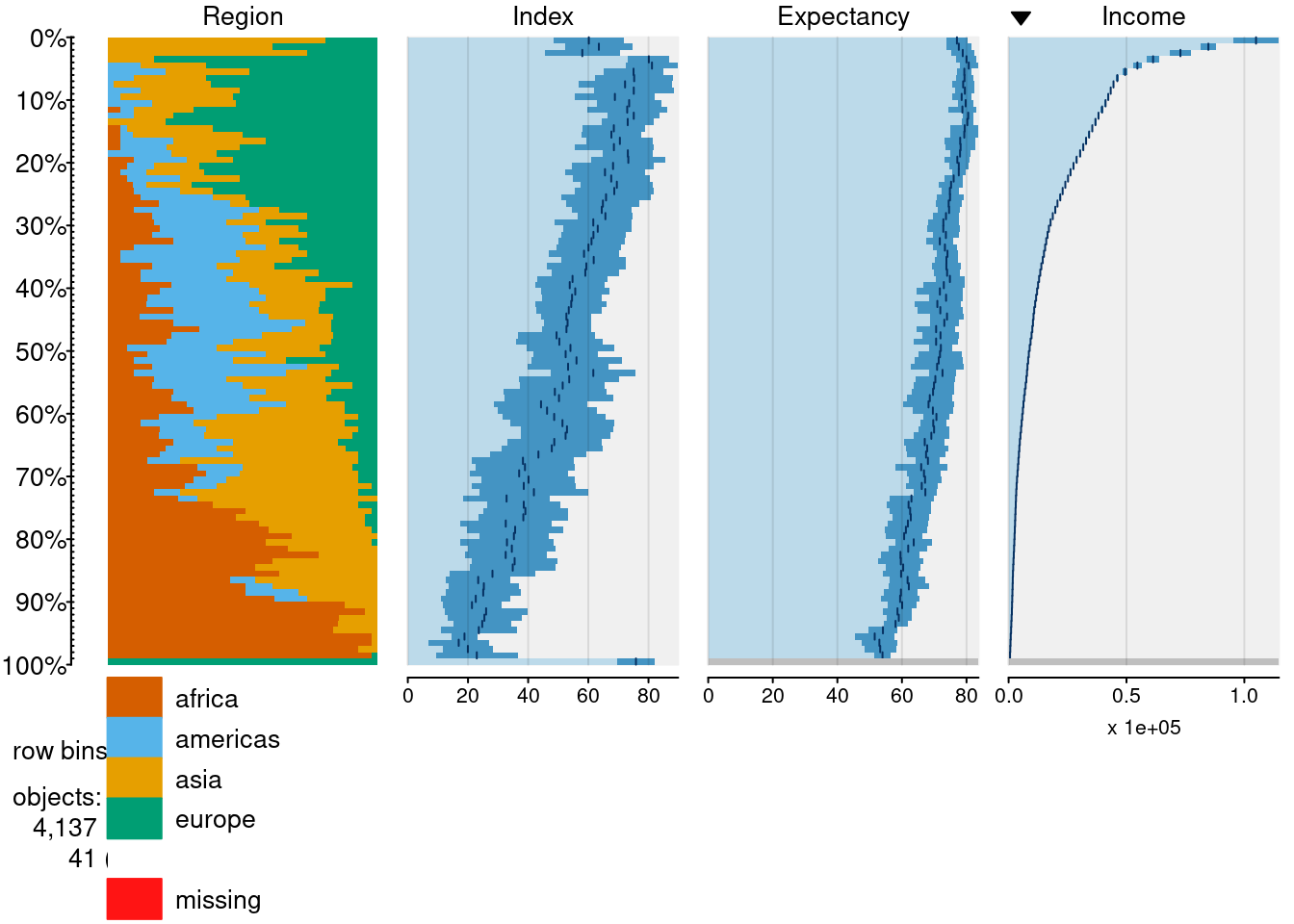
Nun zeigen sich deutliche Muster - alle Variablen sortieren sich mit der Variable Income mit:
- Region: Die Länder im oberen Bereich der Income-Verteilung befinden sich vorrangig in Asien und Europa (gelbe und rote Anteile), während die Länder im unteren Bereich der Income-Verteilung vorrangig in Afrika liegen
- Index: Die Länder im oberen Bereich der Income-Verteilung weisen höhere Werte auf dem Bildungsindex auf als die Länder im unteren Bereich der Income-Verteilung
- Expectancy: Die Länder im oberen Bereich der Income-Verteilung weisen auch höhere Werte für die Lebenserwartung auf als die Länder im unteren Bereich der Income-Verteilung
