Einführung in lineare Modelle in R
Vorbereitung
Zunächst müssen wir das haven-Paket wieder aktivieren und einen Teil des Code aus dem letzten Tutorial wieder durchführen.
library(haven)
setwd("~/Pfad/zu/Ordner")
data <- read_sav(file = "fb22_mod.sav")
data$geschl_faktor <- factor(data$geschl, # Ausgangsvariable
levels = c(1, 2, 3), # Faktorstufen
labels = c("weiblich", "männlich", "anderes")) # Label für Faktorstufen
data$nr_ges <- rowMeans(data[,c("nr1", "nr2", "nr3", "nr4", "nr5", "nr6")])
data$prok <- rowMeans(data[,c("prok1", "prok4", "prok6", "prok9", "prok10")])
data$wohnen_faktor <- factor(data$wohnen,
levels = c(1, 2, 3, 4),
labels = c("WG", "bei Eltern", "alleine", "sonstiges")) lineare Modellierung
Die Grundlage für die spätere hierarchische Ansetzung ist das lineares Modell ohne Hierarchie, dem wir uns demnach im Folgenden widmen werden.
Syntax
Es gibt eine spezielle Syntax für die Darstellungen von Abhängigkeiten. Dies wollen wir anhand der aggregate-Funktion demonstrieren. Hier wird eine bestimmte Operation an einer Variable in Abhängigkeit einer anderen Variable durchgeführt.
aggregate(extra ~ geschl_faktor, data = data, FUN = mean)## geschl_faktor extra
## 1 weiblich 3.373967
## 2 männlich 3.250000
## 3 anderes 2.750000Einfaches lineares Modell
Nun übertragen wir die eben gelernte Syntaxlogik und schauen uns die Variable extra (Extraversion) in Abhängigkeit von lz (Lebenszufriedenheit) an.
lm(extra ~ lz, data = data)##
## Call:
## lm(formula = extra ~ lz, data = data)
##
## Coefficients:
## (Intercept) lz
## 2.7746 0.1273Das Model selbst hat offenbar erstmal nur eine sehr beschränkte Ausgabe. Häufig kann man mehr aus Funktionen herausholen, wenn man ihren Output zunächst in einem Objekt ablegt:
mod <- lm(extra ~ lz, data = data)Das Objekt mod erscheint damit im Environment. Es ist vom Typ Liste, das ist etwas anderes als ein Datensatz mit einer festen Anzahl an Spalten pro Reihe und umgekehrt. Bei Listen können in verschiedenen Bestandteilen der Liste ganz unterschiedliche Sachen liegen. Beispielsweise können auch Datensätze Bestandteile von Listen sein. Die Auswahl von Listenbestandteilen funktioniert aber ebenfalls durch das $.
mod$coefficients## (Intercept) lz
## 2.7745981 0.1273186mod$call## lm(formula = extra ~ lz, data = data)Genau wie Variablen (numeric etc.) können auch Listen verschiedene Klassen haben. Beispielsweise liegt hier die class lm vor, entsprechend der Funktion mit der wir das Objekt erstellt haben.
Datensätze hingegen haben meist die class data.frame.
class(data)## [1] "tbl_df" "tbl" "data.frame"class(mod)## [1] "lm"Neben der händischen Exploration eines Objektes können wir auch automatische Funktionen nutzen, wie beispielsweise die summary-Funktion, die wohl am häufigsten verwendet wird.
summary(mod)##
## Call:
## lm(formula = extra ~ lz, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.78851 -0.48758 -0.01305 0.51706 1.63974
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.77460 0.25420 10.915 <2e-16 ***
## lz 0.12732 0.05291 2.406 0.0173 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.7003 on 151 degrees of freedom
## Multiple R-squared: 0.03693, Adjusted R-squared: 0.03055
## F-statistic: 5.79 on 1 and 151 DF, p-value: 0.01732Sie zeigt uns die wichtigsten Parameter an. Die summary-Funktion ist auch auf Objekte anderer Klassen anwendbar. Wenn wir sie auf den Datensatz anwenden, werden uns Zusammenfassungen der Variablen angezeigt. Auch in den nächsten Blöcken werden wir sie noch verwenden.
summary(data)## prok1 prok2 prok3 prok4
## Min. :1.000 Min. :1.000 Min. :1.000 Min. :1.000
## 1st Qu.:2.000 1st Qu.:2.000 1st Qu.:2.000 1st Qu.:2.000
## Median :3.000 Median :3.000 Median :2.000 Median :3.000
## Mean :2.667 Mean :2.588 Mean :2.235 Mean :2.569
## 3rd Qu.:3.000 3rd Qu.:3.000 3rd Qu.:3.000 3rd Qu.:3.000
## Max. :4.000 Max. :4.000 Max. :4.000 Max. :4.000
##
## prok5 prok6 prok7 prok8 prok9
## Min. :1.000 Min. :1.000 Min. :1.000 Min. :1.00 Min. :1.000
## 1st Qu.:3.000 1st Qu.:2.000 1st Qu.:2.000 1st Qu.:2.00 1st Qu.:2.000
## Median :3.000 Median :3.000 Median :3.000 Median :3.00 Median :3.000
## Mean :2.974 Mean :2.725 Mean :2.725 Mean :2.81 Mean :2.745
## 3rd Qu.:3.000 3rd Qu.:3.000 3rd Qu.:3.000 3rd Qu.:3.00 3rd Qu.:4.000
## Max. :4.000 Max. :4.000 Max. :4.000 Max. :4.00 Max. :4.000
##
## prok10 nr1 nr2 nr3 nr4
## Min. :1.000 Min. :1.000 Min. :1.00 Min. :1.000 Min. :1.000
## 1st Qu.:2.000 1st Qu.:2.000 1st Qu.:3.00 1st Qu.:2.000 1st Qu.:3.000
## Median :3.000 Median :3.000 Median :4.00 Median :3.000 Median :4.000
## Mean :2.739 Mean :2.765 Mean :3.68 Mean :3.124 Mean :3.699
## 3rd Qu.:4.000 3rd Qu.:4.000 3rd Qu.:4.00 3rd Qu.:4.000 3rd Qu.:4.000
## Max. :4.000 Max. :5.000 Max. :5.00 Max. :5.000 Max. :5.000
##
## nr5 nr6 lz extra vertr
## Min. :1.000 Min. :1.000 Min. :1.400 Min. :1.500 Min. :2.50
## 1st Qu.:3.000 1st Qu.:2.000 1st Qu.:4.200 1st Qu.:3.000 1st Qu.:3.75
## Median :3.000 Median :3.000 Median :4.800 Median :3.250 Median :4.00
## Mean :3.327 Mean :2.915 Mean :4.684 Mean :3.371 Mean :4.09
## 3rd Qu.:4.000 3rd Qu.:4.000 3rd Qu.:5.400 3rd Qu.:3.750 3rd Qu.:4.50
## Max. :5.000 Max. :5.000 Max. :6.600 Max. :5.000 Max. :5.00
##
## gewis neuro intel nerd
## Min. :2.000 Min. :1.250 Min. :1.250 Min. :1.500
## 1st Qu.:3.500 1st Qu.:3.250 1st Qu.:3.250 1st Qu.:2.667
## Median :4.000 Median :3.750 Median :3.500 Median :3.167
## Mean :3.856 Mean :3.621 Mean :3.564 Mean :3.127
## 3rd Qu.:4.250 3rd Qu.:4.250 3rd Qu.:4.000 3rd Qu.:3.500
## Max. :5.000 Max. :5.000 Max. :5.000 Max. :4.667
##
## grund fach ziel lerntyp
## Length:153 Length:153 Length:153 Length:153
## Class :character Class :character Class :character Class :character
## Mode :character Mode :character Mode :character Mode :character
##
##
##
##
## geschl job ort ort12
## Min. :1.000 Min. :1.00 Min. :1.000 Length:153
## 1st Qu.:1.000 1st Qu.:1.00 1st Qu.:1.000 Class :character
## Median :1.000 Median :1.00 Median :1.000 Mode :character
## Mean :1.161 Mean :1.35 Mean :1.361
## 3rd Qu.:1.000 3rd Qu.:2.00 3rd Qu.:2.000
## Max. :3.000 Max. :2.00 Max. :2.000
## NA's :10 NA's :10 NA's :9
## wohnen uni1 uni2 uni3
## Min. :1.000 Min. :0.0000 Min. :0.0000 Min. :0.0000
## 1st Qu.:1.500 1st Qu.:0.0000 1st Qu.:1.0000 1st Qu.:0.0000
## Median :2.000 Median :0.0000 Median :1.0000 Median :0.0000
## Mean :2.238 Mean :0.2026 Mean :0.8693 Mean :0.3791
## 3rd Qu.:3.000 3rd Qu.:0.0000 3rd Qu.:1.0000 3rd Qu.:1.0000
## Max. :4.000 Max. :1.0000 Max. :1.0000 Max. :1.0000
## NA's :10
## uni4 geschl_faktor nr_ges prok
## Min. :0.0000 weiblich:121 Min. :1.000 Min. :1.200
## 1st Qu.:0.0000 männlich: 21 1st Qu.:2.833 1st Qu.:2.200
## Median :0.0000 anderes : 1 Median :3.333 Median :2.800
## Mean :0.1111 NA's : 10 Mean :3.252 Mean :2.689
## 3rd Qu.:0.0000 3rd Qu.:3.667 3rd Qu.:3.200
## Max. :1.0000 Max. :5.000 Max. :4.000
##
## wohnen_faktor
## WG :36
## bei Eltern:55
## alleine :34
## sonstiges :18
## NA's :10
##
## Weitere Beispiele für solche Funktionen, die auf Objekte verschiedener Klassen angewandt werden können, sind plot() und resid().
Die einfache lineare Modellierung kann hier vertieft werden.
Multiple Regression
Die multiple Regression ist eine Erweiterung des Modells mit der Aufnahme von Effekten. Zur multiplen Regression gibt es viele Themen in der Übersicht von PsyBSc7.
Kontinuierliche Prädiktoren
Schauen wir uns zunächst eine einfache Erweiterung der Syntax um eine Addition an.
mod_kont <- lm(lz ~ neuro + intel, data = data)Die class bleibt gleich und auch die summary ist daher gleich aufgebaut. Die Coefficients werden logischerweise um einen Eintrag erweitert.
class(mod_kont)## [1] "lm"summary(mod_kont)##
## Call:
## lm(formula = lz ~ neuro + intel, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.4246 -0.6164 0.0396 0.7188 1.8736
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.6670 0.6245 5.872 2.67e-08 ***
## neuro -0.2566 0.1184 -2.167 0.0318 *
## intel 0.5460 0.1360 4.016 9.34e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.017 on 150 degrees of freedom
## Multiple R-squared: 0.1149, Adjusted R-squared: 0.1031
## F-statistic: 9.74 on 2 and 150 DF, p-value: 0.0001054Aufnahme kategorialer Prädiktor
Nun nehmen wir zunächst einmal die Variable geschl (Geschlecht) auf, so wie sie ursprünglich vorlag. Die Syntax bleibt dabei genau gleich.
mod_kat <- lm(lz ~ intel + geschl, data = data)
summary(mod_kat)##
## Call:
## lm(formula = lz ~ intel + geschl, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.6753 -0.5007 0.0738 0.7247 2.0197
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.1983 0.5188 6.165 7.09e-09 ***
## intel 0.5967 0.1389 4.296 3.24e-05 ***
## geschl -0.5097 0.2219 -2.297 0.0231 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.004 on 140 degrees of freedom
## (10 Beobachtungen als fehlend gelöscht)
## Multiple R-squared: 0.1284, Adjusted R-squared: 0.1159
## F-statistic: 10.31 on 2 and 140 DF, p-value: 6.654e-05Wir sehen, dass geschl ein eigenes Steigungsgewicht bekommt. Das ist überraschend, da es drei Ausprägungen in dieser Variable gibt.
Daher ist die Verwandlung in einen Faktor essentiell.
mod_kat <- lm(lz ~ intel + geschl_faktor, data = data)
summary(mod_kat)##
## Call:
## lm(formula = lz ~ intel + geschl_faktor, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.6774 -0.5032 0.0709 0.7226 2.0124
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.7046 0.5003 5.406 2.73e-07 ***
## intel 0.5932 0.1395 4.253 3.84e-05 ***
## geschl_faktormännlich -0.5548 0.2412 -2.300 0.0229 *
## geschl_faktoranderes -0.5740 1.0198 -0.563 0.5745
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.007 on 139 degrees of freedom
## (10 Beobachtungen als fehlend gelöscht)
## Multiple R-squared: 0.1298, Adjusted R-squared: 0.1111
## F-statistic: 6.914 on 3 and 139 DF, p-value: 0.0002258Die summary zeigt uns direkt an, in welcher Kategorie der Unterschied besteht. Die fehlende Kategorie wird als Referenz genutzt. Standardmäßig liegt hier also eine Dummykodierung vor.
Moderierte Regression
Nun soll der Interaktionseffekt zwischen zwei Variablen aufgenommen werden. Bevor wir dies tun, müssen wir die Variablen zentrieren, damit Multikollinearität vorgebeugt wird.
data$neuro_center <- scale(data$neuro, scale = F, center = T)
data$intel_center <- scale(data$intel, scale = F, center = T)Wir überprüfen die Funktionalität; diese ist nicht immer genau null, aber maschinell gesehen schon.
mean(data$neuro_center)## [1] -1.450156e-17mean(data$intel_center)## [1] -2.176752e-16Setzen wir nun die lineare Modellierung mit Moderationseffekt um. Da eine Moderation eine Multiplikation der Effekte ist, würde man intuitiv den Code folgendermaßen schreiben.
mod_inter_nocenter <- lm(lz ~ neuro + intel + neuro * intel, data = data)
mod_inter_center <- lm(lz ~ neuro_center + intel_center + neuro_center * intel_center, data = data)
summary(mod_inter_nocenter)##
## Call:
## lm(formula = lz ~ neuro + intel + neuro * intel, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.4151 -0.6220 0.0753 0.7150 1.9449
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.65678 3.14284 0.845 0.399
## neuro 0.01942 0.84978 0.023 0.982
## intel 0.83316 0.88602 0.940 0.349
## neuro:intel -0.07825 0.23856 -0.328 0.743
##
## Residual standard error: 1.02 on 149 degrees of freedom
## Multiple R-squared: 0.1156, Adjusted R-squared: 0.09777
## F-statistic: 6.491 on 3 and 149 DF, p-value: 0.0003705summary(mod_inter_center)##
## Call:
## lm(formula = lz ~ neuro_center + intel_center + neuro_center *
## intel_center, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.4151 -0.6220 0.0753 0.7150 1.9449
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.68648 0.08288 56.543 < 2e-16 ***
## neuro_center -0.25945 0.11908 -2.179 0.0309 *
## intel_center 0.54981 0.13687 4.017 9.32e-05 ***
## neuro_center:intel_center -0.07825 0.23856 -0.328 0.7434
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.02 on 149 degrees of freedom
## Multiple R-squared: 0.1156, Adjusted R-squared: 0.09777
## F-statistic: 6.491 on 3 and 149 DF, p-value: 0.0003705Wir sehen, dass die Zentralisierung wie erwartet die Standardfehler reduziert hat. Kommen wir jetzt nochmal zurück zum Code: die intuitive Lösung mit der Multiplikation benötigt theoretisch nicht die einzelne Aufführung der Variablen, die Teil der Interaktion sind.
mod_inter_center <- lm(lz ~ neuro_center * intel_center, data = data)
summary(mod_inter_center)##
## Call:
## lm(formula = lz ~ neuro_center * intel_center, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.4151 -0.6220 0.0753 0.7150 1.9449
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.68648 0.08288 56.543 < 2e-16 ***
## neuro_center -0.25945 0.11908 -2.179 0.0309 *
## intel_center 0.54981 0.13687 4.017 9.32e-05 ***
## neuro_center:intel_center -0.07825 0.23856 -0.328 0.7434
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.02 on 149 degrees of freedom
## Multiple R-squared: 0.1156, Adjusted R-squared: 0.09777
## F-statistic: 6.491 on 3 and 149 DF, p-value: 0.0003705Allerdings hat das natürlich den Nachteil, dass man nicht spezifisch auswählt und damit nicht so stark über sein Modell nachdenken muss. Es besteht daher die Möglichkeit, Interaktionen sehr präzise mit dem : auszuwählen.
mod_inter_center <- lm(lz ~ neuro_center + intel_center + neuro_center:intel_center, data = data)
summary(mod_inter_center)##
## Call:
## lm(formula = lz ~ neuro_center + intel_center + neuro_center:intel_center,
## data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.4151 -0.6220 0.0753 0.7150 1.9449
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.68648 0.08288 56.543 < 2e-16 ***
## neuro_center -0.25945 0.11908 -2.179 0.0309 *
## intel_center 0.54981 0.13687 4.017 9.32e-05 ***
## neuro_center:intel_center -0.07825 0.23856 -0.328 0.7434
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.02 on 149 degrees of freedom
## Multiple R-squared: 0.1156, Adjusted R-squared: 0.09777
## F-statistic: 6.491 on 3 and 149 DF, p-value: 0.0003705Kommen wir nun zur grafischen Darstellung: Es gibt ein Paket, dass diese sehr gut unterstützt. Es erstellt automatisch Grafen im Rahmen von ggplot(), wozu es auf PandaR einen ganzen Workshop oder auch ein einzelnes, einführendes Tutorial gibt.
install.packages("interactions")
library(interactions)library(interactions)Die Festlegung des Moderators kann R natürlich nicht für uns übernehmen.
interact_plot(model = mod_inter_center, pred = intel_center, modx = neuro_center)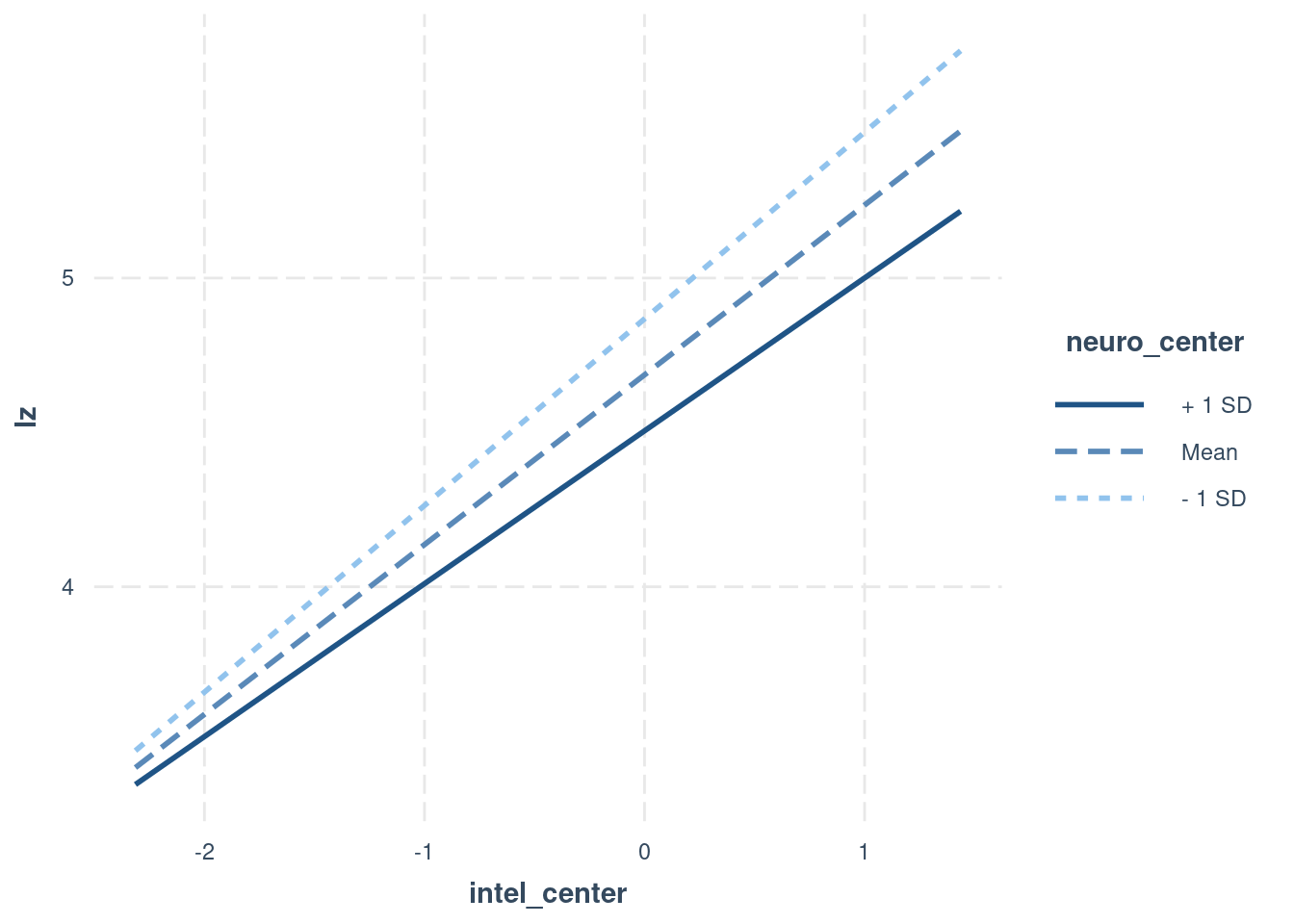
Weitere Infos zur Moderation, besonders zum Zusammenspiel mit quadratischen Effekten, finden sich hier.
Anwendungen
- Erstelle eine multiple Regression mit Extraversion als abhängiger Variable und Art des Wohnens sowie Verträglichkeit als unabhängigen Variablen.
Lösung
mod_extra <- lm(extra ~ wohnen_faktor + vertr, data = data)
summary(mod_extra)##
## Call:
## lm(formula = extra ~ wohnen_faktor + vertr, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.5411 -0.4500 0.0080 0.5113 1.5992
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.75211 0.42948 4.080 7.59e-05 ***
## wohnen_faktorbei Eltern -0.26918 0.14279 -1.885 0.0615 .
## wohnen_faktoralleine -0.04909 0.15898 -0.309 0.7580
## wohnen_faktorsonstiges -0.31833 0.19275 -1.652 0.1009
## vertr 0.42926 0.09992 4.296 3.26e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.6648 on 138 degrees of freedom
## (10 Beobachtungen als fehlend gelöscht)
## Multiple R-squared: 0.161, Adjusted R-squared: 0.1367
## F-statistic: 6.619 on 4 and 138 DF, p-value: 6.661e-05- Finde mit Hilfe des Internets heraus, wie standardisierte Regressionsparameter mit Hilfe einer Funktion ausgegeben werden können.
Lösung
library(lm.beta)
lm.beta(mod_extra)##
## Call:
## lm(formula = extra ~ wohnen_faktor + vertr, data = data)
##
## Standardized Coefficients::
## (Intercept) wohnen_faktorbei Eltern wohnen_faktoralleine
## NA -0.18368741 -0.02931193
## wohnen_faktorsonstiges vertr
## -0.14810607 0.33734839summary(lm.beta(mod_extra))##
## Call:
## lm(formula = extra ~ wohnen_faktor + vertr, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.5411 -0.4500 0.0080 0.5113 1.5992
##
## Coefficients:
## Estimate Standardized Std. Error t value Pr(>|t|)
## (Intercept) 1.75211 NA 0.42948 4.080 7.59e-05 ***
## wohnen_faktorbei Eltern -0.26918 -0.18369 0.14279 -1.885 0.0615 .
## wohnen_faktoralleine -0.04909 -0.02931 0.15898 -0.309 0.7580
## wohnen_faktorsonstiges -0.31833 -0.14811 0.19275 -1.652 0.1009
## vertr 0.42926 0.33735 0.09992 4.296 3.26e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.6648 on 138 degrees of freedom
## (10 Beobachtungen als fehlend gelöscht)
## Multiple R-squared: 0.161, Adjusted R-squared: 0.1367
## F-statistic: 6.619 on 4 and 138 DF, p-value: 6.661e-05Eine geschachtelte Funktion ist teilweise schwierig zu lesen. Es gibt als Lösung die Pipe, die ein Objekt in eine weitere Funktion weitergibt.
mod_extra |> lm.beta() |> summary()##
## Call:
## lm(formula = extra ~ wohnen_faktor + vertr, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.5411 -0.4500 0.0080 0.5113 1.5992
##
## Coefficients:
## Estimate Standardized Std. Error t value Pr(>|t|)
## (Intercept) 1.75211 NA 0.42948 4.080 7.59e-05 ***
## wohnen_faktorbei Eltern -0.26918 -0.18369 0.14279 -1.885 0.0615 .
## wohnen_faktoralleine -0.04909 -0.02931 0.15898 -0.309 0.7580
## wohnen_faktorsonstiges -0.31833 -0.14811 0.19275 -1.652 0.1009
## vertr 0.42926 0.33735 0.09992 4.296 3.26e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.6648 on 138 degrees of freedom
## (10 Beobachtungen als fehlend gelöscht)
## Multiple R-squared: 0.161, Adjusted R-squared: 0.1367
## F-statistic: 6.619 on 4 and 138 DF, p-value: 6.661e-05- Zur Veranschaulichung des Codes - keine Empfehlung für solch ein Modell: Nun sollen statt Art des Wohnens die Skalenscores für Prokrastination und Naturverbundenheit genutzt werden. Außerdem soll die Dreifachinteraktion der Prädiktoren aufgenommen werden, aber keine Interaktionen zwischen zwei Prädiktoren.
Lösung
data$nr_ges_center <- scale(data$nr_ges, scale = F, center = T)
data$prok_center <- scale(data$prok, scale = F, center = T)
data$vertr_center <- scale(data$vertr, scale = F, center = T)mod_falsch <- lm(extra ~ nr_ges_center * prok_center * vertr_center, data = data)
summary(mod_falsch)##
## Call:
## lm(formula = extra ~ nr_ges_center * prok_center * vertr_center,
## data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.74002 -0.43244 -0.04961 0.43520 1.48942
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.371832 0.054627 61.725 < 2e-16
## nr_ges_center 0.021812 0.068152 0.320 0.749
## prok_center -0.003785 0.085937 -0.044 0.965
## vertr_center 0.445074 0.099212 4.486 1.47e-05
## nr_ges_center:prok_center -0.165077 0.108148 -1.526 0.129
## nr_ges_center:vertr_center 0.080309 0.107238 0.749 0.455
## prok_center:vertr_center 0.092026 0.156887 0.587 0.558
## nr_ges_center:prok_center:vertr_center -0.095016 0.199032 -0.477 0.634
##
## (Intercept) ***
## nr_ges_center
## prok_center
## vertr_center ***
## nr_ges_center:prok_center
## nr_ges_center:vertr_center
## prok_center:vertr_center
## nr_ges_center:prok_center:vertr_center
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.6732 on 145 degrees of freedom
## Multiple R-squared: 0.1454, Adjusted R-squared: 0.1042
## F-statistic: 3.526 on 7 and 145 DF, p-value: 0.001588mod_korrekt <- lm(extra ~ nr_ges_center + prok_center + vertr_center + nr_ges_center:prok_center:vertr_center, data = data)
summary(mod_korrekt)##
## Call:
## lm(formula = extra ~ nr_ges_center + prok_center + vertr_center +
## nr_ges_center:prok_center:vertr_center, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.70159 -0.48198 -0.05594 0.42549 1.55172
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.37225 0.05447 61.905 < 2e-16 ***
## nr_ges_center 0.01607 0.06802 0.236 0.814
## prok_center 0.01132 0.08477 0.134 0.894
## vertr_center 0.44291 0.09685 4.573 1.01e-05 ***
## nr_ges_center:prok_center:vertr_center -0.14871 0.19278 -0.771 0.442
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.6735 on 148 degrees of freedom
## Multiple R-squared: 0.1269, Adjusted R-squared: 0.1033
## F-statistic: 5.38 on 4 and 148 DF, p-value: 0.0004508Anmerkung: Es ist empfehlenswert, keine Modelle zu bestimmen, in denen Interaktionen niedrigerer Ordnung nicht drin sind.
