Metaanalysen in R
Mittelwertsunterschiede
Einführung
Metaanalysen sind empirische Zusammenfassungen von Studien unter Verwendung mathematischer/statistischer Modelle. Auf diese Weise können Ergebnisse aus jahrelanger Forschung integriert und zusammengefasst werden, was oft Aufschluss darüber liefert, ob Effekte im Mittel vorhanden sind oder nicht. Somit können Metaanalysen lange Debatten beenden und Licht in das Dunkel von sich widersprechenden Studienergebnissen bringen.
Mithilfe des metafor-Paketes (meta-analysis for r) von Viechtbauer (2010) lassen sich eindimensionale und mehrdiemensionale Metaanalysen (in welchen ein oder mehrere Koeffizient über mehrere Studien “gemittelt” werden soll) leicht berechnen. Zunächst müssen wir dazu das R-Paket installieren ("install.packages("metafor")). Nachdem dies geschehen ist, können wir es laden:
library(metafor)## Loading required package: Matrix## Loading required package: metadat##
## Loading the 'metafor' package (version 3.4-0). For an
## introduction to the package please type: help(metafor)Wie auch beim Laden des Paketes schon erwähnt wird (For an overview and introduction to the package please type: help(metafor)), können wir uns mit der sehr nützlichen R-internen Hilfe-Funktion einen Überblick über das Paket verschaffen.
help("metafor")Wenn wir diesen Befehl ausführen, so geht in R-Studio ein Fenster mit der Überschrift “metafor: A Meta-Analysis Package for R” auf, in welchem die grundlegenden Funktionen erklärt werden.
Effekte bestimmen
Im Datensatz, den wir in dieser Sitzung betrachten wollen, wurden die Effektstärken (standardisierte Mittelwertsdifferenzen) bereits bestimmt. Mithilfe der escalc-Funktion hätten wir diese auch selbst erstellen können, angenommen wir hätten einen Metaanalysedatensatz, der aus 2 Studien besteht, welche jeweils zwei unabhängige Gruppen in einer Variable untersucht hatten. Wir nehmen mal folgende Mittelwerte, Standardabweichungen und Stichprobengrößen an: Studie 1: und , Studie 2: und . Wir fügen diese Daten kurz in einen data.frame, um dann die escalc-Funktion schöner darauf anwenden zu können (dabei müssen wir die Daten jeweils nach Variablen sortieren):
df <- data.frame("Studie" = c("Studie 1", "Studie 2"),
"X1" = c(1.5, 2.5), "SD1" = c(0.7, 0.9), "n1" = c(35, 132),
"X2" = c(2.7, 2.8), "SD2" = c(1.3, 1.1), "n2" = c(27, 126))
df| Studie | X1 | SD1 | n1 | X2 | SD2 | n2 |
|---|---|---|---|---|---|---|
| Studie 1 | 1.5 | 0.7 | 35 | 2.7 | 1.3 | 27 |
| Studie 2 | 2.5 | 0.9 | 132 | 2.8 | 1.1 | 126 |
Der escalc Funktion müssen wir zunächst sagen, welche Transformation wir wünschen: measure = "SMD" für Standardized Mean Difference. Anschließend braucht die Funktion alle Informationen, die wir auch selbst zum Bestimmen der Effektstärke brauchen: Mittelwerte (m1i, m2i), Standardabweichungen (sd1i, sd2i) und Stichprobengrößen (n1i, n2i).
escalc(measure = "SMD", m1i = X1, m2i = X2, sd1i = SD1, sd2i = SD2,
n1i = n1, n2i = n2,
data = df)| Studie | X1 | SD1 | n1 | X2 | SD2 | n2 | yi | vi |
|---|---|---|---|---|---|---|---|---|
| Studie 1 | 1.5 | 0.7 | 35 | 2.7 | 1.3 | 27 | -1.1790461 | 0.0768194 |
| Studie 2 | 2.5 | 0.9 | 132 | 2.8 | 1.1 | 126 | -0.2983287 | 0.0156847 |
Zurückgegeben wird uns ein Metaanalysedatensatz, der um die beiden Variablen yi (Standardized Mean Difference) und vi (Standardfehler im Quadrat der SMD, also ) erweitert wurde. In den Zeilen stehen die zwei Studien. Bei der 2. Studie ist die SMD geringer, gleichzeitig ist aber die Präzision höher, was ausgedrückt wird durch die kleinere Varianz vi - diese Studie würde in einer Metaanalyse prinzipiell ein größeres Gewicht erhalten (sowohl mit Stichprobengewichtung als auch mit [quadrierter] Standardfehlergewichtung). Zum Glück liegen die Daten schon vor, sodass wir das nicht für unsere Metaanalyse tun müssen!
Daten
In dieser Sitzung wollen wir einen Datensatz von López-López et al. (2019), der mit dem metafor-Paket mitgeliefert wird, verwenden. Dieser heißt dat.lopez2019. Die Autor:innen haben die Effektivität der CBT (cognitive behavioural therapy [kognitive Verhaltenstherapie]) bei Depression untersucht und diese mit verschiedenen Kontrollbedingungen und unterschiedlichen Arten der CBT verglichen. Weitere Informationen zum Datensatz erhalten Sie bspw. mit ?dat.lopez2019 (das metafor-Paket muss natürlich vorher geladen sein).
head(dat.lopez2019)| study | treatment | scale | n | diff | se | group | tailored | sessions | length | intensity | multi | cog | ba | psed | home | prob | soc | relax | goal | final | mind | act |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Andersson (2005) | Placebo | BDI | 49 | -0.2140 | 0.0208 | 0 | 0 | NA | NA | NA | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Andersson (2005) | Multimedia CBT | BDI | 36 | -1.5529 | 0.0425 | 1 | 0 | 5 | NA | NA | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| Arean (1993) | Wait list | BDI | 20 | -0.4032 | 0.0531 | 0 | 0 | NA | NA | NA | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Arean (1993) | F2F CBT | BDI | 19 | -1.5505 | 0.0831 | 1 | 1 | 12 | 90 | 10.8 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Beckenridge (1985) | Wait list | BDI | 19 | 0.2131 | 0.0542 | 0 | 0 | NA | NA | NA | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Beckenridge (1985) | F2F CBT | BDI | 17 | -1.5438 | 0.0934 | 0 | 1 | 18 | NA | NA | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
In study steht die verwendete Studie, treatment zeigt an, welche Art der Therapie oder Kontrollgruppe in der jeweiligen Studie verwendet wurde (“F2F CBT” = “Angesicht zu Angesicht” CBT, “Multimedia CBT” = Online-CBT, “Placebo” = Placebo-Kontrollgruppe, “Wait list” = Wartelistenkontrollgruppe, “Hybrid CBT” = Mischung aus F2F und Multimedia, “No treatment” = klassische Kontrollgruppw, “TAU” = Treatment as Usual [Standardtherapie]), scale gibt an, wie die Depression erfasst wurde, n ist die Stichprobengröße der Studie, diff ist die standardisierte Differenz (Cohen’s ) zwischen vor und nach der Intervention, se ist der Standardfehler von diff, group [Dummy-Variable] zeigt an, ob es sich um eine Einzel- (0) oder Gruppentherapie (1) gehandelt hat. tailored gibt an, ob die Therapie auf den jeweiligen Patienten/die jeweilige Patientin zugeschnitten wurde, sessions ist die Anzahl an Therapiesitzungen, length ist die durchschnittliche Sitzungslänge, intensity ist das Produkt aus session und length. Außerdem werden noch weitere mögliche Moderatorvariablen aufgeführt, die sich jeweils auf die Therapie beziehen. Für mehr Informationen siehe bspw. ?dat.lopez2019. Wir schauen uns die Moderatoren genauer an, wenn es um die Moderatoranalysen im Rahmen von Metaanalysen geht.
Wir wollen uns zunächst nur auf die klassische “Face-to-Face” CBT konzentrieren und kürzen daher den Datensatz. Wir kopieren den Originaldatensatz in F2F_CBT, damit dat.lopez2019 erhalten bleibt.
F2F_CBT <- dat.lopez2019[dat.lopez2019$treatment == "F2F CBT",] # wähle nur Fälle mit F2F CBTFragestellungen
Insgesamt wollen wir nun untersuchen, ob
- die CBT zu einem Therapieerfolg bei Depression führt
- ob die CBT über Studien hinweg zu einer homogenen Verbesserung der Depressivität führt
- ob Heterogenität durch Moderatoren (Therapiemerkmale) erklärt werden kann
Um die erste Fragestellung zu beantworten, müssen wir eine durchschnittliche Differenz von Prä-Post bestimmen. Ist diese bedeutsam negativ, so gibt es eine Symptomverbesserung der CBT für die Depressivität auch in der Population.
Fixed Effects Modell
Das simpelste Vorgehen wäre es, die Differenzen der Studien einfach zu mitteln. Allerdings sind die Studien unterschiedlich groß. Somit müssen wir zumindest ein gewichtetes Mittel bestimmen. Von nun an nennen wir die Effektgrößen (also die standardisierte Prä-Post-Differenz) .
Fixed Effects Modell: händisch
Wir mitteln (gewichtet) zunächst händisch via:
Für die Stichproben wird hier jede standardisierte Prä-Post-Differenz mit der Stichprobengröße multipliziert und dann werden diese Werte aufsummiert (eine gewichtete Summe entsteht). Teilen wir diese Summe anschließend durch die Gesamtstichprobe so erhalten wir einen gewichteten Mittelwert, der berücksichtigt, dass einige Stichproben größer sind und dass dort die geschätzte standardisierte Differenz präziser ist. Dies sieht in R so aus:
sum(F2F_CBT$n*F2F_CBT$diff)/sum(F2F_CBT$n)## [1] -1.744116sum summiert hierbei alle Einträge des Vektors, den wir der Funktion übergeben. Werden Vektoren gleicher Länge miteinander multipliziert, dann entsteht elementenweise Multiplikationen, also der erste Eintrag des ersten Vektors wird mit dem ersten Eintrag des zweiten Vektors multipliziert, usw.
Fixed Effects Modell: Modellgleichung
Wir haben hier, ohne es zu wissen, das sogenannte “Fixed Effects”-Modell bestimmt, wobei wir die Stichprobengröße als als Gewichtung verwendet haben. Das Fixed-Effects-Modell besagt, dass
die Effektstärken zufällig um den wahren Wert streuen. ist hierbei die zufällige Abweichung vom wahren Effekt, quasi das Residuum, welches als normalverteilt angenommen wird.
Fixed Effects Modell: metafor
Ein Fixed-Effects-Modell lässt sich leicht mit dem metafor-Paket schätzen. Die Funktion dazu heißt rma (für R und Metaanalyse). Da bei Metaanalysen die Effekte in den Studien die abhängigen Variablen sind, werden sie im Paket als yi bezeichnet. Wir brauchen dann noch ein Streumaß vi, den Datensatz in data und wir müssen die Methode als Fixed Effects method = "FE" festlegen. Das Modell nennen wir FEM_n für Fixed-Effects Modell gewichtet mit Stichprobengrößen.
FEM_n <- rma(yi = diff, vi = 1/n, data = F2F_CBT, method = "FE")
summary(FEM_n)##
## Fixed-Effects Model (k = 71)
##
## logLik deviance AIC BIC AICc
## -1561.4161 3206.6098 3124.8321 3127.0948 3124.8901
##
## I^2 (total heterogeneity / total variability): 97.82%
## H^2 (total variability / sampling variability): 45.81
##
## Test for Heterogeneity:
## Q(df = 70) = 3206.6098, p-val < .0001
##
## Model Results:
##
## estimate se zval pval ci.lb ci.ub
## -1.7441 0.0217 -80.3430 <.0001 -1.7867 -1.7016 ***
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Die summary gibt uns, wie immer, eine Übersicht über die Ergebnisse.
In der Summary sehen wir Folgendes:
## Fixed-Effects Model (k = 71)zeigt uns, dass ein Fixed Effects Modell mit =71 Studien gerechnet wurde.
## logLik deviance AIC BIC AICc
## -1561.4161 3206.6098 3124.8321 3127.0948 3124.8901sind Modell-Fit Ergebnisse. Das Modell wurde mit der Maximum-Likelihood (ML)-Methode geschätzt, weswegen uns die Log-Liklihood (logLik), die Devianz (deviance), sowie weitere Informationskriterien (AIC, BIC, AICc) ausgegeben werden. Das zeigt uns, dass wenn Modelle mit ML geschätzt werden, auch Modellvergleiche möglich sind.
## I^2 (total heterogeneity / total variability): 97.82%
## H^2 (total variability / sampling variability): 45.81sind Heterogenitätsmaße. Sie beschreiben, wie viel der Variation der Studienergebnisse durch mögliche Subpopulationen zu Stande gekommen sind. ist ein häufig berichtetes Maß, welches den Anteil an der Gesamtvariation der Effektstärken schätzt, die durch Heterogenität zwischen den Studien resultiert.
Diese Heterogenität wird hier auf Signifikanz geprüft mithilfe von Cochran’s .
## Test for Heterogeneity:
## Q(df = 70) = 3206.6098, p-val < .0001Das signifikante Ergebnis zeigt uns, dass die Heterogenität statistisch bedeutsam ist, es also Unterschiede zwischen den Stichproben gibt. Diese Heterogenitätsvarianz, die hier de facto auf Signifikanz geprüft wurde, lässt sich vergleichen mit der Between-Varianz in HLM-Modellen. Die Sampling-Varianz entspricht der Within-Varianz.
Wie immer wird unter Model Results eine Übersicht über die Parameterschätzung gegeben (estimate = Schätzung, se = SE, zval = zugehöriger -Wert, pval = zugehöriger -Wert). Da wir hier nur einen einzigen Parameter schätzen, wird hier nicht viel angezeigt. ci.lb und ci.ub ist das Konfidenzintervall der Schätzung, wobei lb für lower-bound (untere Grenze) und ub für upper-bound (obere Grenze) steht.
## Model Results:
##
## estimate se zval pval ci.lb ci.ub
## -1.7441 0.0217 -80.3430 <.0001 -1.7867 -1.7016 ***
##
## ---
## Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Wir kommen zum selben Ergebnis wie mit unserer händischen Berechnung. Im “Fixed Effects”-Modell wird als Gewicht verwendet ( ist die Varianz des Schätzers; beim Mittelwert ist dies dessen Standardfehler im Quadrat). Wenn wir der R-Funktion v_i= 1/n_i übergeben, so ist das Gewicht einfach die Stichprobengröße (Studien mit größeren Stichproben erhalten mehr Gewicht).
Wir haben nun eine relativ einfache Zusammenfassung der Studienergebnisse durchgeführt. Die Stichprobengröße wird als Gewichtung verwendet, weil sie uns Informationen über die Präzision der Effektstärken gibt: je größer die Stichprobe, desto präziser der Effekt, desto mehr Gewicht sollte diese Stichprobe haben. Nun ist es so, dass wir über Mittelwertsdifferenzen noch zusätzliche Informationen haben. Der Standardfehler enthält sowohl Informationen über die Variabilität innerhalb der Stichprobe, als auch Informationen über die Stichprobengröße. Die lässt sich leicht einsehen, wenn wir uns zurückerinnern, dass der Standardfehler des Mittelwerts gerade durch gegeben ist. In gleicher Weise enthält der der Effektstärken auch Informationen über Variabilität und Stichprobengröße, also insgesamt über die Präzision der Effektstärken. Aus diesem Grund wiederholen wir das Fixed-Effects-Modell nochmals und verwenden diesmal den se von diff als Gewicht. Das nötige Argument heißt sei. Wir können aber auch vi verwenden. Dafür müssen wir den SE nur quadrieren.
FEM <- rma(yi = diff, vi = se^2, data = F2F_CBT, method = "FE")
summary(FEM)##
## Fixed-Effects Model (k = 71)
##
## logLik deviance AIC BIC AICc
## -8468.9399 17146.2694 16939.8798 16942.1425 16939.9377
##
## I^2 (total heterogeneity / total variability): 99.59%
## H^2 (total variability / sampling variability): 244.95
##
## Test for Heterogeneity:
## Q(df = 70) = 17146.2694, p-val < .0001
##
## Model Results:
##
## estimate se zval pval ci.lb ci.ub
## -1.1130 0.0035 -319.7116 <.0001 -1.1198 -1.1062 ***
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1FEM2 <- rma(yi = diff, sei = se, data = F2F_CBT, method = "FE")
summary(FEM2)##
## Fixed-Effects Model (k = 71)
##
## logLik deviance AIC BIC AICc
## -8468.9399 17146.2694 16939.8798 16942.1425 16939.9377
##
## I^2 (total heterogeneity / total variability): 99.59%
## H^2 (total variability / sampling variability): 244.95
##
## Test for Heterogeneity:
## Q(df = 70) = 17146.2694, p-val < .0001
##
## Model Results:
##
## estimate se zval pval ci.lb ci.ub
## -1.1130 0.0035 -319.7116 <.0001 -1.1198 -1.1062 ***
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Das Ergebnis ist komplett identisch. Der mittlere Effekt unterscheidet sich deutlich vom mittleren Effekt, den wir mit Stichprobengewichten bestimmt haben. Dies liegt vermutlich an der Heterogenität, die sich vermutlich auch auf unterschiedliche Streuungen innerhalb der Studien bezieht.
Würden wir selbst eine Metaanalyse durchführen wollen, und wollten wir bspw. Mittelwerte zusammenfassen, dann können wir den SE über die oben genannte Formel selbst bestimmen. Dies ist ein guter Tipp, da in Studien sehr häufig nur Mittelwert und SD berichtet werden.
Random Effects Modell
Da wir nun bereits wissen, dass es signifikante Heterogenität zwischen den Studien gibt, sollten wir diese auch in unserem Modell berücksichtigen. Dies schaffen wir mit dem Random Effects Modell.
Random Effects Modell: Modellgleichung
Im Random Effects Modell wird, wie bei Hierarchischen Regressionsmodellen, eine zusätzliche Variable aufgenommen, die die Heterogenität abbildet:
wobei und die selbe Bedeutung haben, wie beim Fixed Effects Modell. ist die systematische Abweichung vom durchschnittlichen Effekt , der auf Charakteristika der Studie zurückzuführen ist. Die Varianz von wird als Heterogenitätsvarianz bezeichnet und häufig mit bezeichnet. Die Varianzen von und lassen sich mit der Within- und der Between-Varianz vom HLM-Modell vergleichen.
Um nun das Modell zu schätzen, muss die Heterogenität zwischen Studien berücksichtigt werden. Im “Random Effects”-Modell wird die Heterogenitätsvarianz als Gewichtung mitverwendet: . Das Mitteln funktioniert für beide Modelle gleich, nämlich genau so wie der gewichtete Mittelwert, den wir uns zuvor angesehen haben:
Verwenden wir nun das “Random Effects”-Modell, so ergibt sich ein etwas anderer Mittelwert (offensichtlich scheinen die Effektstärken heterogen zu sein, denn das Wählen des “Random Effects”-Modells hat einen Einfluss auf den geschätzten Mittelwert und die Heterogenitätsvarianz ist auch statistisch signifikant). Das Modell nennen wir REM für Random-Effects-Modell:
REM <- rma(yi = diff, sei = se, data = F2F_CBT)
summary(REM)##
## Random-Effects Model (k = 71; tau^2 estimator: REML)
##
## logLik deviance AIC BIC AICc
## -113.9313 227.8626 231.8626 236.3596 232.0417
##
## tau^2 (estimated amount of total heterogeneity): 1.4347 (SE = 0.2480)
## tau (square root of estimated tau^2 value): 1.1978
## I^2 (total heterogeneity / total variability): 99.93%
## H^2 (total variability / sampling variability): 1454.46
##
## Test for Heterogeneity:
## Q(df = 70) = 17146.2694, p-val < .0001
##
## Model Results:
##
## estimate se zval pval ci.lb ci.ub
## -2.0523 0.1438 -14.2714 <.0001 -2.3342 -1.7705 ***
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Der Output des Random Effects Modells unterscheidet sich kaum vom Fixed Effects Modell. Gleich am Anfang der summary fällt uns auf, dass das Modell mit REML anstatt mit ML geschätzt wurde. Dies ist wichtig für die folgenden Modellvergleiche! Außerdem wird uns jetzt ein Maß für die Herterogenitätsvarianz (tau^2) angegeben. In Klammern dahinter steht sein Standardfehler.
## Random-Effects Model (k = 71; tau^2 estimator: REML)
##
## logLik deviance AIC BIC AICc
## -113.9313 227.8626 231.8626 236.3596 232.0417
##
## tau^2 (estimated amount of total heterogeneity): 1.4347 (SE = 0.2480)
## tau (square root of estimated tau^2 value): 1.1978
## I^2 (total heterogeneity / total variability): 99.93%
## H^2 (total variability / sampling variability): 1454.46Der mittlere Effekt liegt beim “Random Effects” -Modell deutlich höher (-2.052) als beim “Fixed Effects”-Modell (-1.113). Dem Random-Effects-Modell ist hier stärker zu vertrauen, da es die systematische Variation zwischen den Studien in die Modellierung integriert.
In beiden Analysen ist die mittlere Differenz negativ und signifikant von 0 verschieden. Niedrigere Mittelwertsdifferenzen sprechen für eine höhere Reduktion der Depressionssymptomatik.
Homogenität “annehmen”
Wollen wir von Homogenität sprechen, schlagen Döring und Bortz (2016) zwei Kriterien vor: 1) der p-Wert der Q-Statistik sollte größer als 0.1 sein () und die Power des Homogenitätstests sollte hoch sein. Die Power können wir recht leicht mit folgendem Code bestimmen:
power <- 1 - pchisq(q = qchisq(p = .95, df = REM$k.all - 1), df = REM$k.all - 1, ncp = REM$QE)
power## [1] 1ncp ist der Non-centrality-parameter der -Verteilung. Er beschreibt im Grunde die -Verteilung unter einer spezifischen Alternativ-Hypothese. In diesem Beispiel liegt die Power bei 1 (also bei ). Das ist wenig verwunderlich, da viele Studien eingegangen sind und der Q-Wert sehr groß ausfällt. Die Power sollte bei mindestens , also () liegen (bei weiterem Interesse an Power-Analysen, die mit dem folgenden allerdings nichts zu tun haben, finden sich in der Sitzung zu Simulation und Poweranalysen aus dem Bachelor).
Analyse Plots
Das metafor-Paket bietet außerdem noch einige grafische Veranschaulichungen der Daten. Beispielsweise lässt sich ganz leicht ein Funnel-Plot erstellen mit der funnel-Funktion, welche lediglich unser Metaanalyse-Objekt REM entgegen nehmen muss.
Funnel Plot und Trim-and-Fill Methode
Der Funnel-Plot wird verwendet, um auf das bekannte Problem des Publication-Bias zu untersuchen. Hier wird der gefundene Effekt (hier Effektstärken von Prä-Post Veränderungen) gegen den Standardfehler jeder Studie geplottet. Es wird die Annahme zugrundegelegt, dass alle Studien in der Metaanalyse eine gewisse zufällige Schwankung um den wahren Effekt haben, und dabei diese zufällige Schwankung größer ist, je größer der Standardfehler in einer Studie ist und je kleiner die Stichprobe war. Sofern eine Studie unabhängig von der Effektgröße sowie der Streuung (und damit auch der Signifikanz) publiziert wurde, sollte so das typische symmetrische Dreieck (Funnel = Trichter) entstehen.
# funnel plot
funnel(REM)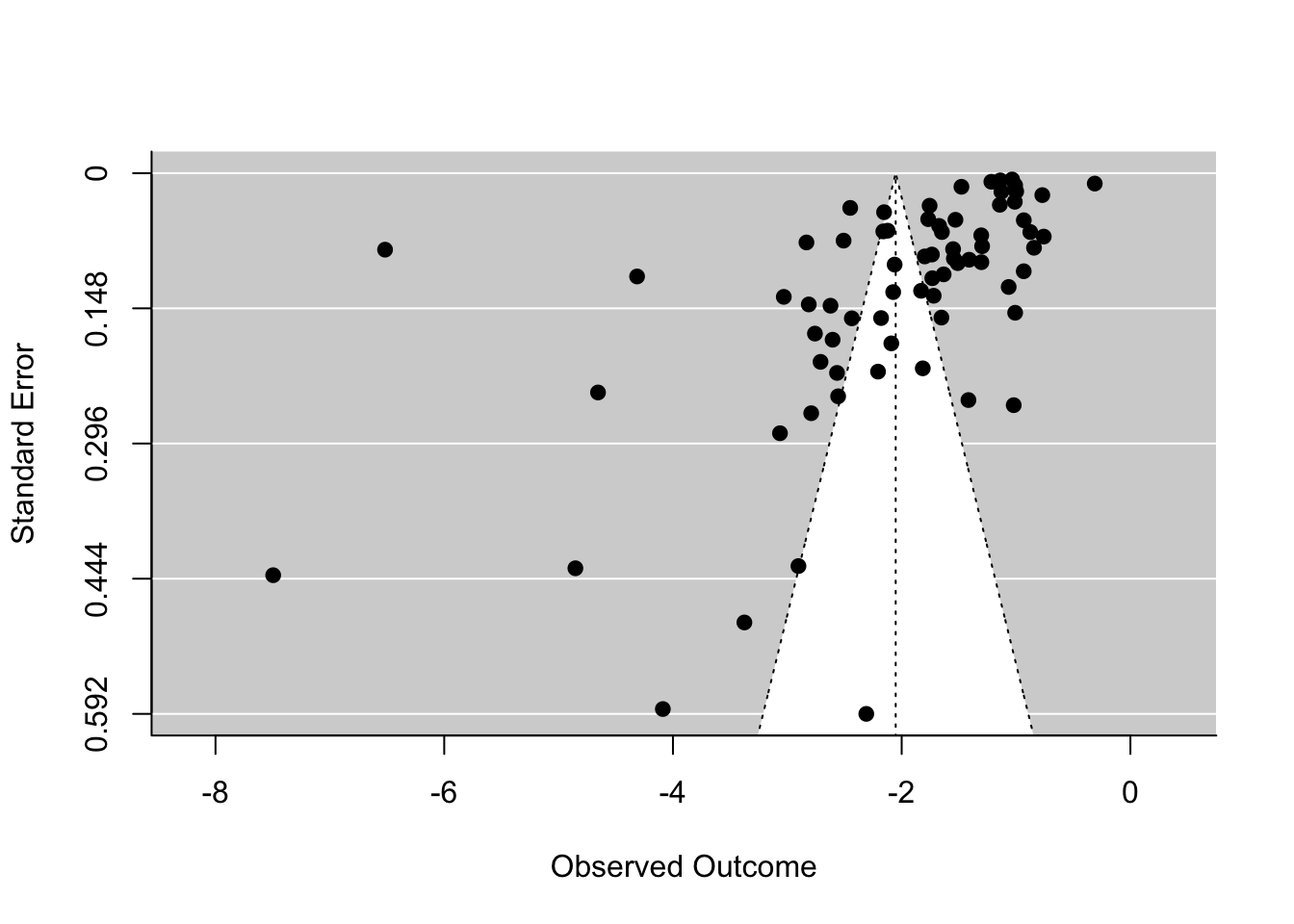
Der Grafik ist zu entnehmen, dass sich fast alle Effektstärken im negativen Bereich tummeln. Je kleiner der Effekt, desto präziser die Schätzung (je kleiner der SE - desto höher dargestellt im Funnel-Plot). Dies könnte Indizien auf einen Publication Bias zeigen. Außerdem gibt es wenige Studien mit sehr großen Standardfehlern (und damit geringen Stichprobengrößen). Der Funnel (Trichter) ist kaum befüllt. Dies liegt vermutlich an den wenigen extremen Ergebnissen, die links im Plot dargestellt sind. Allerdings ist die Punktewolke, auch wenn etwas schief, im oberen rechten Bereich recht gut ausgefüllt. Es gibt keine einzige Studie mit positiven Effektstärken. Insgesamt spricht dies dann doch dagegen, dass die Signifikanz des Effekts durch einen Bias in Veröffentlichungen entstanden ist. Allerdings könnte die ausgesprochen große Effektstärke verzerrt sein.
Die Trim-and-Fill Methode wird verwendet, um zu bestimmen, wie viel Studien hinzugenommen (fill) oder entfernt werden (Trim) müssten werden müssten, damit der Funnel-Plot symmetrisch ist. Die Methode kann auch verwendet werden, um einen (um einen möglichen Publication-Bias) bereinigten Effekt zu schätzen. Es gibt verschiedene Schätzmethoden, um die Anzahl an Studien, die Fehlen, zu schätzen. Wenn wir uns die Hilfe der Funktion ?trimfill anschauen, steht dort “Three different estimators for the number of missing studies were proposed by Duval and Tweedie (2000a, 2000b). Based on these articles and Duval (2005), ”R0” and ”L0” are recommended. An advantage of estimator ”R0” is that it provides a test of the null hypothesis that the number of missing studies (on the chosen side) is zero.”. Aus diesem Grund verwenden wir estimator = "R0":
trimfill(REM, estimator = "R0")##
## Estimated number of missing studies on the right side: 6 (SE = 3.7417)
## Test of H0: no missing studies on the right side: p-val = 0.0078
##
## Random-Effects Model (k = 77; tau^2 estimator: REML)
##
## tau^2 (estimated amount of total heterogeneity): 2.5002 (SE = 0.4122)
## tau (square root of estimated tau^2 value): 1.5812
## I^2 (total heterogeneity / total variability): 99.96%
## H^2 (total variability / sampling variability): 2343.39
##
## Test for Heterogeneity:
## Q(df = 76) = 20128.0649, p-val < .0001
##
## Model Results:
##
## estimate se zval pval ci.lb ci.ub
## -1.7697 0.1817 -9.7400 <.0001 -2.1258 -1.4136 ***
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Die Funktion bestimmt selbst, auf welcher Seite mögliche fehlende (nicht publizierte) Werte ergänzt werden sollten. Der Output sieht dem REM sehr ähnlich. In den ersten beiden Zeilen steht:
##
## Estimated number of missing studies on the right side: 6 (SE = 3.7417)
## Test of H0: no missing studies on the right side: p-val = 0.0078
## Es werden also 6 Studien ergänzt. Der p-Wert ist mit 0.0078 kleiner als .05, was bedeutet, dass die geschätzte Anzahl an ergänzten Stichproben auch in der Population (mit einer Irrtumswahrscheinlichkeit von 5%) von 0 abweicht und somit eine Einschränkung der beobachteten Studien vorliegt. Es könnte sich hierbei also um einen Publikationsbias handeln.
Der weitere Output hat sich deutlich verändert. Der mittlere Effekt ist etwas weniger stark negativ (-2.05 vs. -1.77). Wenn wir nun wieder die funnel-Funktion darauf anwenden, sehen wir auch, welche Studien hinzugefügt wurden:
funnel(trimfill(REM, estimator = "R0"))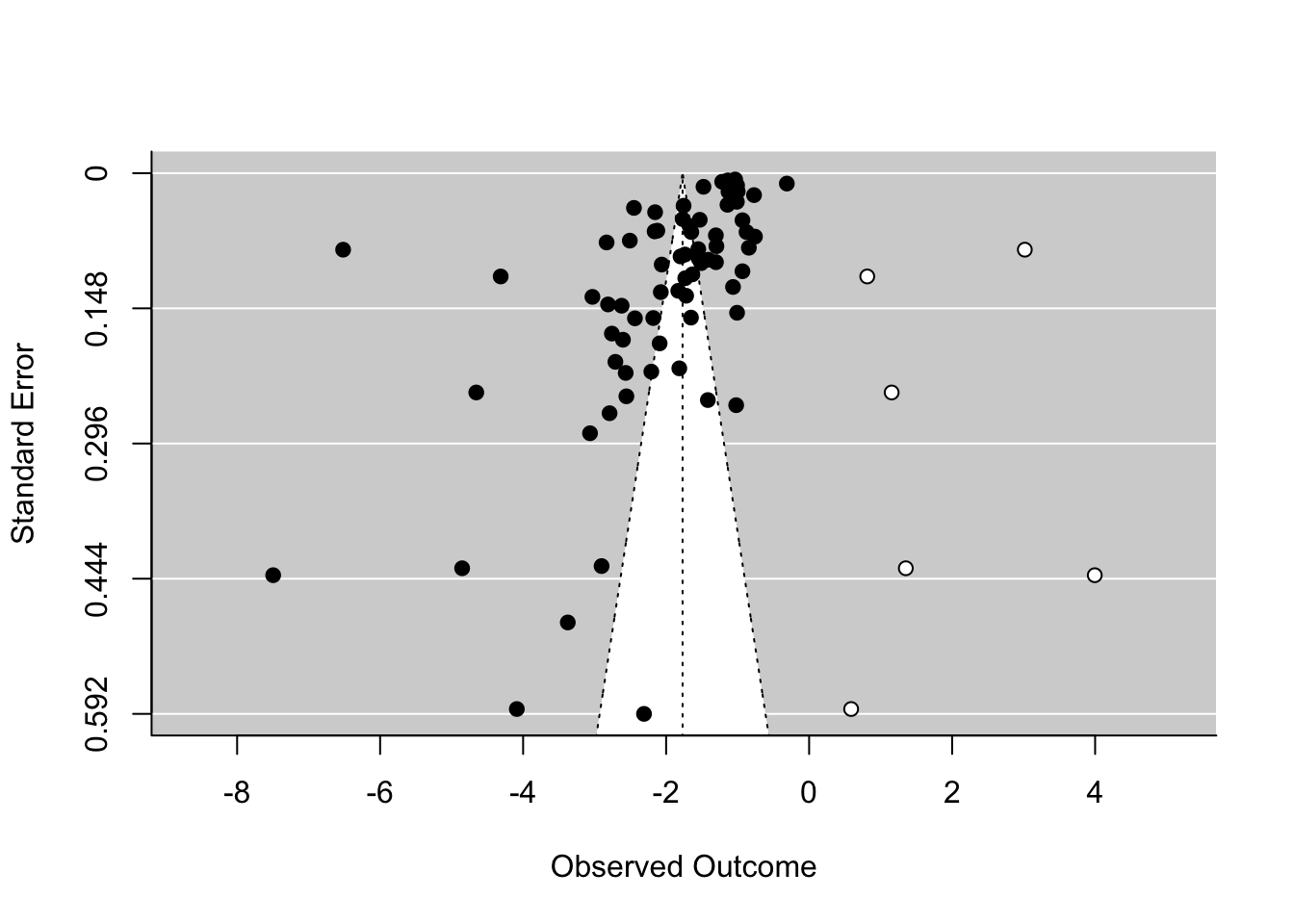
Wir sehen, dass die 6 Studien ziemlich weit auf der rechten Seite eingefügt wurden, was auch erklärt, warum sich die mittleren Effekte unterscheiden. Der geschätzte Effekt mittels Trim-and-Fill ist kleiner geworden! Wir gehen somit insgesamt davon aus, dass kein Publication Bias vorliegt und verwerfen die eben betrachteten Trim-and-Fill-Ergebnisse. Es könnte nun mit diesem Modell weitergerechnet werden. Wir verbleiben aber beim nicht befüllten Modell.
Forest-Plot
Auch Forest-Plots funktionieren auf die gleiche Weise mit der forest-Funktion. Der Forest-Plot stellt die unterschiedlichen Studien hinsichtlich ihrer Parameterschätzung (Effektstärken) und die zugehörige Streuung grafisch dar. So können beispielsweise Studien identifiziert werden, welche besonders hohe oder niedrige Werte aufweisen oder solche, die eine besonders große oder kleine Streuung zeigen.
# forest plot
forest(REM)
Wir sehen sehr deutlich, dass alle Studien Konfidenzintervalle aufweisen, die die Null nicht einschließen. Auch ein kumulativer Forest-Plot wäre möglich. Dazu müssen wir auf unser REM-Objekt noch die Funktion cumul.rma.uni anwenden:
# kumulativer Forest Plot
forest(cumul.rma.uni(REM))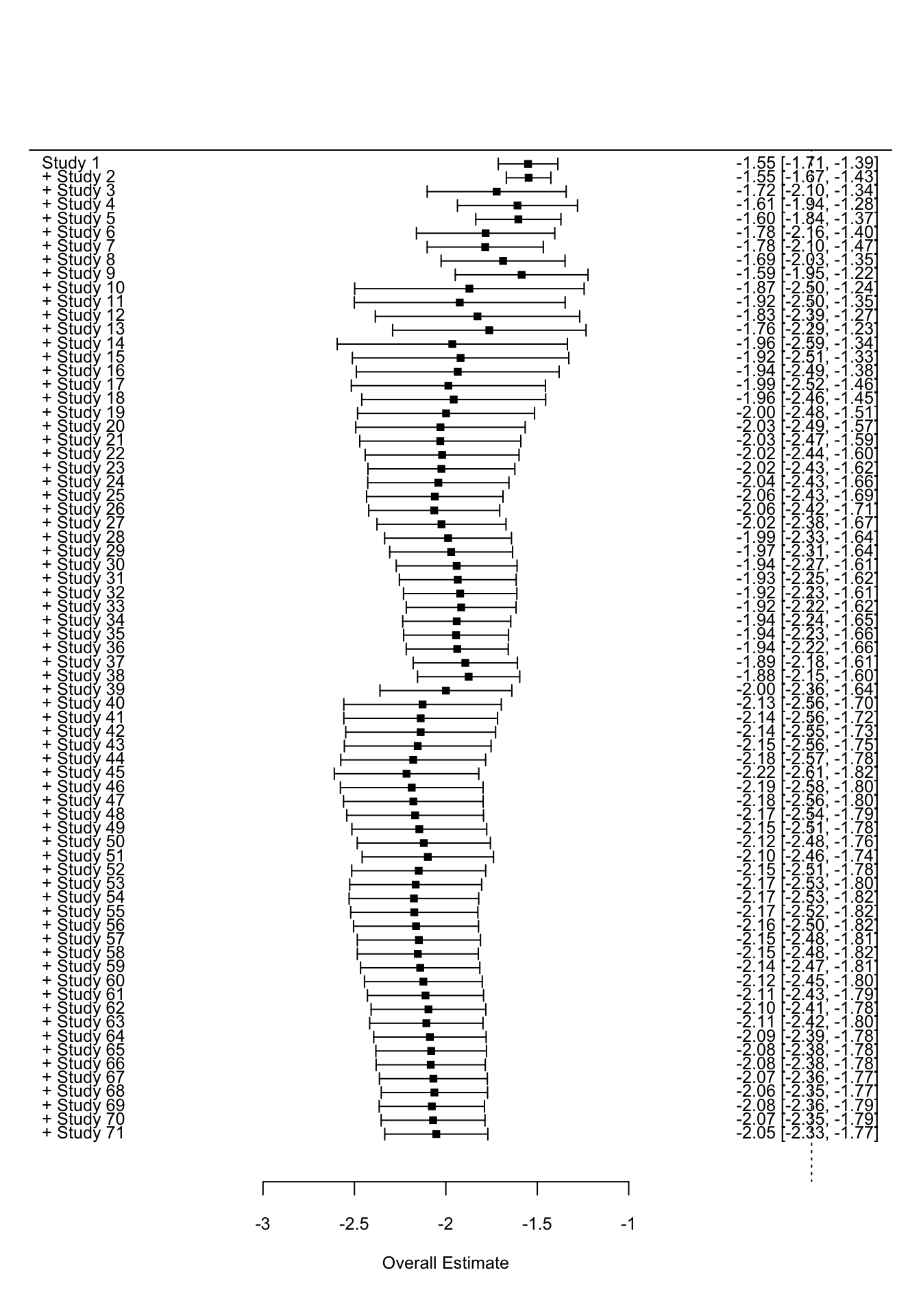
Die Funktion cumul.rma.uni führt skuzessive immer wieder eine Metaanalyse durch, wobei nach und nach eine Studie hinzugefügt wird. Anders als beim ersten Forest-Plot wird immer das Ergebnis der jeweiligen Metaanalyse dargestellt und nicht jede Studie einzeln. Wir sehen, dass sich sowohl mittlere Effektstärke als auch Streuung von oben nach unten einpendeln. Das finale Ergebnis ist identisch mit unserer Metaanalyse. Die gestrichelte Linie der Forest-Plots symbolisiert die 0, da in den meisten Fällen gegen 0 getestet wird und es daher von Interesse ist, wie viele Studien sich von 0 unterscheiden und ob sich der mittlere Effekt von 0 unterscheidet. Die Achsenbeschriftung unterscheidet sich, sodass die beiden Forest-Plots nicht ideal vergleichbar sind. Mit dem Zusatzargument xlim können wir die x-Achse explizit einstellen:
# kumulativer Forest Plot
forest(cumul.rma.uni(REM), xlim = c(-10, 2)) Nun sehen wir schöner, wie gut sich die Ergebnisse um den mittleren Wert einpendeln.
Nun sehen wir schöner, wie gut sich die Ergebnisse um den mittleren Wert einpendeln.
Insgesamt zeigen uns die Plots, dass von einem stabilen Effekt ausgegangen werden kann.
Moderatormodell
Im Random-Effects-Modell hatten wir bemerkt, dass erhebliche Heterogenität in den Daten herrscht. Diese Heterogenität zwischen den Studien lässt sich mit einem Moderatormodell untersuchen. Hier wird quasi eine Regressionsgleichung zwischen Studien aufgestellt, um die Heterogenitätsvarianz zu erklären.
Hingegen würde es keinen Sinn ergeben, ein Moderatormodell aufzustellen, wenn es keine von Null verschiedene Heterogenitätsvariabilität gibt!
Moderatormodell: Modellgleichung
Die Modellgleichung wird um die Moderatoren (Variablen die die Variation zwischen Studien erklären sollen) erweitert.
wobei der durchschnittliche Effekt ist, wenn alle Moderatoren den Wert 0 annehmen (also das Interzept - Zentrierung der Moderatoren ist sehr wichtig für die Interpretation!), ist der Moderatoreffekt des -ten Moderators , ist wieder eine Variable die die verbleibende Heterogenitätsvarianz beschreibt und ist das Residuum.
Moderatormodell: metafor
Augenscheinlich würde für die intensity der Therapie Sinn ergeben, dass sie für Heterogenität zwischen den Studien sorgt. Zunächst muss diese Variable zentriert werden, damit der durchschnittliche bedingte Effekt sinnvoll interpretierbar bleibt. Wir überschreiben die Ursprungsvariable.
F2F_CBT$intensity <- scale(F2F_CBT$intensity, center = T, scale = F) # nur zentrierenWir stellen ein Modell auf (hierbei müssen die Moderatoren, wie in einer normalen Regressionsanlyse mit einer Formel eingegeben werden; diese Formel wird dem Argument mods übergeben) und lassen dieses diesmal mit “ML” schätzen, um später einen geeigneten Modellvergleich durchführen zu können:
MEM1 <- rma(yi = diff, sei = se, data = F2F_CBT,
mods =~ intensity,
method = "ML")## Warning: Studies with NAs omitted from model fitting.summary(MEM1)##
## Mixed-Effects Model (k = 61; tau^2 estimator: ML)
##
## logLik deviance AIC BIC AICc
## -99.6787 375.9617 205.3574 211.6901 205.7785
##
## tau^2 (estimated amount of residual heterogeneity): 1.4485 (SE = 0.2686)
## tau (square root of estimated tau^2 value): 1.2035
## I^2 (residual heterogeneity / unaccounted variability): 99.91%
## H^2 (unaccounted variability / sampling variability): 1135.43
## R^2 (amount of heterogeneity accounted for): 3.05%
##
## Test for Residual Heterogeneity:
## QE(df = 59) = 10944.1843, p-val < .0001
##
## Test of Moderators (coefficient 2):
## QM(df = 1) = 1.6842, p-val = 0.1944
##
## Model Results:
##
## estimate se zval pval ci.lb ci.ub
## intrcpt -2.1560 0.1560 -13.8172 <.0001 -2.4618 -1.8501 ***
## intensity -0.0517 0.0398 -1.2978 0.1944 -0.1298 0.0264
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Uns wird eine “Warning” ausgegeben: Warning: Studies with NAs omitted from model fitting. Diese bedeutet, dass nicht alle Studien zu allen Moderatoren Angaben haben. Für jetzt ignorieren wir diesen Sachverhalt gekonnt.
Die summary wird um einen erklärten Varianzanteil
## R^2 (amount of heterogeneity accounted for): 3.05%sowie um einen Omnibustest der Moderatoren erweitert (quasi F-Test des gesamten Modells aus der Regression, nur dass hier -verteilt ist).
## Test of Moderators (coefficient 2):
## QM(df = 1) = 1.6842, p-val = 0.1944Der Moderator scheint keinen signifikanten Heterogenitätsvarianzanteile zu erklären ( 1.68, , 0.1944). Insgesamt werden nur Heterogenitätsvariation durch die Intensität erklärt. Unter
## Model Results:findet sich ein Output, der einem Regressionsoutput sehr ähnlich sieht. intrcpt ist das Interzept und damit der durchschnittliche Effekt, wenn die intensity den Wert 0 annimmt. Der Effekt von intensity ist nicht statistisch bedeutsam.
Wir nehmen zusätzlich die Moderatoren Psychoedukation (psed, Dummy-Variable, 0 = nein, 1 = ja), soziales Kompetenztraining (soc, Dummy-Variable, 0 = nein, 1 = ja), Verhaltensaktivierung (ba, Dummy-Variable, 0 = nein, 1 = ja) und Hausaufgaben (home, Dummy-Variable, 0 = nein, 1 = ja) in das Modell mit auf. Zunächst wandeln wir die Variablen als Factor um und geben den Ausprägungen sinnvolle Label:
# factors erzeugen und den Ausprägungen Labels geben:
F2F_CBT$psed <- factor(F2F_CBT$psed, levels = c(0, 1), labels = c("no", "yes"))
F2F_CBT$soc <- factor(F2F_CBT$soc, levels = c(0, 1), labels = c("no", "yes"))
F2F_CBT$ba <- factor(F2F_CBT$ba, levels = c(0, 1), labels = c("no", "yes"))
F2F_CBT$home <- factor(F2F_CBT$home, levels = c(0, 1), labels = c("no", "yes"))Das haben wir gemacht, um sicherzustellen, dass wir die Ergebnisse auch richtig interpretieren. Das Modell wird nun um diese vier Variablen erweitert:
MEM2 <- rma(yi = diff, sei = se, data = F2F_CBT,
mods =~ intensity + psed + soc + ba + home,
method = "ML")## Warning: Studies with NAs omitted from model fitting.summary(MEM2)##
## Mixed-Effects Model (k = 61; tau^2 estimator: ML)
##
## logLik deviance AIC BIC AICc
## -89.7698 356.1439 193.5397 208.3158 195.6529
##
## tau^2 (estimated amount of residual heterogeneity): 1.0327 (SE = 0.1931)
## tau (square root of estimated tau^2 value): 1.0162
## I^2 (residual heterogeneity / unaccounted variability): 99.75%
## H^2 (unaccounted variability / sampling variability): 407.62
## R^2 (amount of heterogeneity accounted for): 30.88%
##
## Test for Residual Heterogeneity:
## QE(df = 55) = 7042.6184, p-val < .0001
##
## Test of Moderators (coefficients 2:6):
## QM(df = 5) = 25.6159, p-val = 0.0001
##
## Model Results:
##
## estimate se zval pval ci.lb ci.ub
## intrcpt -2.8435 0.2350 -12.0980 <.0001 -3.3042 -2.3829 ***
## intensity -0.0879 0.0352 -2.5002 0.0124 -0.1568 -0.0190 *
## psedyes 0.7806 0.2941 2.6543 0.0079 0.2042 1.3570 **
## socyes 0.0341 0.3883 0.0878 0.9301 -0.7270 0.7952
## bayes 0.8994 0.3016 2.9823 0.0029 0.3083 1.4905 **
## homeyes -0.5052 0.3124 -1.6173 0.1058 -1.1174 0.1070
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Das Ergebnis sieht nun anders aus. Der Omnibustest zeigt an, dass die 5 Prädiktoren gemeinsam signifikante Varianzanteile erklären ( 25.62, , 0.0001). Insgesamt können 30.88% der Heterogenitätsvariation durch die Prädiktoren erklärt werden. Der Effekt der Intensität ist nun bedeutsam ( -0.09, 0.04, 0.0124). Auch die Psychoedukation ( 0.78, 0.29, 0.0079) und Verhaltensaktivierung ( 0.9, 0.3, 0.0029) trugen zu Unterschieden zwischen den Studien bei. Ob soziale Kompetenztrainings durchgeführt ( 0.03, 0.39, 0.9301) oder ob Hausaufgaben aufgegeben wurden ( -0.51, 0.31, 0.1058), führte zu keiner Heterogenität zwischen den Studien.
Der Effekt der Intensität erscheint plausibel. Je intensiver die Betreuung, desto besser das Ergebnis. Erstaunlich ist, dass Verhaltensaktivierung und Psychoedukation zu einer niedrigeren Verbesserung von Prä zu Post führten. Dies könnte (Achtung Interpretation!) allerdings daran liegen, dass Studien, die so ins Detail gehen, vielleicht grundsätzlich “sauberer” durchgeführt wurden, was zu ggf. kleineren Effekten geführt haben könnte.
Zwei Moderatormodelle lassen sich leicht mit der anova-Funktion inferenzstatistisch vergleichen: Wir führen wie folgt einen Likelihood-Ratio-Test durch
anova(MEM1, MEM2, test = "LRT")##
## df AIC BIC AICc logLik LRT pval QE tau^2
## Full 7 193.5397 208.3158 195.6529 -89.7698 7042.6184 1.0327
## Reduced 3 205.3574 211.6901 205.7785 -99.6787 19.8178 0.0005 10944.1843 1.4485
## R^2
## Full
## Reduced 28.7015%Der Modellvergleich ist statistisch bedeutsam ( 19.82, 0.0005). Somit passt das restriktivere Modell mit nur einem Prädiktor signifikant schlechter zu den Daten. Wir entscheiden uns für das Modell mit 5 Prädiktoren, welches insgesamt mehr Heterogenitätsvariation erklärt als das Modell mit nur der Intensität als Moderator. Die Heterogenitätvarianz reduziert sich von auf durch Hinzunahme der vier Prädiktoren.
Mit Hilfe der reporter-Funktion lässt sich ein Mini-Report anfordern, der die Analyse beschreibt. Natürlich kann dieser nicht komplett übernommen werden, er hilft aber bei der Einordnung mancher Effekte. Außerdem können wir so prüfen, ob alles so ist, wie wir es erwarten würden. In diesem Report werden auch noch weitere Statistiken aufgeführt, wie beispielsweise geprüft werden kann, ob der Funnel-Plot asymmetrisch ist.
reporter(REM)Für MEM (Moderator-Analysen) ist diese Funktion leider noch nicht ausgebaut.
Literatur
Döring, N., & Bortz, J. (2016). Meta-Analyse. In Forschungsmethoden und Evaluation in den Sozial- und Humanwissenschaften (pp. 893-943). Springer, Berlin, Heidelberg.
López-López, J. A., Davies, S. R., Caldwell, D. M., Churchill, R., Peters, T. J., Tallon, D., Dawson, S., Wu, Q., Li, J., Taylor, A., Lewis, G., Kessler, D. S., Wiles, N., & Welton, N. J. (2019). The process and delivery of CBT for depression in adults: A systematic review and network meta-analysis. Psychological Medicine, 49(12), 1937–1947. https://doi.org/10.1017/S003329171900120X
Viechtbauer, W. (2010). Conducting meta-analyses in R with the metafor package. Journal of Statistical Software, 36(3), 1–48. https://www.jstatsoft.org/v036/i03.
- Blau hinterlegte Autor:innenangaben führen Sie direkt zur universitätsinternen Ressource.
