Modelle für Gruppenvergleiche
Multi Sample Analysis
In einer Multi-Sample-Analysis wird in mehreren Gruppen gleichzeitig ein Strukturgleichungsmodell geschätzt. Wir könnten uns bspw. fragen, ob die gleichen Beziehungen zwischen Zeitdruck, Emotionaler Erschöpfung und psychosomatischen Beschwerden, wie wir sie in der letzten Sitzung zu SEM beobachtet haben, gleichermaßen für Männer und Frauen gelten. Im Datensatz StressAtWork der SEM Sitzung ist die Variable sex enthalten. Hier sind Frauen mit 1 und Männer mit 2 kodiert. Wir können diesen wie gewohnt laden:
Sie können den im Folgenden verwendeten Datensatz “StressAtWork.rda” hier herunterladen.
Wir laden zunächst die Daten: entweder lokal von Ihrem Rechner:
load("C:/Users/Musterfrau/Desktop/StressAtWork.rda")oder wir laden sie direkt über die Website:
load(url("https://pandar.netlify.app/post/StressAtWork.rda"))Als Paket brauchen wir erneut lavaan und semPlot:
library(lavaan)
library(semPlot)Wir verwenden das gleiche Modell wie in der vorherigen Sitzung zu SEM für die Variablen Zeitdruck, emotionale Erschöpfung und psychosomatische Beschwerden (als manifesten Skalenmittelwert, siehe dazu die Diskussion zu reflexiven vs. formativen Messmodellen in der Sitzung zu SEM), welches so aussah (für Details, wie etwa das erstellen der Skalenmittelwerte für BFs schaue gerne nochmal in der vorherigen Sitzung zu SEM vorbei):
StressAtWork$BFs <- rowMeans(StressAtWork[,paste0("bf",1:20)])
model_sem <- '
# Messmodelle
ZD =~ zd1 + zd2 + zd6
BOEE =~ bo1 + bo6 + bo12 + bo19
# Strukturmodell
BOEE ~ ZD
BFs ~ BOEE + ZD
'
fit_sem <- sem(model_sem, StressAtWork)
semPaths(object = fit_sem, what = "model", layout = "tree2",
rotation = 2, curve = T, col = list(man = "skyblue", lat = "yellow"),
curvePivot = T, edge.label.cex=1.2, sizeMan = 5, sizeLat = 8)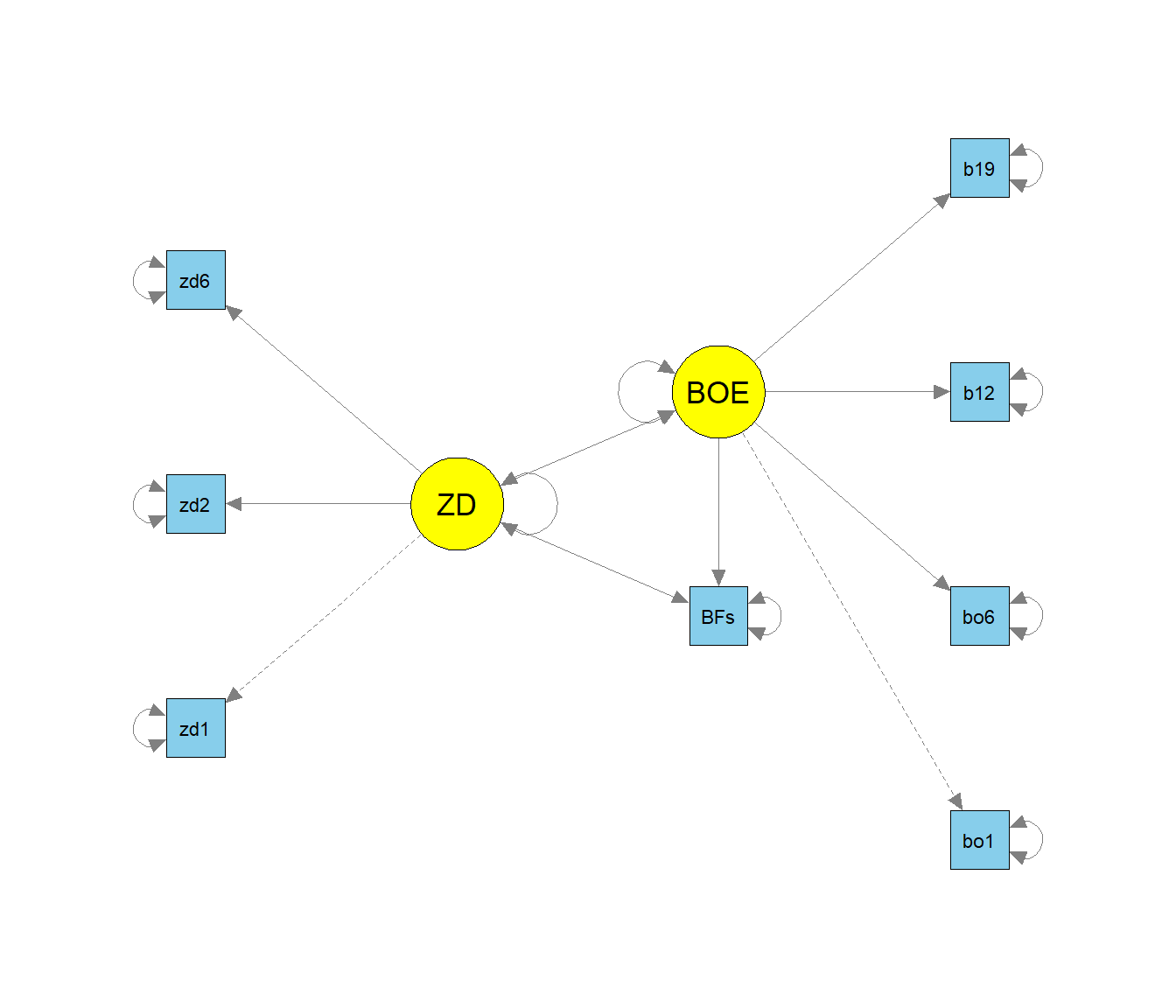
Wenn wir die Variable Geschlecht als Gruppierung verwenden, können wir die Invarianz der Parameter über das Geschlecht untersuchen. Um die Gruppierung in das Modell mit aufzunehmen, können wir in sem einfach dem Argument group den Namen der Gruppierungsvariable übergeben (hierbei sind die “Gänsefüßchen” wichtig!).
fit_sem_MSA <- sem(model_sem, data = StressAtWork, group = "sex")
summary(fit_sem_MSA)Wir sehen, dass im Output nun für jede Gruppe das Modell einzeln geschätzt wurde. Alle Parameter werden sowohl für Frauen, als auch für Männer geschätzt. Wir entnehmen,
## [...]
## Number of observations per group:
## 1 225
## 2 80
## [...]… dass insgesamt 225 der Probanden Frauen und 80 Männer waren. Auch erhalten wir einen globalen sowie einen substichprobenspezifischen Modellfitwert:
## [...]
## Model Test User Model:
##
## Test statistic 35.803
## Degrees of freedom 36
## P-value (Chi-square) 0.478
## Test statistic for each group:
## 1 21.400
## 2 14.403
## [...]Der \(\chi^2\)-Wert für das gesamte Modell liegt bei 35.803 bei \(df=\) 36 mit zugehörigem \(p\)-Wert von 0.478. Demnach verwerfen unsere Daten das Modell nicht. Die Freiheitsgrade sind doppelt so hoch, wie im Ein-Stichprobenfall, da wir alle Parameter für beide Stichproben schätzen müssen. Die \(\chi^2\)-Werte der beiden Stichproben waren 21.400 für die Frauen und 14.403 für die Männer. Der \(\chi^2\)-Wert für das gesamte Modell ist also einfach die Summe der subpopulationsspezifischen \(\chi_g^2\)-Werte (wobei \(g=1\) und \(g=2\) für die erste und zweite Gruppe steht): \[\chi^2=\chi^2_{1}+\chi^2_{2}.\] Wenn wir uns jetzt die Ergebnisse des Modells etwas genauer ansehen, erhalten wir für jede Gruppe eine detaillierte Ausgabe:
## [...]
## Group 1 [1]:
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## ZD =~
## zd1 1.000
## zd2 0.861 0.073 11.853 0.000
## zd6 0.830 0.068 12.214 0.000
## BOEE =~
## bo1 1.000
## bo6 0.900 0.063 14.356 0.000
## bo12 0.936 0.067 14.011 0.000
## bo19 1.033 0.070 14.667 0.000
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## BOEE ~
## ZD 0.499 0.087 5.751 0.000
## BFs ~
## BOEE 0.348 0.041 8.548 0.000
## ZD 0.049 0.046 1.072 0.284
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|)
## .zd1 3.622 0.083 43.758 0.000
## .zd2 3.093 0.083 37.148 0.000
## .zd6 3.849 0.078 49.598 0.000
## .bo1 2.991 0.099 30.280 0.000
## .bo6 2.258 0.095 23.659 0.000
## .bo12 2.262 0.101 22.418 0.000
## .bo19 2.582 0.108 23.905 0.000
## .BFs 2.486 0.050 49.238 0.000
## ZD 0.000
## .BOEE 0.000
## [...]## [...]
## Group 2 [2]:
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## ZD =~
## zd1 1.000
## zd2 0.682 0.123 5.555 0.000
## zd6 0.725 0.129 5.637 0.000
## BOEE =~
## bo1 1.000
## bo6 0.941 0.099 9.472 0.000
## bo12 1.011 0.106 9.525 0.000
## bo19 1.082 0.108 10.041 0.000
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## BOEE ~
## ZD 0.519 0.145 3.580 0.000
## BFs ~
## BOEE 0.418 0.059 7.108 0.000
## ZD 0.023 0.062 0.367 0.714
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|)
## .zd1 3.413 0.128 26.593 0.000
## .zd2 2.788 0.122 22.833 0.000
## .zd6 3.487 0.127 27.360 0.000
## .bo1 3.000 0.157 19.093 0.000
## .bo6 2.138 0.155 13.803 0.000
## .bo12 2.188 0.166 13.184 0.000
## .bo19 2.475 0.172 14.366 0.000
## .BFs 2.176 0.078 28.072 0.000
## ZD 0.000
## .BOEE 0.000
## [...]Uns fällt auf, dass sowohl die Faktorladungen, als auch die Pfadkoeffizienten sich kaum über die Gruppen hinweg unterscheiden. Da sich die Subpopulationen auch hinsichtlich der Mittelwerte unterscheiden können, werden diese nun per Default im Output mit ausgegeben (es ist also nicht mehr notwendig, mit meanstructure = TRUE zu arbeiten). Natürlich können sich die Subpopulationen auch in allen weiteren Koeffizienten unterscheiden.
Im Beitrag zu den Strukturgleichungsmodellen hatten wir Parameterlabel benutzt, um den indirekten Effekt als neuen Modellparameter bestimmen zu können. Da wir nun zwei Gruppen haben, müssen wir die Labels als Vektor schreiben, also bspw. BOEE ~ c(a1, a2)*ZD, um den Effekt der unabhängigen Variable auf den Mediator in den Gruppen jeweils a1 und a2 zu nennen.
Wir nutzen diese Schreibweise, um den indirekten Effekt sowohl für Frauen, als auch für Männer zu berechnen und erweitern unser Modell entsprechend:
model_sem_IE_TE_MSA <- '
# Messmodelle
ZD =~ zd1 + zd2 + zd6
BOEE =~ bo1 + bo6 + bo12 + bo19
# Strukturmodell
BOEE ~ c(a1, a2)*ZD
BFs ~ c(b1, b2)*BOEE + c(c1,c2)*ZD
# Neue Parameter
IE1 := a1*b1
TE1 := IE1 + c1
IE2 := a2*b2
TE2 := IE2 + c2
'
fit_sem_IE_TE_MSA <- sem(model_sem_IE_TE_MSA, StressAtWork, group = "sex")
summary(fit_sem_IE_TE_MSA)Nun sind alle Pfadkoeffizienten benannt. In Gruppe 1 (Frauen):
## [...]
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## BOEE ~
## ZD (a1) 0.499 0.087 5.751 0.000
## BFs ~
## BOEE (b1) 0.348 0.041 8.548 0.000
## ZD (c1) 0.049 0.046 1.072 0.284
## [...]Und in Gruppe 2 (Männer):
## [...]
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## BOEE ~
## ZD (a2) 0.519 0.145 3.580 0.000
## BFs ~
## BOEE (b2) 0.418 0.059 7.108 0.000
## ZD (c2) 0.023 0.062 0.367 0.714
## [...]Bis auf die hinzukommenden indirekten und totalen Effekte:
## [...]
## Defined Parameters:
## Estimate Std.Err z-value P(>|z|)
## IE1 0.174 0.035 4.938 0.000
## TE1 0.223 0.048 4.611 0.000
## IE2 0.217 0.065 3.320 0.001
## TE2 0.240 0.077 3.114 0.002
## [...]… hat sich nichts am Output geändert. Wir haben ja auch nur Labels vergeben und neu definierte Parameter hinzugefügt, die allerdings, wie im Beitrag zu SEM schon erwähnt, die Modellstruktur (und somit auch die \(df\)) nicht tangieren. Auch können wir die Modelle in den beiden Gruppen darstellen via (die Dreiecke haben eine 1 in der Mitte stehen und stellen die Mittelwertsstruktur dar, die Kante/das Gewicht eines Dreiecks auf bspw die manifesten Variablen stellt dann den Mittelwert dieser manifesten Variable dar):
semPaths(object = fit_sem_IE_TE_MSA, what = "est", layout = "tree2",
rotation = 2, curve = T, col = list(man = "skyblue", lat = "yellow"),
curvePivot = T, edge.label.cex=1, sizeMan = 5, sizeLat = 8, fade = F)
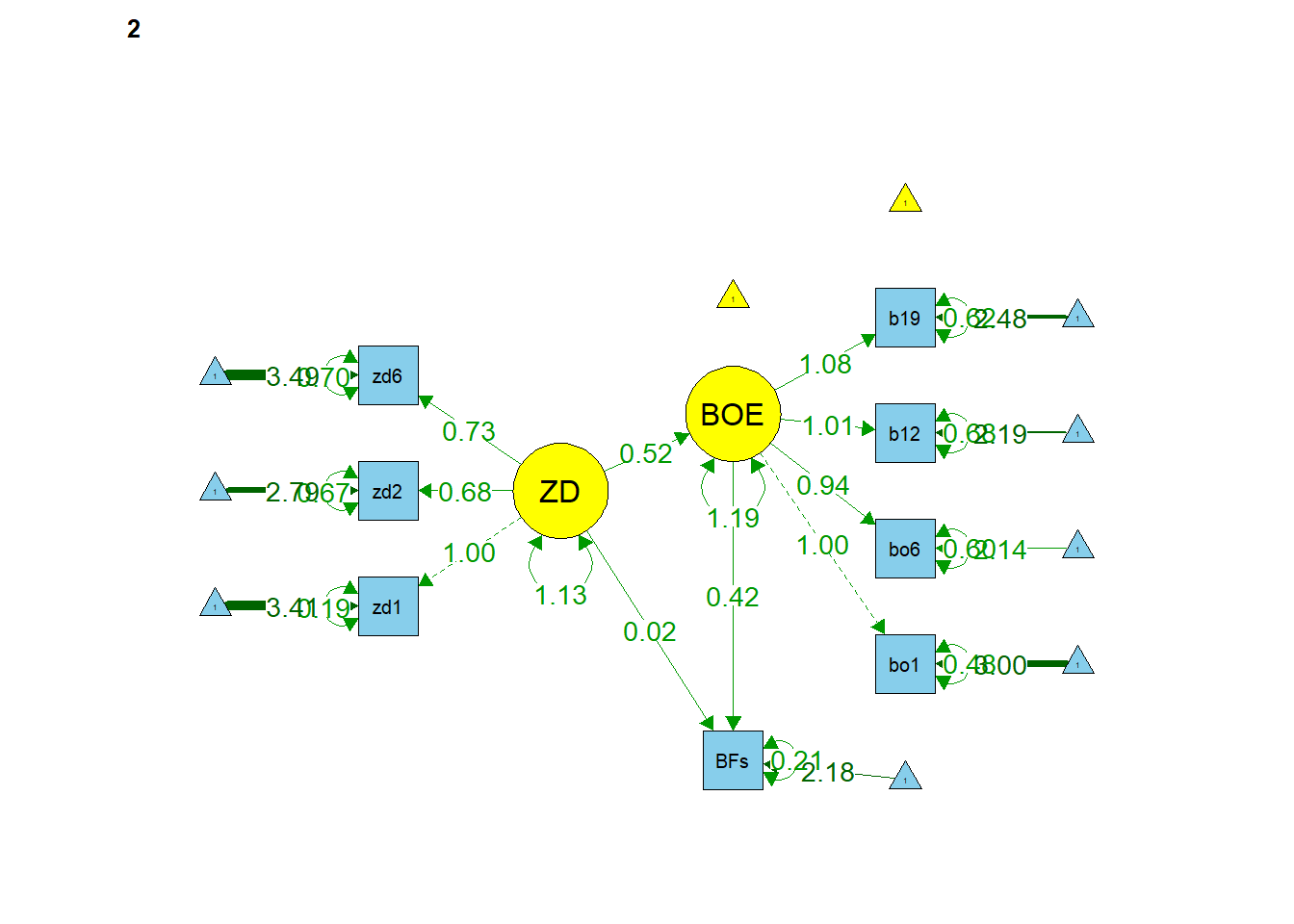
Die totalen und die indirekten Effekte müssten in einer wissenschaftlichen Untersuchung erneut mithilfe von Bootstrapping inferenzstatistisch geprüft werden. Diesen Schritt überlassen wir an dieser Stelle dem/der aufmerksamen Leser/in. Auch können die indirekten Effekte bspw. gegeneinander untersucht werden via Bootstrapping, indem die Differenz der Effekte als neuer Parameter definiert wird. Allerdings können wir auch mittels des \(\chi^2\)-Tests einen “richtigen” Invarianztest durchführen. Das schauen wir uns im Folgenden genauer an.
Invarianzstufen
Mit Invarianz meinen wir die Gleichheit von Parametern über Gruppen hinweg, also bspw., dass es keine Unterschiede über das Geschlecht hinweg gibt. Ein ähnliches Konzept hatten wir im Beitrag zur CFA schon einmal gesehen, als es im Appendix um die Hierarchie der Messmodelle ging. Welche Stufen der Invarianz es in der MSA gibt, was diese bedeuten und wie wir diese spezifizieren, gucken wir uns im Folgenden nochmal kurz an.
So wie wir die indirekten Effekte bestimmt und die Koeffizienten für beide Gruppen benannt haben, lassen sich auch Invarianzen händisch prüfen. Wenn zwei Koeffizienten das selbe Label tragen, werden diese Parameter in den Gruppen auf den gleichen Wert gesetzt. Wir könnten nun für die jeweiligen Invarianzstufen die Parameter händisch gleichsetzen. Dieses ganze Prozedere erscheint recht aufwendig. Allerdings kann so in jedem Schritt überprüft werden, dass die Parameter richtig restringiert wurden. Zudem lassen sich so auch leicht partielle Invarianzen einbauen, in welchen bspw. nicht alle Faktorladungen über die Gruppen hinweg gleich sind. Außerdem könnten Invarianzen nur für bestimmte Variablen angenommen werden. Diesen kompletten, händischen Prozess sehen Sie in Appendix A. Glücklicherweise enthält das lavaan-Paket aber Möglichkeiten, Invarianzen global zu definieren. Dazu müssen wir lediglich in der Schätzung unserer Modelle in sem das Zusatzargument group.equal spezifizieren. Für partielle Invarianzen gibt es zusätzlich group.partial. Bevor wir mit den Analysen beginnen, sehen Sie in der folgenden Tabelle noch einmal eine Übersicht über die Invarianzstufen. Eine detaillierte Wiederholung dessen, was auch in den inhaltlichen Sitzungen zu den Invarianzstufen behandelt wurde, finden Sie im Exkurs zu Invarianzstufen. Die beiden Spalten “Annahme” und “Implikation” sind kumulativ: Invarianzstufen, die weiter unten stehen, enthalten immer auch alle vorherigen Annahmen und erlauben auch immer alle vorherigen Aussagen. Die jeweiligen Einträge einer Zeile sind lediglich für diese Stufe zusätzlich.
| Invarianzstufe | Annahme | Implikation |
|---|---|---|
| konfigural | gleiche Modellstruktur | gleiche Konstruktdefinition |
| metrisch (schwach) | gleiche Faktorladungen | latente Variablen haben gleiche Bedeutung; Beziehungen zwischen latenten Variablen vergleichbar |
| skalar (stark) | gleiche Interzepte | mittlere Gruppenunterschiede in manifesten Variablen auf Unterschiede in latenten Mittelwerten zurückführbar; latente Mittelwerte vergleichbar |
| strikt | gleiche Residualvarianzen | Varianzunterschiede in manifesten Variablen auf Varianzunterschiede in latenten Varianzen zurückführbar |
Die zwei verschiedenen Bezeichnungstypen für die beiden mittleren Invarianzstufen (entweder schwach und stark oder metrisch und skalar) kommen aus unterschiedlichen Traditionen in der MSA Literatur und können austauschbar benutzt werden.
Probieren wir dies doch gleich einmal aus (das Modell sollte hierzu keine Parameterbenennungen haben, da diese die gloablen Invarianzeinstellungen in sem überschreiben könnten):
model_sem <- '
# Messmodelle
ZD =~ zd1 + zd2 + zd6
BOEE =~ bo1 + bo6 + bo12 + bo19
# Strukturmodell
BOEE ~ ZD
BFs ~ BOEE + ZD
'Um BFs hier wie eine latente Variable zu behandeln, müssen wir bestimmen, dass das Interzept und die Residualvarianz nicht mit den manifesten Variablen zusammen gleichgesetzt werden, sondern erst mit den latenten Variablen über die Gruppen restringiert werden (bei der Testung der vollständigen Invarianz). Dazu müssen wir zusätzlich die partielle Invarianzeinstellung verwenden: group.partial = c("BFs~1", "BFs~~BFs"). Hiermit wird bestimmt, welche Koeffizienten nicht von den Invarianzeinstellungen betroffen sein sollen. Auch wenn diese Einstellungen erst bei der skalaren/starken Invarianz ("BFs~1") und bei der strikten Invarianz ("BFs~~BFs") zum Tragen kommen, stellen wir diese auch beim konfigural-invarianten und beim metrisch-invarianten (schwach-invarianten) Modell mit ein, um aufzuzeigen, dass wir in jedem Punkt genau wissen, was wir tun. Fangen wir mit dem Fitten des konfigural-invarianten Modells an.
Konfigurale Invarianz
Bei der konfiguralen Invarianz geht es darum, dass in beiden Gruppen die gleichen Modelle aufgestellt werden. Gilt diese Annahme bereits nicht, so macht es keinen Sinn, das Modell weiter einzuschränken und Parameter über die Gruppen zu restringieren. Glücklicherweise passt das Modell zu den Daten, in welchem das Modell für das Geschlecht jeweils geschätzt wurde. Hier schauen wir uns dies noch einmal zur Wiederholung und zum Umbenennen des geschätzten Modells an und spezifizieren mit group.equal = c(""), dass keine Parameter über die Gruppen als identisch angenommen werden sollen:
fit_sem_sex_konfigural <- sem(model_sem, data = StressAtWork,
group = "sex",
group.equal = c(""),
group.partial = c("BFs~1", "BFs~~BFs"))
summary(fit_sem_sex_konfigural, fit.measures = T)Dem Modell-Fit Teil der Summary entnehmen wir, dass das Modell gut zu den Daten passt:
## [...]
## Model Test User Model:
##
## Test statistic 35.803
## Degrees of freedom 36
## P-value (Chi-square) 0.478
## Test statistic for each group:
## 1 21.400
## 2 14.403
##
## Model Test Baseline Model:
##
## Test statistic 1325.901
## Degrees of freedom 56
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 1.000
## Tucker-Lewis Index (TLI) 1.000
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -3377.320
## Loglikelihood unrestricted model (H1) -3359.418
##
## Akaike (AIC) 6858.639
## Bayesian (BIC) 7052.095
## Sample-size adjusted Bayesian (BIC) 6887.176
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.000
## 90 Percent confidence interval - lower 0.000
## 90 Percent confidence interval - upper 0.057
## P-value RMSEA <= 0.05 0.902
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.031
## [...]Der \(\chi^2\)-Wert ist nicht signifikant und auch die Fit-Indizes CFI, TLI, RMSEA und SRMR sind unauffällig und deuten auf guten Modell-Fit hin. Dies bedeutet, dass wir frohen Mutes das Modell einschränken können, um zu prüfen, welche Invarianz über das Geschlecht hinweg gilt.
Metrische Invarianz
Unter metrischer oder schwacher Invarianz verstehen wir, dass die Faktorladungen (\(\lambda\), bzw. \(\Lambda\)) über die Gruppen hinweg gleich sind. Somit ist der Anteil jedes Items, der auf die latenten Variablen zurückzuführen ist, über die Gruppen hinweg gleich. Dies ist wichtig, um zu prüfen, ob die Konstrukte über die beiden Gruppen hinweg die gleiche Bedeutung haben. Wir erreichen dies, indem wir group.equal = c("loadings") spezifizieren.
fit_sem_sex_metrisch <- sem(model_sem, data = StressAtWork,
group = "sex",
group.equal = c("loadings"),
group.partial = c("BFs~1", "BFs~~BFs"))
summary(fit_sem_sex_metrisch, fit.measures = T)Wir entnehmen,
## [...]
## Model Test User Model:
##
## Test statistic 37.543
## Degrees of freedom 41
## P-value (Chi-square) 0.625
## Test statistic for each group:
## 1 21.770
## 2 15.773
##
## Model Test Baseline Model:
##
## Test statistic 1325.901
## Degrees of freedom 56
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 1.000
## Tucker-Lewis Index (TLI) 1.004
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -3378.190
## Loglikelihood unrestricted model (H1) -3359.418
##
## Akaike (AIC) 6850.380
## Bayesian (BIC) 7025.234
## Sample-size adjusted Bayesian (BIC) 6876.173
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.000
## 90 Percent confidence interval - lower 0.000
## 90 Percent confidence interval - upper 0.048
## P-value RMSEA <= 0.05 0.958
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.035
## [...]… dass das Modell immer noch gut zu den Daten passt. Die Frage ist nur, ob das metrisch-invariante Modell nicht doch vielleicht signifikant schlechter zu den Daten passt als das konfigural-invariante Modell. Bevor wir dieser Frage nachgehen, schauen wir uns noch schnell an, wie Parameter hier per Default benannt werden:
## [...]
## Group 1 [1]:
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## ZD =~
## zd1 1.000
## zd2 (.p2.) 0.826 0.063 13.119 0.000
## zd6 (.p3.) 0.813 0.060 13.496 0.000
## BOEE =~
## bo1 1.000
## bo6 (.p5.) 0.912 0.053 17.191 0.000
## bo12 (.p6.) 0.959 0.057 16.955 0.000
## bo19 (.p7.) 1.048 0.059 17.780 0.000
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## BOEE ~
## ZD 0.481 0.084 5.764 0.000
## BFs ~
## BOEE 0.353 0.041 8.703 0.000
## ZD 0.048 0.045 1.073 0.283
## [...]## [...]
## Group 2 [2]:
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## ZD =~
## zd1 1.000
## zd2 (.p2.) 0.826 0.063 13.119 0.000
## zd6 (.p3.) 0.813 0.060 13.496 0.000
## BOEE =~
## bo1 1.000
## bo6 (.p5.) 0.912 0.053 17.191 0.000
## bo12 (.p6.) 0.959 0.057 16.955 0.000
## bo19 (.p7.) 1.048 0.059 17.780 0.000
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## BOEE ~
## ZD 0.581 0.153 3.795 0.000
## BFs ~
## BOEE 0.412 0.054 7.576 0.000
## ZD 0.013 0.069 0.193 0.847
## [...]Wir erkennen, dass “einfach” nur die Parameter durchnummeriert werden, wobei Parameter, die auf 1 restringiert sind, mitgezählt werden, aber nicht ihr eigenes Label erhalten. So heißt \(\lambda_{21}^x\), der Ladungskoeffizient von zd2, hier .p2., wobei das p für Parameter steht und die Punkte andeuten, dass es sich hierbei um ein intern vergebenes (also ein durch die Funktion selbst vergebenes) Label handelt. Wollen wir nun wissen, ob sich die Modelle statistisch signifikant voneinander unterscheiden, können wir wieder den Likelihood-Ratio-Test (\(\chi^2\)-Differenzentest) heranziehen.
lavTestLRT(fit_sem_sex_metrisch, fit_sem_sex_konfigural)## Chi-Squared Difference Test
##
## Df AIC BIC Chisq Chisq diff Df diff Pr(>Chisq)
## fit_sem_sex_konfigural 36 6858.6 7052.1 35.803
## fit_sem_sex_metrisch 41 6850.4 7025.2 37.543 1.7405 5 0.8838Die \(\chi^2\)-Differenz liegt bei 1.7405 bei \(\Delta df=\) 5 mit dem zugehörigen \(p\)-Wert von 0.8838 (die Null-Hypothese war: \(H_0: \Sigma_{konfigural}=\Sigma_{metrisch}\)). Das metrische Modell ist hier das restriktivere, da Koeffizienten gleichgesetzt wurden. Weil es keine signifikanten Unterschiede zwischen den Modellen gibt, entscheiden wir uns — Ockhams Rasiermesser folgend (siehe Eid et al., 2017, p. 787) — für das sparsamere Modell, also jenes, welches weniger Parameter enthält und somit restriktiver ist, hier: das metrisch-invariante Modell. Somit können wir weiter von metrischer Invarianz ausgehen. Dies bedeutet, dass sich Unterschiede zwischen Frauen auf der latenten Variable in gleicher Weise in den beobachtbaren Variablen niederschlagen, wie sie es bei Männern tun.
Skalare Invarianz
Als nächstes wollen wir prüfen, ob zusätzlich zu den Faktorladungen auch die Interzepte (\(\tau\)) über die Gruppen hinweg gleich sind (insgesamt also \(\lambda\)s und \(\tau\)s gleich über die Gruppen hinweg). Dazu passen wir erneut unser Modell an. Hierbei ist zu beachten, dass wir nicht das Interzept von BFs über die Gruppen hinweg gleichsetzen, da sich die Interzepte auf die manifesten Variablen beziehen, wir BFs hier allerdings wie eine latente Variable behandeln wollen, bzw. diese zu einer der Variablen der Strukturgleichung zählen wollen. Dazu haben wir die group.partial = c("BFs~1", "BFs~~BFs") Einstellungen verwendet. Eine Besonderheit der skalaren Invarianz ist, dass wir, sobald wir die Interzepte über die Gruppen hinweg gleichsetzen, die Freiheitsgrade haben, mit welchen wir die latenten Interzepte von ZD und BOEE schätzen können. Dies ist dann eine Art Effektkodierung, wobei der Mittelwert der einen Gruppe auf 0 gesetzt und in der anderen Gruppe dann die Abweichung zu dieser Gruppe mitgeführt wird. Andernfalls würden wir fälschlicherweise Invarianz der latenten Mittelwerte annehmen, was wir hier noch gar nicht prüfen wollen! Wir schauen uns dies im Output an.
fit_sem_sex_skalar <- sem(model_sem, data = StressAtWork,
group = "sex",
group.equal = c("loadings", "intercepts"),
group.partial = c("BFs~1", "BFs~~BFs"))
summary(fit_sem_sex_skalar, fit.measures = T)## [...]
## Group 1 [1]:
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## ZD =~
## zd1 1.000
## zd2 (.p2.) 0.841 0.063 13.321 0.000
## zd6 (.p3.) 0.829 0.061 13.682 0.000
## BOEE =~
## bo1 1.000
## bo6 (.p5.) 0.913 0.053 17.171 0.000
## bo12 (.p6.) 0.961 0.057 16.943 0.000
## bo19 (.p7.) 1.050 0.059 17.764 0.000
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## BOEE ~
## ZD 0.488 0.084 5.792 0.000
## BFs ~
## BOEE 0.353 0.041 8.683 0.000
## ZD 0.048 0.045 1.070 0.284
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|)
## .zd1 (.21.) 3.644 0.082 44.440 0.000
## .zd2 (.22.) 3.075 0.079 39.155 0.000
## .zd6 (.23.) 3.822 0.075 50.822 0.000
## .bo1 (.24.) 3.014 0.095 31.582 0.000
## .bo6 (.25.) 2.240 0.092 24.481 0.000
## .bo12 (.26.) 2.259 0.097 23.304 0.000
## .bo19 (.27.) 2.570 0.104 24.790 0.000
## .BFs 2.486 0.050 49.238 0.000
## ZD 0.000
## .BOEE 0.000
## [...]## [...]
## Group 2 [2]:
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## ZD =~
## zd1 1.000
## zd2 (.p2.) 0.841 0.063 13.321 0.000
## zd6 (.p3.) 0.829 0.061 13.682 0.000
## BOEE =~
## bo1 1.000
## bo6 (.p5.) 0.913 0.053 17.171 0.000
## bo12 (.p6.) 0.961 0.057 16.943 0.000
## bo19 (.p7.) 1.050 0.059 17.764 0.000
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## BOEE ~
## ZD 0.590 0.156 3.782 0.000
## BFs ~
## BOEE 0.413 0.055 7.564 0.000
## ZD 0.012 0.071 0.166 0.868
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|)
## .zd1 (.21.) 3.644 0.082 44.440 0.000
## .zd2 (.22.) 3.075 0.079 39.155 0.000
## .zd6 (.23.) 3.822 0.075 50.822 0.000
## .bo1 (.24.) 3.014 0.095 31.582 0.000
## .bo6 (.25.) 2.240 0.092 24.481 0.000
## .bo12 (.26.) 2.259 0.097 23.304 0.000
## .bo19 (.27.) 2.570 0.104 24.790 0.000
## .BFs 2.207 0.068 32.380 0.000
## ZD -0.288 0.143 -2.013 0.044
## .BOEE 0.103 0.165 0.624 0.533
## [...]In dieser Ausgabe tauchen jetzt mitunter nur Zahlen zwischen den Punkten auf, dabei handelt es sich aber lediglich um eine Abkürzung im Output. In lavaan werden konsistent alle diese Label als .p[Parameternummer]. vergeben. (Wenn Sie sich davon selbst überzeugen möchten, nutzen Sie z.B. die parameterEstimates-Funktion, um eine detaillierte Ausgabe über die Parameter zu erhalten.)
Hier greift nun tatsächlich die Einstellung "BFs~1" in group.partial. BFs hat zwei unterschiedliche Interzepte. Bei ZD und BOEE fällt auf, dass diese in Gruppe 1 auf 0 gesetzt sind (ohne Unsicherheit) und in Gruppe 2 hier eine Effektkodierung durchgeführt wurde: hier wurden die Interzepte geschätzt. Unterscheidet sich dieser Interzept nun von 0, so unterscheiden sich die Gruppe in ihren Interzepten ([möglicherweise bedingten] Mittelwerten). Dazu später mehr!
Nun wollen wir untersuchen, ob das metrisch- und das skalar-invariante Modell sich signifikant in der Modellbeschreibung unterscheiden.
lavTestLRT(fit_sem_sex_skalar, fit_sem_sex_metrisch)## Chi-Squared Difference Test
##
## Df AIC BIC Chisq Chisq diff Df diff Pr(>Chisq)
## fit_sem_sex_metrisch 41 6850.4 7025.2 37.543
## fit_sem_sex_skalar 46 6844.5 7000.8 41.694 4.1504 5 0.528Die \(\chi^2\)-Differenz ist erneut klein (4.15) und der p-Wert zeigt auch hier an, dass es sich um keine signifikante Verschlechterung des Modells handelt (p = 0.528). Die Null-Hypothese, dass die Interzepte über die Faktorladungen hinaus über das Geschlecht hinweg gleich sind, wird somit nicht verworfen (die Null-Hypothese war: \(H_0: \Sigma_{metrisch}=\Sigma_{skalar}\)). Dies bedeutet nun, dass Unterschiede im Mittelwert der Items zwischen den beiden Gruppen tatsächlich auch auf Unterschiede der Mittelwerte der latenten Variablen zurückzuführen sind. Das heißt, dass es erst ab dieser Invarianzstufe zulässig ist, Mittelwerte zwischen den Gruppen zu vergleichen.
Strikte Invarianz
Unter strikter Invarianz verstehen wir, dass zusätzlich zu den Faktorladungen und den Interzepten auch die Residualvarianzen (\(\theta\)) gleich sind (insgesamt also \(\lambda\)s, \(\tau\)s und \(\theta\)s gleich über die Gruppen hinweg). Wir passen entsprechend das Modell an:
fit_sem_sex_strikt <- sem(model_sem, data = StressAtWork,
group = "sex",
group.equal = c("loadings", "intercepts", "residuals"),
group.partial = c("BFs~1", "BFs~~BFs"))Hier greift nun tatsächlich die Einstellung "BFs~~BFs" in group.partial. Wir vergleichen das skalar- und das strikt-invariante Modell hinsichtlich der Modellbeschreibung.
lavTestLRT(fit_sem_sex_strikt, fit_sem_sex_skalar)## Chi-Squared Difference Test
##
## Df AIC BIC Chisq Chisq diff Df diff Pr(>Chisq)
## fit_sem_sex_skalar 46 6844.5 7000.8 41.694
## fit_sem_sex_strikt 53 6836.7 6966.9 47.850 6.1563 7 0.5216Die \(\chi^2\)-Differenz ist erneut klein (6.156) und der p-Wert zeigt auch hier an, dass es sich um keine signifikante Verschlechterung des Modells handelt (p = 0.522). Die Null-Hypothese, dass die Fehlervarianzen über die Faktorladungen und Interzepte hinaus über das Geschlecht hinweg gleich sind, wird somit nicht verworfen (die Null-Hypothese war: \(H_0: \Sigma_{skalar}=\Sigma_{strikt}\)). Dies bedeutet nun, dass Unterschiede in der Varianz der manifesten Variablen tatsächlich auf Unterschiede in den Varianzen der latenten Variablen zurückzuführen sind. In anderen Worten, wenn wir z.B. beobachten, dass Männer in den beobachtbaren Verhaltensweisen homogener sind als Frauen, können wir bei dieser Varianzstufe davon ausgehen, dass dies daher kommt, dass Männer im Konstrukt ähnlicher sind und nicht nur daher, dass sie z.B. aufgrund der Formulierung der Fragen genauer gemessen werden konnten.
Vollständige Invarianz
Unter vollständiger Invarianz verstehen wir das Gleichsetzen aller Strukturparameter. Hier werden nun alle Varianzen, Residualvarianzen, ungerichtete und gerichtete Effekte des Strukturmodells über die Gruppen hinweg gleichgesetzt (insgesamt also \(\lambda\)s, \(\tau\)s, \(\theta\)s, \(\gamma\)s, \(\beta\)s, \(\kappa\)s, \(\phi\)s und \(\psi\)s gleich über die Gruppen hinweg). Wir passen entsprechend das Modell an. Außerdem müssen wir nun das Interzept und die Residualvarianz von BFs invariant zwischen den Gruppen setzen, was wir erreichen, indem wir die group.partial Option rausnehmen.
fit_sem_sex_voll <- sem(model_sem, data = StressAtWork,
group = "sex",
group.equal = c("loadings", "intercepts", "residuals",
"means", # latente Mittelwerte
"lv.variances", # latente Varianzen
"lv.covariances", # latente Kovarianzen
"regressions")) # Strukturparameter (Regressionsgewichte)Wenn wir nun den Modellvergleich zwischen dem strikt invarianten und dem vollständig invarianten Modell durchführen,
lavTestLRT(fit_sem_sex_voll, fit_sem_sex_strikt)## Chi-Squared Difference Test
##
## Df AIC BIC Chisq Chisq diff Df diff Pr(>Chisq)
## fit_sem_sex_strikt 53 6836.7 6966.9 47.85
## fit_sem_sex_voll 62 6844.0 6940.7 73.14 25.29 9 0.002667 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1… erhalten wir diesmal eine große \(\chi^2\)-Differenz (25.29) und der p-Wert zeigt an, dass es sich um eine signifikante Verschlechterung des Modells handelt \(p = 0.003 < 0.05\), wenn wir die Restriktion der vollständigen Invarianz in das Modell aufnehmen. Die Null-Hypothese, dass alle Parameter im Modell über das Geschlecht hinweg gleich sind, wird somit verworfen (die Null-Hypothese war: \(H_0: \Sigma_{strikt}=\Sigma_{vollständig}\)). Dies bedeutet also, dass es Geschlechtsunterschiede in den Beziehungen zwischen den latenten Variablen gibt.
Natürlich ist es nun interessant, wo diese Unterschiede liegen. Deshalb schauen wir uns dies an, indem wir uns den Output der Summary des strikt-invarianten Modells ansehen, da sich hier Pfadkoeffizienten, sowie die Mittelwerte und Varianzen der latenten Variablen (bzw. von BFs, was wir als latente Variable mitführen) noch unterscheiden:
summary(fit_sem_sex_strikt)## [...]
## Group 1 [1]:
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## ZD =~
## zd1 1.000
## zd2 (.p2.) 0.842 0.063 13.351 0.000
## zd6 (.p3.) 0.828 0.061 13.632 0.000
## BOEE =~
## bo1 1.000
## bo6 (.p5.) 0.909 0.053 17.127 0.000
## bo12 (.p6.) 0.955 0.057 16.871 0.000
## bo19 (.p7.) 1.046 0.059 17.681 0.000
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## BOEE ~
## ZD 0.490 0.084 5.805 0.000
## BFs ~
## BOEE 0.349 0.040 8.688 0.000
## ZD 0.050 0.045 1.115 0.265
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|)
## .zd1 (.21.) 3.644 0.082 44.513 0.000
## .zd2 (.22.) 3.078 0.078 39.236 0.000
## .zd6 (.23.) 3.818 0.076 50.443 0.000
## .bo1 (.24.) 3.011 0.096 31.468 0.000
## .bo6 (.25.) 2.242 0.092 24.477 0.000
## .bo12 (.26.) 2.259 0.097 23.306 0.000
## .bo19 (.27.) 2.572 0.104 24.811 0.000
## .BFs 2.486 0.050 49.238 0.000
## ZD 0.000
## .BOEE 0.000
## [...]## [...]
## Group 2 [2]:
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## ZD =~
## zd1 1.000
## zd2 (.p2.) 0.842 0.063 13.351 0.000
## zd6 (.p3.) 0.828 0.061 13.632 0.000
## BOEE =~
## bo1 1.000
## bo6 (.p5.) 0.909 0.053 17.127 0.000
## bo12 (.p6.) 0.955 0.057 16.871 0.000
## bo19 (.p7.) 1.046 0.059 17.681 0.000
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## BOEE ~
## ZD 0.583 0.155 3.752 0.000
## BFs ~
## BOEE 0.423 0.056 7.606 0.000
## ZD 0.004 0.071 0.060 0.952
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|)
## .zd1 (.21.) 3.644 0.082 44.513 0.000
## .zd2 (.22.) 3.078 0.078 39.236 0.000
## .zd6 (.23.) 3.818 0.076 50.443 0.000
## .bo1 (.24.) 3.011 0.096 31.468 0.000
## .bo6 (.25.) 2.242 0.092 24.477 0.000
## .bo12 (.26.) 2.259 0.097 23.306 0.000
## .bo19 (.27.) 2.572 0.104 24.811 0.000
## .BFs 2.206 0.069 32.084 0.000
## ZD -0.292 0.143 -2.038 0.042
## .BOEE 0.104 0.165 0.627 0.531
## [...]Dem jeweiligen Unterpunkt Regressions in beiden Gruppen entnehmen wir, dass die Pfadkoeffizienten recht ähnlich groß zu sein scheinen. Die Standardfehler der Koeffizienten in beiden Gruppen überlappen sich stark, wenn wir jeweils Estimate \(\pm\) Std.Err für einen Koeffizienten rechnen (zur Erinnerung: ein 95% Konfidenzintervall würden wir mit \(Est \pm 1.96SE\) erhalten, was noch viel größer wäre und sich diese also “noch stärker” überlappen würde). Schauen wir uns jeweils die Interzepte in den Unterpunkten Intercepts in den beiden Gruppen an, erkennen wir an der Effektkodierung für ZD und BOEE, dass die latenten Interzepte (\(\kappa\)) in der einen Gruppe auf 0 gesetzt und in der anderen Gruppe frei geschätzt wurden. Das Interzept in Gruppe 2 (den Männern) von Zeitdruck ist signifikant von 0 verschieden, das von emotionaler Erschöpfung nicht. Dies bedeutet, dass sich Männer und Frauen in ihrem latenten Mittelwert von Zeitdruck unterscheiden. Da der Mittelwert von Zeitdruck in der Gruppe der Frauen auf 0 gesetzt war und der Mittelwert von Zeitdruck der Männer signifikant von 0 abweicht (Est = -0.292, \(p < .05\)), verrät uns das negative Vorzeichen, dass Männer im Durchschnitt weniger Zeitdruck erleben. Auch wenn wir Konfidenzintervalle um die Interzeptschätzung von BFs legen, erhalten wir einen signifikanten Unterschied: die untere Grenze des Konfidenzintervalls in Gruppe 1 liegt bei \(2.486-1.96*0.05 \approx 2.38\) und und die obere Grenze in Gruppe 2 liegt bei \(2.206+1.96*0.069 \approx 2.35\); hier haben wir konservativer “gerundet”, um den \(\beta\)-Fehler zu minimieren; — die Konfidenzintervalle überlappen sich nicht! Diese signifikanten Unterschiede könnten der Grund gewesen sein, warum die vollständige Invarianz verworfen wurde. Um dies genauer zu prüfen, müssten wir sukzessive alle Parameter über die Gruppen gleichsetzen und schauen, für welchen Parameter diese Gleichsetzung zu einer signifikanten Verschlechterung des Modells führt.
Zusammenfassend können wir also nur von strikter Invarianz des Modells über das Geschlecht ausgehen. Wie sieht nun unser finales Modell aus?
semPaths(object = fit_sem_sex_strikt, what = "est", layout = "tree2",
rotation = 2, curve = T, col = list(man = "skyblue", lat = "yellow"),
curvePivot = T, edge.label.cex=1, sizeMan = 5, sizeLat = 8)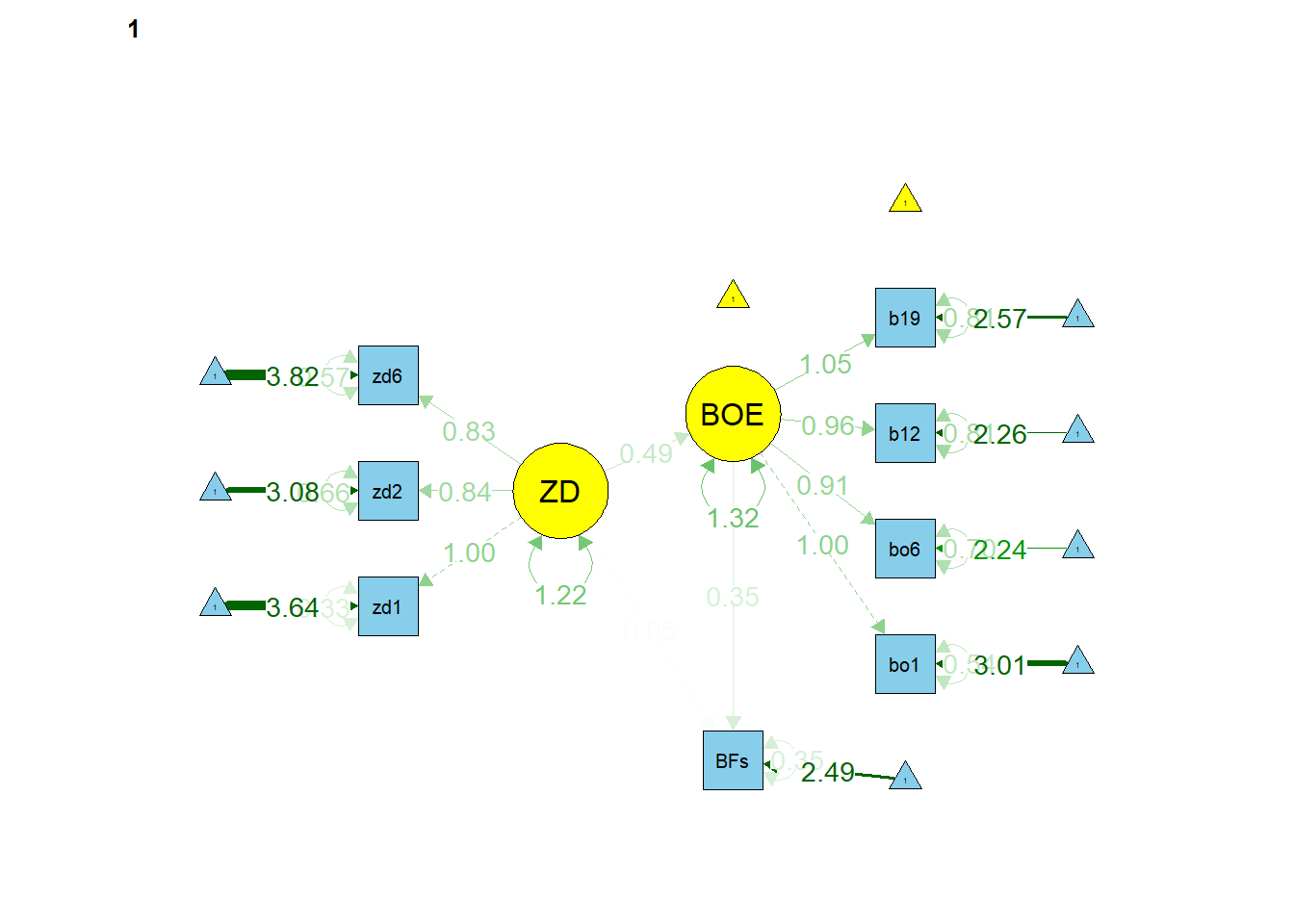
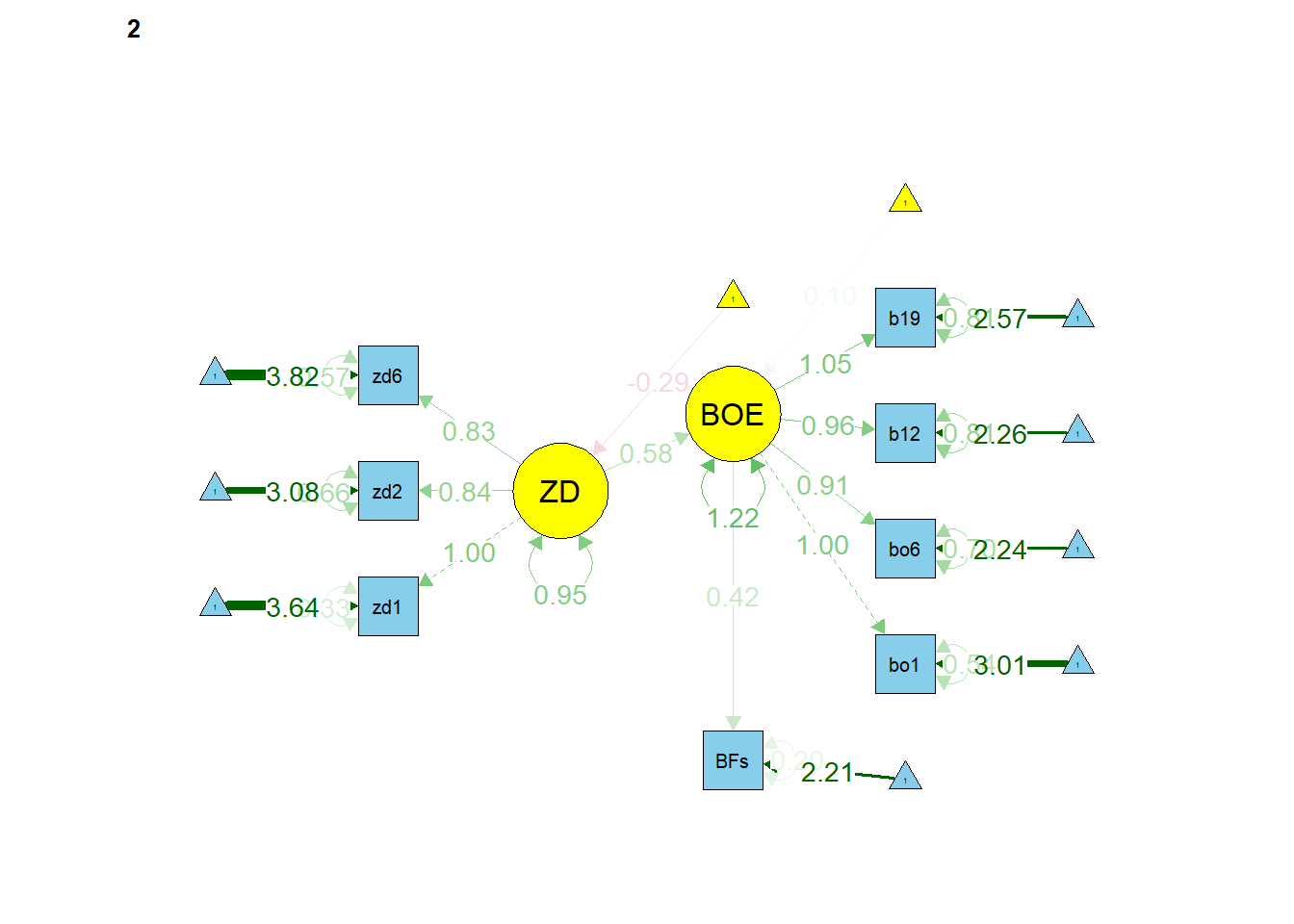
Wir erkennen deutlich, dass einige Koeffizienten gleich sind und bspw. der Mittelwert von ZD in einer Gruppe auf 0 ist (kein Pfeil) und in der zweiten Gruppe bei -0.29 liegt. Wenn wir hier what = "model" wählen, können wir das Modell mit allen Gleichsetzungen betrachten.
Multi Gruppen Modelle und moderierte Regression
Auch wenn in unserem Beispiel die Regressionsgewichte über beide Gruppen hinweg gleich waren, ist das bei weitem nicht immer der Fall. In vielen Fällen zielen inhaltliche Fragestellungen genau darauf ab, in welchem Ausmaß es Unterschiede in den Beziehungen latenter Variablen über Gruppen hinweg gibt. Wir hatten bereits gesehen, dass Männer im Mittel weniger Zeitdruck erleben. Könnte es daher sein, dass Männer, die - entgegen der üblichen männlichen Erfahrung - erhöhten Zeitdruck empfinden, darauf stärker mit psychosomatischen Beschwerden reagieren als Frauen? Diese Frage impliziert einen Interkationseffekt. Gleichzeitig bedeutet diese Frage auch nichts anderes als: “Gibt es einen Unterschied in den Regressionsgewichten zwischen Männern und Frauen?”. In diesem Abschnitt gucken wir uns an, wie diese beiden Ansätze in Bezug zueinander stehen.
Vereinfachen wir unser Beispiel für einen Moment auf die manifeste Ebene, wie es schon bei den Pfadanalysen im letzten Beitrag der Fall war. Dazu nutzen wir neben den Skalenwerten der psychosomatischen Beschwerden (BFs) auch einen Skalenwert des Zeitdrucks (ZDs). Generell hält die folgende Beschreibung auch für den Fall mit latenten Variablen, aber für den Vergleich der beiden Ansätze ist ein übersichtliches Beispiel sinnvoller.
StressAtWork$ZDs <- rowMeans(StressAtWork[,paste0("zd",c(1, 2, 6))])Das einfache Multi Gruppen Modell sieht für diesen Fall in lavaan so aus:
model_pfad_msa <- 'BFs ~ ZDs'
fit_pfad_msa <- sem(model_pfad_msa, StressAtWork,
group = 'sex')Als Ergebnis erhalten wir zwei gruppenspezifische Regressionen, die so notiert werden können:
\[\begin{align} BF &= \beta_{01} + \beta_{11} ZD + \varepsilon \\ BF &= \beta_{02} + \beta_{12} ZD + \varepsilon \end{align}\]
Auf die Daten angepasst erhalten wir folgende Parameterschätzungen:
summary(fit_pfad_msa)## [...]
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## BFs ~
## ZDs 0.220 0.045 4.885 0.000
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|)
## .BFs 1.710 0.166 10.310 0.000
## [...]## [...]
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## BFs ~
## ZDs 0.213 0.078 2.742 0.006
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|)
## .BFs 1.487 0.262 5.677 0.000
## [...]Die beiden Gruppen unterscheiden sich geringfügig im Regressionsgewicht und Intercept. Um uns die Mühe zu ersparen, einfache Subtraktion per Hand betreiben zu müssen, können wir diese Differenzen mit in das Modell aufnehmen. Dazu können wir wieder mit Labels arbeiten und neue Parameter definieren:
model_pfad_msa <- '
# Regressionen
BFs ~ c(b11, b12)*ZDs
# Interzepte
BFs ~ c(b01, b02)*1
# Differenzen
b0d := b02 - b01
b1d := b12 - b11'
fit_pfad_msa <- sem(model_pfad_msa, StressAtWork,
group = 'sex')## [...]
## Defined Parameters:
## Estimate Std.Err z-value P(>|z|)
## b0d -0.223 0.310 -0.720 0.472
## b1d -0.007 0.090 -0.077 0.939
## [...]Wir behalten diese Ergebnisse mal im Hinterkopf und gucken uns die moderierte Regression als Möglichkeit an, die gleiche Frage zu bearbeiten.
Für die moderierte Regression benötigen wir einen Interaktionsterm, der in das Modell aufgenommen werden muss. In unserem Datensatz ist das Geschlecht mit 1 und 2 kodiert, sodass wir hier etwas nachhelfen müssen, bevor wir einen sinnvollen Interaktionsterm bestimmen können:
StressAtWork$sexDum <- StressAtWork$sex - 1
StressAtWork$Int <- StressAtWork$ZDs * StressAtWork$sexDumDurch die Subtraktion der 1 wird die Variable in eine dummy-kodierte Variable umgewandelt. Das hat folgende Auswirkungen auf die Variablen, die in die Regression eingehen:
head(StressAtWork[, c('ZDs', 'sexDum', 'Int')])## ZDs sexDum Int
## 1 2.666667 0 0.000000
## 2 3.666667 0 0.000000
## 3 2.333333 0 0.000000
## 4 2.333333 1 2.333333
## 5 3.333333 0 0.000000
## 6 3.666667 0 0.000000Personen mit einer 0 auf sexDum erhalten also eine 0 im Interaktionsterm, Personen mit sexDum = 1 hingegen erhalten dort ihren ursprünglichen ZDs-Wert. Diese drei Variablen können wir dann im Rahmen einer moderierten Regression nutzen:
\[\begin{align} BF &= \beta_{0} + \beta_{1} ZD + \beta_2 sex + \beta_3 (ZD \cdot sex) + \varepsilon \end{align}\]
die in lavaan folgendermaßen aussieht:
model_pfad_moderiert <- 'BFs ~ ZDs + sexDum + Int'
fit_pfad_moderiert <- sem(model_pfad_moderiert, StressAtWork, meanstructure = T)Hier haben wir meanstructure = T gewählt, um auch das Interzept von BFs angezeigt zu bekommen. Als Ergebnis dieser moderierten Regression ergibt sich dann:
## [...]
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## BFs ~
## ZDs 0.220 0.044 4.986 0.000
## sexDum -0.223 0.323 -0.692 0.489
## Int -0.007 0.094 -0.074 0.941
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|)
## .BFs 1.710 0.163 10.523 0.000
## [...]Diese Ergebnisse sollten Ihnen außerordentlich bekannt vorkommen, weil wir alle drei Parameterschätzer vor wenigen Zeilen im Multi Gruppen Modell gesehen haben. Das liegt daran, dass beide Ansätze sich sehr leicht ineinander überführen lassen. Für die Gruppe der Frauen (\(sex = 0\)):
\[\begin{align} BF &= \beta_{0} + \beta_{1} ZD + \beta_2 0 + \beta_3 (ZD \cdot 0) + \varepsilon \\ BF &= \beta_{0} + \beta_{1} ZD \end{align}\]
und für die Gruppe der Männer (\(sex = 1\)):
\[\begin{align} BF &= \beta_{0} + \beta_{1} ZD + \beta_2 1 + \beta_3 (ZD \cdot 1) + \varepsilon \\ BF &= \beta_{0} + \beta_2 + (\beta_{1} + \beta_3) ZD \end{align}\]
Zusammengefasst ergibt sich also:
| Gruppe | Parameter | MSA | Mod. Reg | Ergebnis |
|---|---|---|---|---|
| Frauen | Interzept | \(\beta_{01}\) | \(\beta_{0}\) | 1.710 |
| Frauen | Gewicht | \(\beta_{11}\) | \(\beta_{1}\) | 0.220 |
| Männer | Interzept | \(\beta_{02}\) | \(\beta_{0} + \beta_2\) | 1.487 |
| Männer | Gewicht | \(\beta_{12}\) | \(\beta_{1} + \beta_3\) | 0.213 |
| Differenz | Interzept | \(\beta_{02} - \beta_{01}\) | \(\beta_2\) | -0.223 |
| Differenz | Gewicht | \(\beta_{12} - \beta_{11}\) | \(\beta_3\) | -0.007 |
Analog hätten wir auch eine Regression mit factor(sex) verwenden können, wie es in der Bachelor-Sitzung zur quadratischen und moderierten Regression gemacht wurde; allerdings war die Umsetzung in lavaan überaus sinnvoll.
reg <- lm(BFs ~ factor(sex)*ZDs, data = StressAtWork)
summary(reg)##
## Call:
## lm(formula = BFs ~ factor(sex) * ZDs, data = StressAtWork)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.31507 -0.50409 -0.05418 0.49895 2.58601
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.710453 0.163628 10.453 < 2e-16 ***
## factor(sex)2 -0.223201 0.324913 -0.687 0.493
## ZDs 0.220296 0.044477 4.953 1.22e-06 ***
## factor(sex)2:ZDs -0.006929 0.094498 -0.073 0.942
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.7103 on 301 degrees of freedom
## Multiple R-squared: 0.1233, Adjusted R-squared: 0.1145
## F-statistic: 14.11 on 3 and 301 DF, p-value: 1.256e-08Grafisch sehen wir, dass sich die Regressionsgerade über die Gruppen hinweg nur geringfügig unterscheiden (signifikant war der Unterschied nicht!). Allerdings ist dies eine gängige Form eine solche Interaktion darzustellen:
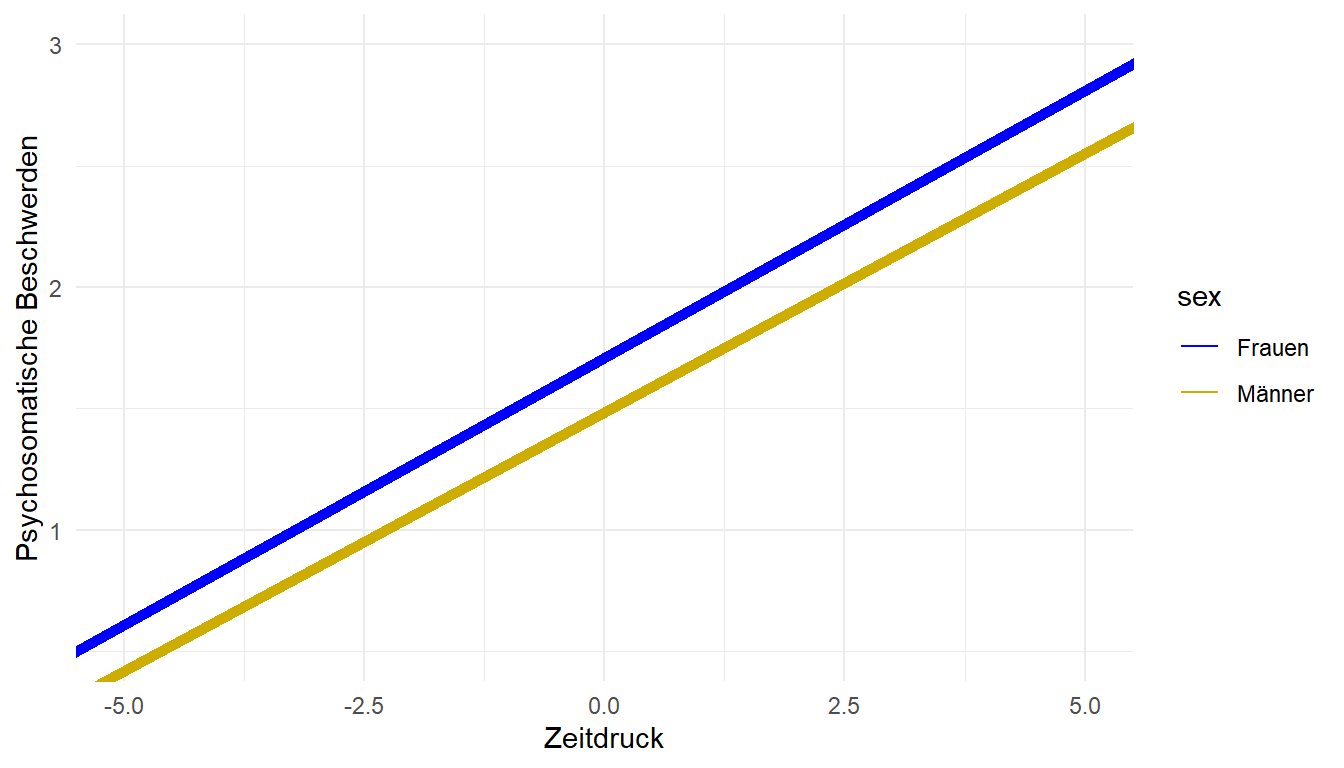
Abgetragen sehen wir auch die Gruppenunterschiede. Wirklich erkennen tun wir nur ein leichten (nicht signifikanten) Unterschied im Interzept. Der Unterschied in der Slope (der ebenfalls nicht signifikant war), lässt sich höchstens erahnen. Diese Darstellungsform wird Simple Slopes genannt. Für mehr Informationen dazu und wie man das Ganze noch in 3D darstellen kann, können sich Interessierte in der Sitzung zur moderierten Regression aus dem Bachelor ansehen/wiederholen. Wir bitten ebenfalls darauf zu achten, dass i.d.R. Prädiktoren zentriert werden sollten, wenn mit Interaktionseffekten oder quadratischen Effekten gearbeitet wird. Dies haben wir hier nicht berücksichtigt, um die Sitzung nicht in die Länge zu ziehen.
Dieses Prinzip gilt in der MSA für alle Parameter: wir implizieren eine Interaktion mit der Gruppierungsvariable, wenn wir keine Gleichheit über die Gruppen hinweg annehmen. Im Umkehrschluss gilt also auch: wenn wir eine Gruppenvariable als einen Prädiktor in ein SEM aufnehmen, ohne sie als Gruppierungsvariable in einer MSA einzuarbeiten, behaupten wir, dass es keinerlei Interaktionseffekt gibt. Dies gilt auf der Ebene des Messmodells genauso wie auf der Ebene des Strukturmodells.
Den gesamten R-Code, der in dieser Sitzung genutzt wird, können Sie hier herunterladen.
Appendix A
MSA zu Fuß
Wir wollen uns die Invarianztestung auch noch einmal zu Fuß ansehen. Um das ganze abzukürzen, schauen wir uns immer mit fitMeasures nur den \(\chi^2\)-Wert, die \(df\) sowie den \(p\)-Wert an und vergleichen diese mit dem bereits geschätzten Modell aus dem Abschnitt zur MSA.
Konfigurale Invarianz
Wir beginnen mit der Spezifikation des konfigural invarianten Modells. Hier muss nichts gleichgesetzt werden. Wir kopieren also einfach das Modell model_sem:
model_sem <- '
# Messmodelle
ZD =~ zd1 + zd2 + zd6
BOEE =~ bo1 + bo6 + bo12 + bo19
# Strukturmodell
BOEE ~ ZD
BFs ~ BOEE + ZD
'und schätzen dies anschließend. Wir verwenden das Anhängsel 2, um zu zeigen, welches die händisch gleichgesetzte Variante ist:
fit_sem_sex_konfigural <- sem(model_sem, data = StressAtWork, group = "sex",
group.equal = c(""), group.partial = c("BFs ~ 1", "BFs ~~*BFs"))
fit_sem_sex_konfigural2 <- sem(model_sem, data = StressAtWork, group = "sex")
# chi^2, df, p-Wert
fitmeasures(fit_sem_sex_konfigural, c("chisq", 'df', "pvalue"))
fitmeasures(fit_sem_sex_konfigural2, c("chisq", 'df', "pvalue"))## group.equal:## chisq df pvalue
## 35.803 36.000 0.478## zu Fuß/händisch:## chisq df pvalue
## 35.803 36.000 0.478Wir erkennen keine Unterschiede, was nicht verwunderlich ist. Hier wurde noch nichts gleichgesetzt.
Metrische Invarianz
Wir müssen nun ein neues Modell spezifizieren, in welchem wir allen Faktorladungen (\(\lambda\)s) jeweils über die Gruppen hinweg das gleiche Label geben. Hierbei verwenden wir l als Label für die Faktorladungen und nummerieren alle Faktorladungen nacheinander durch (wie genau hier vorgegangen wird, ist immer den Anwendenden überlassen. Es muss lediglich darauf geachtet werden, nicht mehrfach das gleiche Label für unterschiedliche Parameter zu verwenden, wenn dies nicht explizit gewünscht ist).
model_sem_metrisch <- '
# Messmodelle
ZD =~ zd1 + c(l1, l1)*zd2 + c(l2, l2)*zd6
BOEE =~ bo1 + c(l3,l3)*bo6 + c(l4, l4)*bo12 + c(l5, l5)*bo19
# Strukturmodell
BOEE ~ ZD
BFs ~ BOEE + ZD'fit_sem_sex_metrisch <- sem(model_sem, data = StressAtWork,
group = "sex",
group.equal = c("loadings"),
group.partial = c("BFs~1", "BFs ~~BFs"))
fit_sem_sex_metrisch2 <- sem(model_sem_metrisch, data = StressAtWork,
group = "sex")
# chi^2, df, p-Wert
fitmeasures(fit_sem_sex_metrisch, c("chisq", 'df', "pvalue"))
fitmeasures(fit_sem_sex_metrisch2, c("chisq", 'df', "pvalue"))## group.equal:## chisq df pvalue
## 37.543 41.000 0.625## zu Fuß/händisch:## chisq df pvalue
## 37.543 41.000 0.625Erneut erkennen wir keine Unterschiede zwischen den Modellen. Beide Vorgehensweisen kommen zum selben Ergebnis!
Skalare Invarianz
Erneut müssen wir ein neues Modell spezifizieren, in welchem wir jeweils allen Faktorladungen und Interzepten (\(\lambda\)s und \(\tau\)s) über die Gruppen hinweg das gleiche Label geben. Hierbei verwenden wir tau als Label für die Interzepte und nummerieren alle Interzepte der manifesten Variablen nacheinander durch. Wir fügen außerdem die Effektkodierung ein via ZD ~ c(0, NA)*1 und BOEE ~c(0, NA)*1, womit der latente Mittelwert in einer Gruppe auf 0 gesetzt und in der zweiten frei geschätzt wird und erweitern das Modell model_sem_metrisch zu:
model_sem_skalar <- '
# Messmodelle
ZD =~ zd1 + c(l1, l1)*zd2 + c(l2, l2)*zd6
BOEE =~ bo1 + c(l3,l3)*bo6 + c(l4, l4)*bo12 + c(l5, l5)*bo19
zd1 ~ c(tau1, tau1)*1
zd2 ~ c(tau2, tau2)*1
zd6 ~ c(tau3, tau3)*1
bo1 ~ c(tau4, tau4)*1
bo6 ~ c(tau5, tau5)*1
bo12 ~ c(tau6, tau6)*1
bo19 ~ c(tau7, tau7)*1
# Strukturmodell
BOEE ~ ZD
BFs ~ BOEE + ZD
BOEE ~ c(0, NA)*1
ZD ~ c(0, NA)*1
'fit_sem_sex_skalar <- sem(model_sem, data = StressAtWork,
group = "sex",
group.equal = c("loadings", "intercepts"),
group.partial = c("BFs~1", "BFs ~~BFs"))
fit_sem_sex_skalar2 <- sem(model_sem_skalar, data = StressAtWork, group = "sex")
# chi^2, df, p-Wert
fitmeasures(fit_sem_sex_skalar, c("chisq", 'df', "pvalue"))
fitmeasures(fit_sem_sex_skalar2, c("chisq", 'df', "pvalue"))## group.equal:## chisq df pvalue
## 41.694 46.000 0.653## zu Fuß/händisch:## chisq df pvalue
## 41.694 46.000 0.653Erneut erkennen wir keine Unterschiede zwischen den Modellen. Beide Vorgehensweisen kommen zum selben Ergebnis!
Strikte Invarianz
Wieder müssen wir ein neues Modell spezifizieren, in welchem wir jeweils allen Faktorladungen, Interzepten und Fehlervarianzen (\(\lambda\)s, \(\tau\)s und \(\theta\)s) über die Gruppen hinweg das gleiche Label geben. Hierbei verwenden wir t als Label für die Fehlervarianzen und nummerieren alle Fehlervarianzen der manifesten Variablen nacheinander durch. Wir erweitern das Modell model_sem_skalar.
model_sem_strikt <- '
# Messmodelle
ZD =~ zd1 + c(l1, l1)*zd2 + c(l2, l2)*zd6
BOEE =~ bo1 + c(l3,l3)*bo6 + c(l4, l4)*bo12 + c(l5, l5)*bo19
zd1 ~ c(tau1, tau1)*1
zd2 ~ c(tau2, tau2)*1
zd6 ~ c(tau3, tau3)*1
bo1 ~ c(tau4, tau4)*1
bo6 ~ c(tau5, tau5)*1
bo12 ~ c(tau6, tau6)*1
bo19 ~ c(tau7, tau7)*1
zd1 ~~ c(t1, t1)*zd1
zd2 ~~ c(t2, t2)*zd2
zd6 ~~ c(t3, t3)*zd6
bo1 ~~ c(t4, t4)*bo1
bo6 ~~ c(t5, t5)*bo6
bo12 ~~ c(t6, t6)*bo12
bo19 ~~ c(t7, t7)*bo19
# Strukturmodell
BOEE ~ ZD
BFs ~ BOEE + ZD
BOEE ~ c(0, NA)*1
ZD ~ c(0, NA)*1
'fit_sem_sex_strikt <- sem(model_sem, data = StressAtWork,
group = "sex",
group.equal = c("loadings", "intercepts", "residuals"),
group.partial = c("BFs~1", "BFs~~BFs"))
fit_sem_sex_strikt2 <- sem(model_sem_strikt, data = StressAtWork, group = "sex")
# chi^2, df, p-Wert
fitmeasures(fit_sem_sex_strikt, c("chisq", 'df', "pvalue"))
fitmeasures(fit_sem_sex_strikt2, c("chisq", 'df', "pvalue"))## group.equal:## chisq df pvalue
## 47.850 53.000 0.674## zu Fuß/händisch:## chisq df pvalue
## 47.850 53.000 0.674Erneut erkennen wir keine Unterschiede zwischen den Modellen. Beide Vorgehensweisen kommen zum selben Ergebnis!
Vollständige Invarianz
Zum letzten Mal müssen wir ein neues Modell spezifizieren, in welchem wir allen Parametern des Modells (insgesamt also \(\lambda\)s, \(\tau\)s, \(\theta\)s, \(\gamma\)s, \(\beta\)s, \(\kappa\)s, \(\phi\)s und \(\psi\)s) über die Gruppen hinweg das gleiche Label geben. Wir müssen die Effektkodierung der latenten Mittelwert wieder herausnehmen und setzen die Mittelwerte in beiden Gruppen auf 0. Als Label verwenden wir wieder die Notation, die wir schon aus den Mediationanalysen kennen (a, b und c). Für die latenten Residualvarianzen führen wir psi als Label ein (hierbei zählen wir weiterhin BFs zu den latenten Variablen). Für die latente Varianz von ZD verwenden wir phi als Label. Für den Mittelwert von BFs verwenden wir ausnahmsweise kappa, da wir BFs, wie zuvor erwähnt, weiter als latente Variable zählen wollen.
model_sem_voll <- '
# Messmodelle
ZD =~ zd1 + c(l1, l1)*zd2 + c(l2, l2)*zd6
BOEE =~ bo1 + c(l3,l3)*bo6 + c(l4, l4)*bo12 + c(l5, l5)*bo19
zd1 ~ c(tau1, tau1)*1
zd2 ~ c(tau2, tau2)*1
zd6 ~ c(tau3, tau3)*1
bo1 ~ c(tau4, tau4)*1
bo6 ~ c(tau5, tau5)*1
bo12 ~ c(tau6, tau6)*1
bo19 ~ c(tau7, tau7)*1
zd1 ~~ c(t1, t1)*zd1
zd2 ~~ c(t2, t2)*zd2
zd6 ~~ c(t3, t3)*zd6
bo1 ~~ c(t4, t4)*bo1
bo6 ~~ c(t5, t5)*bo6
bo12 ~~ c(t6, t6)*bo12
bo19 ~~ c(t7, t7)*bo19
# Strukturmodell
BOEE ~ c(a, a)*ZD
BFs ~ c(b, b)*BOEE + c(c, c)*ZD
BOEE ~ c(0, 0)*1
ZD ~ c(0, 0)*1
BFs ~ c(kappa, kappa)*1
ZD ~~ c(phi, phi)*ZD
BOEE ~~ c(psi1, psi1)*BOEE
BFs ~~ c(psi2, psi2)*BFs
'fit_sem_sex_voll <- sem(model_sem, data = StressAtWork,
group = "sex",
group.equal = c("loadings", "intercepts", "residuals",
"means", # latente Mittelwerte
"lv.variances", # latente Varianzen
"lv.covariances", # latente Kovarianzen
"regressions")) # Strukturparameter (Regressionsgewichte)
fit_sem_sex_voll2 <- sem(model_sem_voll, data = StressAtWork,
group = "sex")
# chi^2, df, p-Wert
fitmeasures(fit_sem_sex_voll, c("chisq", 'df', "pvalue"))
fitmeasures(fit_sem_sex_voll2, c("chisq", 'df', "pvalue"))## group.equal:## chisq df pvalue
## 73.140 62.000 0.157## zu Fuß/händisch:## chisq df pvalue
## 73.140 62.000 0.157Erneut erkennen wir keine Unterschiede zwischen den Modellen. Beide Vorgehensweisen kommen zum selben Ergebnis! Zuvor hatten wir gesehen, dass ein Modellvergleich zwischen der strikten und der vollständigen Invarianz zu Gunsten der strikten Invarianz ausfällt. Somit wird die vollständige Invarianz verworfen und wir entscheiden uns final für die strikte Invarianz über das Geschlecht.
Literatur
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden (5. Auflage, 1. Auflage: 2010). Weinheim: Beltz.
Gregorich, S. E. (2006). Do self-report instruments allow meaningful comparisons across diverse population groups? Testing measurement invariance using the confirmatory factor analysis framework. Medical Care, 44(11), 78-94.
Schermelleh-Engel, K., Moosbrugger, H., & Müller, H. (2003). Evaluation the fit of structural equation models: tests of significance and descriptive goodness-of-fit measures. Methods of Psychological Research Online, 8(2), 23-74.
Inhaltliche Literatur
Büssing, A., & Perrar, K.-M. (1992). Die Messung von Burnout. Untersuchung einer deutschen Fassung des Maslach Burnout Inventory (MBI-D) [The measurement of Burnout. The study of a German version of the Maslach Burnout Inventory (MBI-D)]. Diagnostica, 38, 328 – 353.
Maslach, C., & Jackson, S.E. (1986). Maslach Burnout Inventory (Vol. 2). Palo Alto, CA: Consulting Psychologists Press.
Mohr, G. (1986). Die Erfassung psychischer Befindensbeeinträchtigungen bei Arbeitern [Assessment of impaired psychological well-being in industrial workers]. Frankfurt am Main, Fermany: Lang.
Semmer, N. K., Zapf, D., & Dunckel, H. (1999). Instrument zur Stressbezogenen Tätigkeitsanalyse (ISTA) [Instrument for stress-oriented task analysis (ISTA)]. In H. Dunkel (Ed.), Handbuch psychologischer Arbeitsanalyseverfahren (pp. 179 – 204). Zürich, Switzerland: vdf Hochschulverlag an der ETH.
- Blau hinterlegte Autor:innenangaben führen Sie direkt zur universitätsinternen Ressource.