Verteilungen
Kernfragen dieser Lehreinheit
- Wie können Zufallsexperimente und Bernoulli-Experimente simuliert werden?
- Wie lässt sich die Binomialverteilung darstellen?
- Wie können Wahrscheinlichkeitsverteilung und Verteilungsfunktion erstellt werden?
- Welchem Muster folgt die Arbeit mit Verteilungen in
R? - Mit welchen Befehlen erstellt man die Dichte- und Verteilungsfunktion?
- Wie kann eine empirisch erhobene Variable gegen die Normalverteilung abgetragen werden?
Vorbereitende Schritte
Der Datensatz ist in diesem Tutorial nicht zentral und kommt erst im letzten Abschnitt zum Tragen. Trotzdem beschäftigen wir uns zum Start mit dem Einladen, um die Struktur der Tutorials gleich zu lassen. Den Datensatz haben wir bereits unter diesem Link heruntergeladen und können ihn über den lokalen Speicherort einladen oder Sie können Ihn direkt mittels des folgenden Befehls aus dem Internet in das Environment bekommen. In den vorherigen Tutorials und den dazugehörigen Aufgaben haben wir bereits Änderungen am Datensatz durchgeführt, die hier nochmal aufgeführt sind, um den Datensatz auf dem aktuellen Stand zu haben:
#### Was bisher geschah: ----
# Daten laden
load(url('https://pandar.netlify.app/post/fb22.rda'))
# Nominalskalierte Variablen in Faktoren verwandeln
fb22$geschl_faktor <- factor(fb22$geschl,
levels = 1:3,
labels = c("weiblich", "männlich", "anderes"))
fb22$fach <- factor(fb22$fach,
levels = 1:5,
labels = c('Allgemeine', 'Biologische', 'Entwicklung', 'Klinische', 'Diag./Meth.'))
fb22$ziel <- factor(fb22$ziel,
levels = 1:4,
labels = c("Wirtschaft", "Therapie", "Forschung", "Andere"))
fb22$wohnen <- factor(fb22$wohnen,
levels = 1:4,
labels = c("WG", "bei Eltern", "alleine", "sonstiges"))
# Skalenbildung
fb22$prok2_r <- -1 * (fb22$prok2 - 5)
fb22$prok3_r <- -1 * (fb22$prok3 - 5)
fb22$prok5_r <- -1 * (fb22$prok5 - 5)
fb22$prok7_r <- -1 * (fb22$prok7 - 5)
fb22$prok8_r <- -1 * (fb22$prok8 - 5)
#Prokrastination
fb22$prok_ges <- fb22[, c('prok1', 'prok2_r', 'prok3_r',
'prok4', 'prok5_r', 'prok6',
'prok7_r', 'prok8_r', 'prok9',
'prok10')] |> rowMeans()
#Naturverbundenheit
fb22$nr_ges <- fb22[, c('nr1', 'nr2', 'nr3', 'nr4', 'nr5', 'nr6')] |> rowMeans()
fb22$nr_ges_z <- scale(fb22$nr_ges) # StandardisiertWarum Wahrscheinlichkeit?
In der psychologischen Forschung werden nur Stichproben gezogen. Für die Übertragung der Ergebnisse auf die Grundgesamtheit (Population), aus der die Stichprobe stammt, ist eine Betrachtung der Wahrscheinlichkeitstheorie essentiell. Die Grundlagen der Wahrscheinlichkeitstheorie haben Sie in der Vorlesung vermittelt bekommen. Hier geht es nun um die praktische Anwendung in R. Im weiteren Verlauf werden zuerst Zufallsexperimente und empirische Häufigkeitsverteilungen betrachtet. Anschließend werden verschiedene Verteilungen dargestellt.
Erstellung eines einfachen Zufallsexperiments
Starten wir erstmal mit der Simulation von einem einfachen Zufallsexperiment, dem Werfen von 2 Würfeln. Zwei Würfel können insgesamt 6*6 also 36 verschiedene Kombinationen unter Beachtung der Reihenfolge ergeben. Um dies zu simulieren, definieren wir zunächst einen Würfel als Objekt. Mit expand.grid() können wir uns alle möglichen Kombinationen anzeigen lassen (R kombiniert alle Optionen des ersten Objektes wuerfel einmal mit allen Optionen des zweiten Objektes wuerfel).
wuerfel <- c(1:6)
expand.grid(wuerfel,wuerfel)## Var1 Var2
## 1 1 1
## 2 2 1
## 3 3 1
## 4 4 1
## 5 5 1
## 6 6 1
## 7 1 2
## 8 2 2
## 9 3 2
## 10 4 2
## 11 5 2
## 12 6 2
## 13 1 3
## 14 2 3
## 15 3 3
## 16 4 3
## 17 5 3
## 18 6 3
## 19 1 4
## 20 2 4
## 21 3 4
## 22 4 4
## 23 5 4
## 24 6 4
## 25 1 5
## 26 2 5
## 27 3 5
## 28 4 5
## 29 5 5
## 30 6 5
## 31 1 6
## 32 2 6
## 33 3 6
## 34 4 6
## 35 5 6
## 36 6 6Der Erwartungswert der Augensumme beim Wurf mit zwei Würfeln kann bestimmt werden, indem wir diese Möglichkeiten einem Objekt pos zuweisen. Anschließend bilden wir die Summe für jede Kombination. Wenn man nun alle Möglichkeiten aufaddiert und durch die Anzahl an Möglichkeiten (Anzahl der Reihen aller Möglichkeiten ist 36) teilt, erhält man den Erwartungswert 7.
pos <- expand.grid(wuerfel,wuerfel)
pos$sum <- pos$Var1+pos$Var2
sum(pos$sum) / nrow(pos)## [1] 7Wie aus der Vorlesung und der eigenen Brettspielerfahrung bekannt, ist der Erwartungswert für ein einzelnes Ereignis nicht aussagekräftig - man würfelt nicht mit jedem Wurf 7. Doch gibt es eine Beziehung zwischen beobachteter und erwarteter Häufigkeit, die man durch häufiges Wiederholen abbilden kann. Dafür könnte man 1000 Mal per Hand die Würfel werfen und das Ergebnis jeweils in R notieren, doch natürlich bietet das Programm auch einen Shortcut. Mit der Funktion sample() kann zufällig aus einer definierten Menge gezogen werden. Ein einmaliges Werfen eines Würfels würde dabei so aussehen.
sample(x = wuerfel, size = 1)## [1] 3Unter dem Argument x kann definiert werden, aus welcher Menge an Objekten zufällig gezogen wird - in diesem Fall die Ziffern zwischen 1 und 6, die im Objekt wuerfel hinterlegt sind. size definiert die Anzahl an Wiederholungen. Wenn wir nun also zwei Würfel werfen wollen, können wir die size einfach erhöhen. Dabei ist es außerdem wichtig, ob das Experiment mit oder ohne Zurücklegen durchgeführt wird. Dafür ist das Argument replace verantwortlich, das standardmäßig auf FALSE steht. Da die Würfel jedoch auch die selbe Zahl anzeigen können, agieren wir mit Zurücklegen und müssen das Argument auf TRUE setzen.
sample(x = wuerfel, size = 2, replace = TRUE)## [1] 4 3Für die Verteilung der Ergebnisse ist es vor allem wichtig, wie die Summe aus den beiden Ziffern aussieht. Die Funktionen kann man in einer Zeile kombinieren.
sample(x = wuerfel, size = 2, replace = TRUE) |> sum()## [1] 4Des Weiteren soll der Wurf nicht nur einmal mit den beiden Würfeln durchgeführt werden, sondern häufiger wiederholt werden. Hier hilft Ihnen replicate(), wobei die Anzahl an wiederholten Durchführungen einer Funktion im Argument n festgelegt werden kann. Weiterhin muss im Argument expr die Funktion genannt werden, die wiederholt werden soll.
replicate(n = 10, expr = sum(sample(x = wuerfel, size = 2, replace = TRUE)))## [1] 8 11 12 6 3 4 4 10 5 11Beachten Sie jedoch, dass Sie bei zweimaliger Durchführung desselben Befehls nicht zwei Mal dasselbe Ergebnis bekommen werden, da R den Zufall jeweils neu simuliert.
replicate(n = 10, expr = sum(sample(x = wuerfel, size = 2, replace = TRUE)))## [1] 5 5 12 7 6 5 4 6 12 6Zur Konstanthaltung der Ergebnisse eines Zufallsvorgangs kann set.seed() genutzt werden, durch das der R interne Zufallsgenerator stets an der selben Stelle gestartet wird. Dies ermöglicht die Reproduzierbarkeit des Ergebnisses (Anmerkung: bei verschiedenen Versionen von R könnte der Befehl auch andere Resultate produzieren).
set.seed(500)
replicate(n = 10, expr = sum(sample(x = wuerfel, size = 2, replace = TRUE)))## [1] 8 3 6 8 7 6 8 3 12 10Des Weiteren weisen wir unsere Daten einem Objekt zu, um sie im Folgenden analysieren zu können. Zusätzlich können wir den Code durch die Nutzung des Pipes nochmal verschönern. Wir ziehen zuerst das sample, bilden dann die Summe aus den beiden Werten. Diese Kombination wird dem Argument expr aus der replicate Funktion zugeordnet. R ersetzt also durch den Pipe nicht immer das erste Argument der nachffolgenden Funktion (das wäre ja n), sondern das Argument, welches in der Standardreihenfolge als erstes keine Zuweisung erhalten hat. R checkt demnach, dass n schon besetzt ist und ersetzt stattdessen das zweite Argument expr.
set.seed(500)
results_10 <- sample(x = wuerfel, size = 2, replace = TRUE) |> sum() |> replicate(n = 10)
results_10## [1] 8 3 6 8 7 6 8 3 12 10Häufigkeitsverteilung
Zur Veranschaulichung der Ergebnisse können Sie das bereits besprochene Histogramm nutzen, das Häufigkeiten abbildet. Mit xlim legen wir in diesem Fall die Grenzen der möglichen Ereignisse fest, auch wenn diese noch nicht aufgetreten sind. breaks sind die Übergänge zwischen den Balken. Um die Balken jeweils über der ganzen Zahl (also den möglichen Ereignissen von 2 bis 12) zu haben, setzen wir die Punkte auf 1.5, 2.5, 3.5 und so weiter bis 12.5. Dies wird durch den Doppelpunkt erreicht, der so oft auf den Wert der unteren Grenze eins addiert, bis er bei der oberen angekommen ist.
hist(results_10,xlim = c(1.5,12.5), breaks = c(1.5:12.5))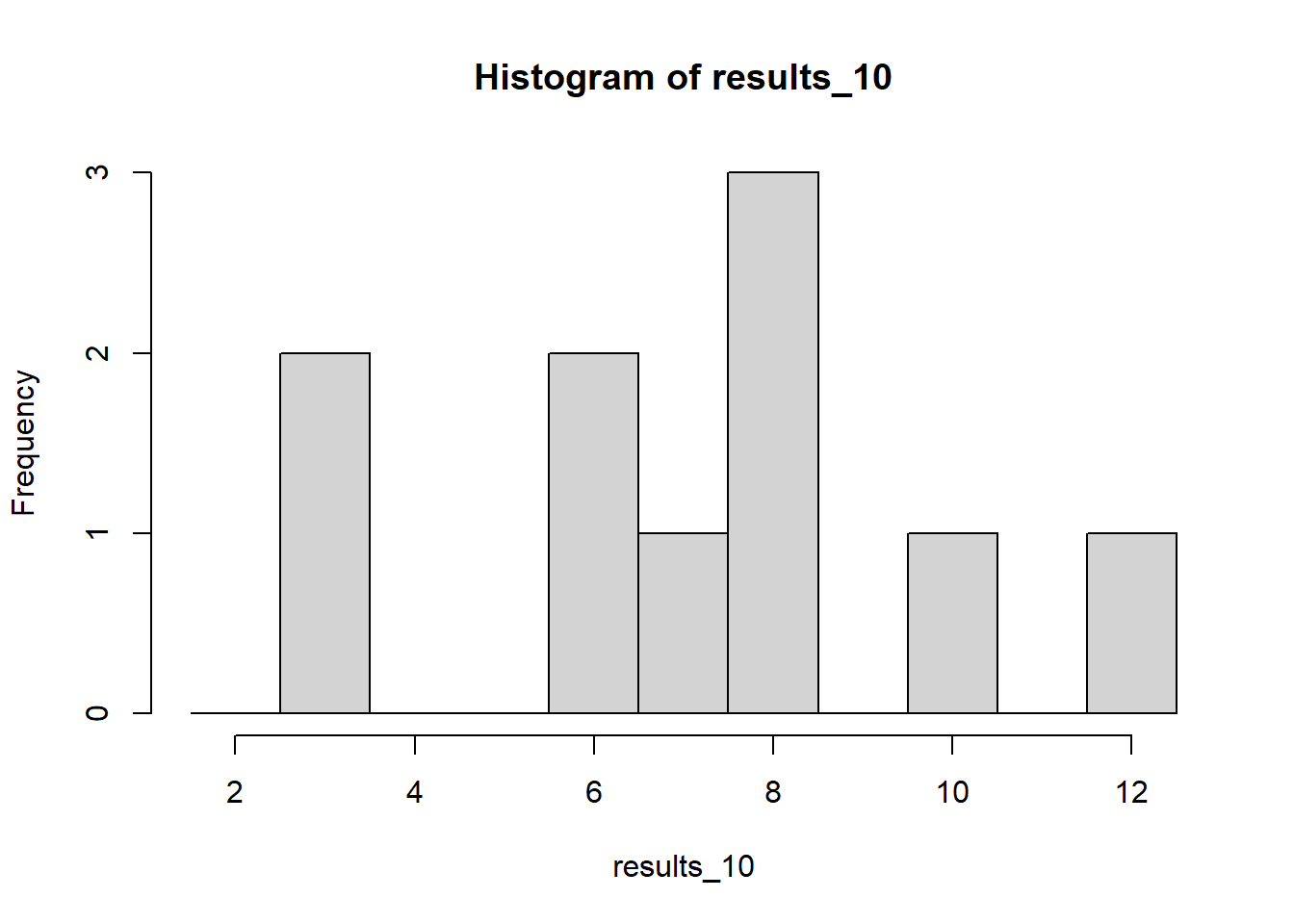
Durch eine Erhöhung der Würfe nähert sich die empirische Wahrscheinlichkeit der einzelnen Ergebnisse den theoretischen Wahrscheinlichkeiten an. Auch dies kann man grafisch darstellen.
set.seed(500)
results_50 <- sample(x = wuerfel, size = 2, replace = TRUE) |> sum() |> replicate(n = 50)
hist(results_50, xlim = c(1.5,12.5), breaks = c(1.5:12.5))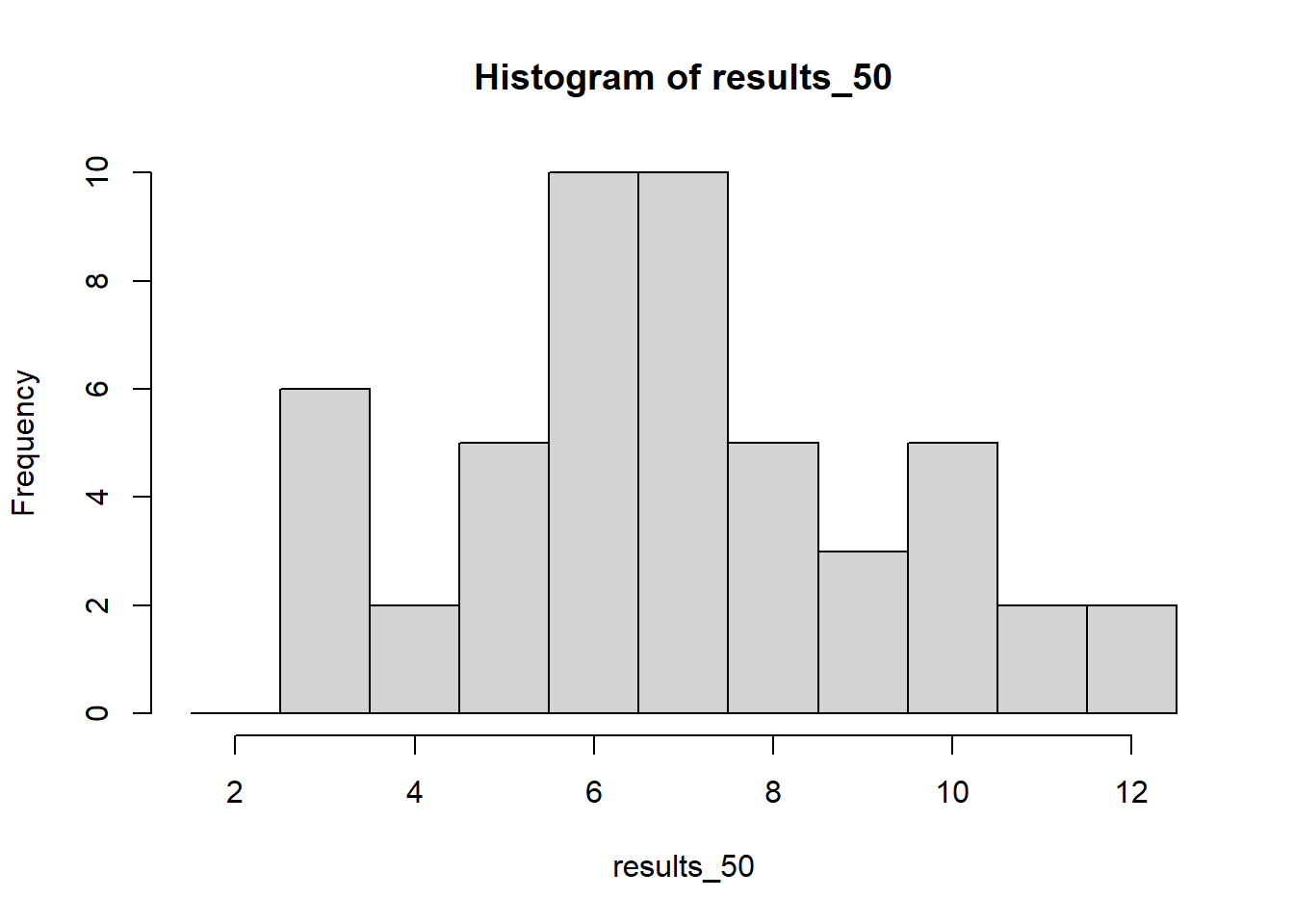
results_250 <- sample(x = wuerfel, size = 2, replace = TRUE) |> sum() |> replicate(n = 250)
hist(results_250, xlim = c(1.5,12.5), breaks = c(1.5:12.5))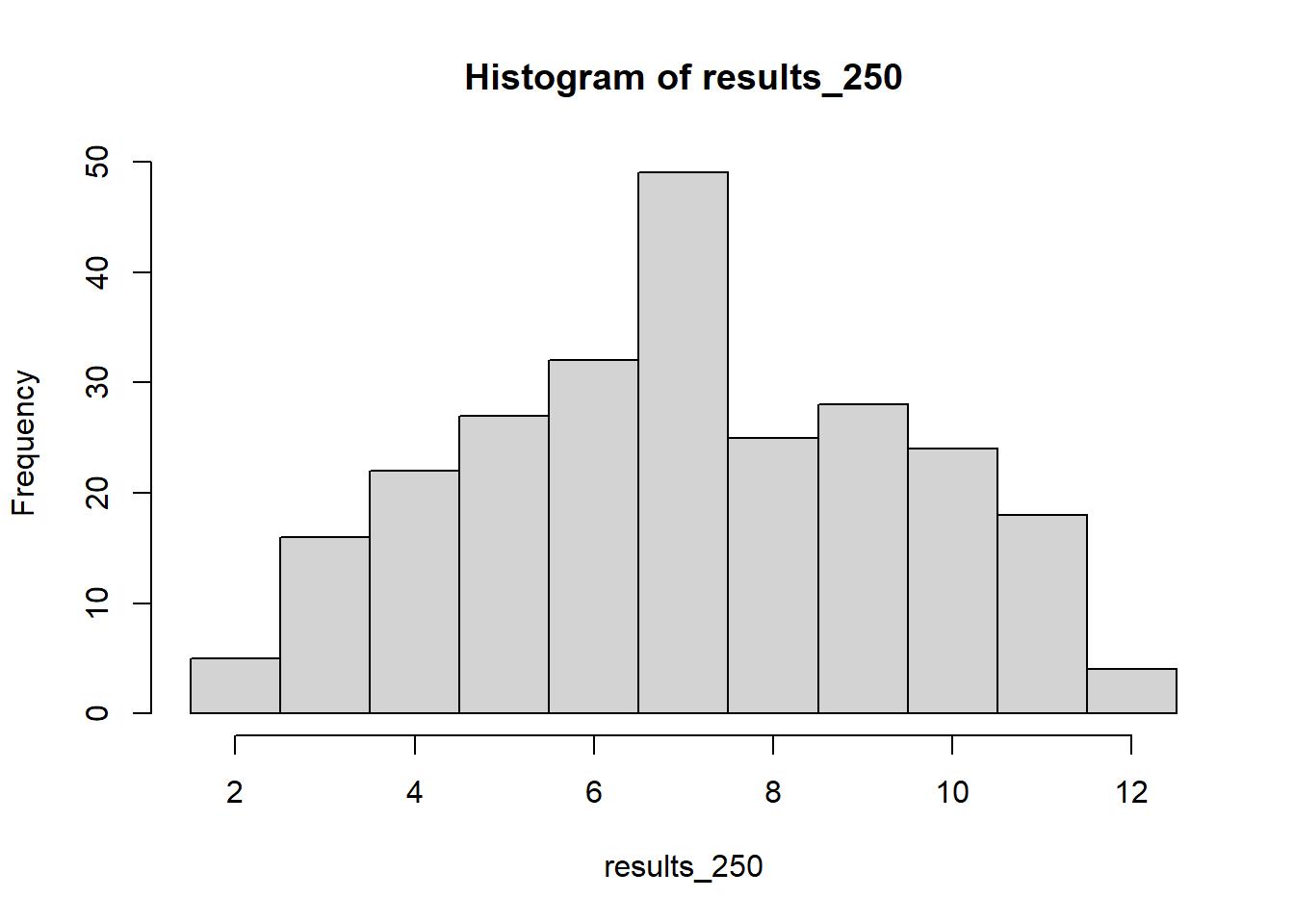
results_10000 <- sample(x = wuerfel, size = 2, replace = TRUE) |> sum() |> replicate(n = 10000)
hist(results_10000, xlim = c(1.5,12.5), breaks = c(1.5:12.5))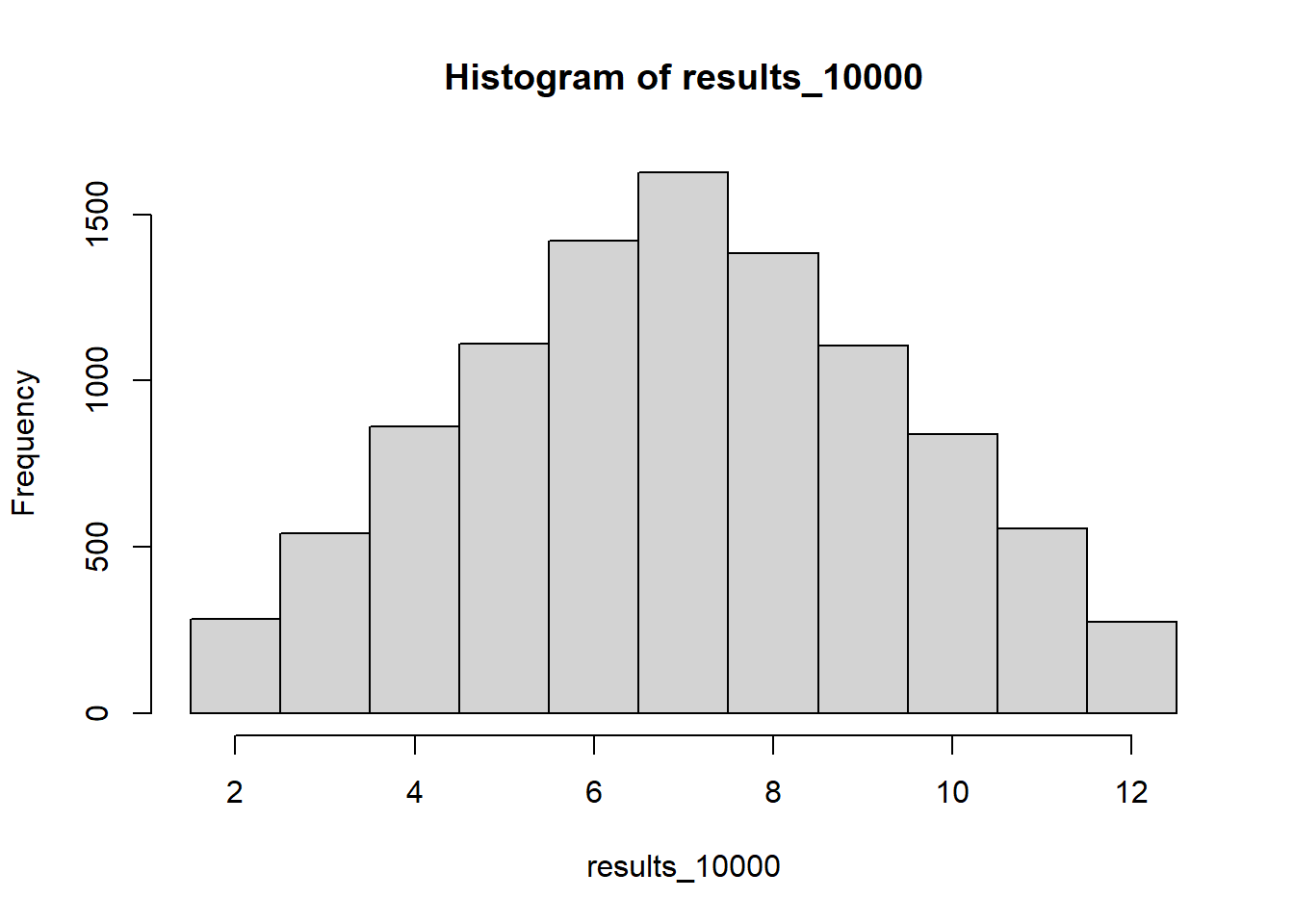
Dies wird auch daran deutlich, dass sich der Mittelwert der Verteilung nun dem Erwartungswert von 7 annähert.
mean(results_10)## [1] 7.1mean(results_50)## [1] 6.88mean(results_250)## [1] 7.016mean(results_10000)## [1] 6.9895Binomialverteilung
Kommen wir nun von der Abbildung empirischer Häufigkeiten zu einer Wahrscheinlichkeitsverteilung - zu der Binomialverteilung. Diese basiert auf einem Bernoulli-Experiment, was bedeutet, dass es nur zwei sich gegenseitig ausschließende Ergebnisse eines Vorgangs gibt. Nehmen wir als Beispiel ein Glücksrad, auf dem 4/5 der Fläche rot markiert sind und 1/5 grün. Diese Ereignisse schließen sich gegenseitig aus und haben bei einer Drehung eine bestimmte Wahrscheinlichkeit von p(rot) = 0.8 und p(grün) = 0.2. Wenn Sie solch ein Spiel anbieten wollen, stellt sich die Frage, wie wahrscheinlich es ist, dass die Teilnehmenden in einer bestimmten Häufigkeit beim Drehen grün treffen. In der Vorlesung haben Sie dafür eine Funktion kennengelernt:
- Anzahl der Treffer
- Anzahl der Wiederholungen
- Wahrscheinlichkeit von Treffern
- Wahrscheinlichkeit von Nieten
- Anzahl der Möglichkeiten / Binomialkoeffizient
Für den Binomialkoeffizienten hat R einen eigenen Eingabebefehl choose() mit den Argumenten n und k. Wenn wir nun also berechnen wollen wie wahrscheinlich es ist, dass bei 100-maligem Drehen 20 mal grün erscheint, kann man dies folgendermaßen machen.
choose(n = 100, k = 20) * 0.2^20 * 0.8^80## [1] 0.09930021Noch simpler geht es mit der Funktion dbinom(). Diese hat als Argumente x statt k, size statt n und prob für die Wahrscheinlichkeit des interessierenden Ereignisses.
dbinom(x = 20, size = 100, prob = 0.2) ## [1] 0.09930021Die berechnete Lösung ist ein Wert aus der Wahrscheinlichkeitsverteilung unseres Beispiels. Es ist also die Wahrscheinlichkeit, dass genau 20 von 100 Versuchen auf grün landen. Für jede mögliche Anzahl k bzw. x gibt es einen zugeordneten Wert. Um sich die gesamte Wahrscheinlichkeitsverteilung anzusehen, gibt es folgende Eingabemöglichkeit:
x <- c(0:100) # alle möglichen Werte für x in unserem Beispiel
probs <- dbinom(x, size = 100, prob = 0.2) #Wahrscheinlichkeiten für alle möglichen Werte
plot(x = x, y = probs, type = "h", xlab = "Häufigkeiten des Ereignis Grün", ylab = "Wahrscheinlichkeit bei 100 Drehungen")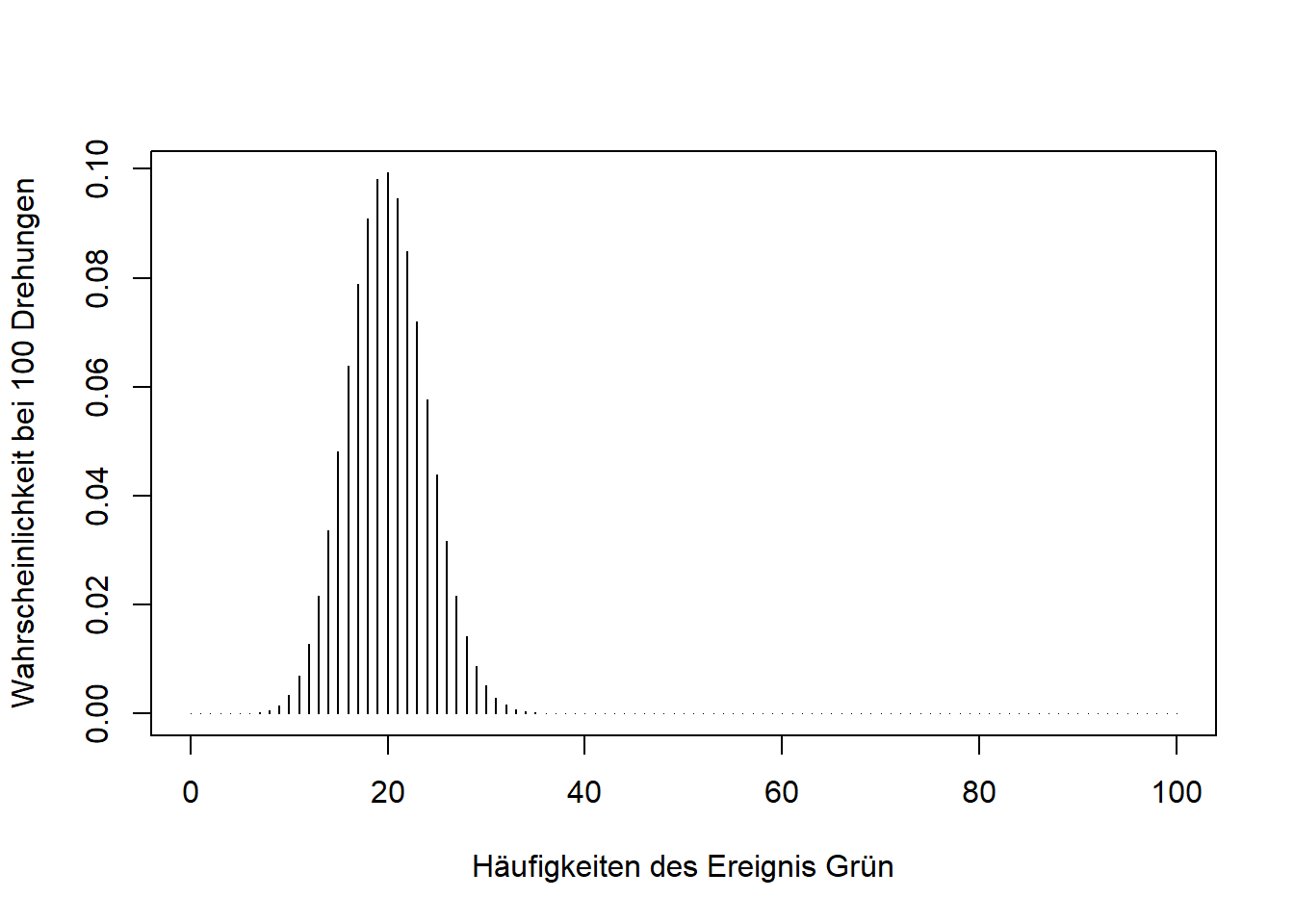
Die Funktion plot() gibt uns die Möglichkeit, eigene x und y Werte zu definieren. Es werden alle Zahlen zwischen 0 und 100 mit der dazugehörigen Wahrscheinlichkeit abgebildet. type gibt uns die Möglichkeit, verschiedene Darstellungsarten zu wählen (h steht in dem Fall für histogrammähnliche Striche). xlab und ylab ermöglichen die Achsenbeschriftung.
Im folgenden Plot ist nochmal abgebildet, was wir mit der Funktion dbinom() für den Wert 20 erreicht haben: Wir konnten die “Höhe” seines Balkens bestimmen - also die Wahrscheinlichkeit für genau 20 Erfolge.
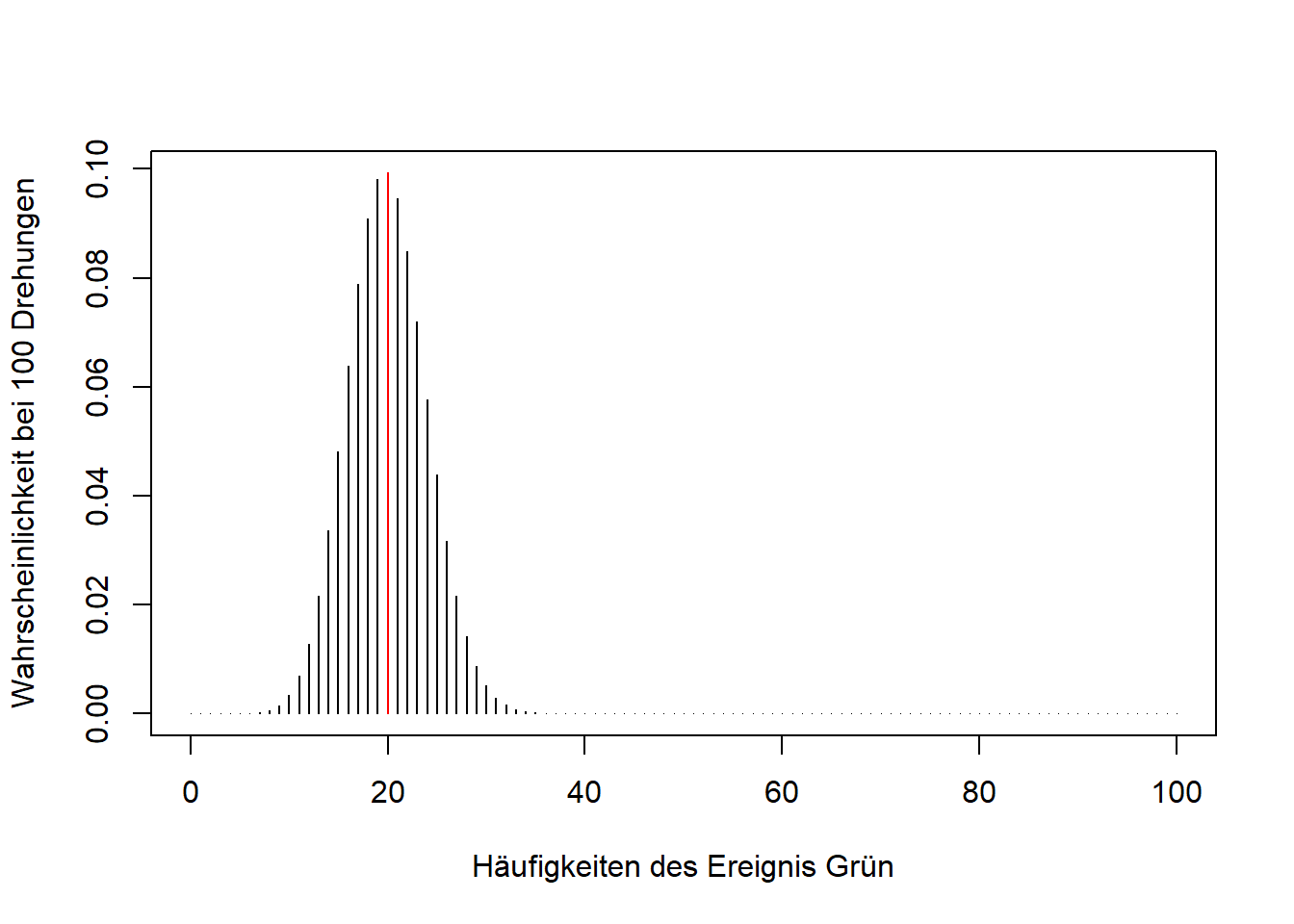
Anmerkung: Grafiken mit gefärbten Bestandteilen werden hier zu didaktischen Zwecken dargestellt. Es wird nicht erwartet, dass dies selber beherrscht wird und aus Gründen des Umfangs auch nicht beschrieben.
Neben der genauen Erfolgszahl gibt es auch häufig Fragestellungen, die sich mit Bereichen befassen: Wie wahrscheinlich ist es, dass höchstens 20 Mal grün gedreht wird bei 100 Versuchen? In unserem Plot der Wahrscheinlichkeitsverteilung würde der erfragte Wert die Summe der Werte vieler Balken sein.
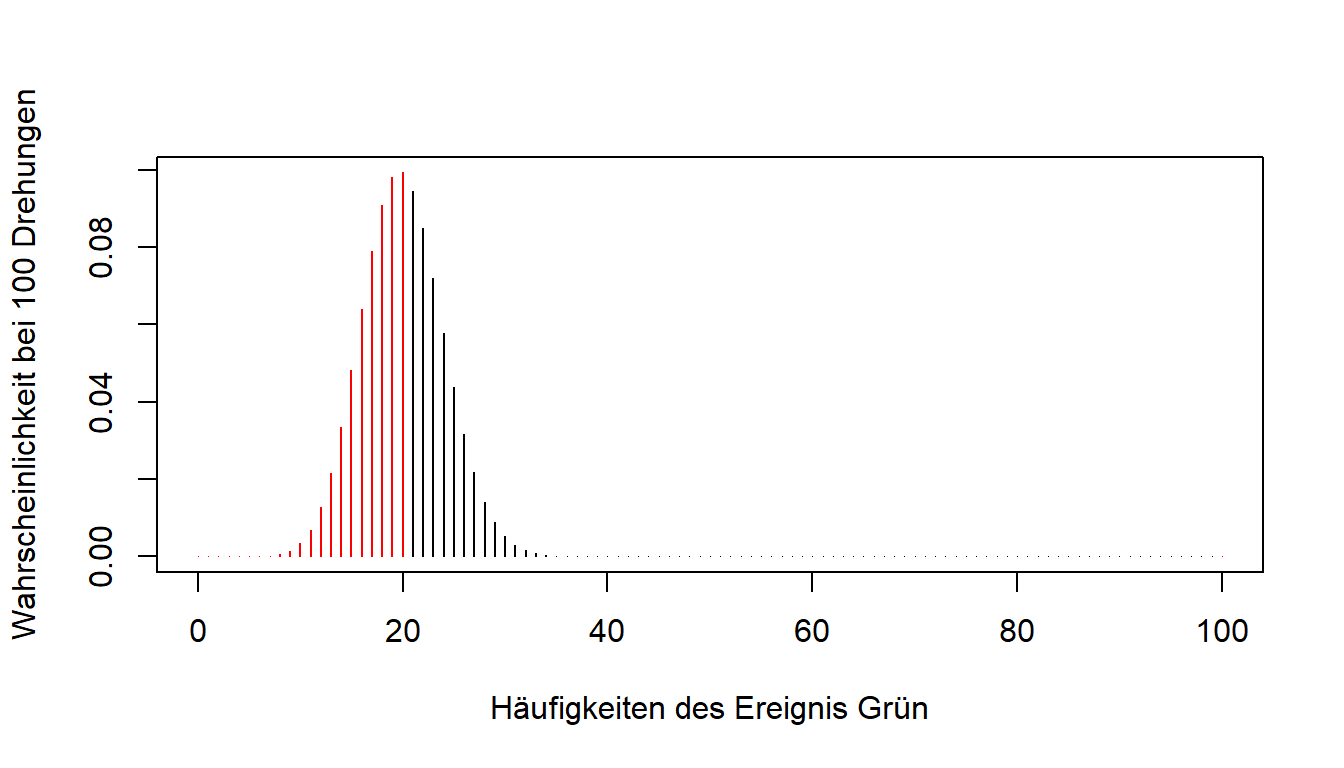 Eine solche Frage kann mit Hilfe der Verteilungsfunktion der Binomialverteilung beantwortet werden. Hier werden die Werte der niedrigeren Zahlen kumuliert - das bedeutet aufaddiert.
Eine solche Frage kann mit Hilfe der Verteilungsfunktion der Binomialverteilung beantwortet werden. Hier werden die Werte der niedrigeren Zahlen kumuliert - das bedeutet aufaddiert.
Auch hierfür ist in R eine Funktion definiert mit dem Namen pbinom(). q gibt nun die Zahl an, bis zu der alle Wahrscheinlichkeiten aufaddiert werden. size und prob erhalten ihre Bedeutung. lower.tail = TRUE (Standardeinstellung) sorgt für eine Aufaddierung der Werte startend bei 0 (also 0 bis 20 Mal grün). Bei lower.tail = FALSE würde von der anderen Seite, also der size zugeordneten Zahl, begonnen werden. Die Aufaddierung der Werte geht dann von dem maximalen Wert (also und in diesem Fall 100) bis zu dem Wert 1 + q (21 bis 100 Mal grün).
Höchstens 20 mal bedeutet dabei, dass die 20 im Intervall mit einbezogen wird (also lower.tail = TRUE).
pbinom(q = 20, size = 100, prob = 0.2, lower.tail = TRUE)## [1] 0.5594616Bei weniger als 20 mal könnte man q = 19 verwenden, da die Binomialverteilung stets diskrete Variablen abbildet.
Um die Wahrscheinlichkeit innerhalb eines Intervalls zu berechnen, kann die Funktion einfach zwei mal genutzt und die Werte voneinander subtrahiert werden. Für die Fragestellung, wie wahrscheinlich Werte im Intervall von 15 und 20 sind, würde die Funktion folgendermaßen aussehen:
pbinom(q = 20, size = 100, prob = 0.2, lower.tail = TRUE) - pbinom(q = 14, size = 100, prob = 0.2, lower.tail = TRUE)## [1] 0.4790179Wie die Wahrscheinlichkeitsverteilung kann die Verteilungsfunktion natürlich auch abgebildet werden. Im Code der Grafikerstellung muss nur die Funktion dbinom() durch pbinom() ersetzt werden.
x <- c(0:100) # alle möglichen Werte für x in unserem Beispiel
probs <- pbinom(x, size = 100, prob = 0.2, lower.tail = TRUE) #Wahrscheinlichkeiten für alle möglichen Werte
plot(x = x, y = probs, type = "h",
xlab = "Häufigkeiten für Ereignis Grün",
ylab = "kumulierte Wahrscheinlichkeit")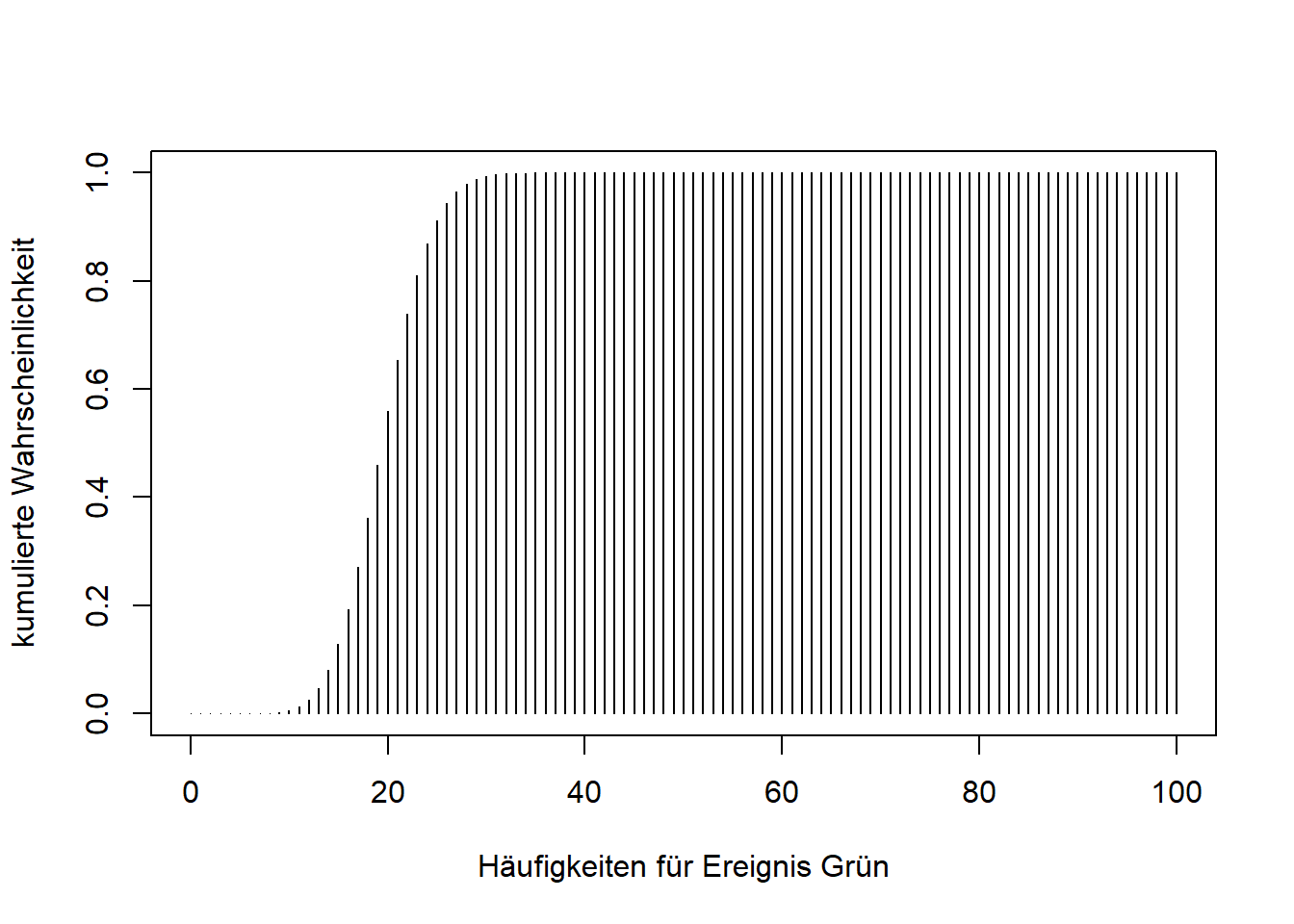
Im Endeffekt haben wir mit pbinom() also wieder einen Wert aus dieser Verteilung ablesen können.
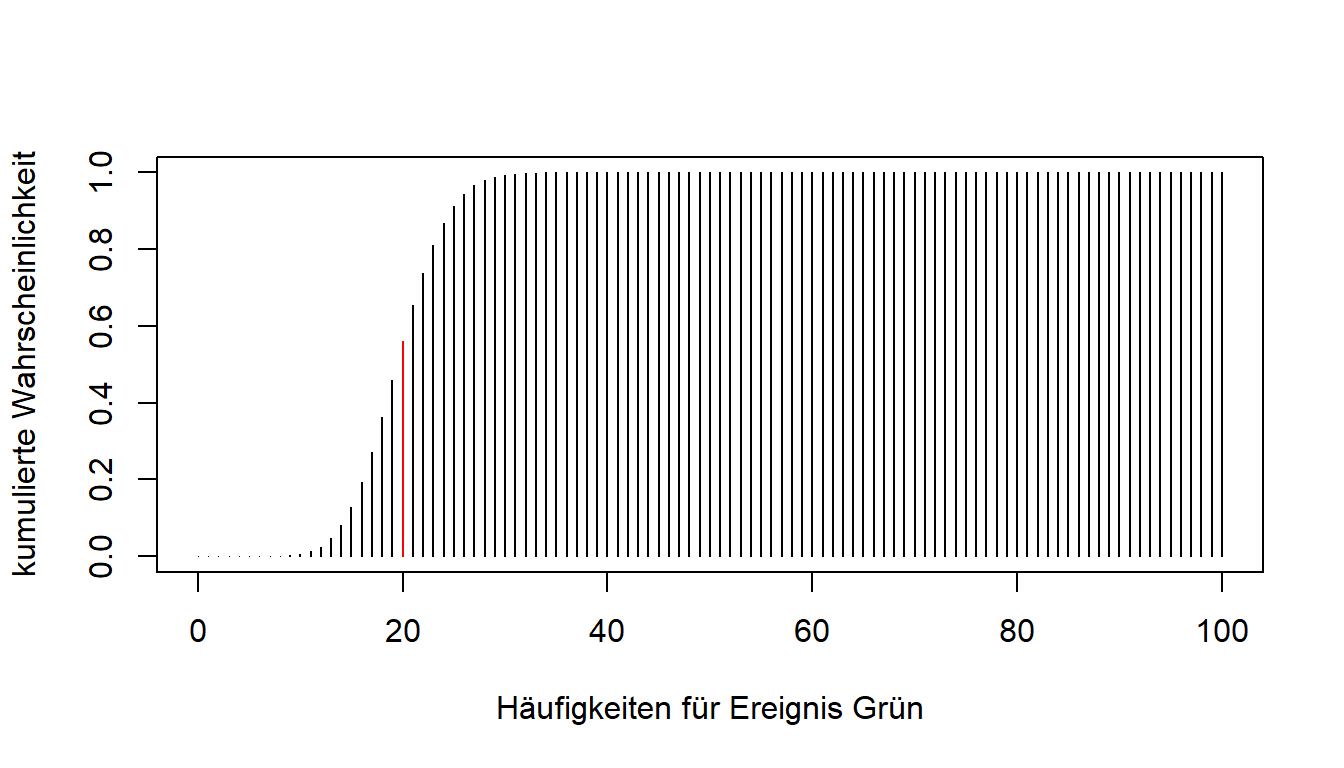
Es ist bereits ein Muster zu erkennen: Der Buchstabe vor dem Funktionsname "binom()" ("d" als Punktwahrscheinlichkeit für ein bestimmtes x bzw. "p" als kumulierte Wahrscheinlichkeit für ein bestimmtes x) verändert die Funktion. Des Weiteren bietet R noch die zufällige Simulation des Experimentes mit "r" und den Präfix "q" für die Quantilfunktion.
Gehen wir nun einmal umgekehrt an unser Experiment heran. Wir wollen hier herausfinden, welche Anzahl an Treffern in den unteren 10 Prozent der Verteilung liegen. Auch hier werden die einzelnen Wahrscheinlichkeiten wieder aufaddiert / kumuliert. Optisch gesehen suchen wir also nach dem Ort in unserer Verteilungsfunktion, wo die 10 Prozent liegen.
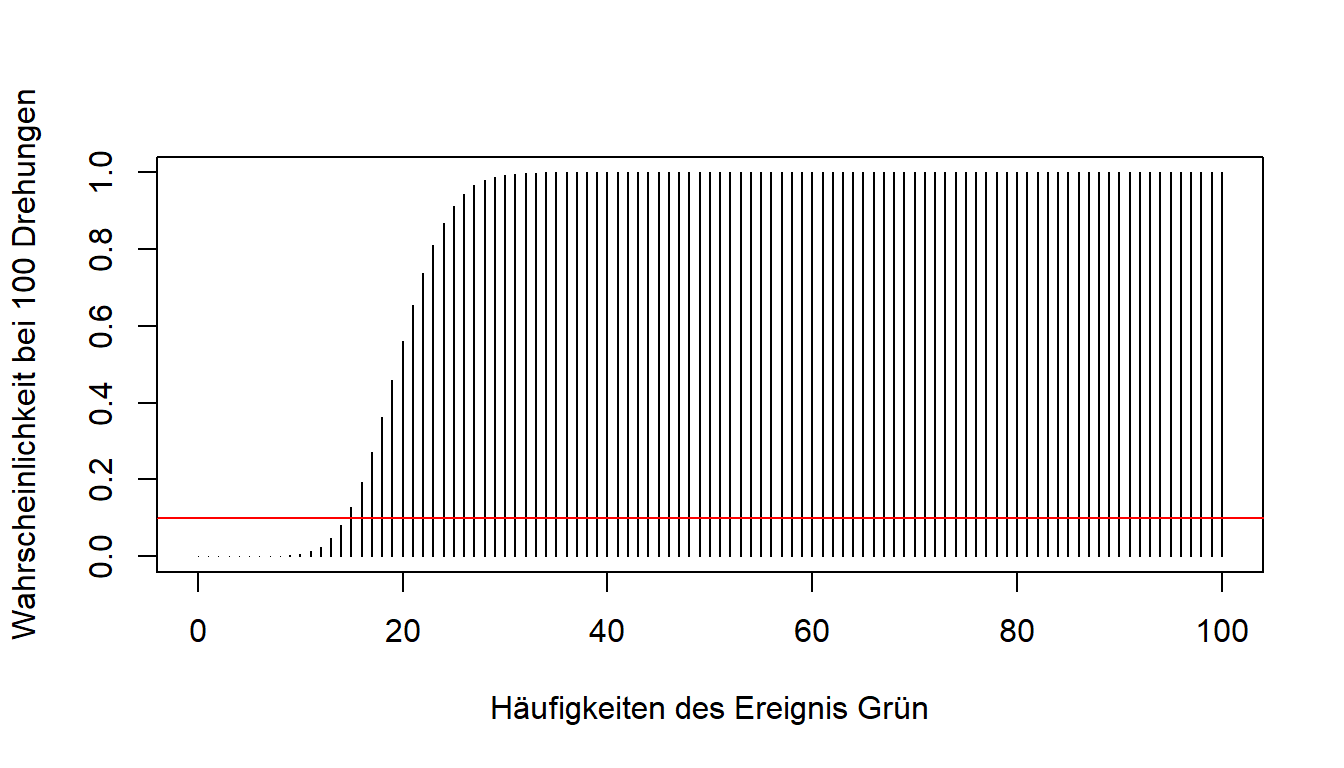
Die Funktion qbinom() beantwortet uns diese entgegengesetzte Fragestellung von pbinom().
qbinom(p = 0.1, size = 100, prob = 0.2, lower.tail = TRUE)## [1] 15p gibt die Anzahl an Prozent an, die die kumulierten Wahrscheinlichkeiten höchstens erreichen dürfen - also 10 Prozent. lower.tail = TRUE steht auch hier dafür, dass wir bei 0 mit der Betrachtung anfangen. Das Ergebnis der Funktion nennt den Wert, der die Grenze überschreitet (in diesem Fall 15). Die kumulierten Wahrscheinlichkeiten von 0 bis 14 Mal grün Drehen übersteigen also nicht unsere Grenze von p = 0.1.
Zum Abschluss noch die Simulation dieses Zufallsexperimentes. Bei rbinom() geben wir in n an, wie oft R unsere 100 Drehungen (size) mit der Wahrscheinlichkeit 0.2 (prob) durchführen soll. Im Bezug auf unser Beispiel wird hier also die Anzahl ausgegeben, wie häufig grün gedreht wird. Beachten Sie, dass bei diesem Befehl ohne set.seed() andere Ergebnisse bei mehrmaliger Durchführung auftreten, da das Experiment ja zufällig durchgeführt wird.
rbinom(n = 1, size = 100, prob = 0.2)## [1] 17Allgemeines Muster
| Präfix | Bedeutung |
|---|---|
| d | density |
| p | probability |
| q | quantile |
| r | random draws |
Diese Präfixe können für alle in R integrierten Verteilungstypen benutzt werden. Eine Übersicht über diese erhält man durch ?distributions.
Stetige Zufallsvariablen
Die Anzahl an Treffern in diesem Experiment stellt eine diskrete Zufallsvariable dar. Zwischen den Werten 4 und 5 Treffer liegen beispielsweise keine anderen Möglichkeiten. Im Gegensatz dazu stehen stetige Zufallsvariablen. Bei diesen liegen zwischen einer Unter- und einer Obergrenze überabzählbar unendlich viele Werte. Beispielsweise liegen zwischen einer Größe von 180 und 181 cm unzählbar viele Abstufungen. Für stetige Zufallsvariablen kann daher nicht einfach eine Wahrscheinlichkeitsfunktion ausgegeben werden, da sie der Theorie nach unendlich viele Balken enthalten würde. Deshalb gibt es hierfür die Dichtefunktion. Die Fläche unter dieser Funktion ergibt einen Wert von 1 - genauso wie die Addition aller Balken einer Wahrscheinlichkeitsfunktion. Viele Merkmale in der Psychologie folgen dabei der Normalverteilung (Größe, IQ, etc.), die Sie in der Vorlesung kennen gelernt haben. Diese stellt eine besondere Form der Dichtefunktion dar mit folgenden Eigenschaften:
- Symmetrisch um
- Glockenförmig
- Wendepunkte bei
- Erwartungswert = Median = Maximum bei
- 68.27% der Verteilung liegen zwischen
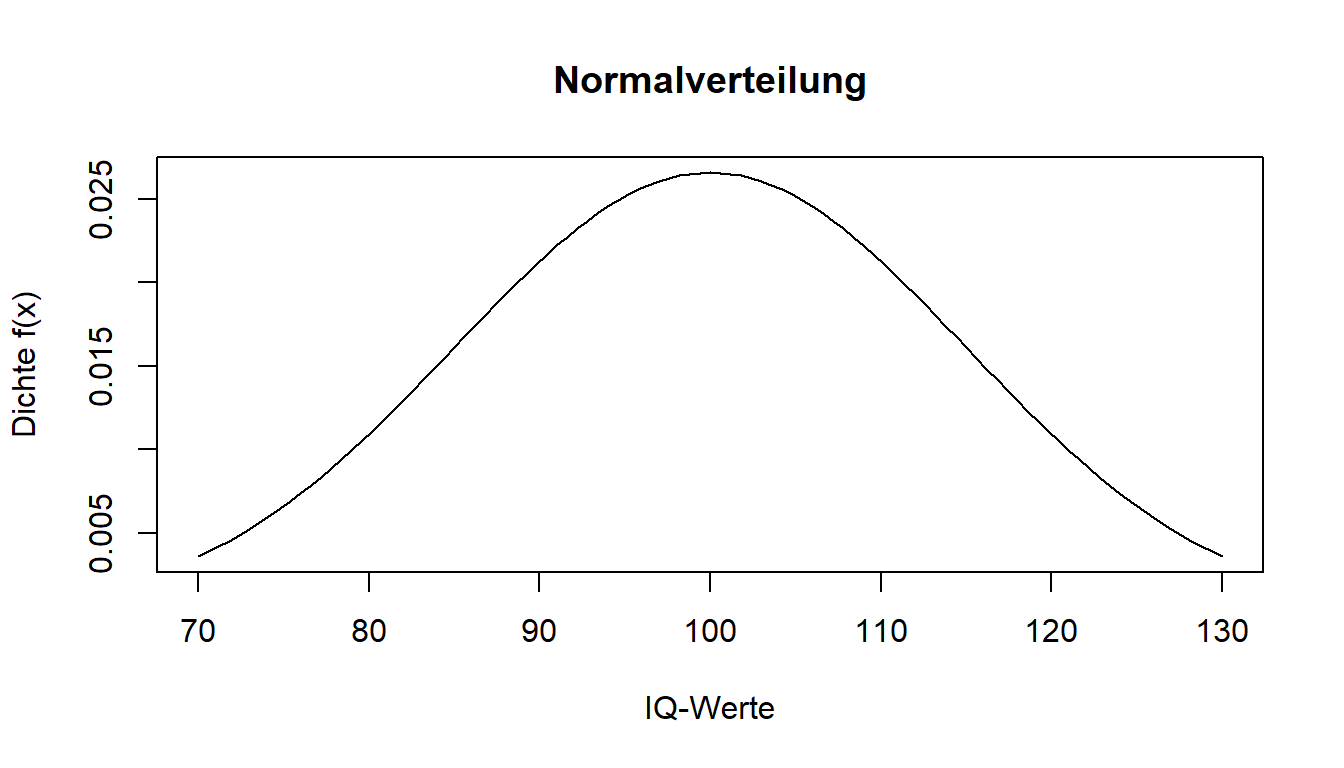
Für die IQ-Verteilung der Population wird angenommen, dass diese den Mittelwert von 100 hat und eine Standardabweichung von 15. Die bewährten Tests werden dahingehend genormt. Wenn wir nun den Wert auf der x-Achse aus der Dichtefunktion eines Probanden erfahren wollen (IQ = 114.3), können wir diesen mit der dnorm() Funktion berechnen. Benötigt werden neben dem x-Wert (in diesem Fall der IQ-Wert) noch der Mittelwert mean und die Standardabweichung sd der zugrundeliegenden Verteilung.
dnorm(x = 114.3, mean = 100, sd = 15) ## [1] 0.01688363Alleine ist der Wert aus der Dichtefunktion noch nicht aussgekräftig für die Anwendung. Trotzdem betrachten wir zunächst den grafischen Aspekt. Wenn wir nun den eben gesehenen Plot zeichnen wollen, verwenden wir bei stetigen Funktionen, wie es die Dichtefunktion eine ist, den Befehl curve(). Dafür muss im Argument expr eine Funktion in Abhängigkeit von x genannt werden. Mit from und to legt man die Grenzen der Bereiche fest. Auf der x-Achse (xlab) sollen die möglichen IQ-Werte, auf der y-Achse (ylab) die zugehörigen Werte der Dichtefunktion f(x) abgebidet werden. Mit main wird ein Titel für die Grafik vergeben.
curve(expr = dnorm(x, mean = 100, sd = 15),
from = 70,
to = 130,
main = "Normalverteilung",
xlab = "IQ-Werte",
ylab = "Dichte f(x)")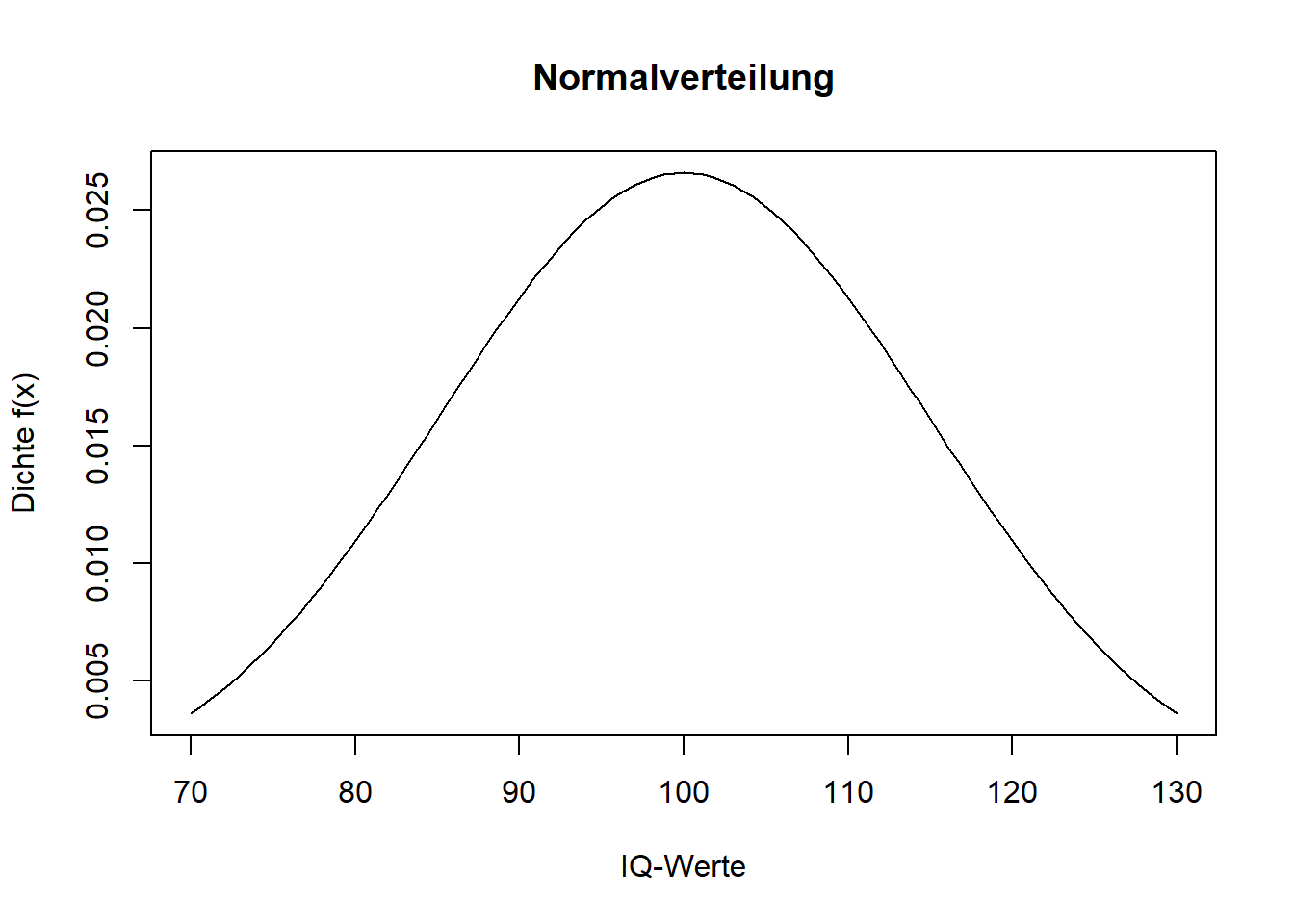
Mit dnorm() konnten wir also einen bestimmten y-Wert aus dieser Verteilung ablesen.
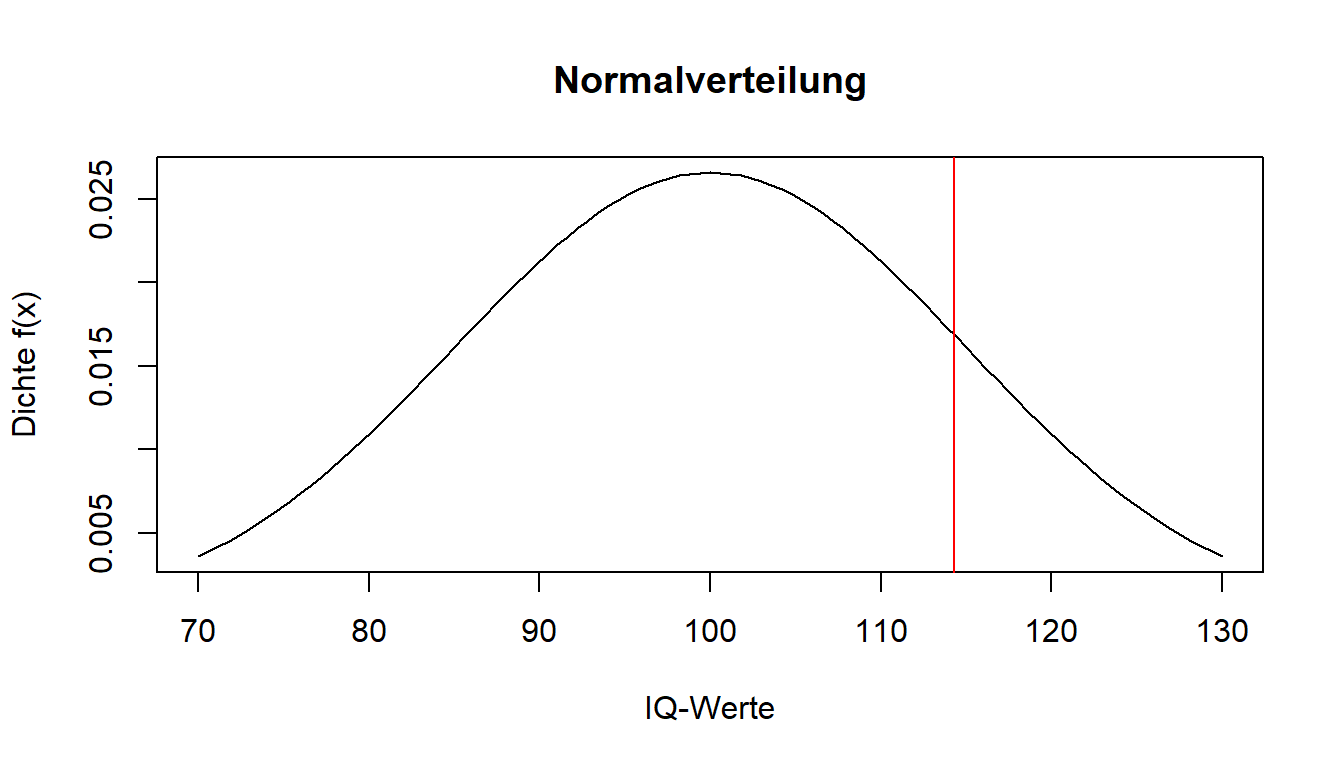
Um für einen bestimmten Wert eine hilfreiche Aussage treffen zu können, wird die Fläche unter der Kurve betrachtet - also die Verteilungsfunktion. Diese ist das Integral (Integrale fungieren zur Flächenbestimmung) der Dichtefunktion. Wie bereits erwähnt ist die Fläche unter der Kurve 1. Nun kann man betrachten, wie groß die Fläche zwischen - und dem Wert einer Person ist, um die Leistung einordnen zu können.
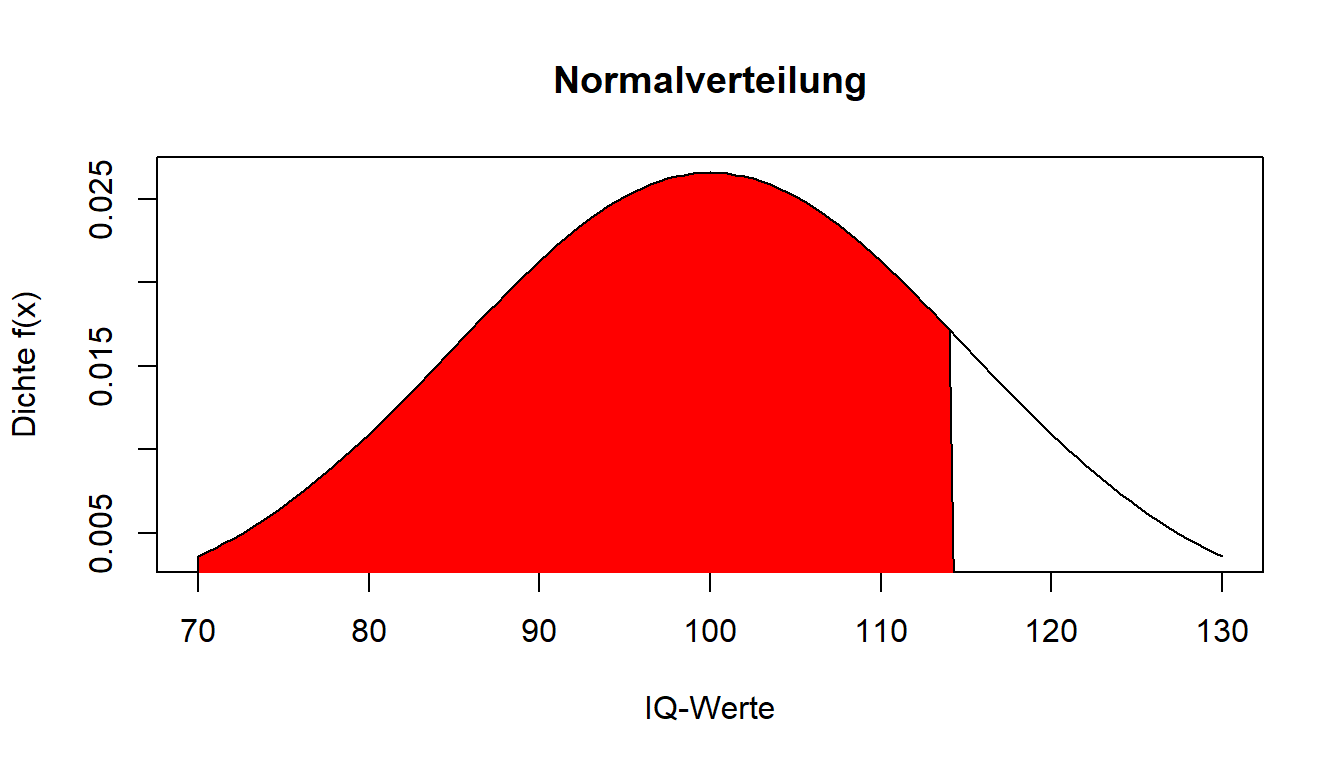
Dafür können auch bei stetigen Variablen die anderen Präfixe wie bei "binom()" genutzt werden. Zur Angabe der Fläche ist der Befehl folglich pnorm(). Das Argument lower.tail steht bei TRUE dafür, dass die Fläche ab - bis zu unserem Wert berechnet wird (FALSE hingegen wäre von unserem Wert bis +).
pnorm(114.3, mean = 100, sd = 15, lower.tail = TRUE)## [1] 0.829789482.98 % der Fläche liegen also unterhalb unseres IQ-Wertes von 114.3. 17.02 % der Fläche liegen hingegen oberhalb unseres IQ-Wertes von 114.3.
Auch hier können wir uns zur Veranschaulichung einmal die Verteilungsfunktion ausgeben lassen. Dafür zeichnen wir die Funktion pnorm(). Die restliche Grafikerstellung funktioniert analog zu dem, was wir bereits gesehen haben, mit der curve() Funktion.
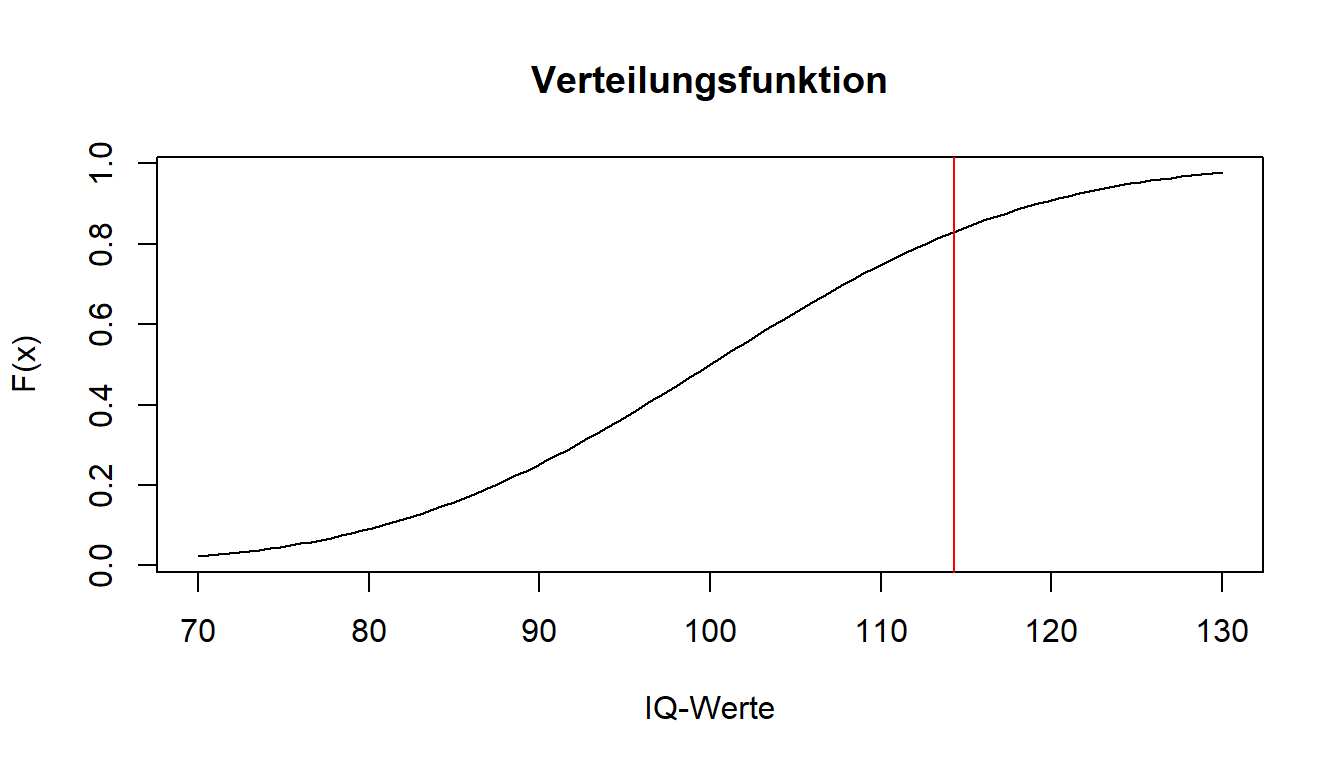
curve(expr = pnorm(x, mean = 100, sd = 15, lower.tail = TRUE),
from = 70,
to = 130,
main = "Verteilungsfunktion",
xlab = "IQ-Werte",
ylab = "F(x)")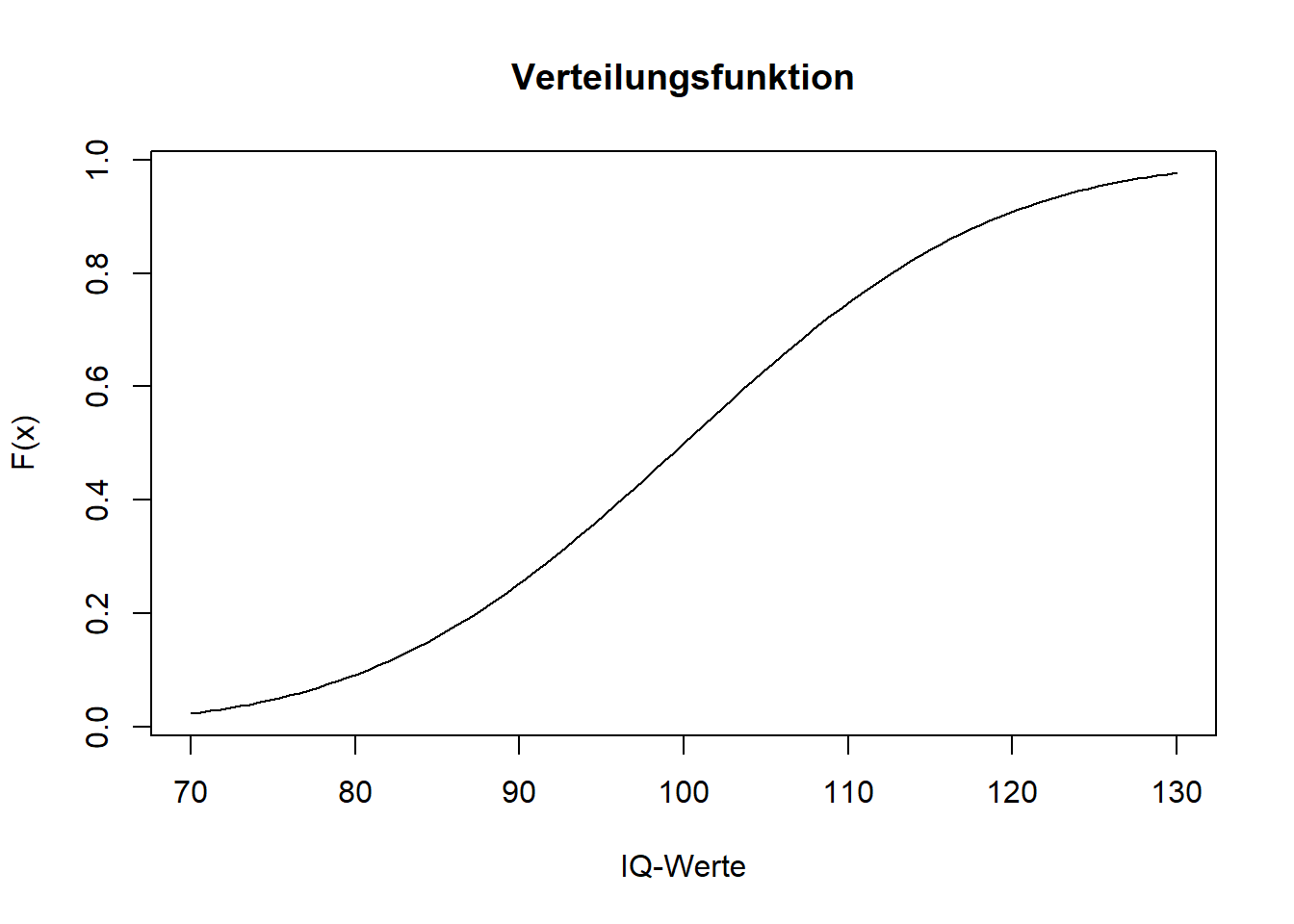
Hier ist schön zu sehen, dass sich die Verteilungsfunktion mit steigendem IQ-Wert der 1 annähert, da dies die Fläche unter der Dichtefunktion ist. Aus der Verteilung haben wir mit pnorm() den y-Wert bei 114.3 ablesen können.
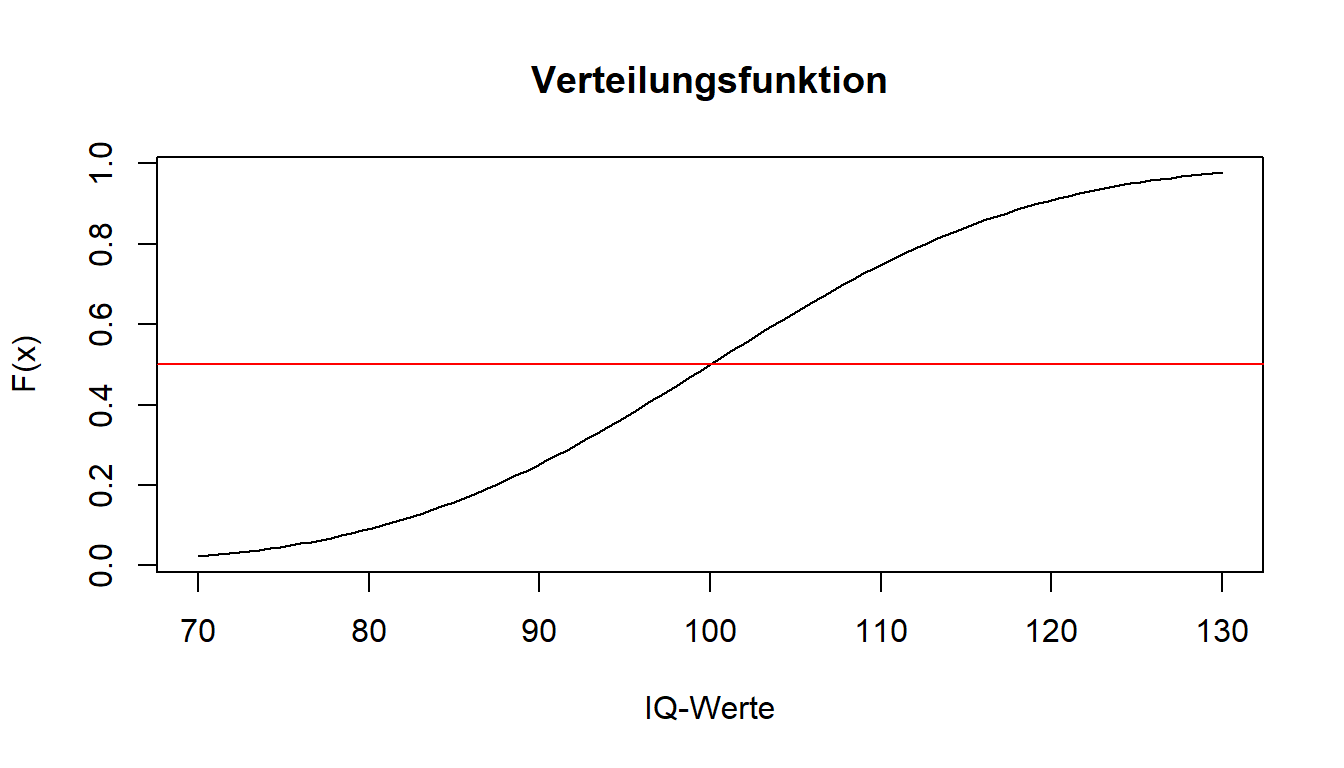
Auch der Präfix "q" funktioniert äquivalent. Durch qnorm() erhalten wir unter Angabe einer Wahrscheinlichkeit den zugehörigen Wert aus der Verteilungsfunktion der Dichte. Wir wollen hier betrachten, welcher Wert die unteren 50% der Verteilung abtrennt.
qnorm(p = 0.5, mean = 100, sd = 15, lower.tail = TRUE)## [1] 100Aufgrund der Symmetrie der Normalverteilung wird hier wie erwartet die Verteilung durch genau ihren Mittelwert (in diesem Fall 100) in 2 Hälften geteilt.
Um die Ziehung aus einer Normalverteilung zu simulieren, können wir mit dem Präfix "r" wieder Daten zufällig auswählen. Anstatt "binom()" folgt nun aber "norm()". Als Argumente werden die Anzahl der Werte, der Mittelwert mean und die Standardabweichung sd der gewünschten Verteilung benötigt. Es werden zufällig 10 Elemente aus einer Normalverteilung gezogen, die den vorgegebenen Parametern entspricht.
set.seed(500) #zur Konstanthaltung der zufälligen Ergebnisse
rnorm(10,mean = 100,sd = 15)## [1] 114.52734 129.48052 113.29484 100.45810 114.24336 91.34905 110.82285
## [8] 109.28648 100.31509 104.12275Normalverteilungsüberprüfung in der Empirie
Kommen wir zum Abschluss des Tutorials nochmal zu einer praktischeren Anwendung. Dafür brauchen wir natürlich den Datensatz, den wir bereits eingeladen haben.
Einige Verfahren, die wir im weiteren Verlauf des Semesters kennenlernen werden, setzen für ihre fehlerfreie Durchführung voraus, dass die untersuchte Variable einer Normalverteilung folgt. Besonders für kleinere Stichproben empfiehlt sich dabei eine optische Prüfung, die wir hier nun vorstellen wollen.
Die erste Möglichkeit besteht darin, dass wir die der Normalverteilung nach erwartete Dichtefunktion über das Histogramm der interessierenden Variable legen und so die Übereinstimmung beurteilen. Wir haben bereits, dass die Funktion hist() ein solches Histogramm zeichnet. Unter xlim legen wir fest, dass das Diagramm nur zwischen 0 und 6 gezeichnet wird, da die Fragebogenscores nur zwischen 1 und 5 sein konnten. Damit stellen wir ein schöneres Aussehen des Plots sicher. Genauso wählen wir eine Überschrift, während wir die Achsenbezeichungen weglassen. Mit dem Argument probability können wir dafür sorgen, dass nicht absolute Häufigkeiten abgetragen werden (sondern wieder Dichte). Die Summe der Fläche der Balken im Plot wird damit auf 1 gesetzt - diesen Wert kennen wir auch von der Dichtefunktion der Normalverteilung. Auch unter dieser Funktion ist die Fläche gleich 1.
hist(fb22$nerd, xlim=c(0,6), main="Score", xlab="", ylab="", probability=T)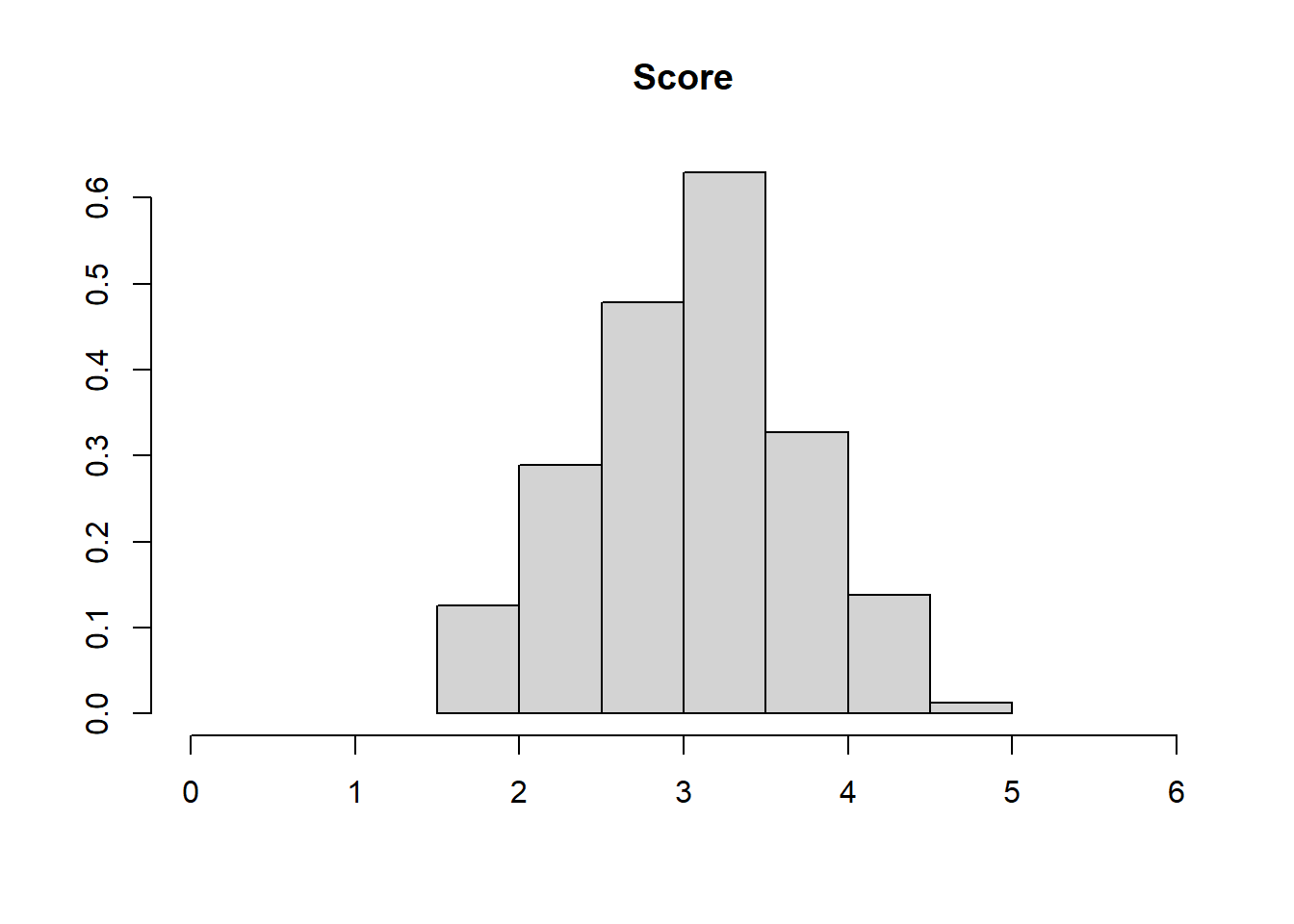
Jetzt müssen wir die Normalverteilung noch dazu zeichnen. Hiefür nutzen wir wieder die curve() Funktion. Da wir bereits einen Plot (das Histogramm) gezeichnet haben, können wir mit dem Argument add dafür sorgen, dass die Kurve in das bestehende Bild integriert wird. Daher müssen wir keine Angaben für from, to und Ähnliches machen. Lediglich die Form der Verteilung als Dichtefunktion der Normalverteilung dnorm() und die dazu gehörigen beschreibenden Maße Mittelwert und Standardabweichung (hervorgehend aus unserer Nerdiness Variable) werden benötigt.
curve(dnorm(x, mean=mean(fb22$nerd), sd=sd(fb22$nerd)), add=T)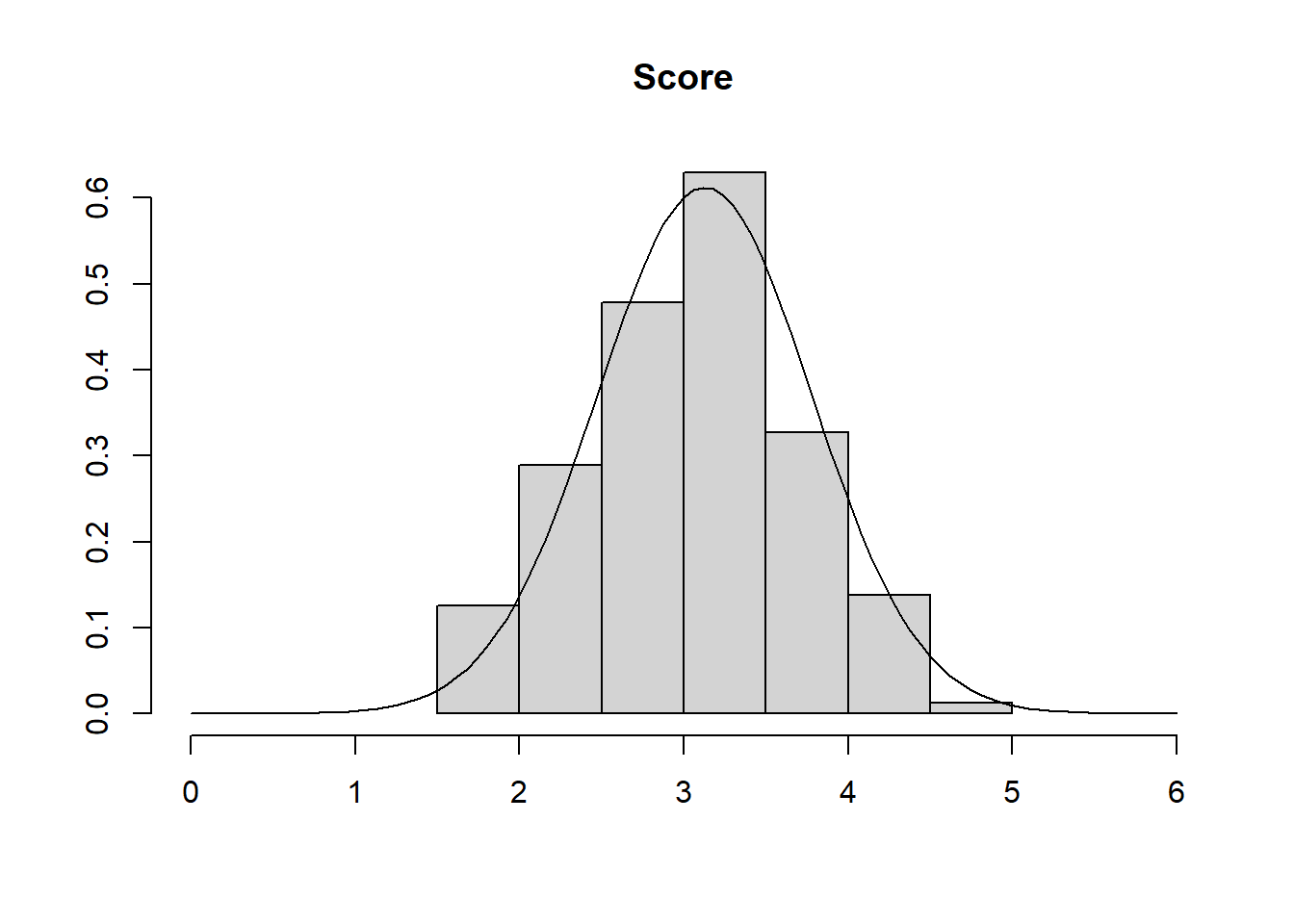
Im Plot sieht man recht gut, dass es kleine Abweichungen der wirklichen empirischen Verteilung von der perfekten Form der Normalverteilung gibt. Kleinere Abweichungen sind jedoch zu erwarten und sollten nicht zu hoch eingestuft werden. Leider wird es bei der optischen Prüfung keine perfekt objektive Lösung geben, doch je mehr Plots man im Laufe der Forschungskarriere betrachtet, umso besser kann man auch diese Verläufe einordnen.
Eine zweite Möglichkeit ist das Erstellen eines sogenannten QQ-Plots (steht für quantile-quantile). Auf der x-Achse sind diejenige Positionen notiert, die unter Gültigkeit der theoretischen Form der Normalverteilung zu erwarten wären. Auf der y-Achse wird die beobachtete Position eines Messwerts abgetragen. Damit die Werte die gleiche Skalierung haben und damit einfacher interpretierbar sind, standardisieren wir zunächst unsere Variable neuro. Hierür erstellen wir eine neue Variable neuro_std in unserem Datensatz. Codetechnisch ist ein QQ-Plot dann schnell erstellt. Mit qqnorm() zeichnet man die Punkte, während qqline() als Unterstützung nochmal die Linien durch die Mitte zeichnet.
fb22$nerd_std <- scale(fb22$nerd, center = T, scale = T)
qqnorm(fb22$nerd_std)
qqline(fb22$nerd_std)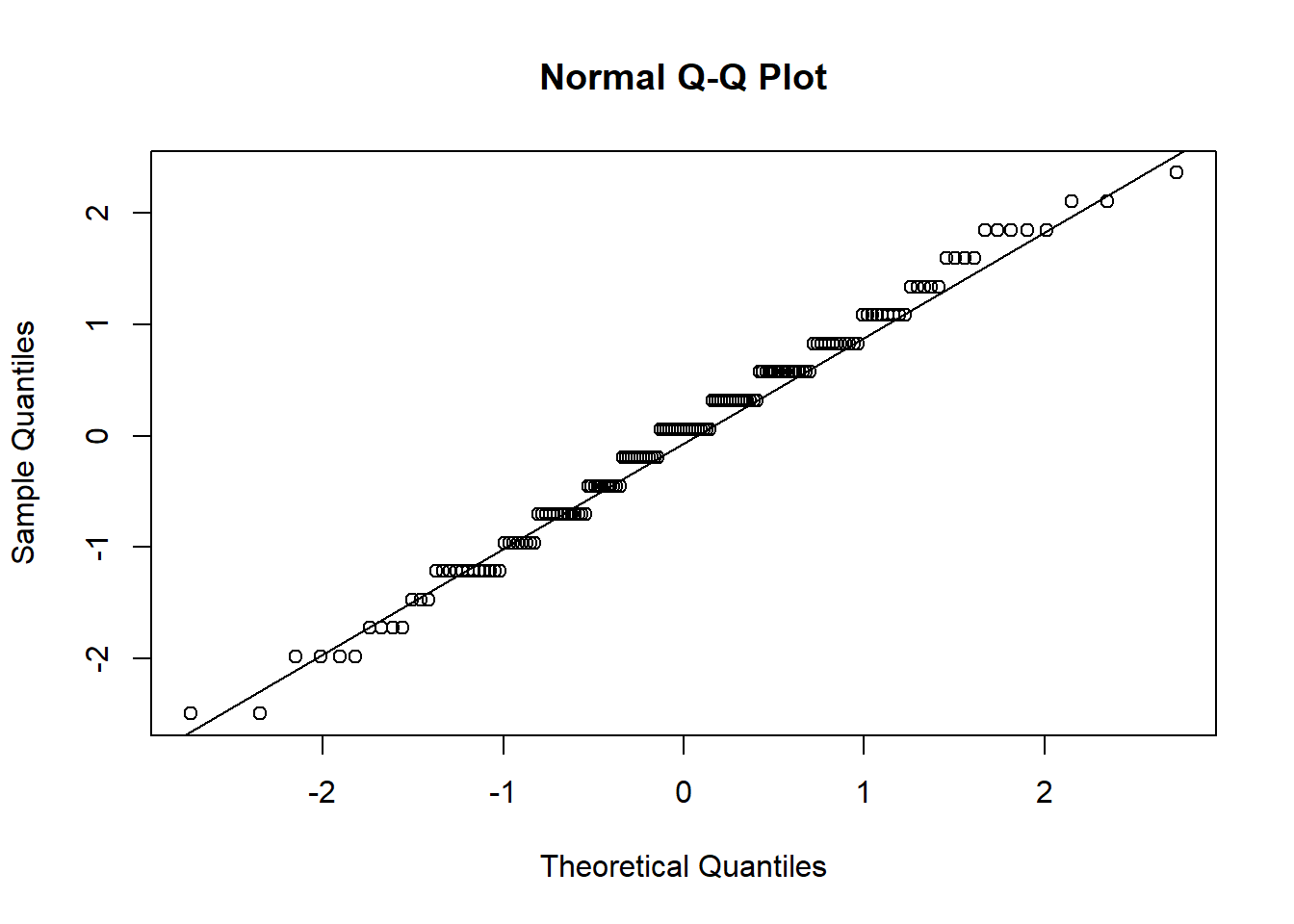
Entspricht nun unsere empirische Datenmenge der angenommenen Normalverteilung perfekt, würden alle Punkte auf der Geraden in der Mitte liegen. Auch hier gilt natürlich, dass die Bewertung letztlich eine gewisse Subjektivität hat. Die Punkte sollten nicht zu weit von der Geraden entfernt liegen. Für unsere Nerdiness Variable können nur leichte Abweichungen festgestellt werden, weshalb wir die Normalverteilung annehmen können.
Die beschriebenen optischen Überprüfungen waren nur eine kleine Einführung zur Normalverteilung in der Empirie. Wir werden in den nächsten Wochen noch andere Aspekte und Überprüfungen kennenlernen.
