ANOVA I: einfaktorielle ANOVA
1-fakt. ANOVA
In den letzten Sitzungen haben wir uns ausführlicher mit dem Zusammenhang zwischen Variablen in Form von Korrelation und Regression beschäftigt. Nun möchten wir untersuchen, ob es einen Unterschied zwischen mehreren Gruppen hinsichtlich der Mittelwerte in einer Variablen gibt. Im letzten Semester haben Sie schon den t-Test kennen gelernt, mit dem Mittelwertsunterschiede zwischen zwei Gruppen untersucht werden können. Wenn wir nun mehr als zwei Gruppen miteinander vergleichen möchten, müssten wir mehrere t-Tests mit allen Kombinationen durchführen. Bei z. B. 3 Gruppen müssten wir t-Tests durchführen. Wie Sie sicherlich noch wissen, führt dies aber zu einer -Fehler-Inflation oder -Kumulierung. In diesem Fall muss demnach eine ANOVA genutzt werden. Da wir den Unterschied auf einer Gruppenvariable wissen wollen, nutzen wir die einfaktorielle ANOVA. Wie das Verfahren für mehrere Gruppenvariablen ist, wird in der nächsten Sitzung besprochen. Mehr zur einfaktoriellen ANOVA finden Sie in Eid, Gollwitzer und Schmitt (2017, Kapitel 13 und insb. 13.1 und folgend).
Die praktische Arbeit soll anhand des Datensatzes conspiracy demonstriert werden, den wir also zunächst in unser Environment laden müssen.
Daten laden
Wenn Sie den Datensatz lokal auf ihrem Rechner haben möchten, können Sie ihn Datensatz “conspiracy.rda” hier herunterladen. Anschließend muss er eingeladen werden - natürlich mit Ihrem Dateipfad.
load("C:/Users/Musterfrau/Desktop/conspiracy.rda")Alternativ kann der Datensatz durch die Nutzung von url auch direkt über die Website eingeladen werden.
load(url("https://pandar.netlify.app/post/conspiracy.rda"))Der Datensatz stammt aus einer Untersuchung zum Thema verschwörungstheoretische Überzegungen. Beginnen wir mit einer kurzen Inspektion.
dim(conspiracy)## [1] 2451 9Der Datensatz enthält die Werte von 2451 Personen auf 9 Variablen.
head(conspiracy)## edu urban gender age GM MG ET PW
## 2 highschool suburban female 14 4.000000 5.000000 4.666667 3.333333
## 3 college suburban female 26 2.000000 4.000000 1.500000 2.000000
## 4 college rural male 25 5.000000 4.333333 1.000000 3.333333
## 5 not highschool suburban male 37 5.000000 4.333333 2.333333 3.333333
## 6 college rural male 34 1.000000 1.000000 1.000000 1.000000
## 7 not highschool suburban male 17 3.333333 2.666667 3.000000 2.666667
## CI
## 2 4.666667
## 3 3.333333
## 4 4.666667
## 5 4.666667
## 6 1.000000
## 7 3.666667Die ersten vier Variablen enthalten Informationen über den demographischen Hintergrund der Personen: höchster Bildungsabschluss (edu), Typ des Wohnortes (urban), Geschlecht (gender) und Alter (age). Die fünf restlichen Variablen sind Skalenwerte bezüglich verschiedener Subdimensionen verschwörungstheoretischer Überzeugungen: GM (goverment malfeasance), MG (malevolent global conspiracies), ET (extraterrestrial cover-up), PW (personal well-being) und CI (control of information).
Aufgestellte Hypothesen
Die Durchführung der ANOVA benötigt natürlich Hypothesen, die uns bei der Auswertung interessieren. In unserem Beispiel soll untersucht werden, ob sich Personen je nach Ländlichkeit ihres Wohnortes (rural, suburban, urban) in der Überzeugung unterscheiden, inwiefern die Existenz von Außerirdischen geheimgehalten wird (Beispielitem: Evidence of alien contact is being concealed from the public).
In der einfaktoriellen ANOVA wird die Gleichheit aller Gruppenmittelwerte als Nullhypothese postuliert - also dass sich Bewohner:innen des ländlichen Raums (rural), des vorstädtischen Raums (suburban) und der Stadt (urban) nicht hinsichtlicher ihrer Zustimmung zur Verschwörungstheorie Extraterrestrial Cover-Up (ET) unterscheiden:
Im Rahmen der vorliegenden Daten müssen wir beachten, dass die der Variablenname urban genauso gewählt wurde, wie eine seiner Ausprägungen (für den städtischen Raum). Für bestimmte Code-Abschnitte ist es wichtig, das im Hinterkopf zu behalten, um nicht verwirrt zu werden.
Bei der Alternativhypothese wird angenommen, dass sich mindestens zwei dieser Subgruppen im Mittel voneinander unterscheiden:
für mindestens ein Paar mit
Wir benutzen hier die Indizes und , um den Vergleich der Mittelwerte von zwei unterschiedlichen Subgruppen darzustellen. Für und könnte dies z. B. den Vergleich der Subgruppen “rural” und “suburban” anzeigen. Die Ungleichung bedeutet in diesem Zusammenhang, dass wir in der Formulierung der Alternativhypothese immer nur unterschiedliche Gruppen miteinander vergleichen, nie aber eine Subgruppe mit sich selbst, was im Übrigen auch ein aussageloser Vergleich wäre, da wir nur einen Datenpunkt für jede Person haben. Dies wäre nur sinnvoll, wenn wir die gleiche Stichprobe mehrfach gemessen hätten. Wie dies dann mitmodelliert wird, erfahren wir im Rahmen der ANOVA mit Messwiederholung.
Voraussetzungsprüfung
Es werden drei Voraussetzungen für die Anwendung einer ANOVA vorgegeben:
- Unabhängigkeit der Residuen
- Homoskedastizität
- Normalverteilung
1) Unabhängigkeit der Residuen
Die Unabhängigkeit der Residuen wäre dann verletzt, wenn abhängige Stichproben vorliegen oder die Stichproben in den Gruppen nicht zufällig zustandegekommen sind (keine Randomisierung). Dies muss also beachtet werden. In unserem Beispiel sind die Stichproben über die Wohnorte hinweg wahrscheinlich nicht abhängig voneinander. Es kann zwar familiäre Bezüge geben, jedoch sollten deren Effekte eher gering ausfallen. Auch die Residuen innerhalb der Gruppen sollten unabhängig sein, da die Personen nicht bewusst einem bestimmten Wohnort zugeordnet wurden, sondern sich dies durch viele Faktoren ergibt. Daher sollte in unserem Beispiel die Unabhängigkeit der Residuen gegeben sein. Wie Sie merken, ist die Unabhängigkeitsannahme schwer zu prüfen und wird daher so gut wie immer durch das Design der Studie “gewährleistet” - bspw. durch Randomisierung.
2) Homoskedastizität
Die Homoskedastizitätsannahme besagt, dass die Varianzen jeder Gruppe über die Gruppen hinweg gleich sind. Deshalb wird diese Annahme auch häufig “Varianzhomogenitätsannahme” genannt. Zur Überprüfung der Homoskedatizität kann der Levene-Test herangezogen werden. Dieser kann mithilfe des car-Pakets angefordert werden. Dazu laden wir zunächst das Paket und führen anschließend die Funktion leveneTest aus. Installiert haben wir das Paket bereits in vorherigen Tutorials und dort auch bereits angewendet.
library(car)## Lade nötiges Paket: carDataleveneTest(conspiracy$ET ~ conspiracy$urban)## Levene's Test for Homogeneity of Variance (center = median)
## Df F value Pr(>F)
## group 2 2.5335 0.07959 .
## 2448
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Die Funktion nimmt die Variable selbst entgegen sowie die Gruppierungsvariable. ET aus dem conspiracy-Datensatz stellt hierbei die AV dar, die Gruppierungsvariable urban ist die UV. Wir erkennen im Output, was genau der Levene-Test eigentlich macht: Levene's Test for Homogeneity of Variance, nämlich die Varianzen auf Homogenität prüfen. Das Ergebnis ist nicht signifikant. In diesem Fall muss die Annahme der Varianzhomogenität über die drei Gruppen hinweg also nicht verworfen werden.
3) Normalverteilung
Innerhalb jeder Gruppe sollte eine Normalverteilung vorliegen. Diese Annahme bezieht sich, entgegen häufiger Vermutung, auf die Residuen der ANOVA. Wir erkennen diese Annahme aus der Regressionsanalyse wieder, wo wir ebenfalls die Normalverteilung der Residuen, behandelt in Regression III, annahmen, um Inferenzstatistik zu betreiben. Um auf die Residuen einer ANOVA zuzugreifen, kann der Befehl residuals oder resid auf ein aov-Objekt angewendet werden. Das Modell muss also zunächst aufgestellt werden. Mehr zum aov-Befehl folgt beim Tukey-Test.
Einfaktorielle ANOVA per Hand
Die einfaktorielle ANOVA arbeitet mit einer Quadratsummenzerlegung. Hierbei werden Unterschiede/Variationen zwischen den Gruppen () und Unterschiede/Variationen innerhalb der Gruppen () getrennt betrachtet und bestimmt. Die Variation zwischen den Gruppen kann als bedingt durch die unterschiedliche Gruppenzugehörigkeit interpretiert werden, wobei die Variation innerhalb einer Gruppe von den Individuen, die der Gruppe zugehörig sind, bedingt wird. Die Gesamtvariation wird als totale Quadratsumme () bezeichnet und ergibt sich wie folgt:
wobei
mit = Index der Personen, = Index der Gruppe, = Anzahl der Gruppen, ist die Gruppengröße der k-ten Gruppen.
Die Quadratsummen der ANOVA können per Hand bestimmt werden. Hierzu nutzen wir den aggregate()-Befehl, der es erlaubt, eine zusammenfassende Statistik (wie Mittelwert oder Standardabweichung) für eine Variable getrennt nach verschiedenen Subgruppen zu berechnen. Dabei übergeben wir aggregate die Variable selbst sowie die Gruppierungsvariable als Liste (deshalb steht im Befehl auch list(conspiracy$urban)), als drittes Argument wird die Funktion übergeben, die durchgeführt werden soll:
mu_k <- aggregate(conspiracy$ET, list(conspiracy$urban), mean)
mu_k## Group.1 x
## 1 rural 2.194386
## 2 suburban 2.150963
## 3 urban 2.307286Unser erstelltes Objekt mu_k enthält also die Mittelwerte der drei Gruppen. Da die Variablennamen nicht sehr aussagekräftig sind, überschreiben wir diese.
names(mu_k) <- c('urban', 'ET_mu_k')Wir wollen nun die Mittelwerte der Gruppen zu unserem ursprünglichen Datensatz hinzufügen. Es soll eine neue Spalte entstehen, die jeder Person den Mittelwert der Gruppe zuweist, in der sie wohnhaft ist. Ein solches Zusammenführen ist mit der Funktion merge möglich. Dafür müssen wir zunächst die beiden Datensätze angeben, die zusammengefügt werden sollen (conspiracy und mu_k). Natürlich müssen wir R auch noch mitteilen, welche Variable das Zusammenfügen ermöglicht. Diese (in beiden Datensätzen gleiche) Variable heißt urban und wird dem Argument by übergeben. Wir nennen das neue Objekt temp für seine temporäre Nutzung.
temp <- merge(conspiracy, mu_k, by = 'urban')
dim(temp)## [1] 2451 10names(temp)## [1] "urban" "edu" "gender" "age" "GM" "MG" "ET"
## [8] "PW" "CI" "ET_mu_k"Anhand der Dimensionen können wir sehen, dass unser neuer Datensatz nun eine Variable mehr hat als conspiracy. Diese zusätzliche Spalte ist genau die, die die Mittelwerte pro Gruppe enthält (ET_mu_k).
Weitere nötige Informationen für die händische Berechnung der Quadratsummen sind der Gesamtmittelwert und auch die Gruppengröße. Diese können mit uns bekannten Funktion einfach bestimmt werden.
# Gesamtmittelwert ermitteln
mu <- mean(conspiracy$ET)
# Gruppengrößen ermitteln
n_k <- table(conspiracy$urban)Nach diesen Vorbereitungen können wir die Quadratsummen und berechnen. beschreibt die quadratischen Abweichungen aller Gruppenmitglieder von ihrem Gruppenmittelwert. Diese beiden Informationen sind in unserem temporären Datensatz temp in den Variablen temp$ET und temp$ET_mu_k festgehalten.
QS_inn <- sum((temp$ET - temp$ET_mu_k)^2)Die Berechnung von benötigt die einzelnen Gruppengrößen, die wir unter n_k abgelegt haben. Diese werden jeweils mit dem quadrierten Unterschied ihres Gruppenmittelwertes vom Gesamtmittelwert multipliziert. Die einzelnen Gruppenmittelwerte sind in mu_k abgelgt. mu_k[, 2] wird hier so verwendet, da in mu_k in der ersten Spalte die Gruppenzugehörigkeiten stehen und in der 2. Spalte die Mittelwerte selbst. Der Gesamtmittelwert liegt in mu.
QS_zw <- sum(n_k * (mu_k[, 2] - mu)^2)Zur inferenzstatistischen Prüfung wird der -Test herangezogen. Um diesen verwenden zu können, brauchen wir die mittleren Quadratsummen und . Dabei steht für die Anzahl aller Personen in der Stichprobe und für die Anzahl an Gruppen. Folglich können die beiden Werten mit diesem Code per Hand bestimmt werden:
MQS_inn <- QS_inn / (nrow(conspiracy) - nlevels(conspiracy$urban))
MQS_zw <- QS_zw / (nlevels(conspiracy$urban)-1)Nun können wir den -Wert bestimmen. Dieser ergibt sich als
Wir erkennen, dass hier einfach die Variation zwischen den Gruppen (Variation der Mittelwerte) relativ zur (zufälligen) Variation innerhalb der Gruppen betrachtet wird. Ist die Variation zwischen den Gruppen relativ zur zufälligen Variation groß, so kann dies nicht durch Zufall passiert sein: die Mittelwerte müssen sich also bei einem großen -Wert unterscheiden.
F_wert <- MQS_zw/MQS_innDas Verhältnis der Quadratsummen ist mit und -verteilt. Daher wird der mit dem mit (Zählerfreiheitsgraden) und (Nennerfreiheitsgraden) verglichen. In R geht das automatisch mit pf (die Verteilungsfunktion/ kumulative Dichtefunktion der -Verteilung). Diese gibt uns den -Wert wieder. Hierbei muss zunächst der angegeben werden, danach und als letztes . lower.tail = FALSE zeigt uns, dass wir gerne die Wahrscheinlichkeit (Fläche unter der Kurve) für extremere Werte als unseren beobachtenen angezeigt bekommen:
pf(F_wert, nlevels(conspiracy$urban)-1, nrow(conspiracy) - nlevels(conspiracy$urban), lower.tail = FALSE)## [1] 0.03240931Grafisch gesehen lassen wir uns also die Fläche für den folgenden Bereich der F-Verteilung anzeigen.

Zur Beurteilung der Signifikanz muss der errechnete p-Wert mit dem vorher festgelegten -Niveau verglichen werden. Nehmen wir die üblichen 5% an, zeigt sich hier ein signifikanter Effekt.
Die ezANOVA
Da das Ausrechnen per Hand nun doch etwas umständlich ist, bietet R uns einige andere Möglichkeiten, z. B. anova oder aov und diverse weitere Pakete (z. B. Anova aus car). Allerdings haben die verschiedenen Ansätze jeweils ihre Vor- und Nachteile, weshalb die ezANOVA-Funktion aus dem ez-Paket erstellt wurde, um als Meta-Funktion zu dienen, die sich situationsspezifisch bei den grundlegenden Funktionen bedient. Da wir das Paket bisher nicht genutzt haben, müssen wir es zunächst installieren.
# Paket installieren
install.packages("ez")Anschließend kann es geladen werden.
# Paket laden
library(ez)## Warning: Paket 'ez' wurde unter R Version 4.2.3 erstelltWeil die Funktion für verschiedene Arten von ANOVAs geeignet ist, benötigt sie einige sehr spezifisiche Argumente. Für die einfaktorielle ANOVA werden vier Argumente benötigt:
data =: der genutzte Datensatzwid =: eine Personen ID-Variabledv =: die abhängige Variable (dependent variable)between =: eine Gruppierungsvariable (die zwischen Personen unterscheidet)
In unserem Datensatz liegt leider noch keine ID-Variable vor, diese muss also zunächst erstellt werden. Der Einfachheit halber nummerieren wir die Personen von 1 bis 2451 durch.
conspiracy$id <- 1:nrow(conspiracy)Damit festgehalten wird, dass es sich bei der ID um eine nominalskalierte Variable und nicht um Zahlen handelt, wandeln wir diese direkt in einen factor um.
conspiracy$id <- as.factor(conspiracy$id)Jetzt kann die ANOVA mit dem ezANOVA-Befehl durchgeführt werden, indem wir einfach den oben stehenden Argumenten unsere Variablen übergeben:
ezANOVA(conspiracy, wid = id, dv = ET, between = urban)## Warning: Data is unbalanced (unequal N per group). Make sure you specified a
## well-considered value for the type argument to ezANOVA().## Coefficient covariances computed by hccm()## $ANOVA
## Effect DFn DFd F p p<.05 ges
## 1 urban 2 2448 3.434118 0.03240931 * 0.002797802
##
## $`Levene's Test for Homogeneity of Variance`
## DFn DFd SSn SSd F p p<.05
## 1 2 2448 3.62836 1752.977 2.533469 0.0795913Zunächst werden wir mit einer ## Warning darauf hingewiesen, dass das Desgin unbalanciert ist: die Gruppen sind nicht alle gleich groß. Das kann Konsequenzen auf die Vertrauenswürdigkeit der Ergebnisse haben, wenn wir ANOVAs mit mehr als einem Faktor bestimmen (dazu mehr in der nächsten Sitzung zur zweifaktoriellen ANOVA.
Die zweite Hälfte der Ergebnisse ($Levene's Test for Homogeneity of Variance) liefern die Überprüfung der Homoskedastizitätsannahme mit dem Levene Test. Dieser wird von ezANOVA immer automatisch mitgeliefert. Wie zu erwarten, zeigt sich das selbe Ergebnis wie mit dem leveneTest aus dem car-Paket.
Der erste Abschnitt der Ausgabe der ezANOVA-Funktion liefert die Ergebnisse der ANOVA selbst. Dabei wird zunächst die unabhängige Variable aufgeführt (Effect), dann die Anzahl der Zählerfreiheitsgrade (DFn = ), dann die Anzahl der Nennerfreiheitsgrade (DFd = ). Darauf wiederum folgt der -Wert (F = ) und der resultierende -Wert. In diesem Fall wird die Nullhypothese bei einem -Fehlerniveau von .05 verworfen: die Mittelwerte der drei Gruppen sind nicht gleich. Der * in der nächsten Spalte liefert uns diesbezüglich einen optischen Hinweis.
Die letzte Spalte liefert das generalisierte (ges = Generalized Eta-Squared), ein Effektstärkemaß für ANOVAs. Dieses berechnet sich in diesem Fall einfach aus . Um die Quadtratsummen (SSn = ,SSd = ) zu erhalten, kann mithilfe des Arguments detailed = TRUE eine detaillierte Ausgabe angefordert werden.
ezANOVA(conspiracy, wid = id, dv = ET, between = urban, detailed = TRUE)## Warning: Data is unbalanced (unequal N per group). Make sure you specified a
## well-considered value for the type argument to ezANOVA().## Coefficient covariances computed by hccm()## $ANOVA
## Effect DFn DFd SSn SSd F p p<.05 ges
## 1 urban 2 2448 12.05839 4297.891 3.434118 0.03240931 * 0.002797802
##
## $`Levene's Test for Homogeneity of Variance`
## DFn DFd SSn SSd F p p<.05
## 1 2 2448 3.62836 1752.977 2.533469 0.0795913Für haben sich - wie für viele Effektgrößen - Konventionen bezüglich der Interpretation etabliert. Für die Varianzanalyse wird als kleiner, als mittlerer und als großer Effekt interpretiert. Der Wert in unserem Beispiel liegt somit noch unter der Schwelle zu einem kleinen Effekt - die Gruppenunterschiede sind zwar statistisch signifikant von null verschieden, praktisch aber kaum bedeutsam.
Post-Hoc Analysen
Die ANOVA ist ein Omnibustest - es wird lediglich die Gleichheit aller Gruppen geprüft. Wenn die Nullhypothese verworfen wird, geben die Ergebnisse zunächst keine Auskunft darüber, welche Gruppen sich unterscheiden. Die detaillierte Untersuchung der Gruppenunterschiede wird in der Post-Hoc-Analyse unternommen.
t-Tests
Die naheliegende Untersuchung wäre hier, alle drei Gruppen mithilfe einfacher -Tests zu vergleichen. Da wir hier nicht nur zwei Ausprägungen in unserer Gruppierungsvariable haben, nutzen wir den Befehl pairwise.t.test. Aufgrund der -Fehler Kumulierung müssen die -Werte adjustiert werden (p.adjust = 'bonferroni'). Dabei ist die Bonferroni-Korrektur einer der einfachsten (und gleichzeitig konservativsten) Ansätze: , wobei die Anzahl der durchgeführten Tests ist.
pairwise.t.test(conspiracy$ET, conspiracy$urban, p.adjust = 'bonferroni')##
## Pairwise comparisons using t tests with pooled SD
##
## data: conspiracy$ET and conspiracy$urban
##
## rural suburban
## suburban 1.000 -
## urban 0.411 0.028
##
## P value adjustment method: bonferroniHier zeigt sich, dass sich ausschließlich Personen aus urban und suburban Umgegbungen in ihrer Überzeugung bezüglich des Extraterrestrial Cover-Ups unterscheiden ( < .05).
Tukey Test
Ein präziserer Ansatz als die einfachen -Tests bietet Tukeys Honest Significant Difference (auch Tukey-Test genannt). Dieser kann in R allerdings nur auf aov-Objekte angewendet werden. Der aov-Befehl führt zum selben Ergebnis wie ezANOVA. Zu Unterschieden kann es erst bei der zweifaktoriellen ANOVA kommen, da dort der Typ der Quadratsumme ein Rolle spielt, wie diese ausfällt.
aov-Befehl
Der benötigte Code in der Funktion aov ähnelt dem der Regressionsanalyse und im Übrigen auch der Gleichung in leveneTest aus dem car-Paket. In unserem Beispiel sieht der aov-Befehl so aus.
alternative<- aov(ET ~ urban, data = conspiracy)Wir können die summary-Funktion, analog zur Regressionanalyse, darauf anwenden, um die Signifikanzentscheidungen zu sehen
summary(alternative)## Df Sum Sq Mean Sq F value Pr(>F)
## urban 2 12 6.029 3.434 0.0324 *
## Residuals 2448 4298 1.756
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Diese entsprechen also wie erwartet unserem vorherigen Ergebnis.
Schauen wir uns nun Tukey’s Test an. Die Funktion TukeyHSD benötigt das durch aov erstellte Objekt und die erwünschte Sicherheit.
TukeyHSD(alternative, conf.level = 0.95)## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = ET ~ urban, data = conspiracy)
##
## $urban
## diff lwr upr p adj
## suburban-rural -0.0434230 -0.21345311 0.1266071 0.8207046
## urban-rural 0.1128996 -0.06507135 0.2908705 0.2969918
## urban-suburban 0.1563226 0.01515294 0.2974922 0.0256251Das Ergebnis bietet neben den einfachen -Werten auch korrigierte Konfidenzintervalle für die Mittelwertsdifferenzen. Darüber hinaus können die Ergebnisse auch in einem Plot dargestellt werden:
tuk <- TukeyHSD(aov(ET ~ urban, data = conspiracy))
plot(tuk)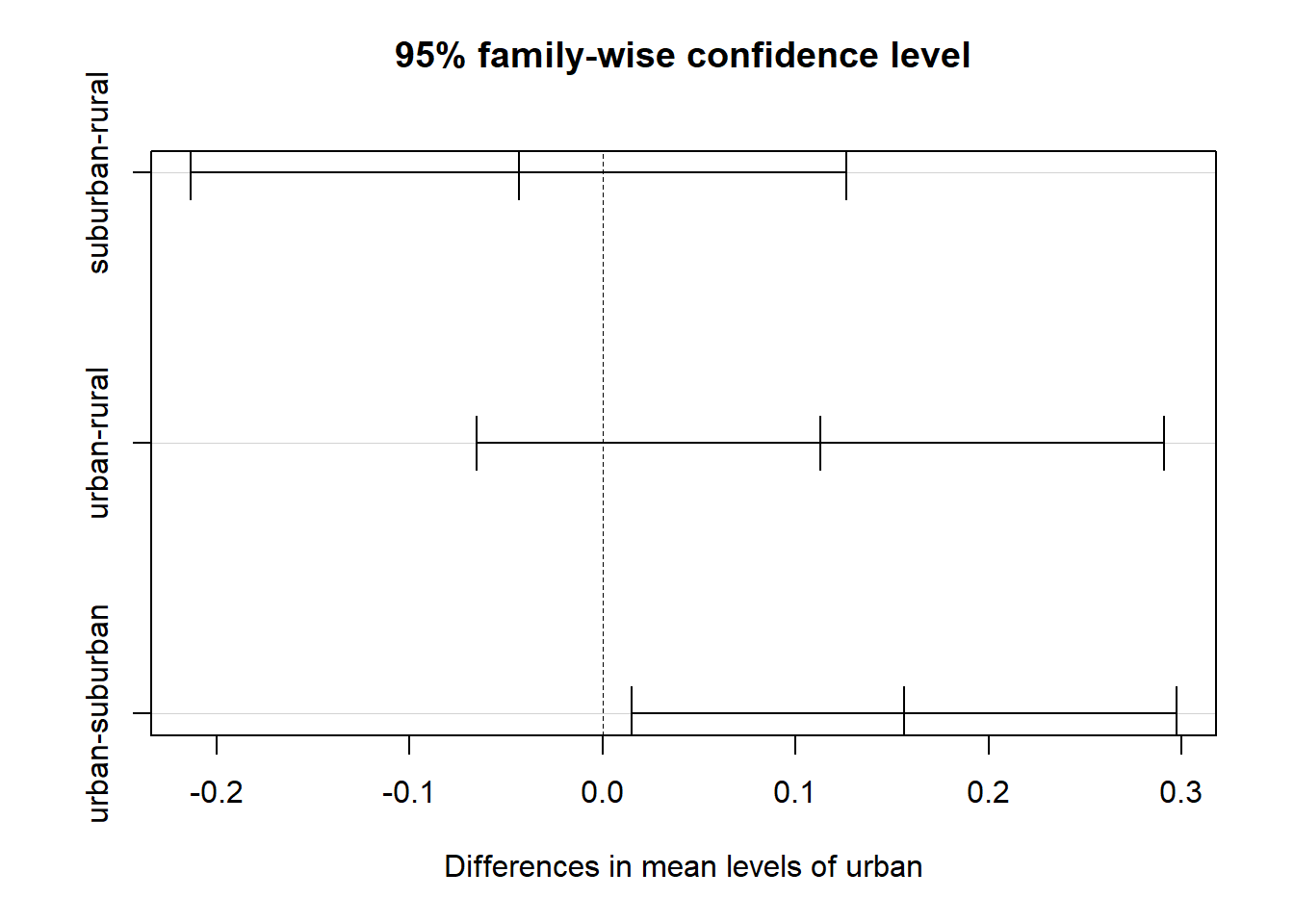
Schließt das Konfidenzintervall für die Mittelwertsdifferenz die Null (gestrichelte Linie) ein, so ist diese Mittelwertsdifferenz statistisch nicht signifikant! In unserer Stichprobe kam es zu Mittelwertsunterschieden auf ET, da sich die Gruppen urban (städtisch) und suburban (vorstädtisch) hinsichtlich der Zustimmung zur Überzeugung, dass die Existenz von Außerirdischen geheimgehalten wird, unterscheiden.
ezANOVA-Befehl
Es ist auch möglich das aov-Objekt gleichzeitig mit der ezANOVA ausgeben zu lassen. Dies ist möglich, indem man im ezANOVA-Befehl die Bedingung return_aov = TRUE hinzufügt und dann mit $aov auf das aov-Objekt zugreift. Dies kann dann im Environment abspeichert und weiterverwendet werden. Durch den Zugriff auf names können wir uns alle Einträge in unserer neu erstellten Liste anzeigen lassen und sehen dabei, dass ein Eintrag aov heißt.
aov_t <- ezANOVA(conspiracy, wid = id, dv = ET, between = urban, return_aov = T)## Warning: Data is unbalanced (unequal N per group). Make sure you specified a
## well-considered value for the type argument to ezANOVA().## Coefficient covariances computed by hccm()names(aov_t)## [1] "ANOVA"
## [2] "Levene's Test for Homogeneity of Variance"
## [3] "aov"Durch die Funktion class können wir uns die Klasse dieses Objektes aus der Liste anzeigen lassen und erhalten als Output, dass die Klasse wie erhofft auch aov ist.
class(aov_t$aov)## [1] "aov" "lm"Die Funktion TukeyHSD kann nun also auf den spezifischen Part des Outputs von ezANOVA angewendet werden (und kommt natürlich zum selben Ergebnis wie zuvor).
TukeyHSD(aov_t$aov, conf.level = 0.95)## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = formula(aov_formula), data = data)
##
## $urban
## diff lwr upr p adj
## suburban-rural -0.0434230 -0.21345311 0.1266071 0.8207046
## urban-rural 0.1128996 -0.06507135 0.2908705 0.2969918
## urban-suburban 0.1563226 0.01515294 0.2974922 0.0256251Literatur
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden (5. Auflage, 1. Auflage: 2010). Weinheim: Beltz.
- Blau hinterlegte Autor:innenangaben führen Sie direkt zur universitätsinternen Ressource.
