Lösungen
Vorwarnung
Achtung! Im Folgenden werden die Lösungen für das fünfte Projekt präsentiert. Falls du das Projekt noch nicht vollständig bearbeitet hast, nutze zunächst die Tipps. Sofern dir die Tipps für einen Teil nicht geholfen haben, kannst du die Lösungen dafür benutzen, einen Schritt weiterzukommen und beim nächsten Abschnitt weiterzumachen.
Lösung zu Aufgabe 1: Lösungsfunktion
Im Folgenden erhältst du eine Erklärung für den Aufbau einer möglichen Lösungsfunktion. Dabei haben wir uns in unserer Lösung allein auf eine einfache Lösungsstrategie beschränkt. Und zwar soll diese Lösungsfunktion immer dann eine bestimmte Zahl in ein freies Feld setzen, wenn alle anderen Zahlen für dieses Feld nicht mehr in Frage kommen. Ein Beispiel dafür ist hier abgebildet:
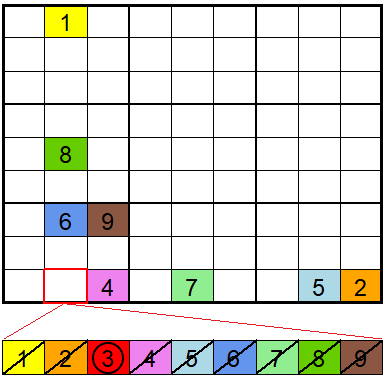
Da alle Zahlen bis auf die 3 für das Feld in Zeile 9 und Spalte 2 ausgeschlossen werden können, muss dort die 3 eingesetzt werden.
Hier kannst du dir anschauen, wie du mit der Lösung umgehen solltest:
Vorbereitungen
Bevor wir anfangen, legen wir erst einmal unseren Grundstein fest - das Sudoku. Das Sudoku ist eine Matrix mit 9 Zeilen und 9 Spalten. Eine solche Matrix erstellt man folgendermaßen in R:
Sudoku <- matrix(nrow = 9, ncol = 9)Das solltest du dir für später im Kopf behalten. Fürs Erste solltest du dir eines der Beispielsudokus hier oder hier herunterladen, damit du dir die folgenden Befehle auch selbst einmal anschauen kannst. Dabei ist es ratsam die Variablen (f und g) zuvor manuell zu definieren.
Wenn du dir dann alle Schritte anschaust, gleiche dabei immer die Ausgabe der Operationen mit dem Sudoku ab, um zu verstehen, was eine bestimmte Funktion genau macht.
Wir werden die Lösungsfunktion nun äquivalent zu der Reihenfolge in den Tipps nach und nach aufbauen.
Überprüfen, welche Zahlen bereits vorhanden sind
Zuerst geht es darum, wie du überprüfen kannst, welche Zahlen in einer gewissen Zeilen-Spalten-Kombination bereits vorhanden sind. Diese rufst du folgendermaßen ab:
Sudoku[f, ] -> Zeile_f
Sudoku[, g] -> Spalte_gDie kompliziertere Frage ist: Wie rufe ich die Zahlen eines bestimmten 3x3-Quadrates ab? Die perfekte Antwort darauf haben wir vielleicht nicht gefunden, aber hier siehst du eine Möglichkeit:
Zuerst definieren wir die einzelnen 3x3-Quadrate.
Qua1 <- Sudoku[1:3, 1:3]
Qua2 <- Sudoku[1:3, 4:6]
Qua3 <- Sudoku[1:3, 7:9]
Qua4 <- Sudoku[4:6, 1:3]
Qua5 <- Sudoku[4:6, 4:6]
Qua6 <- Sudoku[4:6, 7:9]
Qua7 <- Sudoku[7:9, 1:3]
Qua8 <- Sudoku[7:9, 4:6]
Qua9 <- Sudoku[7:9, 7:9]Damit können wir schon mal auf die 3x3-Quadrate zugreifen. Jetzt müssen wir nur noch das richtige Quadrat abhängig vom betrachteten Feld abrufen.
if (is.element(f, 1:3) & is.element(g, 1:3)) {z <- Qua1}
if (is.element(f, 1:3) & is.element(g, 4:6)) {z <- Qua2}
if (is.element(f, 1:3) & is.element(g, 7:9)) {z <- Qua3}
if (is.element(f, 4:6) & is.element(g, 1:3)) {z <- Qua4}
if (is.element(f, 4:6) & is.element(g, 4:6)) {z <- Qua5}
if (is.element(f, 4:6) & is.element(g, 7:9)) {z <- Qua6}
if (is.element(f, 7:9) & is.element(g, 1:3)) {z <- Qua7}
if (is.element(f, 7:9) & is.element(g, 4:6)) {z <- Qua8}
if (is.element(f, 7:9) & is.element(g, 7:9)) {z <- Qua9}Auch das haben wir hier nicht sehr filigran gelöst, aber es funktioniert. Gehen wir davon aus, dass f die Zeilenangabe und g die Spaltenangabe ist und spielen das für das 3x3-Quadrat oben links durch: Wenn f einen Wert zwischen 1 und 3 annimmt (also Zeile 1-3) UND g auch einen Wert zwischen 1 und 3 (also Spalte 1-3), dann liegt das Feld im 3x3-Quadrat oben links (Qua1). Um mit diesem Quadrat weiterarbeiten zu können, speichern wir es in der Variable z ab. Dadurch können wir mithilfe der Variable z auf das zu jedem Zeitpunkt richtig ausgewählte Quadrat zugreifen.
Wählen wir nun aus dem Sudoku das Feld in Zeile f und Spalte g aus, so können wir eine zusammenfassende Aussage über das Vorkommen von Zahlen treffen, indem wir die Informationen aus Zeile f, Spalte g und 3x3-Quadrat z folgendermaßen zusammenfassen:
c(Zeile_f, Spalte_g, as.vector(z)) -> vorkommendeZahlenZahl in ein Feld einsetzen
Zu diesem Zeitpunkt können wir für jedes beliebige Feld überprüfen, welche Zahlen sich in der jeweiligen Zeile, der Spalte und im dazugehörigen 3x3-Quadrat befinden. In ein Feld wollen wir dann eine Zahl einsetzen, wenn alle anderen 8 Zahlen durch vorkommendeZahlen ausgeschlossen werden. In anderen Worten: Wenn die Länge eines Vektors aller möglichen Zahlen minus vorkommendeZahlen eins ergibt, dann soll diese eine übrig gebliebene Zahl in das betrachtete Feld eingesetzt werden. Das sieht in R so aus:
fehlendeZahlen <- subset(1:9, !is.element(1:9, vorkommendeZahlen))Damit haben wir jetzt erreicht, dass im Objekt fehlendeZahlen alle Zahlen zwischen 1 und 9 abgespeichert sind, die kein Element der vorkommenden Zahlen (vorkommendeZahlen) sind.
Wenn in diesem Objekt (fehlendeZahlen) nur eine Zahl vorhanden ist, die Länge des Objekts/Vektors also 1 beträgt, soll die enthaltene Zahl an der Stelle [f, g] im Sudoku eingesetzt werden:
if(length(fehlendeZahlen) == 1) {
Sudoku[f, g] <- fehlendeZahlen
}Bisher können wir also für ein Feld die Zahlen bestimmen, die in Zeile, Spalte und 3x3-Quadrat noch fehlen - und wenn das nur eine Zahl ist, wird diese eingesetzt.
Das soll jetzt eine Funktion für alle Felder automatisch erledigen. Dafür verwenden wir zwei for-Schleifen, eine für die Zeilen und eine für die Spalten. Das sieht dann zusammengesetzt folgendermaßen aus:
for (f in 1:9) {
for (g in 1:9) {
Qua1 <- Sudoku[1:3, 1:3]
Qua2 <- Sudoku[1:3, 4:6]
Qua3 <- Sudoku[1:3, 7:9]
Qua4 <- Sudoku[4:6, 1:3]
Qua5 <- Sudoku[4:6, 4:6]
Qua6 <- Sudoku[4:6, 7:9]
Qua7 <- Sudoku[7:9, 1:3]
Qua8 <- Sudoku[7:9, 4:6]
Qua9 <- Sudoku[7:9, 7:9]
if (is.element(f, 1:3) & is.element(g, 1:3)) {z <- Qua1}
if (is.element(f, 1:3) & is.element(g, 4:6)) {z <- Qua2}
if (is.element(f, 1:3) & is.element(g, 7:9)) {z <- Qua3}
if (is.element(f, 4:6) & is.element(g, 1:3)) {z <- Qua4}
if (is.element(f, 4:6) & is.element(g, 4:6)) {z <- Qua5}
if (is.element(f, 4:6) & is.element(g, 7:9)) {z <- Qua6}
if (is.element(f, 7:9) & is.element(g, 1:3)) {z <- Qua7}
if (is.element(f, 7:9) & is.element(g, 4:6)) {z <- Qua8}
if (is.element(f, 7:9) & is.element(g, 7:9)) {z <- Qua9}
Zeile_f <- Sudoku[f, ]
Spalte_g <- Sudoku[, g]
Quadrat_fg <- as.vector(z)
vorkommendeZahlen <- c(Zeile_f, Spalte_g, Quadrat_fg)
fehlendeZahlen <- subset(1:9, !is.element(1:9, fehlendeZahlen))
if(length(fehlendeZahlen) == 1) {
Sudoku[f, g] <- fehlendeZahlen
}
}
}Diese Funktion geht jetzt von oben links nach unten rechts alle Felder des Sudokus durch, überprüft die jeweils fehlenden Zahlen und setzt, wenn möglich, Zahlen ein.
Aus diesem Grund wird auch der “Inhalt” der einzelnen Quadrate in jedem Durchgang aktualisiert: Wenn eine Zahl eingesetzt wurde, ändert sich der Inhalt eines Quadrats. Natürlich sind neun Zeilen Code dafür etwas umständlich, aber auf jeden Fall macht man damit nichts falsch. Fällt dir dafür eine Verbesserung ein?
Das Problem der Funktion liegt darin, dass sie alle Felder nur einmal durchgeht. Derart einfach und schnell lässt sich jedoch so gut wie kein Sudoku lösen. Deshalb müssen wir den gesamten Vorgang mehrfach wiederholen. Das machen wir mit einer repeat-Funktion. Diese Funktion beenden wir mit einem break-Befehl, der die Funktion dann stoppen soll, wenn das Sudoku-Gitter vollständig mit 81 Zahlen befüllt wurde.
repeat {
for (f in 1:9) {
for (g in 1:9) {
Qua1 <- Sudoku[1:3, 1:3]
Qua2 <- Sudoku[1:3, 4:6]
Qua3 <- Sudoku[1:3, 7:9]
Qua4 <- Sudoku[4:6, 1:3]
Qua5 <- Sudoku[4:6, 4:6]
Qua6 <- Sudoku[4:6, 7:9]
Qua7 <- Sudoku[7:9, 1:3]
Qua8 <- Sudoku[7:9, 4:6]
Qua9 <- Sudoku[7:9, 7:9]
if (is.element(f, 1:3) & is.element(g, 1:3)) {z <- Qua1}
if (is.element(f, 1:3) & is.element(g, 4:6)) {z <- Qua2}
if (is.element(f, 1:3) & is.element(g, 7:9)) {z <- Qua3}
if (is.element(f, 4:6) & is.element(g, 1:3)) {z <- Qua4}
if (is.element(f, 4:6) & is.element(g, 4:6)) {z <- Qua5}
if (is.element(f, 4:6) & is.element(g, 7:9)) {z <- Qua6}
if (is.element(f, 7:9) & is.element(g, 1:3)) {z <- Qua7}
if (is.element(f, 7:9) & is.element(g, 4:6)) {z <- Qua8}
if (is.element(f, 7:9) & is.element(g, 7:9)) {z <- Qua9}
Zeile_f <- Sudoku[f, ]
Spalte_g <- Sudoku[, g]
Quadrat_fg <- as.vector(z)
vorkommendeZahlen <- c(Zeile_f, Spalte_g, Quadrat_fg)
fehlendeZahlen <- subset(1:9, !is.element(1:9, fehlendeZahlen))
if(length(fehlendeZahlen) == 1) {
Sudoku[f, g] <- fehlendeZahlen
}
}
}
if(length(subset(as.vector(Sudoku), is.element(Sudoku, 1:9))) == 81) break
}Bei der break-Bedingung ist zu beachten, dass auch NAs als Eintrag gewertet werden würden und das Sudoku deshalb von Anfang an als ‘voll’ gelten würde. Aus diesem Grund werden mithilfe der subset-Funktion nur Objekte aus der Sudoku-Matrix ausgewählt, die Zahlen zwischen 1 und 9 darstellen.
Um den Vorgang zu beschleunigen, können wir jetzt in jedem Durchgang nur die unbesetzten Felder betrachten. Dafür setzen wir am Anfang der beiden for-Schleifen eine if-Bedingung ein, sodass alle Operationen nur dann ausgeführt werden, wenn das ausgewählte Feld keine Zahl bzw. ein NA enthält.
repeat {
for (f in 1:9) {
for (g in 1:9) {
if(is.na(Sudoku[f, g])) {
Qua1 <- Sudoku[1:3, 1:3]
Qua2 <- Sudoku[1:3, 4:6]
Qua3 <- Sudoku[1:3, 7:9]
Qua4 <- Sudoku[4:6, 1:3]
Qua5 <- Sudoku[4:6, 4:6]
Qua6 <- Sudoku[4:6, 7:9]
Qua7 <- Sudoku[7:9, 1:3]
Qua8 <- Sudoku[7:9, 4:6]
Qua9 <- Sudoku[7:9, 7:9]
if (is.element(f, 1:3) & is.element(g, 1:3)) {z <- Qua1}
if (is.element(f, 1:3) & is.element(g, 4:6)) {z <- Qua2}
if (is.element(f, 1:3) & is.element(g, 7:9)) {z <- Qua3}
if (is.element(f, 4:6) & is.element(g, 1:3)) {z <- Qua4}
if (is.element(f, 4:6) & is.element(g, 4:6)) {z <- Qua5}
if (is.element(f, 4:6) & is.element(g, 7:9)) {z <- Qua6}
if (is.element(f, 7:9) & is.element(g, 1:3)) {z <- Qua7}
if (is.element(f, 7:9) & is.element(g, 4:6)) {z <- Qua8}
if (is.element(f, 7:9) & is.element(g, 7:9)) {z <- Qua9}
Zeile_f <- Sudoku[f, ]
Spalte_g <- Sudoku[, g]
Quadrat_fg <- as.vector(z)
vorkommendeZahlen <- c(Zeile_f, Spalte_g, Quadrat_fg)
fehlendeZahlen <- subset(1:9, !is.element(1:9, fehlendeZahlen))
if(length(fehlendeZahlen) == 1) {
Sudoku[f, g] <- fehlendeZahlen
}
}
}
}
if(length(subset(as.vector(Sudoku), is.element(Sudoku, 1:9))) == 81) break
}Unter bestimmten Umständen kann es sein, dass unsere Funktion ein Sudoku nicht lösen kann. Das könnte entweder daran liegen, dass das Sudoku nicht lösbar ist oder aber daran, dass wir nur eine von vielen Lösungsstrategien impliziert haben. Um dadurch nicht auf Probleme zu stoßen, falls die Funktion mal ein solches Sudoku lösen soll und deshalb nicht zum Ende kommt, werden wir eine weitere break-Bedingung definieren. Die Überlegung dahinter ist die Folgende: Gehen wir davon aus, dass ein Sudoku 11 vorgegebene Zahlen beinhaltet (Das ist sehr unwahrscheinlich und wäre ein sehr schweres Sudoku.) und gehen wir zusätzlich davon aus, dass dieses mit unserer Funktion lösbar wäre. In diesem Fall würde unsere Funktion jedes Mal, wenn sie alle Felder durchgeht, mindest eine neue Zahl einsetzen, denn sonst würde sie sich aufhängen. Das heißt, dass die Funktion für das Fertigstellen des Sudokus höchsten 81 - 11 = 70 Runden brauchen würde.
Aus diesem Grund werden wir im Folgenden die Lösungsfunktion zur Sicherheit nach höchstens 70 Durchgängen abbrechen. Um das nachvollziehbar machen zu können, lassen wir außerdem eine Nachricht ausgeben, sofern das Sudoku nicht lösbar ist.
Durchgaenge <- 0
repeat {
Durchgaenge <- Durchgaenge + 1
for (f in 1:9) {
for (g in 1:9) {
if(is.na(Sudoku[f, g])) {
Qua1 <- Sudoku[1:3, 1:3]
Qua2 <- Sudoku[1:3, 4:6]
Qua3 <- Sudoku[1:3, 7:9]
Qua4 <- Sudoku[4:6, 1:3]
Qua5 <- Sudoku[4:6, 4:6]
Qua6 <- Sudoku[4:6, 7:9]
Qua7 <- Sudoku[7:9, 1:3]
Qua8 <- Sudoku[7:9, 4:6]
Qua9 <- Sudoku[7:9, 7:9]
if (is.element(f, 1:3) & is.element(g, 1:3)) {z <- Qua1}
if (is.element(f, 1:3) & is.element(g, 4:6)) {z <- Qua2}
if (is.element(f, 1:3) & is.element(g, 7:9)) {z <- Qua3}
if (is.element(f, 4:6) & is.element(g, 1:3)) {z <- Qua4}
if (is.element(f, 4:6) & is.element(g, 4:6)) {z <- Qua5}
if (is.element(f, 4:6) & is.element(g, 7:9)) {z <- Qua6}
if (is.element(f, 7:9) & is.element(g, 1:3)) {z <- Qua7}
if (is.element(f, 7:9) & is.element(g, 4:6)) {z <- Qua8}
if (is.element(f, 7:9) & is.element(g, 7:9)) {z <- Qua9}
Zeile_f <- Sudoku[f, ]
Spalte_g <- Sudoku[, g]
Quadrat_fg <- as.vector(z)
vorkommendeZahlen <- c(Zeile_f, Spalte_g, Quadrat_fg)
fehlendeZahlen <- subset(1:9, !is.element(1:9, fehlendeZahlen))
if(length(fehlendeZahlen) == 1) {
Sudoku[f, g] <- fehlendeZahlen
}
}
}
}
if(Durchgaenge == 70) break
if(Durchgaenge == 70) {
print('Nicht lösbar!')
}
if(length(subset(as.vector(Sudoku), is.element(Sudoku, 1:9))) == 81) break
}Lösung zu Aufgabe 2: Ausgefülltes 9x9-Gitter erstellen
Der nächste Schritt zum eigenen Sudoku ist es, ein 9x9-Gitter nach den geltenden Regeln vollständig mit Zahlen zu befüllen. Eine schrittweise Erklärung zur Erstellung einer solchen Funktion gibt es im Folgenden.
9x9-Gitter mit Zahlen befüllen
Mit dem matrix( ) Befehl erstellen wir unser Sudoku-Gitter mit 9 Zeilen (nrow) und 9 Spalten (ncol):
Sudoku <- matrix(nrow = 9, ncol = 9)Um die neun Boxen zu erstellen, weisen wir jeweils die richtigen Zeilen und Spalten einer neuen Variablen zu.
Qua1 <- Sudoku[1:3, 1:3]
Qua2 <- Sudoku[1:3, 4:6]
Qua3 <- Sudoku[1:3, 7:9]
Qua4 <- Sudoku[4:6, 1:3]
Qua5 <- Sudoku[4:6, 4:6]
Qua6 <- Sudoku[4:6, 7:9]
Qua7 <- Sudoku[7:9, 1:3]
Qua8 <- Sudoku[7:9, 4:6]
Qua9 <- Sudoku[7:9, 7:9]Bei uns steht f für die Zeile und g für die Spalte. Deshalb geht die Funktion hier von links nach rechts und von oben nach unten jedes Feld ab, bis sie unten rechts angekommen ist.
for (f in 1:9){
for (g in 1:9){
}
}Für unsere Zufallszahl brauchen wir zwei verschiedene Variablen. Eine davon definiert, aus welchen Zahlen wir eine Zufallsziehung vornehmen (b) und in der anderen (a) wird die eigentliche Zufallszahl gespeichert.
b <- 1:9
a <- sample(b, 1)Um herauszufinden, ob die Zahl in dem 3x3-Quadrat bereits vorhanden ist, müssen wir zunächst wissen in welchem 3x3-Quadrat das betrachtete Feld liegt. Dafür müssen wir verknüpfte if-Bedingungen benutzten. Für jede 3x3-Box testen wir, ob das betrachtete Feld darin liegt. Wenn es das tut, dann speichern wir diese Information im Objekt z.
if (is.element(f, 1:3) & is.element(g, 1:3)) {z <- Qua1}
if (is.element(f, 1:3) & is.element(g, 4:6)) {z <- Qua2}
if (is.element(f, 1:3) & is.element(g, 7:9)) {z <- Qua3}
if (is.element(f, 4:6) & is.element(g, 1:3)) {z <- Qua4}
if (is.element(f, 4:6) & is.element(g, 4:6)) {z <- Qua5}
if (is.element(f, 4:6) & is.element(g, 7:9)) {z <- Qua6}
if (is.element(f, 7:9) & is.element(g, 1:3)) {z <- Qua7}
if (is.element(f, 7:9) & is.element(g, 4:6)) {z <- Qua8}
if (is.element(f, 7:9) & is.element(g, 7:9)) {z <- Qua9}Nun müssen wir überprüfen, ob die Zahl in der Zeile f, in der Spalte g oder im 3x3-Quadrat z bereits vorhanden ist. Diese drei Bedingungen können wir mit is.element erstellen und durch logische unds (&) verknüpfen. Das ! davor kehrt die Bedeutung um. Daher fragen wir hier, ob diese Zahl kein Element der Zeile, der Spalte und der Box ist. Wenn dies der Fall ist, weisen wir die Zufallszahl dem betrachteten Feld zu.
if(!is.element(a, Sudoku[, g]) & !is.element(a, Sudoku[f, ]) & !is.element(a, z)) {
a -> Sudoku[f, g]
}Wenn im ersten Versuch nicht direkt eine passende Zahl ausgewählt wurde, müssen wir die Zufallsziehung wiederholen, bis eine passende Zahl gefunden wurde. Dafür benutzen wir eine repeat-Schleife. In dieser Schleife wollen wir mit einer neuen Zufallszahl aus der Menge b, unter Abzug der Zahl a aus dem vorherigen Versuch, einen neuen Versuch starten. Da wir in b die Zahlen von eins bis neun gespeichert haben, können wir die benutzte Zahl einfach entfernen und aus den restlichen Zahlen eine neue Zahl ziehen.
else {
repeat {
b <- subset(b, b != a)
a <- sample(b, 1)
...
}
}Diese neue Zufallszahl müssen wir nun erneut mit den anderen Zahlen in der Zeile, Spalte und in der Box vergleichen. Ist die Zahl nicht enthalten, weisen wir sie dem betrachteten Feld zu. Dann brechen wir die Schleife ab, um beim nächsten Feld fortzufahren.
if(!is.element(a, Sudoku[, g]) & !is.element(a, Sudoku[f, ]) & !is.element(a, z)) {
a -> Sudoku[f, g]
break
}Es besteht jedoch die Möglichkeit, dass alle 9 Zahlen in einem betrachteten Feld ausprobiert werden, jedoch keine eingesetzt werden kann. In diesem Fall hat die Besetzung des Sudokus nicht geklappt und es muss mit einem leeren 9x9-Gitter von vorne angefangen werden. Ist dieser Fall eingetreten, so ist die Länge des Objekts b= 0. Mithilfe dieser Information kann man nun einen neuen break-Befehl erstellen, der die repeat-Schleife für die Suche nach einer passenden Zahl beendet. Dieser Befehl muss direkt nach b <- subset(b, b != a) eingefügt werden, da erst an diesem Punkt die Menge der noch nicht getesteten Zahlen aktualisiert wird. Das sieht dann im Gesamtergebnis so aus:
b <- 1:9
a <- sample(b, 1)
if(!is.element(a, Sudoku[, g]) & !is.element(a, Sudoku[f, ]) & !is.element(a, z)) {
a -> Sudoku[f, g]
} else {
repeat {
b <- subset(b, b != a)
if(length(b)==0) break
a <- sample(b, 1)
if(!is.element(a, Sudoku[, g]) & !is.element(a, Sudoku[f, ]) & !is.element(a, z)) {
a -> Sudoku[f, g]
break
}
}
}Um am Ende zu überprüfen, ob alle Felder gefüllt sind, können wir schauen, ob 81 Zahlen in das Sudoku eingefügt wurden. Ist das der Fall, so sind wir fertig und haben ein volles Sudoku erstellt.
if(length(subset(as.vector(Sudoku), is.element(Sudoku, 1:9))) == 81) breakZusammengesetzt sieht das folgendermaßen aus:
repeat {
Sudoku <- matrix(nrow = 9, ncol = 9)
for (f in 1:9){
for (g in 1:9){
Qua1 <- Sudoku[1:3,1:3]
Qua2 <- Sudoku[1:3,4:6]
Qua3 <- Sudoku[1:3,7:9]
Qua4 <- Sudoku[4:6,1:3]
Qua5 <- Sudoku[4:6,4:6]
Qua6 <- Sudoku[4:6,7:9]
Qua7 <- Sudoku[7:9,1:3]
Qua8 <- Sudoku[7:9,4:6]
Qua9 <- Sudoku[7:9,7:9]
if (is.element(f, 1:3) & is.element(g, 1:3)) {z <- Qua1}
if (is.element(f, 1:3) & is.element(g, 4:6)) {z <- Qua2}
if (is.element(f, 1:3) & is.element(g, 7:9)) {z <- Qua3}
if (is.element(f, 4:6) & is.element(g, 1:3)) {z <- Qua4}
if (is.element(f, 4:6) & is.element(g, 4:6)) {z <- Qua5}
if (is.element(f, 4:6) & is.element(g, 7:9)) {z <- Qua6}
if (is.element(f, 7:9) & is.element(g, 1:3)) {z <- Qua7}
if (is.element(f, 7:9) & is.element(g, 4:6)) {z <- Qua8}
if (is.element(f, 7:9) & is.element(g, 7:9)) {z <- Qua9}
b <- 1:9
a <- sample(b, 1)
if(!is.element(a, Sudoku[, g]) & !is.element(a, Sudoku[f, ]) & !is.element(a, z)) {
a -> Sudoku[f, g]
} else {
repeat {
b <- subset(b, b != a)
if(length(b)==0) break
a <- sample(b, 1)
if(!is.element(a, Sudoku[, g]) & !is.element(a, Sudoku[f, ]) & !is.element(a, z)) {
a -> Sudoku[f, g]
break
}
}
}
}
}
if(length(subset(as.vector(Sudoku), is.element(Sudoku, 1:9))) == 81) break
}Wie bereits erklärt, kann es dazu kommen, dass b == 0 wird - ein Feld also nicht besetzt werden kann. In diesem Fall macht es keinen Sinn, die folgenden freien Felder weiter zu besetzen, weshalb auch die beiden for-Schleifen unterbrochen werden sollten, wenn b == 0 gilt. Dann wird auch die End-Bedingung eines vollen Sudokus nicht erfüllt und die Schleife beginnt direkt von vorne mit einer leeren 9x9-Matrix:
repeat { #Funktion wird so lange wiederholt, bis break-Bedingung eintritt
Sudoku <- matrix(nrow = 9, ncol = 9) #leeres Sudoku-Gitter erstellen
for (f in 1:9){ #alle Zeilen durchgehen
for (g in 1:9){ #alle Spalten durchgehen
Qua1 <- Sudoku[1:3,1:3] #3x3-Quadrate bestimmen
Qua2 <- Sudoku[1:3,4:6]
Qua3 <- Sudoku[1:3,7:9]
Qua4 <- Sudoku[4:6,1:3]
Qua5 <- Sudoku[4:6,4:6]
Qua6 <- Sudoku[4:6,7:9]
Qua7 <- Sudoku[7:9,1:3]
Qua8 <- Sudoku[7:9,4:6]
Qua9 <- Sudoku[7:9,7:9]
if (is.element(f, 1:3) & is.element(g, 1:3)) {z <- Qua1} #betrachtetes Feld zu Quadrat zuordnen
if (is.element(f, 1:3) & is.element(g, 4:6)) {z <- Qua2}
if (is.element(f, 1:3) & is.element(g, 7:9)) {z <- Qua3}
if (is.element(f, 4:6) & is.element(g, 1:3)) {z <- Qua4}
if (is.element(f, 4:6) & is.element(g, 4:6)) {z <- Qua5}
if (is.element(f, 4:6) & is.element(g, 7:9)) {z <- Qua6}
if (is.element(f, 7:9) & is.element(g, 1:3)) {z <- Qua7}
if (is.element(f, 7:9) & is.element(g, 4:6)) {z <- Qua8}
if (is.element(f, 7:9) & is.element(g, 7:9)) {z <- Qua9}
b <- 1:9 #ab hier: passende Zahl für betrachtetes Feld ermitteln
a <- sample(b, 1)
if(!is.element(a, Sudoku[, g]) & !is.element(a, Sudoku[f, ]) & !is.element(a, z)) {
a -> Sudoku[f, g]
} else {
repeat {
b <- subset(b, b != a)
if(length(b)==0) break
a <- sample(b, 1)
if(!is.element(a, Sudoku[, g]) & !is.element(a, Sudoku[f, ]) & !is.element(a, z)) {
a -> Sudoku[f, g]
break
}
}
} #bis hier: entweder eine passende Zahl wurde eingesetzt oder die Funktion beginnt von vorne (b == 0)
if(length(b)==0) break
}
if(length(b)==0) break
}
if(length(subset(as.vector(Sudoku), is.element(Sudoku, 1:9))) == 81) break
}An diesem Punkt ist die Schleife in der Lage, so lange wiederholt 9x9-Gitter mit Zahlen von 1 bis 9 zu befüllen, bis ein vollständig und unter Beachtung der Regeln befülltes Sudoku erstellt wurde.
Zur weiteren Überprüfung kann man sich die absolute Häufigkeit jeder Zahl mithilfe einer Tabelle ausgeben lassen. Sind alle Zahlen 9 Mal vorhanden, so hat man mit großer Wahrscheinlichkeit ein korrekt aufgefülltes Sudoku erstellt.
table(Sudoku)## Sudoku
## 1 2 3 4 5 6 7 8 9
## 9 9 9 9 9 9 9 9 9Und so sollte das Sudoku jetzt aussehen:
Sudoku## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
## [1,] 9 1 2 6 8 5 4 7 3
## [2,] 3 8 7 9 2 4 1 6 5
## [3,] 5 6 4 1 7 3 8 2 9
## [4,] 7 4 5 8 9 2 3 1 6
## [5,] 6 2 8 5 3 1 9 4 7
## [6,] 1 9 3 4 6 7 2 5 8
## [7,] 2 7 6 3 4 8 5 9 1
## [8,] 8 5 9 2 1 6 7 3 4
## [9,] 4 3 1 7 5 9 6 8 2Lösung zu Aufgabe 3: Letzte Schritte zum eigenen Sudoku
In diesem Teil der Lösung werden wir erklären, wie wir anhand unserer Lösungsfunktion und einem vollständig gefüllten Sudoku-Gitter ein eigenes lösbares Sudoku erstellen.
Vorbereitungen
Bevor du mit diesem Abschnitt anfängst und ihn selbst durchführst, solltest du mithilfe der Funktion in Teilaufgabe 2 ein vollständig gefülltes Sudoku erstellt haben und in zwei Objekten, beispielsweise Sudoku und Gitter hinterlegt haben. Das eine Objekt (z.B. Sudoku) wird im folgenden zur Bearbeitung genutzt, während das zweite Objekt (z.B. Gitter) als Reset fungiert, um zum Ausgangszustand zurückgelangen zu können.
Die dafür zuständige Funktion werden wir nun äquivalent zu der Reihenfolge in den Tipps nach und nach aufbauen.
Zahlen aus dem Sudoku entfernen
Der Ausgangspunkt ist ein vollständig gefülltes Gitter. Um daraus ein lösbares Sudoku zu erstellen, müssen wir Zahlen entfernen; und damit fangen wir an.
Zum Löschen können wir folgenden Befehl verwenden, der in ein Feld [f, g] im Sudoku ein NA einfügt:
Sudoku[f, g] <- NADie Frage ist, welche Zahlen wir überhaupt löschen wollen. Im Vorhinein spezifische Felder auszuwählen, wäre sehr aufwendig und könnte in einem unlösbaren Sudoku enden. Die Feld-Koordinate aus Zeile und Spalte sollte also zufällig gewählt sein. Dadurch wird die Funktion auch in der Lage sein, völlig verschiedene Sudokus aus dem selben vollständig gefüllten Sudoku-Gitter zu erstellen.
f <- sample(1:9, 1)
g <- sample(1:9, 1)Im letzten Schritt wollen wir bestimmen, wann die Funktion aufhören soll, Zahlen aus dem Sudoku zu löschen. Es könnte problematisch sein, die Anzahl der Wiederholungen der Funktion einfach zu begrenzen, da zufällig mehrfach das selbe Feld ausgewählt werden könnte (Das ist bei 50 zu löschenden Zahlen sogar sehr wahrscheinlich!). Aus diesem Grund wollen wir hier mit der Anzahl der Zahlen arbeiten, die jeweils nach dem Löschen im Sudoku übrig geblieben sind. Das Ziel sollte also sein, die Funktion dann zu beenden, wenn nur noch XX Zahlen im Gitter übrig sind.
if(length(subset(as.vector(Sudoku), is.element(Sudoku, 1:9))) == XX) breakDie einzelnen Schritte wären damit erstellt. Fügen wir das nun zu einer Funktion zusammen:
repeat {
f <- sample(1:9, 1)
g <- sample(1:9, 1)
Sudoku[f, g] <- NA
if(length(subset(as.vector(Sudoku), is.element(Sudoku, 1:9))) == XX) break
}Es entsteht ein Sudoku mit XX vorgegebenen Zahlen. Speichere auch dieses an diesem Punkt in einem weiteren neuen Objekt ab, damit wir mit dem Sudoku-Objekt weiterarbeiten können.
Lösungsfunktion das Sudoku lösen lassen
Zu diesem Zeitpunkt haben wir ein eigens erstelltes Sudoku mit XX Zahlen, das in diesem Schritt auf seine Lösbarkeit überprüft werden soll.
Dafür übernehmen wir also die Lösungsfunktion aus Teilaufgabe 1 und lassen sie das Sudoku lösen. Jetzt kann es zu zwei Ausgängen kommen:
- Das Sudoku ist durch die Lösungsfunktion lösbar.
- Das Sudoku ist durch die Lösungsfunktion nicht lösbar.
Für uns gilt es jetzt, alle erarbeiteten Schritte in eine einzige Funktion zu verpacken, die erst dann stoppt, wenn ein lösbares Sudoku mit XX vorgegebenen Zahlen erstellt wurde. Dabei müssen die zwei Ausgänge beachtet werden:
- Wenn 1. eintrifft, muss die Funktion gestoppt werden. Zu diesem Zeitpunkt enthält das
Sudoku-Objekt ein vollständig gelöstes Sudoku. Deshalb sollte man das Sudoku zuvor in einem neuen Objekt (z.B.meinSudoku) abspeichern, um es jetzt wieder abrufen zu können. - Wenn 2. eintrifft, muss die Funktion von vorne anfangen. Das heißt, dass ausgehend von demselben vollständig gefüllten Gitter (
Gitter) erneut ein Sudoku erstellt und danach wiederum durch die Lösungsfunktion überprüft werden soll. Diese Schleife sollte erst dann enden, wenn ein lösbares Sudoku erstellt wurde.
Übernehmen wir erst einmal alles, was wir bereits haben:
#Lösch-Funktion
repeat {
f <- sample(1:9, 1)
g <- sample(1:9, 1)
Sudoku[f, g] <- NA
if(length(subset(as.vector(Sudoku), is.element(Sudoku, 1:9))) == XX) break
}
#Lösungsfunktion
Durchgaenge <- 0
repeat {
Durchgaenge <- Durchgaenge + 1
for (f in 1:9) {
for (g in 1:9) {
if(is.na(Sudoku[f, g])) {
Qua1 <- Sudoku[1:3, 1:3]
Qua2 <- Sudoku[1:3, 4:6]
Qua3 <- Sudoku[1:3, 7:9]
Qua4 <- Sudoku[4:6, 1:3]
Qua5 <- Sudoku[4:6, 4:6]
Qua6 <- Sudoku[4:6, 7:9]
Qua7 <- Sudoku[7:9, 1:3]
Qua8 <- Sudoku[7:9, 4:6]
Qua9 <- Sudoku[7:9, 7:9]
if (is.element(f, 1:3) & is.element(g, 1:3)) {z <- Qua1}
if (is.element(f, 1:3) & is.element(g, 4:6)) {z <- Qua2}
if (is.element(f, 1:3) & is.element(g, 7:9)) {z <- Qua3}
if (is.element(f, 4:6) & is.element(g, 1:3)) {z <- Qua4}
if (is.element(f, 4:6) & is.element(g, 4:6)) {z <- Qua5}
if (is.element(f, 4:6) & is.element(g, 7:9)) {z <- Qua6}
if (is.element(f, 7:9) & is.element(g, 1:3)) {z <- Qua7}
if (is.element(f, 7:9) & is.element(g, 4:6)) {z <- Qua8}
if (is.element(f, 7:9) & is.element(g, 7:9)) {z <- Qua9}
Zeile_f <- Sudoku[f, ]
Spalte_g <- Sudoku[, g]
Quadrat_fg <- as.vector(z)
vorkommendeZahlen <- c(Zeile_f, Spalte_g, Quadrat_fg)
fehlendeZahlen <- subset(1:9, !is.element(1:9, fehlendeZahlen))
if(length(fehlendeZahlen) == 1) {
Sudoku[f, g] <- fehlendeZahlen
}
}
}
}
if(Durchgaenge == 70) break
if(Durchgaenge == 70) {
print('Nicht lösbar!')
}
if(length(subset(as.vector(Sudoku), is.element(Sudoku, 1:9))) == 81) break
}Wie in den Vorbereitung erwähnt, sollte das vollständige Sudoku-Gitter in einem Objekt gespeichert sein (Gitter). Dieses Gitter soll am Anfang jeden Durchlaufs auf das Sudoku-Objekt übertragen werden.
Außerdem muss das erstellte Sudoku mit XX vorgegebenen Zahlen vor der Überprüfung der Lösbarkeit in einem neuen Objekt abgespeichert werden (meinSudoku).
Fügen wir nun das alles zusammen in eine repeat-Schleife:
repeat {
Sudoku <- Gitter
repeat {
f <- sample(1:9, 1)
g <- sample(1:9, 1)
Sudoku[f, g] <- NA
if(length(subset(as.vector(Sudoku), is.element(Sudoku, 1:9))) == XX) break
}
meinSudoku <- Sudoku
Durchgaenge <- 0
repeat {
Durchgaenge <- Durchgaenge + 1
for (f in 1:9) {
for (g in 1:9) {
if(is.na(Sudoku[f, g])) {
Qua1 <- Sudoku[1:3, 1:3]
Qua2 <- Sudoku[1:3, 4:6]
Qua3 <- Sudoku[1:3, 7:9]
Qua4 <- Sudoku[4:6, 1:3]
Qua5 <- Sudoku[4:6, 4:6]
Qua6 <- Sudoku[4:6, 7:9]
Qua7 <- Sudoku[7:9, 1:3]
Qua8 <- Sudoku[7:9, 4:6]
Qua9 <- Sudoku[7:9, 7:9]
if (is.element(f, 1:3) & is.element(g, 1:3)) {z <- Qua1}
if (is.element(f, 1:3) & is.element(g, 4:6)) {z <- Qua2}
if (is.element(f, 1:3) & is.element(g, 7:9)) {z <- Qua3}
if (is.element(f, 4:6) & is.element(g, 1:3)) {z <- Qua4}
if (is.element(f, 4:6) & is.element(g, 4:6)) {z <- Qua5}
if (is.element(f, 4:6) & is.element(g, 7:9)) {z <- Qua6}
if (is.element(f, 7:9) & is.element(g, 1:3)) {z <- Qua7}
if (is.element(f, 7:9) & is.element(g, 4:6)) {z <- Qua8}
if (is.element(f, 7:9) & is.element(g, 7:9)) {z <- Qua9}
Zeile_f <- Sudoku[f, ]
Spalte_g <- Sudoku[, g]
Quadrat_fg <- as.vector(z)
vorkommendeZahlen <- c(Zeile_f, Spalte_g, Quadrat_fg)
fehlendeZahlen <- subset(1:9, !is.element(1:9, fehlendeZahlen))
if(length(fehlendeZahlen) == 1) {
Sudoku[f, g] <- fehlendeZahlen
}
}
}
}
if(Durchgaenge == 70) break
if(Durchgaenge == 70) {
print('Nicht lösbar!')
}
if(length(subset(as.vector(Sudoku), is.element(Sudoku, 1:9))) == 81) break
}
}Jetzt brauchen wir nur noch die Bedingung, mit der die große Schleife beendet wird. Diese ist bereits in der Lösungsfunktion vorhanden. Denn wenn wir ein selbst erstelltes Sudoku vollständig gelöst haben, braucht die Funktion nicht weiter nach einem lösbaren Sudoku suchen. Also fügen wir diesen break-Befehl nochmals ganz am Ende der Funktion ein.
repeat {
Sudoku <- Gitter
repeat {
f <- sample(1:9, 1)
g <- sample(1:9, 1)
Sudoku[f, g] <- NA
if(length(subset(as.vector(Sudoku), is.element(Sudoku, 1:9))) == XX) break
}
meinSudoku <- Sudoku
Durchgaenge <- 0
repeat {
Durchgaenge <- Durchgaenge + 1
for (f in 1:9) {
for (g in 1:9) {
if(is.na(Sudoku[f, g])) {
Qua1 <- Sudoku[1:3, 1:3]
Qua2 <- Sudoku[1:3, 4:6]
Qua3 <- Sudoku[1:3, 7:9]
Qua4 <- Sudoku[4:6, 1:3]
Qua5 <- Sudoku[4:6, 4:6]
Qua6 <- Sudoku[4:6, 7:9]
Qua7 <- Sudoku[7:9, 1:3]
Qua8 <- Sudoku[7:9, 4:6]
Qua9 <- Sudoku[7:9, 7:9]
if (is.element(f, 1:3) & is.element(g, 1:3)) {z <- Qua1}
if (is.element(f, 1:3) & is.element(g, 4:6)) {z <- Qua2}
if (is.element(f, 1:3) & is.element(g, 7:9)) {z <- Qua3}
if (is.element(f, 4:6) & is.element(g, 1:3)) {z <- Qua4}
if (is.element(f, 4:6) & is.element(g, 4:6)) {z <- Qua5}
if (is.element(f, 4:6) & is.element(g, 7:9)) {z <- Qua6}
if (is.element(f, 7:9) & is.element(g, 1:3)) {z <- Qua7}
if (is.element(f, 7:9) & is.element(g, 4:6)) {z <- Qua8}
if (is.element(f, 7:9) & is.element(g, 7:9)) {z <- Qua9}
Zeile_f <- Sudoku[f, ]
Spalte_g <- Sudoku[, g]
Quadrat_fg <- as.vector(z)
vorkommendeZahlen <- c(Zeile_f, Spalte_g, Quadrat_fg)
fehlendeZahlen <- subset(1:9, !is.element(1:9, fehlendeZahlen))
if(length(fehlendeZahlen) == 1) {
Sudoku[f, g] <- fehlendeZahlen
}
}
}
}
if(Durchgaenge == 70) break
if(Durchgaenge == 70) {
print('Nicht lösbar!')
}
if(length(subset(as.vector(Sudoku), is.element(Sudoku, 1:9))) == 81) break
}
if(length(subset(as.vector(Sudoku), is.element(Sudoku, 1:9))) == 81) break
}Bis hierhin haben wir eine Funktion erstellt, die anhand eines vollständigen Gitters (Gitter) ein eigenes lösbares Sudoku erstellt (meinSudoku). Jetzt kannst du dir dein erstes eigenes Sudoku abspeichern. Du wirst es noch brauchen.
save(meinSudoku, file = "meinSudoku.rda")Anmerkung: Bevor du jetzt vielleicht einen Lösungsversuch deines eigenen Sudoku beginnst, widme dich doch auch noch dem letzten Aufgabenteil zum Thema Sudoku. Da wirst du deinem Sudoku den letzten äußerlichen Schliff verpassen.
Lösung zu Aufgabe 4: Sudokuausgabe in R verschönern
Für eine verschönerte Darstellung des Sudokus werden wir dieses jetzt als Plot darstellen. Dafür kann man zum Beispiel das plot.matrix-Paket benutzen, das das Plotten von Matrizen ermöglicht.
Vorbereitung
Damit du diesen Teil der Lösungen dürchführen kannst, solltest du sichergehen, dass die Pakete plot.matrix und graphics geladen sind.
install.packages("plot.matrix")
library(plot.matrix)
library(graphics)Verschönern des Sudokus
Am besten schauen wir uns jetzt erst einmal an, wie unsere Matrix nun durch die plot-Funktion dargestellt wird. Deshalb plotten wir das Sudoku erst einmal ohne weitere Argumente.
plot(Sudoku)Das kann dann z.B. so aussehen:
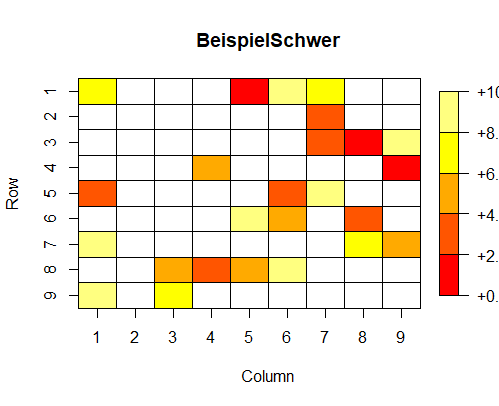
Diesen Plot müssen wir jetzt so bearbeiten, dass er einem echten Sudoku ähnlicher wird. Dafür müssen wir folgendes tun:
- eine neue Überschrift erstellen
- die Beschriftungen von den Achsen entfernen
- die Achsen entfernen
- jeder Zahl eine eigene Farbe zuweisen
- das Gitter entfernen
- die Zahlen in den Feldern anzeigen lassen
- das
+vor den Zahlen entfernen - die
NA-Felder neu in leere weiße Felder umformatieren - die Legende entfernen
- das Gitter neu formatieren
In der genannten Reihenfolge werden wir die Argumente dazu durchgehen:
- Eine neue Überschrift erstellt man mithilfe des
main-Arguments. Dieplot-Funktion benennt das Sudoku automatisch nach seinem Objektnamen (meinSudoku). Das können wir umändern, z.B. inmain = 'Sudoku'. - Die Beschriftung von den Achsen nimmt die
plot-Funktion auch automatisch vor. Mitxlabundylabkann man diese manuell bestimmen. Wir brauchen keine, deshalb bestimmen wir diese beiden einfach so:ylab = ''undxlab = ''. - Die Achsen entfernt man mithilfe des
par()-Arguments, das auch außerhalb derplot-Funktion stehen kann. Hierin müssen wir nun x- und y-Achsen löschen. Das geht folgendermaßen:par(xaxt = 'n', yaxt = 'n'). - Die Farbenzuweisung ist etwas komplizierter. Die
plot-Funktion geht automatisch von intervallskalierten Werten aus, obwohl im Falle eines Sudokus Absolutskalierung mit den Werten 1 bis 9 vorliegt. Das ist ungünstig, aber wir sorgen einfach dafür, dass trotzdem jede Zahl eine eigene Farbe hat. Dafür legen zuerst manuell die Abschnitte fest:breaks = c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10). Jetzt gibt es also Abschnitte von 1 bis 2, von 2 bis 3, … und von 9 bis 10, die jeweils mit einer unterschiedlichen Farbe kodiert werden. Diese Farben können wir nun auch noch manuell bestimmen:col = c("yellow" , "orange", "red", "violet", "lightblue", "cornflowerblue", "lightgreen", "chartreuse3", "lightsalmon4"). Damit bleibt zwar die Skalierung falsch, aber das Ziel wurde trotzdem erreicht. - Das Gitter entfernen wir, da in einem Sudoku typischerweise unterschiedlich starke Gitternetzlinien verwendet werden, um die Umrandung der 3x3-Quadrate zu verdeutlichen. Wie wir das machen, erklären wir in Schritt 10. Erst einmal entfernen wir die Gitterlinien mit
border = F. - Die Zahlen lässt man in den einzelnen Feldern folgendermaßen anzeigen:
text.cell = list(cex = 1). Innerhalb deslist-Arguments kann man dabei die Schrift formatieren.cexbestimmt beispielsweise die Schriftgröße,coldie Schriftfarbe. - Das Problem ist, dass die Zahlen mit einem
+davor angezeigt werden. Das beseitigen wir durch dieses Argument:fmt.cell='%.0f'. - Die leeren Felder werden momentan durch weiße
NA-Felder repräsentiert. Das ändern wir durch folgende Argumente:na.col = 'white'legt die Farbe des Feldes auf weiß fest undna.print = ''legt fest, dass in diesen Felder nichts stehen soll. - Die Legende können wir entfernen, indem wir Achsenbegrenzungen setzen. Das sollte z.B. so aussehen: xlim =
c(0.5, 9.5)undylim = c(0.5, 9.5).
Bevor wir jetzt mit dem Gitter weitermachen, setzen wir erst einmal alle Argumente zusammen:
par(yaxt = "n", xaxt = "n")
plot(meinSudoku,
main = "Sudoku",
xlab = "", ylab = "",
breaks = c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10),
par(yaxt = "n", xaxt = "n"),
col = c("yellow" , "orange", "red", "violet", "lightblue",
"cornflowerblue", "lightgreen", "chartreuse3", "lightsalmon4"),
border = F,
text.cell = list(cex = 1),
fmt.cell='%.0f',
na.print = '', na.col = "white",
xlim = c(0.5, 9.5), ylim = c(0.5, 9.5))Das Ergebnis sollte dann ein Sudoku ohne Gitterlinien sein.
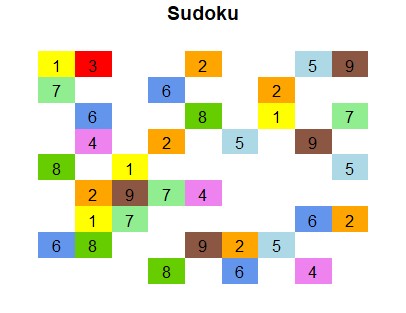
- Im letzten Schritt fügen wir die Gitterlinien hinzu. Da quasi jede Gitterlinie individuell angepasst werden muss, haben wir auch jede Linie einzeln mit der
abline-Funktion erstellt. Mit den Argumentenh = XXundv = XXkann man die Position der Linien auf der Horizontalen (h) oder Vertikalen (v) festlegen. Mitlwd = X.xxlegt man die Dicke der Linien fest. Wir haben folgende Linien eingesetzt:
abline(h = 0.5, lwd = 5)
abline(h = 1.5, lwd = 0.5)
abline(h = 2.5, lwd = 0.5)
abline(h = 3.5, lwd = 2)
abline(h = 4.5, lwd = 0.5)
abline(h = 5.5, lwd = 0.5)
abline(h = 6.5, lwd = 2)
abline(h = 7.5, lwd = 0.5)
abline(h = 8.5, lwd = 0.5)
abline(h = 9.5, lwd = 5)
abline(v = 0.5, lwd = 5)
abline(v = 1.5, lwd = 0.5)
abline(v = 2.5, lwd = 0.5)
abline(v = 3.5, lwd = 2)
abline(v = 4.5, lwd = 0.5)
abline(v = 5.5, lwd = 0.5)
abline(v = 6.5, lwd = 2)
abline(v = 7.5, lwd = 0.5)
abline(v = 8.5, lwd = 0.5)
abline(v = 9.5, lwd = 5)Daraus ergibt sich folgendes Endergebnis:
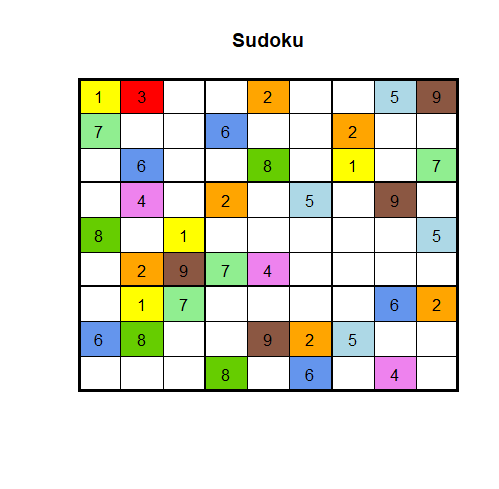
Falls du nun noch darauf verzichten möchtest, alle 20 Gitterlienen einzeln einzufügen, kannst du mit dem dplyr-Paket die Pipe-Funktion (%>%) benutzen. Dadurch werden die abline-Befehle aneinandergehängt und R kann alle Gitterlinien in einem Rutsch einfügen.
install.packages("dplyr")
library(dplyr)
abline(h = 0.5, lwd = 5) %>%
abline(h = 1.5, lwd = 0.5) %>%
abline(h = 2.5, lwd = 0.5) %>%
abline(h = 3.5, lwd = 2) %>%
abline(h = 4.5, lwd = 0.5) %>%
abline(h = 5.5, lwd = 0.5) %>%
abline(h = 6.5, lwd = 2) %>%
abline(h = 7.5, lwd = 0.5) %>%
abline(h = 8.5, lwd = 0.5) %>%
abline(h = 9.5, lwd = 5) %>%
abline(v = 0.5, lwd = 5) %>%
abline(v = 1.5, lwd = 0.5) %>%
abline(v = 2.5, lwd = 0.5) %>%
abline(v = 3.5, lwd = 2) %>%
abline(v = 4.5, lwd = 0.5) %>%
abline(v = 5.5, lwd = 0.5) %>%
abline(v = 6.5, lwd = 2) %>%
abline(v = 7.5, lwd = 0.5) %>%
abline(v = 8.5, lwd = 0.5) %>%
abline(v = 9.5, lwd = 5)