Tipps

Hier soll es um das Prinzip von Sudokus gehen. In anderen Worten: Welche Regeln gibt es? Die Regeln sind erst einmal einfach. In jeder Zeile und Spalte sowie auch in jedem der neun 3x3-Quadrate dürfen die Zahlen von 1 bis 9 jeweils nur ein Mal vorkommen.

Reihen und Spalten einzeln zu betrachten, sollte dabei kein Problem darstellen. Doch wie überprüft man das mit den 3x3-Quadraten? Für jedes Feld muss das richtige 3x3-Quadrat ausgewählt und abgeglichen werden. Auf die Lösung dieses Problems solltest du dich erst einmal konzentrieren. Wie kann man das in R umsetzen?

Bis hierhin sollte man sich Gedanken gemacht haben, wie man den Abgleich mit den Regeln gestalten könnte. Darauf folgt nun die Frage: Wie geht man beim Lösen eines Sudokus vor?

Um beim Lösen eines Sudokus voranzukommen, muss man nach Feldern suchen, die eindeutig besetzt werden können. Dafür gibt es zwei einfache Möglichkeiten (die schwierigeren lassen wir einmal außen vor), die wir uns am Beispiel eines beliebigen 3x3-Quadrats anschauen:

1. Ein Feld des Quadrats kann nur durch eine Zahl besetzt werden, weil alle anderen Zahlen bereits in der gleichen Zeile oder Spalte oder dem gleichen 3x3-Quadrat vorkommen.
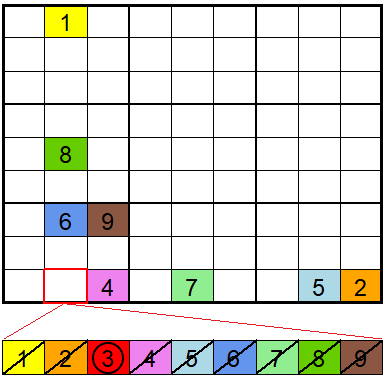
2. Ein Feld des Quadrats kann deshalb besetzt werden, weil eine Zahl, die in diesem 3x3-Quadrat noch fehlt, nur an eine freie Position des Quadrats gesetzt werden kann. Das kann dann passieren, wenn jene Zahl in anderen 3x3-Quadraten bereits vorhanden ist und dadurch gewisse Zeilen und Spalten blockiert.

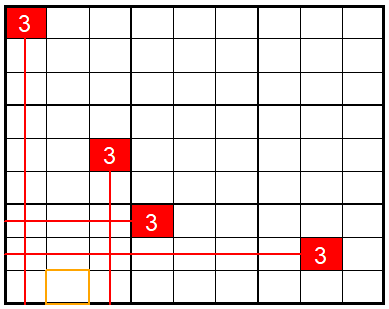
Versuch doch mal, den ersten Punkt in R umzusetzen!

Danach stellt sich die Frage: Wann soll die erstellte Funktion abgebrochen werden? - Falls du dazu keine Idee hast, kannst du dir hier einen kleine Anregung holen.

Zusatz: Ein weiterer Punkt, den du beachten kannst, ist, dass du von deiner Funktion alle Operationen immer nur für jene Felder durchführen lässt, die noch nicht belegt sind. Das kannst du mit einer if-Funktion machen und es erspart dir sehr viel Zeit.

Eine Matrix braucht nur Angaben zu Zeilen- und Spaltenzahl. Diese kannst du einfach mit den Argumenten nrow und ncol bestimmen. Versuch dir über die Hilfefunktion von R den Befehl für Matrizen anzuschauen und herauszufinden, welche Argumente du noch benötigst.

Dieser Tipp soll dir dabei helfen, die richtige Schleifenart zu finden, um jedes Feld mithilfe von Zeilen- und Spaltenvariable einmal abzugehen.

Am besten benutzt du in diesem Fall die for-Schleife. Du kannst eine for-Schleife für die Zeilen 1 bis 9 erstellen und darin eine weitere for-Schleife für die Spalten 1 bis 9. So beginnt die Funktion in Zeile 1 und geht dann alle Felder von Spalte 1 bis Spalte 9 durch, ehe die Funktion zu Zeile 2 übergeht und dort auch alle Felder von Spalte 1 bis 9 durchgeht, bis am Ende das Feld in Zeile 9 und Spalte 9 erreicht wird.

Um herauszufinden, in welchem 3x3-Quadrat du dich gerade befindest, musst du jedes Quadrat einzeln testen. Hierfür benutzen wir beispielhaft die erste Box:

• Mit dem logischen und & kannst du eine if-Funktion an mehrere Bedingungen knüpfen.
• Mit is.elememt überprüft man, ob eine Zahl Element eines bestimmten Objektes ist.

In unserem Fall steht f für die Zeilen und g für die Spalten. Wir schauen nun, ob sich das betrachtete Feld in Zeile 1 bis 3 und in Spalte 1 bis 3 befindet, was dem ersten Quadrat entsprechen würde. Wenn dies der Fall ist, speichern wir das zuvor als erstes Quadrat definierte Qua1 in einem neuen Objekt z. Diese Überprüfung sollte dann mit allen Quadraten durchgeführt werden, um unter allen Umständen das richtige Quadrat zu ermitteln.

if (is.element(f, 1:3) & is.element(g, 1:3)) {z <- Qua1}

Für die Zufallsziehung brauchst du von Anfang an zwei Variablen. In der einen definierst du, aus welchen Zahlen gezogen werden sollen (am Anfang immer 1 bis 9); nennen wir sie b. In der anderen speicherst du die ausgeloste Zahl; nennen wir sie a. Nun muss in der ersten Variable (b) die benutzte Zahl a immer wieder ausgeschlossen werden. Das Ganze kann man mit subset machen, indem alle Zahlen von b, die ungleich a sind, wieder in b übernommen werden. So befinden sich mit jedem Durchgang für ein Feld eine Zahl weniger im Objekt b.

Wenn der Füllversuch des Sudoku an einer Stelle nicht mehr nach den Regeln möglich ist, dann sollte die Funktion erneut bei einer leeren 9x9-Matrix mit dem Füllen beginnen. Das ist dann der Fall, wenn in einem Feld alle 9 Zahlen probiert wurden und nicht eingesetzt werden konnten. In Folge dessen ist die Länge des Vektors b = 0. Mithilfe dieser Information solltest du einen break-Befehl erstellen, den du zum Abbruch dreier Schleifen an der richtigen Stelle einsetzen musst: die repeat-Schleife zum Einsetzen einer zufälligen Zahl in das betrachtete Feld muss beendet werden und die beiden for-Schleifen, die ansonsten trotzdem noch alle weiteren Felder durchgehen würden.

In diesem Tipp soll es darum gehen, wie wir von einem vollständig gefüllten Sudoku-Gitter so lange Zahlen entfernen, bis eine bestimmte Anzahl an Zahlen im Gitter übrig geblieben ist (Anmerkung: Wähle am besten eine Anzahl zwischen 25 und 40).

Wichtig: Speichere dir das vollständige Gitter in einem zweiten Objekt ab, sonst geht es dir im Folgenden verloren und du musst immer wieder ein neues erstellen.

Zunächst einmal musst du dir überlegen, wie du wiederholt Zahlen aus dem Gitter löschen kannst bzw. durch NA ersetzen kannst.

Hast du das geschafft, solltest du überlegen, welche Zahlen du löschen willst. Im Vorhinein spezifische Felder auszuwählen, wäre sehr aufwendig und könnte auch in einem unlösbaren Sudoku enden. Die Feld-Koordinate aus Zeile und Spalte sollte also zufällig gewählt sein.

Bist du damit fertig, erfüllt die Funktion schon fast ihren Zweck. Es fehlt nur noch die Bedingung, mit der du sie beendest. Probier das erst einmal selbst!

Zu diesem Zeitpunkt sollte man ein Sudoku-Gitter mit einer beliebigen Anzahl an Zahlen erstellt haben. Jetzt soll es darum gehen, die Funktion aus Tipp 1 (die Lösungsfunktion) sowie einige Ergänzungen so in eine neue Funktion zu implementieren, dass die Funktion ein lösbares Sudoku generiert.

Zu diesem Zeitpunkt gibt es zwei Möglichkeiten:

1. Das Sudoku ist mit der Lösungsfunktion lösbar.
2. Das Sudoku ist mit der Lösungsfunktion nicht lösbar.

Wenn 1. zutrifft, sollte die Funktion stoppen. Das erstellte Sudoku war lösbar und muss nur noch abgerufen werden. Wichtig ist dabei natürlich, dass du es vor dem Lösungsversuch in einer neuen Variable abgespeichert hast!

Wenn 2. zutrifft, sollte die Funktion komplett von vorne anfangen und von dem am Anfang erstellten vollständigen Gitter erneut zufällig Zahlen entfernen. Damit das Ganze automatisch abläuft, musst du die Funktion aus Tipp 1 sowie die Lösungsfunktion in eine Schleife packen.

Das Endergebnis sollte eine Schleife sein, die anhand eines vollständigen 9x9-Sudoku-Gitters ein lösbares Sudoku mit X gegebenen Zahlen generiert.

Anmerkung: Je weniger Zahlen gegeben sein sollen, desto länger wird der Vorgang andauern. Außerdem nutzt die von uns (in den Lösungen) erstellte Lösungsfunktion nur eine Lösungsstrategie von vielen. Deshalb ist ihre Fähigkeit beschränkt.

Unser Ausgangspunkt ist vergleichbar mit einem normalen Datensatz aus einem Experiment. Nur möchten wir diesen Datensatz nun irgendwie abbilden. Abbildungen zum Veranschaulichen von Daten kann man mithilfe von Plots erstellen. Diese sind jedoch eher nicht für die Darstellung von Matrizen geeignet; wir sind also auf der Suche nach Plots für Matrizen.

Eine mögliche Lösung dafür stellt das Paket plot.matrix dar. Lade jenes Paket herunter und plotte dein Sudoku einmal ohne weitere Argumente.

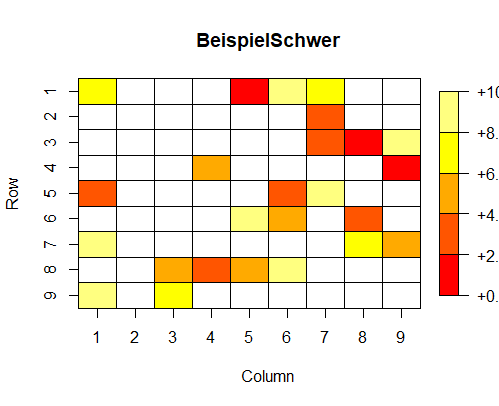
Das Ergebnis ist schon einmal vielversprechend: Es erscheint ein Koordinatensystem, das mit einem teilweise gefärbten Gitter durchsetzt ist. Einige Bearbeitungsschritte sind nötig, um das zu einem Sudoku zu verwandeln:

• Schreibe eine neue Überschrift!
• Entferne die Beschriftungen von den Achsen!
• Entferne die Achsen!
• Weise jeder Zahl eine eigene Farbe zu!
• Entferne das Gitter!
• Lass die Zahlen in den Feldern anzeigen!
• Entferne das + vor den Zahlen!
• Formatiere die NA-Felder neu in leere weiße Felder!

Viele dieser Formatierung sind auf den Websites in der Problemstellung beschrieben. Falls du nicht weiter weißt, schaue dich auch noch auf anderen Seiten um.

Offen bleibt das Gitter-Problem. Normale Sudokus haben verstärkte Rahmen um die 3x3-Quadrate. Eine etwas aufwendige Möglichkeit zur Umsetzung bietet die abline-Funktion in R. Diese fügt einzelne, formatierbare Linien in die Abbildung ein. Weitere Erklärungen zu dieser Funktion findest du in der R-internen Hilfefunktion oder hier.