Regression
Kernfragen dieser Lehreinheit
- Wie kann ein Modell für den Zusammenhang von zwei Variablen erstellt werden?
- Wie können Streudiagramme in R erstellt werden? Wie kann die Regressionsgerade in den Plot eingefügt werden?
- Wie können standardisierte Regressionsgewichte geschätzt werden? Was ist der Unterschied zu nicht-standardisierten Regressionsgewichten?
- Wie wird der Determinationskoeffizient berechnet und was sagt er aus?
- Wie werden der Determinationskoeffizient und der Regressionsparameter b inferenzstatistisch überprüft?
Vorbereitende Schritte
Zu Beginn laden wir wie gewohnt den Datensatz und verteilen die relevanten Labels. Beachten Sie, dass diese Befehle bereits angewendet wurden. Wenn Sie die veränderten Daten abgespeichert oder noch aktiv haben, sind die folgenden Befehle natürlich nicht nötig.
#### Was bisher geschah: ----
# Daten laden
load(url('https://pandar.netlify.app/post/fb22.rda'))
# Nominalskalierte Variablen in Faktoren verwandeln
fb22$geschl_faktor <- factor(fb22$geschl,
levels = 1:3,
labels = c("weiblich", "männlich", "anderes"))
fb22$fach <- factor(fb22$fach,
levels = 1:5,
labels = c('Allgemeine', 'Biologische', 'Entwicklung', 'Klinische', 'Diag./Meth.'))
fb22$ziel <- factor(fb22$ziel,
levels = 1:4,
labels = c("Wirtschaft", "Therapie", "Forschung", "Andere"))
fb22$wohnen <- factor(fb22$wohnen,
levels = 1:4,
labels = c("WG", "bei Eltern", "alleine", "sonstiges"))
fb22$ort <- factor(fb22$ort, levels=c(1,2), labels=c("FFM", "anderer"))
fb22$job <- factor(fb22$job, levels=c(1,2), labels=c("nein", "ja"))
# Skalenbildung
fb22$prok2_r <- -1 * (fb22$prok2 - 5)
fb22$prok3_r <- -1 * (fb22$prok3 - 5)
fb22$prok5_r <- -1 * (fb22$prok5 - 5)
fb22$prok7_r <- -1 * (fb22$prok7 - 5)
fb22$prok8_r <- -1 * (fb22$prok8 - 5)
# Prokrastination
fb22$prok_ges <- fb22[, c('prok1', 'prok2_r', 'prok3_r',
'prok4', 'prok5_r', 'prok6',
'prok7_r', 'prok8_r', 'prok9',
'prok10')] |> rowMeans()
# Naturverbundenheit
fb22$nr_ges <- fb22[, c('nr1', 'nr2', 'nr3', 'nr4', 'nr5', 'nr6')] |> rowMeans()
fb22$nr_ges_z <- scale(fb22$nr_ges) # Standardisiert
# Weitere Standardisierungen
fb22$nerd_std <- scale(fb22$nerd)
fb22$neuro_std <- scale(fb22$neuro)Lineare Regression
Nachdem wir mit der Korrelation mit der gemeinsamen Betrachtung von zwei Variablen begonnen haben, werden wir jetzt lineare Modelle erstellen, uns Plots - inklusive Regressionsgerade - für Zusammenhänge anzeigen lassen und Determinationskoeffizienten berechnen. Hierzu betrachten wir folgende Fragestellung:
- Zeigt die Extraversion (extra) aus dem Selbstbericht einen linearen Zusammenhang mit der selbst eingeschätzten “Nerdiness” (nerd)?
Voraussetzungen:
- Linearität: Zusammenhang muss linear sein Grafische Überprüfung (Scatterplot)
- Varianzhomogenität (Homoskedastizität) der Fehler: der Fehler jedes Wertes der UV hat annährend die gleiche Varianz
- Normalverteilung der Fehlervariablen
- Unabhängigkeit der Fehler
Die Voraussetzungen 2-4 können erst geprüft werden, nachdem das Modell schon gerechnet wurde, weil sie sich auf die Fehler (Residuen: Differenz aus beobachtetem und vorhergesagtem Wert für y) beziehen!
Deshalb erstellen wir zunächst das Regressionsmodell - wir werden weiter unten diesen Befehl - die Funktion lm() genauer besprechen, für’s erste ist wichtig zu wissen, dass die relevanten Ergebnisse des Regressionsmodells im Objekt lin_mod abgespeichert werden.
lin_mod <- lm(nerd ~ extra, fb22) #Modell erstellen und Ergebnisse im Objekt lin_mod ablegenzu 1. Linearität: Zusammenhang muss linear sein Grafische Überprüfung (Scatterplot)
plot(fb22$extra, fb22$nerd, xlab = "Extraversion", ylab = "Nerdiness",
main = "Zusammenhang zwischen Extraversion und Nerdiness", xlim = c(0, 6), ylim = c(1, 5), pch = 19)
lines(loess.smooth(fb22$extra, fb22$nerd), col = 'blue') #beobachteter, lokaler Zusammenhang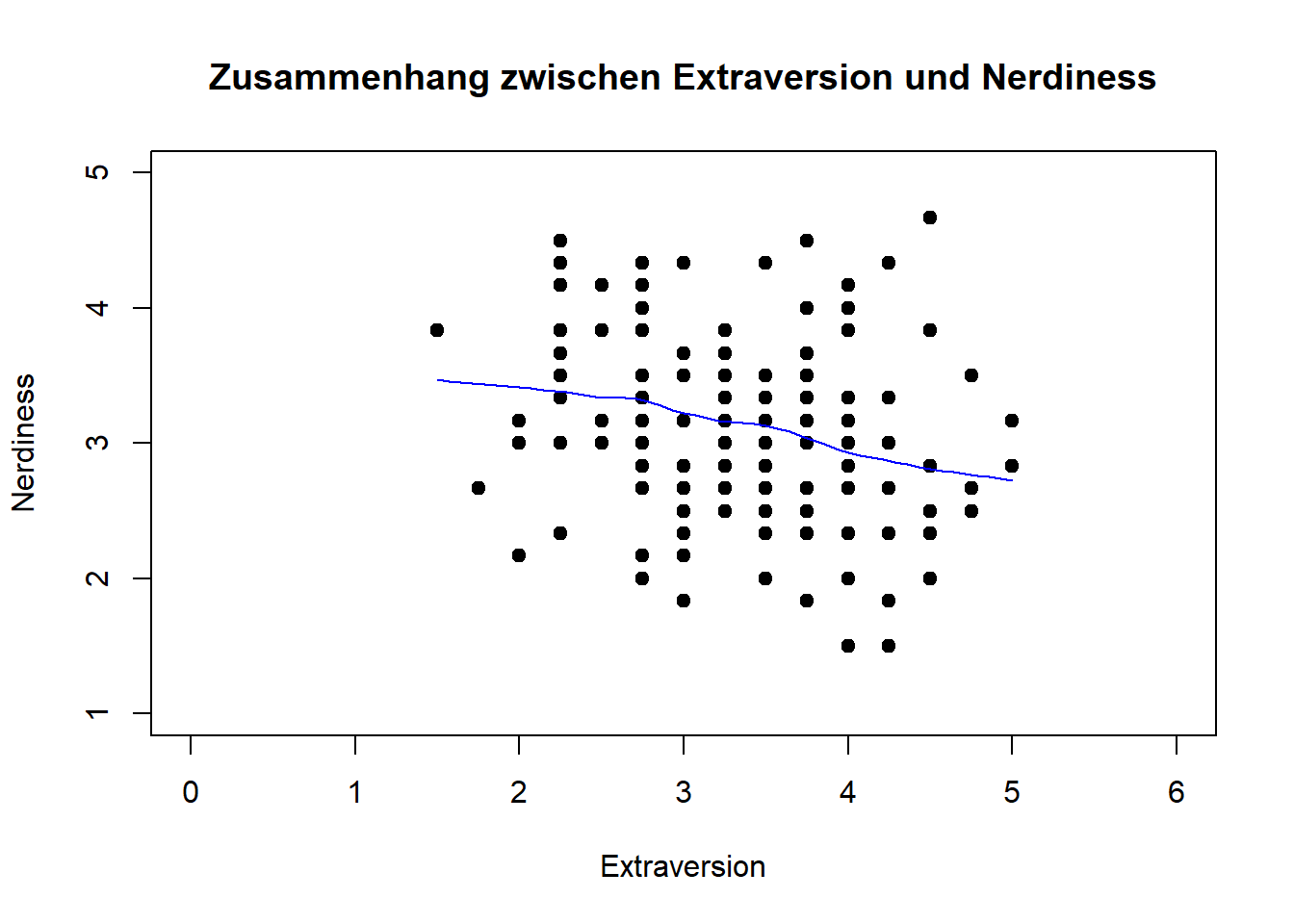
pchverändert die Darstellung der Datenpunktexlimundylimveränderen die X- bzw. Y-Achse- mit
cexkönnte man noch die Größe der Datenpunkte anpassen
Interpretation: Eine lineare Beziehung scheint den Zusammenhang aus extra und nerd akkurat zu beschreiben. Ein bspw. u-förmiger Zusammenhang ist nicht zu erkennen.
zu Voraussetzungen 2-4:
Mithilfe der Ergebnisse aus dem Regressionsmodell im Objekt lin_mod können wir nun überprüfen, ob die weiteren Voraussetzungen der linearen Regression erfüllt sind.
par(mfrow = c(2, 2)) #vier Abbildungen gleichzeitig
plot(lin_mod)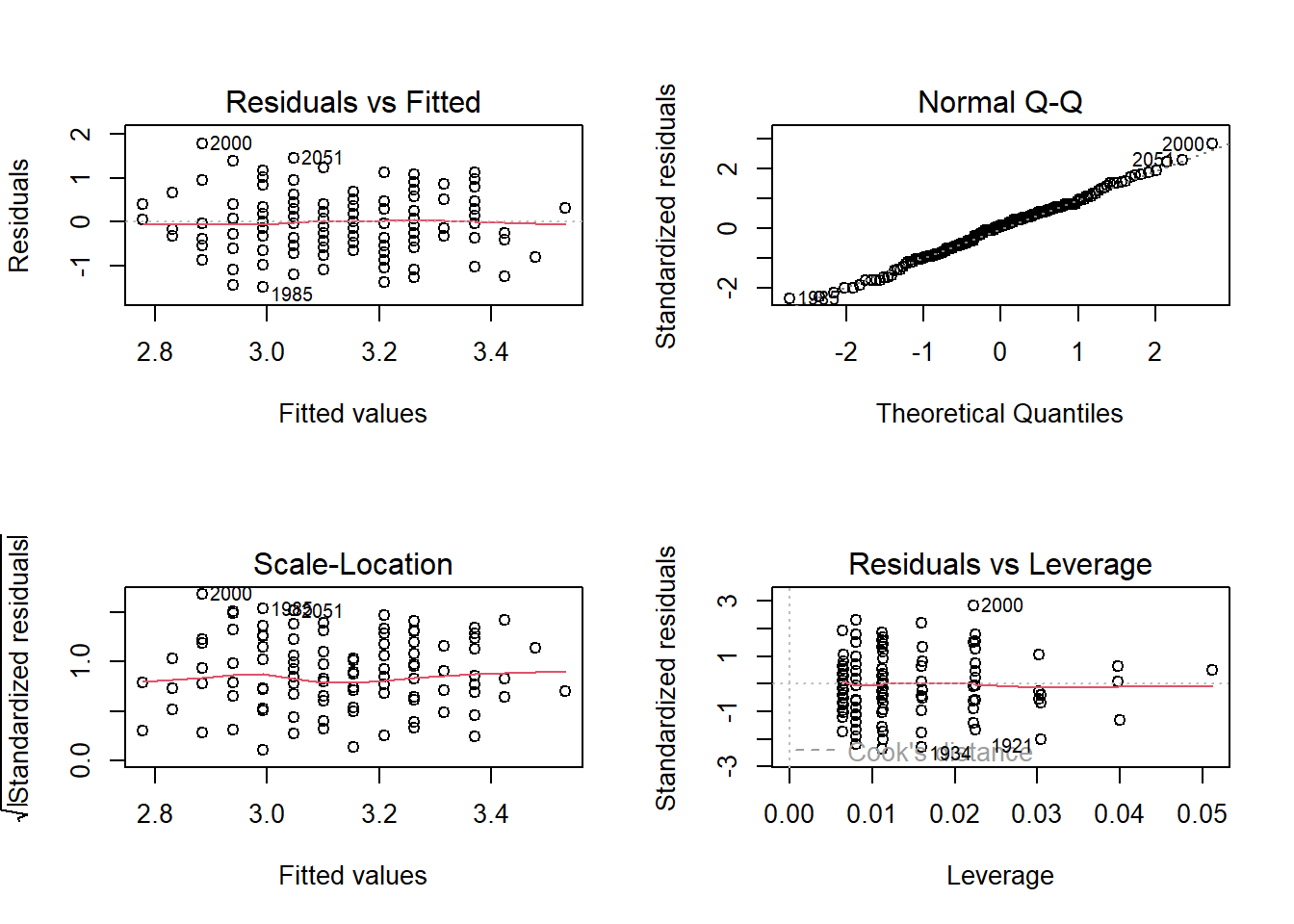
par(mfrow = c(1, 1)) #wieder auf eine Abbildung zurücksetzenInterpretation der Abbildungen:
- Residuals vs. Fitted: geeignet um Abweichungen von der Linearität und Verletzungen der Homoskedastizität aufzudecken soll möglichst unsystematisch aussehen, rote Anpassungslinie (y-MW bedingt auf X) verläuft parallel zur x-Achse
- Normal Q-Q: Zeigt Annäherung der Normalverteilung durch Residuen Punkte sollen auf die Diagonalen liegen
- Scale-Location: Prüfung der Homoskedastizität, zeigt Zusammenhang zwischen Streuung der Residuen und vorhergesagten Werten rote Anpassungslinie (y-MW bedingt auf X) sollte parallel zur x-Achse verlaufen
- Residuals vs. Leverage: Einflussreiche Datenpunkte liegen „weit draußen“, außerhalb einer der grau gestrichelten Linie. Dies trifft auf keine Beobachtung in unserer Stichprobe zu (die grau gestrichelte Linie ist in dieser Abbildung nicht zu sehen; kein Punkt liegt außerhalb dieses Bereichs) Somit lassen sich hier keine potentiell problematischen einflussreichen Datenpunkte identifizieren
In diesem Fall ist alles weitestgehend erfüllt. Da wir uns hier im Rahmen einer grafischen Überprüfung befinden, ist es natürlich schwer direkte Richtlinien festzulegen. Die Fähigkeit zur Einordnung einer Verletzung stärkt sich mit der Erfahrung - also der Betrachtung im Rahmen von sehr vielen Analysen. Wir verweisen hier zur Veranschaulich auch auf ein Beispiel mit starken Verletzungen.
Alternativer Weg zur Prüfung der Normalverteilung der Residuen
Da wir uns die Residuen (also die Fehler in der Vorhersage) direkt vom Modell ausgeben lassen können, können wir zur Überprüfung ihrer Verteilung auch unsere schon bekannten Befehle nutzen. Hier wird nochmal ein Histogramm und ein QQ-Plot gezeichnet, weiterhin wird die inferenzstatistische Testung durchgeführt.
res1 <- residuals(lin_mod) #Residuen speichern
#QQ
qqnorm(res1)
qqline(res1)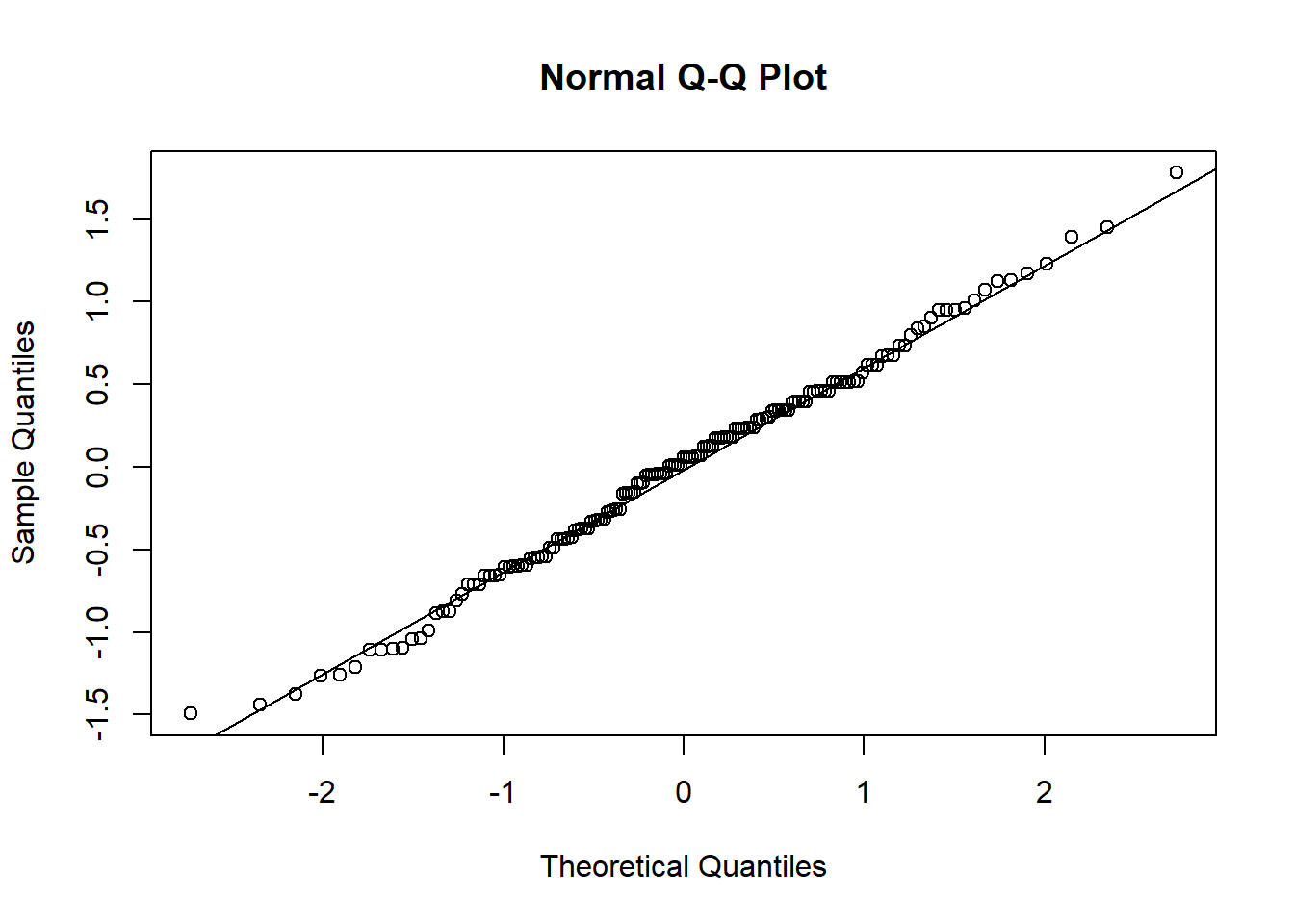
#Histogramm
hist(res1, prob = T,ylim = c(0,1)) #prob: TRUE, da wir uns auf die Dichte beziehen
curve(dnorm(x,
mean = mean(res1, na.rm = T),
sd = sd(res1, na.rm = T)),
main = "Histogram of residuals", ylab = "Residuals",
col = "blue", add = T) #add: soll Kurve in Grafik hinzugefügt werden?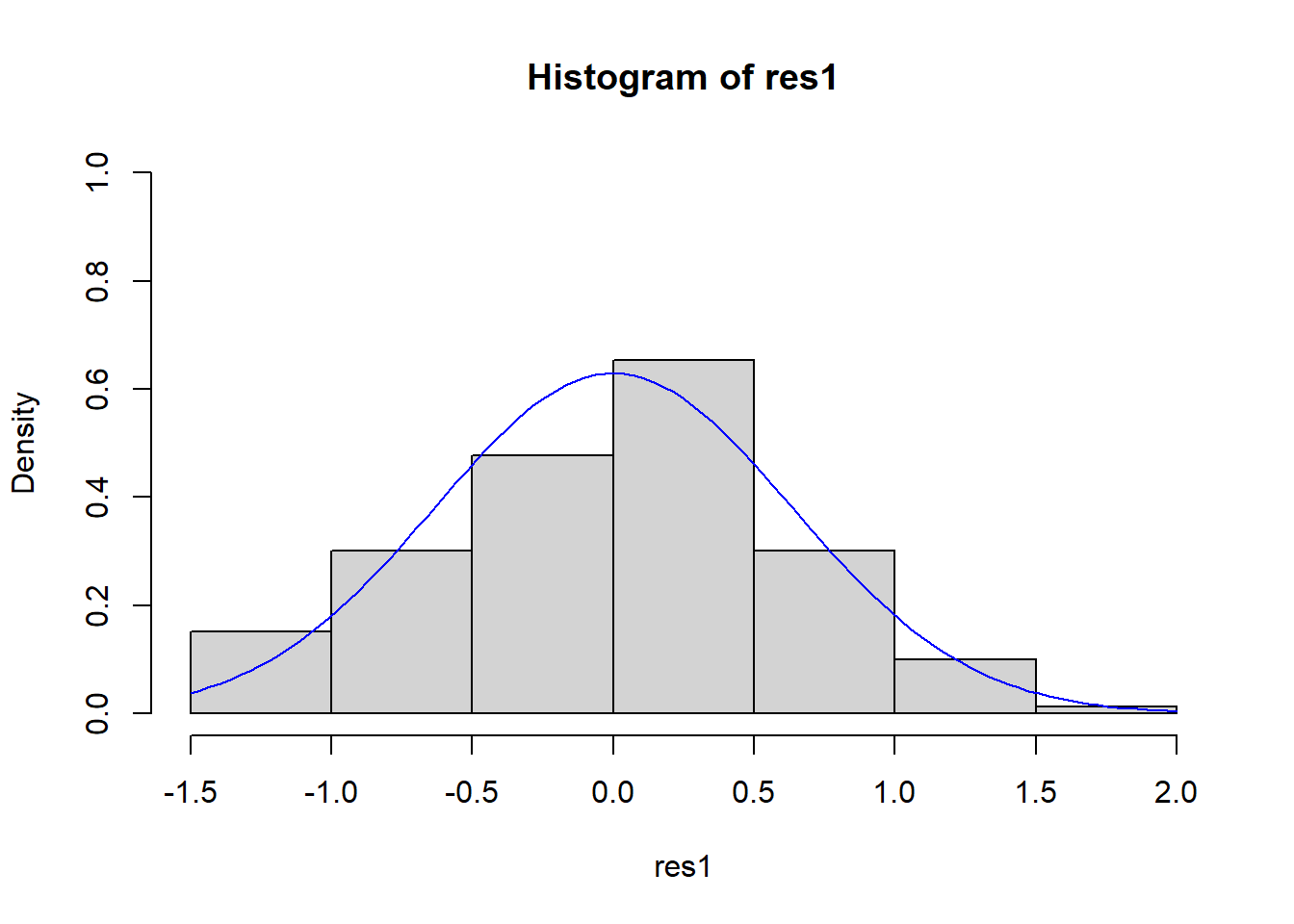
#Shapiro
shapiro.test(res1)##
## Shapiro-Wilk normality test
##
## data: res1
## W = 0.99446, p-value = 0.8122Die Plots weisen auf keine Verletzung der Annahme hin. Auch der p-Wert ist größer als .05 Die Nullhypothese konnte nicht verworfen werden und wird beibehalten: Für die Residuen wird also Normalverteilung angenommen. Somit sind alle Voraussetzungen zur Durchführung der linearen Regression erfüllt.
Modellschätzung
Die Modellgleichung für die lineare Regression, wie sie in der Vorlesung besprochen wurde, lautet:
In R gibt es eine interne Schreibweise, die sehr eng an diese Form der Notation angelehnt ist. Mit ?formula können Sie sich detailliert ansehen, welche Modelle in welcher Weise mit dieser Notation dargestellt werden können. R verwendet diese Notation für (beinahe) alle Modelle, sodass es sich lohnt, sich mit dieser Schreibweise vertraut zu machen. Die Kernelemente sind im Fall der linearen Regression
y ~ 1 + xDiese Notation enthält fünf Elemente:
y: die abhängige Variable~: die Notation für “regrediert auf” oder “vorhergesagt durch”1: die Konstante 1+: eine additive Verknüpfung der Elemente auf der rechten Seite der Gleichungx: eine unabhängige Variable
Die Notation beschreibt also die Aussage “ wird regrediert auf die Konstante und die Variable ”. Die zu schätzenden Parameter und werden in dieser Notation nicht erwähnt, weil sie uns unbekannt sind.
R geht generell davon aus, dass immer auch der Achsenabschnitt geschätzt werden soll, sodass y ~ x ausreichend ist, um eine Regression mit einem Achsenabschnitt zu beschreiben. Wenn das Intercept unterdrückt werden soll, muss das mit y ~ 0 + x explizit gemacht werden.
In unserem Beispiel ist die Extraversion (extra) und die Nerdiness (nerd). Um das Modell zu schätzen, wird dann der lm() (für “linear model”) Befehl genutzt:
lm(formula = nerd ~ 1 + extra, data = fb22)##
## Call:
## lm(formula = nerd ~ 1 + extra, data = fb22)
##
## Coefficients:
## (Intercept) extra
## 3.8554 -0.2156So werden die Koeffizienten direkt ausgegeben. Wir haben das Modell bereits abgespeichert, da wir es für die Überprüfung der Voraussetzungen benötigt haben. Hierzu muss das Modell einem Objekt zugewiesen werden. Hier in verkürzter Schreibweise (wir lassen die 1 als Repräsentant für den Achsenabschnitt weg):
lin_mod <- lm(nerd ~ extra, fb22)Aus diesem Objekt können mit coef() die geschätzten Koeffizienten extrahiert werden:
coef(lin_mod)## (Intercept) extra
## 3.8553535 -0.2156064Falls man sich unsicher ist, wie dieses Modell zustande gekommen ist, kann man dies ausdrücklich erfragen:
formula(lin_mod)## nerd ~ extraWie wir bereits weiter oben gesehen haben, werden mit dem Befehl lm() auch automatisch immer die Residuen () geschätzt, die mit residuals() (oder alternativ: resid()) abgefragt werden können.
residuals(lin_mod)## 1897 1898 1899 1900 1901 1902
## -0.595769219 0.953170506 1.394307035 0.173738771 0.850329183 0.458132379
## 1903 1904 1905 1906 1907 1908
## 0.570897447 -0.434064425 0.668776898 0.389345163 -0.424140680 0.129760918
## 1909 1910 1912 1914 1915 1916
## 1.173738771 0.007072104 -0.541867621 -0.046829494 -0.095769219 0.070897447
## 1917 1918 1919 1920 1921 1922
## 0.840405437 -0.875200955 0.065935575 0.394307035 -1.257474013 0.119837173
## 1923 1924 1925 1926 1927 1928
## 0.345367310 0.394307035 -0.149670817 0.678700643 0.232602241 0.232602241
## 1929 1930 1931 1932 1934 1935
## -0.051791367 0.453170506 0.060973702 0.619837173 -1.439026298 -0.321299357
## 1936 1937 1938 1939 1940 1941
## -0.541867621 0.345367310 0.737564114 0.345367310 0.178700643 1.070897447
## 1942 1943 1944 1945 1946 1947
## 0.516995849 -0.375200955 -0.257474013 0.948208633 0.291465712 0.453170506
## 1948 1949 1950 1951 1953 1954
## -0.811375611 1.124799045 0.173738771 -0.546829494 0.119837173 -1.100731092
## 1955 1956 1957 1958 1959 1960
## 0.458132379 1.007072104 0.340405437 0.056011829 -0.257474013 0.963094251
## 1961 1962 1963 1964 1965 1966
## -1.262435886 0.286503839 -0.164556435 -0.159594563 -1.105692965 0.056011829
## 1967 1968 1969 1970 1971 1972
## 0.904230781 0.512033977 0.232602241 0.345367310 -0.600731092 -0.385124700
## 1974 1975 1976 1977 1978 1979
## -0.331223102 -0.380162827 -0.375200955 0.012033977 0.012033977 -0.272359631
## 1980 1981 1982 1985 1986 1987
## -0.434064425 -1.213496161 -0.595769219 -1.492927896 0.232602241 0.301389457
## 1988 1989 1990 1991 1992 1994
## -0.767397759 -0.046829494 0.296427585 0.178700643 -0.875200955 0.512033977
## 1995 1996 1997 1998 1999 2000
## -0.100731092 0.237564114 -0.154632690 0.070897447 -0.605692965 1.781541967
## 2001 2002 2003 2004 2006 2008
## 0.012033977 -1.041867621 -0.654632690 -0.321299357 -0.267397759 -0.992927896
## 2009 2011 2012 2013 2017 2018
## -0.046829494 0.678700643 -0.713496161 0.178700643 -0.713496161 -0.708534288
## 2021 2022 2023 2024 2027 2028
## 0.516995849 0.173738771 -0.159594563 0.953170506 0.463094251 -1.095769219
## 2031 2032 2034 2035 2036 2039
## 0.512033977 -0.036905749 -0.600731092 -0.429102553 0.012033977 -0.316337484
## 2040 2041 2042 2043 2044 2045
## -1.036905749 -0.262435886 0.399268908 -0.659594563 -0.659594563 -0.370239082
## 2046 2047 2048 2049 2050 2051
## 0.129760918 -1.105692965 0.512033977 0.345367310 -0.041867621 1.453170506
## 2052 2054 2058 2060 2061 2062
## 0.619837173 0.796427585 -0.434064425 0.178700643 -0.487966023 -0.326261229
## 2063 2065 2066 2067 2068 2069
## 1.129760918 0.286503839 1.232602241 -0.659594563 -0.546829494 0.237564114
## 2070 2071 2072 2073 2074 2075
## 0.737564114 -0.487966023 -0.551791367 -1.375200955 0.237564114 0.619837173
## 2076 2077 2078 2079 2080 2081
## 0.512033977 0.060973702 -0.605692965 -0.041867621 0.399268908 0.458132379
## 2082 2083 2084
## -0.041867621 -0.100731092 -0.885124700Diese können auch als neue Variable im Datensatz angelegt werden und hätten dort die Bedeutung des “Ausmaßes an Nerdiness, das nicht durch Extraversion vorhergesagt werden kann” - also die Differenz aus vorhergesagtem und tatsächlich beobachtetem Wert der y-Variable (Nerdiness).
fb22$res <- residuals(lin_mod)Die folgenden Ergebnisse aus lin_mod werden wir verwenden. In lin_mod$coef stehen die Regressionskoeffizienten unter (Intercept) zur Konstanten gehörend und unter dem Namen der Variable, die wir als Prädiktor nutzen. In diesem Fall also extra. Die Regressionsgleichung hat daher die folgende Gestalt: .
Regressionsgleichung (unstandardisiert):
Interpretation der Regressionskoeffizienten:
- b0 (Regressionsgewicht): beträgt die Extraversion 0, wird eine Nerdiness von 3.86 vorhergesagt
- b1 (Regressionsgewicht): mit jeder Steigerung der Extraversion um 1 Einheit wird eine um 0.22 Einheiten niedrigere (!) Nerdiness vorhergesagt
Vorhergesagte Werte
Die vorhergesagten Werten können mit predict() ermittelt werden:
predict(lin_mod)## 1897 1898 1899 1900 1901 1902 1903 1904
## 3.262436 3.046829 2.939026 2.992928 3.316337 3.208534 3.262436 3.100731
## 1905 1906 1907 1908 1909 1910 1912 1914
## 2.831223 2.777322 3.424141 3.370239 2.992928 2.992928 3.208534 3.046829
## 1915 1916 1917 1918 1919 1920 1921 1922
## 3.262436 3.262436 2.992928 3.208534 3.100731 2.939026 3.424141 3.046829
## 1923 1924 1925 1926 1927 1928 1929 1930
## 3.154633 2.939026 3.316337 3.154633 3.100731 3.100731 2.885125 3.046829
## 1931 1932 1934 1935 1936 1937 1938 1939
## 2.939026 3.046829 2.939026 3.154633 3.208534 3.154633 3.262436 3.154633
## 1940 1941 1942 1943 1944 1945 1946 1947
## 3.154633 3.262436 3.316337 3.208534 3.424141 2.885125 3.208534 3.046829
## 1948 1949 1950 1951 1953 1954 1955 1956
## 3.478042 3.208534 2.992928 3.046829 3.046829 3.100731 3.208534 2.992928
## 1957 1958 1959 1960 1961 1962 1963 1964
## 2.992928 2.777322 3.424141 3.370239 3.262436 3.046829 2.831223 2.992928
## 1965 1966 1967 1968 1969 1970 1971 1972
## 2.939026 2.777322 3.262436 3.154633 3.100731 3.154633 3.100731 2.885125
## 1974 1975 1976 1977 1978 1979 1980 1981
## 2.831223 3.046829 3.208534 3.154633 3.154633 2.939026 3.100731 3.046829
## 1982 1985 1986 1987 1988 1989 1990 1991
## 3.262436 2.992928 3.100731 3.531944 3.100731 3.046829 3.370239 3.154633
## 1992 1994 1995 1996 1997 1998 1999 2000
## 3.208534 3.154633 3.100731 3.262436 3.154633 3.262436 2.939026 2.885125
## 2001 2002 2003 2004 2006 2008 2009 2011
## 3.154633 3.208534 3.154633 3.154633 3.100731 2.992928 3.046829 3.154633
## 2012 2013 2017 2018 2021 2022 2023 2024
## 3.046829 3.154633 3.046829 3.208534 3.316337 2.992928 2.992928 3.046829
## 2027 2028 2031 2032 2034 2035 2036 2039
## 3.370239 3.262436 3.154633 3.370239 3.100731 3.262436 3.154633 3.316337
## 2040 2041 2042 2043 2044 2045 2046 2047
## 3.370239 3.262436 3.100731 2.992928 2.992928 3.370239 3.370239 2.939026
## 2048 2049 2050 2051 2052 2054 2058 2060
## 3.154633 3.154633 3.208534 3.046829 3.046829 3.370239 3.100731 3.154633
## 2061 2062 2063 2065 2066 2067 2068 2069
## 3.154633 2.992928 3.370239 3.046829 3.100731 2.992928 3.046829 3.262436
## 2070 2071 2072 2073 2074 2075 2076 2077
## 3.262436 3.154633 2.885125 3.208534 3.262436 3.046829 3.154633 2.939026
## 2078 2079 2080 2081 2082 2083 2084
## 2.939026 3.208534 3.100731 3.208534 3.208534 3.100731 2.885125Per Voreinstellung werden hier die vorhergesagten Werte aus unserem ursprünglichen Datensatz dargestellt. predict() erlaubt uns aber auch Werte von “neuen” Beobachtungen vorherzusagen. Nehmen wir an, wir würden die Extraversion von 5 neuen Personen beobachten (sie haben - vollkommen zufällig - die Werte 1, 2, 3, 4 und 5) und diese Beobachtungen in einem neuem Datensatz extra_neu festhalten:
extra_neu <- data.frame(extra = c(1, 2, 3, 4, 5))Anhand unseres Modells können wir für diese Personen auch ihre Nerdiness vorhersagen, obwohl wir diese nicht beobachtet haben:
predict(lin_mod, newdata = extra_neu)## 1 2 3 4 5
## 3.639747 3.424141 3.208534 2.992928 2.777322Damit diese Vorhersage funktioniert, muss im neuen Datensatz eine Variable mit dem Namen extra vorliegen.
Streu-Punktdiagramm mit Regressionsgerade
Das Streudiagramm haben wir zu Beginn schon abbilden lassen. Hier kann zusätzlich noch der geschätzte Zusammenhang zwischen den beiden Variablen als Regressiongerade eingefügt werden. Hierzu wird der Befehl plot() durch abline() ergänzt:
# Scatterplot zuvor im Skript beschrieben
plot(fb22$extra, fb22$nerd,
xlim = c(0, 6), ylim = c(1, 5), pch = 19)
lines(loess.smooth(fb22$extra, fb22$nerd), col = 'blue') #beobachteter, lokaler Zusammenhang
# Ergebnisse der Regression als Gerade aufnehmen
abline(lin_mod, col = 'red')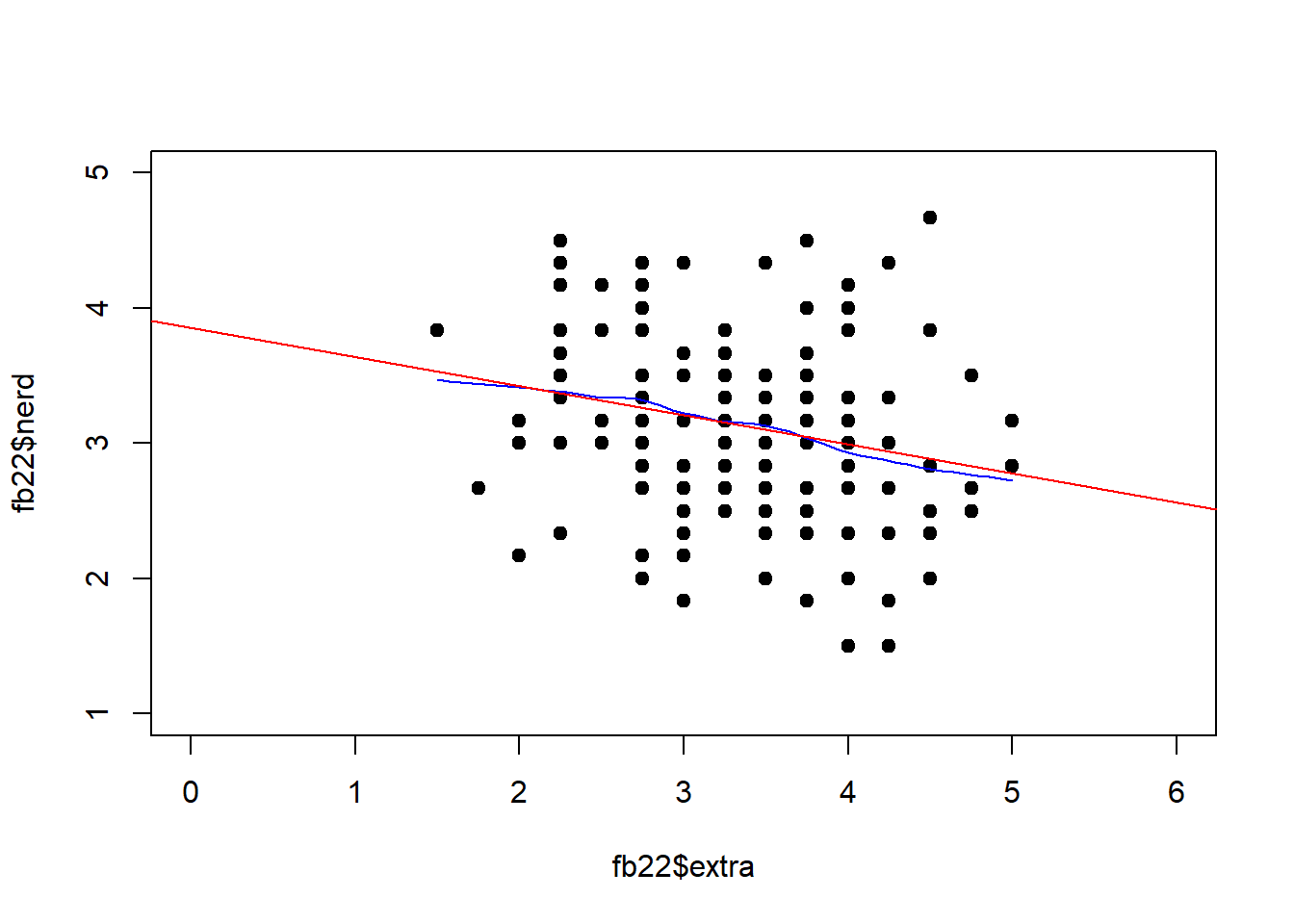
Standardisierte Regressionsgewichte
Bei einer Regression (besonders wenn mehr als ein Prädiktor in das Modell aufgenommen wird) kann es sinnvoll sein, die standardisierten Regressionskoeffizienten zu betrachten, um die Erklärungs- oder Prognosebeiträge der einzelnen unabhängigen Variablen (unabhängig von den bei der Messung der Variablen gewählten Einheiten) miteinander vergleichen zu können, z. B. um zu sehen, welche Variable den größten Beitrag zur Prognose der abhängigen Variable leistet. Außerdem ist es hierdurch möglich, die Ergebnisse zwischen verschiedenen Studien zu vergleichen, die nerd und extra gemessen haben, jedoch in unterschiedlichen Einheiten. Durch die Standardisierung werden die Regressionskoeffizienten vergleichbar.
Die Variablen werden mit scale() standardisiert (z-Transformation; Erwartungswert gleich Null und die Varianz gleich Eins gesetzt). Mit lm() wird das Modell berechnet.
s_lin_mod <- lm(scale(nerd) ~ scale(extra), fb22)
s_lin_mod##
## Call:
## lm(formula = scale(nerd) ~ scale(extra), data = fb22)
##
## Coefficients:
## (Intercept) scale(extra)
## 8.719e-17 -2.335e-01Determinationskoeffizient
Der Determinationskoeffizient ist eine Kennzahl zur Beurteilung der Anpassungsgüte einer Regression. Anhand dessen kann bewertet werden, wie gut Messwerte zu einem Modell passen. Das Bestimmtheitsmaß ist definiert als der Anteil, der durch die Regression erklärten Quadratsumme an der zu erklärenden totalen Quadratsumme. Es gibt somit an, wie viel Streuung in den Daten durch das vorliegende lineare Regressionsmodell „erklärt“ werden kann. Bei einer einfachen Regression entspricht dem Quadrat des Korrelationskoeffizienten.
Um zu berechnen, gibt es verschiedene Möglichkeiten.
Für die Berechnung per Hand werden die einzelnen Varianzen benötigt:
# Anhand der Varianz von lz
var(predict(lin_mod)) / var(fb22$nerd, use = "na.or.complete")## [1] 0.05451483# Anhand der Summe der Varianzen
var(predict(lin_mod)) / (var(predict(lin_mod)) + var(resid(lin_mod)))## [1] 0.05451483Jedoch kann dieser umständliche Weg umgangen werden.
Mit der Funktion summary() kann ein Überblick über verschiedene Ergebnisse eines Modells gewonnen werden. Für lineare Modelle werden mit diesem Befehl unter anderem auch die Koeffizienten angezeigt. Anhand des p-Werts kann hier auch die Signifikanz des überprüft werden.
#Detaillierte Modellergebnisse
summary(lin_mod)##
## Call:
## lm(formula = nerd ~ extra, data = fb22)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.49293 -0.43406 0.05601 0.39927 1.78154
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.85535 0.24733 15.588 < 2e-16 ***
## extra -0.21561 0.07166 -3.009 0.00306 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.6359 on 157 degrees of freedom
## Multiple R-squared: 0.05451, Adjusted R-squared: 0.04849
## F-statistic: 9.052 on 1 and 157 DF, p-value: 0.003057Determinationskoeffizient ist signifikant, da .
Der Determinationskoeffizient kann auch direkt über den Befehl summary(lin_mod)$r.squared ausgegeben werden:
summary(lin_mod)$r.squared## [1] 0.054514835.45% der Varianz von nerd können durch extra erklärt werden. Dieser Effekt ist nach Cohens (1988) Konvention als schwach bis mittelstark zu bewerten, wenn keine Erkenntnisse in dem spezifischen Bereich vorliegen.
Cohens (1988) Konvention zur Interpretation von :
Konventionen sind, wie bereits besprochen, heranzuziehen, wenn keine vorherigen Untersuchungen der Fragestellung oder zumindest in dem Forschungsbereich vorliegen. Die vorgeschlagenen Werte von entsprechen dabei dem Quadrat der in der letzten Sitzung genannten Konventionen für .
- ~ .01: schwacher Effekt
- ~ .09: mittlerer Effekt
- ~ .25: starker Effekt
Korrelation vs. Regression
Im Falle einer einfachen linearen Regression (1 Prädiktor) ist das standardisierte Regressionsgewicht identisch zur Produkt-Moment-Korrelation aus Prädiktor (extra) und Kriterium (nerd)
cor(fb22$nerd, fb22$extra) # Korrelation## [1] -0.2334841s_lin_mod <- lm(scale(nerd) ~ scale(extra), fb22) # Regression mit standardisierten Variablen
s_lin_mod##
## Call:
## lm(formula = scale(nerd) ~ scale(extra), data = fb22)
##
## Coefficients:
## (Intercept) scale(extra)
## 8.719e-17 -2.335e-01round(coef(s_lin_mod)["scale(extra)"],3) == round(cor(fb22$nerd, fb22$extra),3)## scale(extra)
## TRUEEntsprechend ist das Quadrat der Korrelation identisch zum Determinationskoeffizienten des Modells mit standardisierten Variablen…
cor(fb22$nerd, fb22$extra)^2 # Quadrierte Korrelation## [1] 0.05451483summary(s_lin_mod)$ r.squared # Det-Koeffizient Modell mit standardisierten Variablen## [1] 0.05451483round((cor(fb22$nerd, fb22$extra)^2),3) == round(summary(s_lin_mod)$ r.squared, 3)## [1] TRUE… und unstandardisierten Variablen
cor(fb22$nerd, fb22$extra)^2 # Quadrierte Korrelation## [1] 0.05451483summary(lin_mod)$ r.squared # Det-Koeffizient Modell mit unstandardisierten Variablen## [1] 0.05451483round((cor(fb22$nerd, fb22$extra)^2),3) == round(summary(lin_mod)$ r.squared, 3)## [1] TRUEDer standardisierte Korrelationskoeffizient in einer einfachen linearen Regression liefert also dieselben Informationen wie eine Produkt-Moment-Korrelation. Daraus wird auch ersichtlich, dass ein Regressionskoeffizient (genau wie eine Korrelation) nicht zulässt, auf die Richtung des Effekts (Kausalität) zu schließen.
Inferenzstatistische Überprüfung der Regressionsparameter b
Signifikanztestung der Regressionskoeffizienten:
Zuerst kann die Betrachtung der Konfidenzintervalle helfen. Der Befehl confint() berechnet die Konfidenzintervalle der Regressionsgewichte.
#Konfidenzintervalle der Regressionskoeffizienten
confint(lin_mod)## 2.5 % 97.5 %
## (Intercept) 3.3668258 4.34388110
## extra -0.3571501 -0.07406269Das Konfidenzintervall von -0.357 und -0.074 ist der Bereich, in dem wir den wahren Wert vermuten können. Zur Erinnerung: das 95% Konfidenzintervall besagt, dass, wenn wir diese Studie mit der selben Stichprobengröße sehr oft wiederholen, 95% aller realisierten Konfidenzintervalle den wahren Wert für enthalten werden. Da die 0 nicht in diesem Intervall enthalten ist, ist 0 ein eher unwahrscheinlicher wahrer Wert für .
- H0: , das Regressionsgewicht ist nicht von Null verschieden.
- H1: , das Regressionsgewicht ist von Null verschieden.
- H0: , das Regressionsgewicht ist nicht von Null verschieden.
- (häufig nicht von Interesse)
- H0: , der y-Achsenabschnitt ist nicht von Null verschieden.
- H1: , der y-Achsenabschnitt ist von Null verschieden.
- H0: , der y-Achsenabschnitt ist nicht von Null verschieden.
Für beide Parameter ( uns ) wird die H0 auf einem alpha-Fehler-Niveau von 5% verworfen, da die 0 nicht im jeweiligen 95% Konfidenzintervall enthalten ist.
Eine andere Möglichkeit zur interenzstatitschen Überpüfung ergibt sich über die p-Werte der Regressionskoeffizienten. Diese werden über die summary()Funktion ausgegeben.
#Detaillierte Modellergebnisse
summary(lin_mod)##
## Call:
## lm(formula = nerd ~ extra, data = fb22)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.49293 -0.43406 0.05601 0.39927 1.78154
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.85535 0.24733 15.588 < 2e-16 ***
## extra -0.21561 0.07166 -3.009 0.00306 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.6359 on 157 degrees of freedom
## Multiple R-squared: 0.05451, Adjusted R-squared: 0.04849
## F-statistic: 9.052 on 1 and 157 DF, p-value: 0.003057Aus summary(): H1: Das Regressionsgewicht für den Prädiktor Extraversion ist signifikant von Null verschieden. Der Zusammenhang von Extraversion und Nerdiness ist statistisch bedeutsam.
Aus summary(): H1: der Achsenabschnitt ist signifikant von Null verschieden. Beträgt die Extraversion Null wird eine von 0 verschiedene Nerdiness vorhergesagt.
Konfidenzinteralle und p-Werte für Regressionskoeffizienten kommen immer zu denselben Schlussfolgerungen in Bezug darauf, ob die H0 beibehalten oder verworfen wird!
