Logistische Regression
Generalisiertes lineares Modell: dichotome abhängige Variablen
Einleitung
In dieser Sitzung wollen wir dichotome abhängige Variablen mit der logistischen Regression (vgl. bspw. Eid, Gollwitzer & Schmitt, 2017, Kapitel 22 und Pituch und Stevens, 2016, Kapitel 11) analysieren. Diese Daten sind dahingehend speziell, dass die abhängige Variable nur zwei Ausprägungen hat, welche in der Regel mit 00 und 11 kodiert werden. Dies führt dazu, dass der Wertebereich der abhängigen Variable so gut wie gar nicht durch die Vorhersage innerhalb einer normalen Regressionsanalyse “getroffen” wird, die Residuen nicht länger unabhängig von der Ausprägung der abhängigen Variablen sind und auch die Normalverteilungsannahme der Residuen verletzt ist. Wir wollen uns ein reales Datenbeispiel (Datensatz Titanic aus dem gleichnamigen .rda File Titanic.rda) ansehen, in welchem die Überlebenswahrscheinlichkeit des Titanicunglücks durch das Alter sowie die Klassenzugehörigkeit auf dem Schiff vorhergesagt werden soll. Der Datensatz ist öffentlich zugänglich auf Open-Daten-Soft zu finden. Sie können sich den vollständigen Datensatz hier ansehen. Bevor wir Ihn verwenden, wurden alle fehlenden Werte entfernt (wir gehen einfach mal davon aus, dass das keine Effekte auf die Ergebnisse hat, obwohl wir dies selbstverständlich prüfen müssten) und es wurden einige Variablen rekodiert bzw. entfernt. Sie können den im Folgenden verwendeten Datensatz “Titanic.rda” hier herunterladen.
Daten laden
Wir laden zunächst die Daten: entweder lokal von Ihrem Rechner:
load("C:/Users/Musterfrau/Desktop/Titanic.rda")oder wir laden sie direkt über die Website:
load(url("https://pandar.netlify.app/post/Titanic.rda"))Nun sollte in R-Studio oben rechts in dem Fenster unter der Rubrik “Data” unser Datensatz mit dem Namen “Titanic” erscheinen.
Übersicht über die Daten
Wir wollen uns einen Überblick über die Daten verschaffen:
head(Titanic)## survived pclass sex age
## 1 1 1 2 28
## 2 0 3 2 36
## 3 1 2 1 3
## 4 1 2 1 40
## 5 0 3 2 32
## 6 0 2 2 34dim(Titanic) # Dimensionen des Datensatzes## [1] 714 4Die Variable survived gibt an, ob eine Person das Unglück überlebt hat. sex kodiert das Geschlecht, wobei 1 für weiblich und 2 für männlich steht. Die Variablen age und pclass beschreiben das Alter und die Klasse, in der die Person reiste (Klasse 1 bis 3). In dieser Analyse werden 714 Personen berücksichtigt.
Hypothesen
Während das Schiff sank, galt die Devise: Frauen und Kinder zuerst! Zumindest wird einem dies vermittelt, wenn man sich den gleichnamigen Spielfilm von James Cameron aus dem Jahr 1997 mit Kate Winslet und Leonardo DiCaprio in den Hauptrollen ansieht. Außerdem waren die Klassen an Board so angeordnet, dass die erste Klasse oberhalb der 2. lag, welche wiederum oberhalb der 3. Klasse lag. Daher hatten es Passagiere aus der 3. Klasse schwerer an Deck des Schiffs zu gelangen. Folglich sind unsere Hypothesen die Folgenden:
- Das Überleben des Unglücks hängt vom Alter ab
- Das Überleben des Unglücks hängt vom Geschlecht ab
- Das Überleben des Unglücks hängt von der Klasse an Bord ab
Modellspezifikation
Um das Überleben zu modellieren, könnten wir eine Regressionsanalyse heranziehen und das Überleben (survived) durch bspw. das Alter (age) vorhersagen:
lm(survived ~ 1 + age, data = Titanic)
In dieser Analyse sind einige Annahmen der Regressionsanalyse verletzt: Normalverteilung der Residuen, Homoskedastizität und auch Unabhängigkeit der Residuen. Aus diesem Grund wollen wir die logistische Regression heranziehen. In einer Regressionsanalyse wird der Mittelwert gegeben die unabhängigen Variablen modelliert. Es handelt sich also um einen bedingten Mittelwert. Dies ist daran ersichtlich, dass die Residuen im Mittel zu jeder Ausprägung von ˆy^y gerade Null sind und somit im Mittel immer der vorhergesagte Wert eintritt. Dieser mittlere Wert ist gerade der Mittelwert oder (korrekter) der Erwartungswert an dieser Stelle.
Gleiches wollen wir auf eine 0-1-Variable verallgemeinern. Wenn Sie einen Münzwurf durchführen und Kopf als 1 und Zahl als 0 kodieren, so erhalten Sie eine Zahlenfolge von 0en und 1en. Wenn Sie nun die relative Häufigkeit (also die Wahrscheinlichkeit) untersuchen wollen, dass Kopf auftritt, so müssen Sie lediglich den Mittelwert über alle 0en und 1en bestimmen. Dieser Mittelwert ist dann genau die Wahrscheinlichkeit, dass die Münze Kopf zeigt. Im folgenden Beispiel ist die relative Häufigkeit Kopf zu werfen 25%:
Münze <- c(0, 1, 0, 0)
mean(Münze)## [1] 0.25Diese 25% sind selbstverständlich nur eine Schätzung für die wahre Wahrscheinlichkeit, Kopf zu werfen. In einer idealen Welt würden wir davon ausgehen, dass die Wahrscheinlichkeit bei 50% liegt! Für Interessierte unter Ihnen: dieser Mittelwert ist der Maximum-Likelihood (ML) Schätzer für die Auftretenswahrscheinlichkeit von Kopf.
Im Grunde wird bei der logistischen Regression die Wahrscheinlichkeit des Erfolgs (was auch immer das ist: Kopf bei einem Münzwurf, Überleben eines Unglücks ja/nein, befördert ja/nein, oder besonders im psychologischen oder medizinischen Kontext relevant: erkrankt ja/nein, genesen ja/nein etc.) modelliert, welche eigentlich einfach wieder dem Mittelwert entspricht (bzw. der bedingten Erwartung). Die Funktion in R hierzu heißt glm, was für Generalized Linear Model steht. Um den Wertebereich der AV einzuhalten, wird die Erfolgswahrscheinlichkeit so transformiert, dass sie linear durch die UVs vorhergesagt werden kann, aber die Wahrscheinlichkeit trotzdem zwischen 0 und 1 liegt. Gehen wir bspw. von zwei Prädiktoren X1X1 und X2X2 aus:
p=P(Y=1|X1=x1,X2=x2)=eβ0+β1x1+β2x21+eβ0+β1x1+β2x2odds(p)=P(Y=1|X1=x1,X2=x2)1−P(Y=1|X1=x1,X2=x2)=eβ0+β1x1+β2x2logit(p)=ln(P(Y=1|X1=x1,X2=x2)1−P(Y=1|X1=x1,X2=x2))=β0+β1x1+β2x2
Hier ist ln der natürlich Logarithmus zur Basis e (e ist die Eulersche Zahl ≈2.718282). Der logit stellt hierbei die Link-Funktion dar, die den Erwartungswert den wir Untersuchen wollen, linear durch die Prädiktoren darstellen lässt. Die odds und p sind dann nur Retransformationen, die aus der Link-Funktion resultieren. Einige Wiederholungen zu Exponenten- oder Logarithmusregeln können Sie am Anfang der Sitzung zu exponentiellem Wachstum aus dem Bachelor nachlesen.
Eine Schreibweise für die normale Regression ist E[Y|X1=x1,X2=x2]=β0+β1x1+β2x2. Gilt für Y=0,1, so ist E[Y|X1=x1,X2=x2]=P(Y=1|X1=x1,X2=x2)=p, also der (bedingte) Mittelwert über Y ist die (bedingte) Wahrscheinlichkeit, dass Y=1 (wie wir oben am Münzwurfbeispiel gesehen haben). Somit ist ersichtlich, dass bei der logistischen Regression im Grunde nichts anderes als der (bedingte) Mittelwert/die (bedingte) Erwartung, dass Y=1 ist, modelliert wird.
Analysen mit dem Beispieldatensatz
Um die Probleme einer normalen Regression besser zu erkennen, führen wir eine solche durch.
Hypothese 1: Alter als Prädiktor
Für die erste Hypothese müssen wir den Einfluss des Alters auf die Überlebenswahrscheinlichkeit (im logistischen Regressionsfall) bzw. das Überleben (im linearen Regressionsfall) bestimmen.
Lineares Modell: Einfache Regressionsanalyse
Wir nennen unser Modell zur Modellierung des Überlebens reg_model.
library(lm.beta) # std. Koeffizienten
reg_model <- lm(survived ~ 1 + age, data = Titanic)
summary(lm.beta(reg_model))##
## Call:
## lm(formula = survived ~ 1 + age, data = Titanic)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.4811 -0.4158 -0.3662 0.5789 0.7252
##
## Coefficients:
## Estimate Standardized Std. Error t value Pr(>|t|)
## (Intercept) 0.483753 0.000000 0.041788 11.576 <2e-16 ***
## age -0.002613 -0.077221 0.001264 -2.067 0.0391 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4903 on 712 degrees of freedom
## Multiple R-squared: 0.005963, Adjusted R-squared: 0.004567
## F-statistic: 4.271 on 1 and 712 DF, p-value: 0.03912Laut der einfachen Regressionsanalyse scheint das Alter nur gering mit dem Überleben des Unglücks zusammenzuhängen. Wir führen noch einige Analysen zur Diagnostik durch.
library(car) # nötiges Paket ladenavPlots(model = reg_model, pch = 16)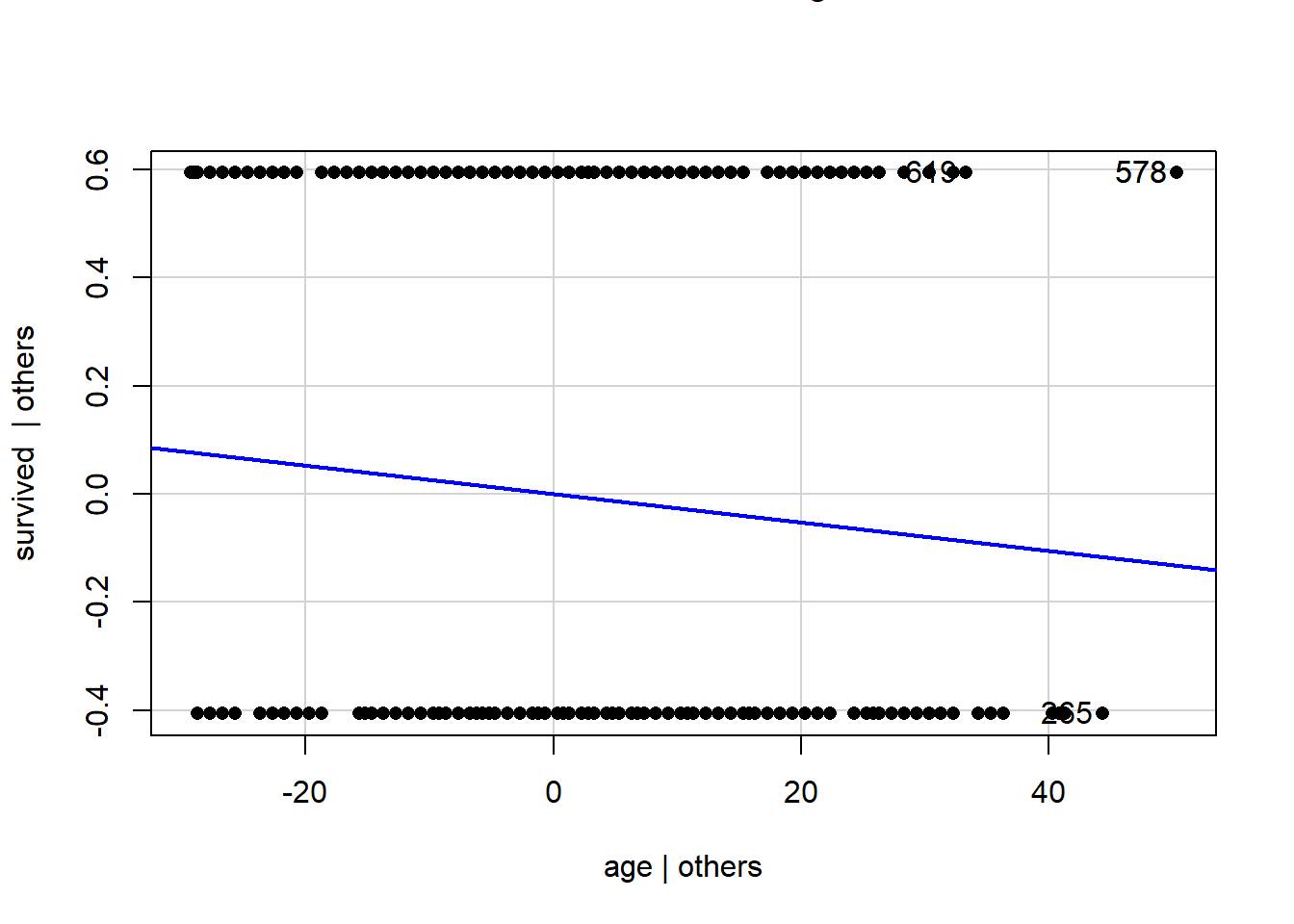
residualPlots(model = reg_model, pch = 16)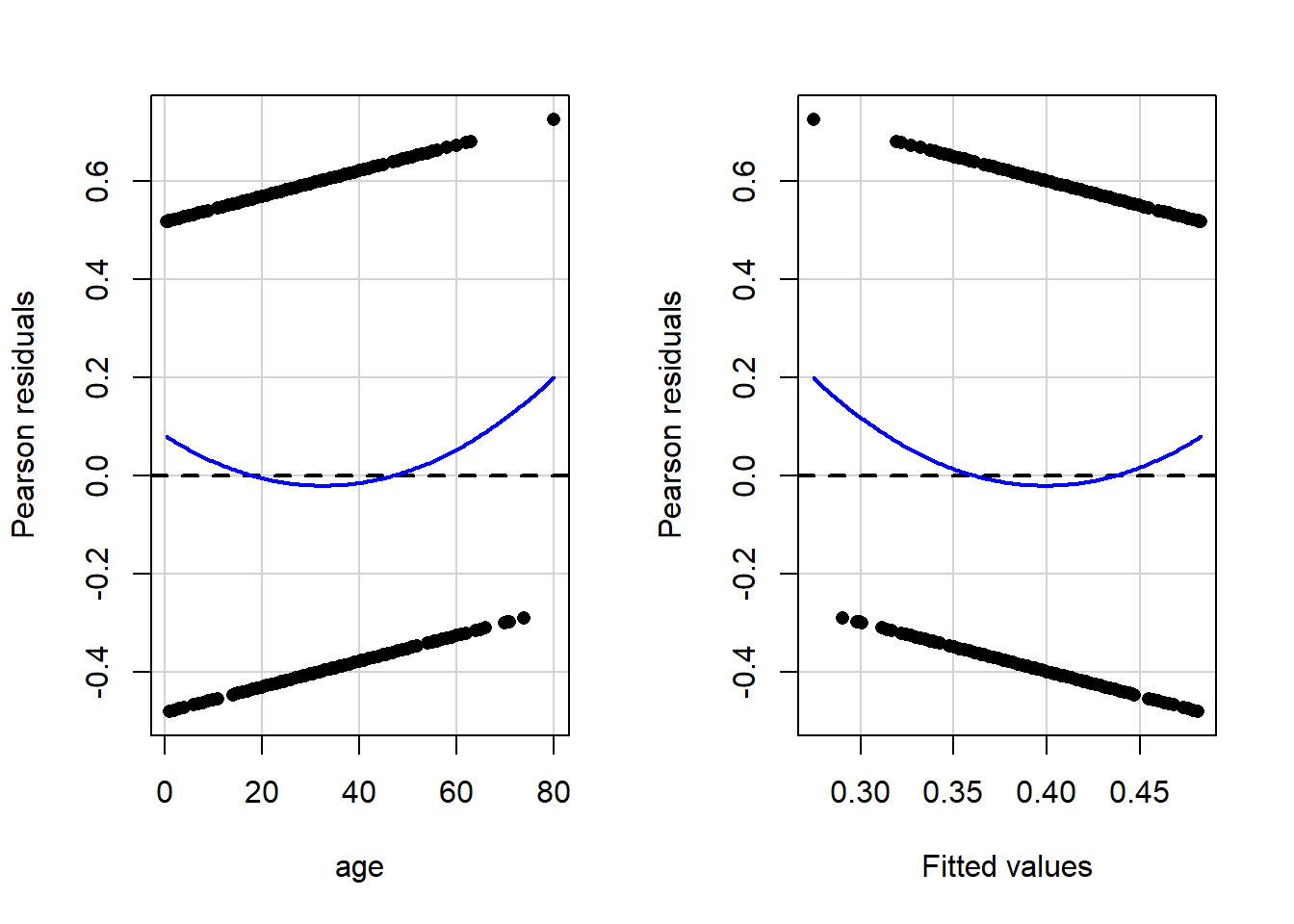
## Test stat Pr(>|Test stat|)
## age 1.5925 0.1117
## Tukey test 1.5925 0.1113library(MASS)# nötiges Paket laden
res <- studres(reg_model) # Studentisierte Residuen als Objekt speichern
hist(res, freq = F)
xWerte <- seq(from = min(res), to = max(res), by = 0.01)
lines(x = xWerte, y = dnorm(x = xWerte, mean = mean(res), sd = sd(res)), lwd = 3)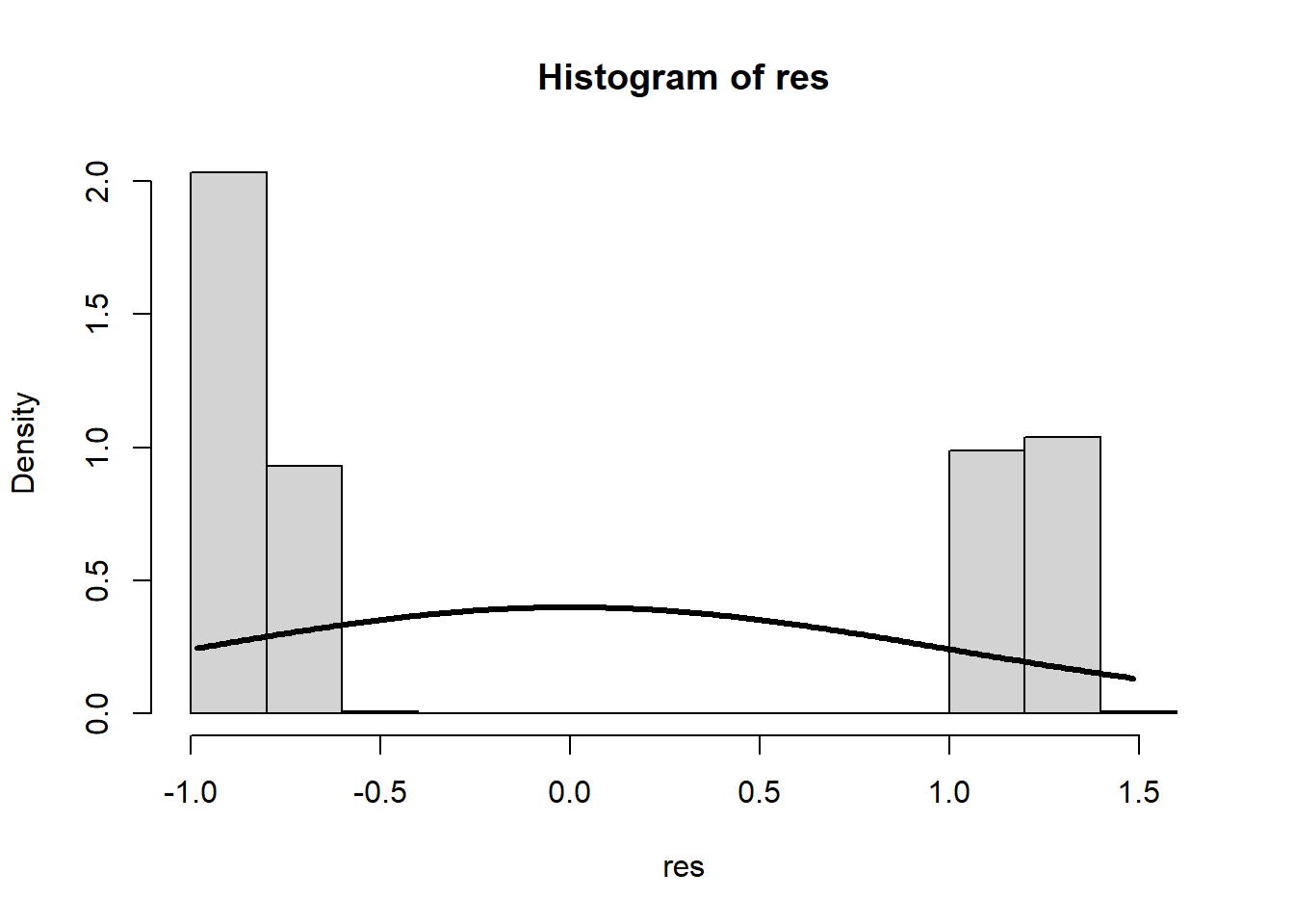
Den Verteilungen der Residuen können wir deutlich entnehmen, dass diese höchst systematisch ausfallen (mit steigendem Alter fallen die Residuen linear ab) und auch die Normalverteilungsannahme ist deutlich verletzt. Eine Regression erscheint nicht sinnvoll. Den Ergebnisse der Signifikanzentscheidungen kann nicht getraut werden. Wir müssen uns also irgendwie anders mit den Daten auseinandersetzen!
Generalisiertes Lineares Modell: Logistische Regressionsanalyse
Nun wollen wir eine logistische Regressionsanlyse durchführen. In dieser werden die Residuen nicht länger als normalverteilt angenommen, sondern die AV wird als (bedingt) binomialverteilt modelliert. Wir nennen das Modell m1, da es die erste Hypothese untersucht. Die Funktion glm übernimmt für uns die richtige Transformation, nämlich den Logit als Link-Funktion, indem wir noch das Zusatzargument family = "binomial" festlegen. Die Binomialverteilung ist gerade jene Verteilung, die beschreibt, wie häufig bei n Versuchen Erfolg eintritt (also genau die richtige Verteilung für unser Modell!).
m1 <- glm(survived ~ 1 + age, family = "binomial", data = Titanic)
summary(m1)##
## Call:
## glm(formula = survived ~ 1 + age, family = "binomial", data = Titanic)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.1488 -1.0361 -0.9544 1.3159 1.5908
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.05672 0.17358 -0.327 0.7438
## age -0.01096 0.00533 -2.057 0.0397 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 964.52 on 713 degrees of freedom
## Residual deviance: 960.23 on 712 degrees of freedom
## AIC: 964.23
##
## Number of Fisher Scoring iterations: 4Der Output der Summary unterscheidet sich geringfügig von der der normalen Regressionsanalyse:
##
## Call:
## glm(formula = survived ~ 1 + age, family = "binomial", data = Titanic)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.1488 -1.0361 -0.9544 1.3159 1.5908zeigt uns, dass wir kein lm-Objekt sondern ein glm-Objekt vor uns haben. Außerdem werden uns dieses Mal Deviance Residuals angezeigt anstatt normale Residuen. Das Schätzverfahren ist ein anderes. Es wird nicht das Kleinste-Quadrate-Verfahren angewandt, sondern die Maximum-Likelihood-Schätzmethode (ML).
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.05672 0.17358 -0.327 0.7438
## age -0.01096 0.00533 -2.057 0.0397 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Der Überblick über die (ML-)Parameterschätzung unterscheidet sich kaum von der normalen Regression. Lediglich die t-Werte werden durch z-Werte ersetzt. Die Idee hinter der Signifikanzentscheidung ist aber komplett identisch (außerdem geht die t-Verteilung für große n in die z-(Standardnormal-)Verteilung über). Hier scheint sich ein signifikanter Effekt des Alters zu zeigen.
## Null deviance: 964.52 on 713 degrees of freedom
## Residual deviance: 960.23 on 712 degrees of freedom
## AIC: 964.23
##
## Number of Fisher Scoring iterations: 4In diesem Abschnitt werden die Devianzen angezeigt. Diese beschreiben gerade die Log-Likelihooddifferenz zum saturierten Modell (also de facto die Abweichung des Modells zu den Daten). Die Null deviance beschreibt hier den Unterschied eines Modells ohne Prädiktoren zu den Daten. Dieses hat hier 713 Freiheitsgrade. Unter Residual deviance wird nun die Devianz unseres angenommenen Modells verstanden. Da wir einen Prädiktor mit in das Modell aufgenommen haben (das Alter), geht ein Freiheitsgrad für diesen Parameter verloren, weswegen die Residualdevianz hier 712 Freiheitsgrade hat (siehe bspw. Eid, et al., 2017, Kapitel 22.8 und insbesondere Seiten 823-824). Der AIC (Akaike’s Information Criterion) unseres Modells liegt bei AIC: 964.23. Mit Hilfe dieses AICs können auch nicht geschachtelte Modelle sowie Modelle mit unterschiedlichen Annahmen verglichen werden. Eine Signifikanzentscheidung ist allerdings nicht möglich (siehe bspw. Eid, et al., 2017, Seite 750). Number of Fisher Scoring iterations: 4 gibt an, wie lange der Fisher-Scoring-Algorithmus gebraucht hat, um die Standardfehler zu bestimmen. Dies kann Auskunft über mögliche Konvergenzschwierigkeiten liefern. Hier ist ein Wert von 4 aber sehr niedrig!
Fazit der Analyse
Der Effekt des Alters ist statistisch signifikant. Wir haben dieses Mal ein sinnvolleres Modell eingesetzt, was bedeutet, dass wir den Ergebnissen eher trauen können. Insgesamt stützen die Daten unsere erste Hypothese. Allerdings ist dieser Effekt sehr klein (dazu später mehr, wenn wir zur Ergebnisinterpretation und zur Einordnung der Koeffizienten kommen). Wenn wir den Wertebereich entlang der x-Achse sehr/unrealistisch groß wählen und das Alter von -500 bis 500 laufen lassen, so können wir uns die linearen und nichtlinearen Beziehungen zwischen Alter und Logit und Alter und Odds und Wahrscheinlichkeit ansehen, andernfalls ist der Effekt so klein, dass wir kaum etwas erkennen. m_age$coefficients[1] + m_age$coefficients[2]*AltersWerte ist hierbei die Formel für den Logit, da die Parameterschätzungen einfach die β-Koeffizienten sind, welche linear verknüpft den Logit ergeben. Wir könnten hier auch mit predict arbeiten, um die vorhergesagten Werte des Logit dieser Analyse zu erhalten – allerdings nur für jede Person und nicht für ein hypothetisches Alter von -500 bis 500. Glücklicherweise sind Logit, Odds und Wahrscheinlichkeit sehr leicht ineinander überführbar:
AltersWerte <- seq(-500, 500, 0.1)
logit <- m1$coefficients[1] + m1$coefficients[2]*AltersWerte
plot(x = AltersWerte, y = logit, type = "l", col = "blue", lwd = 3)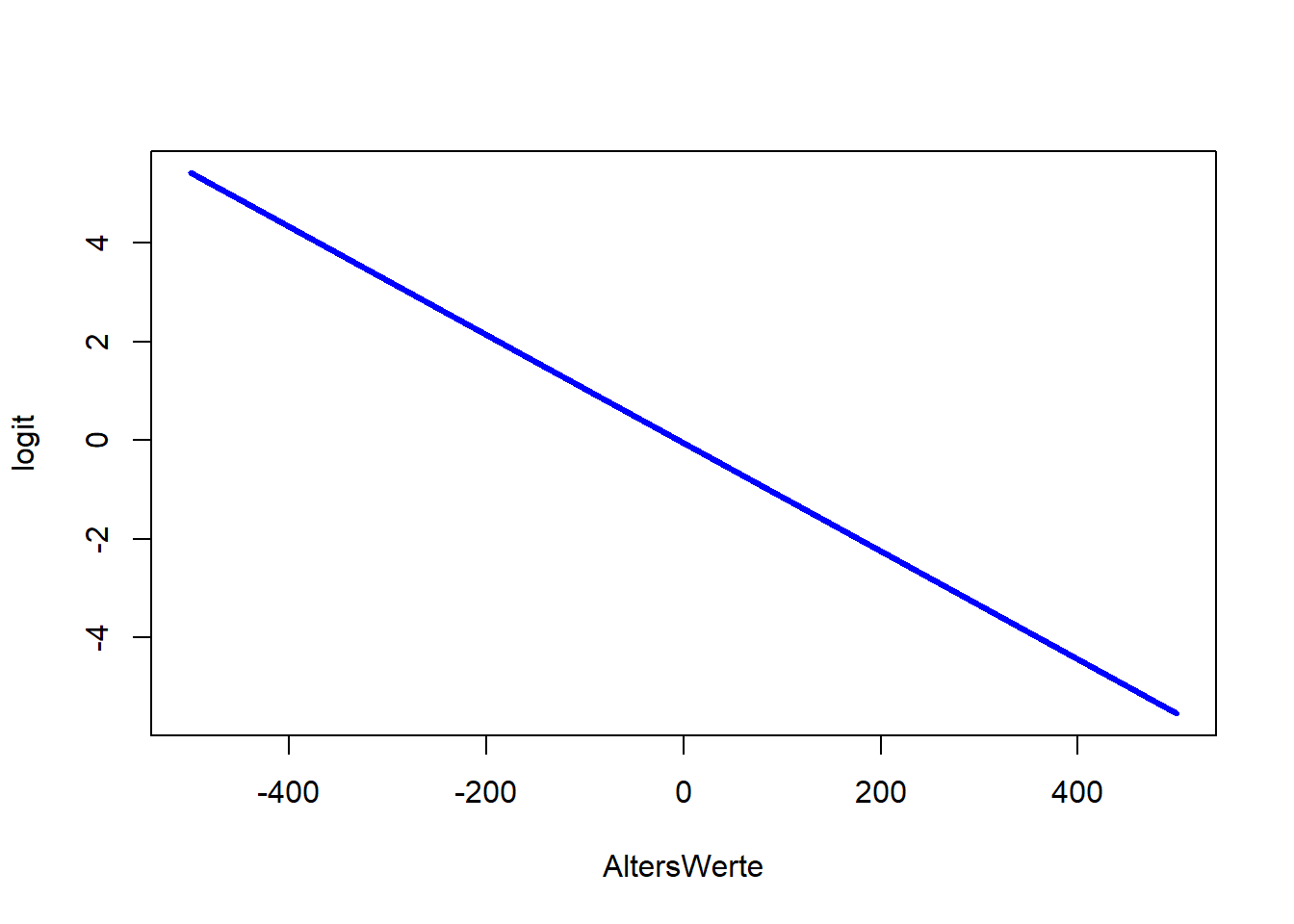
odds <- exp(logit)
plot(x = AltersWerte, y = odds, type = "l", col = "blue", lwd = 3)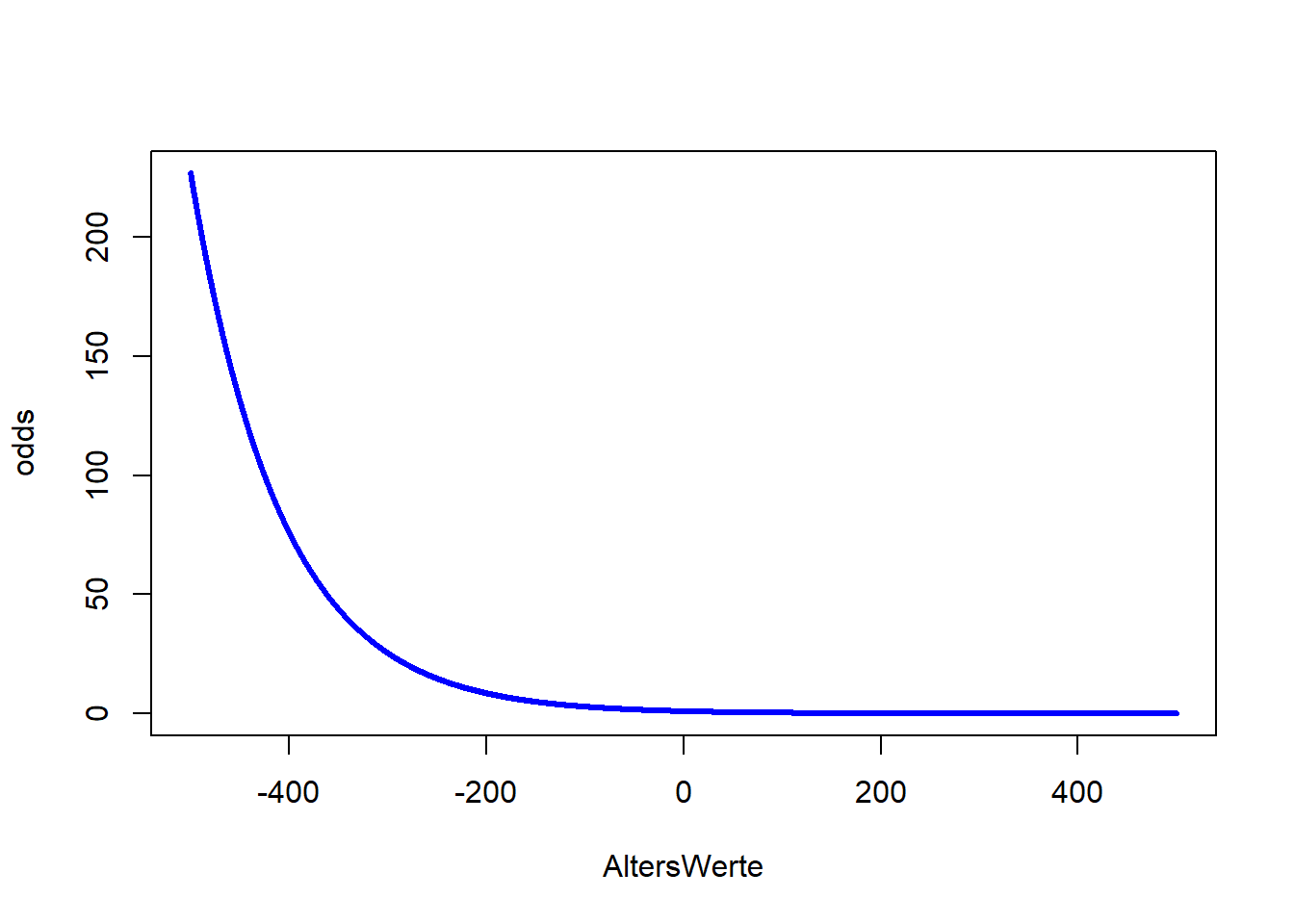
p <- odds/(1 + odds)
plot(x = AltersWerte, y = p, type = "l", col = "blue", lwd = 3)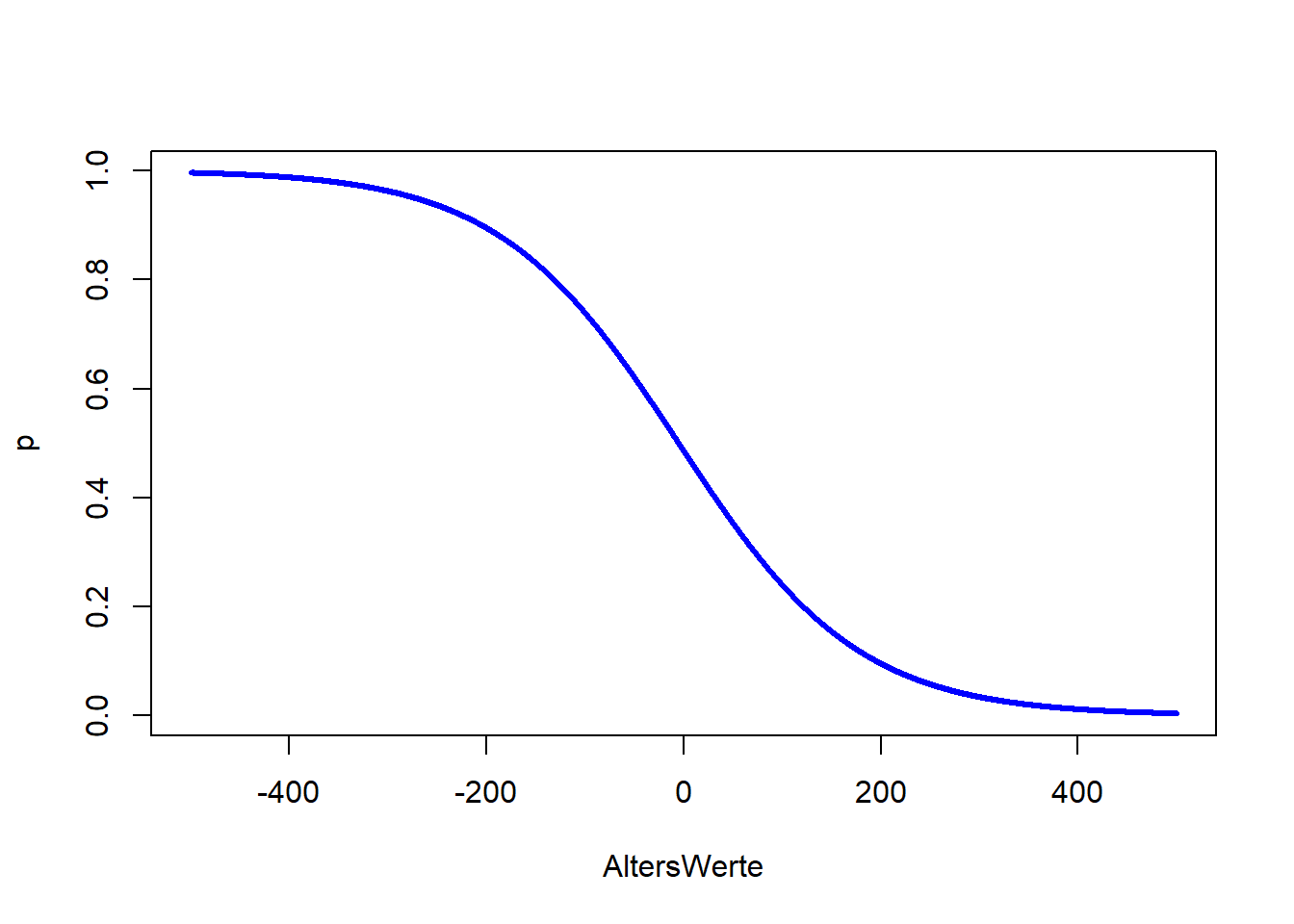
type = "l" fordert eine Linie anstatt von Punkten an, lwd = 3 sagt, dass diese Linie dreimal so dick wie der Default sein soll und col = "blue" sagt, dass die Linie blau sein soll. Wir erkennen in allen drei Plots die negative Beziehung zwischen Überleben und Alter. Der Logit ist eine lineare Funktion (Wertebereich [−∞,∞]). Somit steigt (bzw. sinkt) der Logit um β1, wenn der Prädiktor (hier Alter) um eine Einheit erhöht wird. Die Odds sind eine Exponentialfunktion (Wertebereich [0,∞]) und bei der Wahrscheinlichkeit handelt es sich um eine sogenannte Ogive (Wertebereich [0,1]). Die Odds steigen (bzw. sinken) um den Faktor eβ1 (auch Odds-Ratio genannt), wenn der Prädiktor (hier Alter) um eine Einheit erhöht wird - die Beziehung zwischen Odds und Prädiktor ist somit multiplikativ! Wir schauen uns die Parameterinterpretation der Odds im nächsten Abschnitt genauer an. Wie sich die Wahrscheinlichkeit verändert, ist nicht pauschal zu sagen. Diese Veränderung hängt von der Ausprägung des Prädiktors ab und lässt sich nicht durch eine einzige Zahl quantifizieren. Wir erkennen aber, dass die Ogive erst deutlich nach einem Alter von Null nach links laufend flacher gegen 1 geht. Im Intervall von 0 bis 80 (also realistischem Alter) ist die Wahrscheinlichkeit zu überleben kleiner als 50% und fallend mit dem Alter. In Appendix A haben Sie die Möglichkeit, spielerisch die Einflüsse der Parameter in der logistischen Regression kennen zu lernen.
Hypothese 2
Nun wollen wir das Geschlecht mit in unser Modell aufnehmen und somit Hypothese 2 untersuchen. Da das Geschlecht hier auch nur 2 Ausprägungen hat, kann dieser Effekt als Vergleich zwischen Gruppen verstanden werden. Intern wird dann mit “Dummy”-Variablen gerechnet. Wir können sicher gehen, dass mit “Dummy”-Variablen gerechnet wird (dies ist analog dazu, dass wir das Geschlecht mit 0 und 1 kodieren, anstatt 1 und 2 - so wie wir dies in den anderen Sitzungen getan hatten!), indem wir R sagen, dass es sich bei der Variable Geschlecht um einen “Faktor” handelt, der Gruppenzugehörigkeit symbolisiert. Wir können prüfen, ob diese Variable ein Faktor ist, indem wir is.factor auf die Variable sex anwenden.
is.factor(Titanic$sex)## [1] TRUEEs scheint sich also um einen Faktor zu handeln. Falls dies nicht der Fall gewesen wäre, so hätten wir as.factor auf die Variable anwenden können. Wäre das Geschlecht über Strings kodiert (bspw. “m” und “w”), so würde R dies automatisch in einen Faktor umwandeln, sobald es in einem Modell als Variable verwendet wird. Mit der Funktion table erhalten wir einen Überblick über die Kombination an Überlebenden und dem Geschlecht.
table(Titanic$survived, Titanic$sex)##
## 2 1
## 0 360 64
## 1 93 197In der Tabelle wird entlang der Spalten das Geschlecht vs. der Überlebensstatus in den Zeilen abgetragen. Dieser Tabelle ist zu entnehmen, dass der relative Anteil an Frauen, die das Unglück überlebt haben, höher ist als der der Männer: 197 vs. 64 für die Frauen und 93 vs. 360 für die Männer. Auch absolut gesehen haben mehr Frauen das Unglück überlebt. Folglich würden wir einen Geschlechtereffekt erwarten. Diese 4-Feldertafel könnten wir auch heranziehen, um einen χ2-Unabhängigkeitstest durchzuführen. Wir wollen aber den Effekt des Geschlechts über das Alter hinaus auf die Überlebenswahrscheinlichkeit des Titanicunglücks modellieren:
m2 <- glm(survived ~ 1 + age + sex, family = "binomial", data = Titanic)
summary(m2)##
## Call:
## glm(formula = survived ~ 1 + age + sex, family = "binomial",
## data = Titanic)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.7405 -0.6885 -0.6558 0.7533 1.8989
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1.188647 0.222432 -5.344 9.1e-08 ***
## age -0.005426 0.006310 -0.860 0.39
## sex1 2.465920 0.185384 13.302 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 964.52 on 713 degrees of freedom
## Residual deviance: 749.96 on 711 degrees of freedom
## AIC: 755.96
##
## Number of Fisher Scoring iterations: 4Das besondere an diesem Output ist, dass bei der Variable Geschlecht eine kleine 1 dahinter steht:
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1.188647 0.222432 -5.344 9.1e-08 ***
## age -0.005426 0.006310 -0.860 0.39
## sex1 2.465920 0.185384 13.302 < 2e-16 ***Dies gibt an, dass hier dummy-kodiert wurde und der Effekt von 1 (Frauen) im Vergleich zur Referenzgruppe (also 2, der Männer) dargestellt ist. Wir bekommen einen Überblick über die Kodierung, indem wir entweder die Variable Geschlecht ansehen oder die Funktion levels auf das Geschlecht anwenden:
Titanic$sex## [1] 2 2 1 1 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 2 1 2 2 2 2 2 1 1 2 1 1 1 2
## [38] 2 2 1 1 1 1 1 1 2 2 1 2 2 2 1 1 1 2 1 1 1 1 2 1 2 2 1 1 2 2 2 2 1 2 1 1 1
## [75] 1 2 1 2 2 1 2 1 2 2 2 2 2 2 2 1 1 2 1 1 1 2 1 2 2 1 2 2 2 1 1 2 2 2 2 1 2
## [112] 2 2 2 1 1 1 2 2 2 1 2 2 2 2 2 2 2 1 2 2 2 2 1 2 2 2 2 1 1 2 2 2 2 2 2 2 1
## [149] 2 1 1 2 1 1 1 1 2 1 1 1 1 2 2 1 2 2 2 2 1 2 2 1 1 2 1 1 1 2 2 2 2 2 2 1 2
## [186] 1 1 2 1 1 1 2 2 2 2 1 2 1 2 2 1 1 1 1 2 2 1 2 1 1 2 2 1 2 2 2 2 1 2 2 2 1
## [223] 2 2 2 2 2 2 2 1 1 1 2 2 2 2 1 2 2 2 2 1 2 2 2 2 2 1 1 2 1 2 1 1 2 1 1 2 2
## [260] 2 1 1 2 2 2 1 1 2 1 1 1 1 1 2 1 2 2 2 1 2 2 2 2 2 1 2 2 2 1 2 2 2 2 2 1 1
## [297] 1 1 1 2 1 2 2 1 1 2 1 2 1 2 1 1 2 2 2 2 1 1 1 2 2 2 2 1 2 2 2 2 2 1 2 1 1
## [334] 1 1 2 2 2 1 2 1 2 2 2 2 2 1 2 2 1 2 1 1 2 2 2 1 1 2 2 1 2 2 2 2 2 1 2 1 1
## [371] 2 1 1 2 2 2 1 2 2 1 1 1 2 1 2 2 1 2 1 2 2 2 2 2 1 2 2 1 2 1 1 2 1 2 1 2 2
## [408] 2 1 2 1 1 2 1 1 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 1
## [445] 1 2 1 2 2 2 2 1 2 2 1 2 2 1 1 2 2 2 2 2 2 1 2 1 2 1 2 1 2 2 2 2 2 1 2 2 2
## [482] 2 2 1 2 1 1 2 1 2 2 2 2 2 2 1 2 1 1 2 1 1 2 2 1 1 2 2 2 2 1 1 2 2 2 2 1 2
## [519] 2 2 2 1 1 2 2 2 2 1 2 2 2 2 1 1 2 2 2 2 2 2 2 2 2 1 1 2 2 1 2 2 2 1 1 1 2
## [556] 1 1 2 2 2 2 2 2 2 2 2 2 1 2 2 2 2 1 1 2 1 2 2 2 1 1 1 1 2 1 1 1 2 2 2 2 2
## [593] 2 1 2 2 2 1 2 1 2 1 1 2 2 2 2 2 2 2 2 2 1 2 2 2 2 1 2 2 2 1 2 2 1 2 2 1 1
## [630] 2 2 2 2 2 1 1 2 1 2 2 1 2 1 1 2 2 1 2 2 2 2 2 1 1 1 2 1 2 1 1 1 2 1 2 2 2
## [667] 1 1 2 2 1 2 2 1 2 1 2 2 1 1 2 2 1 2 2 2 2 2 2 2 1 2 1 2 1 2 2 2 2 2 2 2 2
## [704] 2 2 2 2 1 2 2 2 1 2 2
## Levels: 2 1levels(Titanic$sex)## [1] "2" "1"Bei ersterer Wahl wird, nachdem alle Ausprägungen ausgegeben wurden, ## Levels: 2 1 dargestellt. Dies ist der gleiche Output, den auch die Funktion levels erzeugt. Er ist folgendermaßen zu verstehen: es gibt hier zwei Faktoren/Gruppenzugehörigkeiten/Kategorien, wobei der Faktor mit dem Namen 2 (also die Männer) als Referenz für die Kodierung verwendet wird. Somit sind alle Effekt immer im Vergleich zur Referenzkategorie zu interpretieren. Mit Hilfe von relevel könnten wir die Referenzkategorie ändern und dann der Variable erneut zuordnen via Titanic$sex_relevel <- relevel(Titanic$sex, ref = "1") (hier würde eine neue Variable mit mit dem Namen sex_relevel dem Datensatz angehängt werden, in welchem die Frauen die Referenzkategorie darstellen würden).
Ergebnisinterpretation
Die β-Gewichte zu interpretieren, hat wenig inhaltliche Aussagekraft. Wir könnten bspw. für das Geschlecht lediglich die Aussage treffen, dass (unter Konstanthaltung aller weiteren Prädiktoren im Modell), wenn Frauen im Vergleich zu Männern betrachtet werden, der Logit (der Überlebenswahrscheinlichkeit) um 2.46 steigt. Wenn wir allerdings anstatt des Logits die Odds heranziehen, so können wir mit Hilfe des Odds-Ratio doch eine Aussage über die Überlebenswahrscheinlichkeit treffen. Dazu müssen wir die β-Gewichte transformieren via eβ:
exp(m2$coefficients) # Odds-Ratios## (Intercept) age sex1
## 0.3046332 0.9945888 11.7743113Nun können wir die Ergebnisse (einigermaßen) sinnvoll interpretieren. Das Interzept wird an der Stelle interpretiert, wo alle Prädiktoren den Wert 0 annehmen. Das Alter am Wert 0 ist wenig sinnvoll, wir könnten uns allerdings einen Säugling vorstellen, der ein Alter von 0 Jahren hat. Außerdem ist noch die Variable sex1 im Modell. Dies ist eine Dummy-Variable, die den Wert 1 annimmt, wenn das Geschlecht den Wert 1 (im Vergleich zu 2; der Referenzkategorie) annimmt; also wenn wir eine Frau im Vergleich zu einem Mann betrachten. Folglich hat diese Dummy-Variable gerade den Wert 0, wenn ein Mann betrachtet wird. Wir interpretieren das Interzept bzgl. der Odds wie folgt: Ein männlicher Säugling hat Überlebens-Odds von 0.305. Dies bedeutet, dass es für ihn 0.305-mal so wahrscheinlich ist zu überleben wie nicht zu überleben. Leider spricht dieses Ergebnis für recht schlechte Aussichten. Der Effekt des Alters lässt sich wie folgt interpretieren: Steigt das Alter um 1 Jahr (unter Konstanthaltung aller weiteren Prädiktoren im Modell), so verändern sich die Odds zu überleben um den Faktor (multiplikativ) 0.995. Insgesamt sinken die Odds zu überleben und damit die Überlebenswahrscheinlichkeit mit dem Alter, denn das Odds-Ratio ist genau dann kleiner 1, wenn der β-Koeffizient des Logit kleiner 0 ist und es sich somit um eine negative/abfallende Beziehung handelt! Dieser Effekt ist allerdings nicht statistisch signifikant und wird somit nur für die Stichprobe, nicht aber für die Population interpretiert. Wird nun eine Frau im Vergleich zu einem Mann betrachtet, so steigen die Odds zu überleben um den Faktor 11.774. Somit haben (unter Konstanthaltung aller weiteren Prädiktoren im Modell) Frauen eine 11.774 mal so hohe Überlebenswahrscheinlichkeit wie die Männer. Hier ist extrem wichtig, zu beachten, dass die Odds sich multiplikativ ändern und nicht additiv, wie wir es von der linearen Regression (und im Übrigen auch vom Logit) gewohnt sind.
Grafische Veranschaulichung
Wir können uns dieses Modell auch grafisch ansehen und damit die oben aufgezeigten Effekte verdeutlichen. Dazu werden wir diesmal ggplot aus dem ggplot2 Paket verwenden. Dieses muss natürlich installiert sein (install.packages("ggplot2")) und geladen werden.
library(ggplot2)Wir können hier sehr leicht Gruppierungen in Grafiken darstellen. Zunächst müssen wir allerdings die Prädiktionen unseres Modells bestimmen, denn wir wollen uns die Vorhersage/Erwartung (unter) unseres Modells ansehen. Die Funktion, mit der wir dies machen können, heißt genauso wie die Funktion die sie ausführt: predict. Wir sagen damit den Logit für alle Konstellationen von Alter und Geschlecht in unseren Daten vorher, indem wir der Funktion das Modell übergeben. Wir bestimmen also für jede Personen die erwartete Überlebenswahrscheinlichkeit unter diesem Modell (der Prädiktion durch Geschlecht und Alter). Anschließend können wir den Logit so transformieren, dass wir die Odds oder die Wahrscheinlichkeit erhalten. Um dies leichter nachvollziehbar zu machen, führen wir die Transformationen mit neu erstellten Variablen durch, ehe wir diese dem Datensatz anhängen (denn ggplot hat es am liebsten, wenn wir mit data.frames, also ganzen Datensätzen arbeiten).
logit_m2 <- predict(m2) # Logit unter Modell m2 bestimmen
odds_m2 <- exp(logit_m2) # Logit unter Modell m2 in Odds transformieren
p_m2 <- odds_m2/(1 + odds_m2) # Odds in Wahrscheinlichkeiten transformieren
# dem Datensatz anhängen:
Titanic$logit_m2 <- logit_m2
Titanic$odds_m2 <- odds_m2
Titanic$p_m2 <- p_m2
head(Titanic)| survived | pclass | sex | age | logit_m2 | odds_m2 | p_m2 |
|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 28 | -1.340572 | 0.2616959 | 0.2074160 |
| 0 | 3 | 2 | 36 | -1.383979 | 0.2505794 | 0.2003707 |
| 1 | 2 | 1 | 3 | 1.260995 | 3.5289329 | 0.7791974 |
| 1 | 2 | 1 | 40 | 1.060237 | 2.8870558 | 0.7427359 |
| 0 | 3 | 2 | 32 | -1.362276 | 0.2560774 | 0.2038707 |
| 0 | 2 | 2 | 34 | -1.373128 | 0.2533135 | 0.2021150 |
Eine Grafik erhalten wir nun mit ggplot sehr einfach:
ggplot(data = Titanic, mapping = aes(x = age, y = logit_m2, col = sex)) +
geom_line(lwd = 2) +
ggtitle("Logit vs Age and Sex")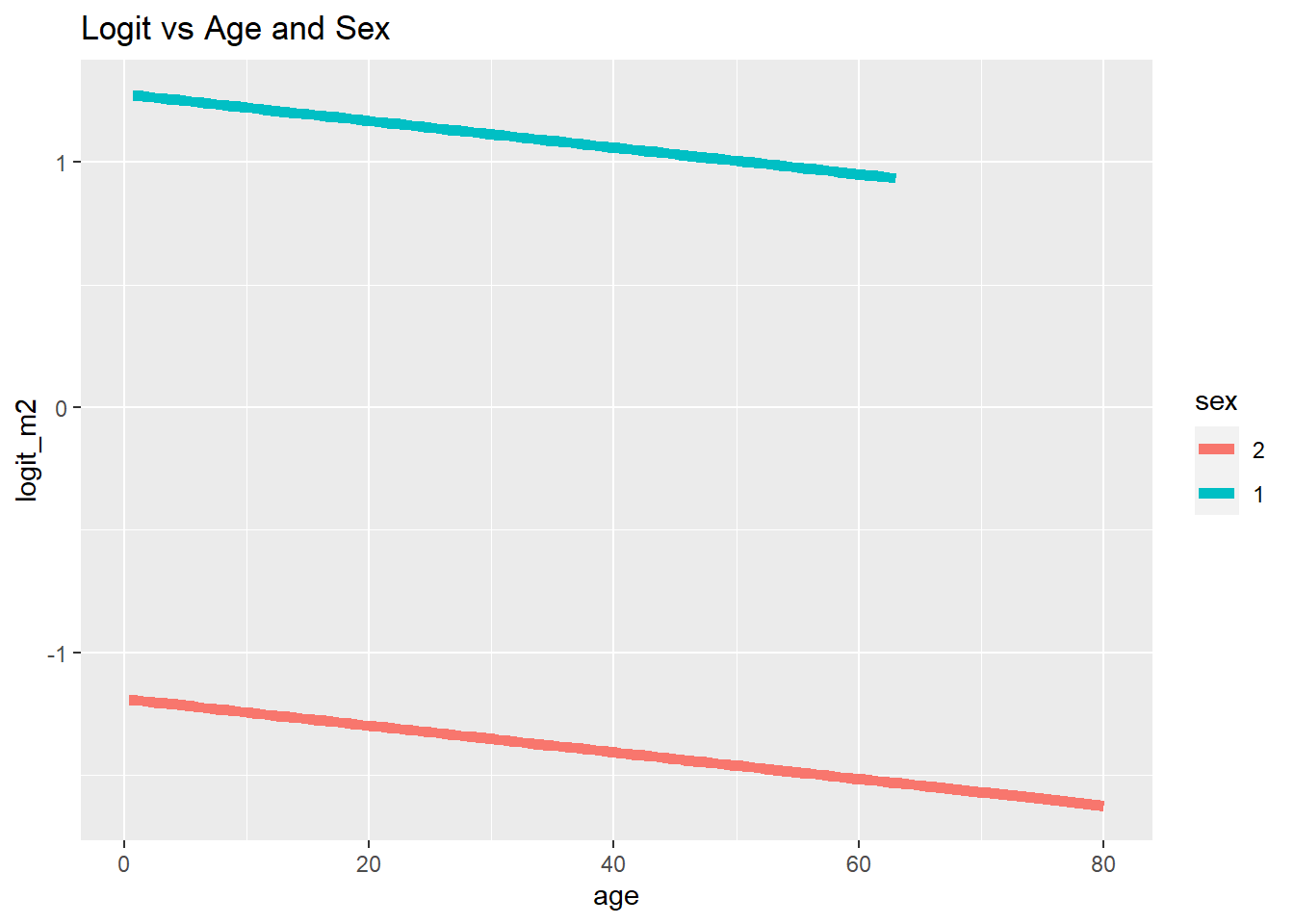
ggplot arbeitet etwas anders als die Basisfunktion plot. Zunächst übergeben wir ihr die Daten data = Titanic. Dem mapping übergeben wir sozusagen das Achsenkreuz und Gruppenzugehörigkeiten und Farbkodierungen innerhalb von aes(x = age, y = logit_m2, col = sex). Hier wird gesagt, dass das Alter auf die x-Achse soll und wir den Logit entlang der y-Achse plotten wollen. Außerdem soll für das Geschlecht eine separate Linie eingezeichnet werden und diese soll farblich kodiert sein. Damit dies funktioniert, müssen natürlich die Variablen im richtigen Format vorliegen. Bspw. müssen Gruppierungen, wie etwa das Geschlecht, als Faktor vorliegen. Anschließend fügen wir mit + hinzu, was genau geplottet werden soll. In diesem Beispiel wollen wir Linien haben. Deshalb verwenden wir die Funktion geom_line mit dem Argument lwd = 2 für zweifache Liniendicke. Würden wir hier bspw. geom_point verwenden, so würden Punkte gezeichnet werden. Wieder mit dem + fügen wir außerdem einen Titel hinzu mit der Funktion ggtitle. Gleiches können wir auch für die Odds oder die Wahrscheinlichkeit durchführen:
ggplot(data = Titanic, mapping = aes(x = age, y = odds_m2, col = sex)) +
geom_line(lwd = 2) +
ggtitle("Odds vs Age and Sex")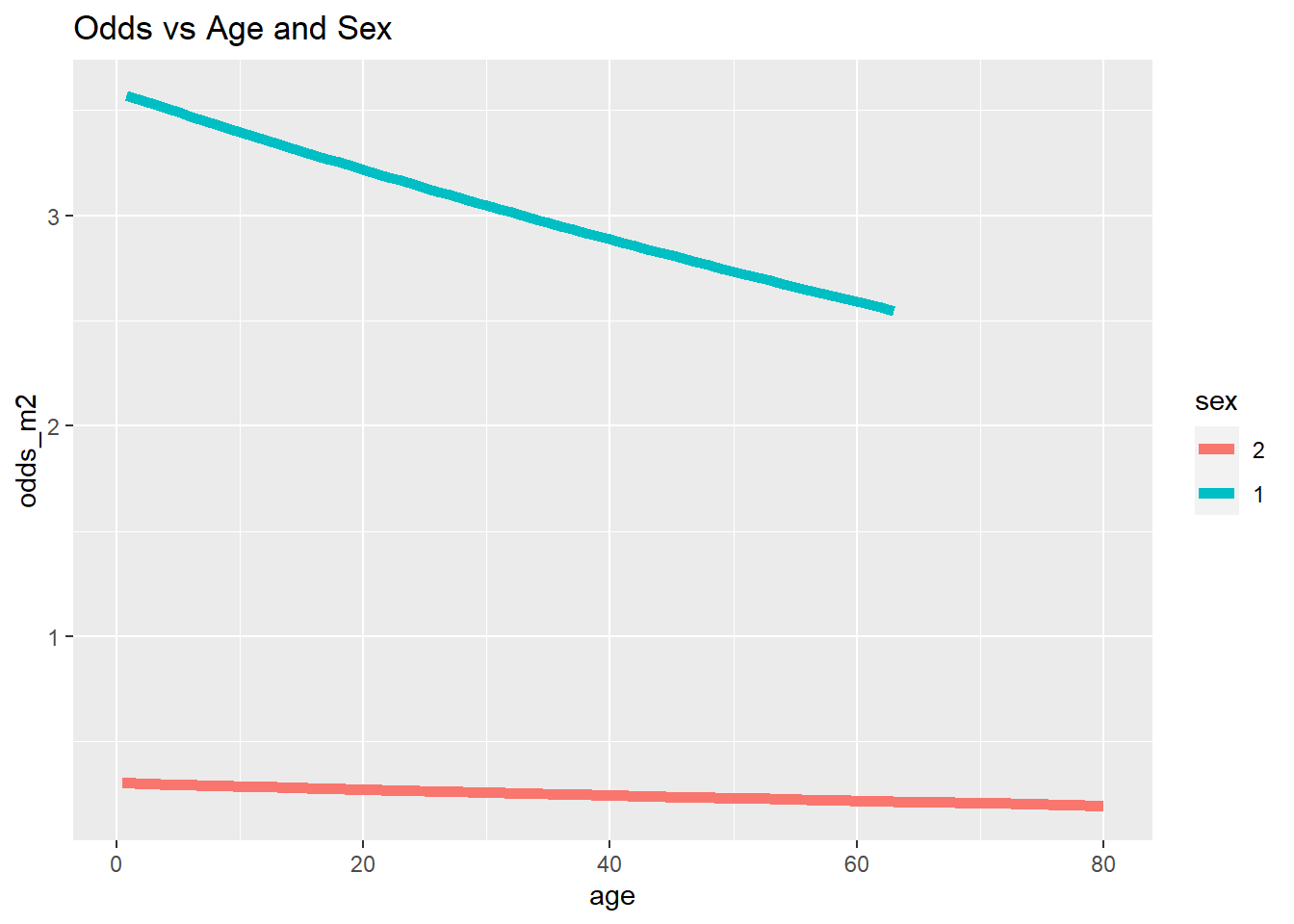
ggplot(data = Titanic, mapping = aes(x = age, y = p_m2, col = sex)) +
geom_line(lwd = 2) +
ggtitle("P vs Age and Sex")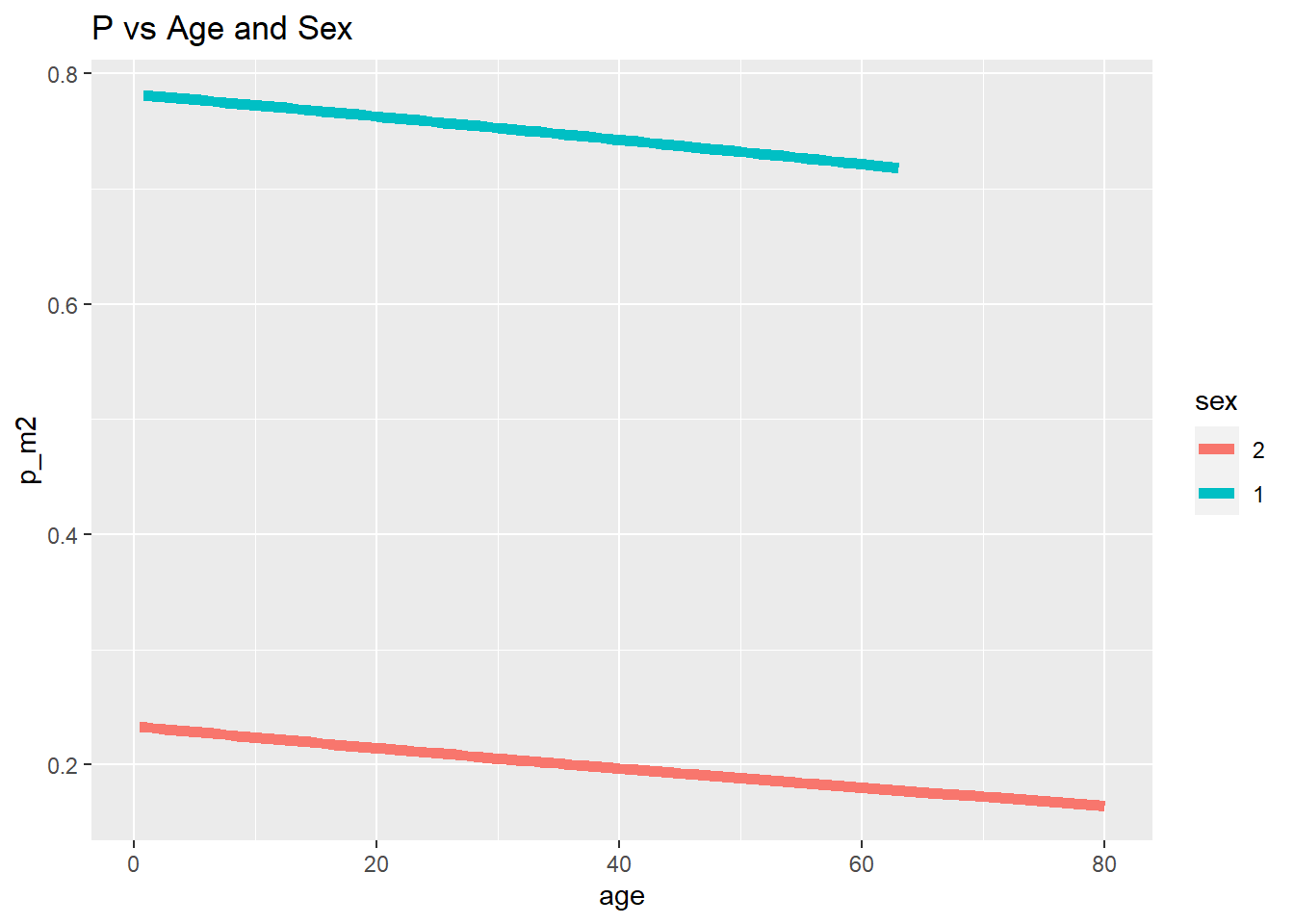
Einen drastischen Alterseffekt können wir in keiner der Grafiken erkennen. Dass sich Unterschiede über das Geschlecht abbilden, sehen wir allerdings recht deutlich! Weitere Informationen zu ggplot2 erhalten Sie bspw. auf Tidyverse. Außerdem können Sie sich auch eine Einführung in ggplot2 auf dieser Website ansehen.
Hypothese 3
Nun wollen wir die Reiseklasse mit in unser Modell aufnehmen und somit Hypothese 3 untersuchen. Die Klasse ist auch ein Faktor, der 3 Ausprägungen hat. Wir schauen uns die Level an:
levels(Titanic$pclass)## [1] "3" "1" "2"Die drei Klassen sind mit 1, 2 und 3 kodiert, wobei die 3. Klasse die Referenz ist (da sie an erster Stelle steht). Dies müssen wir bei der Interpretation berücksichtigen. Schauen wir uns die Ergebnisse an:
m3 <- glm(survived ~ 1 + age + sex + pclass, family = "binomial", data = Titanic)
summary(m3)##
## Call:
## glm(formula = survived ~ 1 + age + sex + pclass, family = "binomial",
## data = Titanic)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.7303 -0.6780 -0.3953 0.6485 2.4657
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1.326394 0.247892 -5.351 8.76e-08 ***
## age -0.036985 0.007656 -4.831 1.36e-06 ***
## sex1 2.522781 0.207391 12.164 < 2e-16 ***
## pclass1 2.580625 0.281442 9.169 < 2e-16 ***
## pclass2 1.270826 0.244048 5.207 1.92e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 964.52 on 713 degrees of freedom
## Residual deviance: 647.28 on 709 degrees of freedom
## AIC: 657.28
##
## Number of Fisher Scoring iterations: 5Dieses Mal sind alle Prädiktoren signifikant - auch das Alter. Bevor wir zur Interpretation übergehen, wollen wir die Hinzunahme der Klasse noch insgesamt auf Signifikanz prüfen. Wir sehen am Output, dass jede Dummy-Variable für sich signifikante Vorhersagekraft leistet, allerdings wollen wir eine Signifikanzentscheidung für die Variable Reiseklasse als Ganzes durchführen und ziehen dazu den Likelihood-Ratio-Test (χ2-Differenzen-Test) heran.
Modellvergleich
Diesen kennen wir bereits aus der hierarchischen Regressionssitzung. Da wir hier keine Varianzen prüfen, können wir die p-Werte so interpretieren, wie sie ausgegeben werden.
anova(m2, m3, test = "LRT")## Analysis of Deviance Table
##
## Model 1: survived ~ 1 + age + sex
## Model 2: survived ~ 1 + age + sex + pclass
## Resid. Df Resid. Dev Df Deviance Pr(>Chi)
## 1 711 749.96
## 2 709 647.28 2 102.67 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Der Test liefert eine signifikante Likelihood-Differenz, χ2(df=2)= 102.674, p<.001. Der Test hat hier 2 Freiheitsgrade, da auch zwei Dummy-Variablen mit in das Modell aufgenommen wurden! Hätten wir eine Gruppierungsvariable mit 5 Ausprägungen gehabt, so wären es 4 Freiheitsgrade gewesen. Folglich verbessert die Klassenzugehörigkeit die Prädiktion der Überlebenswahrscheinlichkeit des Titanicunglücks.
Ergebnisinterpretation
Um die Ergebnisse sinnvoll zu interpretieren, schauen wir uns wieder die Odds-Ratios an:
exp(m3$coefficients) # Odds-Ratio## (Intercept) age sex1 pclass1 pclass2
## 0.2654328 0.9636903 12.4632077 13.2053931 3.5637952Das Interzept wird an der Stelle interpretiert, an dem alle Prädiktoren den Wert 0 annehmen. Dies ist der Fall, wenn das Alter sowie alle Dummy-Variablen den Wert 0 annehmen, wir uns also für alle kategorialen Prädiktoren in der Referenzkategorie befinden. Somit hat ein männlicher Säugling aus der 3. Klasse eine um den Faktor 0.265 kleinere Wahrscheinlichkeit zu überleben im Vergleich zu zu sterben. Unter Konstanthaltung aller weiteren Prädiktoren im Modell sinken die Odds zu Überleben um den Faktor 0.964, wenn das Alter um ein Jahr steigt. Unter Konstanthaltung aller weiteren Prädiktoren im Modell steigen die Odds zu Überleben um den Faktor 12.463, wenn Frauen im Vergleich zu Männern betrachtet werden. Unter Konstanthaltung aller weiteren Prädiktoren im Modell steigen die Odds zu überleben um den Faktor 13.205, wenn eine Person aus der 1. Klasse im Vergleich zu einer Person aus der 3. Klasse betrachtet wird. Unter Konstanthaltung aller weiteren Prädiktoren im Modell steigen die Odds zu überleben um den Faktor 3.564, wenn eine Person aus der 2. Klasse im Vergleich zu einer Person aus der 3. Klasse betrachtet wird. Es scheint also so, dass je höher das Alter ist, desto geringer ist die Überlebenswahrscheinlichkeit, während je besser die Reiseklasse war, die Überlebenswahrscheinlichkeit höher ausfiel.
Grafische Veranschaulichung
Die selbigen Ergebnisse wollen wir uns auch noch einmal grafisch ansehen. Dazu müssen wir wieder einer Prädiktion mittels unseres Modells m3 durchführen. Die Prädiktion und das Anhängen an den Datensatz erfolgt analog zu oben:
logit_m3 <- predict(m3) # Logit unter Modell m3 bestimmen
odds_m3 <- exp(logit_m3) # Logit unter Modell m3 in Odds transformieren
p_m3 <- odds_m3/(1 + odds_m3) # Odds in Wahrscheinlichkeiten transformieren
# dem Datensatz anhängen:
Titanic$logit_m3 <- logit_m3
Titanic$odds_m3 <- odds_m3
Titanic$p_m3 <- p_m3
head(Titanic)| survived | pclass | sex | age | logit_m2 | odds_m2 | p_m2 | logit_m3 | odds_m3 | p_m3 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 28 | -1.340572 | 0.2616959 | 0.2074160 | 0.2186443 | 1.2443886 | 0.5544444 |
| 0 | 3 | 2 | 36 | -1.383979 | 0.2505794 | 0.2003707 | -2.6578631 | 0.0700979 | 0.0655060 |
| 1 | 2 | 1 | 3 | 1.260995 | 3.5289329 | 0.7791974 | 2.3562576 | 10.5513898 | 0.9134303 |
| 1 | 2 | 1 | 40 | 1.060237 | 2.8870558 | 0.7427359 | 0.9878028 | 2.6853277 | 0.7286537 |
| 0 | 3 | 2 | 32 | -1.362276 | 0.2560774 | 0.2038707 | -2.5099221 | 0.0812746 | 0.0751655 |
| 0 | 2 | 2 | 34 | -1.373128 | 0.2533135 | 0.2021150 | -1.3130666 | 0.2689939 | 0.2119741 |
Nun können wir die Grafiken analog zu oben erstellen, wobei wir lediglich die Benennung für die Farbe, die Linienform, das Modell sowie den Titel ein wenig abändern müssen. Das fantastische an ggplot ist nun, dass wir einfach eine neue Gruppierungsvariable in der aes vermerken können. Bspw. können wir mit lty die Linienart verändern. Wenn wir hier das Geschlecht festlegen, also lty = sex, dann wird für das Geschlecht jeweils eine eigene Linienart eingeführt (durchgezogen vs. gestrichelt). Wenn wir nun der Reiseklasse jeweils eine eigene Farbe geben (wie vorher dem Geschlecht) via col = pclass, dann erhalten wir einen sehr übersichtlichen Plot:
ggplot(data = Titanic, mapping = aes(x = age, y = logit_m3, col = pclass, lty = sex)) +
geom_line(lwd = 1) +
ggtitle("Logit vs Age, Sex and Class")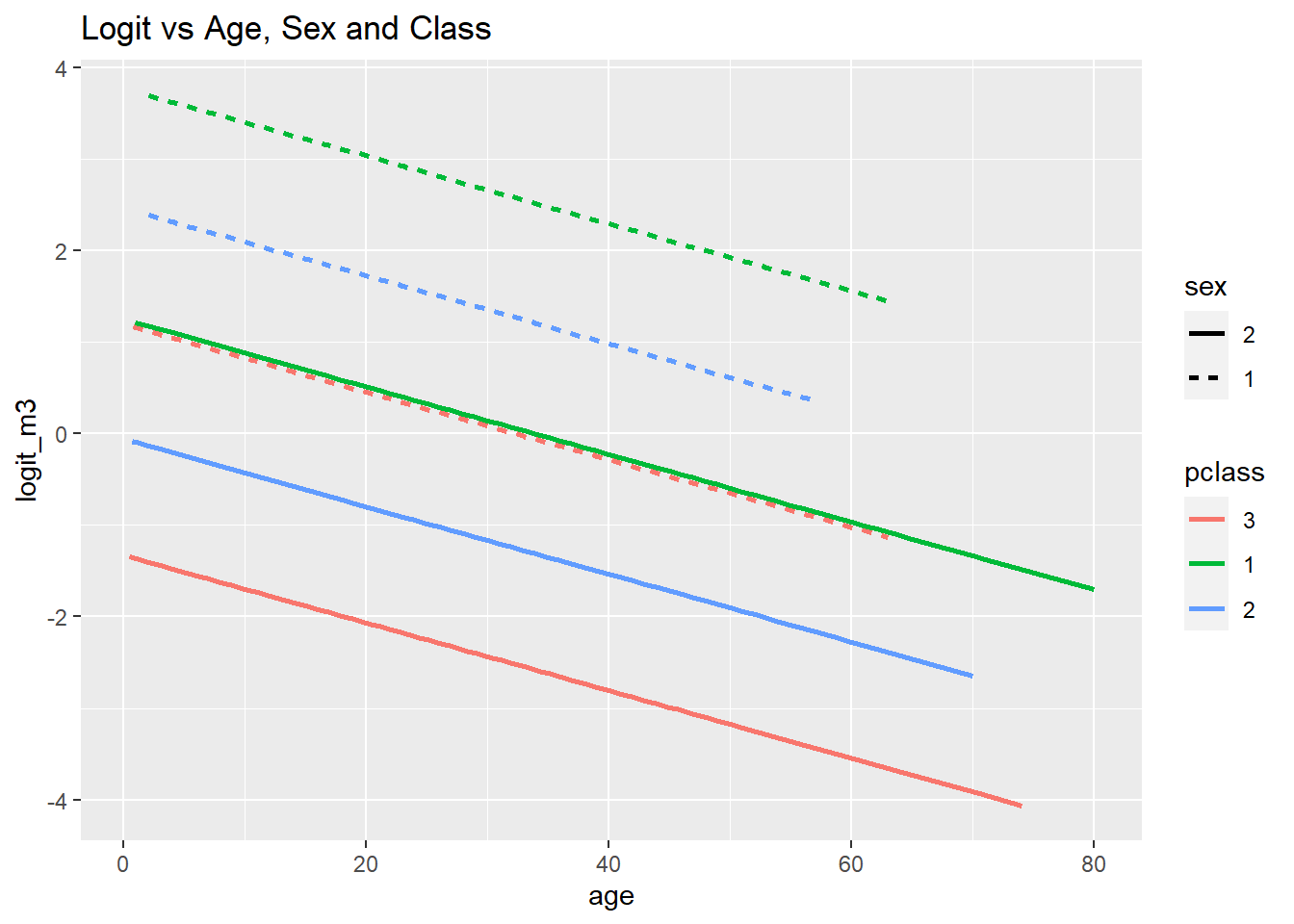
ggplot(data = Titanic, mapping = aes(x = age, y = odds_m3, col = pclass, lty = sex)) +
geom_line(lwd = 1) +
ggtitle("Odds vs Age, Sex and Class")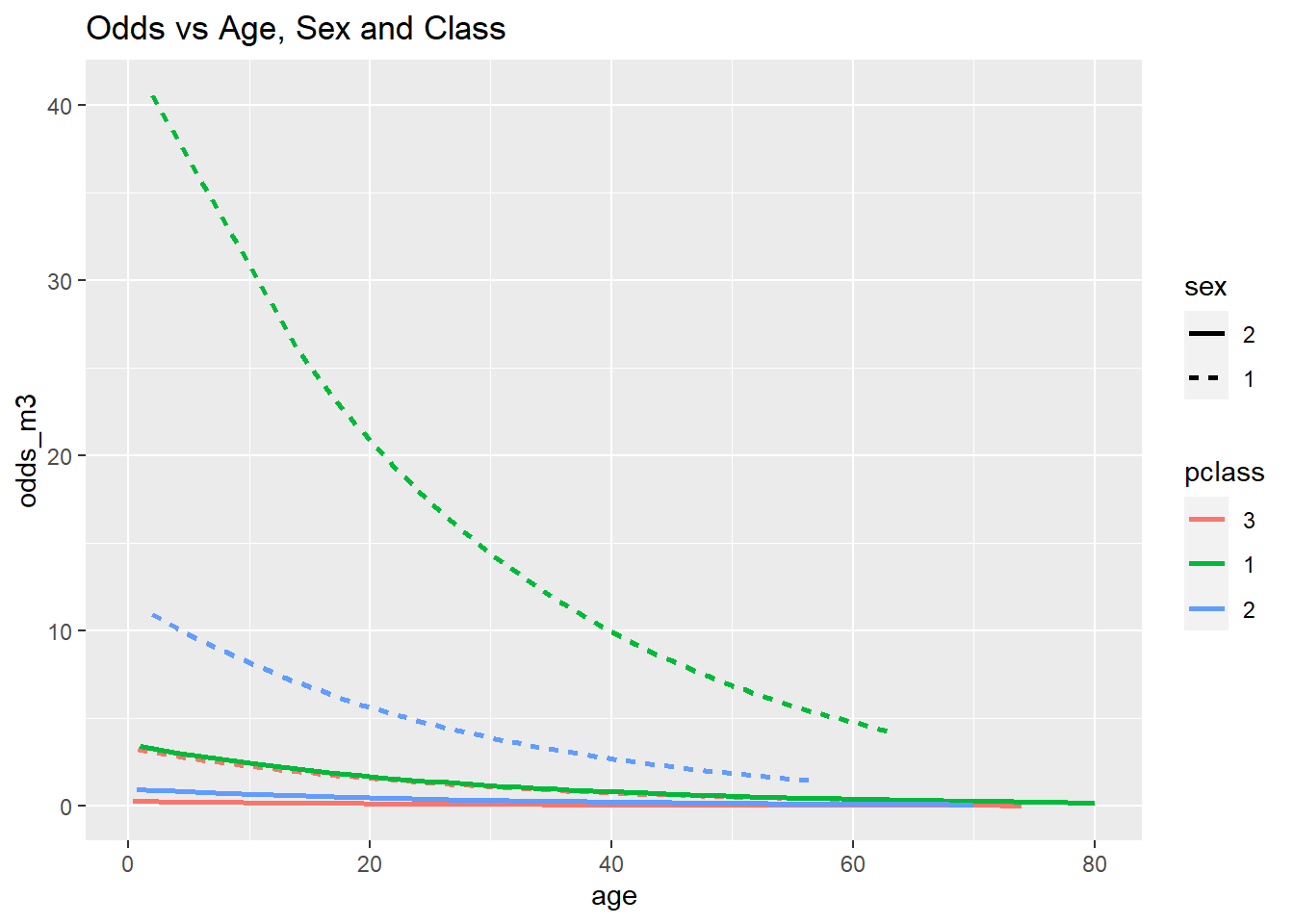
ggplot(data = Titanic, mapping = aes(x = age, y = p_m3, col = pclass, lty = sex)) +
geom_line(lwd = 1) +
ggtitle("P vs Age, Sex and Class")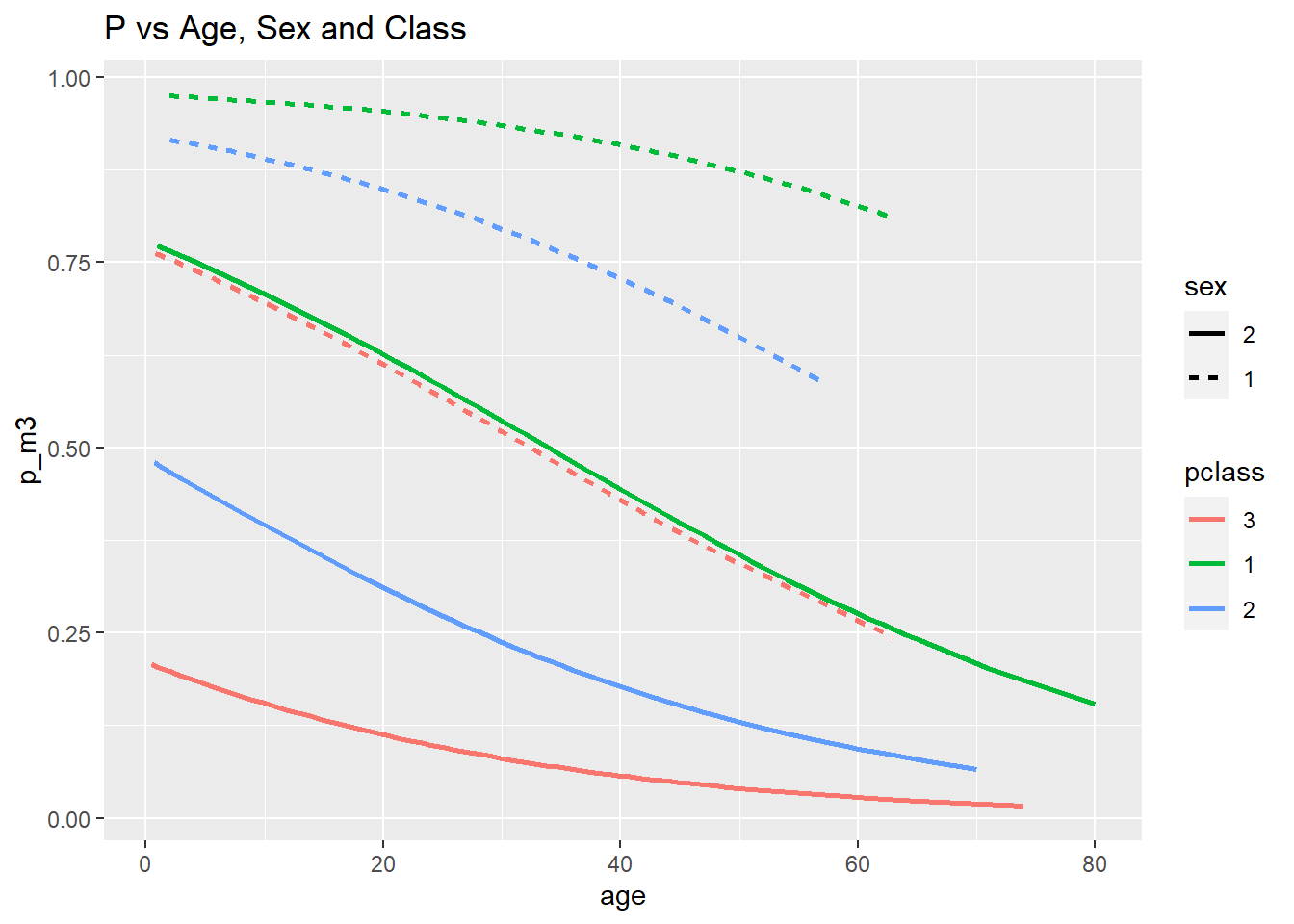
Alle drei Grafiken zeigen deutlich die Haupteffekte der Analyse: Die Überlebenswahrscheinlichkeit des Titanicunglücks sinkt mit dem Alter. Frauen haben eine höhere Überlebenswahrscheinlichkeit als Männer (bei vergleichbarem Alter) sowie deskriptiv gesprochen hatten Menschen die in der 1. Klasse reisen eine höhere Überlebenswahrscheinlichkeit als jene aus der 2. und 3. Klasse und die aus der 2. Klasse hatten ebenfalls eine höhere Überlebenswahrscheinlichkeit als jene aus der 3. Klasse (jeweils immer für vergleichbares Alter und Geschlecht). Der Zusatz “für vergleichbares Alter” ist im Grunde das Gleiche wie der Zusatz “unter Konstanthaltung aller weiteren Prädiktoren im Modell”, denn wir können schlecht die Überlebenswahrscheinlichkeit eines zwanzigjährigen Mannes aus der 1. Klasse mit der einer sechzigjährigen Frau aus der 3. Klasse vergleichen, denn dann wissen wir nicht, ob die Wahrscheinlichkeiten unterschiedlich sind, weil es sich um eine Frau oder einen Mann aus der jeweiligen Klasse handelt oder, ob es sich auf das Alter zurückführen lässt, oder ob eine Kombination der Variablen das Ergebnis erzeugt. Was wir aber tun können, ist für ein gleiches Alter die 6 Linien jeweils zu vergleichen! Außerdem erkennen wir insbesondere an der Modellierung des Logit oder der Wahrscheinlichkeit, dass Frauen, die in der 3. Klasse reisten, eine annähernd gleiche Überlebenswahrscheinlichkeit hatten wie Männer aus der 1. Klasse (erneut: jeweils für vergleichbares Alter!). Innerhalb der Geschlechter waren die Klassen allerdings auf die gleiche Art und Weise sortiert: 1>2>3. Insgesamt suggeriert dies also, dass dem Motto “Frauen und Kinder zuerst” Folge geleistet wurde.
Final können wir festhalten, dass wahrscheinlich alle drei Hypothesen erfüllt sind und sowohl das Alter als auch das Geschlecht und die Klassenzugehörigkeit die Überlebenswahrscheinlichkeit des Titanicunglücks beeinflussten.
Appendix
Appendix A
Parametereinflüsse
Die folgende Funktion stellt vier Grafiken dar: den Logit, die Odds, die Wahrscheinlichkeit und die Wahrscheinlichkeit vs. eine Zufallserhebung. Sie können β0 und β1 dieses Modells so einstellen, wie Sie wünschen und können sich den Effekt auf die verschiedenen Darstellungsformen der logistischen Regression ansehen. In hellblau wird jeweils die Funktion mit β0=0 und β1=1 als Referenz dargestellt. Die gestrichelten Linien stellen jeweils die x- und die y-Achse dar. In roten Punkten werden Realisierungen von Y=0,1 dargestellt, die mit der angezeigten Wahrscheinlichkeit gezogen wurden. Um die Ergebnisse vergleichbar zu machen, wird set.seed(1234) verwendet (vgl. Einführungssitzung).
Logistic_functions <- function(beta0 = 0, beta1 = 1)
{
par(mfrow=c(2,2)) # 4 Grafiken in einer
xWerte <- seq(-5, 5, 0.1)
logit <- beta0 + beta1*xWerte
plot(x = xWerte, y = logit, type = "l", col = "blue", lwd = 3, main = "Logit vs X", xlab = "X")
lines(xWerte, xWerte, col = "skyblue")
abline(h = 0, lty = 3); abline(v = 0, lty = 3)
odds <- exp(logit)
plot(x = xWerte, y = odds, type = "l", col = "blue", lwd = 3, main = "Odds vs X", xlab = "X")
abline(h = 0, lty = 3); abline(v = 0, lty = 3)
lines(xWerte, exp(xWerte), col = "skyblue")
p <- odds/(1 + odds)
plot(x = xWerte, y = p, type = "l", col = "blue", lwd = 3, main = "P vs X", ylim = c(0,1), xlab = "X")
lines(xWerte, exp(xWerte)/(1 + exp(xWerte)), col = "skyblue")
abline(h = 0, lty = 3); abline(v = 0, lty = 3)
set.seed(1234) # Vergleichbarkeit
Y <- rbinom(n = length(xWerte), size = 1, prob = p)
plot(x = xWerte, y = p, type = "l", col = "blue", lwd = 3, main = "P vs X und zufällige Realisierungen",
ylim = c(0,1), xlab = "X", ylab = "P und Y")
abline(h = 0, lty = 3); abline(v = 0, lty = 3)
points(x = xWerte, y = Y, pch = 16, cex = .5, col = "red")
}Sie führen diese Funktion aus, indem Sie alles von Logistic_functions <- function(beta0 = 0, beta1 = 1){ bis } kopieren und in Ihrem R-Studio Fenster ausführen, sodass in der Rubrik oben rechts (dort wo auch immer Data erscheint) unter Functions Logistic_functions als Funktion aufgeführt wird. Sie können sich bspw. die Konstellation für β0=1 und β1=−0.5 im Vergleich zu β0=0 und β1=1 ansehen:
Logistic_functions(beta0 = 1, beta1 = -.5)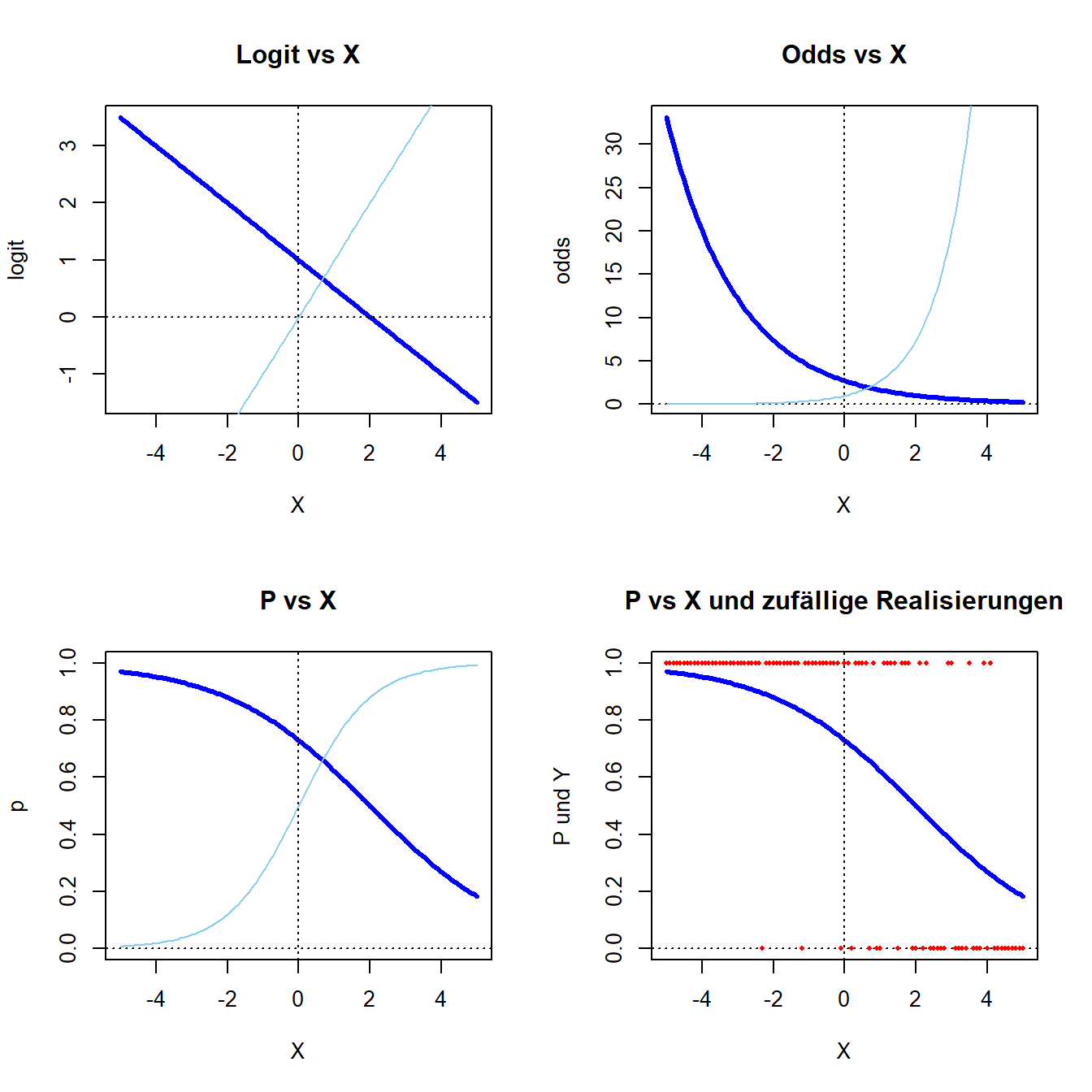
Literatur
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden (5. Auflage, 1. Auflage: 2010). Weinheim: Beltz.
Pituch, K. A. & Stevens, J. P. (2016). Applied Multivariate Statistics for the Social Sciences (6th ed.). New York: Taylor & Francis.
- Blau hinterlegte Autor:innenangaben führen Sie direkt zur universitätsinternen Ressource.
