Meta-Analysen in R
Die Kunst des Zusammenfassens von Studien und das metafor-Paket
Einführung
Meta-Analysen sind empirische Zusammenfassungen von Studien unter Verwendung mathematischer Modelle. Auf diese Weise können Ergebnisse aus jahrelanger Forschung integriert und zusammengefasst werden, was oft Aufschluss darüber liefert, ob Effekte im Mittel vorhanden sind oder nicht. Somit können Meta-Analysen lange Debatten beenden und Licht in das Dunkel von sich widersprechenden Studienergebnissen bringen.
Mit Hilfe des metafor-Paketes (meta-analysis for r) von Viechtbauer (2010) lassen sich eindimensionale Meta-Analysen (in welchen ein Koeffizient über mehrere Studien “gemittelt” werden soll) leicht berechnen. Zunächst müssen wir dazu das R-Paket installieren.
install.packages("metafor")Eine solche Installation ist nur einmalig vonnöten (es sei denn wir wollen eine ggf. neuerer Version des Pakets installieren). Anschließend lässt sich das Paket laden; wir machen es so in R verfügbar und können auf dessen Funktionen zugreifen.
library(metafor)## Warning: Paket 'metafor' wurde unter R Version 4.1.3 erstellt## Lade nötiges Paket: Matrix##
## Loading the 'metafor' package (version 3.0-2). For an
## introduction to the package please type: help(metafor)Wie auch beim Laden des Paketes schon erwähnt wird (For an overview and introduction to the package please type: help(metafor)), können wir uns mit der sehr nützlichen R-internen Hilfe-Funktion einen Überblick über das Paket verschaffen.
help("metafor")## starting httpd help server ... doneWenn wir diesen Befehl ausführen, so geht in R-Studio ein Fenster mit der Überschrift “metafor: A Meta-Analysis Package for R” auf, in welchem die grundlegenden Funktionen erklärt werden.
Daten
In diesem kleinen Tutorial wollen wir einen von diesem Paket mitgelieferten Datensatz untersuchen. Dieser heißt dat.mcdaniel1994. Wie wir eigene Daten einlesen, haben wir in der letzten Sitzungen gelernt! Wir erhalten mit folgenden Befehl mehr Informationen über diesen Datensatz.
?dat.mcdaniel1994 # Studies on the Validity of Employment InterviewsFühren wir diese Zeile aus, geht in R-Studio erneut ein Erklärungsfenster mit der Überschrift “Studies on the Validity of Employment Interviews” auf. Es geht also um eine Meta-Analysen über Studien, die die Validität von Einstellungsinterviews untersucht haben. Die Studie wurde von McDaniel, Whetzel, Schmidt und Maurer (1994) durchgeführt. Die Daten im Datensatz dat.mcdaniel1994 stammen aus Tabelle A.2 in Rothstein, Sutton, and Borenstein (2005, p. 325-329). In dieser Übersicht sehen wir, dass es 5 Variablen in diesem Datensatz gibt. Mit head (zeigt die ersten 6 Zeilen des Datensatzes) oder mit names (zeigt die Variablennamen des R-Objektes) können wir uns einen Überblick über die Variablen im Datensatz verschaffen.
head(dat.mcdaniel1994)## study ni ri type struct
## 1 1 123 0.00 j s
## 2 2 95 0.06 p u
## 3 3 69 0.36 j s
## 4 4 1832 0.15 j s
## 5 5 78 0.14 j s
## 6 6 329 0.06 j snames(dat.mcdaniel1994)## [1] "study" "ni" "ri" "type" "struct"Mit Hilfe dieser Namen können wir explizit auf die Variablen im Datensatz zugreifen. Wir können bspw. die Korrelationen zwischen Performanz im Einstellungsinterview und Job-Performanz pro Studie abgreifen, die im Datensatz als Variable ri gespeichert sind.
dat.mcdaniel1994$ri## [1] 0.00 0.06 0.36 0.15 0.14 0.06 0.09 0.40 0.39 0.14 0.36 0.28
## [13] 0.62 0.07 0.18 0.42 0.08 0.18 0.43 0.04 -0.04 0.05 -0.14 0.05
## [25] 0.35 -0.08 0.24 0.16 0.25 0.68 0.61 0.81 0.99 0.66 0.45 0.71
## [37] 0.27 -0.02 0.29 0.13 0.03 0.00 0.09 -0.03 0.46 0.30 0.33 0.24
## [49] 0.64 0.12 0.15 0.44 0.00 0.16 0.21 0.29 0.19 0.04 0.56 0.14
## [61] 0.44 0.36 0.34 0.11 0.40 0.23 0.22 0.44 0.27 0.11 0.27 -0.07
## [73] 0.32 0.05 0.20 0.18 0.34 0.03 0.45 0.34 0.51 0.41 0.37 0.25
## [85] -0.17 0.47 0.32 -0.09 0.33 0.22 0.27 0.00 0.41 0.16 0.00 0.03
## [97] 0.01 0.03 0.14 0.11 0.08 -0.13 0.13 0.36 0.06 0.19 0.27 0.17
## [109] 0.34 0.28 0.11 0.07 -0.13 0.12 0.12 0.37 0.26 0.42 0.37 0.17
## [121] 0.19 0.32 0.33 0.24 0.09 0.36 0.26 0.42 0.62 0.87 -0.07 0.65
## [133] 0.17 0.30 0.45 0.24 0.02 0.23 0.17 0.32 0.36 0.09 0.13 0.29
## [145] 0.49 0.40 0.23 0.31 0.46 -0.12 0.22 0.59 0.21 0.02 -0.03 0.28
## [157] -0.04 0.19 0.23 0.30Die Variable heißt hier ri, da auch im zugehörigen Paper von Viechtbauer (2010) die Korrelation für die -te Studie mit bezeichnet wird. Insgesamt gibt es 160 Studien (und somit Korrelationskoeffizienten) in diesem Datensatz. Einen Überblick über solch einen Wust von Daten in diesem Vektor erhalten wir mit der R-internen summary Funktion.
summary(dat.mcdaniel1994$ri)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -0.1700 0.0900 0.2300 0.2404 0.3600 0.9900Die Korrelationskoeffizienten liegen also zwischen -0.17 und 0.99. Auch ein Mittelwert wird uns bereits ausgegeben: 0.24. Dies gibt uns ein erstes Gefühl dafür, wo der tatsächlich gepoolte mittlere Korrelationskoeffizient, der die Beziehung zwischen der Performanz im Einstellungsinterview und Job-Performanz quantifiziert, liegen könnte. Jedoch wurden in diesem Mittelwert etwaige Unterschiede zwischen Studien (Größe, Streuung, Qualität, Kovariaten, etc.) nicht berücksichtigt.
Grafische Veranschaulichung der Beziehung zwischen der Performanz im Einstellungsinterview und der Job-Performanz
Wir wollen uns die Daten zunächst noch etwas genauer ansehen. Plotten wir zunächst die Korrelationskoeffizienten.
Aus dieser Grafik lässt sich noch nicht so viel erkennen, vielleicht wäre ein Boxplot sinnvoller?
boxplot(dat.mcdaniel1994$ri, main = "Empirische Korrelationen zwischen\n Interview Performanz und Job-Performanz")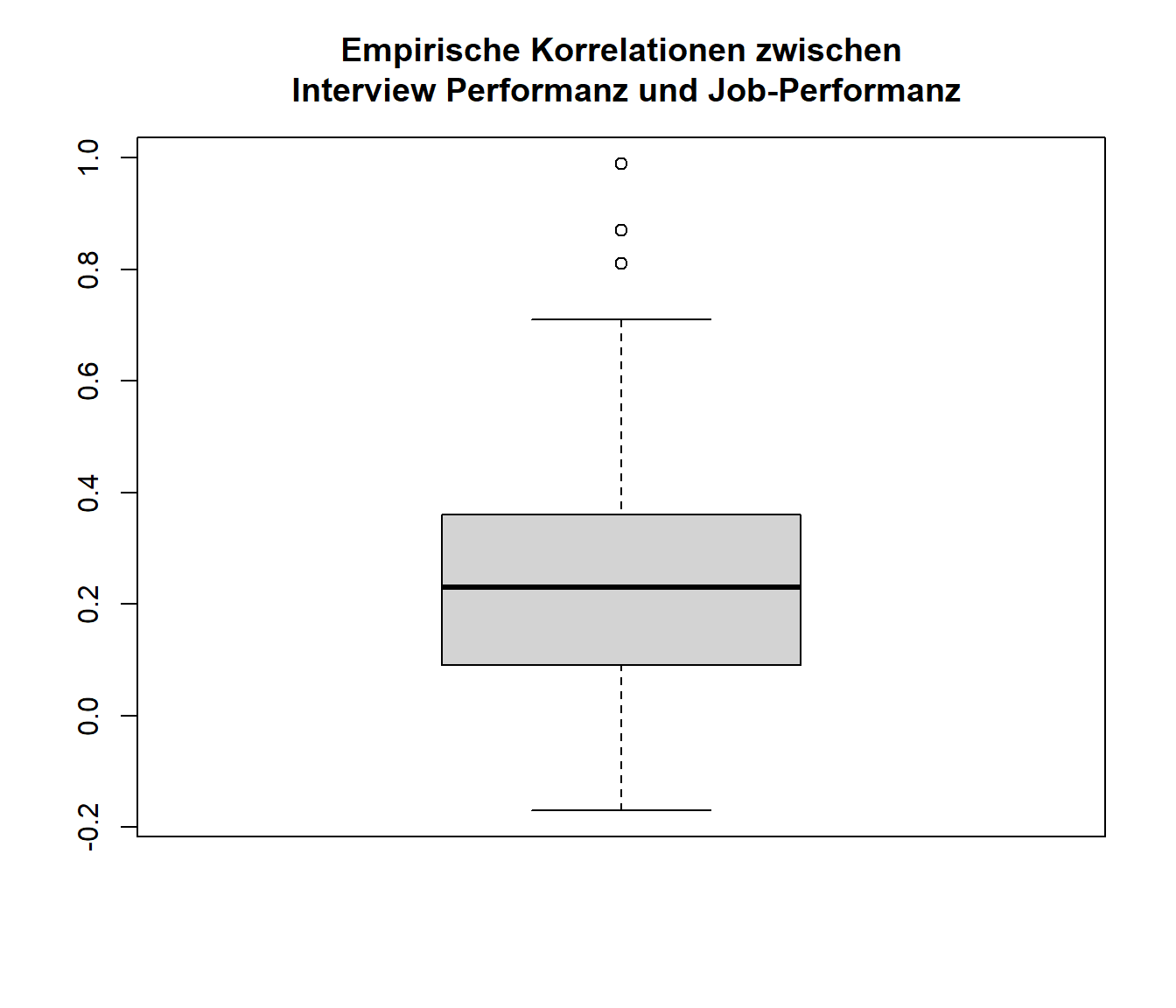
Wir sehen, dass die meisten Korrelationen zwischen -0.17 und 0.71 liegen. 50% der Korrelationen liegen allerdings zwischen 0.09 und 0.36, also im positiven Bereich; der Median liegt bei 0.23.
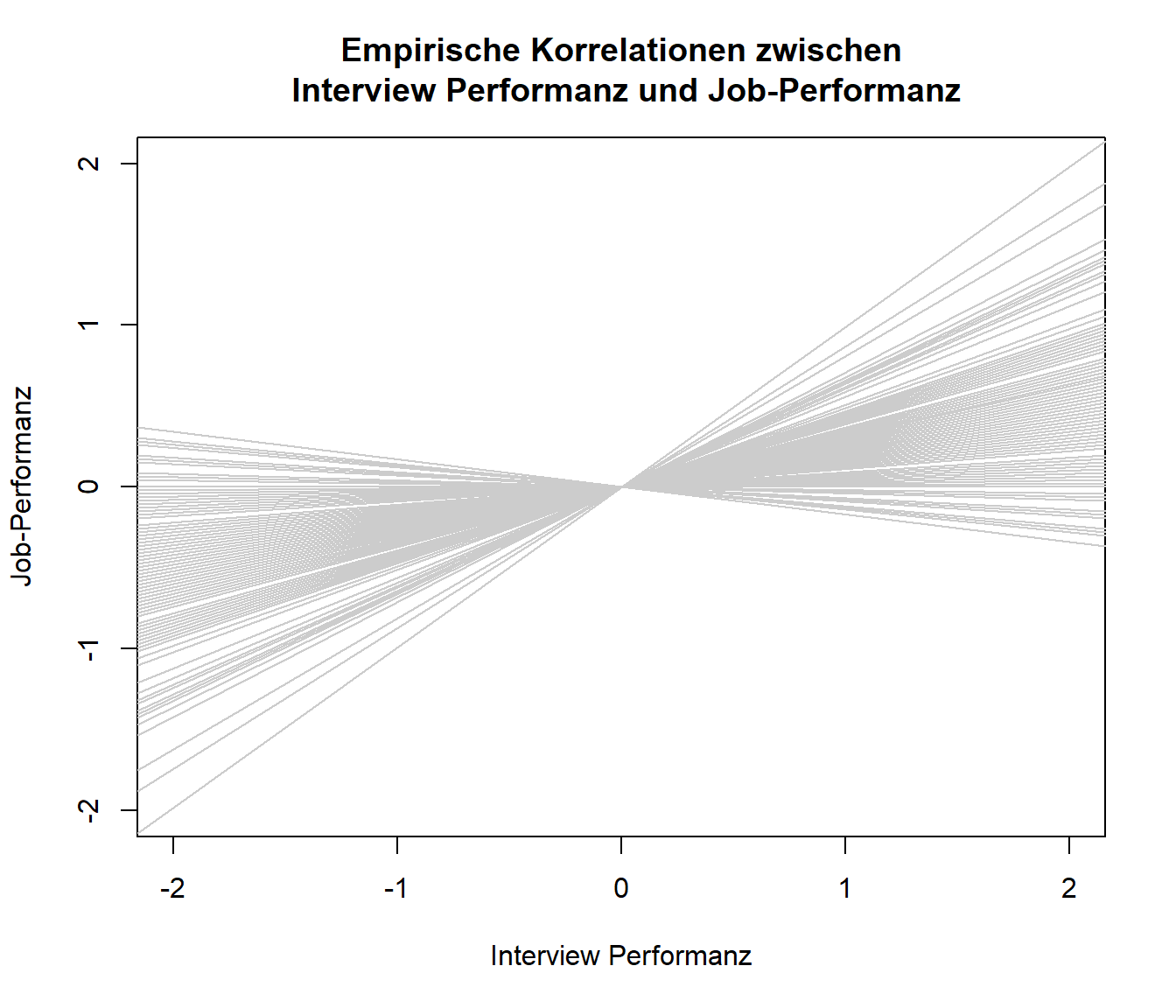
Wir wollen uns außerdem die Unterschiedlichkeit der Korrelationskoeffizienten als Darstellung der verschiedenen Einfach-Regressionen von Job-Performanz auf die Interview-Performanz anschauen. Hierzu plotten wir quasi eine standardisierte Regressionsgerade ( und , wobei Korrelationskoeffizient von Studie ) pro Studie. Um den zu Grunde liegenden Code anzusehen, können Sie Appendix A nachschlagen.
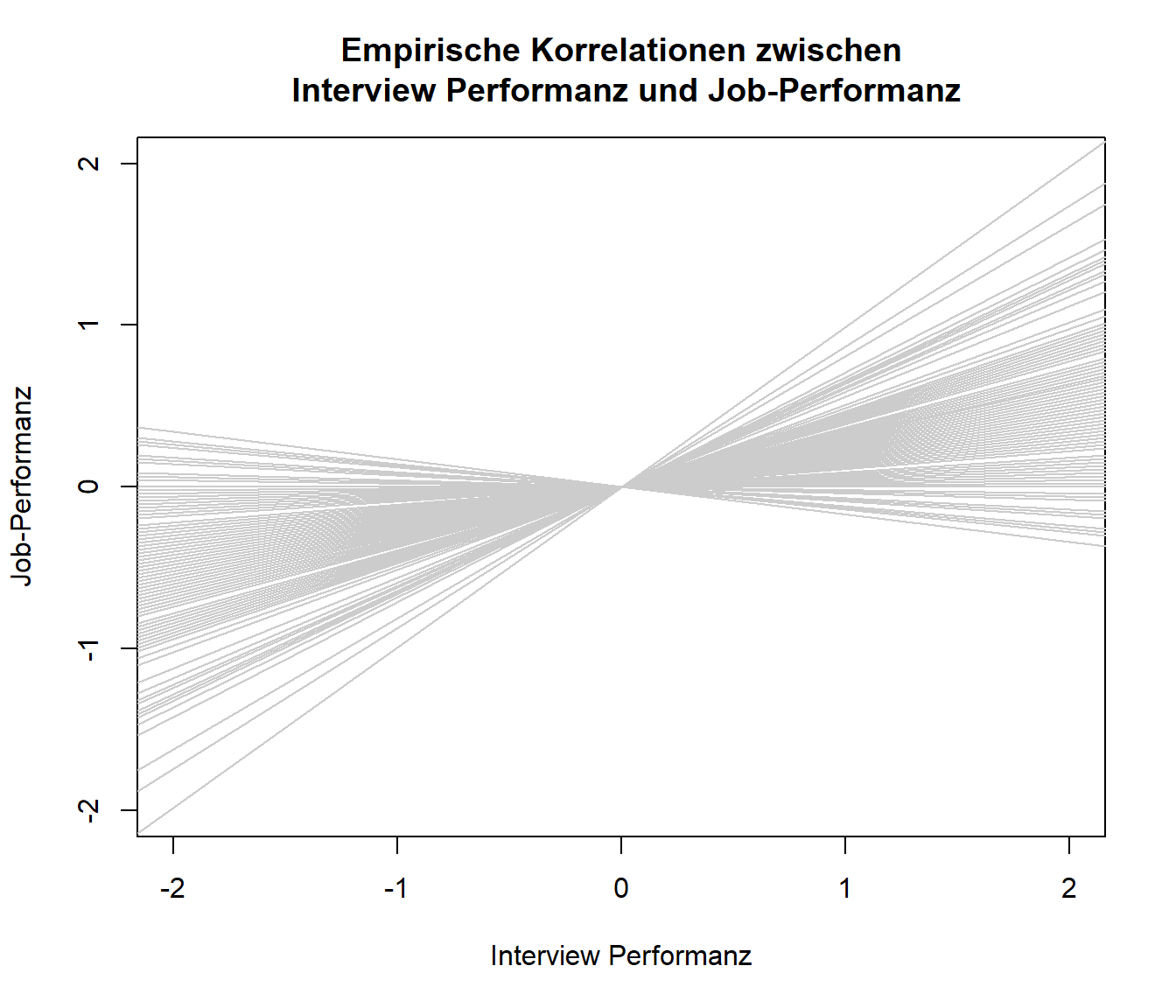
In diese Grafik würden wir gerne eine durchschnittliche Regressionsgerade hineinlegen.
Fisher’s -Transformation
Allerdings können wir dazu, wie wir in den vergangenen inhaltlichen Sitzungen gelernt haben, nicht einfach alle Korrelationskoeffizienten mitteln. Die Korrelation ist außerdem ein besonderer Koeffizient, da er nur Werte zwischen -1 und 1 annehmen kann. Somit ist hier einfaches Mitteln der Korrelationskoeffizienten nicht ohne Weiteres möglich (es ist jedoch zu beachten, dass diese Meinung nicht überall verbreitet ist, weswegen dies für sich ein Thema ist, welches zur Diskussion steht!). Aus diesem Grund werden Korrelationskoeffizienten häufig mit Hilfe von Fisher’s -Transformation in -Werte übertragen. Dies haben wir vielleicht im ersten Semester schon einmal kennengelernt, als wir Korrelationskoeffizienten mitteln wollten. Der zugehörige -Wert zu einer Korrelation lässt sich wie folgt bestimmen:
.
Das Schöne an den transformierten Daten (den -Werten) ist, dass wir nun die Varianz (bzw. die Standardfehler) der Korrelationskoeffizienten kennen. Es gilt nämlich:
wobei die Stichprobengröße der Studie ist. Der Standardfehler wäre . Wir sehen, dass die Variation der Korrelationskoeffizienten unabhängig von ihrer Höhe ist, aber wir im Idealfall die Stichprobengröße der Studie kennen sollten. Das macht es uns leicht, da wir nicht, wie beim Mittelwert bspw., noch die Standardabweichung aus den Studien kennen müssen. Wir müssen diese Transformation selbstverständlich nicht mit Hand durchführen, sondern können uns einfach der Funktion escalc aus dem metafor Paket bedienen.
Um diese Funktion zu verwenden, um die Daten zu -transformieren, müssen wir folgende Argumente an die Funktion übergeben: measure = "ZCOR" bewirkt, dass auch tatsächlich die -to--Transformation (Fisher’s -Transformation) durchgeführt wird. Das Argument ri nimmt die beobachteten Korrelationskoeffizienten entgegen (diese heißen hier auch ri), ni nimmt die Stichprobengröße pro Studie entgegen (diese heißen hier auch ni). Das Argument data nimmt, wie der Namen schon verrät, den Datensatz entgegen, in dem die Studien zusammengefasst sind (hier dat.mcdaniel1994). Die Funktion erzeugt einen neuen Datensatz, welcher um die -Werte sowie deren Varianz erweitert wurde. Diesen wollen wir unter einem neuen Namen abspeichern. Als Beweis meines Einfallsreichtums nennen wir diesen Datensatz einfach data_transformed. Auch die Namen, der neu zu erstellenden Variablen lassen sich in der Funktion festlegen. Dies ergibt insbesondere dann Sinn, wenn wir mehrere Analysen an einem Datensatz durchführen. Dies geht mit dem var.names-Argument, welchem wir einen Vektor mit zwei Einträgen übergeben müssen: dem Namen der -Werte und dem Namen der Varianzen. Wir wollen sie z_ri und v_ri nennen: var.names = c("z_ri", "v_ri"). Der fertige Code sieht folglich so aus (mit head schauen wir uns wieder die ersten 6 Zeilen an):
data_transformed <- escalc(measure="ZCOR", ri=ri, ni=ni, data=dat.mcdaniel1994, var.names = c("z_ri", "v_ri"))
head(data_transformed)## study ni ri type struct z_ri v_ri
## 1 1 123 0.00 j s 0.0000 0.0083
## 2 2 95 0.06 p u 0.0601 0.0109
## 3 3 69 0.36 j s 0.3769 0.0152
## 4 4 1832 0.15 j s 0.1511 0.0005
## 5 5 78 0.14 j s 0.1409 0.0133
## 6 6 329 0.06 j s 0.0601 0.0031Wenn wir den Namen des Datensatzes nicht an die Funktion übergeben, und statt dessen nur die beobachteten Korrelationen und die Stichprobengrößen angeben, werden im erzeugten Datensatz nur die -Werte und die Varianzen gespeichert; die Werte werden nicht an den bestehenden Datensatz angehängt (was für spätere Analysen weniger sinnvoll erscheint).
data_transformed_2 <- escalc(measure="ZCOR", ri=dat.mcdaniel1994$ri, ni=dat.mcdaniel1994$ni, var.names = c("z_ri", "v_ri"))
head(data_transformed_2)## z_ri v_ri
## 1 0.0000 0.0083
## 2 0.0601 0.0109
## 3 0.3769 0.0152
## 4 0.1511 0.0005
## 5 0.1409 0.0133
## 6 0.0601 0.0031Wir entnehmen dem Output, dass die Benennung geklappt hat und das hier nur ein Datensatz mit den -Werten und den Varianzen entstanden ist.
Aus unserem neuen Datensatz data_transformed können wir nun wieder die entsprechenden Werte herausziehen. Wir können bspw. die Berechnung der Streuung der -Werte überprüfen. Mit Hilfe von eckigen Klammern können die bezeichneten Einträge eines Vektors indiziert werden. Mit data_transformed$v_ri[1:4] werden entsprechend die ersten 4 Elemente im Vektor bezeichnet. Somit können wir uns mit [1:4] die ersten 4 Einträge der beiden Vektoren anschauen, um diese zu vergleichen:
1:4## [1] 1 2 3 4data_transformed$v_ri[1:4]## [1] 0.0083333333 0.0108695652 0.0151515152 0.00054674691/(dat.mcdaniel1994$ni - 3)[1:4] ## [1] 0.0083333333 0.0108695652 0.0151515152 0.0005467469Wir sehen, dass unsere Berechnung mit Hand zum gleichen Ergebnis kommt, wie die Berechnung mit escalc, was daran liegt, dass die Funktion escalc mit den oben gewählten Zusatzargument genau das gemacht hat! Was genau hat nun die Transformation bewirkt?
plot(x = data_transformed$ri, y = data_transformed$z_ri, xlab = "r", ylab = "z",
main = "Fisher's z-Transformation")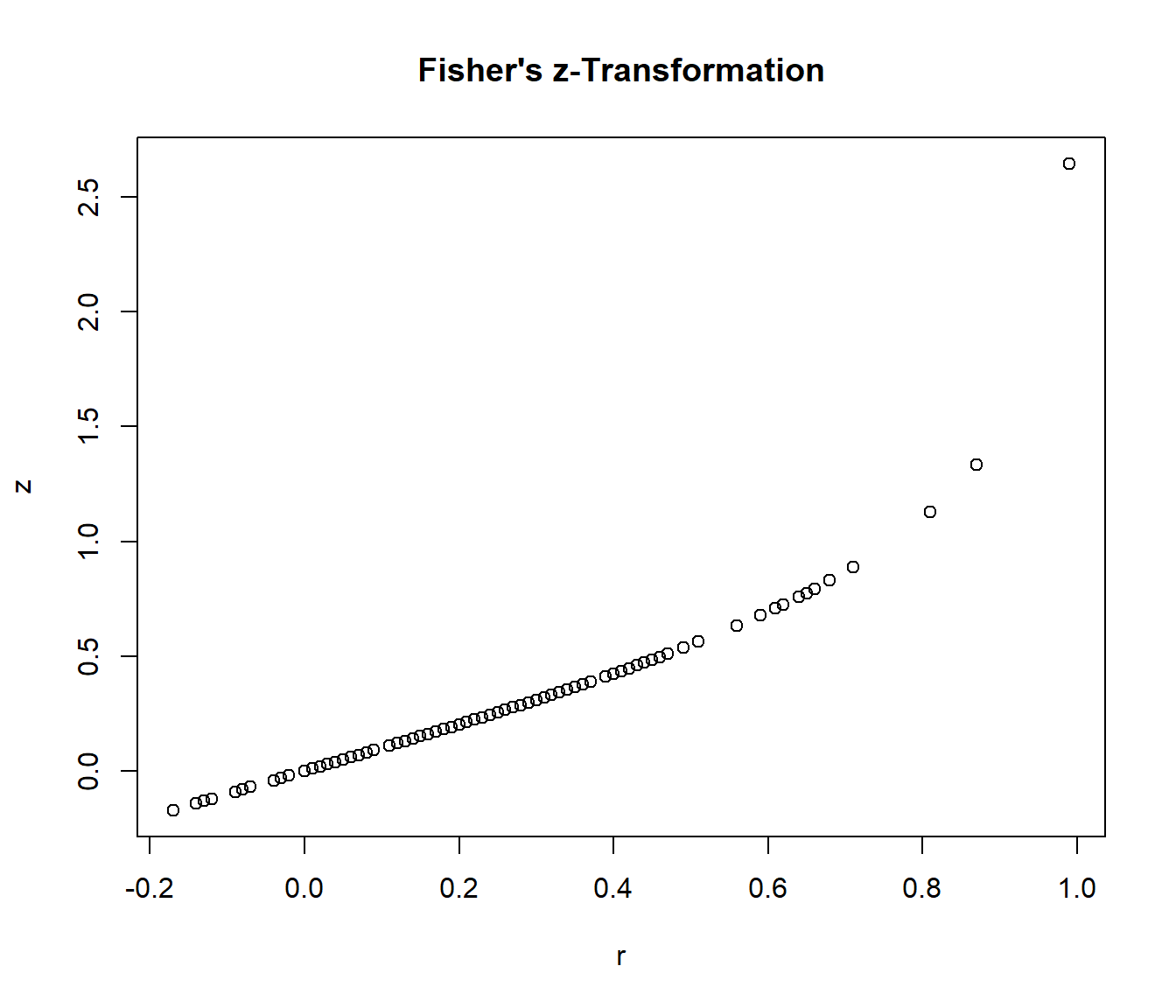
Der Grafik ist zu entnehmen, dass nach Transformation Korrelationswerte nahe 1 stärker gewichtet werden (sie haben größere -Ausprägungen). Dies war das Ziel, da es deutlich unwahrscheinlicher ist, in einer Studie einen Korrelationskoeffizient von .90 zu finden als einen von .20 und die Korrelation von .90 somit stärker ins Gewicht fallen sollte. Vor allem, wenn wir den mittleren Korrelationskoeffizienten gegen 0 testen wollen, sollte berücksichtigt werden, dass einige Korrelationskoeffizienten nahe 1 lagen. Sollten diese Werte aufgrund zufälliger Schwankungen gefunden worden sein, so sollte dies daran liegen, dass der Standardfehler groß, also die Stichprobengröße klein ist, da Standardfehler der Korrelation antiproportional zur Stichprobengröße ist (da ). Somit können wir auch solche Stichproben weniger stark gewichten, die zwar einen hohen Korrelationskoeffizienten aufweisen, aber eine sehr kleine Stichprobe haben, da in solchen Fällen eine hohe Korrelation auch mal durch Zufall auftreten kann! Nach unseren Berechnungen können wir die Transformation natürlich auch wieder ganz leicht rückgängig machen (natürlich gibt es hier auch wieder eine Funktion die dies für uns übernimmt, welche wir uns anschauen, wenn es soweit ist):
Meta-analytische Modellierung
In der inhaltlichen Sitzung haben wir bisher zwei Typen von meta-analytischen Modellen kennengelernt: das Fixed- und das Random Effects Modell (FEM und REM). Das FEM geht davon aus, dass die Studien sich nur durch zufällige, unsystematische Schwankungen unterscheiden. Ein beobachteter Koeffizient der -ten Studie (wird auch oft genannt, weswegen im metafor-R-Paket auch häufig das Argument der Koeffizienten yi genannt wird) lässt sich also zerlegen in einen globalen (wahren) Mittelwert (global, also für alle Studien gültig, daher kein Index ) und zufällige Abweichungen , welche homogen (mit gleicher Varianz) über alle Studien hinweg variieren. Hierbei hat einen Mittelwert von 0 und eine Varianz , zudem wird es als normalverteilt angenommen.
Das REM geht im Gegenteil davon aus, dass es Heterogenität zwischen den Effektmaßen gibt, also, dass sich die Studien systematisch unterscheiden - sie sind heterogen. Diese Annahme wird modelliert, indem ein weiterer Fehlerterm hinzugefügt wird , welcher studienspezifische systematische Abweichungen quantifiziert. Das Modell erweitert sich zu
hat wie ebenfalls einen Mittelwert von 0, wird als normalverteilt angenommen und besitzt die Heterogenitätsvarianz .
Dieses Modell sieht einer einfaktoriellen ANOVA recht ähnlich: Hier hatten wir den Wert einer Person aus Gruppe zerlegt in den globalen Mittelwert , die Abweichung von diesem und ein Residuum (zufällige Abweichung) ; manchmal haben wir auch direkt den gruppenspezifischen Mittelwert wie folgt geschrieben: . Der Wert einer Person ergab sich in diesem Modell wie folgt: . Es gab also bei der einfaktoriellen ANOVA Varianzanteile, die auf Unterschiede zwischen Gruppen zurückzuführen war (Variation der ) und Varianzanteile, die auf Unterschiede der Erhebungen innerhalb einer Gruppe zurückzuführen war (unsystematische Varation von ).
Im sogenannten Mixed-Effects Modell (MEM) gilt es, diese Heterogenitätsvarianz (also die systematische Variation zwischen Studien) weiter durch Moderatoren () zu erklären (im Analogon der ANOVA bedeutet dies, dass wir die Variation zwischen den Gruppen erklären wollen würden, also Kovariaten heranziehen wollen würden, die die Unterschiede zwischen den Gruppen beschreiben).
Es wird also im Grunde eine Regression durchgeführt, wobei die zu erklärenden Beobachtungen hier Studienergebnisse sind. Wie genau gewichtet gemittelt wird oder wie sich “Fixed” und “Random” Effects Modelle unterscheiden, sehen sie skizzenhaft in Appendix B.
Das Random Effects Modell
Wir verwenden die zentrale Funktion rma des metafor Pakets, um ein REM zu schätzen. Dieser Funktion übergeben wir folgende Argumente: yi = die Effektmaße (hier unsere -transformierten Korrelationen), vi = die Streuung dieser Effektmaße, sowie data = den Datensatz.
REM <- rma(yi = z_ri, vi = v_ri, data=data_transformed)
REM##
## Random-Effects Model (k = 160; tau^2 estimator: REML)
##
## tau^2 (estimated amount of total heterogeneity): 0.0293 (SE = 0.0049)
## tau (square root of estimated tau^2 value): 0.1712
## I^2 (total heterogeneity / total variability): 81.29%
## H^2 (total variability / sampling variability): 5.35
##
## Test for Heterogeneity:
## Q(df = 159) = 789.7321, p-val < .0001
##
## Model Results:
##
## estimate se zval pval ci.lb ci.ub
## 0.2374 0.0170 13.9995 <.0001 0.2042 0.2706 ***
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Diesem Output können wir nun einige wichtige Informationen entnehmen. Als Überschrift lesen wir Random-Effects Model, wobei k die Anzahl der Studien angibt (hier k=160). Außerdem wird uns das Schätzverfahren für die Heterogenitätsvarianz angegeben unter tau^2 estimator: (hier REML).
In den darunter liegenden Zeilen können wir die Heterogenitätsvarianz ablesen, welche bei 0.0293 liegt. Der Standardfehler (SE = 0.0049) gibt uns an, dass diese Heterogenitätsvarianz wahrscheinlich signifikant von 0 verschieden ist. In der Zeile von I^2 wird die -Statistik ausgegeben, welche ein Maß für die Heterogenität in den Daten sein soll. Diese liegt hier bei 81.29% und deutet somit auf Heterogenität der Korrelationskoeffizienten hin. Allerdings ist nicht so ein absolutes Maß, wie der Determinationskoeffizient in der linearen Regression (für lineare Regression in R siehe Regressionssitzung aus PsyMSc1).
Auch wird die Heterogenitätsvarianz mit einem Signifikanztest auf Verschiedenheit von 0 geprüft. Die Ergebnisse hierzu entnehmen wir Test for Heterogeneity. Hier zeigt der p-Wert ein signifikantes () Ergebnis an: für die Population wird folglich die Null-Hypothese, dass es im Mittel keine Beziehung zwischen Interview und Job-Performanz gibt verworfen.
Unter Model Results können wir nun (endlich) die Schätzergebnisse unseres REM ablesen. estimate steht hierbei für die gepoolte -transformierte Korrelation, se ist der Standardfehler, zval der zugehörige z-Wert , pval der p-Wert und ci.lb und ci.ub geben die untere und die obere Grenze eines 95%-igen Konfidenzintervall an. Hier ist zu erkennen, dass die mittlere Korrelation wohl von 0 verschieden ist. Den exakten vorhergesagten Wert kennen wir allerdings noch nicht; hierzu müssen wir den -Wert erst wieder in einen Korrelation retransformieren. Selbstverständlich können wir auf das Objekt REM mit $ zugreifen und dadurch noch zahlreiche weitere Informationen erhalten. Welche dies genau sind erfahren wir wieder mit names:
names(REM)## [1] "b" "beta" "se" "zval" "pval"
## [6] "ci.lb" "ci.ub" "vb" "tau2" "se.tau2"
## [11] "tau2.fix" "tau2.f" "I2" "H2" "R2"
## [16] "vt" "QE" "QEp" "QM" "QMdf"
## [21] "QMp" "k" "k.f" "k.eff" "k.all"
## [26] "p" "p.eff" "parms" "int.only" "int.incl"
## [31] "intercept" "allvipos" "coef.na" "yi" "vi"
## [36] "X" "weights" "yi.f" "vi.f" "X.f"
## [41] "weights.f" "M" "ai.f" "bi.f" "ci.f"
## [46] "di.f" "x1i.f" "x2i.f" "t1i.f" "t2i.f"
## [51] "ni" "ni.f" "ids" "not.na" "subset"
## [56] "slab" "slab.null" "measure" "method" "model"
## [61] "weighted" "test" "dfs" "ddf" "s2w"
## [66] "btt" "m" "digits" "level" "control"
## [71] "verbose" "add" "to" "drop00" "fit.stats"
## [76] "formula.yi" "formula.mods" "version" "call" "time"Beispielsweise können wir dem Objekt so auch die mittlere Schätzung ($b) oder ($tau2) entlocken.
REM$b## [,1]
## intrcpt 0.2373935REM$tau2## [1] 0.02931054Diese Ergebnisse können wir mit Hilfe der R-internen predict Funktion unter Angabe des Zusatzarguments transf=transf.ztor (transformiere zu ) retransformieren.
predict(REM, transf=transf.ztor)##
## pred ci.lb ci.ub pi.lb pi.ub
## 0.2330 0.2014 0.2642 -0.0995 0.5187Das Konfidenzintervall reicht von ci.lb (confidence interval lower boundary) bis ci.ub (confidence interval upper boundary). Die Aussage, die wir treffen können ist, dass, wenn wir diese Meta-Analyse an unabhängigen Stichproben unendlich häufig wiederholen könnten, so würde dieses Intervall, welches sich in dieser Meta-Analyse von 0.2014 bis 0.2642 erstreckt (und welches von Meta-Analyse zu Meta-Analyse von unabhängigen Ansammlungen von Stichproben unterscheiden würde), den wahren Populationsmittelwert in 95% der Fälle enthalten. Auf Basis dieses Konfidenzintervalls würden wir die Null-Hypothese, dass es keine Beziehung zwischen Interviews und Job-Performanz gibt, auf dem 95% Signifikanzniveau verwerfen.
Auch dieser Befehl lässt sich erneut als Objekt abspeichern und wir können dann auf diese zugreifen:
pred_REM <- predict(REM, transf=transf.ztor)
names(pred_REM)## [1] "pred" "se" "ci.lb" "ci.ub" "pi.lb" "pi.ub" "cr.lb" "cr.ub"
## [9] "slab" "digits" "method" "transf"pred_REM$pred # retransformierter gepoolter Korrelationskoeffizient## [1] 0.2330323Wir sehen, dass der mittlere -Wert sich kaum vom mittleren Korrelationskoeffizienten unterscheidet. Dies ist im Allgemeinen auch so: -Wert und -Wert sind für betraglich kleine Korrelationen annähernd identisch, also für : hier liegt die betragliche Differenz bei .
Finales Ergebnis des Random Effects Modells
Schauen wir uns die Ergebnisse nun grafisch an:
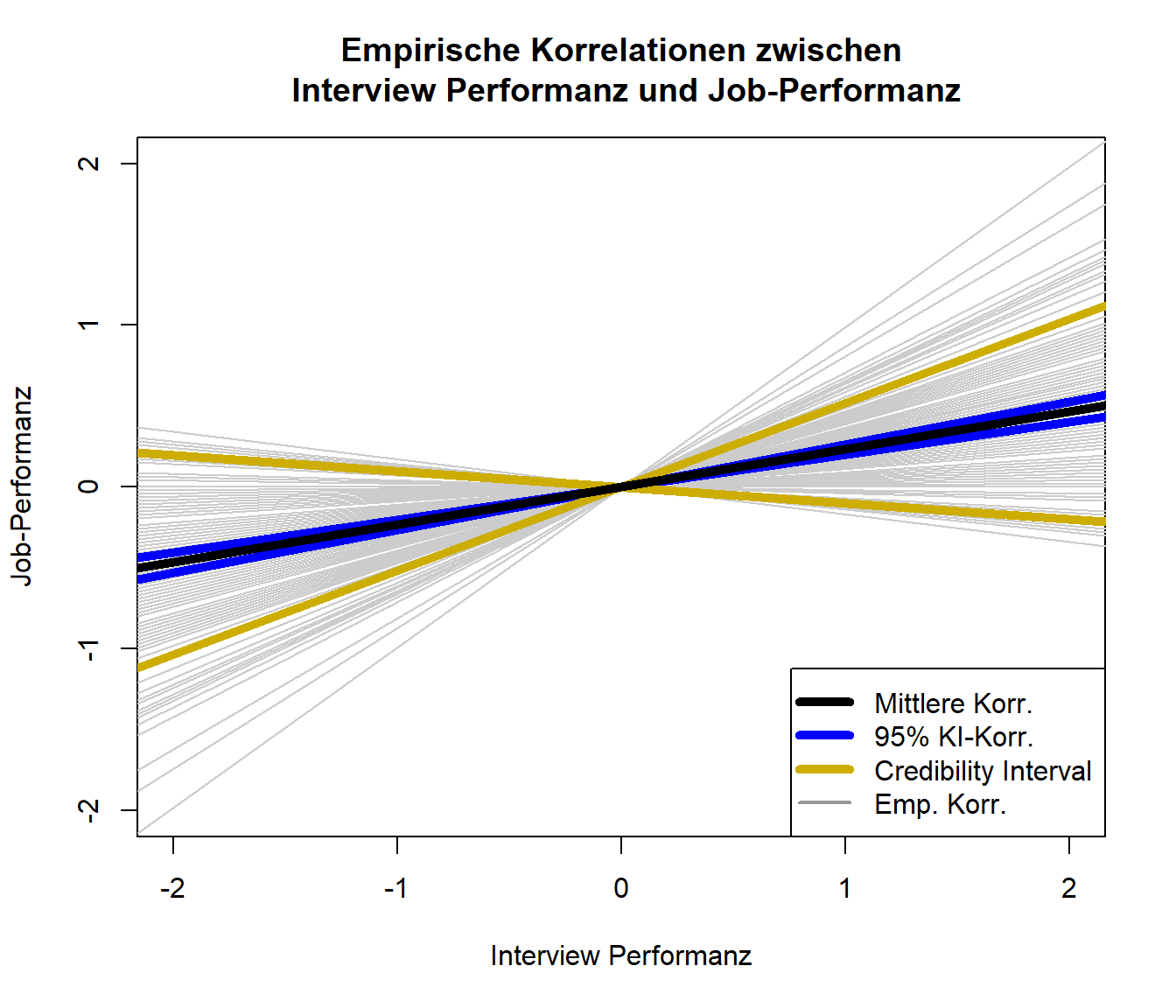
Es scheint wohl eine Beziehung zwischen Einstellungsinterviews und Job-Performanz zu geben. Allerdings ist diese Beziehung mit einer Korrelation von 0.233 nicht sehr stark; lediglich 5.43% der Variation an der Job-Performanz können durch die Interview-Performanz vorhergesagt werden. Das Credibility-Intervall zeigt an, in welchem Bereich ca. 80% der beobachteten Werte liegen.
Analyse Plots
Das metafor Paket bietet außerdem noch einige grafischen Veranschaulichungen der Daten. Beispielsweise lässt sich ganz leicht ein Funnel-Plot erstellen mit der funnel Funktion, welche lediglich unser Meta-Analyse Objekt REM entgegen nehmen muss. Der Funnel-Plot wird verwendet, um auf das bekannte Problem des Publication-Bias zu untersuchen. Hier wird der gefundene Effekt (hier die z-transformierte Korrelation) gegen den Standardfehler jeder Studie geplottet. Es wird die Annahme zugrunde gelegt, dass alle Studien in der Meta-Analyse eine gewisse, zufällige Schwankung um den wahren Effekt haben, und dabei diese zufällige Schwankung größer ist, je größer der Standardfehler in einer Studie ist und je kleiner die Stichprobe war. Sofern eine Studie unabhängig von der Effektgröße sowie der Streuung (und damit auch der Signifikanz) publiziert wurde, sollte so das typische symmetrische Dreieck (Funnel = Trichter) entstehen.
# funnel plot
funnel(REM)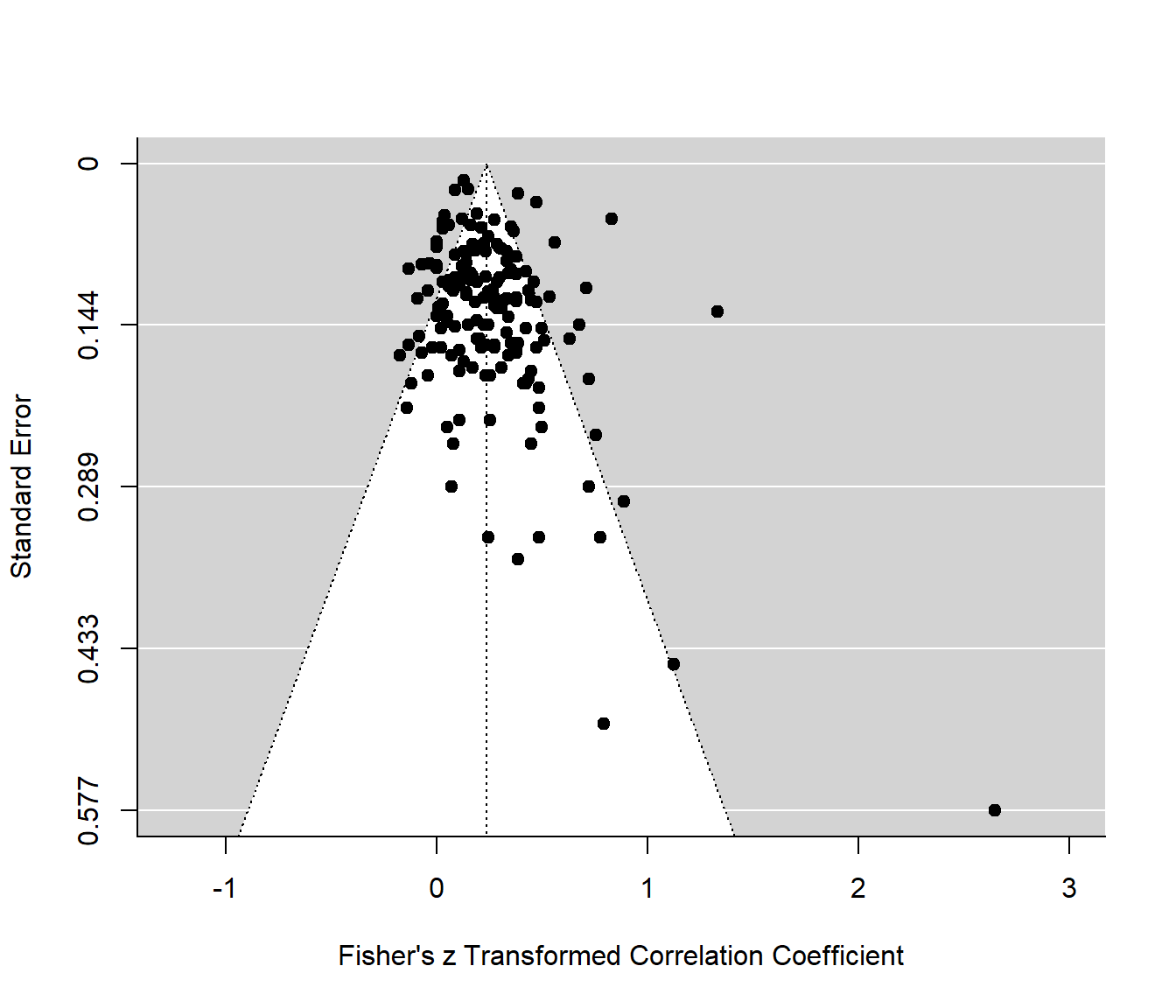
Der Grafik ist zu entnehmen, dass im positiven Bereich mehr Studien zu finden sind. Dies könnte Indizien auf einen Publication Bias zeigen. Außerdem gibt es wenige Studien mit sehr großen Standardfehlern (un damit geringen Stichprobengrößen). Jedoch ist es wenig verwunderlich, dass es mehr Studien gibt, in welchen es eine Beziehung zwischen Interview und Job-Performanz gibt, da die Interviews zum Teil nach diesem Kriterium durchgeführt wurden und eine gewissen Augenscheinvalidität von Einstellungsinterviews (im Idealfall) besteht.
Auch Forest-Plots funktionieren auf die gleiche Weise mit der forest Funktion. Der Forest-Plot stellt die unterschiedlichen Studien hinsichtlich ihrer Parameterschätzung (hier -Wert des Korrelationskoeffizienten) und die zugehörige Streuung grafisch dar. So können beispielsweise Studien identifiziert werden, welche besonders hohe oder niedrige Werte aufweisen oder solche, die eine besonders große oder kleine Streuung zeigen.
# forest plot
forest(REM, xlim = c(-1, 2))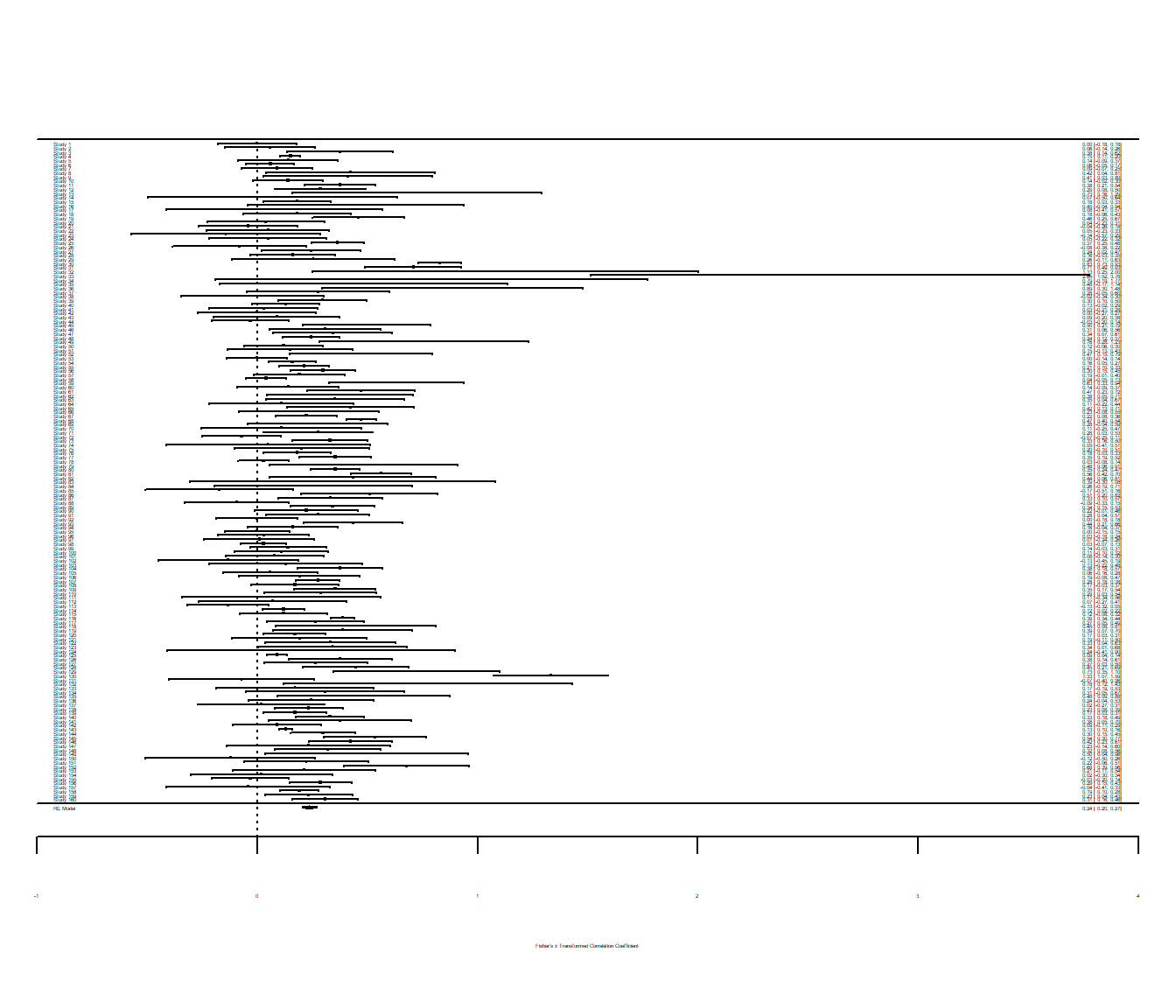
Die Anzahl der Studien ist hierbei so enorm, dass wir die Achsenbeschriftungen nicht mehr lesen können. Mit xlim = c(-1, 2) legen wir das Minimum und das Maximum auf der x-Achse fest (dies machen wir, um Forest-Plots vergleichen zu können). Auch ein kumulativer Forest-Plot wäre möglich. Dazu müssen wir auf unser REM-Objekt noch die Funktion cumul.rma.uni anwenden:
# kumulativer Forest Plot
forest(cumul.rma.uni(REM), xlim = c(-1, 2))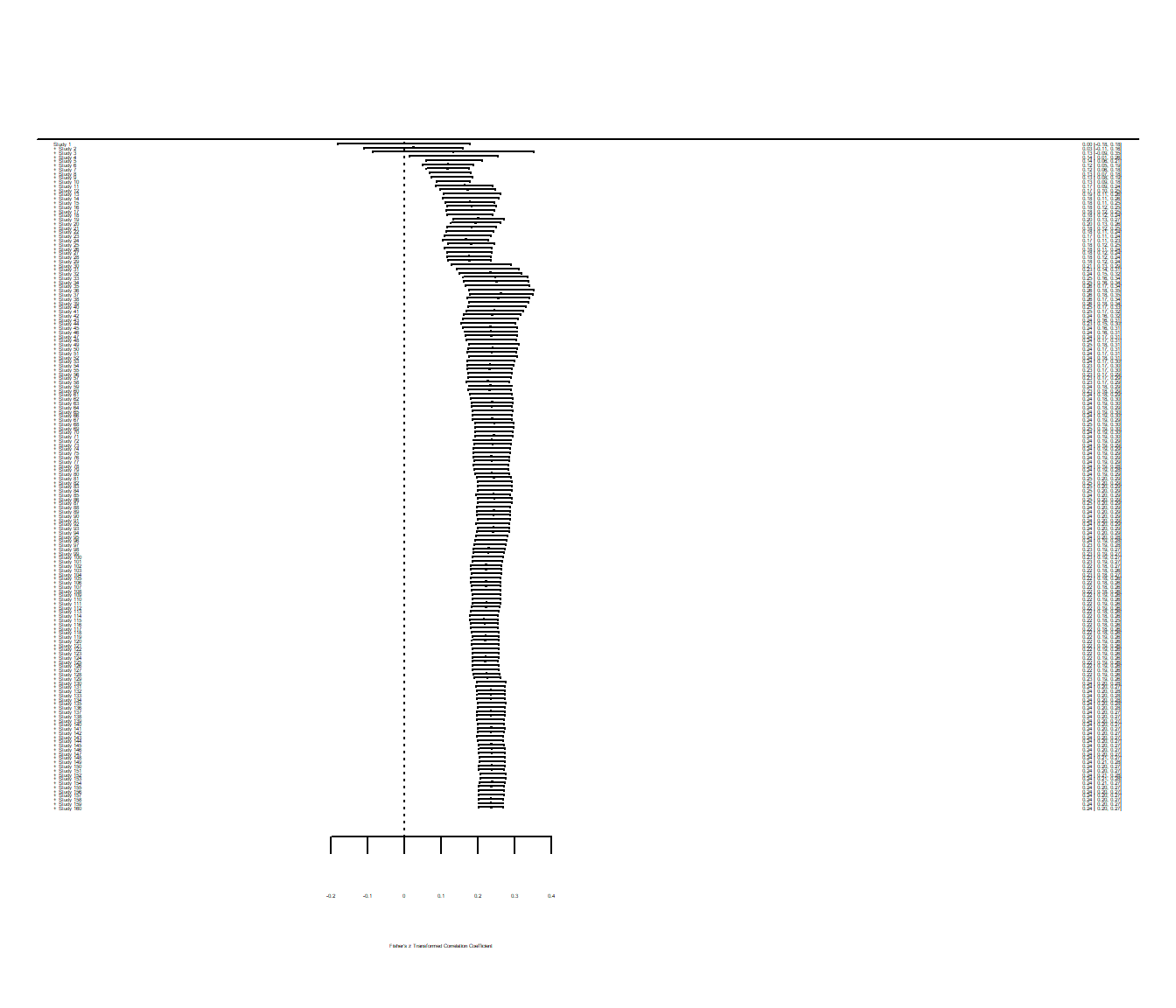
Die Funktion cumul.rma.uni führt skuzessive immer wieder eine Meta-Analyse durch, wobei nach und nach eine Studie hinzugefügt wird. Anders als beim ersten Forest-Plot wird immer das Ergebnis der jeweiligen Meta-Analyse dargestellt und nicht jede Studie einzeln. Wir sehen, dass sich sowohl mittlerer -Wert als auch Streuung von oben nach unten einpendeln. Das finale Ergebnis ist identisch mit unsere Meta-Analyse. Die gestrichelte Linie der Forest-Plots symbolisiert die 0, da in den meisten Fällen gegen 0 getestet wird und es daher von Interesse ist, wie viele Studien sich von 0 unterscheiden und ob sich der mittlere Effekt von 0 unterscheidet. Um die Beschriftungen des Forest-Plot einmal genauer zu sehen, führen wir eine Meta-Analyse nur über die ersten 20 Studien durch:
REM20 <- rma(yi = z_ri, vi = v_ri, data=data_transformed[1:20, ]) # wähle Studie 1 bis 20
# forest plot
forest(REM20, xlim = c(-1, 2))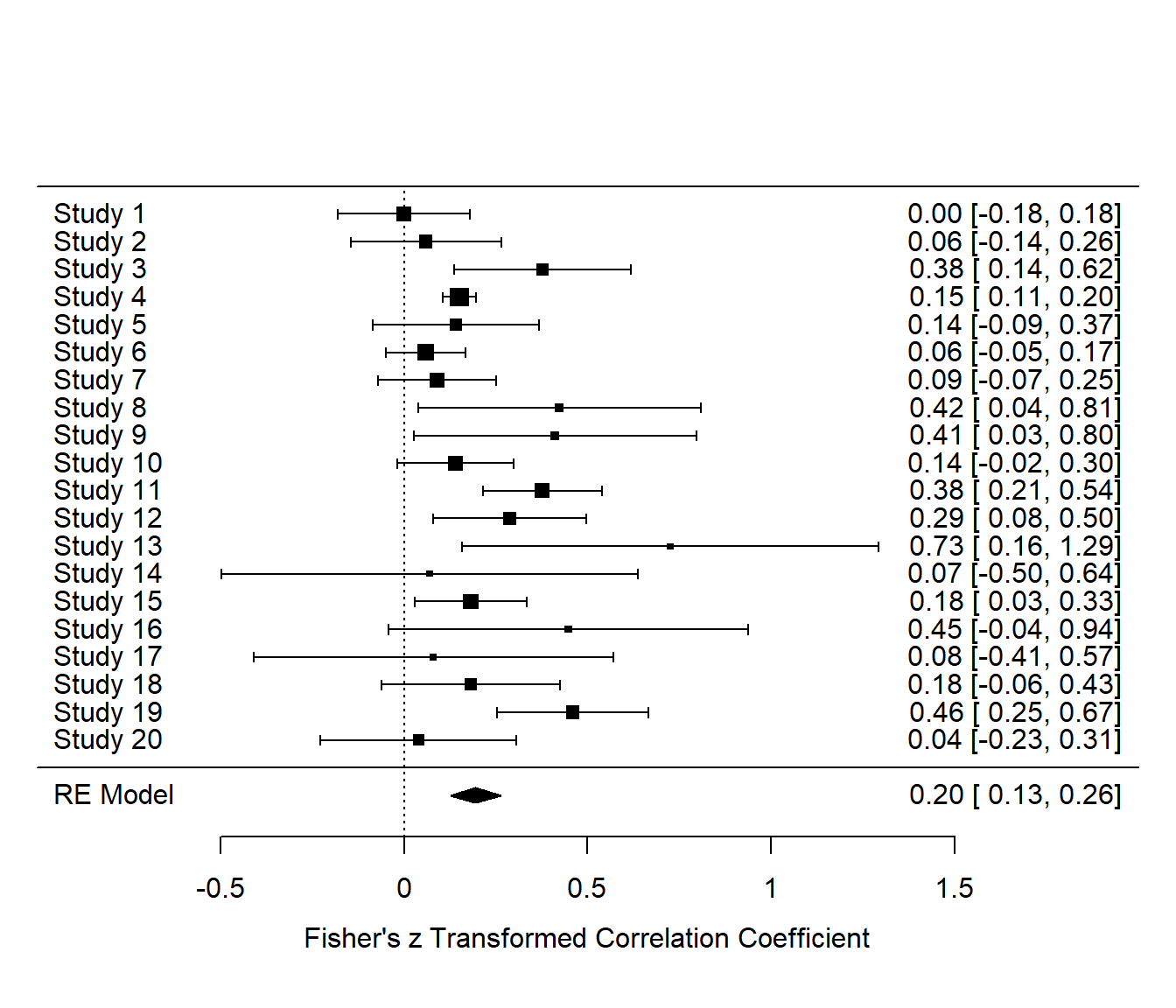
# kumulativer Forest Plot
forest(cumul.rma.uni(REM20), xlim = c(-1, 2))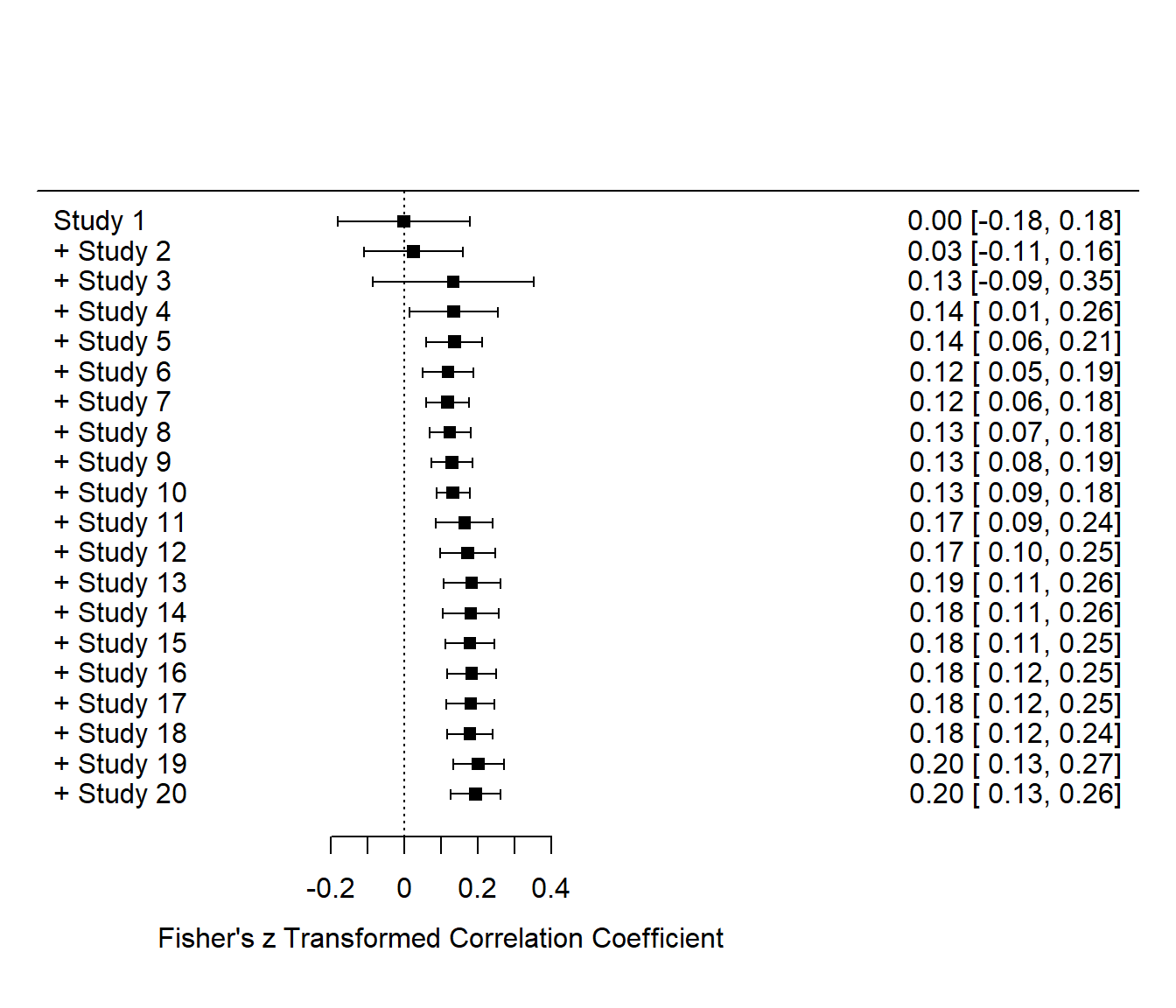 Wir sehen, dass auch hier der durchschnittliche Wert nicht weit von unserem finalen Durchschnitt entfernt liegt. Die kleine Raute in der letzten Zeile des normalen Forest-Plots symbolisiert den durchschnittlichen Wert und dessen Streuung.
Wir sehen, dass auch hier der durchschnittliche Wert nicht weit von unserem finalen Durchschnitt entfernt liegt. Die kleine Raute in der letzten Zeile des normalen Forest-Plots symbolisiert den durchschnittlichen Wert und dessen Streuung.
Mixed Effects Modelle
Da die Heterogenitätsvarianz signifikant von 0 verschieden war, wollen wir versuchen die Variation in den Korrelationskoeffizienten zwischen den Studien mit Hilfe von Moderatoren vorherzusagen.
Interviewtyp als Moderator
Es könnte sein, dass die Art (der Typ) des Interviews eine Rolle in der Bewertung der Performanz hat und dass die verschiedenen Interviewtypen unterschiedlich stark mit der späteren Job-Performanz zusammenhängen. Insgesamt gab es drei Arten von Interviews: j = job-related, s = situational und p = psychological. Diese Typen sind in der Variable type enthalten. Wir wollen uns die (-transformierte) Korrelation pro Interviewtyp anschauen:
data_transformed$type## [1] "j" "p" "j" "j" "j" "j" "j" "j" "s" "s" "s" "j" "j" "j" "j" "j" "j" "p"
## [19] "j" "j" "p" "p" "p" "j" "j" "p" "p" "p" "j" "j" "j" "j" "j" "j" "j" "j"
## [37] "j" "j" "j" "j" "j" "j" "j" "j" "s" "s" "s" "p" "j" "j" "j" "j" "j" "j"
## [55] "p" "j" "j" "j" "j" "j" "j" "j" "j" "j" "j" "j" "j" "j" "j" "j" "j" "j"
## [73] "j" "j" "j" "j" "j" "j" "s" "j" "j" "s" "s" "s" "j" "j" "j" "s" "j" "j"
## [91] "s" "j" "j" "j" "j" "j" "j" "j" "j" "j" "j" "j" "j" "j" "j" "j" "j" "j"
## [109] "j" "s" "j" "j" NA "j" "j" "j" "p" "j" "j" "j" "j" "s" NA "j" NA "j"
## [127] "s" "j" "j" "j" "j" "j" "j" "j" "s" "p" "p" "j" "j" "j" "j" "p" "j" "j"
## [145] "j" "j" "j" "j" "j" "j" "j" "j" "j" "j" "j" "j" "j" "j" "j" "j"plot(z_ri ~ factor(type), data=data_transformed, col = c("blue", "gold3", "red"), xlab = "Interviewtyp",
ylab = "z-transformierte Korrelation", main = "z-transformierte Korrelation pro Interviewtyp")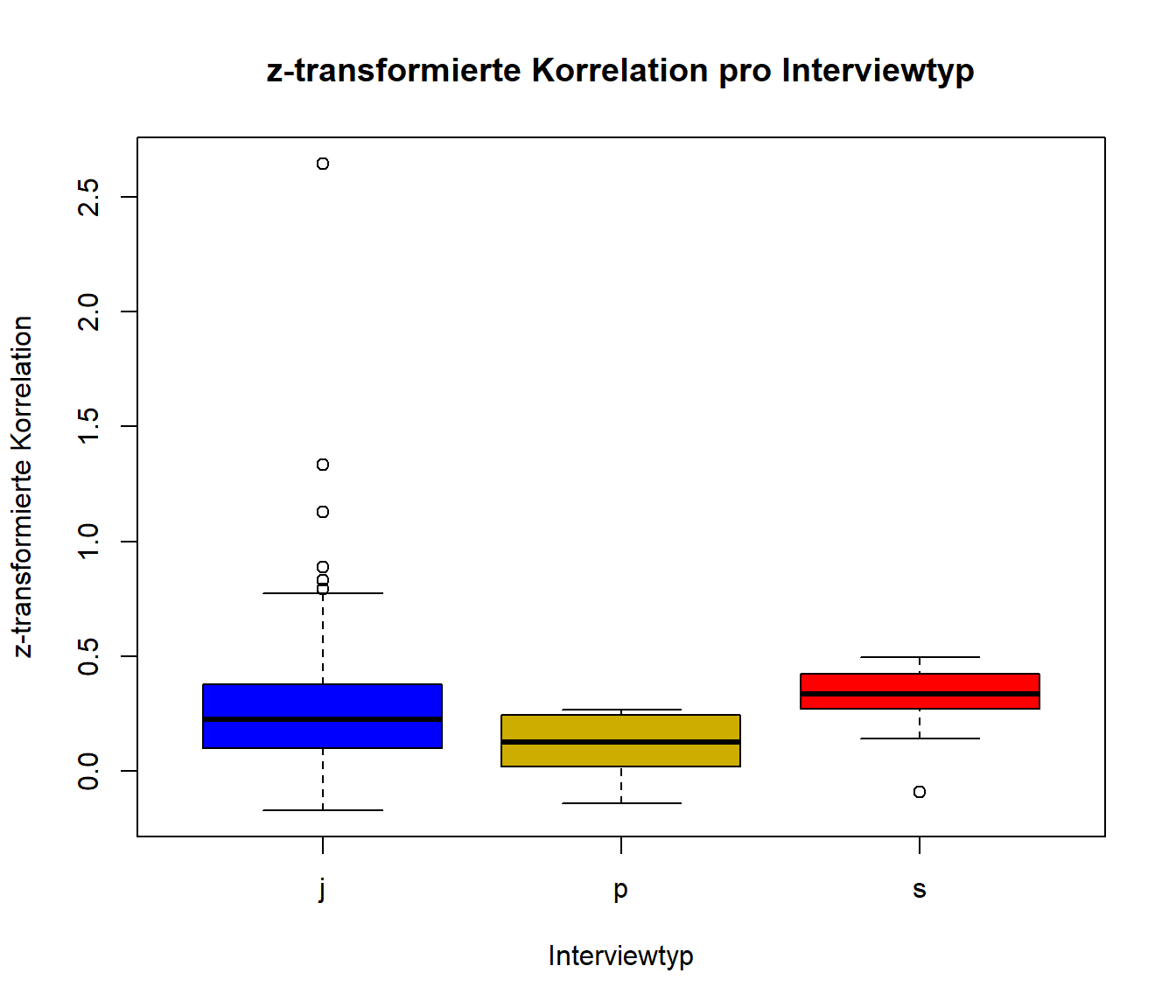
plot(ri ~ factor(type), data=data_transformed, col = c("blue", "gold3", "red"), xlab = "Interviewtyp",
ylab = "Korrelation", main = "Korrelation pro Interviewtyp")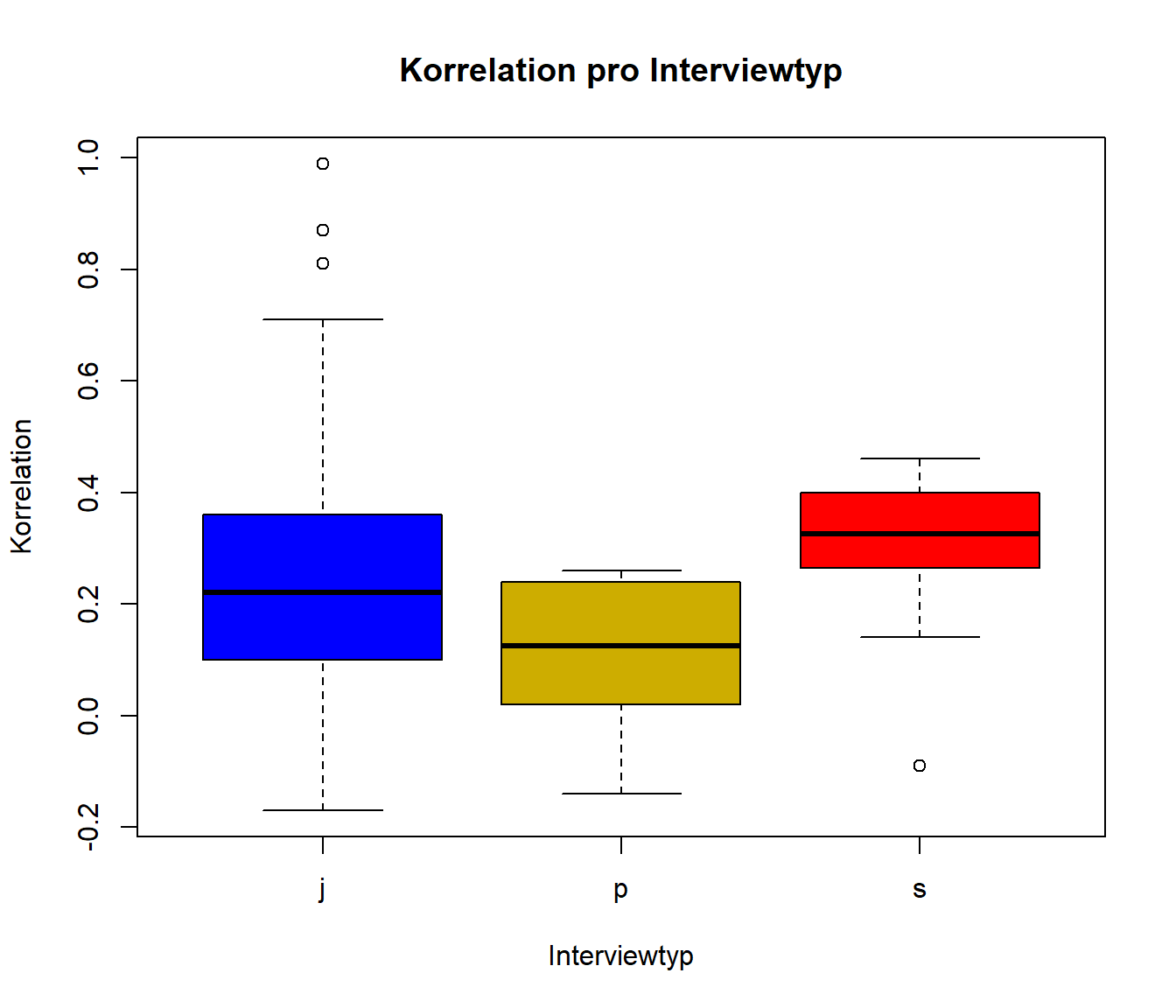
Ein Mixed Effects Model (MEM) können wir wieder mit der rma Funktion schätzen. Wir müssen lediglich dem Argument mods = ~ factor(type) die Namen der Moderatorvariablen übergeben. Die Tilde gibt an, dass es sich hier um eine regressive Beziehung handelt. factor gibt an, dass es sich um eine kategoriale Variable mit Abstufungen handelt und dass die Werte eine Gruppenzugehörigkeit symbolisieren sollen (auch falls type aus Zahlen bestehen würde). Wollen wir kontinuierliche (und nicht kategoriale) Prädiktoren als Moderatoren verwenden, so können wir factor weglassen (dazu müssen allerdings die Daten im richtigen Format vorliegen, also intervallskaliert sein: bspw. Alter, Zustimmung auf einer Likert-Skala mit hinreichend vielen Ausprägungen oder das Einkommen, etc.).
MEM_type <- rma(yi = z_ri, vi = v_ri, mods = ~ factor(type), data = data_transformed)## Warning: Studies with NAs omitted from model fitting.MEM_type##
## Mixed-Effects Model (k = 157; tau^2 estimator: REML)
##
## tau^2 (estimated amount of residual heterogeneity): 0.0282 (SE = 0.0049)
## tau (square root of estimated tau^2 value): 0.1681
## I^2 (residual heterogeneity / unaccounted variability): 79.62%
## H^2 (unaccounted variability / sampling variability): 4.91
## R^2 (amount of heterogeneity accounted for): 1.92%
##
## Test for Residual Heterogeneity:
## QE(df = 154) = 738.4411, p-val < .0001
##
## Test of Moderators (coefficients 2:3):
## QM(df = 2) = 5.8455, p-val = 0.0538
##
## Model Results:
##
## estimate se zval pval ci.lb ci.ub
## intrcpt 0.2474 0.0187 13.2089 <.0001 0.2107 0.2841 ***
## factor(type)p -0.1228 0.0582 -2.1115 0.0347 -0.2368 -0.0088 *
## factor(type)s 0.0573 0.0598 0.9587 0.3377 -0.0599 0.1745
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Wenn wir das Modell schätzen, bekommen wir die Warnmeldung ausgegeben, dass für einige Studien keine Angabe zu dem Moderator Interviewtyp vorliegen (bzw. diese Information nicht auffindbar war). Aus diesem Grund werden diese Studien komplett via listwise deletion (listenweiser Fallauschluss) aus den Analysen ausgeschlossen; es sind nur noch 157 anstatt 160 Studien in der Meta-Analyse enthalten (dies können wir dem Output entnehmen, welcher genauso aufgebaut ist, wie der Output des REM Modells; es ist ja auch die gleiche Funktion, die wir angewendet haben!). Der Output hat zwei Neuheiten: 1) Test of Moderators (coefficients 2:3): gibt einen Omnibustest an, ob die Moderatoren das Modell verbessern, 2) in den Model Results sind “”-Koeffizienten für die Moderatoren (hier als Dummy-kodierte Variablen) angegeben. Die Referenzkategorie für die Dummy-Variablen ist das “job-related” Interview. So gibt factor(type)p gerade den Effekt an, der durch Nutzen von psychologischen im Vergleich zu “job-related” Interviews entsteht. Hier ist die -transformierte Korrelation in den Studien mit psychologischen Interviewtyp um -0.1228 kleiner als in den “job-related” Interviewstudien. Entsprechend steht factor(type)s für den Effekt, der durch Nutzen von “situational” (also situationsbezogenen-) im Vergleich zu “job-related” Interviews entsteht. Hier ist die -transformierte Korrelation in den Studien mit “situational” Interviewtyp um 0.0573 größer als in den “job-related” Interviewstudien.
Modellvergleiche
Wir können Modelle auch miteinander vergleichen, um so den inkrementellen Wert von Moderatoren zu prüfen. Dabei prüfen wir konkret, ob die Heterogenitätsvarianz zwischen den Studien bedeutsam durch die Moderatoren reduziert/aufgeklärt werden kann. So können wir bspw. das Modell mit und das ohne Moderatoren vergleichen (entspricht dann dem Omnibustest) oder wir vergleichen Modelle mit unterschiedlich vielen Moderatoren. Hierbei ist zu beachten, dass diese Modelle geschachtelt sein müssen, da sonst keine Inferenz möglich ist. Um Modelle zu vergleichen, verwenden wir den R-internen anova-Befehl.
anova(REM, MEM_type)Wenn wir diesen Befehl einfach so durchführen, bekommen wir eine Fehlermeldung:
## Error in anova.rma(REM, MEM_type) : Observed outcomes and/or sampling
## variances not equal in the full and reduced model.Dies liegt daran, dass die beiden Modelle auf unterschiedlichen Datengrundlagen beruhen. Beim MEM wurde durch listwise deletion die Stichprobengröße (welche hier der Anzahl an Studien entspricht) reduziert. Um die beiden Modelle dennoch miteinander vergleichen zu können, müssen wir also jene Fälle ausschließen, in welchen keine Information über den Interviewtyp besteht. Wir haben mit data_transformed$type auf den Interviewtyp zugegriffen. Hier steht NA für not available, also fehlend. Mit der Funktion is.na können wir abfragen, welche der Werte fehlend sind. Mit dem which Befehl können wir uns außerdem die Stellen im Vektor ausgeben lassen, in welchem die Werte fehlen.
is.na(data_transformed$type) # fehlt ein Wert = TRUE## [1] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [13] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [25] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [37] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [49] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [61] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [73] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [85] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [97] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [109] FALSE FALSE FALSE FALSE TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [121] FALSE FALSE TRUE FALSE TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [133] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [145] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [157] FALSE FALSE FALSE FALSEwhich(is.na(data_transformed$type)) # welche Werte fehlen?## [1] 113 123 125Fügen wir ein ! vor is.na ein, negieren wir den Befehl. !is.na entspricht also “nicht fehlend”. Darüber wählen wir Studien aus, in denen die Bedingung zutrifft, dass der Wert für type nicht fehlt. So können wir den Datensatz “reinigen” (mit dim können wir uns die Dimensionen des Datensatzes ansehen), indem wir nur die Beobachtungen (Studien) behalten, in denen der Typ vorliegt. Den Datensatz können wir bspw. unter data_transformed_clean_type abspeichern:
dim(data_transformed)## [1] 160 7data_transformed_clean_type <- data_transformed[!is.na(data_transformed$type), ]
dim(data_transformed_clean_type)## [1] 157 7Nun fitten wir nochmal das REM mit den reduzierten Daten:
REM_reduced_type <- rma(yi = z_ri, vi = v_ri, data = data_transformed_clean_type)
REM_reduced_type##
## Random-Effects Model (k = 157; tau^2 estimator: REML)
##
## tau^2 (estimated amount of total heterogeneity): 0.0288 (SE = 0.0049)
## tau (square root of estimated tau^2 value): 0.1697
## I^2 (total heterogeneity / total variability): 79.99%
## H^2 (total variability / sampling variability): 5.00
##
## Test for Heterogeneity:
## Q(df = 156) = 747.1489, p-val < .0001
##
## Model Results:
##
## estimate se zval pval ci.lb ci.ub
## 0.2410 0.0170 14.1438 <.0001 0.2076 0.2744 ***
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Wir sehen nun, dass auch hier die Studienanzahl reduziert ist. Das Ergebnis ändert sich hingegen kaum. Nun können wir erneut versuchen einen Modellvergleich mit Hilfe des anova-Befehls anzufordern:
anova(REM_reduced_type, MEM_type)Auch hier erkennen wir eine Warnung, weswegen wir uns die Ergebnisse noch nicht ansehen wollen:
## Warning in anova.rma(REM_reduced_type, MEM_type): Models with different fixed
## effects. REML comparisons are not meaningful.Wenn wir eine andere Schätzmethoden wählen, wird dieses Problem umgangen. Wir können bespielsweise die “ML” (Maximum Likelihood) anstatt der “REML” (Restricted ML) Schätzmethode verwenden. Dazu müssen wir allerdings die Modelle erneut schätzen und müssen dem Argument method die Methode "ML" zuweisen. Der zugehörige Test, den wir anschließend mit anova durchführen wollen, ist unter Verwendung der “ML”-Schätzmethode der Likelihood-Ratio-Test (LRT), welcher auch häufig -Differenzen-Test genannt wird. Diesen kennen wir bereits aus einigen weiteren Statistikveranstaltungen (siehe bspw. Multi-Level-Modeling oder logistische Regression). Die Freiheitsgrade des -Tests sind in diesem Fall die Parameter, die durch die Hinzunahme der Moderatoren zusätzlich geschätzt werden müssen. Hier sind dies also die beiden Effekte der Vergleiche zwischen p vs. j und s vs. j, also 2.
REM_reduced_type_ML <- rma(yi = z_ri, vi = v_ri, data = data_transformed_clean_type, method = "ML")
MEM_type_ML <- rma(yi = z_ri, vi = v_ri, mods = ~ factor(type), data=data_transformed_clean_type, method = "ML")
anova(REM_reduced_type_ML, MEM_type_ML)##
## df AIC BIC AICc logLik LRT pval QE tau^2
## Full 4 -11.0523 1.1727 -10.7892 9.5262 738.4411 0.0274
## Reduced 2 -9.1793 -3.0668 -9.1014 6.5896 5.8730 0.0530 747.1489 0.0285
## R^2
## Full
## Reduced 3.8338%Unter LRT erkennen wir die Log-Likelihood-Differenz, welche die Loglikelihoods verechnet, welche wir unter logLik ablesen können (es gilt: ). Der angegeben p-Wert des Modellvergleichs liegt bei 0.053 und zeigt somit keine signifikante Reduktion der Heterogenitätsvarianz durch den Moderator Interviewtyp an (dies ist im Übrigen fast identisch zum p-Wert des Omnibustest, der durch das Objekt MEM_type_ML selbst ausgegeben würde).
MEM_type_ML##
## Mixed-Effects Model (k = 157; tau^2 estimator: ML)
##
## tau^2 (estimated amount of residual heterogeneity): 0.0274 (SE = 0.0047)
## tau (square root of estimated tau^2 value): 0.1655
## I^2 (residual heterogeneity / unaccounted variability): 79.13%
## H^2 (unaccounted variability / sampling variability): 4.79
## R^2 (amount of heterogeneity accounted for): 3.83%
##
## Test for Residual Heterogeneity:
## QE(df = 154) = 738.4411, p-val < .0001
##
## Test of Moderators (coefficients 2:3):
## QM(df = 2) = 5.9232, p-val = 0.0517
##
## Model Results:
##
## estimate se zval pval ci.lb ci.ub
## intrcpt 0.2472 0.0185 13.3381 <.0001 0.2109 0.2836 ***
## factor(type)p -0.1223 0.0576 -2.1253 0.0336 -0.2352 -0.0095 *
## factor(type)s 0.0572 0.0592 0.9658 0.3341 -0.0589 0.1733
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Die Beziehung zwischen Einstellungsinterview und Job-Performanz scheint sich also über die Interviewtypen nicht zu unterscheiden. Die Interviewtypen scheinen alle gleich valide zu sein.
Wie wir bspw. Mittelwerte meta-analytisch verrechnen oder wie genau sich das “Fixed Effects” und das “Random Effects” Modell unterscheiden, sehen Sie im Appendix B.
Die Meta-Analyse von Irmer, Kern, Schermelleh-Engel, Semmer und Zapf (2019) wurde mit diesem R-Paket durchgeführt. Sie behandelt die Validierung des Instrument zur stressbezogenen Tätigkeitsanalyse (ISTA) von Semmer, Zapf und Dunckel (1995, 1999), indem die linearen Beziehungen der Skalen des Instrument untereinander sowie mit Kriteriumsvariablen untersucht wurden. Außerdem wurden die Mittelwerte und und Standardabweichungen (meta-analytisch) gemittelt. Alle Koeffizienten (Mittelwerte, Standardabweichungen und Korrelationen) wurden hinsichtlich systematischer Unterschiede über das Geschlecht (% Frauen), der Publikationsstatus (publiziert vs. nicht publiziert), die ISTA-Version sowie die Branche (des Arbeitsplatzes) untersucht. Das genaue meta-analytische Vorgehen ist dem Appendix des Artikels zu entnehmen.
Appendix A
Codes
plot(NA, xlim = c(-2,2), ylim = c(-2,2), xlab = "Interview Performanz", ylab = "Job-Performanz",
main = "Empirische Korrelationen zwischen\n Interview Performanz und Job-Performanz") # erzeuge einen leeren Plot mit vorgegbenen Achsenabschnitten
for(i in 1:length(dat.mcdaniel1994$ri))
{
abline(a = 0, b = dat.mcdaniel1994$ri[i], col = "grey80") # füge Gerade pro Studie hinzu
}
plot(NA, xlim = c(-2,2), ylim = c(-2,2), xlab = "Interview Performanz", ylab = "Job-Performanz",
main = "Empirische Korrelationen zwischen\n Interview Performanz und Job-Performanz") # erzeuge einen leeren Plot mit vorgegbenen Achsenabschnitten
for(i in 1:length(dat.mcdaniel1994$ri))
{
abline(a = 0, b = dat.mcdaniel1994$ri[i], col = "grey80") # füge Gerade pro Studie hinzu
}
abline(a = 0, b = pred_REM$ci.lb, col = "blue", lwd = 5)
abline(a = 0, b = pred_REM$ci.ub, col = "blue", lwd = 5)
abline(a = 0, b = pred_REM$cr.lb, col = "gold3", lwd = 5)
abline(a = 0, b = pred_REM$cr.ub, col = "gold3", lwd = 5)
abline(a = 0, b = pred_REM$pred, col = "black", lwd = 5)
legend(x = "bottomright", col = c("black", "blue", "gold3", "grey60"), pch = NA, lwd = c(5,5,5,2),
legend = c("Mittlere Korr.", "95% KI-Korr.", "Credibility Interval", "Emp. Korr.")) # Legende für Farbzuordnung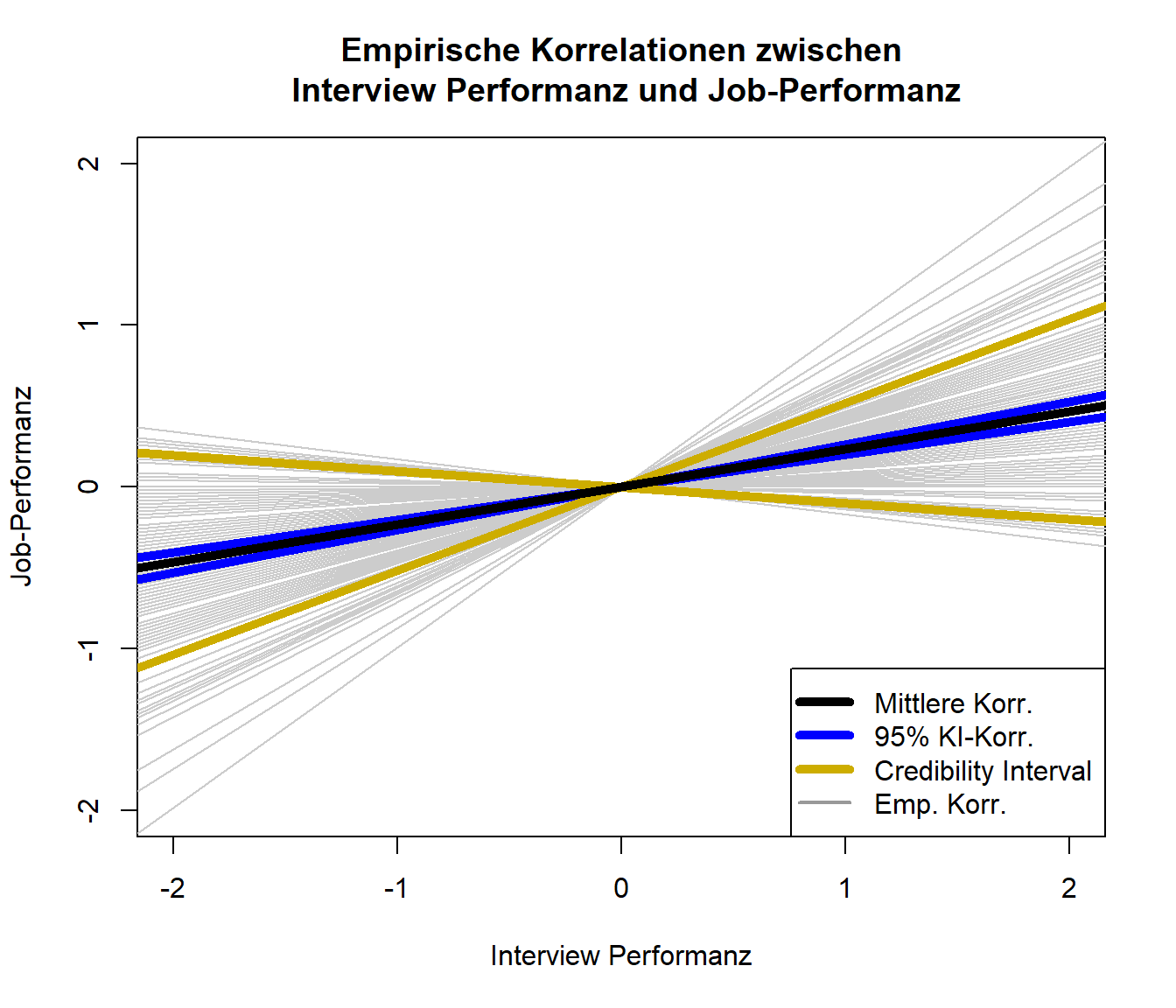
Appendix B
Andere Parameter zusammenfassen: Mittelwerte
Genauso wie Korrelationskoeffizienten können auch Mittelwerte meta-analytisch zusammengefasst werden. Das Vorgehen bleibt weitgehend das Gleiche. Wir müssen jedoch keine Transformation der Daten durchführen, um sie sinnvoll zu mitteln. Dazu verwenden wir diesmal den Datensatz dat.bangertdrowns2004. Mit ?dat.bangertdrowns2004 erhalten Sie weitere Informationen zu dieser Studie. Es geht in diesem Datensatz um die Wirksamkeit einer “Writing-to-Learn Intervention”. yi (Zugriff via dat.bangertdrowns2004$yi) enthält die standardisierte Mittelwertsdifferenz (d), ni ist die Stichprobengröße und vi ist die Varianz der Mittelwertsdifferenz (also ).
head(dat.bangertdrowns2004)## id author year grade length minutes wic feedback info pers imag meta
## 1 1 Ashworth 1992 4 15 NA 1 1 1 1 0 1
## 2 2 Ayers 1993 2 10 NA 1 NA 1 1 1 0
## 3 3 Baisch 1990 2 2 NA 1 0 1 1 0 1
## 4 4 Baker 1994 4 9 10 1 1 1 0 0 0
## 5 5 Bauman 1992 1 14 10 1 1 1 1 0 1
## 6 6 Becker 1996 4 1 20 1 0 0 1 0 0
## subject ni yi vi
## 1 Nursing 60 0.650 0.070
## 2 Earth Science 34 -0.750 0.126
## 3 Math 95 -0.210 0.042
## 4 Algebra 209 -0.040 0.019
## 5 Math 182 0.230 0.022
## 6 Literature 462 0.030 0.009dat.bangertdrowns2004$yi # std. Mittelwertsdiff.## [1] 0.65 -0.75 -0.21 -0.04 0.23 0.03 0.26 0.06 0.06 0.12 0.77 0.00
## [13] 0.52 0.54 0.20 0.20 -0.16 0.42 0.60 0.51 0.58 0.54 0.09 0.37
## [25] -0.01 -0.13 0.18 0.27 -0.02 0.33 0.59 0.84 -0.32 0.12 1.12 -0.12
## [37] -0.44 -0.07 0.70 0.49 0.20 0.58 0.15 0.63 0.04 1.46 0.04 0.25
## attr(,"measure")
## [1] "SMD"
## attr(,"ni")
## [1] 60 34 95 209 182 462 38 542 99 77 40 190 113 50 47 44 24 78 46
## [20] 64 57 68 40 68 48 107 58 225 446 77 243 39 67 91 36 177 20 120
## [39] 16 105 195 62 289 25 250 51 46 56dat.bangertdrowns2004$ni # n## [1] 60 34 95 209 182 462 38 542 99 77 40 190 113 50 47 44 24 78 46
## [20] 64 57 68 40 68 48 107 58 225 446 77 243 39 67 91 36 177 20 120
## [39] 16 105 195 62 289 25 250 51 46 56dat.bangertdrowns2004$vi # Varianz## [1] 0.070 0.126 0.042 0.019 0.022 0.009 0.106 0.007 0.040 0.052 0.107 0.021
## [13] 0.037 0.083 0.086 0.091 0.167 0.052 0.091 0.065 0.073 0.061 0.100 0.060
## [25] 0.083 0.037 0.069 0.018 0.009 0.053 0.017 0.112 0.060 0.044 0.129 0.023
## [37] 0.205 0.033 0.265 0.039 0.021 0.067 0.014 0.168 0.016 0.099 0.087 0.072Wir können nun einfach eine Meta-Analyse mit Stichprobengewichtung durchführen. Wir mitteln (gewichtet) zunächst händisch via:
Hier wird jede Mittelwertsdifferenz mit der Stichprobengröße multipliziert und dann werden diese Werte aufsummiert (eine gewichtete Summe entsteht). Teilen wir diese Summe anschließend durch die Gesamtstichprobe so erhalten wir einen gewichteten Mittelwert, der berücksichtigt, dass einige Stichproben größer sind und dort der Mittelwert präziser ist. Dies sieht in R so aus:
sum(dat.bangertdrowns2004$ni*dat.bangertdrowns2004$yi)/sum(dat.bangertdrowns2004$ni)## [1] 0.1719405Mit Hilfe der rma Funktion geht das Ganze so:
rma_n_FE <- rma(yi = yi, vi = 1/ni, data = dat.bangertdrowns2004, method = "FE")
summary(rma_n_FE)##
## Fixed-Effects Model (k = 48)
##
## logLik deviance AIC BIC AICc
## -169.2493 460.8106 340.4985 342.3697 340.5855
##
## I^2 (total heterogeneity / total variability): 89.80%
## H^2 (total variability / sampling variability): 9.80
##
## Test for Heterogeneity:
## Q(df = 47) = 460.8106, p-val < .0001
##
## Model Results:
##
## estimate se zval pval ci.lb ci.ub
## 0.1719 0.0134 12.8392 <.0001 0.1457 0.1982 ***
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Mit beiden Wegen kommt man zum selben Ergebnis. Allerdings haben wir in diesem Fall ein “Fixed Effects” Modell geschätzt, denn nur so ist zu sehen, dass dies nichts anderes als ein gewichteter Mittelwert ist. Wählen wir hingegen ein “Random Effects” Modell (so wie wir dies bei den Korrelationen getan haben), so müssen wir method = "RE" wählen (oder dieses Argument weglassen, da auch automatisch als Default “RE” eingestellt ist) und uns damit abfinden, dass beim “Random Effects” Modell die Heterogenitätsvarianz ebenfalls als Gewicht verwendet wird. Im “Fixed Effects” Modell wird als Gewicht verwendet ( ist die Varianz des Schätzer; beim Mittelwert ist dies dessen Standardfehler im Quadrat). Wenn wir der R-Funktion v_i= 1/n_i übergeben, so ist das Gewicht einfach die Stichprobengröße (Studien mit größeren Stichproben erhalten mehr Gewicht). Im “Random Effects” Modell wird die Heterogenitätsvarianz ebenfalls als Gewichtung verwendet: . Das Mitteln funktioniert für beide Modelle gleich, nämlich genau so wie der gewichtete Mittelwert, den wir uns zuvor angesehen haben:
Verwenden wir nun das “Random Effects” Modell, so ergibt sich ein etwas anderer Mittelwert (offensichtlich scheinen die Mittelwertsdifferenz heterogen zu sein, denn das Wählen des “Random Effects” Modell hat einen Einfluss auf den geschätzten Mittelwert und die Heterogenitätsvarianz ist auch statistisch signifikant):
rma_n_RE <- rma(yi = yi, vi = 1/ni, data = dat.bangertdrowns2004)
summary(rma_n_RE)##
## Random-Effects Model (k = 48; tau^2 estimator: REML)
##
## logLik deviance AIC BIC AICc
## -22.1023 44.2046 48.2046 51.9049 48.4773
##
## tau^2 (estimated amount of total heterogeneity): 0.1277 (SE = 0.0295)
## tau (square root of estimated tau^2 value): 0.3573
## I^2 (total heterogeneity / total variability): 93.55%
## H^2 (total variability / sampling variability): 15.52
##
## Test for Heterogeneity:
## Q(df = 47) = 460.8106, p-val < .0001
##
## Model Results:
##
## estimate se zval pval ci.lb ci.ub
## 0.2549 0.0547 4.6639 <.0001 0.1478 0.3621 ***
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Der mittlere Effekt liegt beim “Random Effects” Modell etwas höher (0.255) als beim “Fixed Effects” Modell (0.172). Da die Unsicherheit einer Mittelwertsdifferenz allerdings auch stark von der Streuung in der Stichprobe abhängt, wird häufig auch die Variation der Mittelwertsdifferenz verwendet, um die Stichproben zu gewichten. Dies ist quasi der quadrierte Standardfehler ():
rma_vi_RE <- rma(yi = yi, vi = vi, data = dat.bangertdrowns2004)
summary(rma_vi_RE)##
## Random-Effects Model (k = 48; tau^2 estimator: REML)
##
## logLik deviance AIC BIC AICc
## -18.4943 36.9886 40.9886 44.6889 41.2613
##
## tau^2 (estimated amount of total heterogeneity): 0.0499 (SE = 0.0197)
## tau (square root of estimated tau^2 value): 0.2235
## I^2 (total heterogeneity / total variability): 58.37%
## H^2 (total variability / sampling variability): 2.40
##
## Test for Heterogeneity:
## Q(df = 47) = 107.1061, p-val < .0001
##
## Model Results:
##
## estimate se zval pval ci.lb ci.ub
## 0.2219 0.0460 4.8209 <.0001 0.1317 0.3122 ***
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1In allen drei Analysen ist die mittlere Differenz positiv und signifikant von 0 verschieden. Höhere Mittelwertsdifferenzen sprechen für ein höheres mittleres “academic achievment”-Level in der Interventionsgruppe (Bangert-Drowns, Hurley, & Wilkinson, 2004). Somit scheint es einen durchschnittlichen Effekt der Intervention zu geben!
Dass es sich wirklich um den handelt, ist folgender Grafik zu entnehmen:
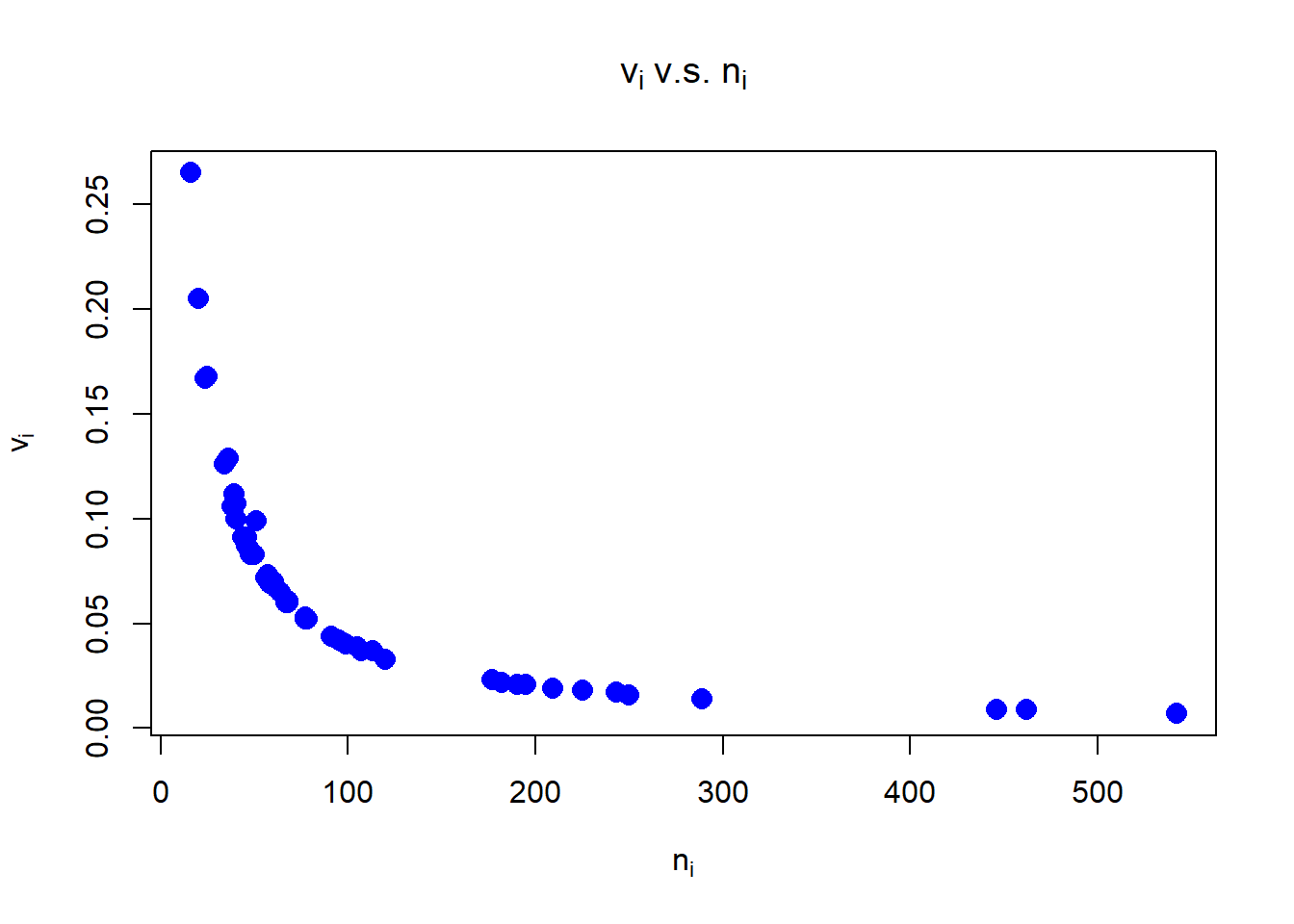
Offensichtlich fällt mit steigendem gleich der Funktion ab, was nur der tut. Die Varianz einer Skala (Stichprobenvarianz) würde sich für steigende Stichprobengröße bei einem Wert “einpendeln”.
Würden wir Skalenmittelwerte mitteln wollen, so könnten wir dies anhand der Stichprobengröße machen oder wir berechnen den Standardfehler des Mittelwerts via , wobei die Varianz der Skala ist (diese oder die Standardabweichung sollten in den Studien berichtet werden). Denn es gilt Somit würden wir dem Argument vi in der Funktion rma gerade übergeben.
Literatur
Bangert-Drowns, R. L., Hurley, M. M., & Wilkinson, B. (2004). The effects of school-based writing-to-learn interventions on academic achievement: A meta-analysis. Review of Educational Research, 74, 29–58.
Irmer, J. P., Kern, M., Schermelleh-Engel, K., Semmer, N. K., & Zapf, D. (2019). The instrument for stress oriented job analysis (ISTA) – a meta-analysis. Zeitschrift für Arbeits- & Organisationspsychologie – German Journal of Work and Organizational Psychology, 63(4), 217-237. https://doi.org/10.1026/0932-4089/a000312
McDaniel, M. A., Whetzel, D. L., Schmidt, F. L., & Maurer, S. D. (1994). The validity of employment interviews: A comprehensive review and meta-analysis. Journal of Applied Psychology, 79, 599–616.
Rothstein, H. R., Sutton, A. J., & Borenstein, M. (2005). Publication bias in meta-analysis: Prevention, assessment, and adjustments. Chichester, England: Wiley.
Semmer, N. K., Zapf, D., & Dunckel, H. (1995). Assessing stress at work: A framework and an instrument. In O. Svane, & C. Johansen (Eds.), Work and health – scientific basis of progress in the working environment, (pp. 105 – 113). Luxembourg, Luxembourg: Office for Official Publications of the European Communities.
Semmer, N. K., Zapf, D., & Dunckel, H. (1999). Instrument zur Stressbezogenen Tätigkeitsanalyse (ISTA) [Instrument for stress-oriented task analysis (ISTA)]. In H. Dunkel (Ed.), Handbuch psychologischer Arbeitsanalyseverfahren (pp. 179 – 204). Zürich, Switzerland: vdf Hochschulverlag an der ETH.
Viechtbauer, W. (2010). Conducting meta-analyses in R with the metafor package. Journal of Statistical Software, 36(3), 1–48. https://www.jstatsoft.org/v036/i03.
- Blau hinterlegte Autor:innenangaben führen Sie direkt zur universitätsinternen Ressource.
